Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Fault line selecting method based on k-means cluster analysis for power distribution network

A distribution network fault and cluster analysis technology, applied in the direction of fault location, etc., can solve the problems of complex fault line selection and low correct rate of line selection

Active Publication Date: 2015-09-09
KUNMING UNIV OF SCI & TECH
View PDF6 Cites 19 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

Judging from the current operation of small current grounding line selection devices, the correct rate of line selection devices in many areas is very low, which fully demonstrates the complexity of fault line selection problems and the necessity of new method research

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Fault line selecting method based on k-means cluster analysis for power distribution network
  • Fault line selecting method based on k-means cluster analysis for power distribution network
  • Fault line selecting method based on k-means cluster analysis for power distribution network

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

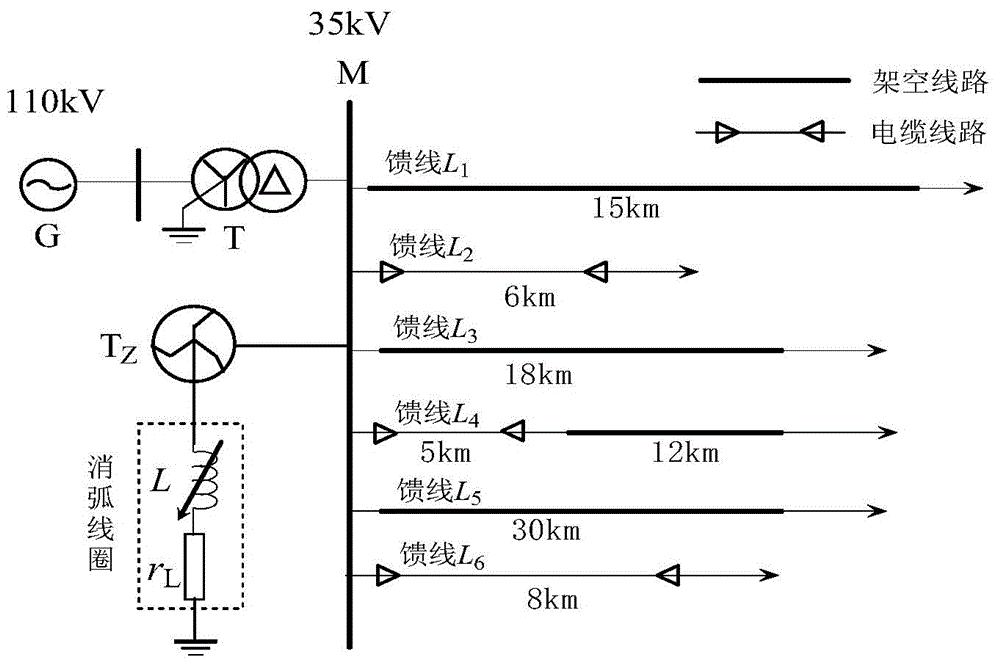
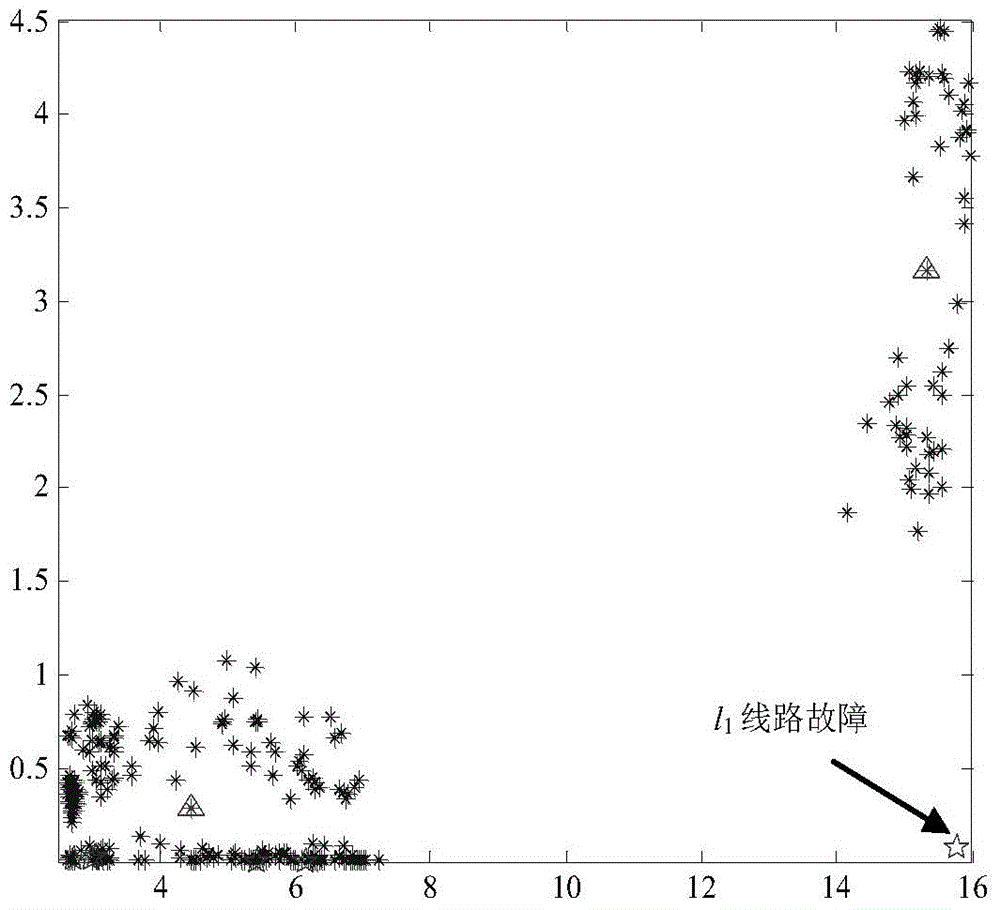
[0039] Example 1: Now select fault points every 2km along the overhead line, every 1km on the cable line, and form 318 fault sample data under the condition that the transition resistance is 20Ω and the fault initial phase angle is 90°. The data length is 5ms. now assume l 1 A phase-to-ground fault occurs 1km away from terminal M, the initial phase angle of the fault is 10°, and the transition resistance is 20Ω.

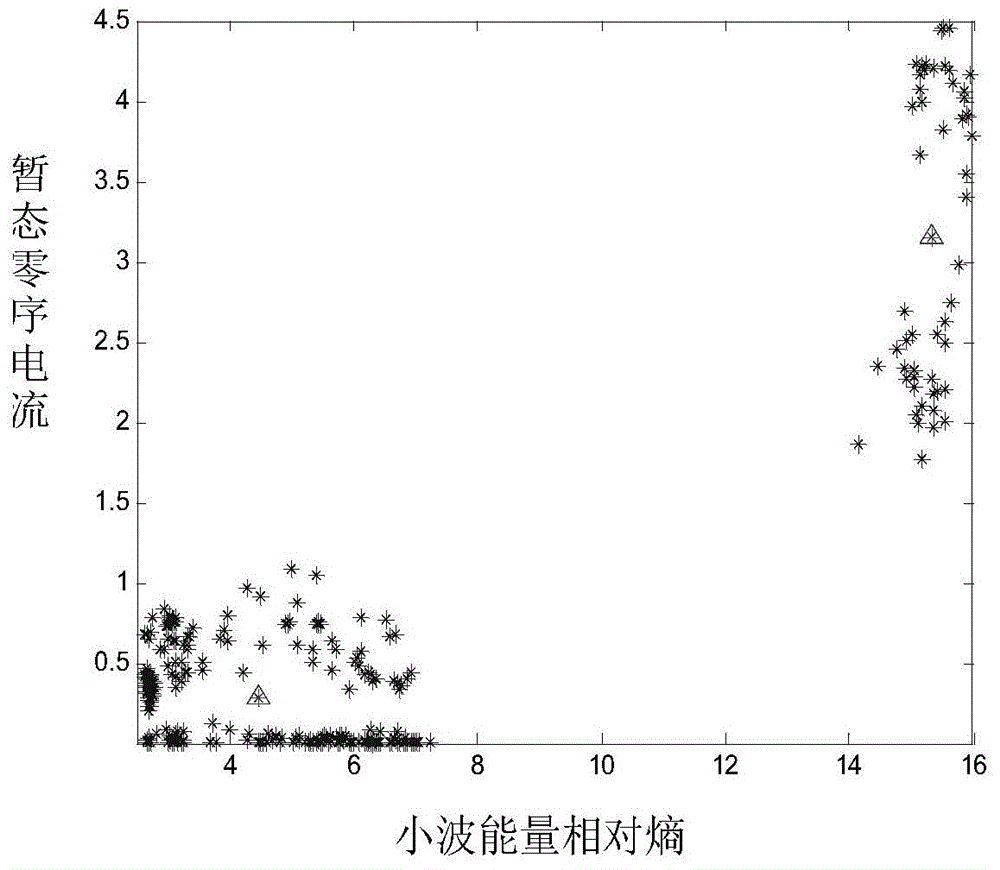
[0040] (1) The two types of cluster centers obtained by the k-means cluster analysis method are the unfaulted centers C 1 , fault center C 2 . where C 1 =(4.476,0.2806),C 2 =(15.347,3.1574). Analysis results such as figure 2 shown.

[0041] (2) After the test data is decomposed by db10 wavelet, its transient zero-sequence current energy and comprehensive wavelet relative energy entropy are calculated, and the fault line is judged according to the Euclidean distance between the test data and the two cluster centers.

[0042] which is

[0043] ...

Embodiment 2

[0046] Example 2: Now select fault points every 2km along the overhead line, every 1km on the cable line, and form 318 fault sample data under the condition that the transition resistance is 20Ω and the fault initial phase angle is 90°. The data length is 5ms. now assume l 1 A phase-to-ground fault occurs 14km away from terminal M, the initial phase angle of the fault is 90°, and the transition resistance is 200Ω.

[0047] (1) The two types of cluster centers obtained by the k-means cluster analysis method are the unfaulted centers C 1 , fault center C 2 . where C 1 =(4.476,0.2806),C 2 =(15.347,3.1574). Analysis results such as figure 2 shown.

[0048] (2) After the test data is decomposed by db10 wavelet, its transient zero-sequence current energy and comprehensive wavelet relative energy entropy are calculated, and the fault line is judged according to the Euclidean distance between the test data and the two cluster centers.

[0049] which is

[0050] ...

Embodiment 3

[0053] Embodiment 3: Now select fault points every 2km along the overhead line, every 1km on the cable line, and form 318 fault sample data under the condition that the transition resistance is 20Ω and the fault initial phase angle is 90°. The data length is 5ms. now assume l 2 A phase-to-ground fault occurs 3km away from terminal M, the initial phase angle of the fault is 30°, and the transition resistance is 20Ω.

[0054] (1) The two types of cluster centers obtained by the k-means cluster analysis method are the unfaulted centers C 1 , fault center C 2 . where C 1 =(4.476,0.2806),C 2 =(15.347,3.1574). Analysis results such as figure 2 shown.

[0055] (2) After the test data is decomposed by db10 wavelet, its transient zero-sequence current energy and comprehensive wavelet relative energy entropy are calculated, and the fault line is judged according to the Euclidean distance between the test data and the two cluster centers.

[0056] which is

[0057] ...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention relates to a fault line selecting method based on k-means cluster analysis for a power distribution network. The method includes setting fault position on lines along a resonant grounding system, selecting zero sequence current 5ms after fault with fault current curve clusters obtained by electromagnetism transient simulation as sample data, carrying out six-layer wavelet decomposition with db wavelets, calculating the total energy of transient zero sequence current under full spectrum band, calculating comprehensive wavelet energy relative entropy, measuring symptom fault characteristics with two dimensions of the total energy of transient zero sequence current and the comprehensive wavelet energy relative entropy, mapping the symptom fault characteristics onto a two dimensional plane, and calculating the cluster centers of the said data on the two dimensional plane by employing k-means cluster analysis algorithm. In a cluster space, the fault lines form a cluster center, and the non-fault lines form a cluster center. After fault line selection element starts, fault current data in 5ms time window serves as a test sample, and whether the line fails or not is determined according to the Euler's distance between the test data and two kinds of cluster centers.

Description

technical field [0001] The invention relates to a fault line selection method of a distribution network based on k-means cluster analysis, and belongs to the technical field of power system fault line selection. Background technique [0002] As the scale of the distribution network continues to grow, the number of lines continues to increase, and the number of cable lines and cable mixed lines is also increasing. When a single-phase fault occurs, the current of the grounding capacitor also increases, and the fault occurs for a long time. If the fault cannot be eliminated in time, the equipment will be damaged, and in severe cases, it will cause serious accidents such as shutdown of power plant units and interruption of process flow, which will destroy the safe operation of the system. [0003] For a long time, due to the weak fault current and unstable fault arc, etc., the single-phase ground fault of the neutral point through the arc suppression coil grounding system often ...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G01R31/08
Inventor 束洪春高利
Owner KUNMING UNIV OF SCI & TECH
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com