Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Blind reconstruction method under modulation broadband converter based on sparse Bayesian

A sparse Bayesian, modulated broadband technology, applied in the field of signal blind reconstruction under the framework of modulated broadband converters, can solve problems such as poor reconstruction performance, and achieve the effect of improving reconstruction performance

Active Publication Date: 2019-04-05
HARBIN INST OF TECH
View PDF19 Cites 5 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0004] The purpose of the present invention is to solve the problem of poor reconstruction performance when the signal contains noise in the reconstruction method under the framework of the existing modulation broadband converter

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Blind reconstruction method under modulation broadband converter based on sparse Bayesian
  • Blind reconstruction method under modulation broadband converter based on sparse Bayesian
  • Blind reconstruction method under modulation broadband converter based on sparse Bayesian

Examples

Experimental program
Comparison scheme
Effect test

specific Embodiment approach 1

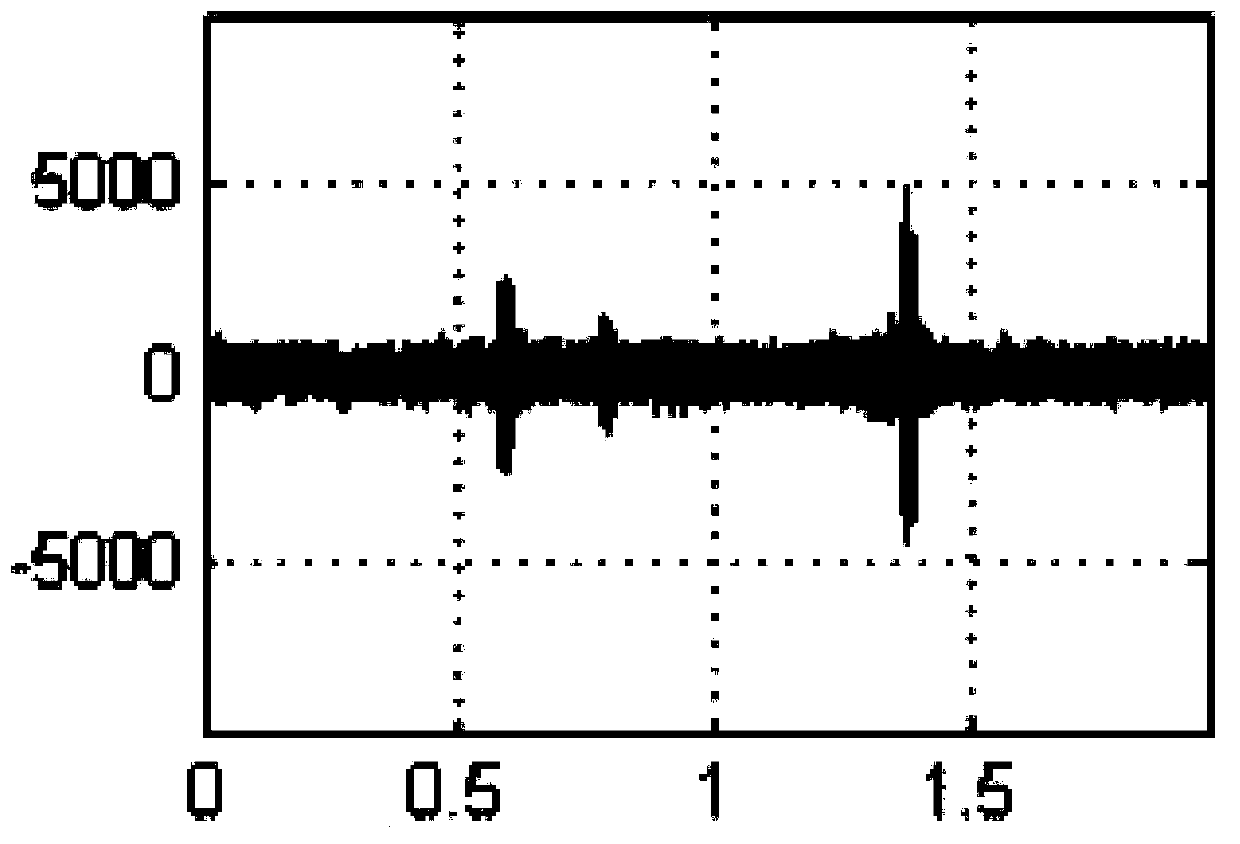
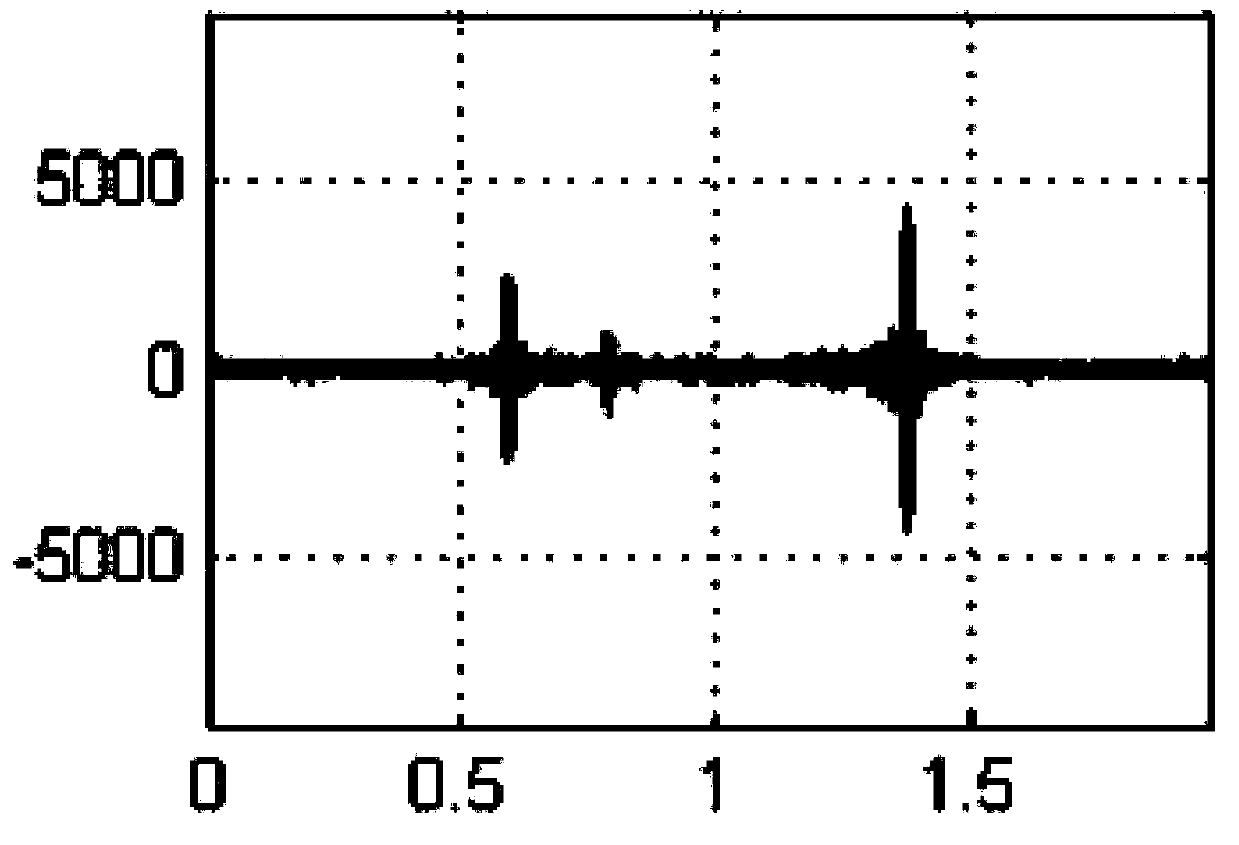
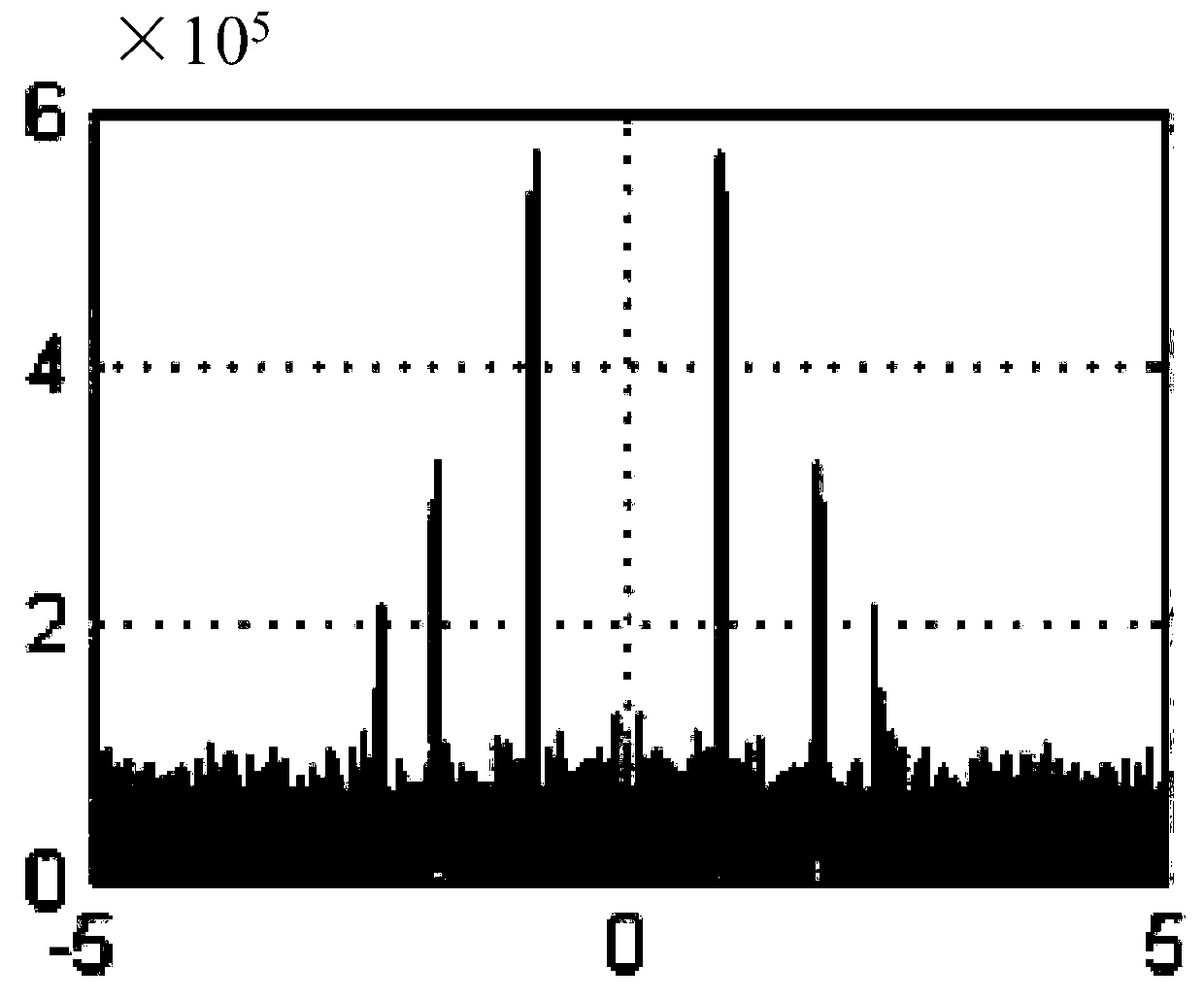
[0022] Specific implementation mode one: the blind signal reconstruction method under the framework of the sparse Bayesian modulation broadband converter described in this implementation mode, the method includes the following steps:

[0023] Step 1: input a sparse signal x(t), and multiply the input sparse signal x(t) with the pseudo-random sequences of m channels of the modulated broadband converter, the pseudo-random sequences of each channel are mutually orthogonal; Then multiply the result corresponding to each channel through F 0 ' sampling frequency to obtain the sampling results of each channel, and filter the sampling results of each channel through a low-pass filter with a cutoff frequency of fs / 2 to obtain the sampling value y output by each channel i (n) frequency-domain DTFT;

[0024] Step 2: Obtain the sampled value y of each channel output i (n) performing windowing processing to obtain a signal after windowing processing;

[0025] Step 3: adding Gaussian whi...

specific Embodiment approach 2

[0028] Specific implementation mode two: this implementation mode further limits the signal blind reconstruction method under the framework of the sparse Bayesian modulation broadband converter described in the first implementation mode, and the specific process of the first step is as follows:

[0029] The pseudo-random sequence for modulating the i-th channel of the wideband converter is p i (t), according to the Fourier transform, the pseudo-random sequence p i The specific expression of (t) is:

[0030] Among them: l is Fourier series, c il is the Fourier coefficient, j is the complex unit, T P is the period of the pseudo-random sequence, and t is time;

[0031] According to the inverse Fourier transform, the Fourier coefficient c is obtained il The expression is:

[0032]

[0033] Input a sparse signal x(t), multiply the input sparse signal x(t) with the pseudo-random sequence of the m channels of the modulated broadband converter, and obtain the frequency domai...

specific Embodiment approach 3

[0042] Specific implementation mode three: this implementation mode further limits the signal blind reconstruction method under the framework of the sparse Bayesian modulation broadband converter described in the first implementation mode, and the specific process of the fourth step is as follows:

[0043] The signal obtained in step 3 after adding Gaussian white noise is expressed as:

[0044] y(f)=Az(f) (5)

[0045] Wherein: intermediate variable z (f)=[z 1 (f),...,z L (f)] T , and z i′ (f)=X(f+(i'-L 0 -1) f p ), 1≤i′≤L, L=2L 0 +1; y(f) is a vector of length m, and A is the observation matrix;

[0046] After sampling and filtering, the Fourier coefficients are given by c il becomes c il ':

[0047]

[0048] Among them: a ik is the value of the pseudo-random sequence of the i-th channel, k=0,1,...,L 0 -1;

[0049] Define the integral term of formula (6) as d l :

[0050]

[0051] where: intermediate variable but

[0052] Then the observation matrix A...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The present invention provides a blind reconstruction method under a modulation broadband converter based on the sparse Bayesian, and is used for the technical field of reconstruction of compressed sensing signals. The problem is solved that a reconstruction method under a current modulation broadband converter is poor in reconstruction performance when the signals contain noise. The method comprises the steps of: multiplying input sparse signals by a pseudo-random sequence, performing low-speed sampling and filtering operation for the signals obtained through multiplying, constructing an observation matrix to show the signals to a representation of compressed sensing, adopting the sparse Bayesian method to estimate the signals in the recovery, and obtaining a variance [gamma] of the inputsparse signals through iteration by employing an EM algorithm to complete reconstruction of the sparse signals. In the condition that the signal-to-noise ratio of the signals is -15dB, compared to the prior art, the reconstruction method provided by the invention can reduce the steady-state mean square error value above 75% so as to effectively improve the reconstruction performance. The blind reconstruction method can be applied to the reconstruction field of the compressed sensing signals.

Description

technical field [0001] The invention belongs to the technical field of reconstruction of compressed sensing signals, and in particular relates to a signal blind reconstruction method under the framework of a modulation broadband converter. Background technique [0002] CS theorists proposed analog information conversion (AIC) on the basis of compressed sensing, one of which is the sub-Nyquist sampler based on random demodulation, which is mainly aimed at multi-tone with multiple discrete components The signal has the advantages of low power consumption and simple circuit structure, but its shortcomings are also obvious. In practice, due to the wide frequency spectrum of the bandwidth, it can be regarded as an infinite number of discrete components. If a random demodulation scheme is used, it should first Discretization of the spectrum, if the selected frequency resolution is too low, will cause serious spectrum distortion, if the selected resolution is high, the burden of st...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): H03M7/30
CPCH03M7/3062
Inventor 高玉龙王威顾云涛白旭
Owner HARBIN INST OF TECH
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com