Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Simulation method of meshless numerical model

A technology of numerical model and simulation method, applied in the field of ship mechanics, can solve the problems such as the inability to fully consider rollover, the influence of the broken flow field, the difficulty of solving the time domain, and the difficulty of describing the interaction of the fluid-solid interface, so as to improve the stress instability. , Improve the effectiveness and accuracy, the effect of high use value

Pending Publication Date: 2021-05-28
中国船舶重工集团公司第七研究院
View PDF0 Cites 5 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0004] (1) The influence of strong nonlinear factors such as rollover, crushing and splashing of the water body on the flow field cannot be fully considered;
[0005] (2) The large-scale motion of the floating body makes the interaction description of the fluid-solid interface difficult;
[0006] (3) The large deformation of the free liquid surface makes it difficult to solve the time domain interaction between the water body and the floating structure

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Simulation method of meshless numerical model
  • Simulation method of meshless numerical model
  • Simulation method of meshless numerical model

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

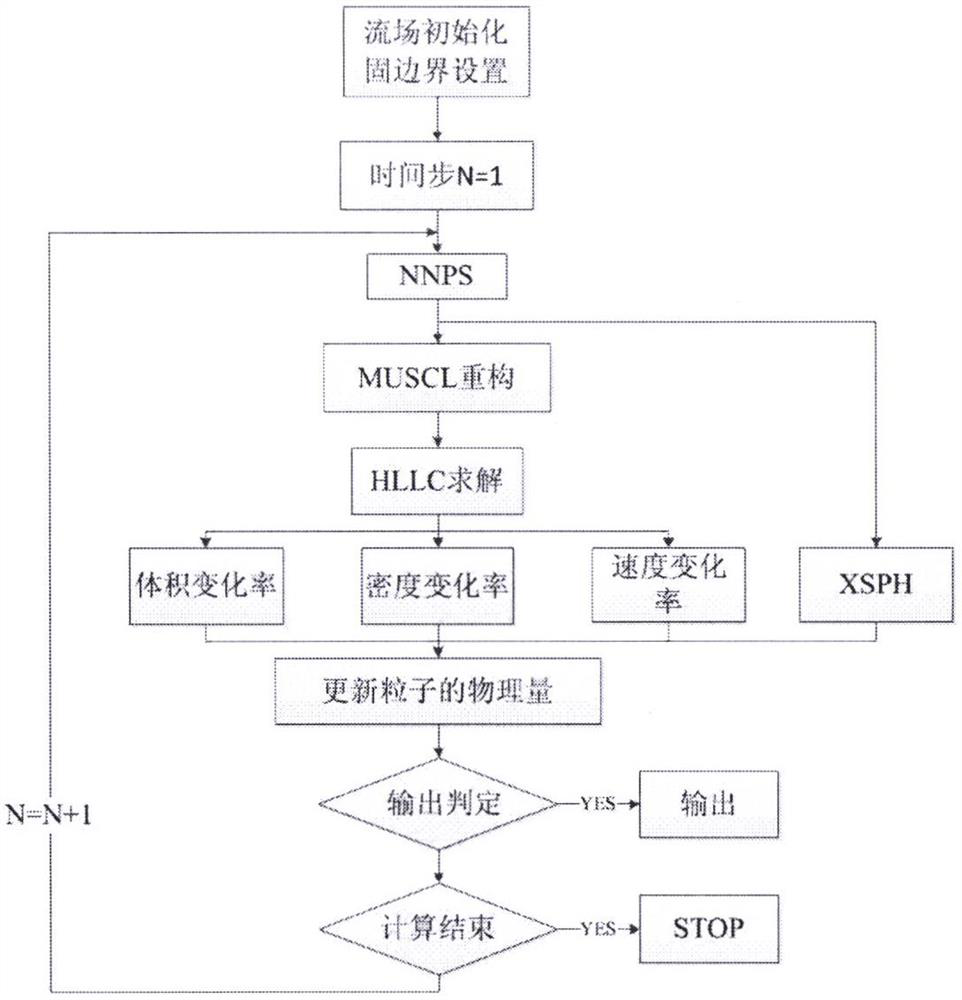
[0086] Such as figure 1 As shown, one embodiment of the present invention provides a simulation method of a meshless numerical model, comprising:

[0087] Step1: Initialize the flow field, and give each fluid particle an initial value of each physical quantity, such as position, density, velocity, and pressure.

[0088] Step2: Arrange solid wall boundary particles.

[0089] Step3: Carry out NNPS particle search, and use the high-order MUSCL format to reconstruct the initial value of the Riemann problem at the particle contact gap (ρ, u, w) RC , the output value (ρ, u, w, p) is obtained by the HLLC Riemann solver E , Substitute it into the governing equation to obtain the particle volume change rate d(ω) / dt, density change rate d(ωρ) / dt, and velocity change rate d(ωρv) / dt.

[0090] Step4: Use the time-stepping method to solve the above-mentioned conservative variables (ω, ωρ, ωρv), and obtain the velocity, density, and volume of the N+1 step particles after division. Substit...

Embodiment 2

[0093] The simulation method of the meshless numerical model in Embodiment 1 specifically provides a fluid governing equation of an improved Riemann solution meshless algorithm.

[0094] Different from the traditional SPH method, the improved Riemann solution meshless numerical model no longer directly substitutes the physical quantities (density, pressure, velocity, etc.) At the contact section, the idea of ​​particle contact algorithm is introduced in the solution process, and the physical quantity of the contact discontinuity of the two particles is approximated by the Riemann solver. At the same time, the TVD-MUSCL format with second-order accuracy is introduced to input the left and right ends of the HLLC Riemann solver. Values ​​are reconstructed to obtain a smooth solution input with high-order accuracy, and a flux limiter that does not reduce the accuracy of the smooth solution region is used to suppress numerical fluctuations near the discontinuity.

[0095] The SPH m...

Embodiment 3

[0101] The method for simulating a meshless numerical model in Embodiment 1 specifically provides an HLLC Riemann solver.

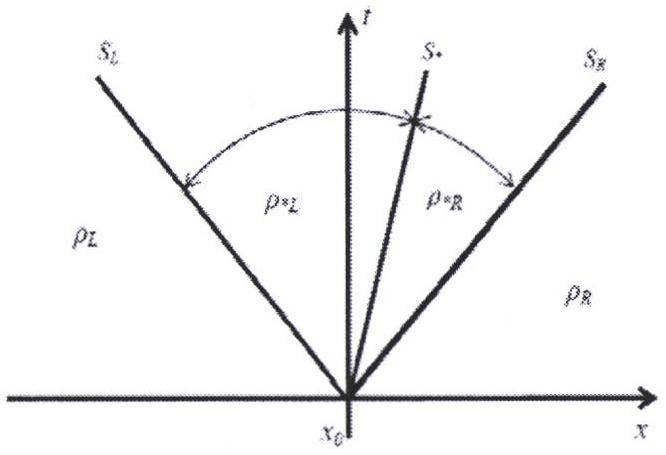
[0102] It is very difficult to solve the Riemann exact solution at the discontinuity, and an approximate solution is generally used. The HLLC Riemann solver is an improvement of the HLL solver. It is a method for approximately solving the Riemann solution. The wave solution is deduced from a double-wave structure to a three-wave structure. The wave solution structure at the discontinuity is as follows: figure 2 shown.

[0103] Define the input flux of the HLLC Riemann solver as Q = [ρ, ρu, ρw] T , the wave velocities of left traveling wave, right traveling wave and star region are respectively S L , S * , S R , the three waves divide the structure of the solution into four states, represented by the density as ρ L , ρ R . In the improved Riemann solution meshless numerical model algorithm, the flux output value of the HLLC Riemann solver is dete...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a simulation method of a meshless numerical model, computer equipment and a computer readable storage medium. According to the simulation method of the meshless numerical model, the floating body and fluid interaction numerical model of the improved Riemannian solution meshless algorithm is constructed, and compared with a meshless method in the related technology, the influence of strong nonlinear factors such as rolling, breaking and splashing of a water body on a flow field is fully considered; the problems of stress instability, particle pressure field oscillation and low free surface expression precision are solved, the flow field pressure calculation precision is improved, and the effectiveness and precision of high-precision and strong-impact solid-liquid interaction are achieved in the wave making problem. Therefore, the invention can be suitable for simulating scenes where nonlinear waves and floating bodies interact, has a wider application environment, can be applied to the fields of ship and ocean engineering, offshore engineering and the like, and has a higher use value.

Description

technical field [0001] The invention relates to the technical field of ship mechanics, in particular to a simulation method of a gridless numerical model, a computer device and a computer-readable storage medium. Background technique [0002] The interaction between fluid and floating body is a very complex problem in ship hydrodynamics. For a long time, the load and response of ships and marine structures in fluid has been the core research content in the field of ship general engineering. After scientific and technological work in various countries After more than half a century of continuous exploration, the numerical simulation and model test research of the interaction between fluid and structure have made great progress, from two-dimensional to three-dimensional, from frequency domain analysis to time domain simulation, from linear assumption to nonlinear Theoretically, the wave environment in which structures are located also gradually develops from the initial regula...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G06F30/28G06F30/25G06F30/15G06F111/10G06F113/08G06F119/14
CPCG06F30/28G06F30/25G06F30/15G06F2111/10G06F2113/08G06F2119/14
Inventor 上官子柠宋鑫刘瀛昊
Owner 中国船舶重工集团公司第七研究院
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com