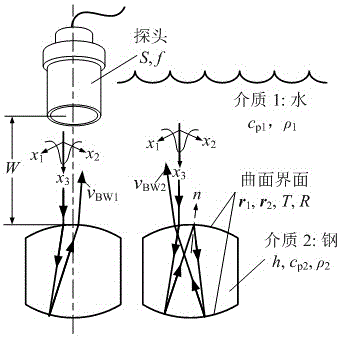
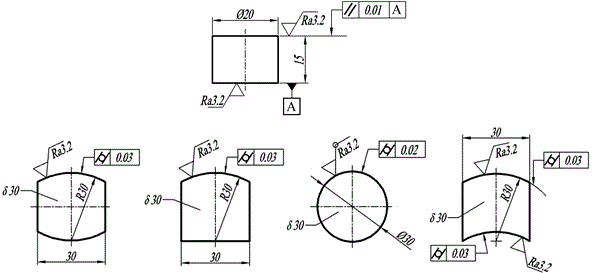
Ultrasonic attenuation evaluation method for crystal grain size of metal without influence of curved-surface diffusion

Abstract

The invention discloses an ultrasonic attenuation evaluation method for the crystal grain size of metal without influence of curved-surface diffusion. The method comprises the following steps: carrying out data acquisition on plane-calibrated metal test blocks; extracting a total testing attenuation spectrum on the basis of acquired primary and secondary bottom wave signals; establishing a diffusion attenuation model of curved-surface test blocks according to the multi-component Gaussian beam theory so as to obtain a scattering attenuation spectrum without a diffusion attenuation component; acquiring an evaluation function for the crystal grain size by using the scattering attenuation spectrum; establishing a multi-frequency weighted evaluation model for the crystal grain size; and evaluating the crystal grain size of a curved-surface test block with an unknown crystal grain size by using the established multi-frequency weighted evaluation model for the crystal grain size. The method can reduce system errors and random errors; and when the method is used for evaluation of test blocks with six different curvatures and with crystal grain sizes of 124.43 [mu]m according to metallographical determination, the mean value of relative errors is 4.28%. Thus, the method provided by the invention inhibits influence of curved-surface diffusion on evaluation of the crystal grain size and improves precision of nondestructive evaluation of the crystal grain size of curved-surface metal.

Description

technical field [0001] The invention relates to the technical field of metal average grain size measurement, in particular to a metal grain size ultrasonic attenuation evaluation method that eliminates the influence of curved surface diffusion. Background technique [0002] Grain size is an important parameter to characterize the microscopic properties of metal materials. For example, fine-grain strengthening is an effective means to improve the strength, plasticity and toughness of polycrystalline castings, and increasing the grain size can reduce the grain boundary energy and improve the metal's resistance. corrosion performance. Therefore, in the production and service process of metal components, strict control of grain size is one of the keys to ensure the mechanical properties of metal materials such as strength, toughness, and weather resistance, and effective detection of grain size is the premise and basis. The methods for obtaining the grain size of metal material...

AI Technical Summary

Problems solved by technology

However, in the actual measurement of curved surface workpieces, the attenuation of sound energy and the change of spectral components also include a large degree of diffusion loss, that is, due to the divergence of sound beams, reflection and refraction of curved surface interfaces during ultrasonic propagation, the probe with limited aperture Only part of the echo signal can be received, so it is necessary to compensate the diffusion of sound energy to reduce the attenuation of sound energy caused by diffraction

Images