Supercharge Your Innovation With Domain-Expert AI Agents!

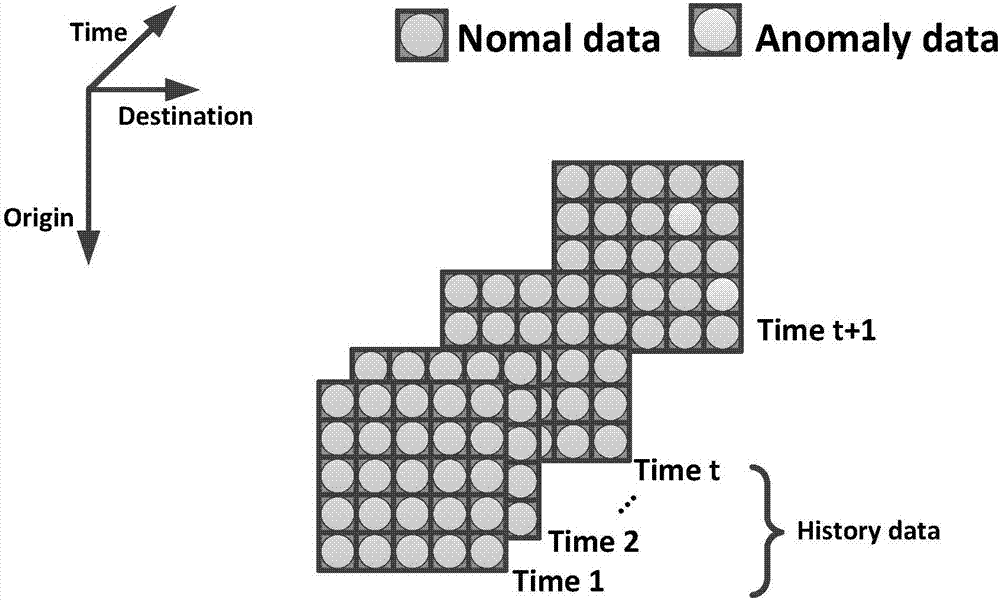
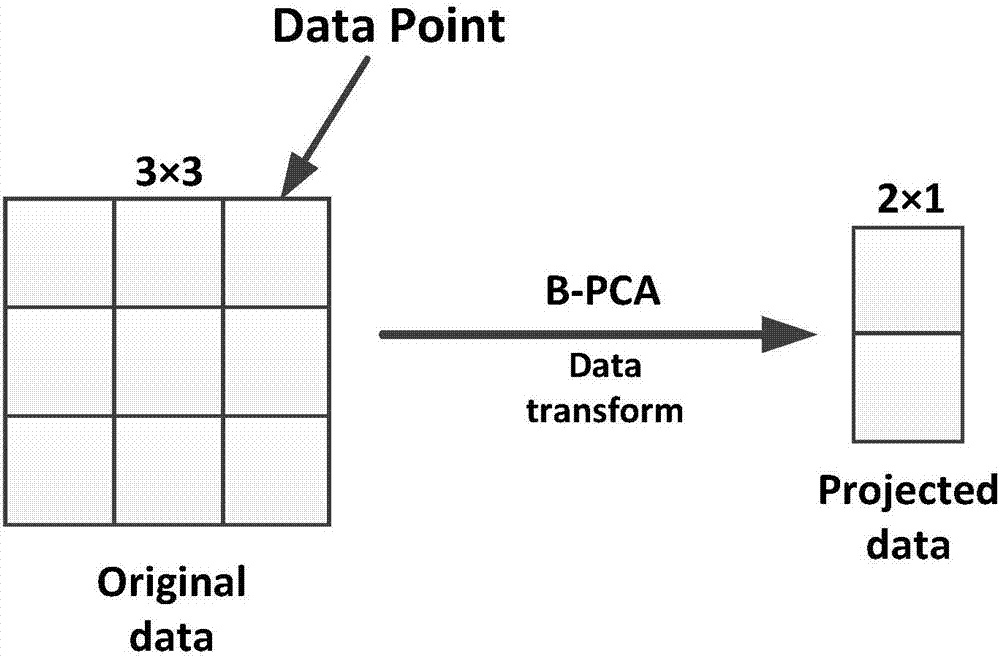
Online network traffic abnormality detection method based on bidirectional two-dimension principal component analysis

A two-dimensional principal component and network traffic technology, which is applied in the field of online network traffic anomaly detection by two-dimensional principal component analysis, can solve the problems of damage, the calculation time cost cannot meet the online detection, and the internal properties and characteristics of the data are destroyed. The effect of convenient network management

Active Publication Date: 2017-07-11
湖南友道信息技术有限公司
View PDF3 Cites 9 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

For example, no matter what the data model is, the traditional principal component analysis method needs to convert the data into vector type data in order to perform dimensionality reduction processing. This method undoubtedly destroys many characteristics that exist among the various data.
In addition, the traditional principal component analysis method only analyzes the data characteristics of the data row space, but ignores the characteristics of the data column space. In addition, the principal component analysis method (PCA) vectorizes the data, which destroys the internal properties and characteristics of the data. , while vectorizing the data will increase both the computational cost and the memory cost
Therefore, the PCA method for online anomaly detection is not only not accurate enough, but also the calculation time cost cannot meet the cost of online detection.

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Online network traffic abnormality detection method based on bidirectional two-dimension principal component analysis
  • Online network traffic abnormality detection method based on bidirectional two-dimension principal component analysis
  • Online network traffic abnormality detection method based on bidirectional two-dimension principal component analysis

Examples

Experimental program
Comparison scheme
Effect test

no. 1 example

[0067] The described BPCA algorithm of the first embodiment of the present invention is as follows:

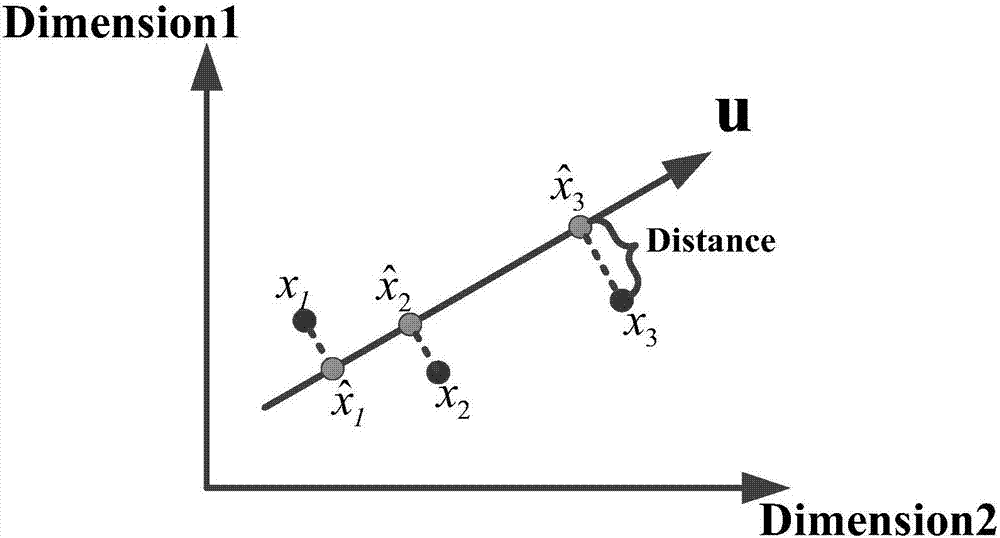
[0068] Given a dataset where X i ∈R N×N , i=1...T, centralize these data in like Figure 1.2 The Distance shown in is expressed in BPCA as:

[0069]

[0070] Where U and V are column and row space vectors respectively, and U T , V T , is U, V transpose. It can be found

[0071] The proof is as follows:

[0072] first order but

[0073]

[0074] because is a constant, so (1) can be expressed as

[0075]

[0076] After derivation, we can get:

[0077]

[0078] if and only if: Equation (3) obtains the minimum value, so it is brought into to (2) formula.

[0079]

[0080] Also the first term is a constant, so:

[0081]

[0082] In order to optimize the objective function (6), when given a U opt , U opt The covariance matrix can be calculated by The first L eigenvectors of the singular value decomposition are obtained. Similarly, g...

no. 2 example

[0092] By observing the calculation process of the above method, it is found that this process requires repeated iterations, so the calculation cost is relatively high. Therefore, in the second embodiment, the present invention proposes a kind of approximate solution algorithm of this BPCA method, and concrete method is as follows:

[0093] By observing the third and fourth steps in the above-mentioned method steps, we can know that when performing singular value decomposition, when R and L are large enough, we can get as well as Therefore this specific embodiment proposes the BPCA method of approximation, and it comprises following specific steps:

[0094] Step 1: Calculate and pass C V The singular value decomposition of i ;

[0095] Step 2: Calculate and pass C U The singular value decomposition of , find the U i ;

[0096] Step Three: End.

no. 3 example

[0098]Proved by a large number of experiments, this approximate BPCA method still can not meet the requirement of online detection, therefore, for this approximate BPCA method, the third embodiment of the present invention proposes a kind of incremental (incremental) method, In this way, the computational cost can be greatly reduced.

[0099] The incremental method includes the following steps:

[0100] Step 1: Input the new sampled data matrix X t+1 , historical sampling data mean matrix And the eigenvectors of historical data in column space and row space and the singular value matrix

[0101] Step 2: Calculate

[0102] Step 3: Calculate the QR decomposition: where Q u , R u ,Q v , R v for the matrix Two matrices obtained by QR decomposition;

[0103] Step 4: Calculate SVD decomposition (Singular Value Decomposition):

[0104]

[0105]

[0106] in for the matrix The three matrices obtained by performing singular value decomposition;

[0107] ...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses an online network traffic abnormality detection method based on bidirectional two-dimension principal component analysis, which relates to the online network traffic abnormality detection technology field. The method comprises three different BPCA methods, including the BPCA computation method through iterative computations, the proximity BPCA method and the BPCA method for acceleration through the incremental method. According to the method proposed by the invention, through the method of principal component analysis, abnormity detection is carried out through the sensitivity of the abnormal data and the normal data. And the method is applied mainly to the detection of network traffic data in real time so as to determine whether abnormal data exist in the acquired real-time data and to further determine that the acquired data are not abnormal. At the same time, the method can also make the network management more convenient by increasing the online abnormity detection accuracy and reducing the computation time.

Description

technical field [0001] The present invention relates to the field of machine learning and computer network, in particular to the application of processing a large amount of flow data generated by modern networks and requiring real-time online detection of abnormal data, specifically an online network based on two-dimensional two-dimensional principal component analysis A method for traffic anomaly detection. Background technique [0002] With the rapid development of computers and the Internet, major operators or IT companies need to collect normal network traffic data for data analysis or network status analysis. However, the continuous increase of network data traffic, the continuous increase of network deployment, and the increasingly diverse and complex computer environment have caused more and more abnormal network traffic data to appear. Therefore, it is necessary to preprocess the collected network data to eliminate abnormal data. However, due to the increase in the...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): H04L29/06G06N99/00
CPCG06N20/00H04L63/14H04L63/1408H04L63/1416
Inventor 李晓灿文吉刚曾彬
Owner 湖南友道信息技术有限公司
Features
  • R&D
  • Intellectual Property
  • Life Sciences
  • Materials
  • Tech Scout
Why Patsnap Eureka
  • Unparalleled Data Quality
  • Higher Quality Content
  • 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com