Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Optimal Latin hypercube design (LHD) method based on adaptive genetic algorithm

A Latin hypercube, experimental design technology, applied in the fields of genetic law, calculation, genetic model, etc., can solve the problems of high optimization cost, premature convergence, falling into local optimal solution, etc., to achieve high sampling efficiency, improve optimization accuracy, Test point characteristic good effect

Inactive Publication Date: 2017-08-11
HARBIN INST OF TECH
View PDF3 Cites 6 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0004] The purpose of the present invention is to solve the shortcomings of premature convergence, local optimal solution, and high optimization cost in the traditional optimization algorithm, and propose an optimal Latin algorithm based on adaptive genetic algorithm (AP-GA). Hypercube Design of Experiments

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Optimal Latin hypercube design (LHD) method based on adaptive genetic algorithm
  • Optimal Latin hypercube design (LHD) method based on adaptive genetic algorithm
  • Optimal Latin hypercube design (LHD) method based on adaptive genetic algorithm

Examples

Experimental program
Comparison scheme
Effect test

specific Embodiment approach 1

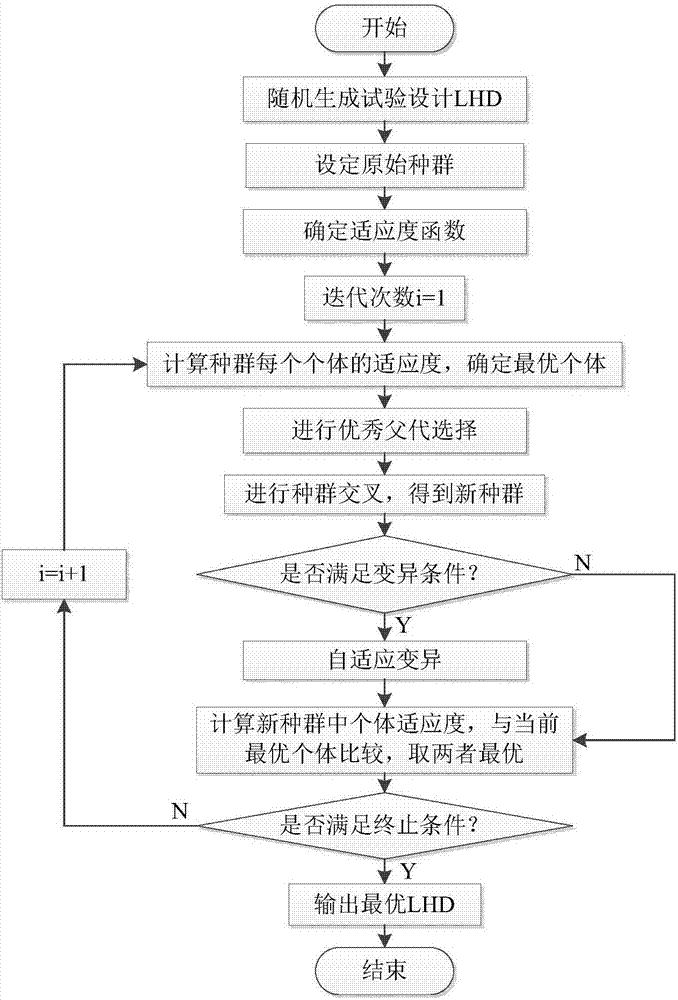
[0024] Specific implementation mode one: as figure 1 and figure 2 As shown, an optimal Latin hypercube experiment design method based on adaptive genetic algorithm includes the following steps:

[0025] Step 1: Randomly generate n Latin hypercube experimental design matrices LHD(N, P), where N is the number of experiments, P is the number of experimental factors, and each LHD(N, P) is a matrix of order N×P, which is recorded as a matrix L; the initial population N consisting of n LHD(N, P) individuals pop Expressed as a matrix of k×N, where k=n×P;

[0026] Step 2: Determine the fitness function of the population individual in the optimization process, and calculate the population N pop The fitness value of the n individuals in the middle, and select the individual with the largest fitness value as the current optimal LHD(N, P);

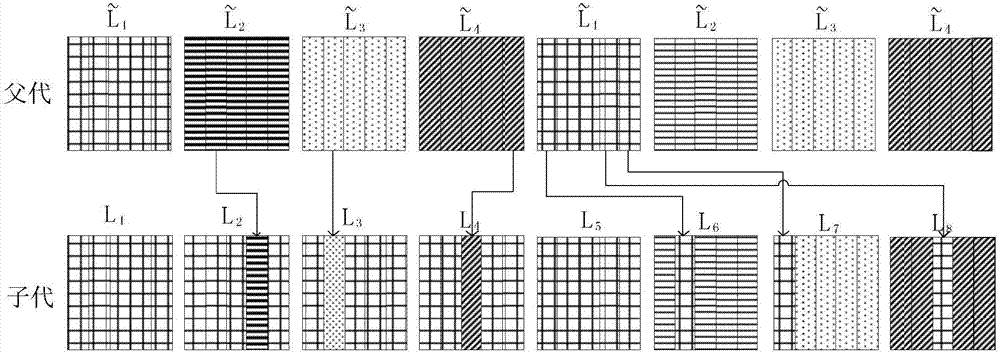
[0027] Step 3: Sort the n fitness values ​​calculated in step 2 from large to small, select the first n / 2 individuals as parents, and the rest a...

specific Embodiment approach 2

[0030] Specific embodiment 2: The difference between this embodiment and specific embodiment 1 is that the column vector of matrix L in the step 1 represents the value of the test factor, and each column is arranged arbitrarily from 1 to N, and the matrix L is arbitrarily arranged. line x i =[x i1 ,x i2 ,...,x iP ], which is a sample point.

[0031] The randomly generated sample size is 6, and the schematic diagram of the Latin hypercube experimental design with a factor number of 2 is LHD (6, 2). figure 2 As shown, the Latin hypercube experimental design matrix L is:

[0032]

[0033] Other steps and parameters are the same as those in Embodiment 1.

specific Embodiment approach 3

[0034] Specific embodiment three: the difference between this embodiment and specific embodiment one or two is: the specific process of determining the fitness function of the population individual in the optimization process in the step two is:

[0035] Firstly, the Audze–Eglais criterion is chosen to describe the property of "filled space". The AE criterion can effectively avoid the defect that the genetic algorithm itself is easy to fall into the local optimum, and can be effectively combined with the genetic algorithm.

[0036] Select the optimization objective function f(x)=G(L), and the fitness function is:

[0037]

[0038] where c max is the maximum estimated value of f(x);

[0039]

[0040] Where G(L) represents the potential energy of a LHD(N, P), ||x i -x j || represents the distance between any two rows in LHD(N, P). x j =[x j1 ,x j2 ,...,x jP ] to distinguish from x i Another sample point of .

[0041] Other steps and parameters are the same as th...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

An optimal Latin hypercube design (LHD) method based on an adaptive genetic algorithm relates to a Latin hypercube design method and aims to solve the defects of premature convergence, local optimal solution and high optimal cost produced in a conventional optimization algorithm optimizing process. The method comprises the steps of I, representing an initial population Npop formed by n LHD(N,P) individuals as a k*N matrix; II, calculating adaptation values of the n individuals in the population Npop, and selecting the individual with a maximum adaptation as a current optimal LHD(N,P); III, ranking the n adaptation values from largest to smallest, selecting first n / 2 individuals as parents, and generating n descendants by use of the selected n / 2 parents and forming a new population; IV, carrying out adaptive variation on the new population to obtain a new altered population; and V, iteratively carrying out steps II-IV, and judging whether an iteration termination condition is satisfied. The method is used for the field of computer simulation experimental design.

Description

technical field [0001] The invention relates to an optimal Latin hypercube experiment design method based on an adaptive genetic algorithm. Background technique [0002] Experimental design is a pre-design of experimental factors, research methods and experimental steps before conducting the experiment according to the research objectives. Experimental design is a method of simultaneously studying the influence of multiple input factors on the output. The selection and use of simulation test methods will directly affect the results of system simulation, and the efficiency of the test determines the efficiency and practicability of the simulation. Latin hypercube design (Latin Hypercube Design, LHD) is a commonly used method in the simulation test method. It is a random test design method with full space filling and non-overlapping. The factors are arranged horizontally and vertically into a random matrix, that is, Latin hypercube design. In the cubic matrix, the level of an...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G06F17/50G06N3/12
CPCG06F30/3323G06F2111/06G06N3/126
Inventor 马萍齐东兴杨明尚晓兵周玉臣
Owner HARBIN INST OF TECH
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com