Elastic beam structure PVDF modal sensor generation method

[0061] The following examples describe the present invention in more detail.

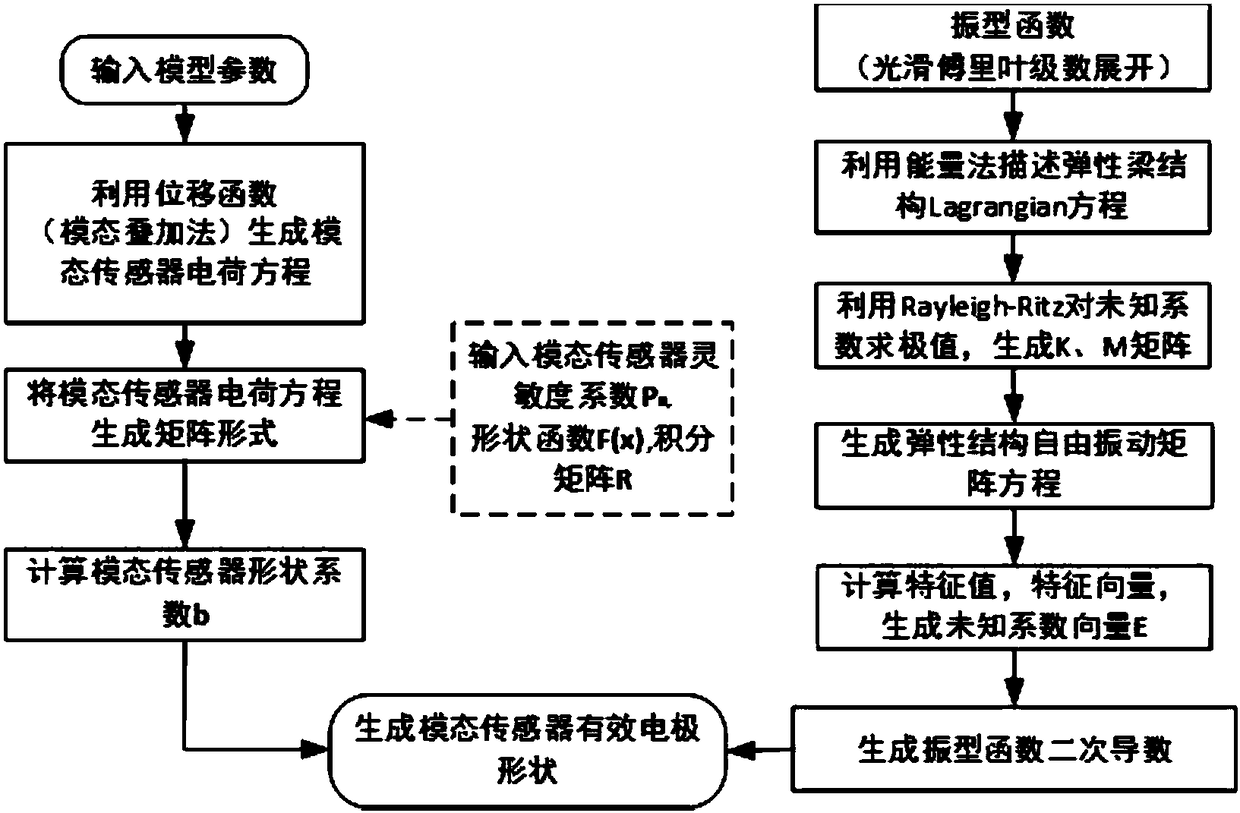
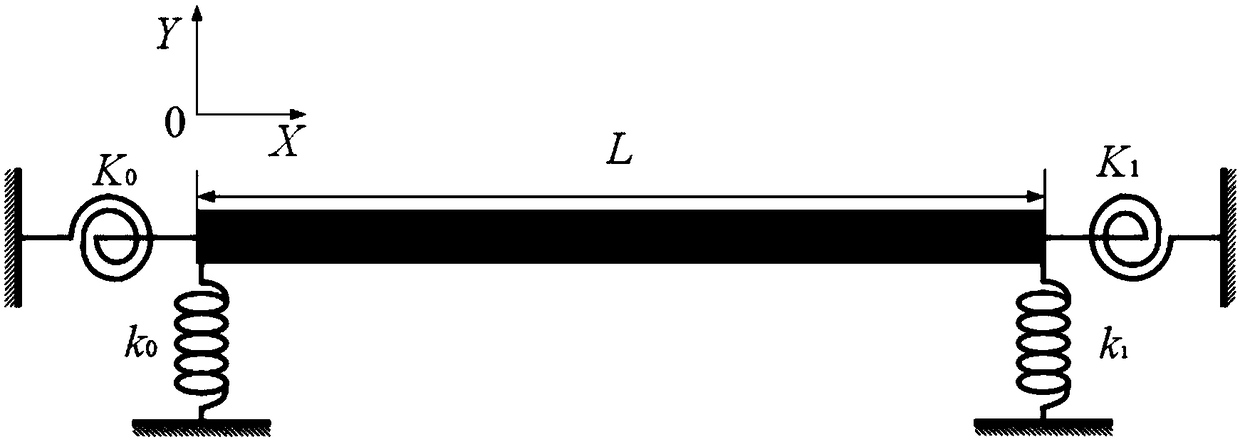
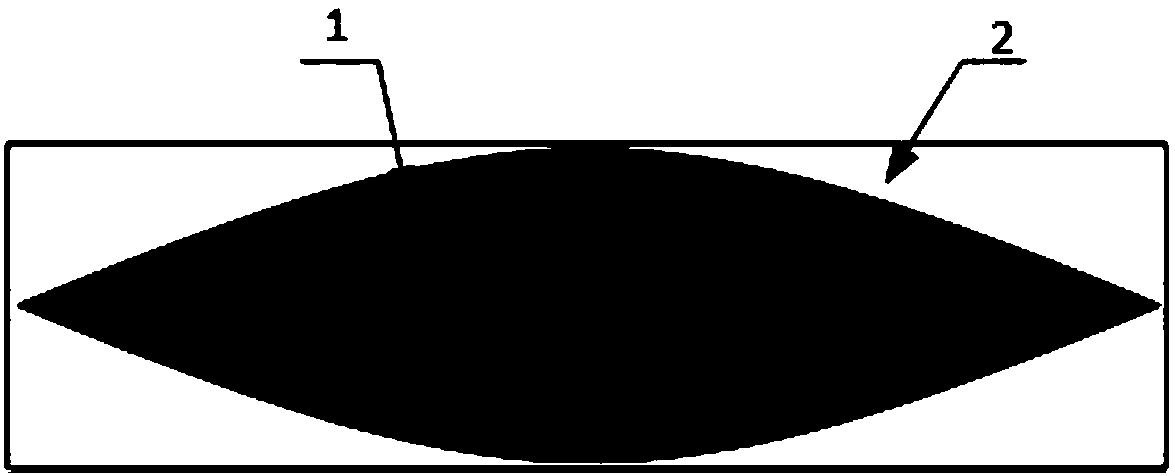
[0062] The method for generating an elastic beam structure PVDF modal sensor of the present invention relates to an effective electrode of a PVDF modal sensor that uses a smooth Fourier series method to generate an elastic boundary. The method for generating the effective electrode of the PVDF modal sensor with the elastic boundary includes: inputting model parameters, using the displacement function (modal superposition method) to generate the modal sensor charge equation, and inputting the modal sensor sensitivity coefficient P n , Shape function F(x) and integral matrix R generate matrix form of modal sensor charge equation, calculate modal sensor shape coefficient b and use smooth Fourier series expansion method to calculate modal function; among them, use smooth Fourier The series expansion method to calculate the mode function includes using the energy method to describe the Lagrangian equation of the total potential energy and total kinetic energy of the elastic beam structure, using the Rayleigh-Ritz to find the extreme value of the unknown coefficients, generating K and M matrices, and generating the free vibration matrix equation of the elastic beam structure , Calculate the eigenvalue eigenvector to generate the unknown coefficient vector E, and generate the second derivative of the mode function. Combine figure 1 The method of the present invention specifically includes the following steps:

[0063] (1) Input the geometric dimensions, material properties, boundary conditions and physical parameters of the PVDF piezoelectric film of the elastic beam structure model;

[0064] (2) Generate the charge output equation of the PVDF modal sensor with elastic beam structure, the expression is as follows:

[0065]

[0066] Among them, Q(t) is the output charge of PVDF modal sensor; h and h p Is the thickness of the elastic beam and the thickness of the PVDF piezoelectric film; e 31 Is the piezoelectric constant in the x direction; w(x,t) is the lateral displacement of the elastic beam; F(x) is the shape function of the PVDF modal sensor; L is the length of the elastic beam;

[0067] (3) Using the theory of mode superposition, the lateral displacement of the elastic beam under the harmonic excitation force can be expressed as:

[0068]

[0069] Where a m And φ m (x) are the complex modal amplitude and mode function of the m-th order structure respectively; M is the modal truncation number; e jωt Is the simple harmonic vibration time factor.

[0070] (4) Input the PVDF modal sensor sensitivity coefficient P m , Substituting the expression in step (1), get:

[0071]

[0072] among them, Is the second derivative of the mode function;

[0073] (5) Generate the matrix form of the PVDF modal sensor charge equation, the expression is as follows:

[0074] Q(t)=γe jωt aP

[0075] Among them, γ is a constant term, defined as γ=e 31 (h+h p )/2; a is the 1×M complex modal amplitude row vector; P represents the M×1 modal sensitivity column vector;

[0076] (6) Input the shape function of the PVDF modal sensor, the expression is as follows:

[0077]

[0078] (7) Substituting step (6) PVDF modal sensor shape function expression F(x) into step (4) to establish the PVDF modal sensor charge equation matrix form, at the same time, combining step (5), the expression is as follows:

[0079] Q(t)=γe jωt aP=γe jωt aRb T

[0080] Among them, R is the integral matrix, and the expression is as follows:

[0081]

[0082] (8) In particular, the PVDF modal sensor generates the medium modal sensitivity vector P m For the default value, the target mode is set to 1, and the other elements in the vector are set to 0. The specific expression is as follows:

[0083]

[0084] Among them, t represents the target order;

[0085] (9) Through the equation in step (7), calculate the unknown coefficient vector b of the PVDF modal sensor, the expression is as follows:

[0086] b=(R -1 P) T

[0087] (10) Further, in order to obtain the PVDF mode transfer shape function F(x) defined in step (6), it is necessary to solve the second derivative of the mode function. More specifically, the mode function φ(x) uses smooth Fourier The series is expanded into the standard cosine series and four correction terms, the expression is as follows:

[0088]

[0089] Among them, A 0 ,A 1 …A n ,B 1 ,B 2 ,B 3 ,B 4 Is the unknown Fourier series coefficient and the corresponding supplementary term function coefficient ξ 1 (x),ξ 2 (x),ξ 3 (x),ξ 4 (x) is a four-term supplementary function that overcomes the discontinuity of the boundary, in particular,

[0090]

[0091]

[0092] (11) Using the energy method to describe the Lagrangian equation of the total potential energy and total kinetic energy of an elastic beam structure, the specific expressions are as follows:

[0093] L=V-T

[0094] Among them, V represents the total potential energy, including the spring potential energy V spring , And the elastic beam potential energy V beam; T represents total kinetic energy,

[0095]

[0096]

[0097] Among them, EI, ρ, S respectively represent the section tensile and bending stiffness, mass density, and section area of ​​the elastic beam structure; K 0 (K 1 ), k 0 (k 1 ) Respectively represent the rotational spring stiffness at the left end (right end) and the linear spring stiffness at the left end (right end) of the boundary;

[0098] (12) Use the Rayleigh-Ritz method to find the extreme values ​​of the unknown coefficients in the expression L in step (11), generate K and M matrices, and express them as matrices:

[0099] (K-ω 2 ρSM)E=0

[0100] Among them, K is the stiffness matrix, M is the mass matrix, E is the vector of unknown coefficients of the improved Fourier series, and ω is the natural angular frequency;

[0101] E=[A 0 A 1 … A n B 1 B 2 B 3 B 4 ] T

[0102] (13) Obtain the position coefficient vector E, the mode function φ(x), and the natural frequency by using the eigenvalues ​​and eigenvectors of step (12);

[0103] (14) Generate the second derivative of the mode function;

[0104] Combine steps (6), (9) and (14) to generate the effective electrode shape of the PVDF modal sensor.

[0105] Combine figure 2 , Set the boundary spring stiffness as K 0 =K 1 = 0, k 0 =k 1 = 1e12, modal cutoff number M=45. Elastic beam structure model material Young's modulus E=200Gpa, density ρ=7800kg/m 3 , Beam length is 0.64m, width is 0.056m and thickness is 0.008m

[0106] According to the effective electrode generation method of the PVDF modal sensor of the present invention, such as Figure 3a-Figure 3d The effective electrode schematic diagram of the first four-order PVDF modal sensor with the elastic beam structure shown, in which, Figure 3a Is the first order, Figure 3b Is the second order, Figure 3c Is the third order, Figure 3d It is the 4th order. 1 represents the effective electrode, 2 represents the elastic beam sticking surface.

[0107] Although the present invention provides specific and detailed implementations in conjunction with the accompanying drawings, the present invention is not limited to the above specific implementations and application fields. The above-mentioned examples are only for a better understanding of the present invention, and are merely illustrative and instructive. , Not restrictive.