Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Frequency Domain GFDM Low Complexity Minimum Mean Square Error Receiving Method and Receiver

A minimum mean square error, low-complexity technology, applied in multi-frequency code systems, digital transmission systems, baseband system components, etc., can solve problems such as the inapplicability of the AWGN channel model

Active Publication Date: 2021-06-04
TIANJIN UNIV
View PDF8 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

However, existing low-complexity algorithm receiver design schemes (such as receivers based on Gabor transform [8] and a two-step MMSE receiver [6] ) only considers the most ideal situation, assuming that the channel is an Additive White Gaussian Noise (AWGN) channel, and the channel impulse response is the unit impulse
Obviously, in practical situations, the channel is random and time-varying, and the AWGN channel model is not applicable

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Frequency Domain GFDM Low Complexity Minimum Mean Square Error Receiving Method and Receiver
  • Frequency Domain GFDM Low Complexity Minimum Mean Square Error Receiving Method and Receiver
  • Frequency Domain GFDM Low Complexity Minimum Mean Square Error Receiving Method and Receiver

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

[0038] A frequency domain GFDM low complexity minimum mean square error receiving method, the receiving method comprises the following steps:

[0039]101: Construct K modulation vectors, perform Fourier transform on the channel matrix H to obtain a diagonal matrix, construct a filter matrix according to a given filter, and then construct a modulation matrix, and perform Fourier transformation on the modulation matrix to obtain the matrix

[0040] 102: Initialize a large matrix of all zeros, and then divide the large matrix into K 2 A sub-block Φ of size M×M i,j ;

[0041] 103: Perform two-dimensional Fourier transform on the first K / 2+1 sub-blocks on the main diagonal and the first K / 2 sub-blocks on the secondary diagonal, and then determine all other sub-blocks Φ according to the symmetric relationship i,j The two-dimensional Fourier transform result of ;

[0042] 104: For the result of two-dimensional Fourier transform Find the inverse transformation, for each sub-blo...

Embodiment 2

[0055] The scheme in embodiment 1 is further introduced below in conjunction with specific examples and calculation formulas, see the following description for details:

[0056] 201: system input;

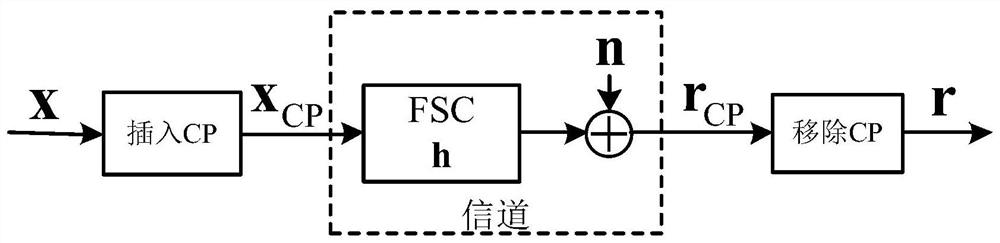
[0057] Among them, the number of subcarriers is defined as K, the number of subsymbols as M, the filter as g, the channel matrix of the frequency selective channel as H, and the noise variance of the receiver as The GFDM receiving block of KM×1 is r, let N=KM.

[0058] 202: Construct K modulation vectors ε k , do DFT on the channel matrix H to obtain the diagonal matrix Construct the filter matrix G according to the given filter g, and then construct the modulation matrix A, and perform DFT on the modulation matrix A to obtain the matrix

[0059] Among them, ε k =diag[1,e j2πk / K ,...,e j2πk(N-1) / K ],k=0,...,K-1, (·) CT represents the conjugate transpose, is the N-point discrete Fourier transform matrix, defined as:

[0060]

[0061] Among them, W=exp(2*pi*i*x / N) / ...

Embodiment 3

[0083] The following is combined with specific mathematical formulas, examples, Figure 1-Figure 9 The scheme in embodiment 1 and 2 is further introduced, see the following description for details:

[0084] 1. GFDM system model;

[0085] 1) Transmitter model;

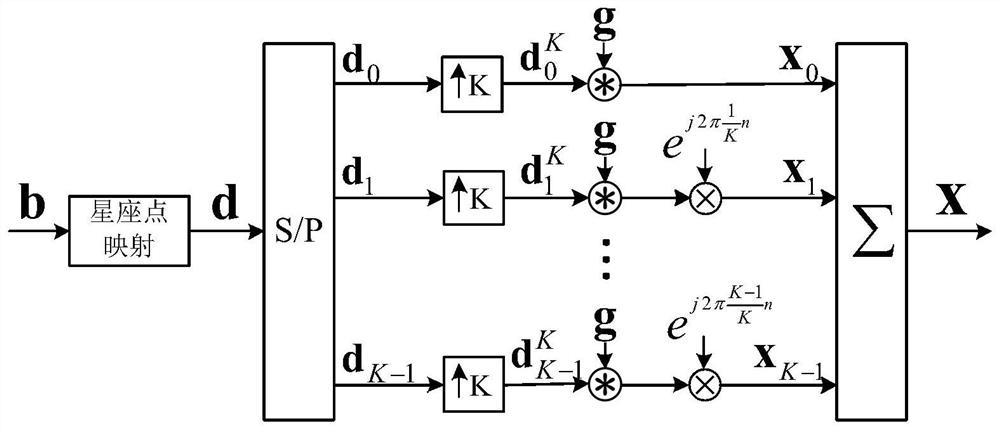
[0086] Assume that the GFDM system model contains K subcarriers and M subsymbols. Such as figure 1 As shown, after the binary source signal of length N=KM is mapped to the QAM constellation, a complex sequence d of length N is generated.

[0087] After serial-to-parallel conversion, the complex sequence d is divided into K segments of length M where d k =[d k (0),...,d k (M-1)] T . Then, each d k Do K-point upsampling to generate an upsampling sequence of length N Can be expressed as:

[0088]

[0089] Among them, δ(n) represents the unit shock function. Afterwards, the upsampling sequence with the shaping filter g=[g(0),...,g(N-1)] T Do circular convolution, then use subcarrier e j2πkn / K Do up-con...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a frequency domain GFDM low-complexity minimum mean square error receiving method and receiver, including: initializing a large matrix of all zeros, and then dividing the large matrix into several sub-blocks Φ i,j ; Do two-dimensional Fourier transform on the first K / 2+1 sub-blocks on the main diagonal and the first K / 2 sub-blocks on the sub-diagonal, and then determine all other sub-blocks Φ according to the symmetric relationship i,j The result of the two-dimensional Fourier transform; the inverse transform is obtained for the two-dimensional Fourier transform result, and the IDFT anti-cornerization operation is performed on each sub-block in the inverse transform result to obtain the anti-cornerization result Ψ i,j ;According to the anti-cornerization result Ψ i,j , Matrix N-point discrete Fourier transform matrix GFDM receiving block r obtains the demodulation output signal receiver includes: GFDM sending module carries out constellation mapping, serial-to-parallel conversion and GFDM modulation on the signal, after completing the modulation, the signal enters the frequency selective channel, when adding the channel delay and noise; the MMSE receiving module demodulates the signal, and finally obtains the demodulated received signal.

Description

technical field [0001] The invention relates to multi-carrier modulation and demodulation technology, channel analysis, and receiver design, in particular to a frequency domain GFDM low-complexity minimum mean square error receiving method and receiver. Background technique [0002] The next-generation mobile communication system needs to be compatible with more scenarios, such as Machine Type Communication (MTC) [1] , Tactile Internet [2] etc., need to face the explosive transmission of a large amount of information; the Internet of Things (the Internet of Things) system and vehicle-to-vehicle (V2V) [3] etc. require lower latency. As the mainstream modulation method in the past decade, the Orthogonal Frequency Division Multiplexing (OFDM) system has gradually exposed its limitations, such as large transmission delay, high out-of-band radiation, and sensitivity to frequency offset. In comparison, the generalized frequency division multiplexing (Generalized Frequency Divis...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Patents(China)
IPC IPC(8): H04L25/02H04L27/26H04B1/06H04L27/36
CPCH04B1/06H04L25/0242H04L25/0256H04L27/2628H04L27/265H04L27/362
Inventor 黄翔东王惠杰黎鸣诗马欣
Owner TIANJIN UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com