Unmanned aerial vehicle flight time optimal real-time trajectory optimization method capable of ensuring convergence

A time-of-flight and trajectory optimization technology, applied in the field of trajectory optimization, can solve problems such as difficulty in meeting real-time requirements, difficulty in explaining the black-box model solution process, and difficulty in path planning methods to generate trajectories with both optimal time and variable speed.

Active Publication Date: 2020-08-21
BEIJING INSTITUTE OF TECHNOLOGYGY
View PDF3 Cites 29 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

Blindly using violent heuristic algorithms is difficult to meet the real-time requirements of agile drones for trajectory optimization; general nonlinear programming algorithms are not always feasible to solve this non-convex problem; sequence optimization based on state iteration or sequence convex The optimization method to solve such problems has the potential of real-time application, but it cannot theoretically ensure the large-scale convergence of the optimization iterative process, so the solution efficiency of this type of algorithm is difficult to be guaranteed theoretically, and it is directly based on the non-convex programming algorithm to solve Although the time-optimal trajectory optimization problem is feasible, the solution efficiency is low and it is d

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Unmanned aerial vehicle flight time optimal real-time trajectory optimization method capable of ensuring convergence
  • Unmanned aerial vehicle flight time optimal real-time trajectory optimization method capable of ensuring convergence
  • Unmanned aerial vehicle flight time optimal real-time trajectory optimization method capable of ensuring convergence

Examples

Experimental program
Comparison scheme
Effect test

Embodiment

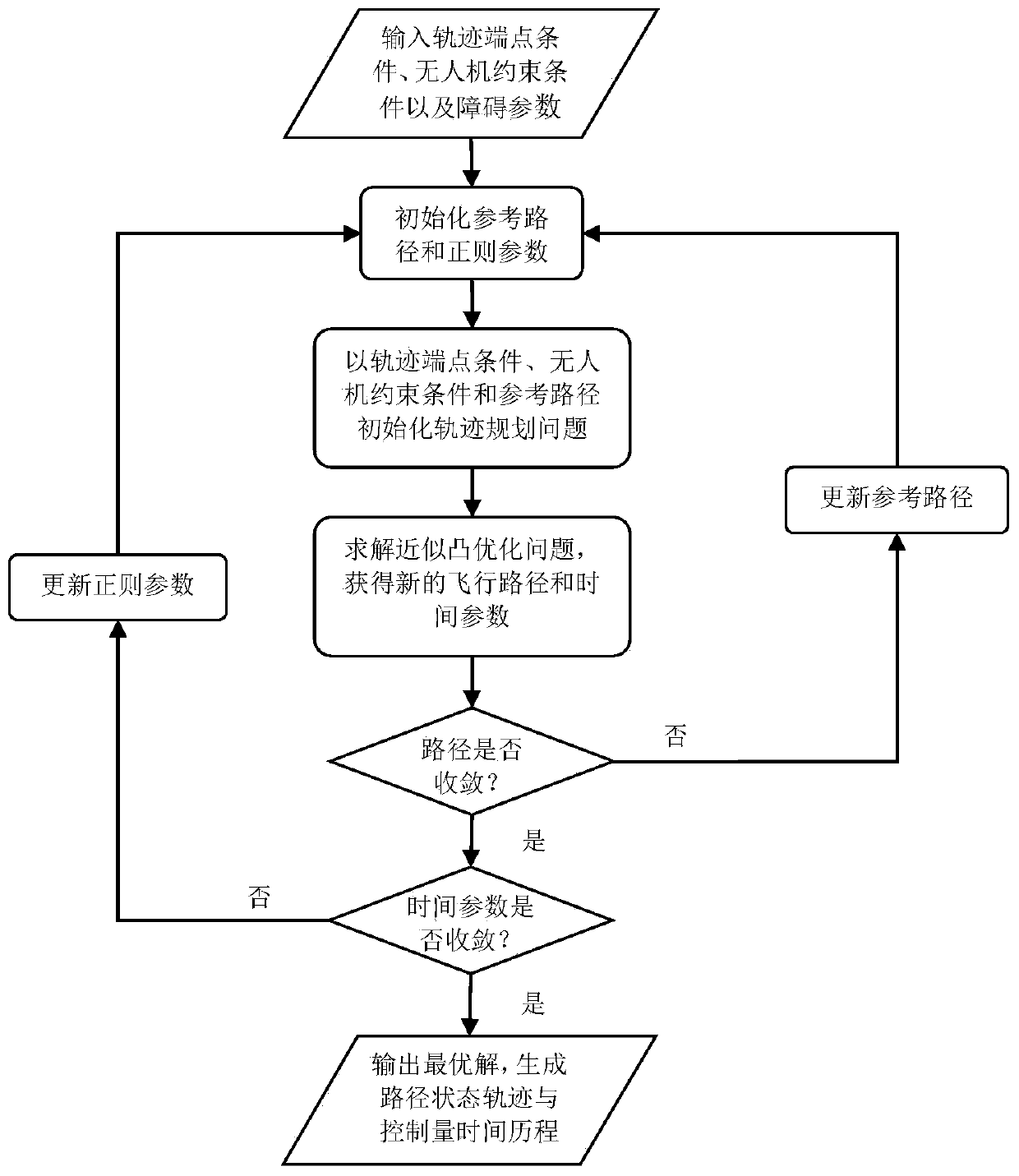
[0167] Such as figure 1 As shown, the optimal real-time trajectory optimization method for the flight time of the unmanned aerial vehicle that ensures convergence is disclosed in this embodiment, and the specific implementation steps are as follows:

[0168] Step 1: UAV kinematics modeling, the dimensionless motion equation of UAV three-dimensional obstacle avoidance is expressed as:

[0169]

[0170] where r = [x, y, z] T is the spatial position of the UAV, z is the height, x, y are the coordinates in the orthogonal direction of the horizontal plane; V is the speed of the UAV; a=[a x a y a z ] T is the maneuvering overload of the UAV, g=[0 0 g] T is the constant vector of gravitational acceleration. In formula (1), the distance variable [x, y, z] T Using the Euclidean distance L of the initial and end positions 0 To normalize, the speed is used Normalized. for time Normalized.

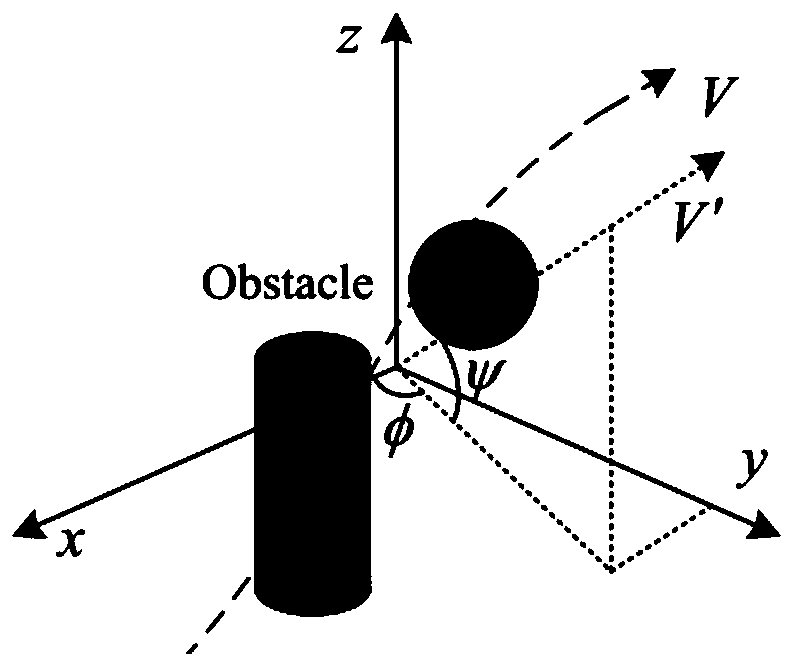
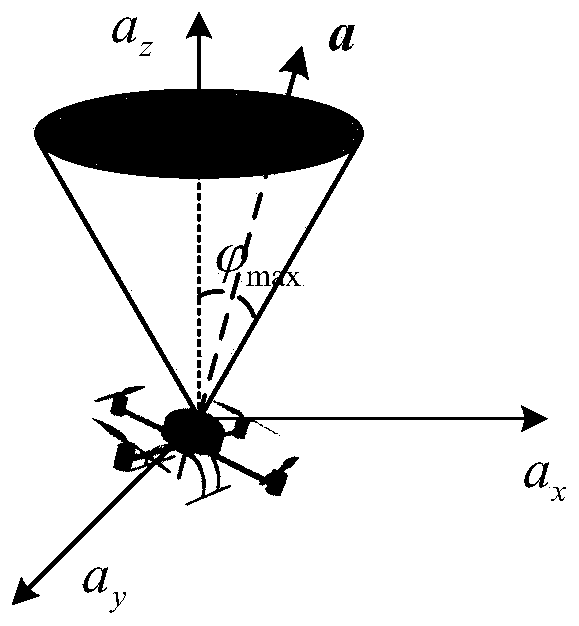
[0171] Step 2: Establish an optimal control problem model for obstacle avoidanc...

Embodiment A

[0296] Example A: Barrier-free trajectory planning

[0297] This subsection aims to illustrate the computational fastness by the proposed method. Design an obstacle-free situation, the initial and terminal conditions are shown in Table 1. In this case, only one calculation of convex optimization is needed to obtain the solution of the problem. Specifically, it only takes 0.1-0.2 seconds to solve the SOCP problem P3. Because there is no obstacle constraint, path iteration is not required, and only the steps shown in Algorithm 1 are used to solve the problem. In this case, the optimal solution is exactly at the support point corresponding to σ=0, and other state variables will be shown in Figure 6.

[0298] Table 1 Initial and terminal conditions of 3D trajectory planning without obstacle avoidance constraints

[0299]

[0300] The optimal flight time is 19.57s. from Figure 5 It can be seen from -6 that the flight path endpoints and the initial and final angles all mee...

Embodiment B

[0301] Example B: 3D Trajectory Planning Considering Obstacles

[0302] In this instance, consider the task of trajectory planning with obstacle avoidance constraints. As a comparison, two elliptical cylinder obstacles are added to the path of the barrier-free task, and the parameters of the obstacle elliptical cylinders are shown in Table II. The minimum flight time is 20.437 seconds. Figure 7-10 The numerical solution plotted in shows that for this obstacle avoidance path task, the initial, terminal, and acceleration constraints are all satisfied. Figure 7 The path of each iteration process is drawn in , where the initial path is a straight line segment connecting the initial and final points, and the optimal obstacle avoidance path is a thick solid line.

[0303] Table 2 Obstacle Constrained Elliptic Cylinder Parameters

[0304]

[0305] Table 3 shows the convergence error of 8 iterations, where the error about the time parameter and Figure 11 Explanation: The rel...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

PUM

No PUM Login to view more

Abstract

The invention discloses an unmanned aerial vehicle flight time optimal real-time trajectory optimization method capable of ensuring convergence, and belongs to the field of trajectory optimization. According to the method, an unmanned aerial vehicle kinematics model is established under the consideration of gravity action, speed and acceleration factors, and a three-dimensional dimensionless motion equation is established. Constraint conditions of speed and control quantity are established according to specific requirements of obstacle avoidance flight of the unmanned aerial vehicle, and the minimum time is selected as an optimization target to establish an optimal control problem P0 of flight path planning of the unmanned aerial vehicle. Nonlinear dynamics in the problem P0 is transformedinto linear dynamics to obtain a fixed initial and end time trajectory optimization problem P1; and the P1 problem is relaxed into an approximate convex optimization problem P2 through convex relaxation, so that the robustness and robustness of real-time solving of the unmanned aerial vehicle are improved. And the problem P2 is discretized to form a second-order cone programming problem P3, and asecond-order cone programming problem P3 is solved iteratively for finite times to obtain an optimal solution, namely the optimal flight time trajectory of the unmanned aerial vehicle. The task response capability of the unmanned aerial vehicle can be further improved.

Description

technical field [0001] The invention belongs to the field of trajectory optimization, and relates to a real-time trajectory planning method with optimal flight time of an unmanned aerial vehicle, in particular to a real-time obstacle avoidance trajectory optimization method with optimal flight time based on an online convex optimization technology and guaranteed convergence. Background technique [0002] In the past few years, as an aerial robot platform, UAV technology has benefited all aspects of human production and life, and trajectory planning has played a key role in the tasks of UAVs such as load delivery, target search, environmental monitoring, and agricultural plant protection. UAVs need to plan flight trajectories in advance to perform large-scale flight missions. In order to maximize the flight performance of UAVs and improve the agility of UAVs to perform tasks, it is important to quickly plan flight trajectories with minimum flight time. technical status. [0...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

Application Information

Patent Timeline
no application Login to view more
IPC IPC(8): G05D1/10G05B13/04
CPCG05B13/041G05D1/101
Inventor 刘新福姜欢
Owner BEIJING INSTITUTE OF TECHNOLOGYGY
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Try Eureka
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap