Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

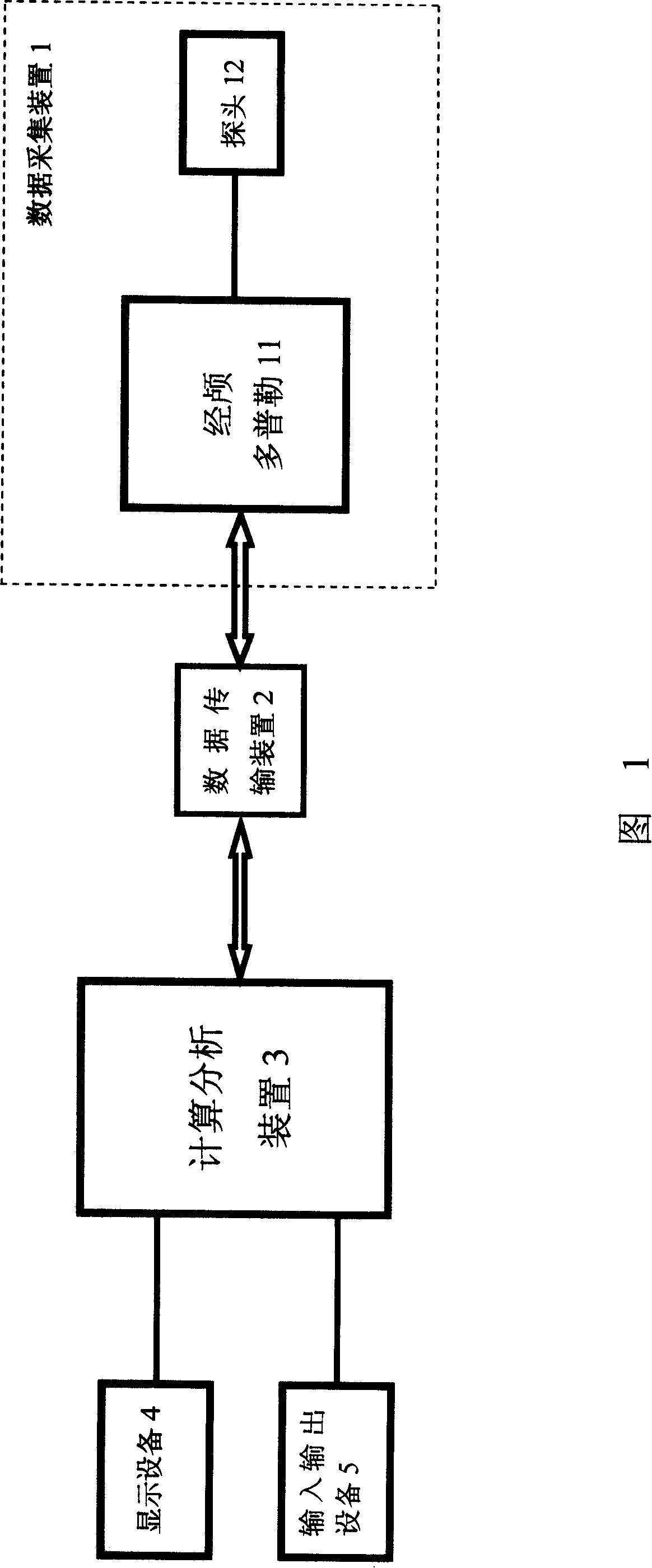
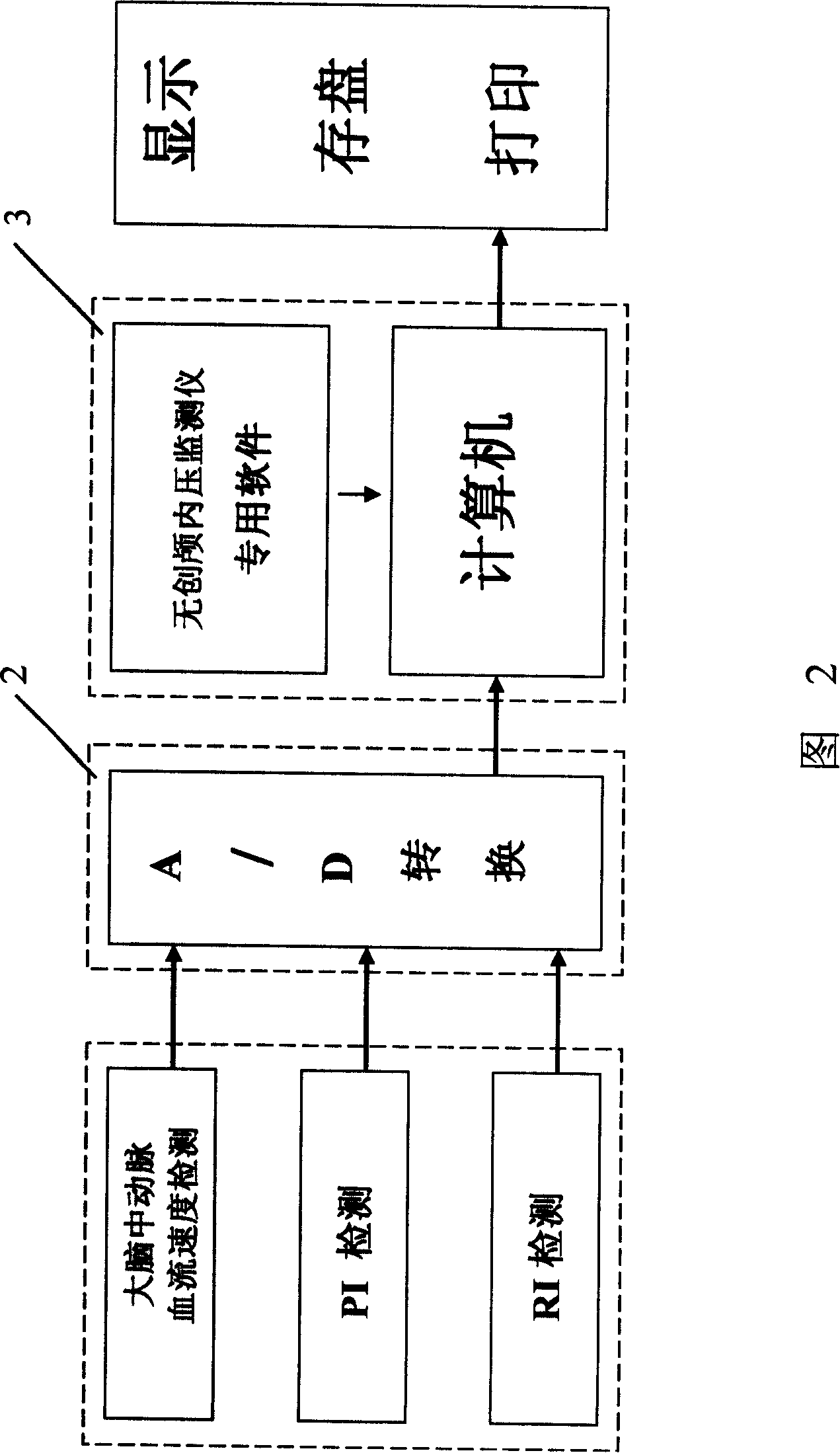
Noninvasive intracranial pressure monitoring equipment

A technology for monitoring equipment and intracranial pressure, applied in diagnostic recording/measurement, sensors, diagnosis, etc., can solve the problems of inaccurate measurement of ICP value, complex reasons for impedance changes, differences in impedance measurement, etc., to achieve convenient detection methods and benefit Rehabilitation, timely effect of treatment

Active Publication Date: 2008-07-23
百睦好科技(北京)有限公司
View PDF0 Cites 15 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

The limitations of this method are: (1) when ICP>300mmH 2 At O, f-VEP is easily affected by factors related to brain metabolism, such as arterial carbon dioxide partial pressure, arterial oxygen partial pressure, hypotension, pH value, etc.
However, this method cannot accurately measure the ICP value due to the following reasons: (1) The causes of impedance changes are complex. In addition to the main factors such as cerebrospinal fluid and cerebral blood flow, changes in the conductivity of other tissues will also affect the electric field distribution of the brain. Some variance is unavoidable in impedance measurements
(2) There is no direct relationship between brain impedance and ICP. Different patients, different conditions, and different volume compensatory abilities have different impedance values ​​measured at the same ICP.
This method is the current international research focus in this field, but there is no mature instrument available for clinical use.

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Noninvasive intracranial pressure monitoring equipment
  • Noninvasive intracranial pressure monitoring equipment
  • Noninvasive intracranial pressure monitoring equipment

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

[0087] The mathematical model for determining CSF production and outflow resistance is:

[0088] R=P 0 t / PVI log[P (t) / P p ×(P p -P 0 ) / (P (t) -P 0 )]

[0089] The graph measured in this embodiment is as Figure 6 As shown, the abscissa in the graph is time, and the ordinate is intracranial pressure. The star-shaped curve in the figure represents the ICP data curve measured by the invasive monitor, and the solid line curve represents the mathematical model estimation based on the generation and outflow resistance of cerebrospinal fluid in the present invention. out the ICP data. Quantitative relationship of CSF production and outflow resistance to intracranial pressure over time is shown. R in the equation is the generation and absorption resistance; PVI is the pressure-volume index, indicating the corresponding relationship between pressure and volume; P 0 is the initial intracranial pressure; P p is the peak intracranial pressure. Depend on Figure 6 It can be ...

Embodiment 2

[0092] The mathematical model for determining intracranial compliance is:

[0093] C = K * PVI P (C: Compliance, compliance)

[0094] C=1 / KP=0.4343(PVI) / P

[0095] In the formula: C is the intracranial compliance; k is the intracranial elastic coefficient

[0096] The brain is in a rigid cranial cavity, and the increase of a certain volume of the contents of the cranial cavity can keep the intracranial pressure constant, which is intracranial compliance. However, if the volume of the cranial cavity further increases, the compliance will decrease and the intracranial pressure will increase. Therefore, the relationship between the two is one of the factors that determine the intracranial pressure. The quantitative relationship between compliance and intracranial pressure can be expressed by this mathematical model. In the process of data processing, conventional paramet...

Embodiment 3

[0098] The model for determining the relationship between cerebral hemodynamics and intracranial pressure is:

[0099] ICP t =c(1)*ABP t +c(2)*PI t +c(3)*RI t+c(4)*CO2 t +c(5)*ABP t-1 +μ t

[0100] mu t =c(6)*μ t-1 +ε t

[0101] This calculation formula obtains the parameter c(1) of the basic parameter by establishing an autoregressive time series model on the data sequence, and then selects the first-period delay and first-order autoregression of the most important response quantity ABP as random disturbance items.

[0102] The simulation curve of the model is as Figure 8 shown.

[0103] The components in the rigid cranial cavity are brain tissue, cerebrospinal fluid, and blood. An increase in any of these components can lead to an increase in intracranial pressure. Cerebral hemodynamics regulates the amount of intracranial blood volume, so it determines intracranial pressure. Key factor. This model contains the main factors affecting cerebral hemodynamics. Su...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention relates to a non-invasive intracranial pressure monitoring equipment, which comprises: a data collection device, which is a transcranial Doppler instrument; a data transmission device, which is used for converting the analog signal of the data collection device to the digital signal; a calculation and analysis device, which is a computer with a data analysis software, the calculation and analysis device receives the output signal of the data transmission device and can call the data in a database by a network; a display equipment, which is used for displaying the analysis results of the calculation and analysis device; an input-output equipment, which is used for the input of the operation command and the output of the analysis results of the calculation and analysis device. The invention can realize the long-term continuous detection, which not only has a convenient detection way, but also has reliable conclusions and high measurement accuracy.

Description

technical field [0001] The invention relates to intracranial pressure monitoring equipment, in particular to a non-invasive intracranial pressure monitoring equipment based on transcranial Doppler. Background technique [0002] Increased intracranial pressure (ICP) is a common syndrome in clinical practice. Increased ICP can cause disturbance of consciousness in patients, and brain herniation in severe cases, which can be life-threatening in a short time. Therefore, ICP monitoring is an important prerequisite for the treatment of craniocerebral diseases. ICP monitoring can help judge the severity of traumatic brain injury or other intracranial lesions, help early detection of intracranial space-occupying lesions, and guide the treatment options for reducing ICP. In addition, ICP monitoring can also assist in the diagnosis of brain death. [0003] Most of the clinically used ICP monitoring methods are invasive. The earliest ICP detection method is lumbar puncture manometry ...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): A61B5/03A61B8/00G06F19/00
Inventor 梁冶矢刘来福
Owner 百睦好科技(北京)有限公司
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com