[0024] In order to make the technical solutions and advantages of the present invention clearer, the present invention will be further described below with reference to specific embodiments and accompanying drawings in the forward-looking array SAR system.
[0025] The invention is mainly applied to the radar imaging of the real aperture array antenna, and is mainly applied to the short-range imaging platform of the high frequency band array radar at present.
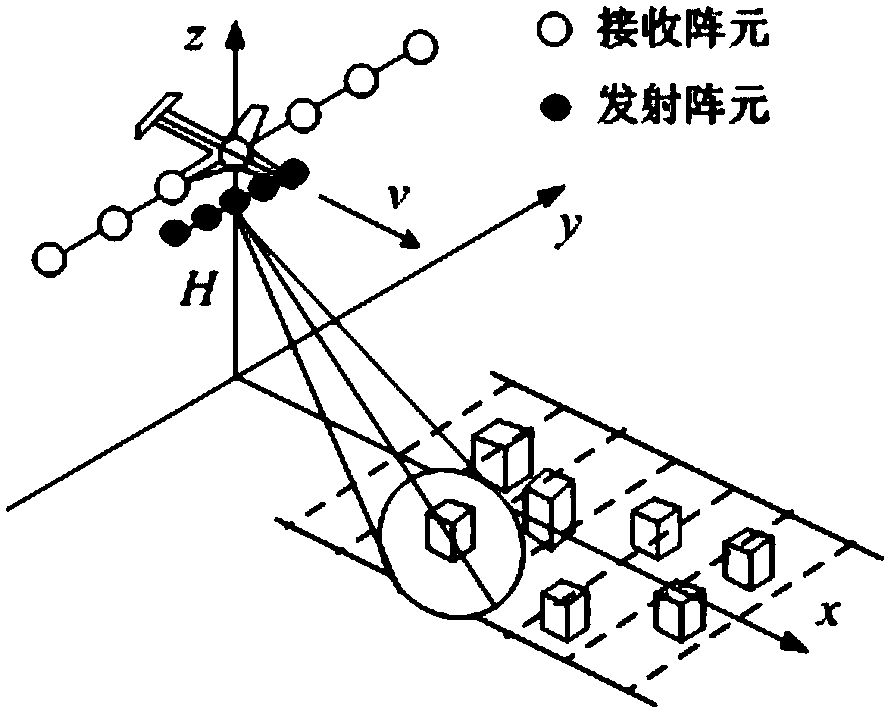
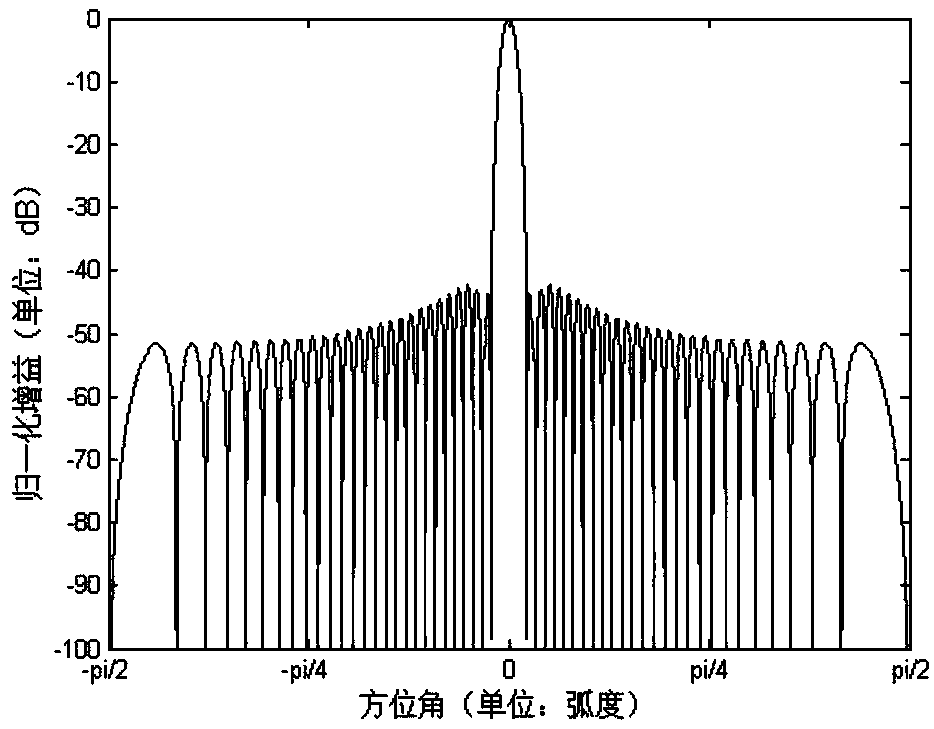
[0026] figure 1 The schematic diagram of the earth observation of the forward looking array SAR system is given. The carrier plane flies horizontally and uniformly along the direction of the observation strip at H meters above the observation strip, and the speed is v. The radar transmit beam points to the front and bottom of the platform (use beam scanning to achieve effective coverage of the observation strip, figure 1 Examples of observations in the two beam case are given). It is assumed that the receiving and transmitting antennas are independent array antennas. The transmitting antenna adopts a short dense array antenna that can be electronically scanned, and the receiving antenna adopts a sparse and evenly arranged long array antenna. The two antennas are arranged in parallel and perpendicular to the flight direction of the platform. ,like figure 1 shown. It is defined that the flight direction of the carrier aircraft is along the heading, represented by the x-axis; the direction of the transceiver array is the cross-course, represented by the y-axis, and the center of the two arrays is the zero point of the y-axis; the height direction is the z-axis, and the horizontal ground is the zero point of the z-axis. The directions of the three coordinate axes are arranged in accordance with the Cartesian Cartesian coordinate system. The steps of sparse antenna design for forward looking array SAR system are as follows:
[0027] Step 1: Adopt a new antenna transceiver mode
[0028] The basic situation of the transceiver antenna is as follows: the transmitting antenna adopts a short dense array antenna that can be electronically scanned, and the receiving antenna adopts a uniform and sparsely arranged long array antenna. Compared with the traditional single dense array antenna, due to the short length of the transmitting antenna, the number of array elements is much smaller; because the receiving antennas are sparsely arranged, the number of array elements is also much smaller, so the total number of array elements is greatly reduced. At the same time, in order to meet the coverage requirements of the observation strip of the forward-looking array SAR, the transmitting antenna needs to scan the observation strip, so it is more suitable to use the phase-shifted electronic scanning method. Therefore, the working method of the system is: for a certain observation area, it is divided into multiple sub-areas according to the beam width, and the transmitting antenna scans each sub-area in turn. The receiving array element simultaneously receives the echo of each sub-area.
[0029] Step 2: Determine the basic parameters of the antenna according to the resolution requirements
[0030] After the system's transceiver mode is determined, the basic parameters of the antenna are determined according to the imaging requirements of the forward-looking array SAR system. The basic parameters of imaging are: radar range R, range resolution ΔR, cross-course resolution ΔA, etc. Together with the operating wavelength λ of the system, the total length of the receiving antenna L r It can be expressed by the following formula:
[0031]
[0032] where β represents the resolution broadening factor.
[0033] Step 3: Determine the correlation between the transmit and receive antenna parameters from the perspective of grating lobe suppression
[0034] Assume that the element spacing of the receiving antenna is d r (d rλ), then the number of array elements of the receiving antenna is N r =L r /d r. Due to the increased spacing of the array elements, the aperture of the receiving array elements can be appropriately increased accordingly to improve the receiving gain. However, the sparse arrangement of the array will bring the receiving grating lobes and reduce the imaging quality. The azimuth angle sinθ of the receiving grating lobes is not considered in the case of phase shift and weighting. r0 will satisfy the following formula:
[0035]
[0036] From the perspective of radar imaging, receiving grating lobes will significantly reduce the cross-course peak-to-side lobe ratio and cross-course integral side lobe ratio of the imaging system, and it is necessary to effectively suppress the grating lobes to achieve cross-course imaging. Experiments have found that a feasible method is to make the zero point of the transmit beam the same as the receive grating lobe, and use the zero point of the transmit beam to effectively reduce the grating lobe level of the total beam for transmission and reception.
[0037] The transmitting antenna adopts a uniform dense array, and it is assumed that the distance between the array elements is d. t is λ/2, and the length of the transmitting antenna is L t, then the number of array elements is If appropriate period weighting is performed on the transmitting antenna, and it is assumed that the beam nulling coefficient is γ (it is closely related to the window function of the transmitting array, in general, γ=1 or 2), then the null position θ of the transmitting beam t0 It can be expressed as
[0038]
[0039] It should be noted that the window function here should be a periodic window function, that is, the position of the beam zero point is periodic. The implementation shows that there are some window functions whose beam nulls are not periodic and cannot be used here. At present, it has been tested that the rectangular window function, the periodic Hamming window and the periodic Hanning window are all acceptable.
[0040] In order to obtain an ideal level of integral sidelobe ratio, the receiving grating lobe must fall into the zero position of the transmitting beam, namely:
[0041]
[0042] Therefore, the receiving array element spacing d r and transmit antenna length L t Satisfy L t =md r , where m≥γ, d rλ.
[0043] Step 4: Determine the expression and constraints of the total number of array elements, and establish an optimization equation.
[0044] According to the constraint relationship in equation (4), the total number of array elements N of the transmitting and receiving antennas tr It can be expressed as:
[0045]
[0046] It can be seen that formula (5) is a monotonically increasing function of variable m, the smaller the value, the smaller the function value, and its minimum value is m=γ, so the variable m in formula (5) can be replaced by γ. If λ, L are assumed r and γ are known, then when m=γ, When the formula (5) takes the minimum value At this time, the length of the transmitting antenna Transmit beam width
[0047] However, since L t When it is larger, the width of the transmit beam will be very narrow, even much smaller than the width θ of the observation strip c , which will result in a large number of scans, difficult beam control, and a small number of receiving array elements, which will affect the sidelobe suppression in subsequent beamforming. Therefore, L t It cannot be infinite, but there is a minimum scanning beamwidth Δθ t , so that L t must be less than a certain value, and then d r must also be less than some value, i.e.
[0048]
[0049] Therefore, according to equations (5) and (6), the total number of array elements can be expressed as d r is an optimization equation with independent variables and linear constraints, as shown in the following equation.
[0050]
[0051] Among them, the objective function is a convex function, and the constraints are also linear.
[0052] Step 5: Solve the optimization equation with constraints to determine the parameters of the transceiver antenna
[0053] The above optimization equation is a linearly constrained convex optimization equation, which can be solved by the Lagrange multiplier method to obtain the optimal solution d of the equation r，min. According to this optimal solution, the following parameters of the system can be uniquely determined, including: the transmitting antenna length L t =γd r，min , the number of transmitting array elements Number of receiving array elements N r =L r /d r，min. So far, there is an unknown parameter γ and the window function of the weighting of the transmitting and receiving antennas has not been determined, and γ depends on the window function of the transmitting antenna.
[0054] Step 6: Determine the window function of the transceiver antenna according to the radar imaging quality requirements
[0055] It can be seen from equation (4) that the smaller γ is, the smaller the total number of transceiver array elements is, but the cross-course integral sidelobe ratio may be higher, so the value of γ should be discussed according to the imaging quality. The array antennas of the forward-looking array SAR are arranged across the course, and the beamforming of the cross-course array antenna is used to achieve high resolution across the course. Therefore, the cross-course resolution, the cross-course peak sidelobe ratio and the cross-course integral sidelobe ratio are three. an indicator. Experiments show that the transceiver split array antenna has the following characteristics: (1) Due to the effective suppression of the receiving grating lobes, the cross-course resolution is only related to the weighting of the receiving array, and is not closely related to the transmitting pattern. (2) Although the cross-course peak sidelobe ratio is also related to the transmit pattern, it mainly depends on the sidelobe level of the receiving array weighted processing, and it is easy to obtain a satisfactory sidelobe level. (3) The cross-course integral side lobe ratio is very closely related to the weighting process of the transmitting pattern and the receiving array. At the same time, the simulation results show that the cross-course integral sidelobe ratio level is related to the following three points: (1) In order to obtain an ideal integral sidelobe level, the zero point of the transmitting beam must be used to effectively suppress all the receiving grating lobes. (2) If a rectangular window is used to weight the transmitting array, even if the receiving array adopts a deeper weighting function, the integral sidelobe ratio will be greater than -10dB, that is, γ cannot take 1; therefore, the weighting window function of the transmitting antenna adopts periodic Hamming Both the window and the periodic Hanning window can be used, and γ=2 at this time. (3) If Hamming or Hanning window is used to weight the transmitting array, as long as the weighting depth of the receiving array is less than -30dB, the integral sidelobe ratio will be less than -10dB, which meets the requirements of cross-course imaging. Therefore, the minimum value of γ should be 2, and the transmitting and receiving antennas all use a periodic window function of a certain depth, so that the imaging requirements of the forward-looking array SAR system can be met. For example, in the following embodiments, the transmitting antenna adopts the Hamming window function, and the receiving antenna adopts the Chebwin window function.
[0056] Specific examples are given below, and the feasibility and imaging quality of the method of the present invention are verified.
[0057] Assuming that the wavelength of the transmitted signal is 3 mm and the length of the receiving antenna is 9.6 m, if a uniformly dense array is used and the spacing between adjacent array elements is 1.5 mm, the number of receiving array elements is 6400. However, if the method in this paper is adopted, assuming that the beam width can be infinitely small, the number of transmitting and receiving array elements corresponding to the optimal solution is 114 respectively, the total number of array elements is 228, and the number of array elements is reduced to 3.6% of the original. At this point, the transmit beamwidth is about 0.035 radians. Assuming that the azimuth beam width is 30 degrees (0.52 radians) and the coincidence of adjacent beams is 10%, the number of scanning beams is about 17. If the minimum beam width is assumed to be 0.07 radian, the number of transmitting array elements is reduced to 56, the number of receiving array elements is increased to 228, the total number of array elements is increased by 25%, and the number of scanning beams is reduced to 9 at this time. At this time, compared with the dense array method, the array elements are about 4.5% of it, which also significantly reduces the number of array elements. The basic parameters of the simulation experiment are shown in Table 1.
[0058] Table 1 Basic parameters of the simulation experiment
[0059] Center wavelength (mm)
[0060] (1): figure 1 The two-way pattern of transmitting and receiving when the number of transmitting array elements is 56 and the number of receiving array elements is 228 is given, in which the transmitting beam is weighted by Hamming window, and the transmitting beam width is 0.07 radian (about 3.7 degrees), like figure 2 shown. The receiving array is windowed during imaging, and the window function is a Chebyshev window of -35dB. image 3 The pattern of the two-way transmission and reception is given, in which the peak sidelobe ratio is -35dB and the integral sidelobe ratio is -17dB, which fully meets the requirements of cross-course imaging.
[0061] (2): Assuming that the slant distance from the center of the scene is 1 km, the cross-course resolution is about 0.5 m. At the same time, assuming that the transmitted pulse is a chirp signal, the signal bandwidth is 500MHz, the pulse width is 2 microseconds, and the range-wise window function is a Chebyshev window of -30dB, the range-wise resolution is about 0.5 meters. Figure 4 A 2D image of a point scattering source at the center of the scene is given, Figure 5 The range and cross-course profiles of the scatter source image are given. Among them, the imaging method adopts Chirp Scaling imaging algorithm.
[0062] (3): Simulate the echoes of 9 point scattering sources in the shape of a field. Among them, the 9 point scattering sources have the same amplitude and random phase, and the distance between adjacent point scattering sources is 1 meter. Image 6 The imaging results of echoes from these nine point scattering sources are given.
[0063] It can be seen that under this antenna configuration, the present invention also achieves effective imaging and accurate positioning of all point scattering sources. The above experimental results show that this method can effectively realize the cross-directional imaging of the forward-looking array SAR, and significantly reduce the number of array elements, which is beneficial to the realization of the forward-looking array SAR antenna.
