Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

High-performance material optimal selection method suitable for space debris protection structure

A technology for protecting structures and space debris, which is applied in computer materials science, astronautical equipment, and spacecraft for astronautics. The effect of reducing trial costs

Active Publication Date: 2020-05-15
BEIJING INST OF SPACECRAFT ENVIRONMENT ENG
View PDF14 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

my country's spacecraft space debris protection research work started late, and foreign countries have been strictly embargoing high-performance protective materials for my country. Facing the increasingly strong demand for space debris protection projects, many domestic companies have carried out research and development of high-performance protective materials. However, there is a big gap between the engineering application of space debris protection materials and the protection ability compared with foreign countries.

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • High-performance material optimal selection method suitable for space debris protection structure
  • High-performance material optimal selection method suitable for space debris protection structure
  • High-performance material optimal selection method suitable for space debris protection structure

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

[0048] see Figure 1-5 , a method for optimizing high-performance materials suitable for space debris protection structures, comprising the following steps: a. selecting a protection material, and looking up a table to obtain the Hugo Neo and thermodynamic parameters of the material, b. according to the impact pressure criterion and Preliminary screening of protective materials based on internal energy conversion criteria, c. further optimization of protective materials through the coefficient of performance model, d. screening of protective screen materials according to the minimum thickness criterion, and optimal protective screen materials, e. filling according to the kinetic energy absorption criterion Layer material is screened to obtain the preferred filling layer material, f. the preferred protective screen material and filling layer material are tested and verified;

[0049]Impact pressure criterion: The impact pressure depends on the impact velocity, the density of th...

Embodiment 2

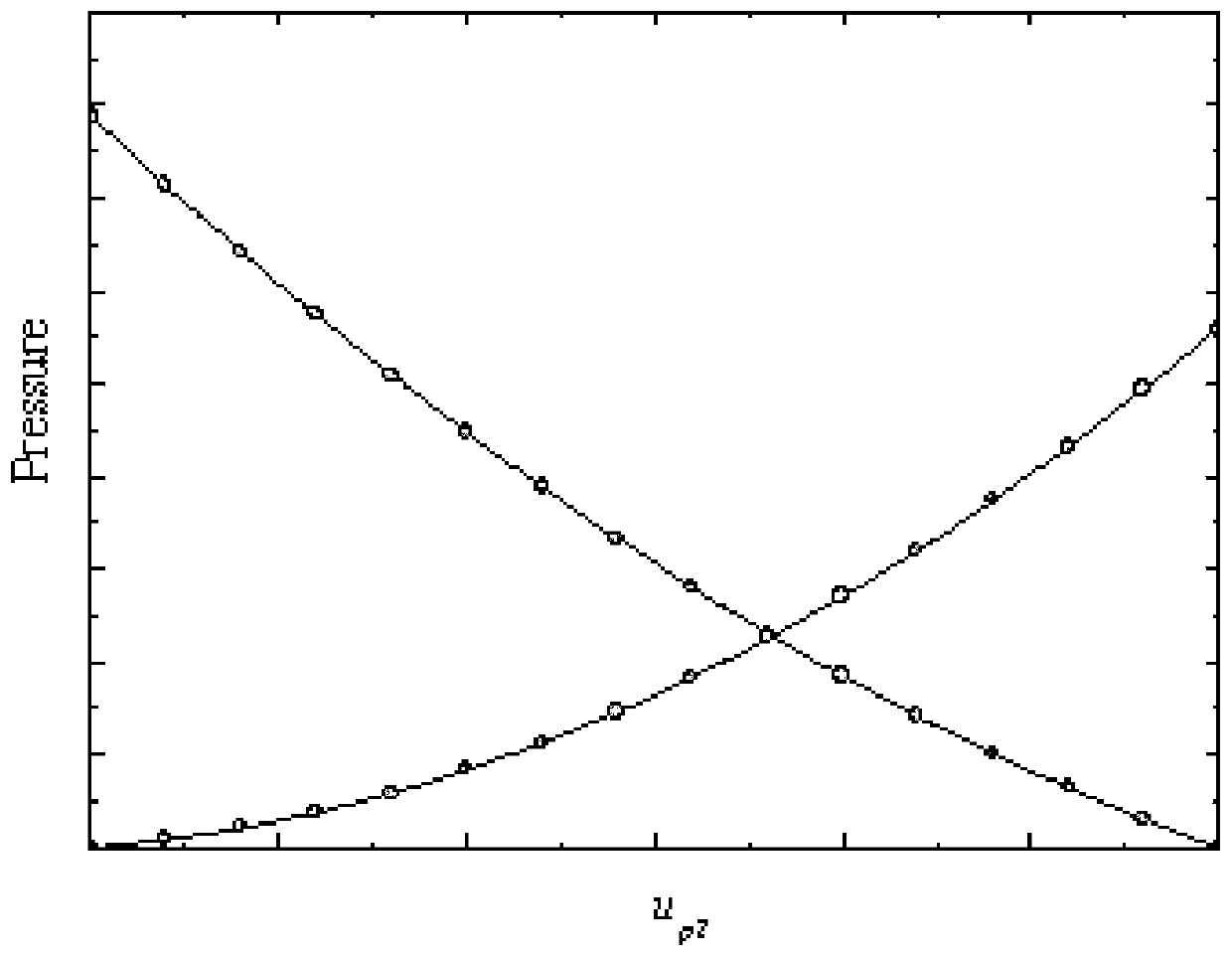
[0056] see figure 2 and image 3 , the impact pressure criterion in step b is based on the one-dimensional shock wave theory, ignoring the initial pressure before the impact of the projectile target, and using the momentum conservation equation to calculate the pressure in the projectile and the target plate, the calculation formula is:

[0057] For projectiles:

[0058] P 1 = ρ 1 u s1 mu p1

[0059] For target board:

[0060] P 2 = ρ 2 u s2 mu p2

[0061] The state equations corresponding to the projectile and the target plate are:

[0062] u s1 =C 1 +S 1 mu p1

[0063] u s2 =C 2 +S 2 mu p2

[0064] Combined with the continuous condition of the interface, we can get:

[0065] P 1 = ρ 1 (C 1 +S 1 mu p1 )μ p1 = ρ 1 C 1 mu p1 +S 1 mu p1 2

[0066] P 2 = ρ 2 (C 2 +S 2 mu p2 )μ p2 = ρ 2 C 2 mu p2 +S 1 mu p2 2 .

[0067] According to the known parameters of the material state equation, the impedance matching method is used to calcul...

Embodiment 3

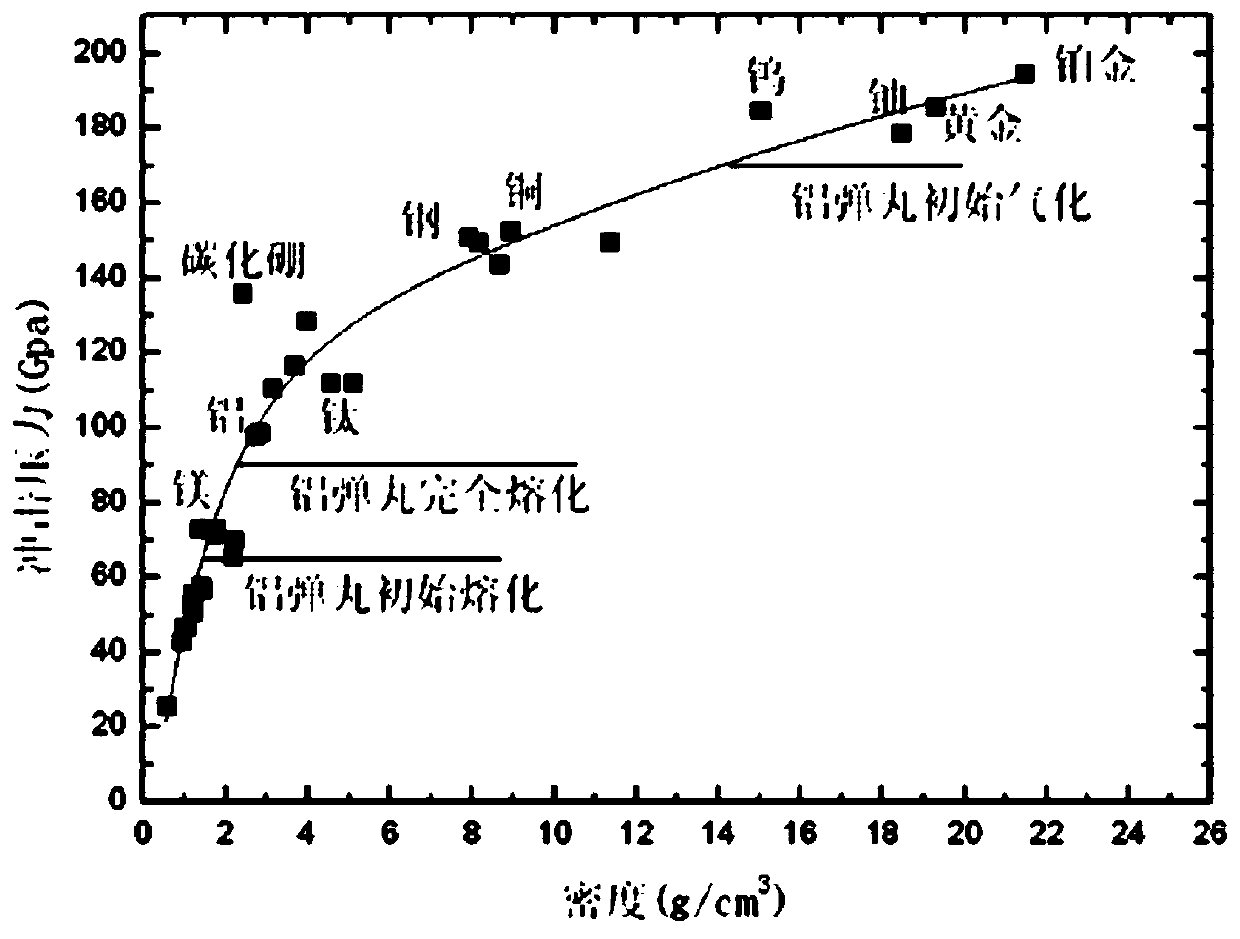
[0070] see Figure 4 , from the theory of shock wave heating, it can be known that the melting or gasification of a material is determined by the residual specific internal energy retained in the material after shock wave compression and isentropic unloading. It will lead to irreversible entropy increase of the projectile target material. The entropy increase process can be considered as adiabatic, while the unloading process under the action of sparse wave is isentropic. After the material undergoes two processes, the entropy increases, that is, the internal energy of the material increases. The increase in internal energy during the impact loading process minus the energy released during the unloading process is the remaining internal energy in the material. When the remaining specific internal energy of the material is greater than the melting specific internal energy, the material melts. When the remaining specific internal energy is greater than the gasification When the ...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a high-performance material optimal selection method suitable for a space debris protection structure. The method comprises the following steps: a, selecting a protective material, and looking up a table to obtain the Hugoniot and thermodynamic parameters of the material; and b, screening the protective material according to an impact pressure criterion, an internal energyconversion criterion, a minimum thickness criterion and a kinetic energy absorption criterion to obtain a preferred material. In the present invention, the protection mechanism of the protective material under the ultrahigh-speed impact effect is deeply analyzed; the mechanical and thermodynamic characteristics of the protective material are comprehensively considered; the impact pressure, the internal energy conversion, the minimum thickness and the kinetic energy absorption characteristic of the protective material are used as optimal criteria; in combination with a performance coefficient model capable of quantitatively characterizing wave impedance characteristics and thermodynamic characteristics of the protective material, the high-performance material optimal selection method suitable for the space debris protection structure is obtained, optimal selection of various protection materials can be achieved, the test cost for material selection is effectively reduced, and theoretical guidance can be provided for design and preparation of novel high-performance protection materials.

Description

technical field [0001] The invention relates to the technical field of space debris protection, in particular to a method for optimizing high-performance materials suitable for space debris protection structures. Background technique [0002] The concept of protective screen was first proposed by American astrophysicist Whipple, which is placed outside the bulkhead of the spacecraft and kept a certain distance from the bulkhead. The protective screen, the rear wall and a certain distance constitute the basic configuration of the space debris protective structure of the spacecraft——Whipple protective structure. By adding a protective screen on the outside of the bulkhead, the spacecraft can make the incident debris collide with the protective screen at a super high speed and be broken, melted or even gasified to form a secondary debris cloud, which minimizes and disperses the kinetic energy of the incident debris and significantly reduces The collision energy flux density ac...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): B64G1/52B64G1/22G16C60/00
CPCB64G1/52B64G1/22G16C60/00
Inventor 武强宋光明李明龚自正张品亮曹燕田东波
Owner BEIJING INST OF SPACECRAFT ENVIRONMENT ENG
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com