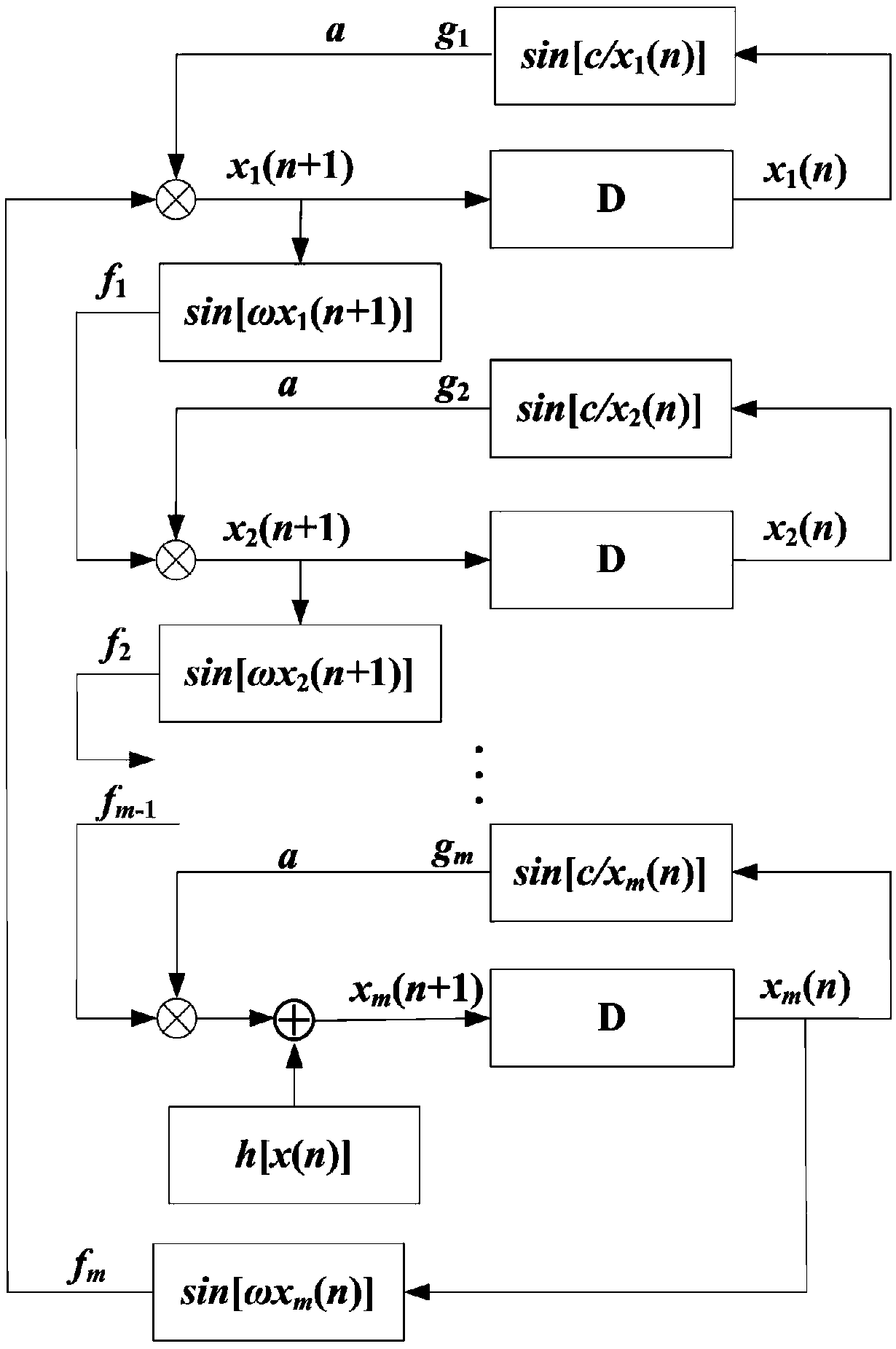Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

A New Grid Sine Cavity Hyperchaotic Mapping System

A super-chaotic and sinusoidal technology, applied in the field of nonlinear systems, can solve complex nonlinear phenomena and other problems, and achieve the effect of clear phase diagram and rich dynamic characteristics

Inactive Publication Date: 2019-01-25
湖南特思科智能科技有限公司
View PDF3 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

However, in practical engineering applications, many physical systems are described by two variables or even multiple variables, making two-dimensional or even multi-dimensional discrete maps have more complex nonlinear phenomena than one-dimensional discrete maps

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • A New Grid Sine Cavity Hyperchaotic Mapping System
  • A New Grid Sine Cavity Hyperchaotic Mapping System
  • A New Grid Sine Cavity Hyperchaotic Mapping System

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

[0051] A new grid sinusoidal cavity hyperchaotic mapping system, the construction of which includes the following steps:

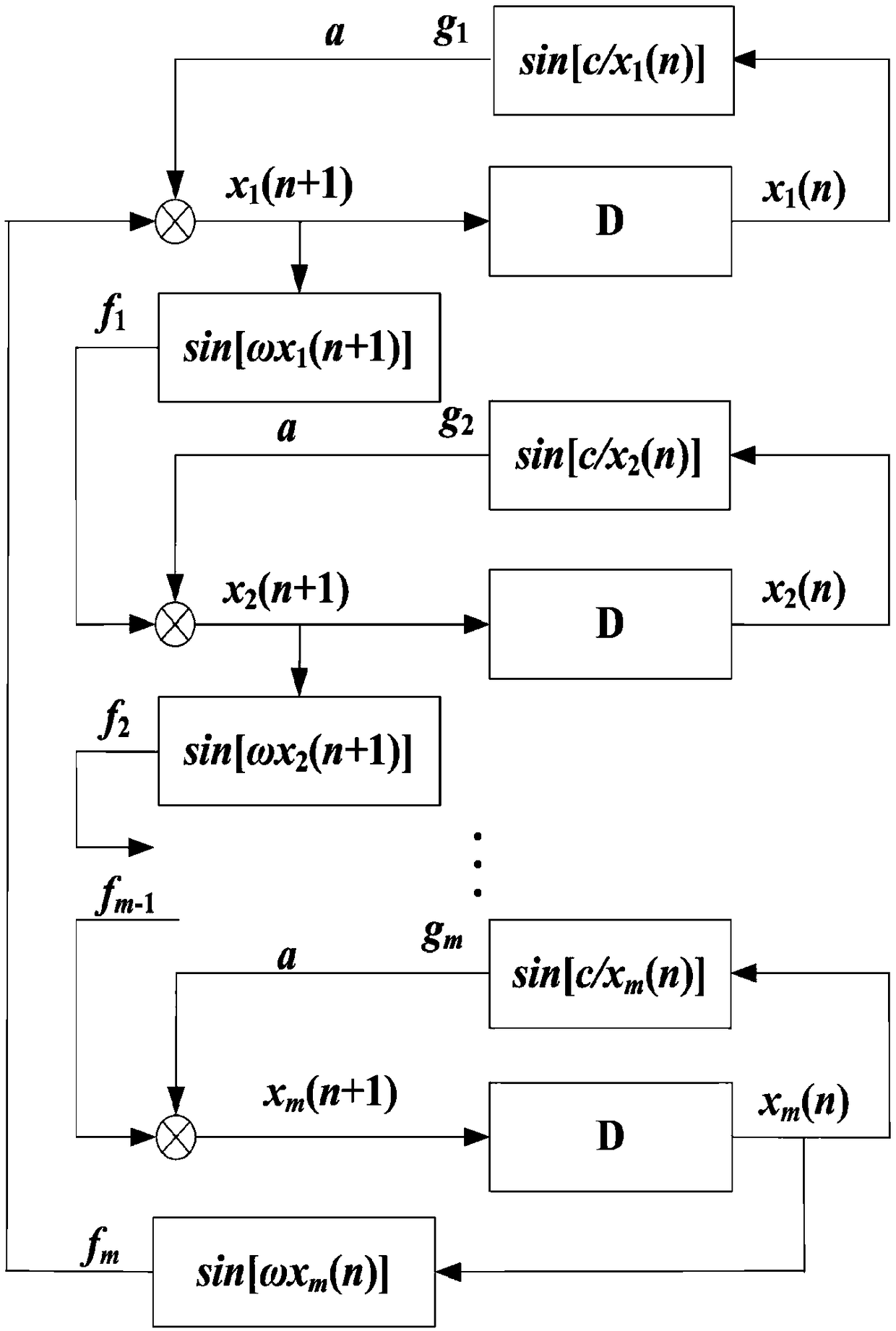
[0052] The first step is to establish a sinusoidal discrete nonlinear function model based on closed-loop modulation coupling. For details, see figure 1 , to obtain the state equation of the m-dimensional control system, the specific process is as follows:

[0053] Step 1.1. Design an m-dimensional discrete-time system with a control parameter ω, specifically, expression 1):

[0054] X(n+1)=Af[x m (n),X(n+1),ω] 1);

[0055] Where: X(n)=[x 1 (n),x 2 (n),...,x m (n)] T , and satisfy m≥2; A is an m×m control matrix; f[x m (n), X(n+1), ω] is a uniformly bounded nonlinear feedback controller whose value is Expression 2):

[0056]

[0057] In expression 2) ω=[ω,ω,...,ω] T ;

[0058] Step 1.2, simplify expression 2) to get expression 3):

[0059] f i [x i (n),ω]=sin[ωx i (n)], i=1,2,...,m 3);

[0060] Step 1.3, take A as an expression 4) containin...

Embodiment 2

[0079] Combining the method of Example 1 to construct a two-dimensional sinusoidal cavity hyperchaotic mapping system, the details are as follows:

[0080] 1. The system equation of the unidirectional sinusoidal cavity is the expression 1-1):

[0081]

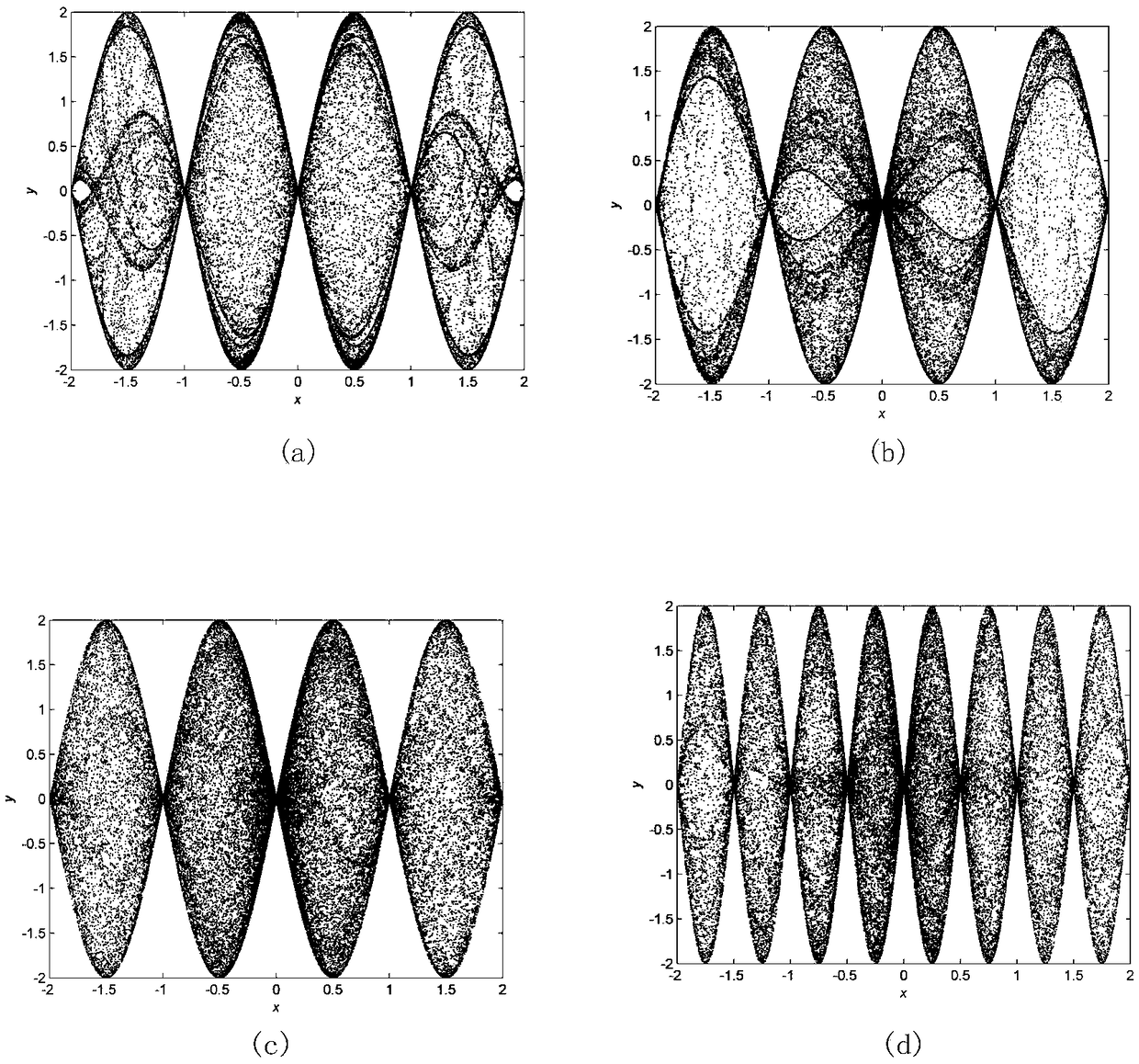
[0082] Among them: x and y are state variables, a is the amplitude, ω is the angular frequency, and c is the internal disturbance frequency. It is worth noting that: x n and y n are not zero, otherwise the system has no meaning, and x 0 and y 0 are not equal to kπ or

[0083] Set the initial value x(1)=0.3, y(1)=0.3, n=50000, under different value parameters, use Matlab to carry out numerical simulation, the chaotic attractor with unidirectional multi-sine cavity can be obtained as image 3 (a), image 3 (b), image 3 (c) and image 3 (d), where image 3 (a)-(d) are chaotic attractors under different parameters ( image 3 The abscissa and ordinate of (a)-(d) are x(n) and y(n) respectively), specifically: image 3...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention provides a novel grid sine cavity hyper-chaos mapping system. A construction method of the system includes following steps: step 1, building a sine discrete nonlinear function model based on closed-loop modulation coupling, and acquiring a state equation of an m-dimension control system; step 2, combining the state equation of the m-dimension control system acquired in the step 1 with a step wave function to acquire a state equation of the novel grid sine cavity hyper-chaos mapping system. Different amounts of one-dimension chaos attractors can be acquired by building the sine discrete nonlinear function model based on closed-loop modulation coupling and then changing system parameters; the sine discrete nonlinear function model is combined with the step wave function, the one-dimension chaos attractors are enabled to extend onto a plane to acquire grid hyper-chaos attractors, novel grid hyper-chaos mapping is constructed, and the attractors have clear phase diagrams and rich dynamic characteristics.

Description

technical field [0001] The invention relates to the technical field of nonlinear systems, in particular to a novel grid hyperchaotic mapping system. Background technique [0002] Existing chaotic maps can be divided into two categories: [0003] The first type, one-dimensional chaotic map, one-dimensional chaotic map has only a small number of parameters and one variable, such as Logistic map, Tent map, Chebyshev map and sinusoidal map. Its advantages are reflected in the implementation efficiency and simplicity of application. Therefore, they are widely used in cryptography and chaotic secure communication. But the complexity is low and the key space is small. With the development of the Internet and cloud computing, the one-dimensional chaotic map based on chaotic encryption can no longer guarantee the security of information transmission, because its orbit, parameters and initial conditions can be predicted by chaotic signal estimation technology. [0004] The second ...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Patents(China)
IPC IPC(8): H04L9/00
CPCH04L9/001
Inventor 孙克辉喻梦瑶刘文浩贺少波王会海
Owner 湖南特思科智能科技有限公司
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com