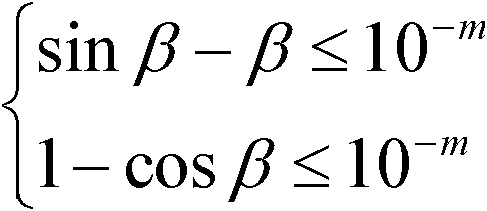Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Sine-cosine function IP core capable of reconfiguring spaceborne computer and control method thereof

A technology of sine and cosine functions and satellite-borne computers, which is applied in calculation, electrical digital data processing, digital data processing parts, etc., and can solve problems such as rounding errors and result effects

Inactive Publication Date: 2011-08-17
HARBIN INST OF TECH
View PDF3 Cites 7 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0008] The present invention solves the problem of rounding error in the initial assignment of the existing iterative algorithm, which has a great influence on the result; and for different angles, the number of iterations required is different, and the larger the angle, the more the number of iterations required. Propose a Sine-Cosine Function IP Core and Its Control Method for Reconfigurable Spaceborne Computer

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Sine-cosine function IP core capable of reconfiguring spaceborne computer and control method thereof
  • Sine-cosine function IP core capable of reconfiguring spaceborne computer and control method thereof
  • Sine-cosine function IP core capable of reconfiguring spaceborne computer and control method thereof

Examples

Experimental program
Comparison scheme
Effect test

specific Embodiment approach 1

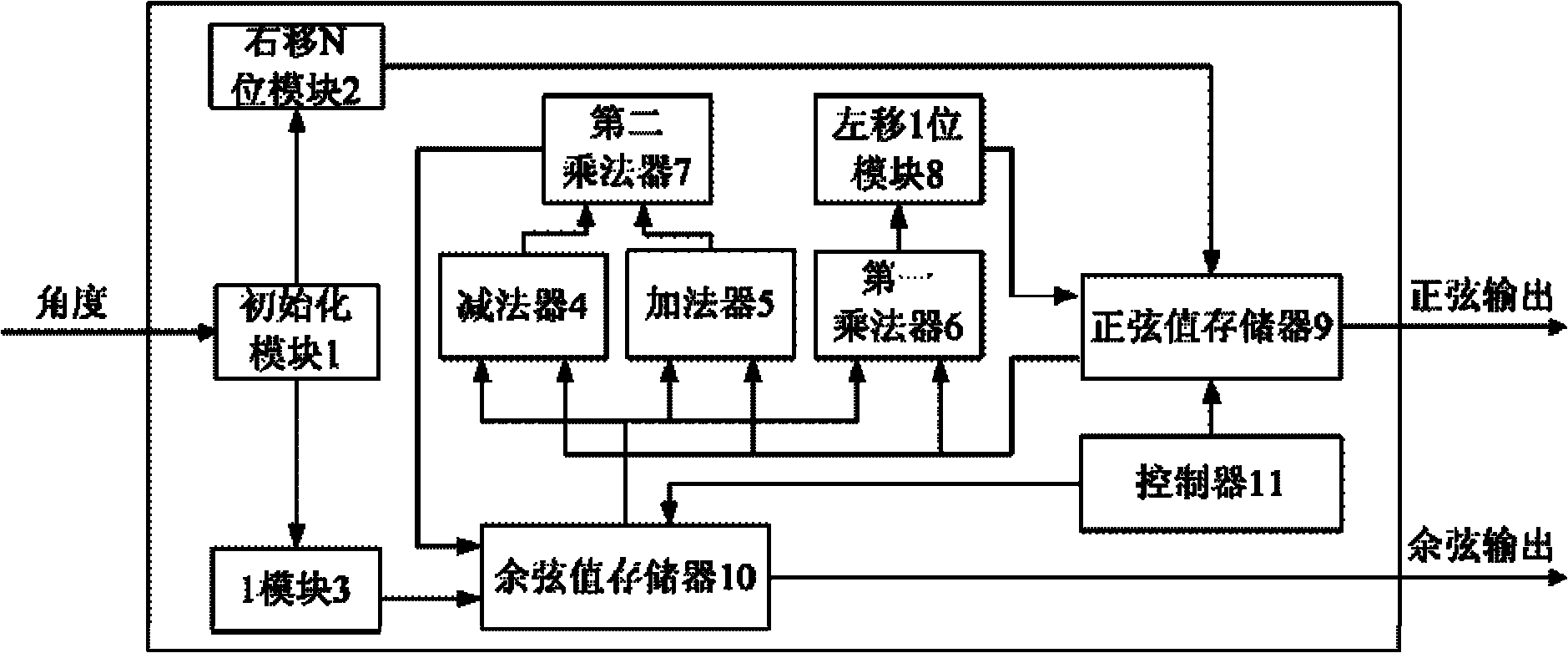
[0028] Specific embodiment one: combination figure 1 To describe this embodiment, the steps of this embodiment are as follows:

[0029] Step 1: According to the periodicity of the trigonometric function, map the angle η to [0, π / 2] to become the input angle θ, and set the sign bit;

[0030] Step 2: Perform pre-judgment to determine whether the input angle θ is less than or equal to the given critical angle β. Yes, that is, when θ≤β, directly use sinθ=θ, cosθ=1 for assignment and proceed to step 4. No, That is, when β<θ≤π / 2, go to step three;

[0031] Step 3: Iterative operation:

[0032] Step 1: Perform an iterative operation on the input angle θ, and divide the input angle θ by 2 N , Get the initial assignment according to the approximate criterion:

[0033] sinα=θ / 2 N

[0034] cosα=1

[0035] n=0

[0036] Among them, N represents the total number of iterations, and n represents the nth iteration;

[0037] Step 2: Use the double angle formula to calculate:

[0038] cos2 n+1 α=(cos2 n α+sin...

specific Embodiment approach 2

[0044] The second embodiment: The difference between this embodiment and the first embodiment is the calculation of the critical angle β in step 2:

[0045] The expected design accuracy is 10 -m , According to the principle of initial assignment, the critical angle β should satisfy:

[0046] sin β - β ≤ 10 - m 1 - cos β ≤ 10 - m

[0047] For example, the expected design accuracy is 10 -7 , The critical angle β should satisfy:

[0048] sin β - β ≤ 10 - 7 1 - cos β ≤ 10 - 7

[0049] The required β = 0.0014. Other components and connection modes are the same as the first embodiment.

specific Embodiment approach 3

[0050] Specific embodiment three: This embodiment and the specific embodiment one or two points are that the total number of iterations N in step 3 is 21; the main errors of implementing the sine and cosine function using the iterative algorithm are: rounding error and truncation error. When the iterative process retains many valid digits, the truncation error has little influence on the calculation result and can be ignored, so only the rounding error generated in the initial assignment is considered.

[0051] Perform Taylor expansion on sinx and cosx, there are:

[0052] sinx=x-x 3 / 3! +x 5 / 5! -...

[0053] cosx = 1-x 2 / 2! +x 4 / 4! -...

[0054] When the value of x is much smaller than 1, it is only necessary to keep the first term of the expansion to meet the calculation accuracy requirements.

[0055] Let α≈θ / 2 N , Suppose the errors of the n-th iterative calculation of sine and cosine are respectively ε n ,Δ n , Using the recursive method to derive the error expression of th...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention relates to a sine-cosine function IP core capable of reconfiguring a spaceborne computer and a control method thereof, relating to the technical field of aerospace electronics, and solving the problems that the result of initial value assignment is largely influenced due to rounding errors, and the larger the angle is, the more the iteration times is needed. An initializing module is connected with a right-shift N-bit module and a module 1, the module 1 is connected with a cosine value storing device, the right-shift N-bit module is connected with a sine value storing device, the cosine value storing device and the sine value storing device are connected with a subtracter-adder and a first multiplier, the subtracter-adder is connected with a second multiplier and then is connected with the cosine value storing device, the first multiplier is connected with a left-shift 1-bit module and then is connected with the sine value storing device, and the a controller is connected with the sine value storing device and the cosine value storing device. The control method comprises the following steps of: mapping eta into [0, pi / 2] to generate theta; judging whether theta is less than and equal to beta; if theta is less than and equal to beta, directly assigning the value and carrying out the last step; otherwise, carrying out the iteration operation, and obtaining an assigned initial value according to an approximate rule; calculating by utilizing a double-angle formula, judging whether n is less than N; if n is less than N, calculating again; otherwise, finishing the operation; finally assigning a sine / cosine function value according to the positive / negative result obtained by the sign bit judgment. The invention is applied to attitude control.

Description

Technical field [0001] The invention relates to the electronic technology field of aerospace. Background technique [0002] With the continuous development of reconfigurable technology in the aerospace field, on-board computers based on FPGA (Field Programmable Gate Array) have become a research hotspot in satellite electronic systems. The use of a satellite electronic system with FPGA as the core can reduce the size, weight, power consumption and cost of micro-satellites, and increase the functional density of the system. [0003] Attitude determination and attitude control processing is one of the important functions of the on-board computer. In traditional on-board computers, the standard sincos function in the C language mathematical function library is mostly used to calculate the attitude control algorithm. The calculation of the sine and cosine functions The time is as high as 2.5μs / time (accurate to 7 digits after the decimal point). It can be seen that the software calcul...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G06F7/548
Inventor 潘瑞于文进兰盛昌徐国栋徐卓异丁玉叶马玉海林晓辉
Owner HARBIN INST OF TECH
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com