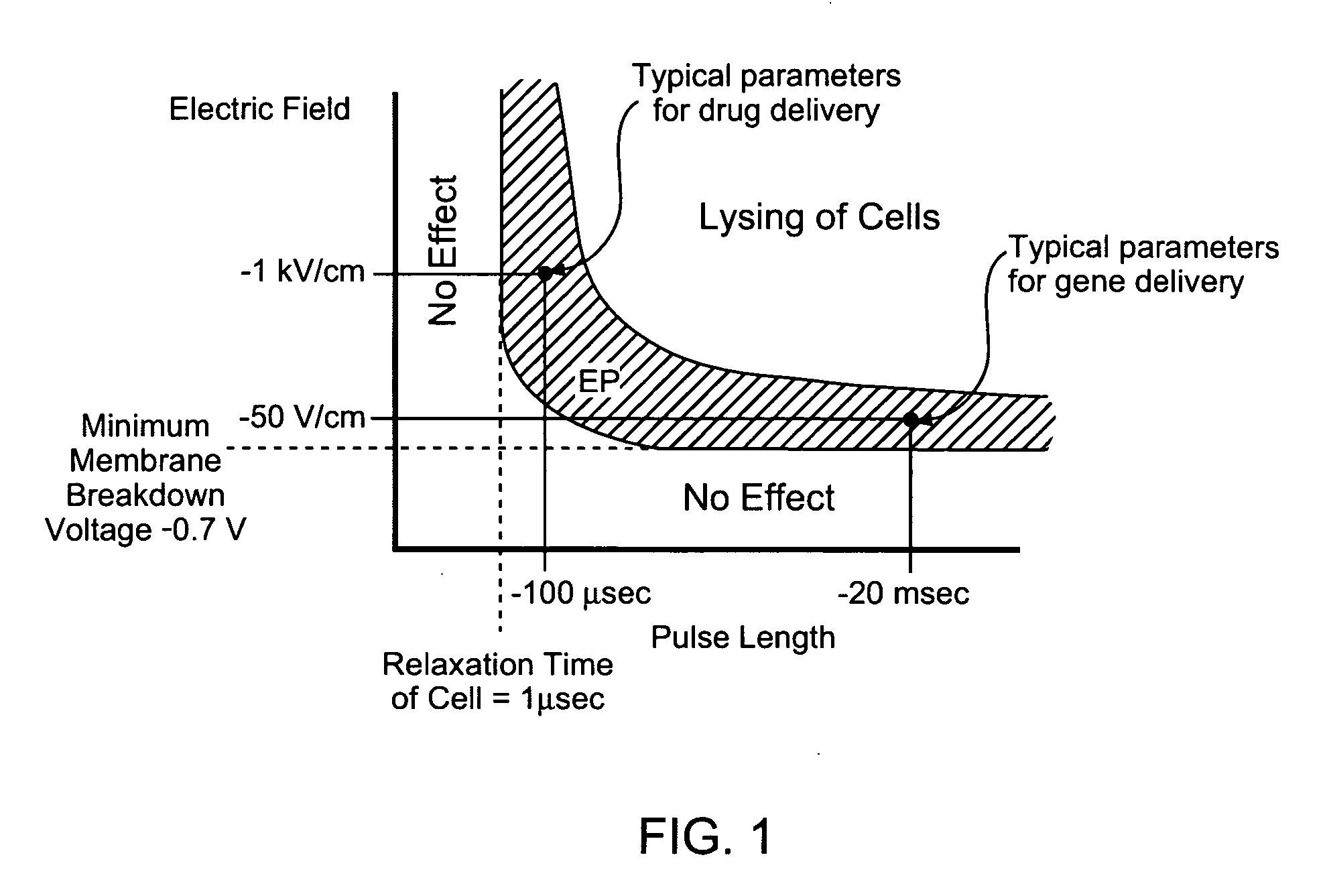
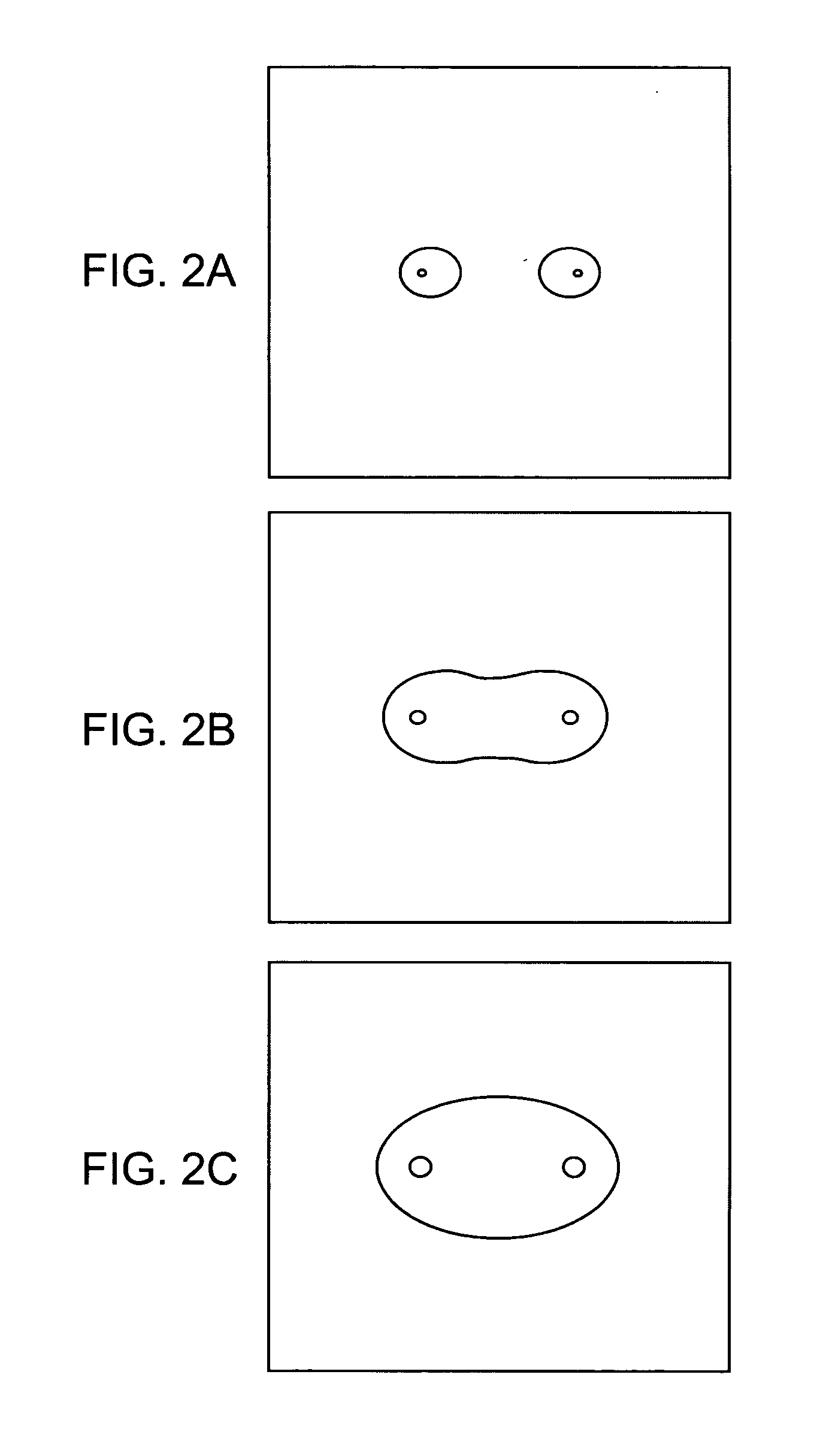
Irreversible electroporation to control bleeding

Inactive Publication Date: 2005-08-04
RGT UNIV OF CALIFORNIA
View PDF8 Cites 260 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Benefits of technology

[0020] The present invention comprises a method whereby blood flow and such bleeding from a vessel is stopped with the application of electrical pulses causing irreversible electroporation of cells making up vessels and blood involved in unwanted bleeding. The electric pulses irreversibly permeate the membranes, thereby invoking cell death. The length of time of the electrica

Problems solved by technology

The electroporation pulse should not have considerable thermal effects, but irreversible break cell membranes of targeted cells and result in cell death.
Of these effects, irreversible el

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Irreversible electroporation to control bleeding
  • Irreversible electroporation to control bleeding
  • Irreversible electroporation to control bleeding

Examples

Experimental program
Comparison scheme
Effect test

Example

Example 1

[0067] The mathematical model provided here shows that irreversible tissue ablation can affect substantial volumes of tissue, without inducing damaging thermal effects. To this end, the present invention uses the Laplace equation to calculate the electrical potential distribution in tissue during typical electroporation pulses and a modified Pennes (bioheat), (Pennes, H. H., Analysis of tissue and arterial blood flow temperatures in the resting forearm. J of Appl. Physiology., 1948. 1: p. 93-122), equation to calculate the resulting temperature distribution. It is important to note that there are several forms of the bioheat equation which have been reviewed (Carney, C. K., Mathematical models of bioheat transfer, in Bioengineering heat transfer, Y. I. Choi, Editor. 1992, Academic Press, Inc: Boston. p. 19-152; Eto, T. K. and B. Rubinsky, Bioheat transfer, in Introduction to bioengineering, S. A. Berger, W. Goldsmith, and E. R. Lewis, Editors. 1996, Oxford Press). While th...

Example

Example 2

[0090] This example was developed to produce a correlation between electroporation pulses and thermal effects. The system analyzed is an infinitesimally small control volume of tissue exposed to an electroporation voltage gradient of V (Volts / cm).The entire electrical energy is dissipated as heat and there is no conduction of heat from the system. The calculations produce the increase in temperature with time during the application of the pulse and the results are a safe lower limit for how long a certain electroporation pulse can be administered until a certain temperature is reached. To generate the correlation an energy balance is made on a control volume between the Joule heating produced from the dissipation of heat of the V (volt / cm) electrical potential dissipating through tissue with an electrical conductivity of σ ( ohm-cm) and the raise in temperature of the control volume made of tissue with a density ρ (g / cc) and specific heat, c, (J / g K). the calculation produ...

Example

Example 3

[0097] The goal of this experiment was to verify the ability of irreversible electroporation pulses to produce substantial tissue ablation in the non-thermal regime. To this end we have performed experiments on the liver of Spraque-Dawley male rats (250 g to 350 g) under an approved animal use and care protocol. After the animals were anesthetized by injection of Nembutal Sodium Solution (50 mg / ml Pentobarbital) the liver was exposed via a midline incisions and one lobed clamped between two cylindrical electrodes of Ag / AgCl, with a diameter of 10 mm (In Vivo Metric, Healdsburg, Calif.). The electrodes had their flat surface parallel; they were concentric and the liver between the electrodes was compressed so that the lobes were separated by 4 mm. A schematic of the electrodes and the liver is shown in FIG. 9. The liver was exposed to a single electroporation pulse of 40 milliseconds. One electrode was set to 400 V and the other grounded. The rest of the liver was not in co...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

PUM

No PUM Login to view more

Abstract

A method of stopping or controlling bleeding by the placement of electrodes into or near the vicinity of vessels is disclosed. Then the application of electrical pulses causing irreversible electroporation of vessel and blood cells throughout the entire area of current flow the bleeding is stopped or controlled. The electric pulses irreversibly permeate the cell membranes, thereby invoking cell death. The irreversibly permeabilized cells are left in situ and are removed by the body immune system. Through the use of irreversible electroporation bleeding can be stopped or controlled without inducing thermal damage.

Description

CROSS-REFERENCE [0001] This application claims the benefit of U.S. Provisional Application No. 60 / 532,588, filed Dec. 24. 2003, which application is incorporated herein by reference.FIELD OF THE INVENTION [0002] This invention resides in the fields of electroporation of tissue and to treatments whereby unwanted bleeding is stopped. BACKGROUND OF THE INVENTION [0003] In many medical procedures, such as the treatment of benign or malignant tumors, it is important to be able to ablate the undesirable tissue in a controlled and focused way without affecting the surrounding desirable tissue. Over the years, a large number of minimally invasive methods have been developed to selectively destroy specific areas of undesirable tissues as an alternative to resection surgery. There are a variety of techniques with specific advantages and disadvantages, which are indicated and contraindicated for various applications. For example, cryosurgery is a low temperature minimally invasive technique in...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

Application Information

Patent Timeline
no application Login to view more
IPC IPC(8): A61B18/04A61B18/12A61B18/18A61N1/00A61N1/04A61N1/05A61N1/32
CPCA61B18/12A61B18/1477A61B2018/1425A61N1/327A61N1/0472A61N1/05A61N1/0412A61B18/1233A61B2018/00577A61B2018/00613A61B2018/00714A61B2018/00761A61B2018/00827
Inventor RUBINSKY, BORISEDD, JONHOROWITZ, LIANA
Owner RGT UNIV OF CALIFORNIA
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Try Eureka
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap