Patents
Literature
638 results about "Viewport" patented technology
Efficacy Topic
Property
Owner
Technical Advancement
Application Domain
Technology Topic
Technology Field Word
Patent Country/Region
Patent Type
Patent Status
Application Year
Inventor
A viewport is a polygon viewing region in computer graphics. In computer graphics theory, there are two region-like notions of relevance when rendering some objects to an image. In textbook terminology, the world coordinate window is the area of interest (meaning what the user wants to visualize) in some application-specific coordinates, e.g. miles, centimeters etc.
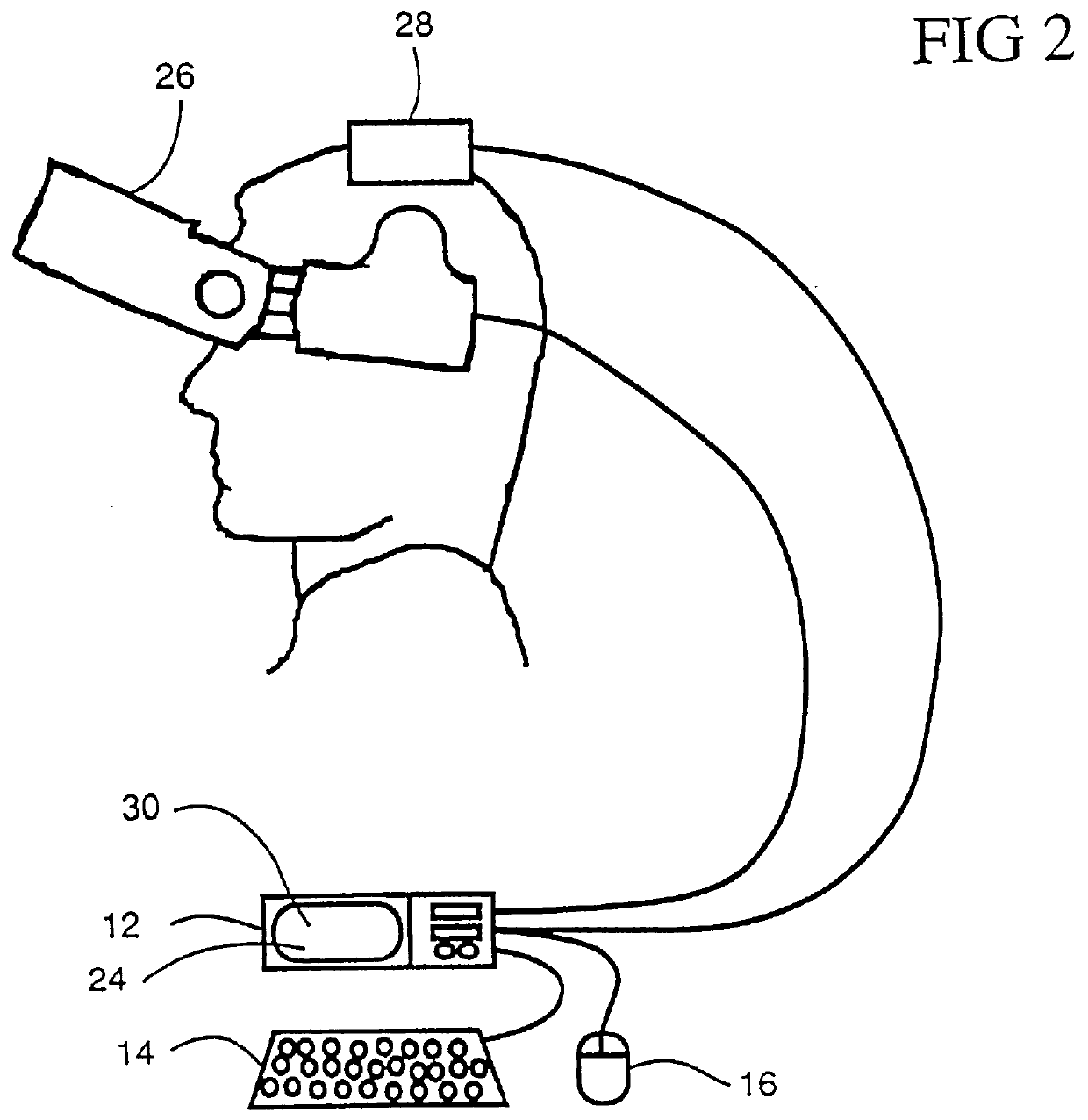
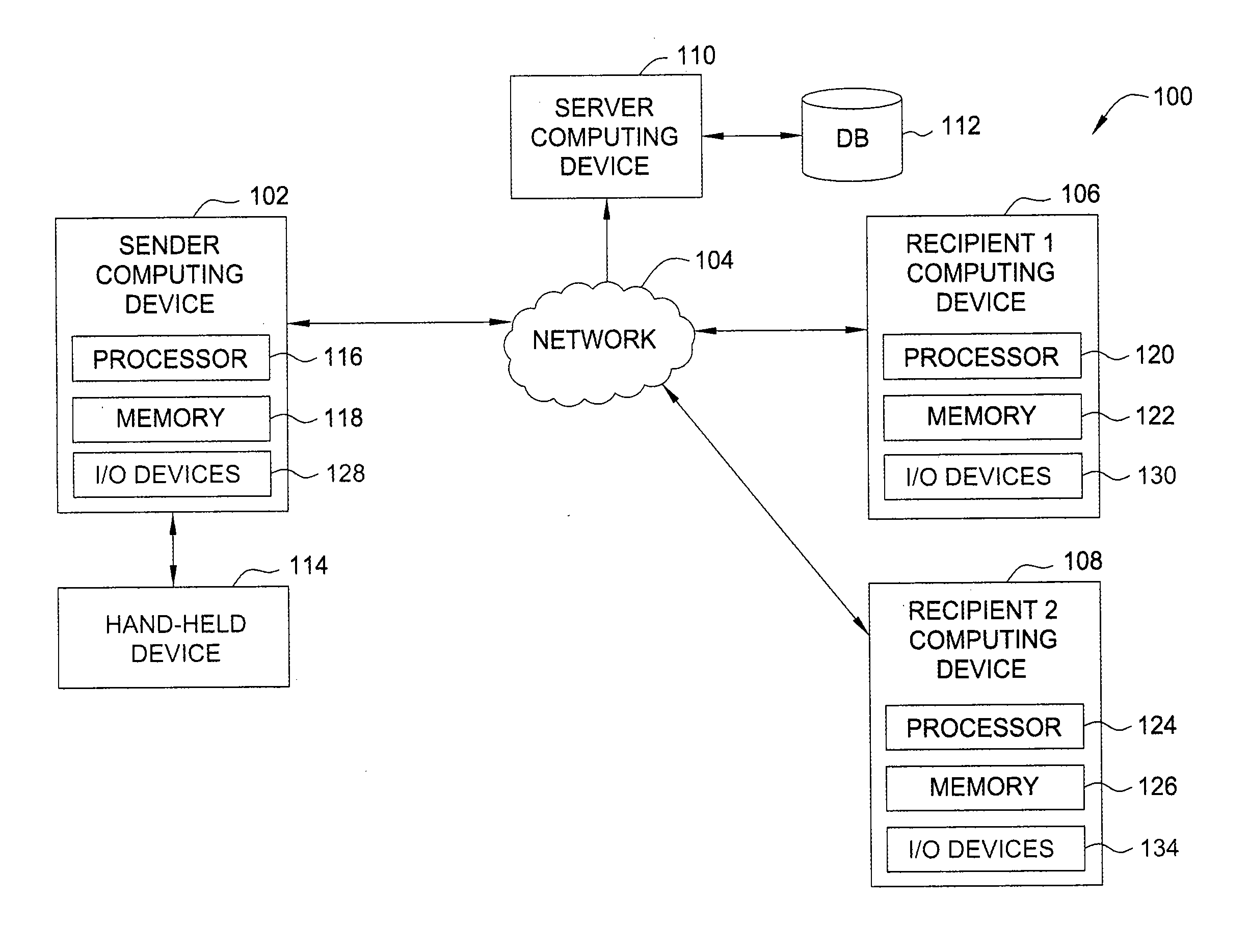
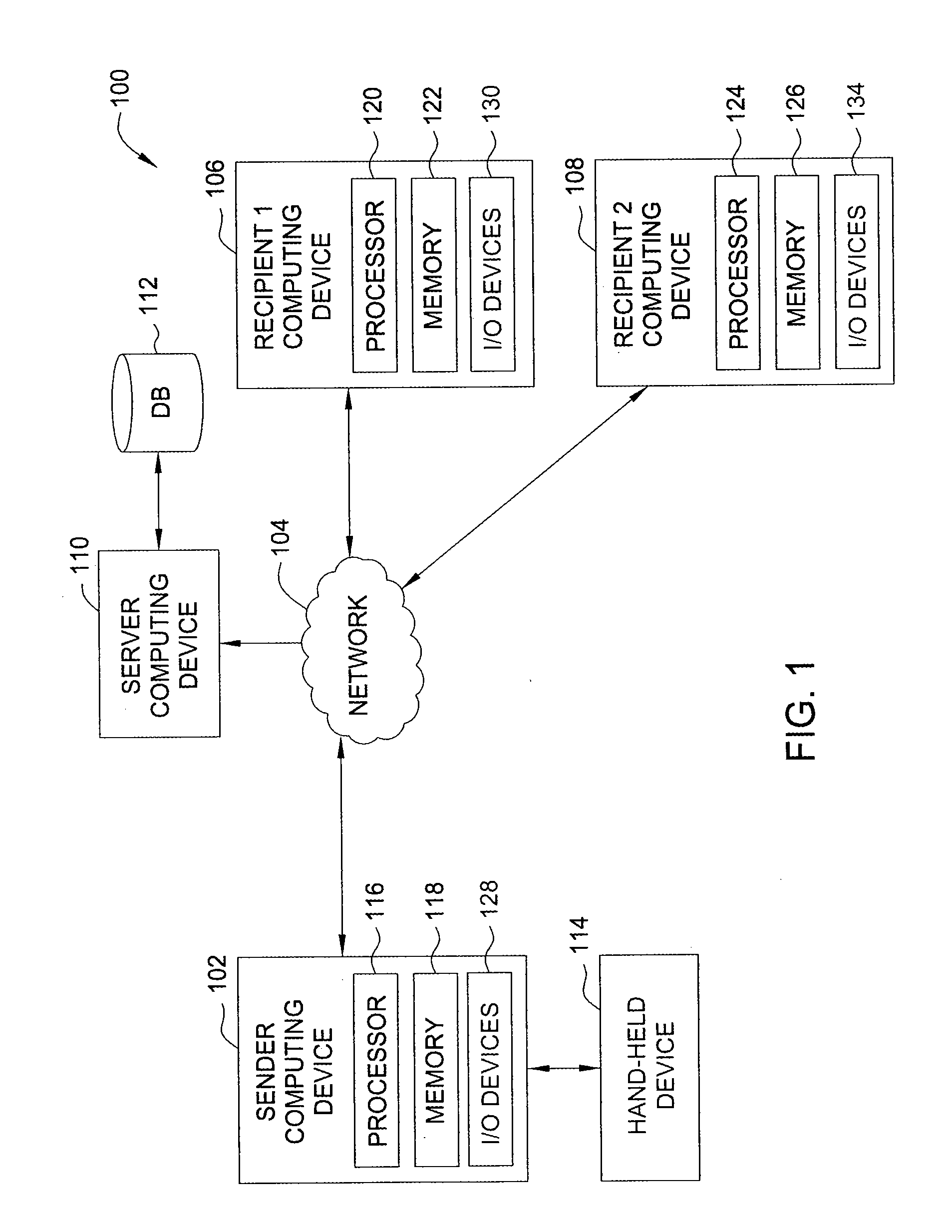
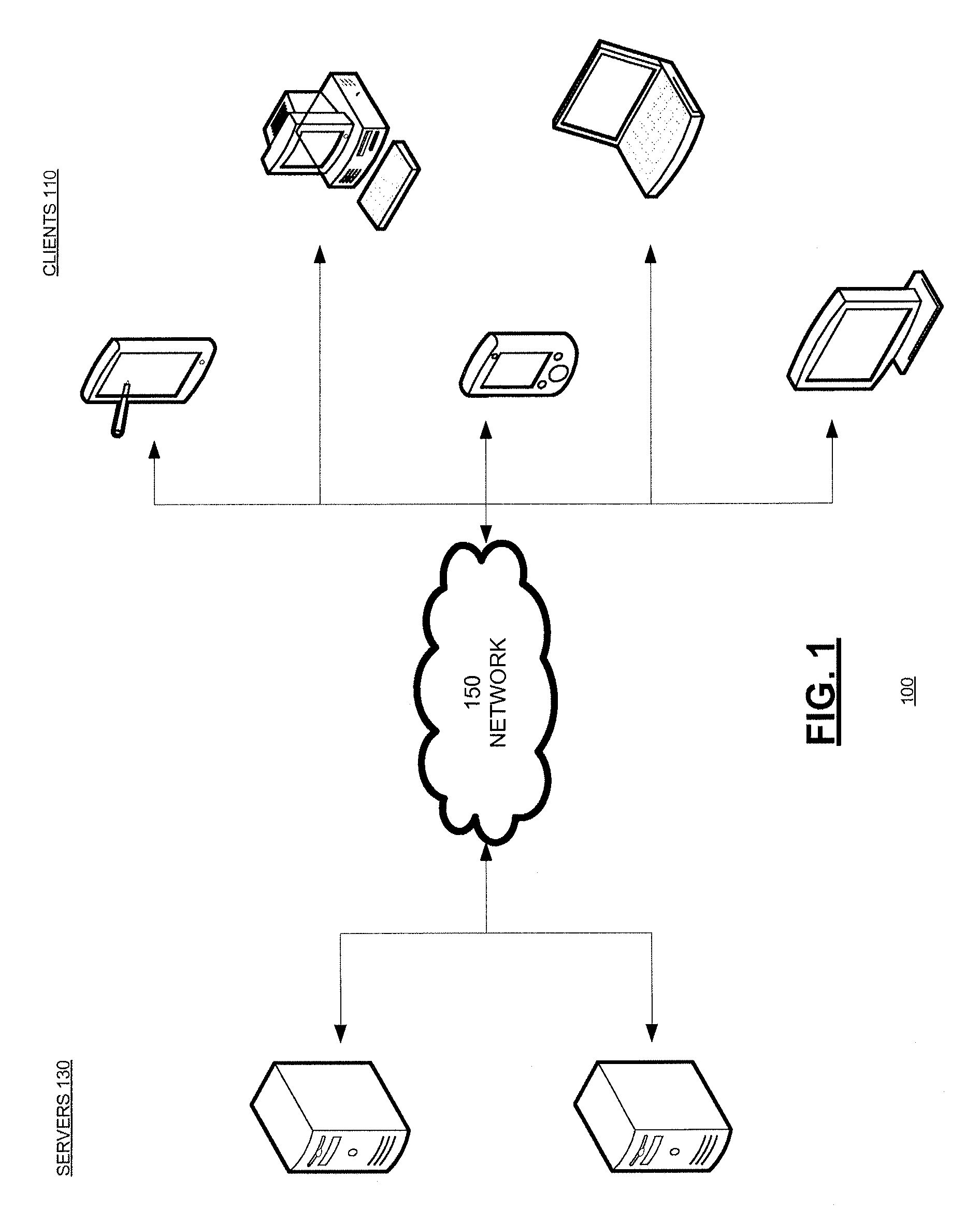
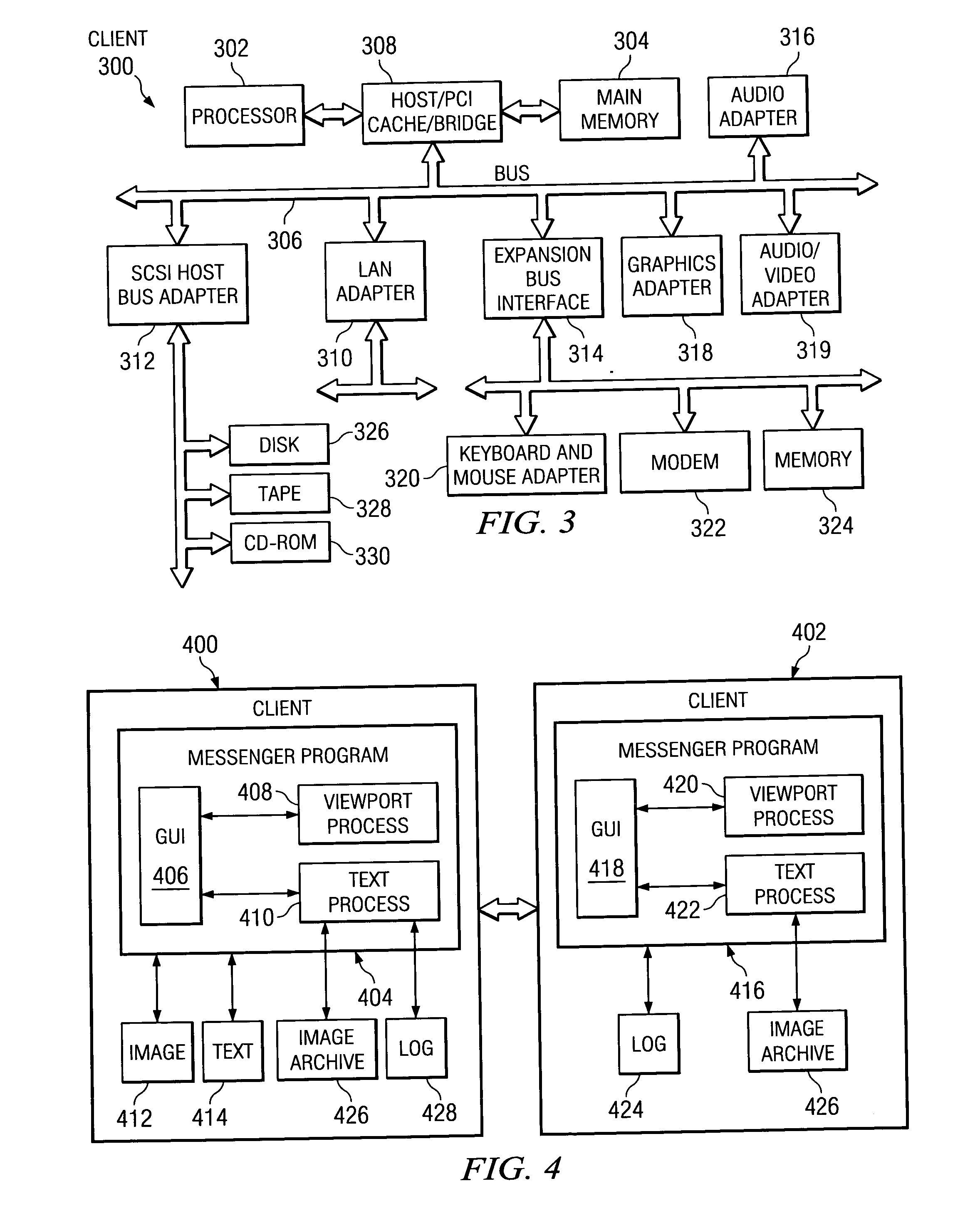
Intuitive control of portable data displays
InactiveUS6184847B1Reduce jitterInput/output for user-computer interactionCathode-ray tube indicatorsVisually impairedData display
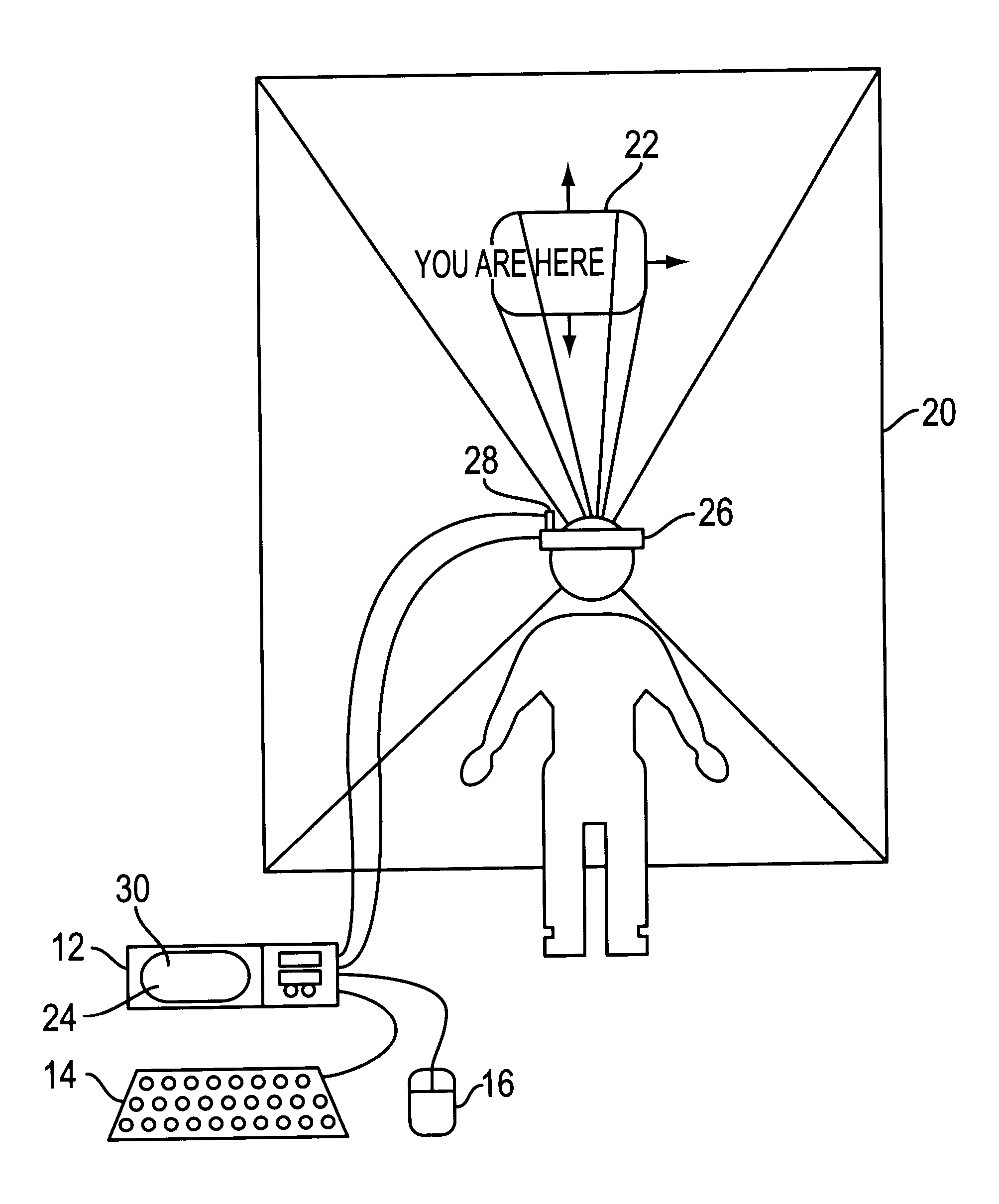
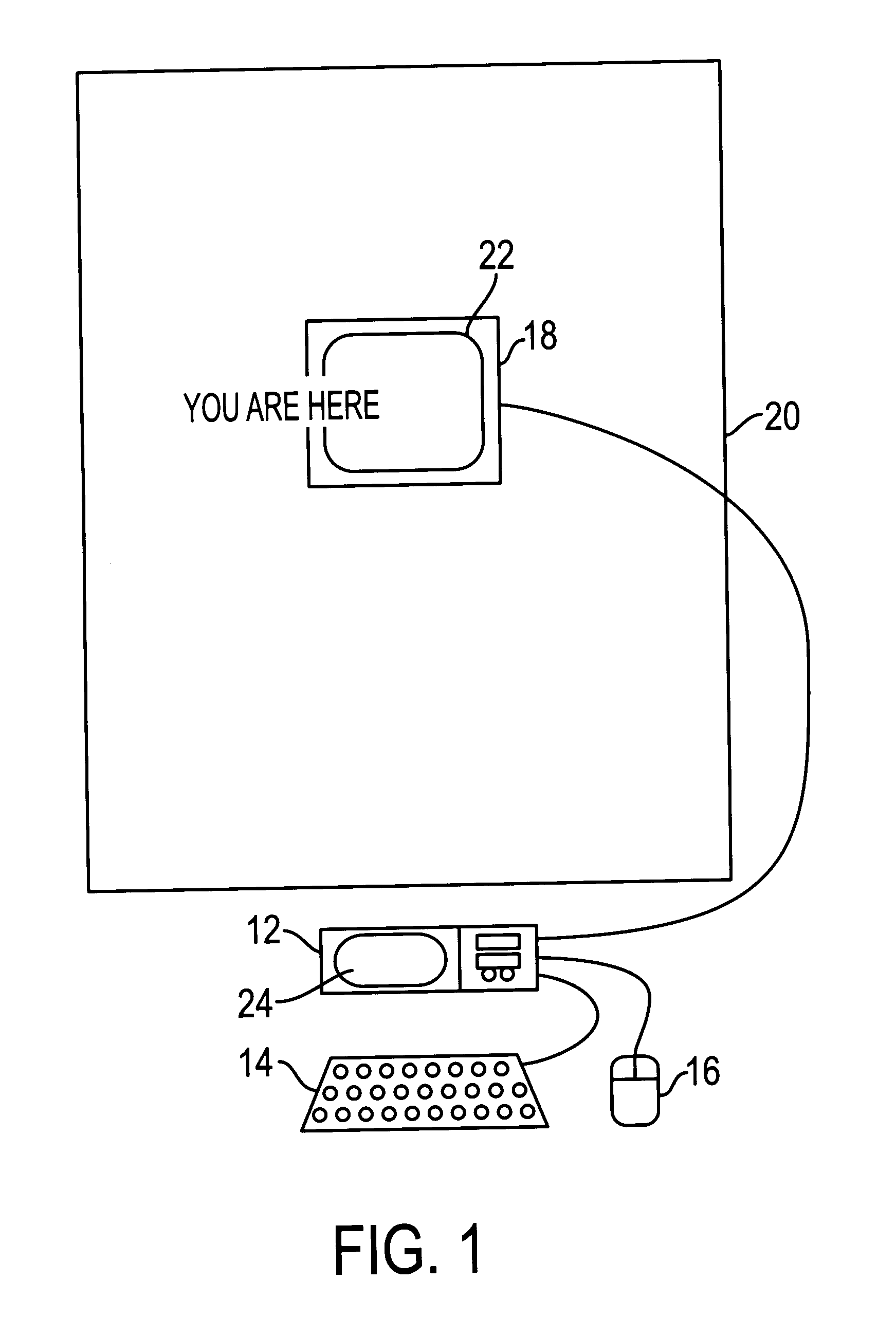
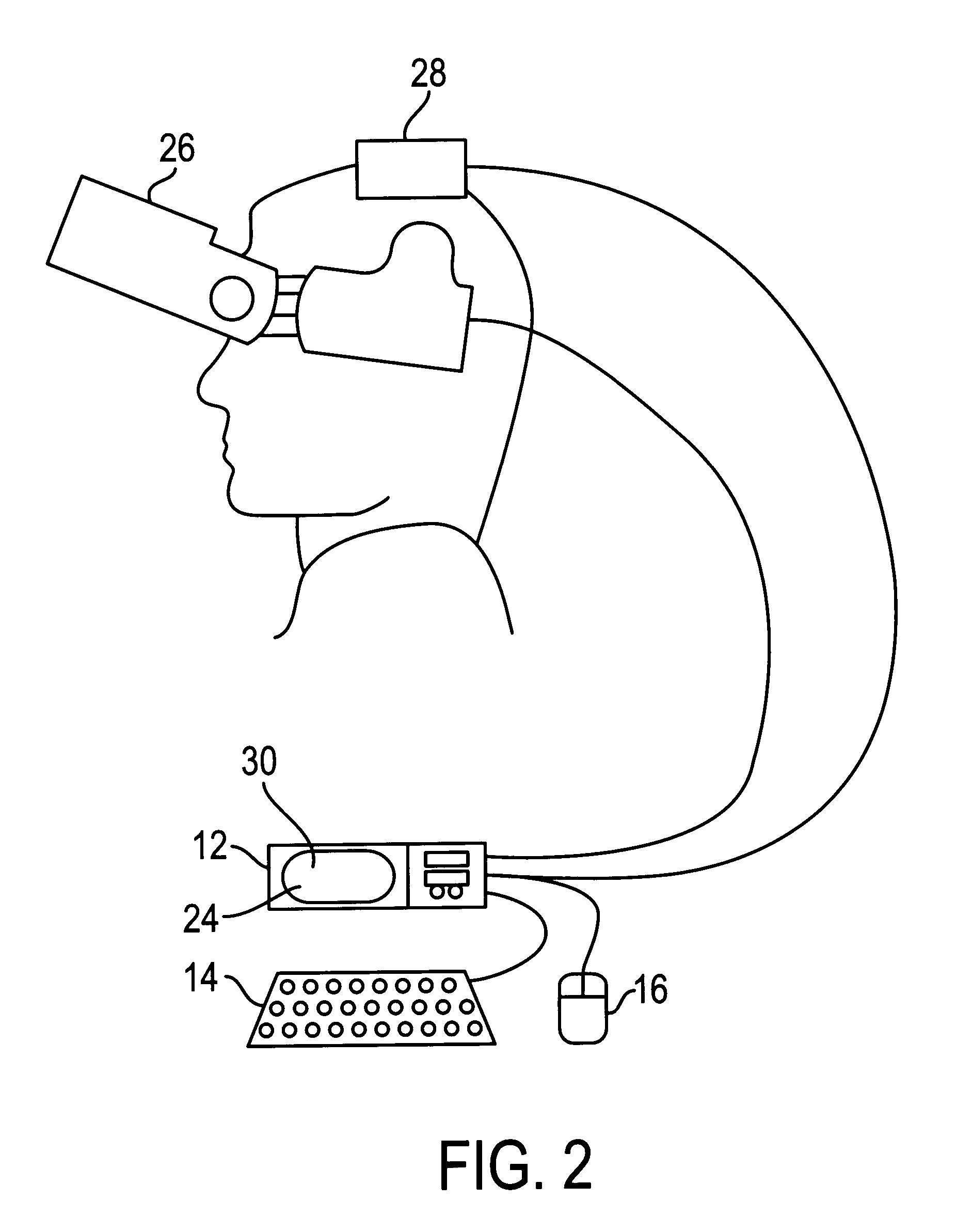
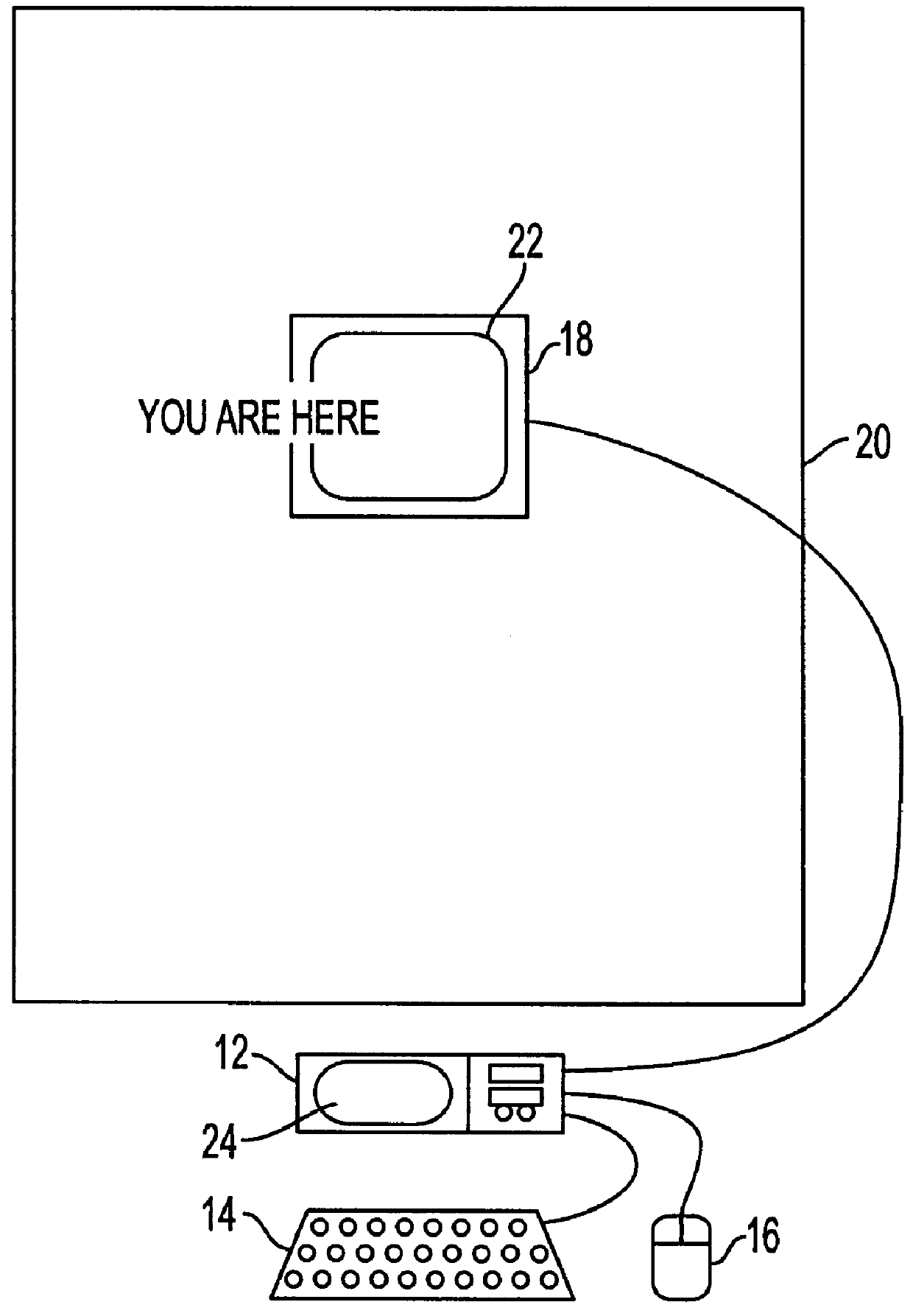
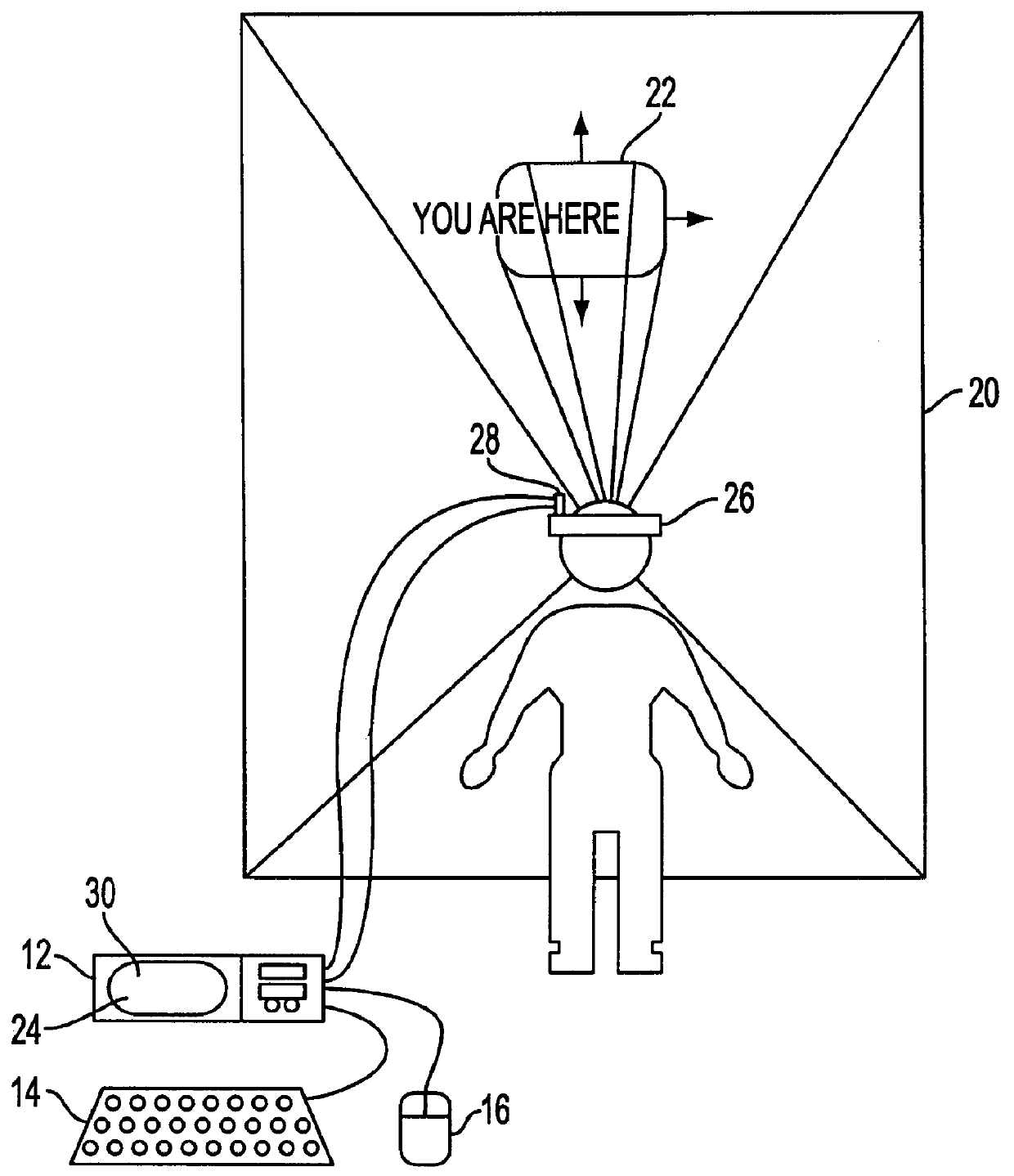
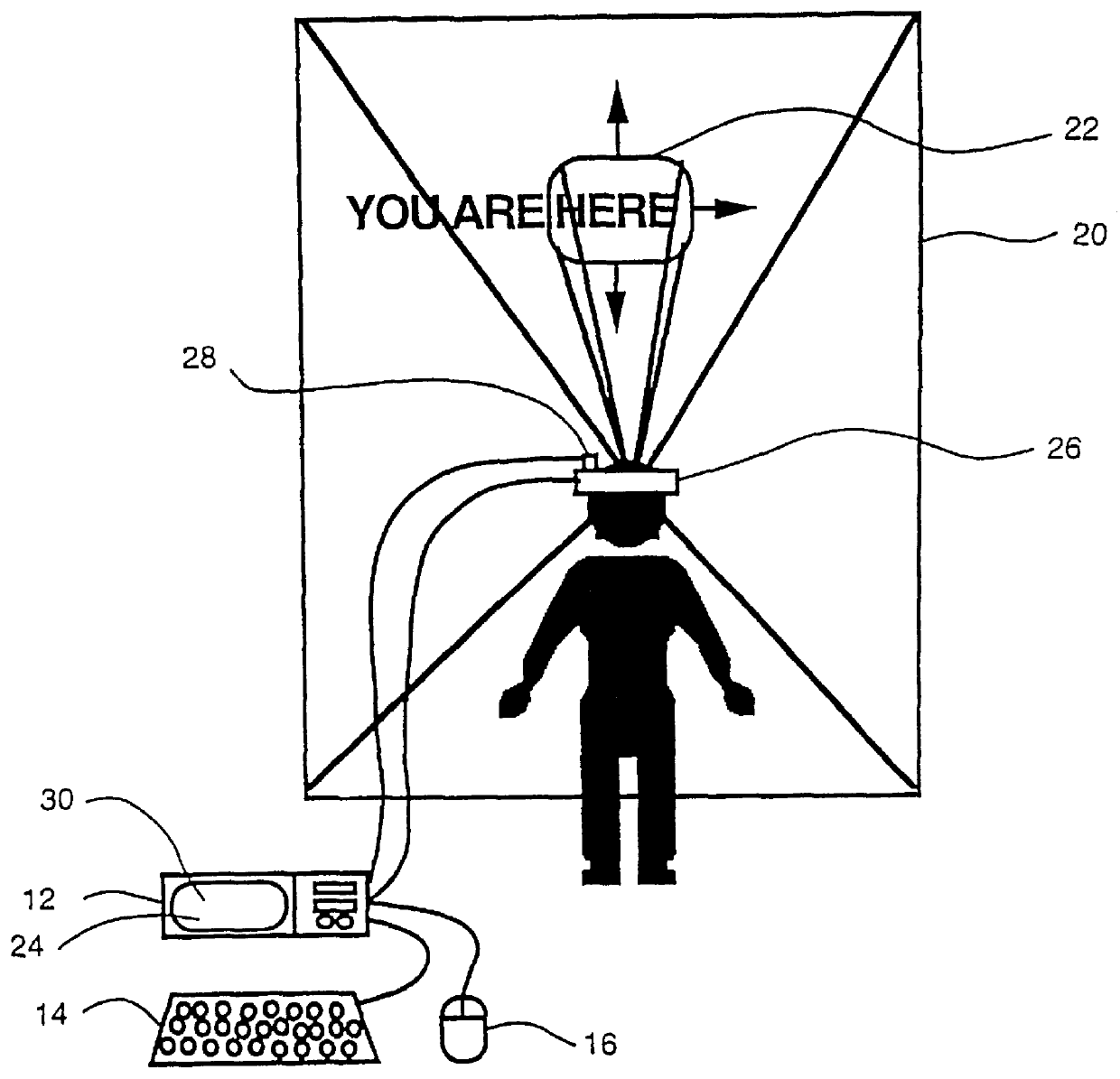
A virtual computer monitor is described which enables instantaneous and intuitive visual access to large amounts of visual data by providing the user with a large display projected virtually in front of the user. The user wears a head-mounted display or holds a portable display containing a head-tracker or other motion tracker, which together allow the user to position an instantaneous viewport provided by the display at any position within the large virtual display by turning to look in the desired direction. The instantaneous viewport further includes a mouse pointer, which may be positioned by turning the user's head or moving the portable display, and which may be further positioned using a mouse or analogous control device. A particular advantage of the virtual computer monitor is intuitive access to enlarged computer output for visually-impaired individuals.
Owner:META PLATFORMS INC +1
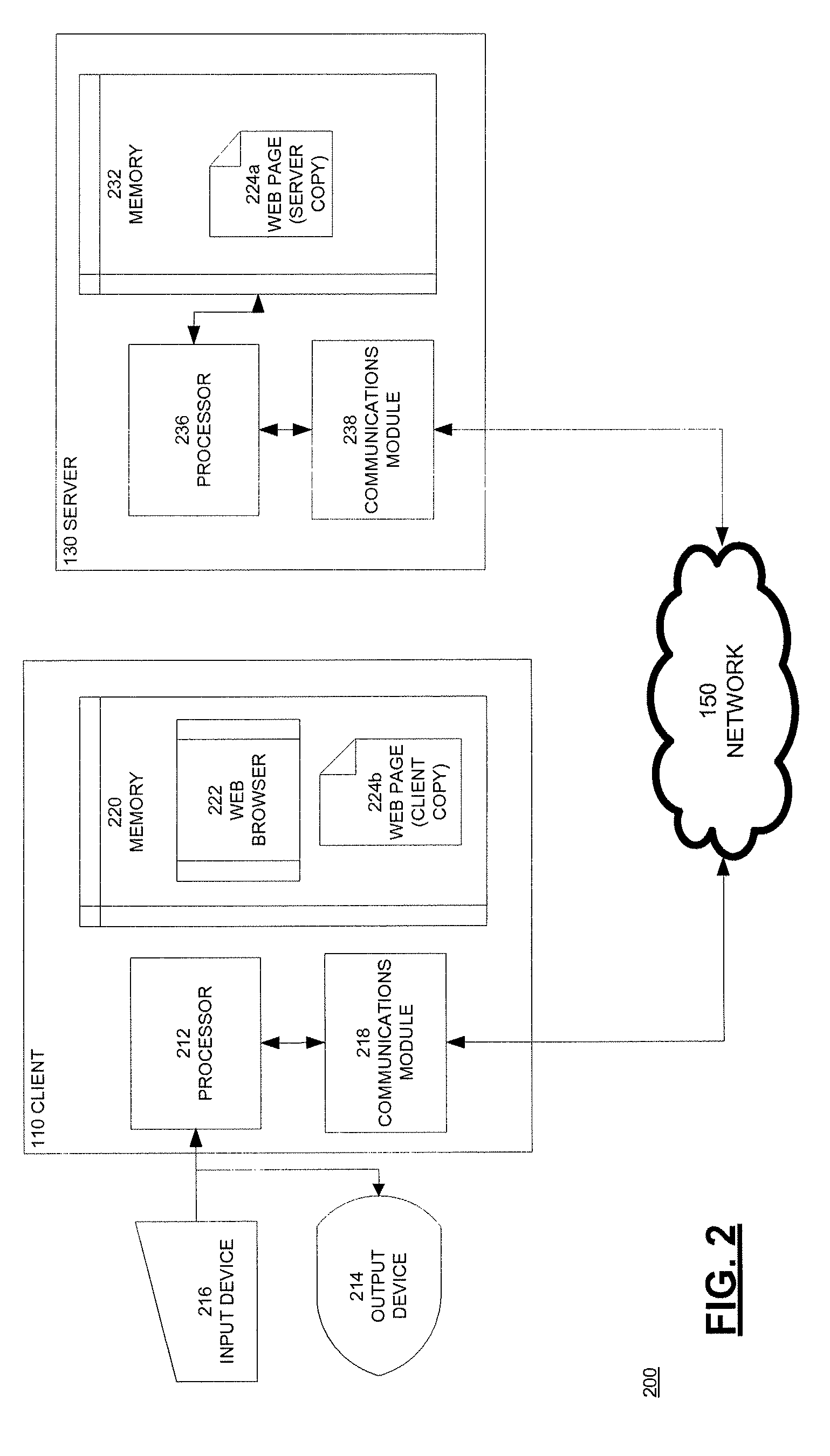
System and method for storing, viewing, editing, and processing ordered sections having different file formats
InactiveUS6026416AImprove practicalityReduce memory usageSpecial data processing applicationsDocument management systemsGraphicsApplication software
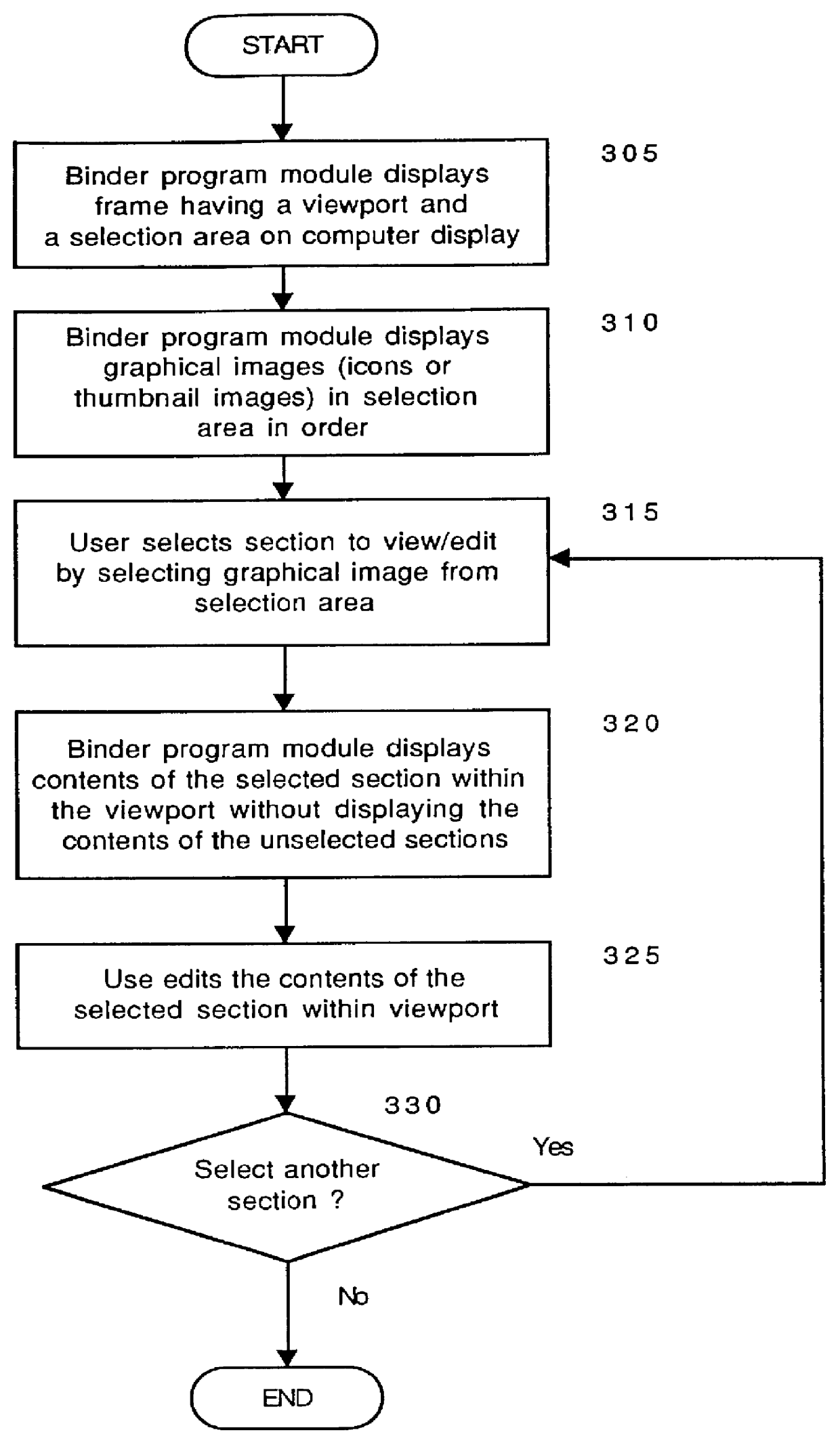
Ordered binder document sections having different file formats stored within a binder file. The binder file maintains the order of binder document sections and the native file format of each section. The ordered sections can be viewed and edited through a viewport of a frame displayed by a binder program module. By selecting graphical images displayed in a selection area of the frame the content of a binder document section can be viewed and edited without viewing the content of other binder document sections. The graphical images can be icons or graphical images derived from the content of sections called thumbnail images. A thumbnail image can be derived from either the first page or from multiple pages of an individual section. The binder program module can also dispatch the underlying application program modules that created each binder document section to print, spell check, and grammar check the binder document sections as a single data processing task. In this manner, selected sections of a binder document can be printed as a single consecutively printed document without having other print jobs interrupting or intervening between printed sections of the binder document.
Owner:MICROSOFT TECH LICENSING LLC
Wearable display and methods for controlling same
InactiveUS6127990AReduce jitterCosmonautic condition simulationsColor television detailsComputer monitorDisplay device
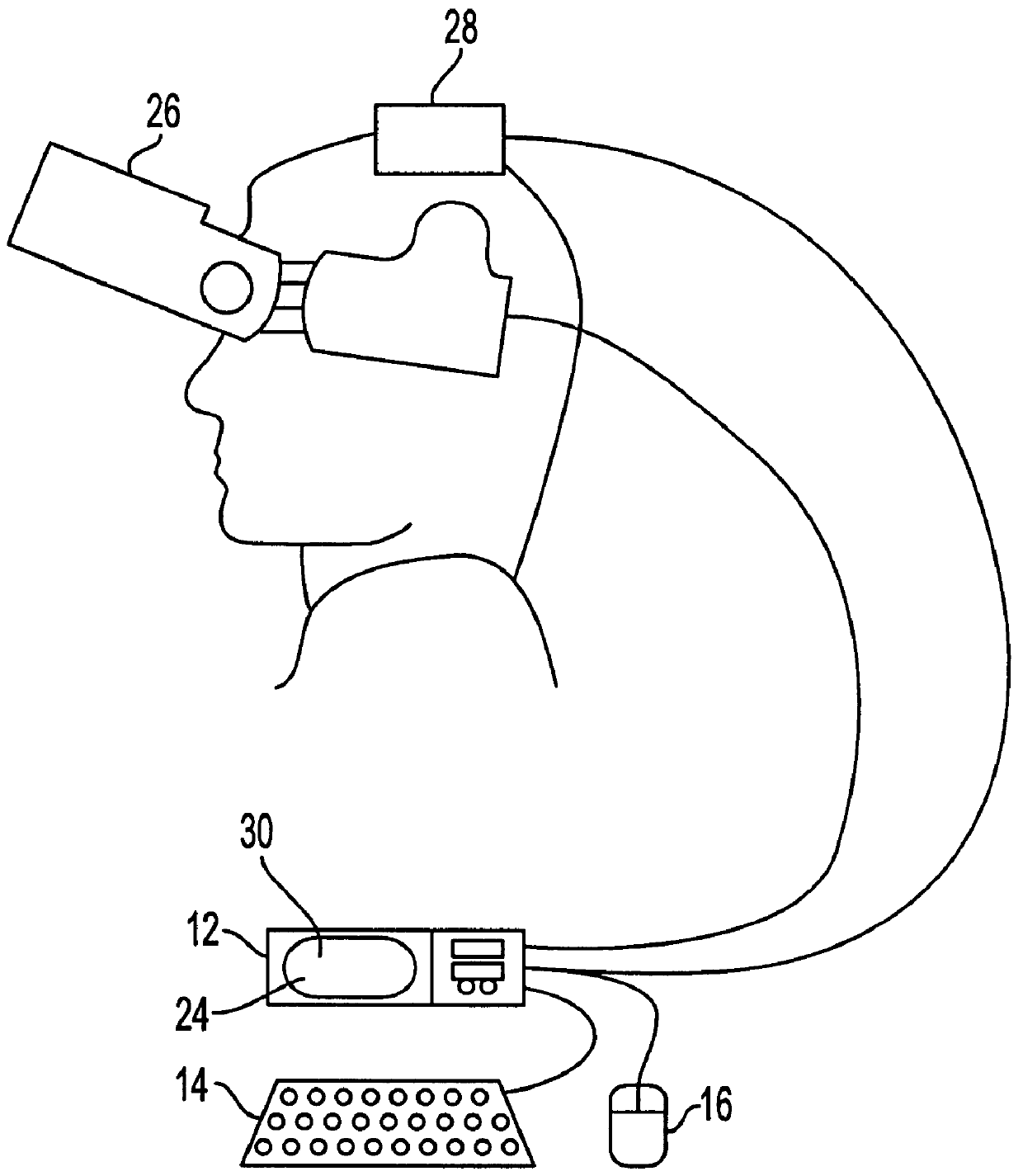
A virtual computer monitor is described which enables instantaneous and intuitive visual access to large amounts of visual data by providing the user with a large display projected virtually in front of the user. The user wears a head-mounted display containing a head-tracker, which together allow the user to position an instantaneous viewport provided by the head-mounted display at any position within the large virtual display by turning to look in the desired direction. The instantaneous viewport further includes a mouse pointer, which may be positioned by turning the user's head, and which may be further positioned using a mouse or analogous control device. A particular advantage of the virtual computer monitor is intuitive access to enlarged computer output for visually-impaired individuals.
Owner:REMBRANDT PORTABLE DISPLAY TECH LP
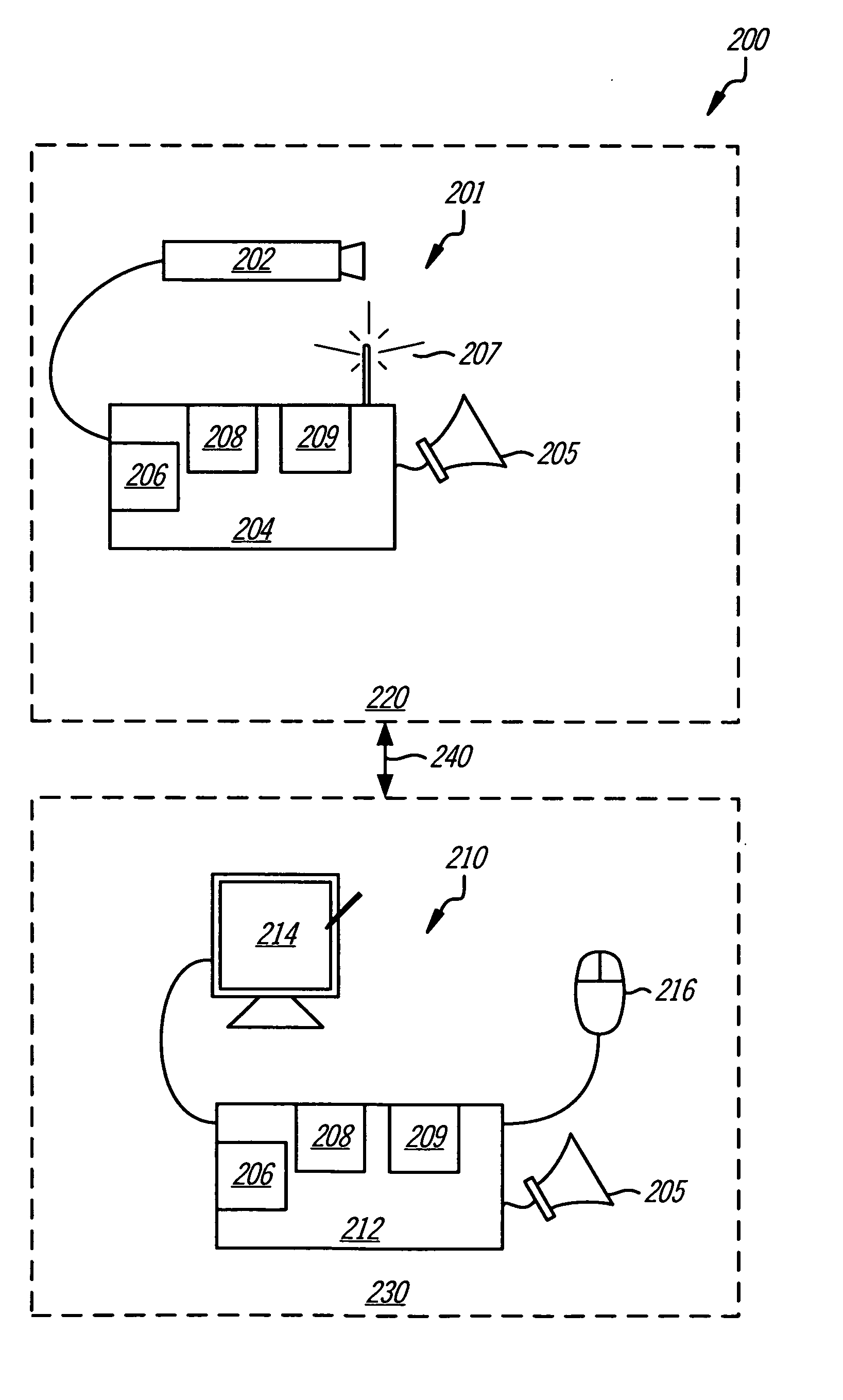
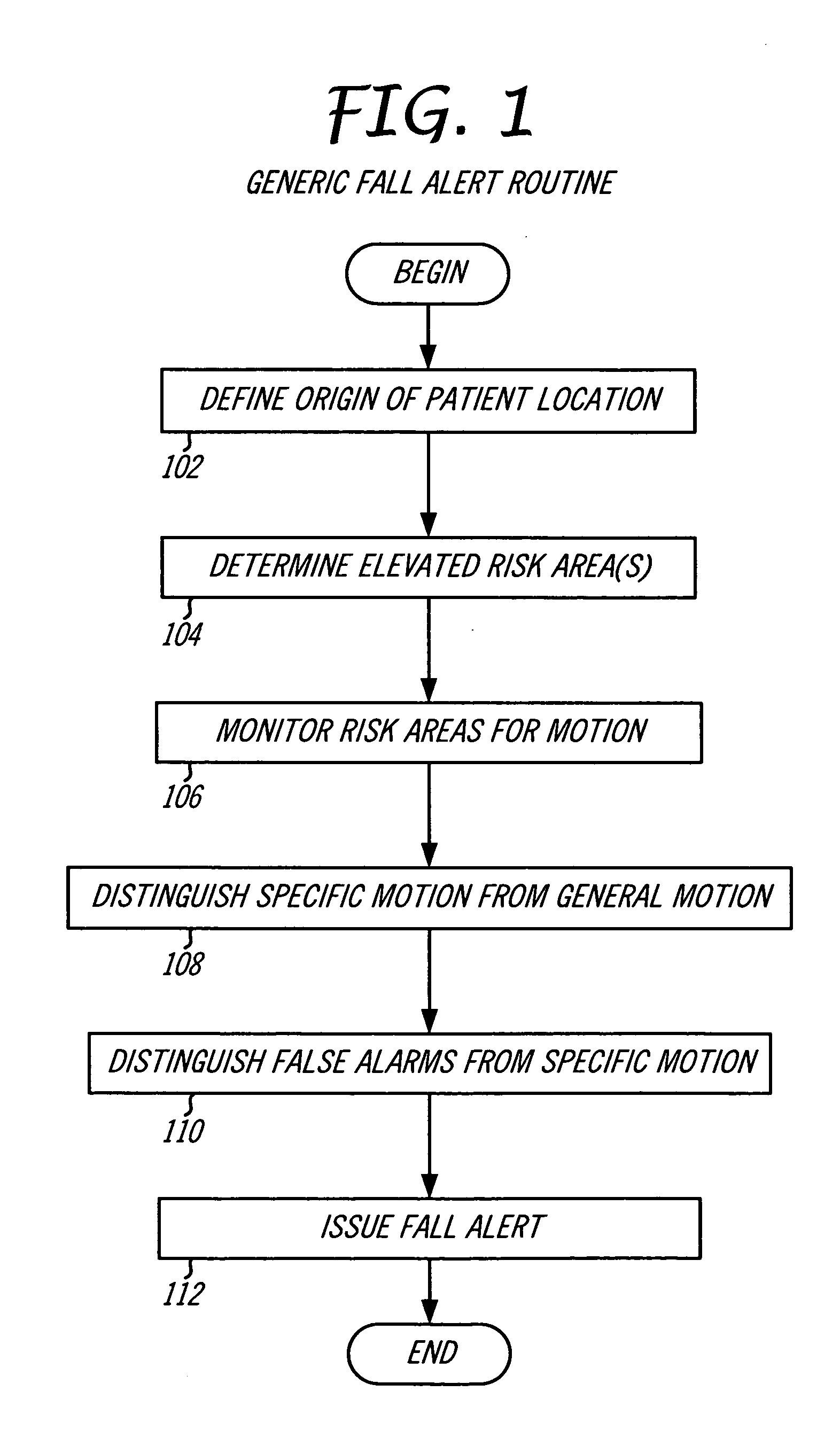
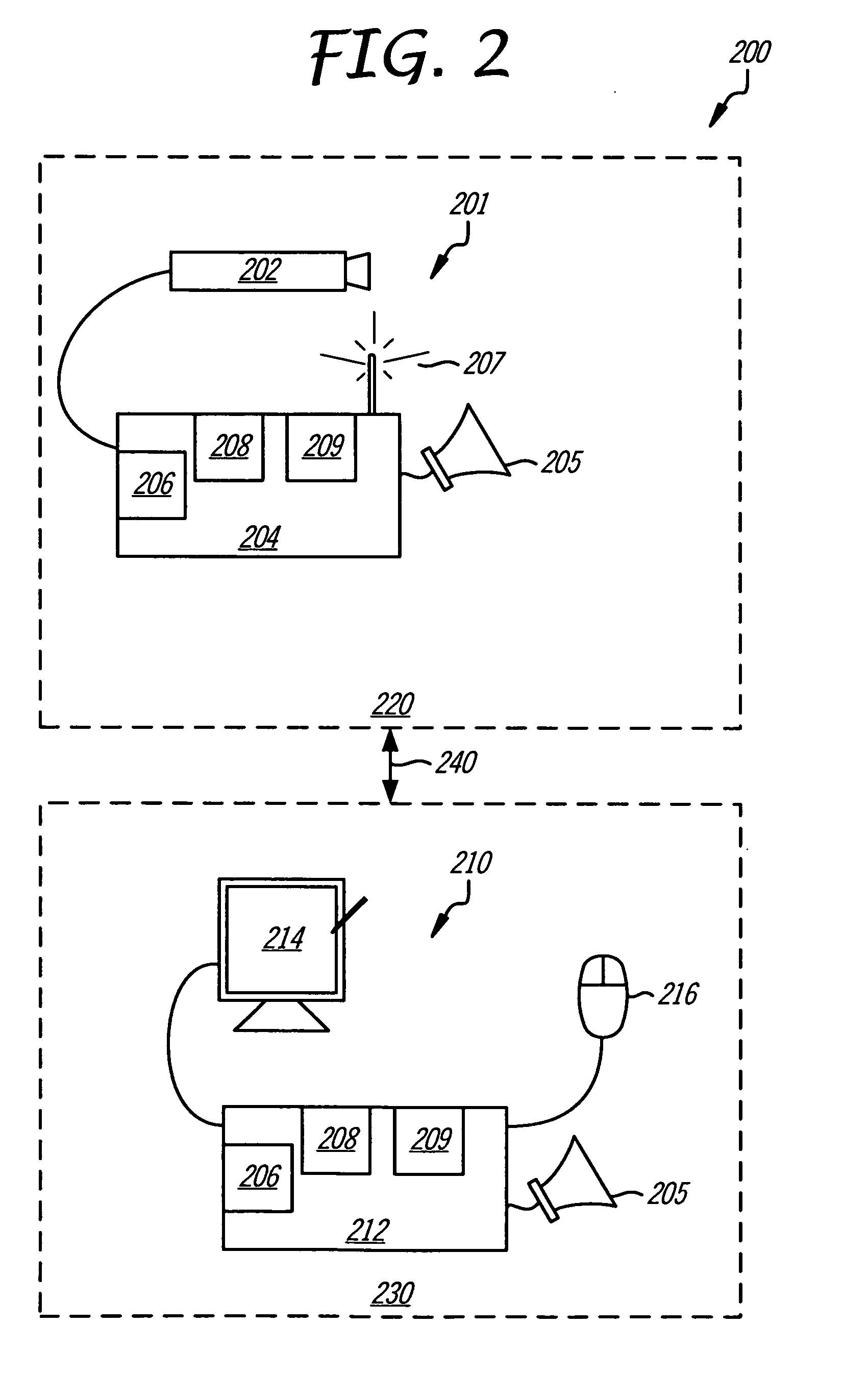
System and method for predicting patient falls
ActiveUS20090278934A1Character and pattern recognitionClosed circuit television systemsGraphicsViewpoints
A patient fall prediction system receives video image frames from a surveillance camera positioned in a patient's room and analyses the video image frames for movement that may be a precursor to a patient fall. In set up phase, the viewpoint of the camera is directed at a risk area associated with patient falls, beds, chairs, wheelchairs, etc. A risk area is defined graphically in the viewport. The patient fall prediction system generates a plurality of concurrent motion detection zones that are situated proximate to the graphic markings of the risk areas. These motion detection zones are monitored for changes between video image frames that indicate a movement. The pattern of detections is recorded and compared to a fall movement detection signature. One fall movement detection signature is a sequential detection order from the motion detection zone closest to the risk area in the frames associated with patient falls, to the motion detection zone farthest away from the risk area. The patient fall prediction system continually monitors the motion detection zones for changes between image frames and compiles detections lists that are compared to known movement detection signatures, such as a fall movement detection signature. Once a match is identified, the patient fall prediction system issues a fall warning to a healthcare provider.
Owner:CAREVIEW COMM INC
Virtual computer monitor
InactiveUS6084556AReduce jitterCosmonautic condition simulationsCathode-ray tube indicatorsComputer monitorDisplay device
A virtual computer monitor is described which enables instantaneous and intuitive visual access to large amounts of visual data by providing the user with a large display projected virtually in front of the user. The user wears a head-mounted display containing a head-tracker, which together allow the user to position an instantaneous viewport provided by the head-mounted display at any position within the large virtual display by turning to look in the desired direction. The instantaneous viewport further includes a mouse pointer, which may be positioned by turning the user's head, and which may be further positioned using a mouse or analogous control device. A particular advantage of the virtual computer monitor is intuitive access to enlarged computer output for visually-impaired individuals.
Owner:META PLATFORMS INC
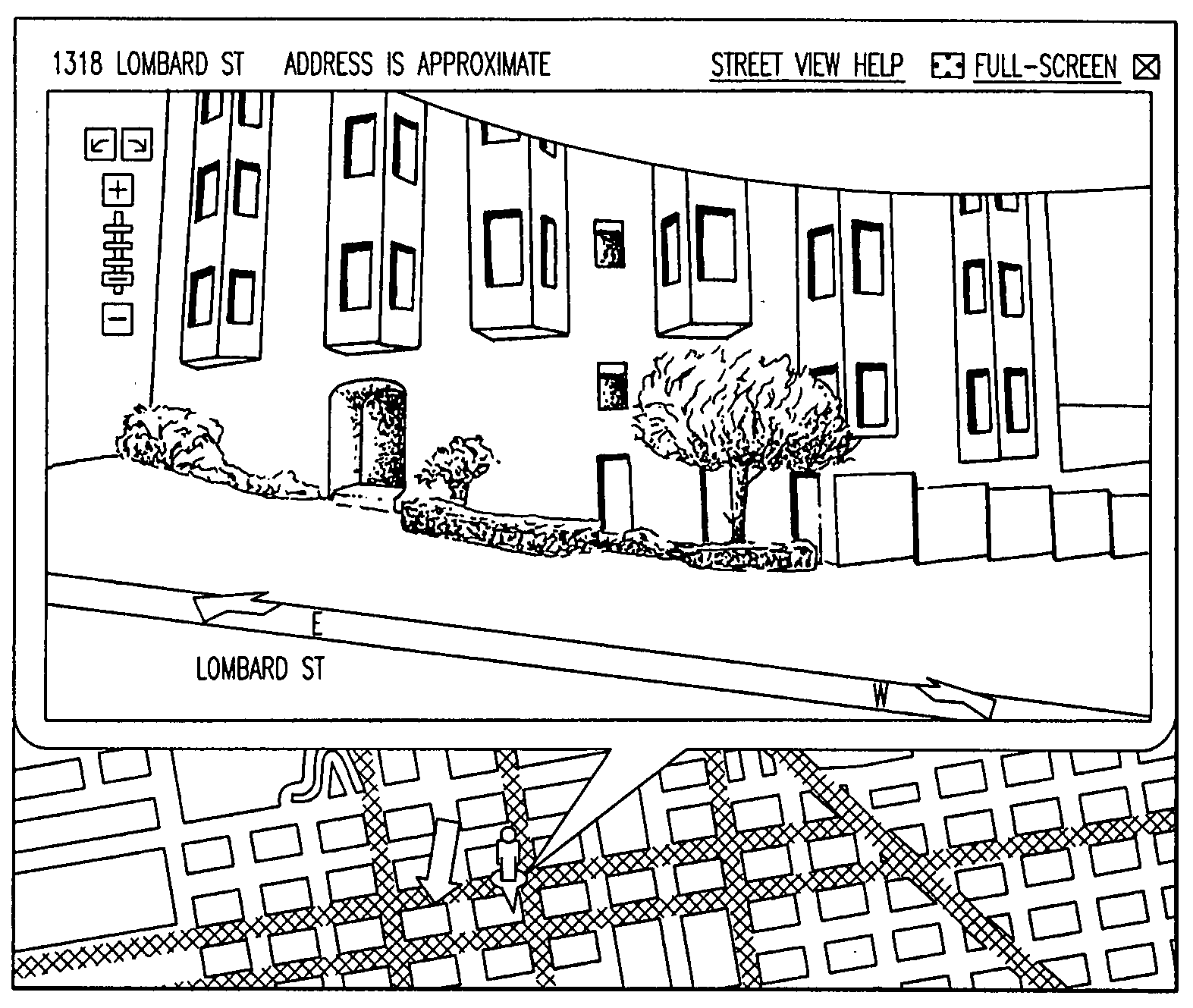
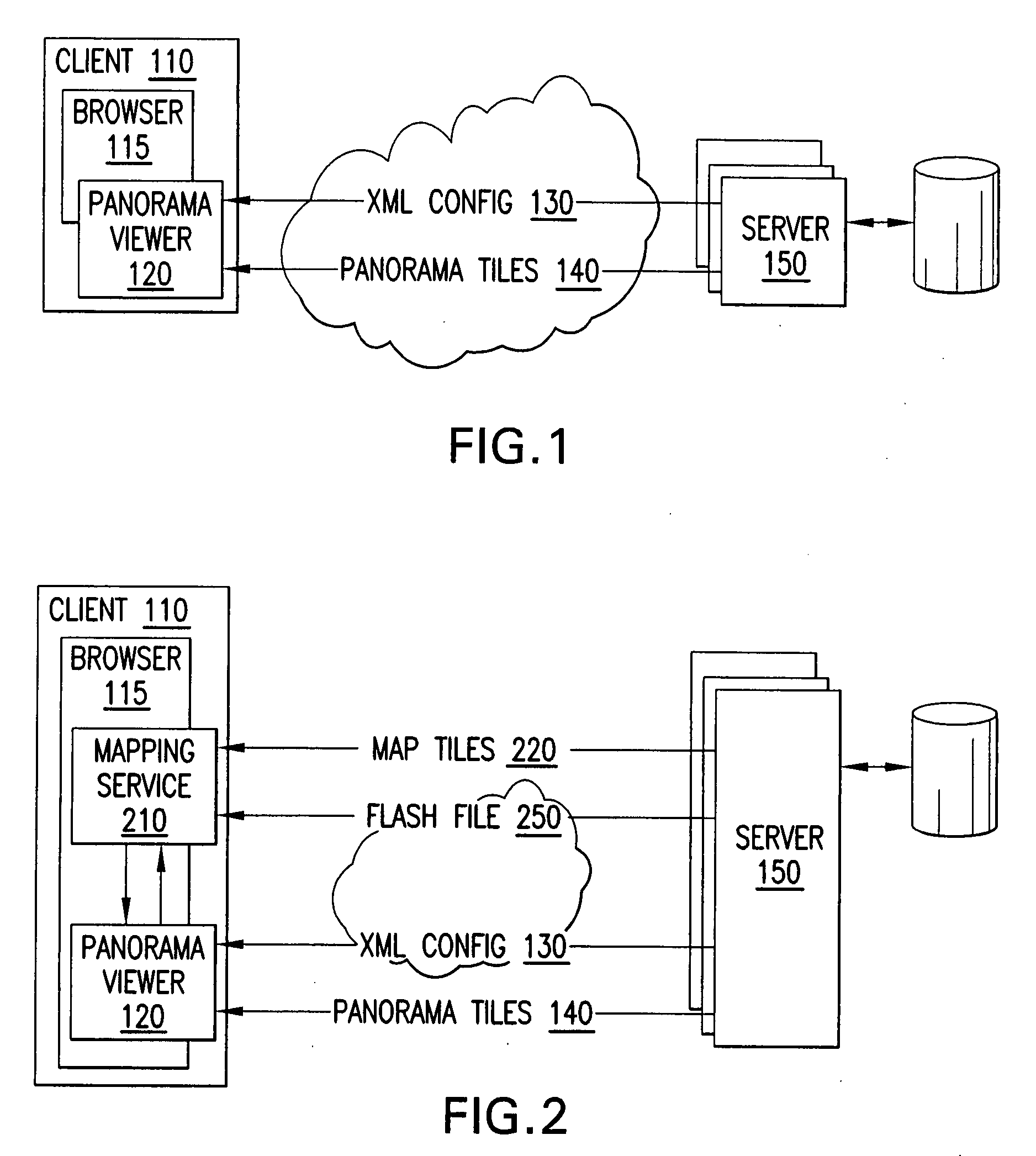
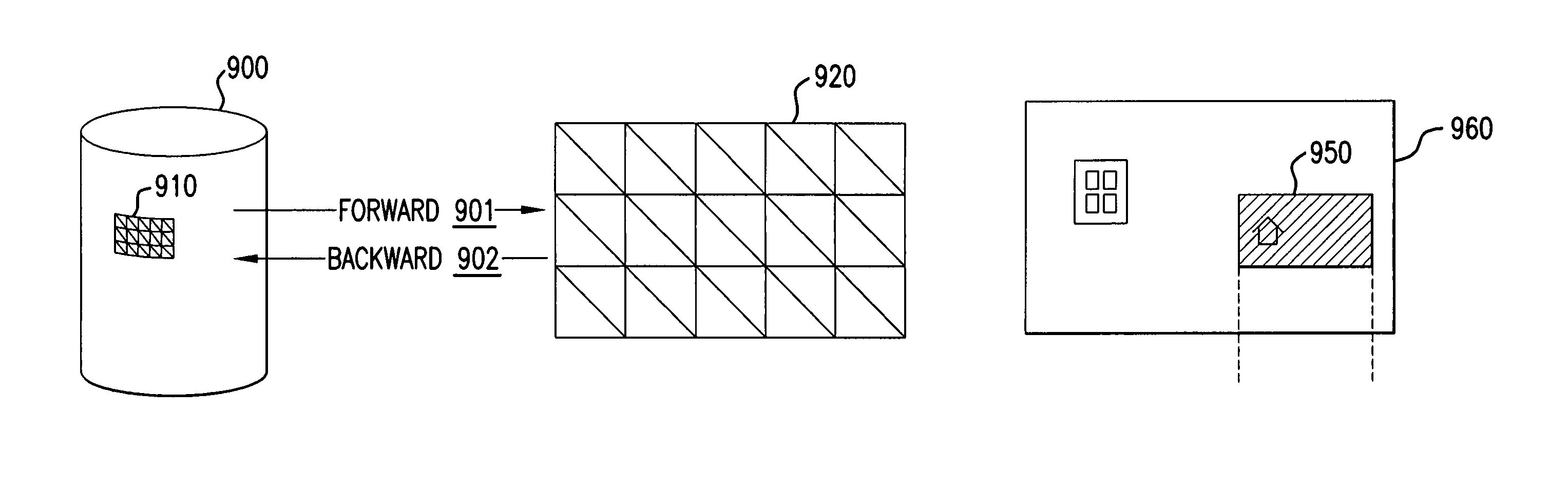
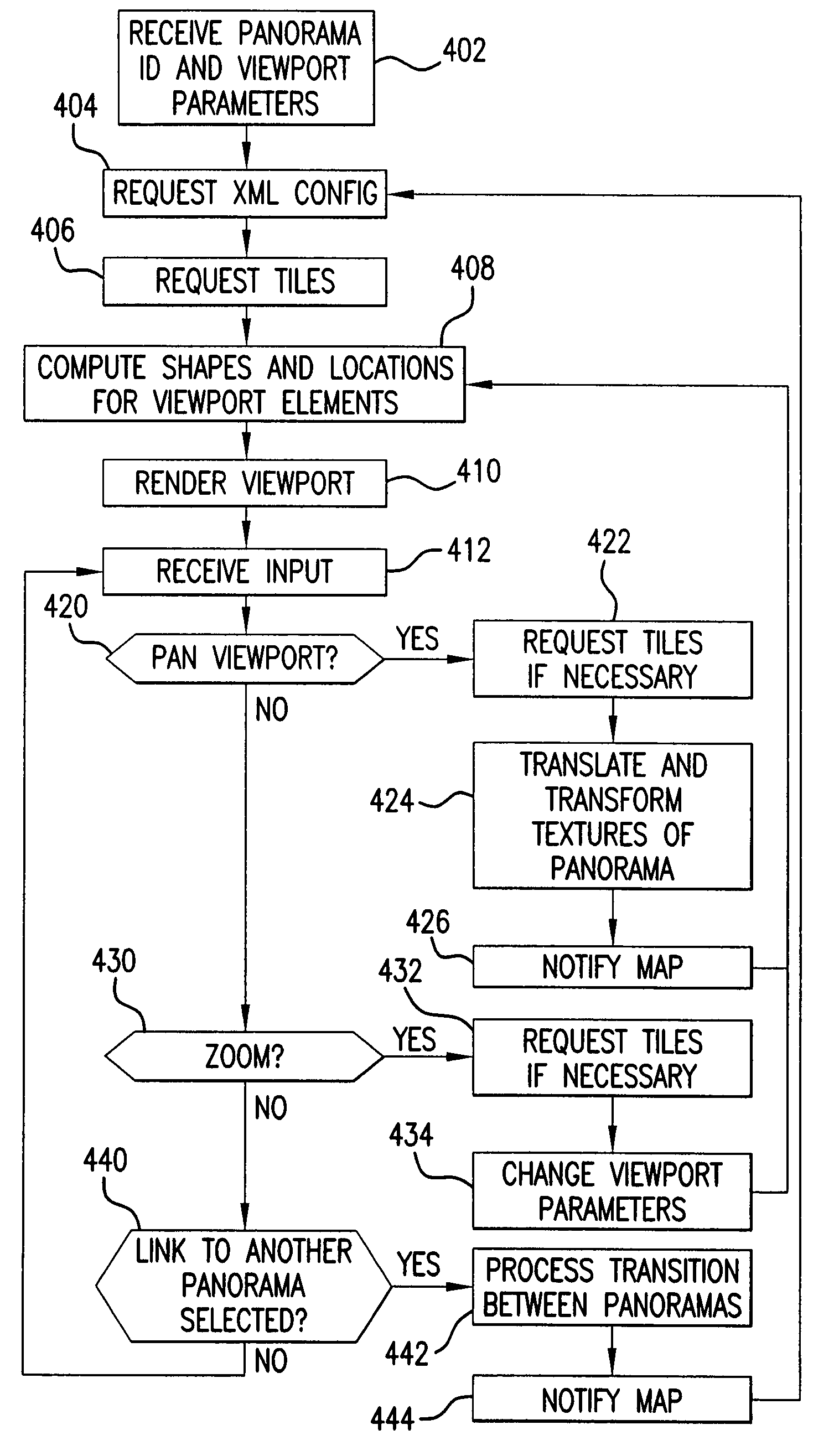
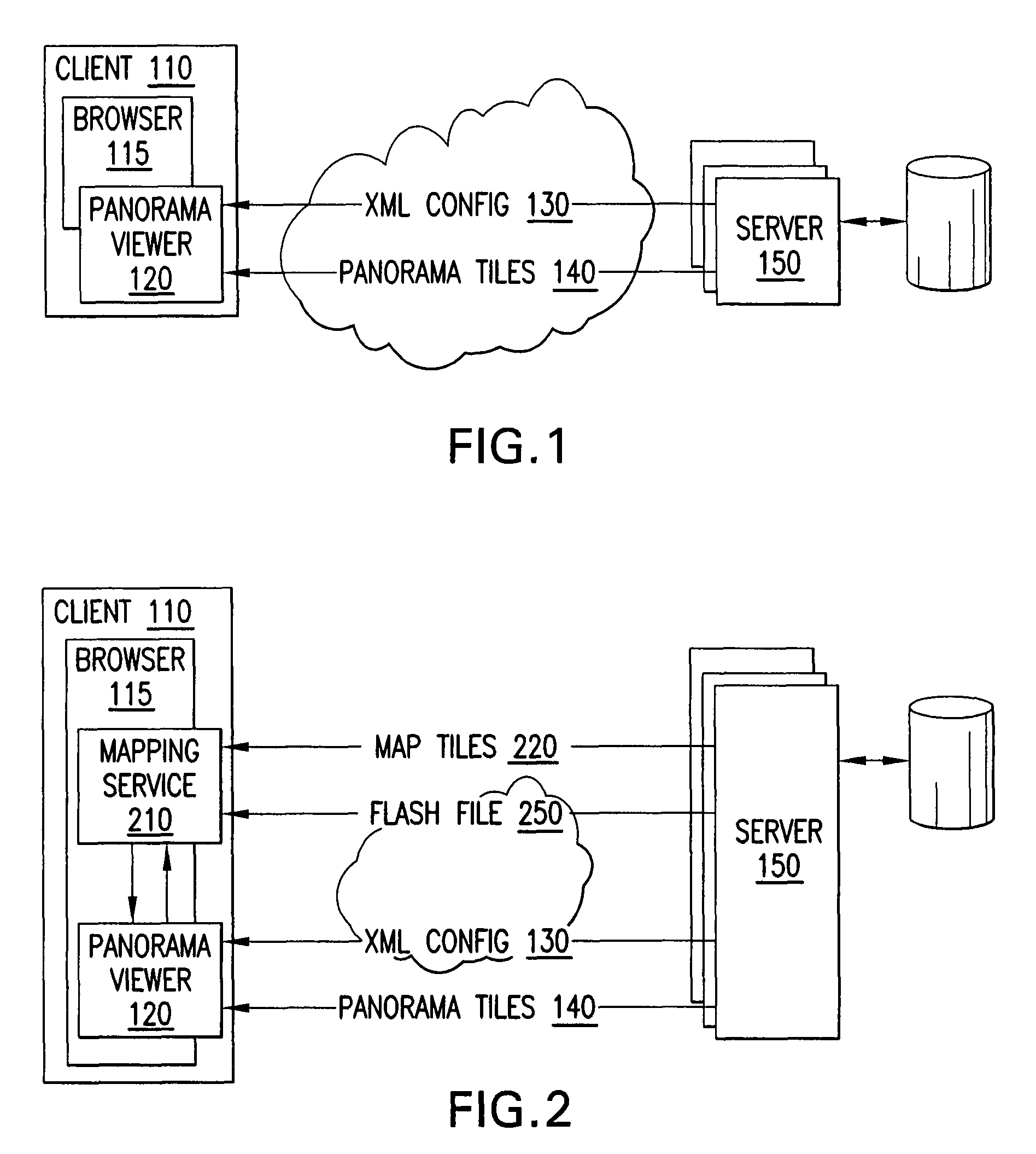
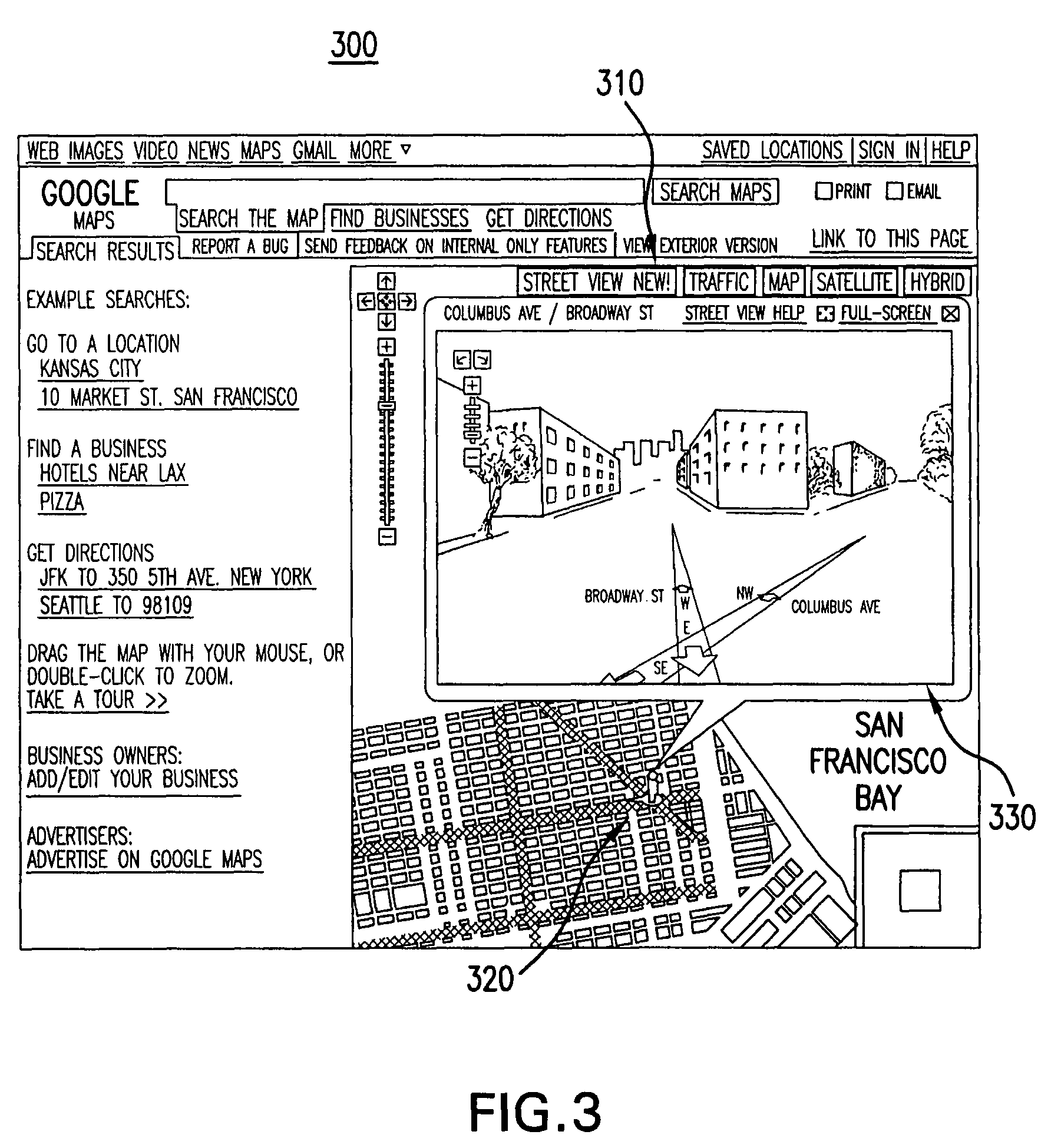
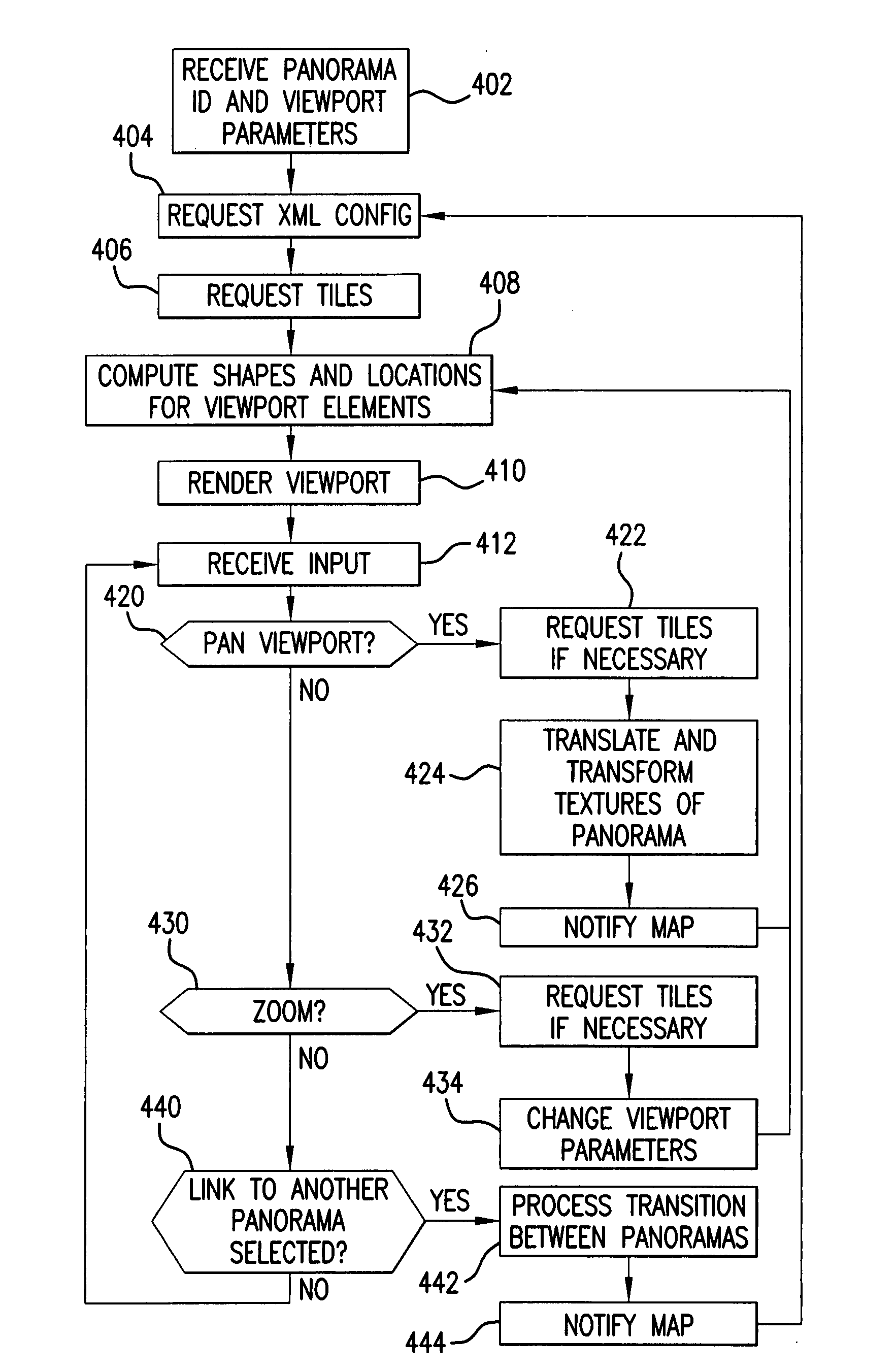
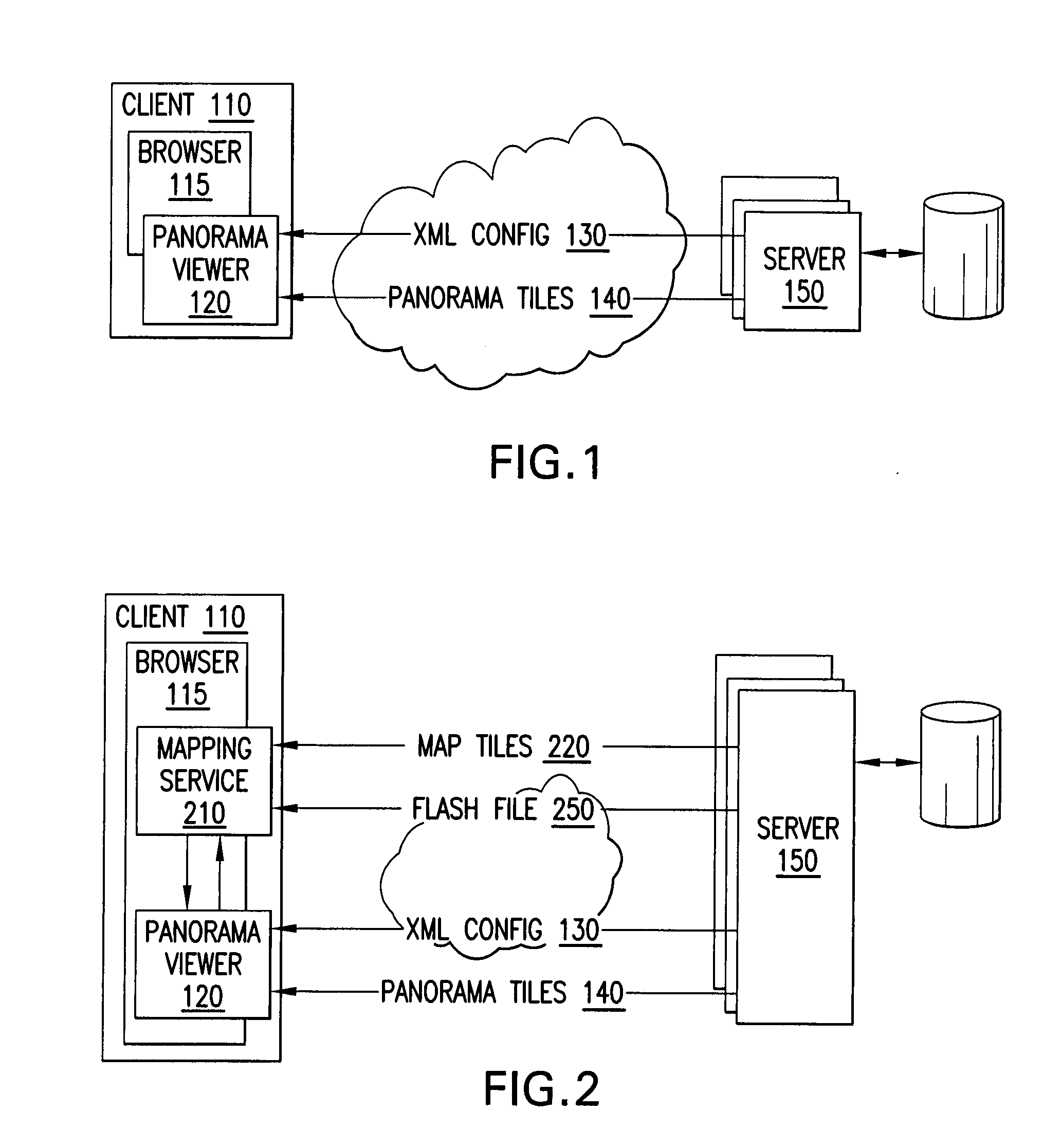
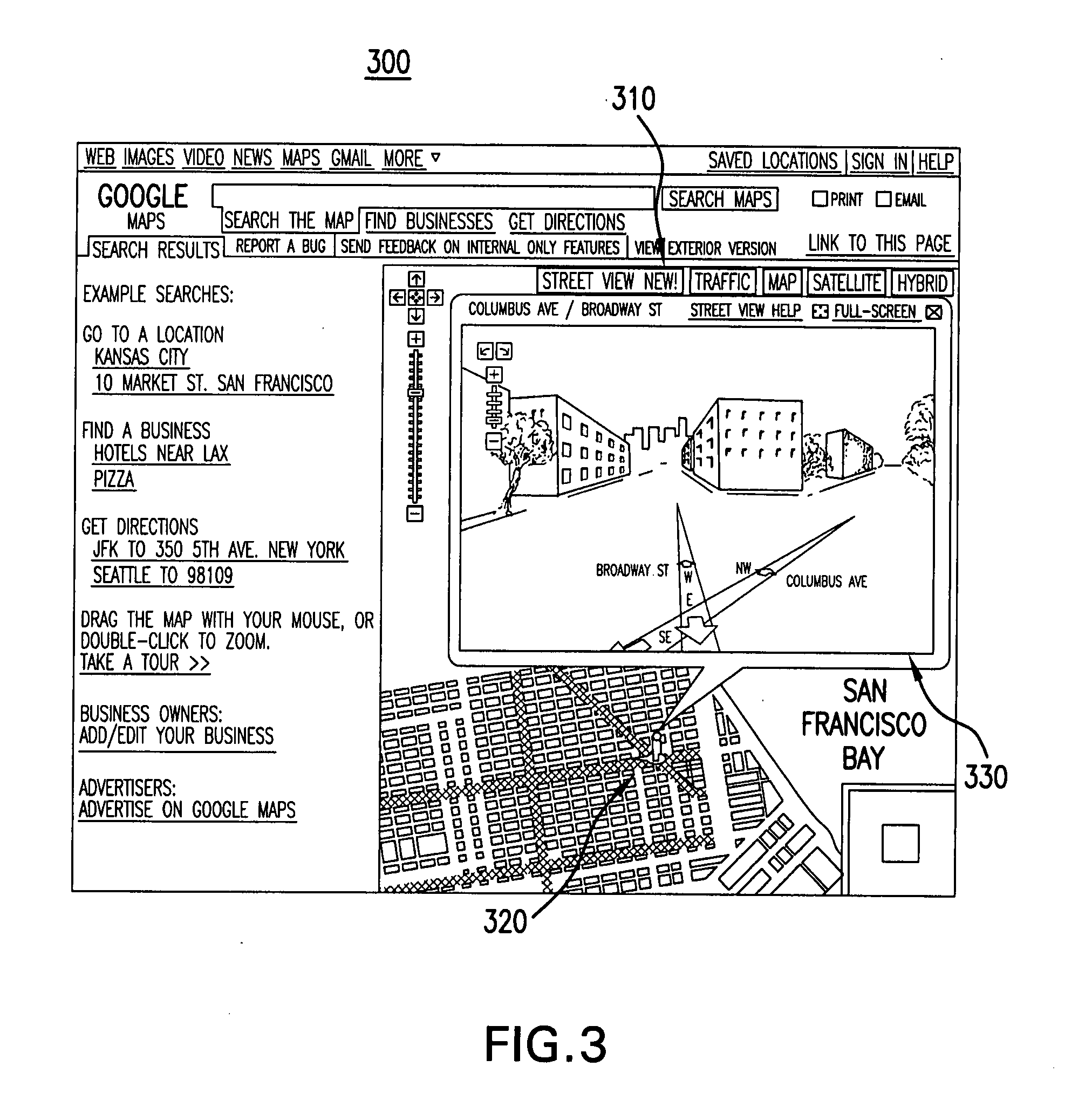
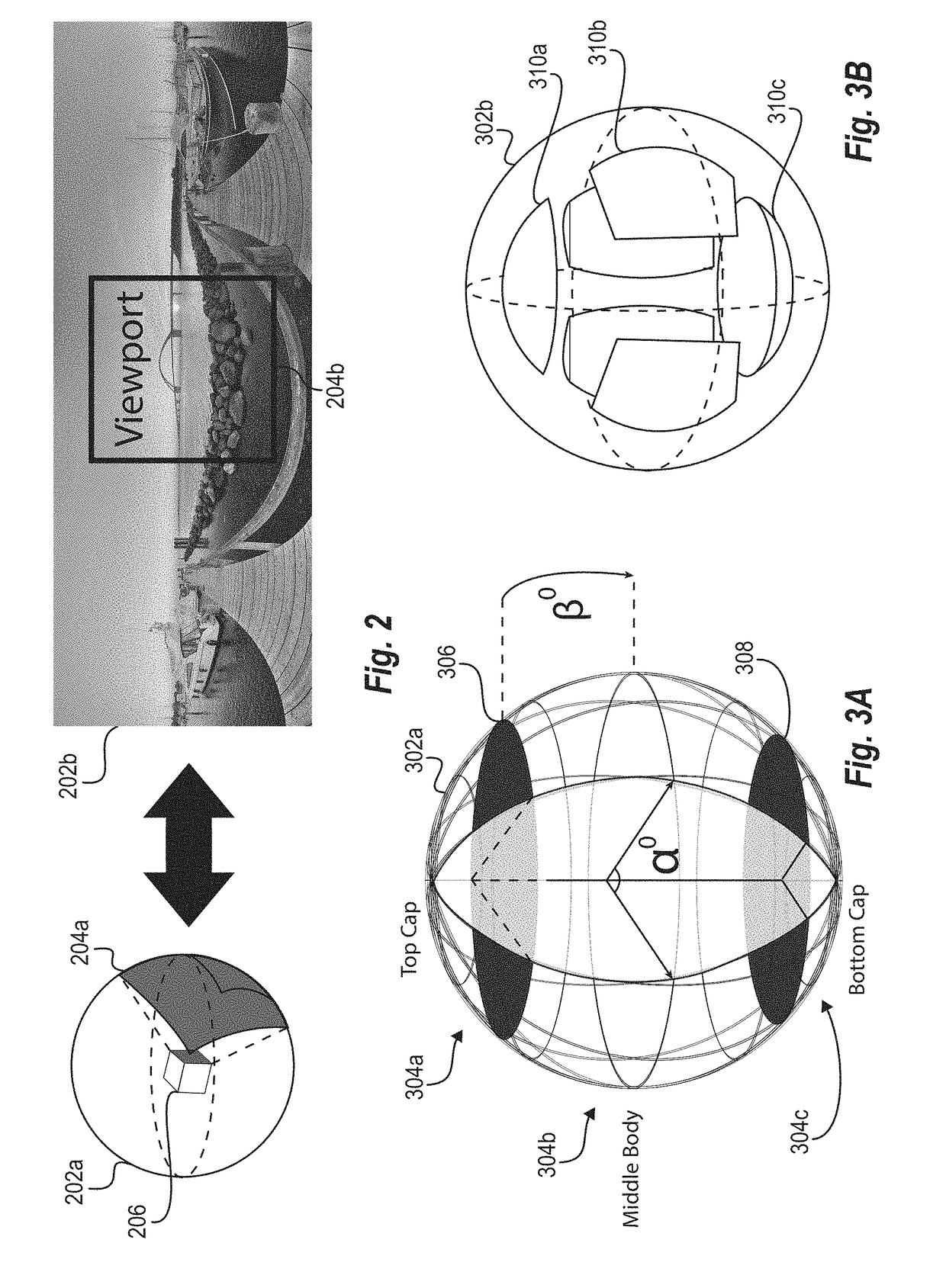
Viewing and navigating within panoramic images, and applications thereof
ActiveUS20080291217A1Easy to navigateCathode-ray tube indicatorsSpecial data processing applicationsThree-dimensional spacePanorama
A panorama viewer is disclosed which facilitates navigation from within the panorama of a larger, structured system such as a map. The panorama viewer presents a viewport on a portion of a panoramic image, the viewport including a three-dimensional overlay rendered with the panoramic image. As the orientation of the viewport within the panoramic image changes, the three-dimensional overlay's orientation in three-dimensional space also changes as it is rendered with the panoramic image in a manner that matches the change in orientation of the viewport.
Owner:GOOGLE LLC
Efficient rendering of panoramic images, and applications thereof
ActiveUS7843451B2Easy to handleQuickly renderedCharacter and pattern recognitionCathode-ray tube indicatorsPrecomputationViewport
A fast renderer for panoramic images is herein disclosed. In an embodiment, a precomputation is made of (a) a region on a surface defined by a first transformation from a viewport to the surface and (b) a second transformation that maps from the precomputed region to the viewport. In order to render the surface on the viewport, the renderer determines what portion of the image intersects with the precomputed region and proceeds to apply the precomputed second transformation to the portion of the image, thereby resulting in a transformed image which can be rendered in the viewport for display.
Owner:GOOGLE LLC
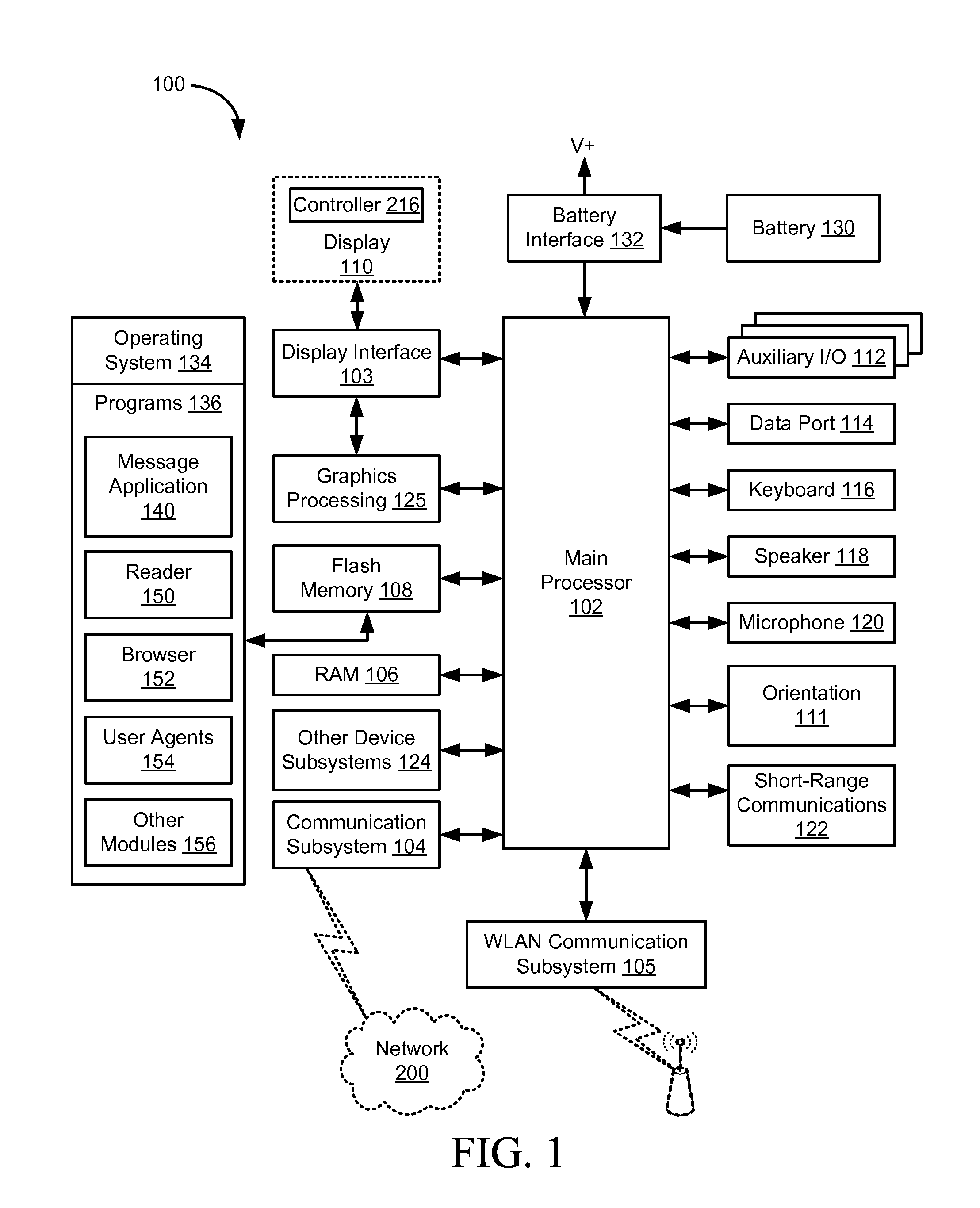
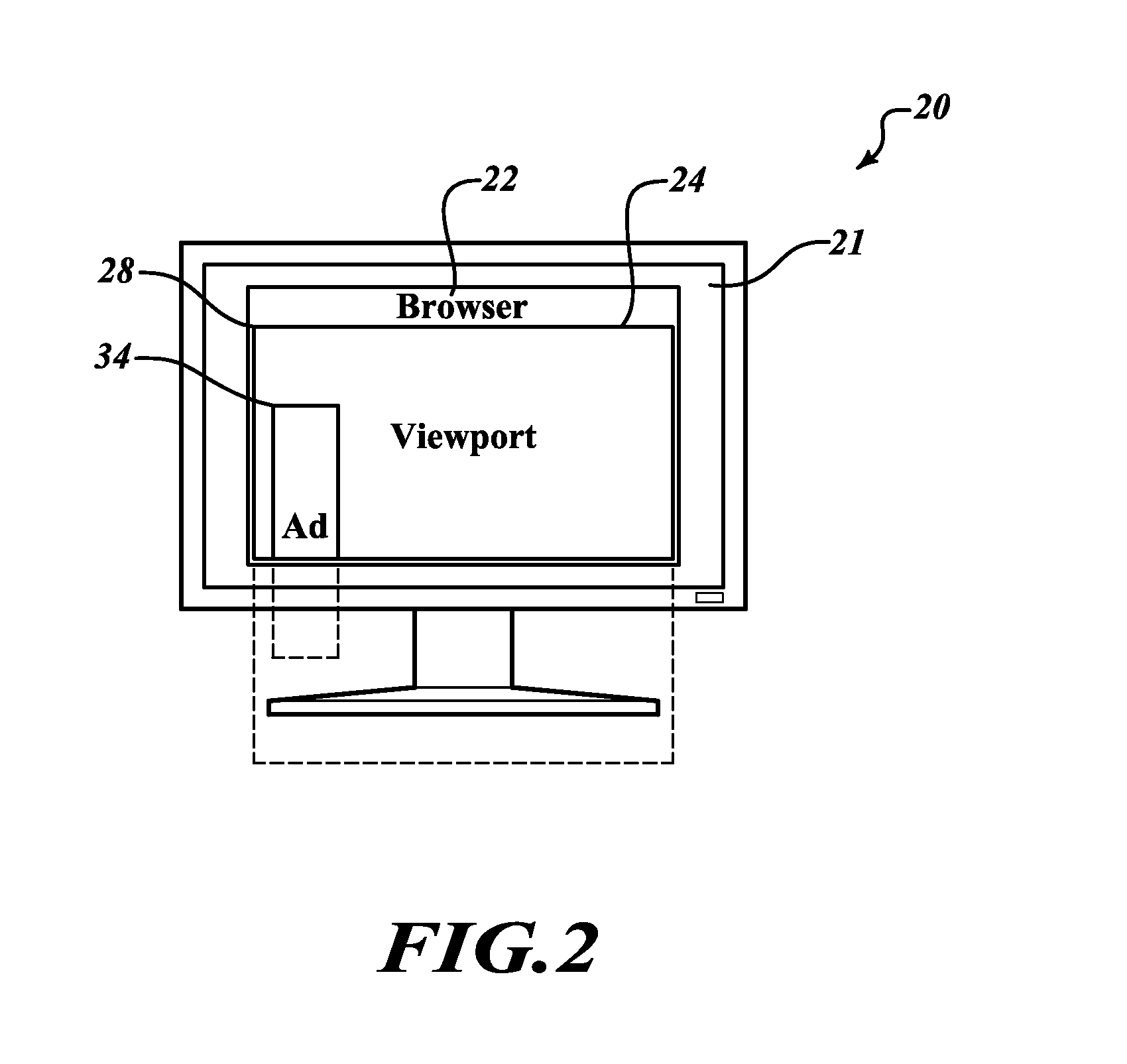
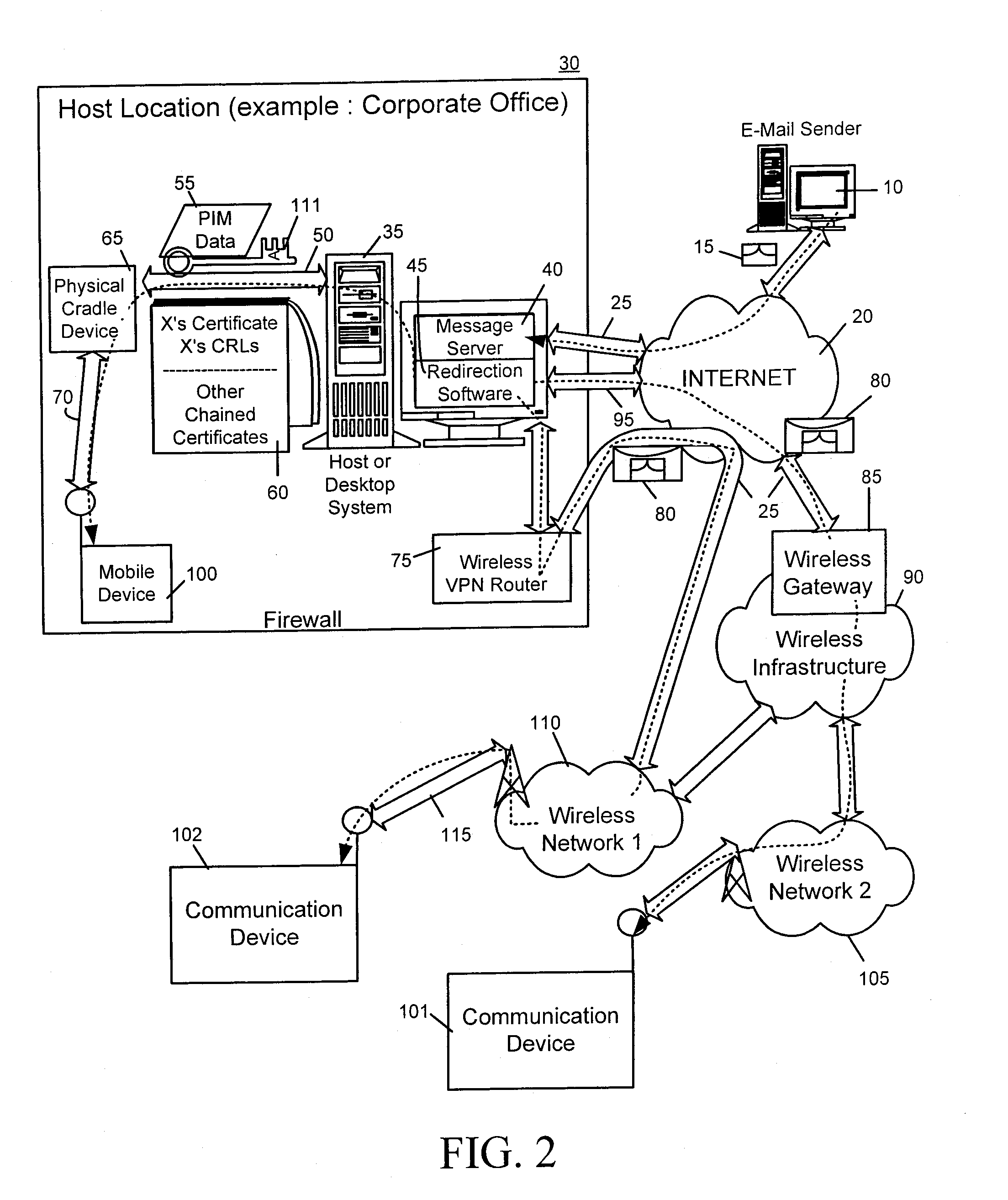
Accelerated compositing of fixed position elements on an electronic device
A device, system and method are provided for processing structured documents for display. Content of a first viewable portion of the structured document having a fixed position in relation to a viewport is rendered as first rendered image data. Content of a second viewable portion that does not have a fixed position is rendered as second rendered image data. The first and second rendered image data are composited, and a resultant composited image is output for display. In response to a scroll or zoom command applied to the document, and in particular to the second viewable portion, the second rendered image data is updated and composited with the first rendered image data. Compositing can be carried out by a graphics processor separate from a main processor in the electronic device. When no fixed position elements are present in the structured document, the main processor renders the entire content without compositing.
Owner:BLACKBERRY LTD
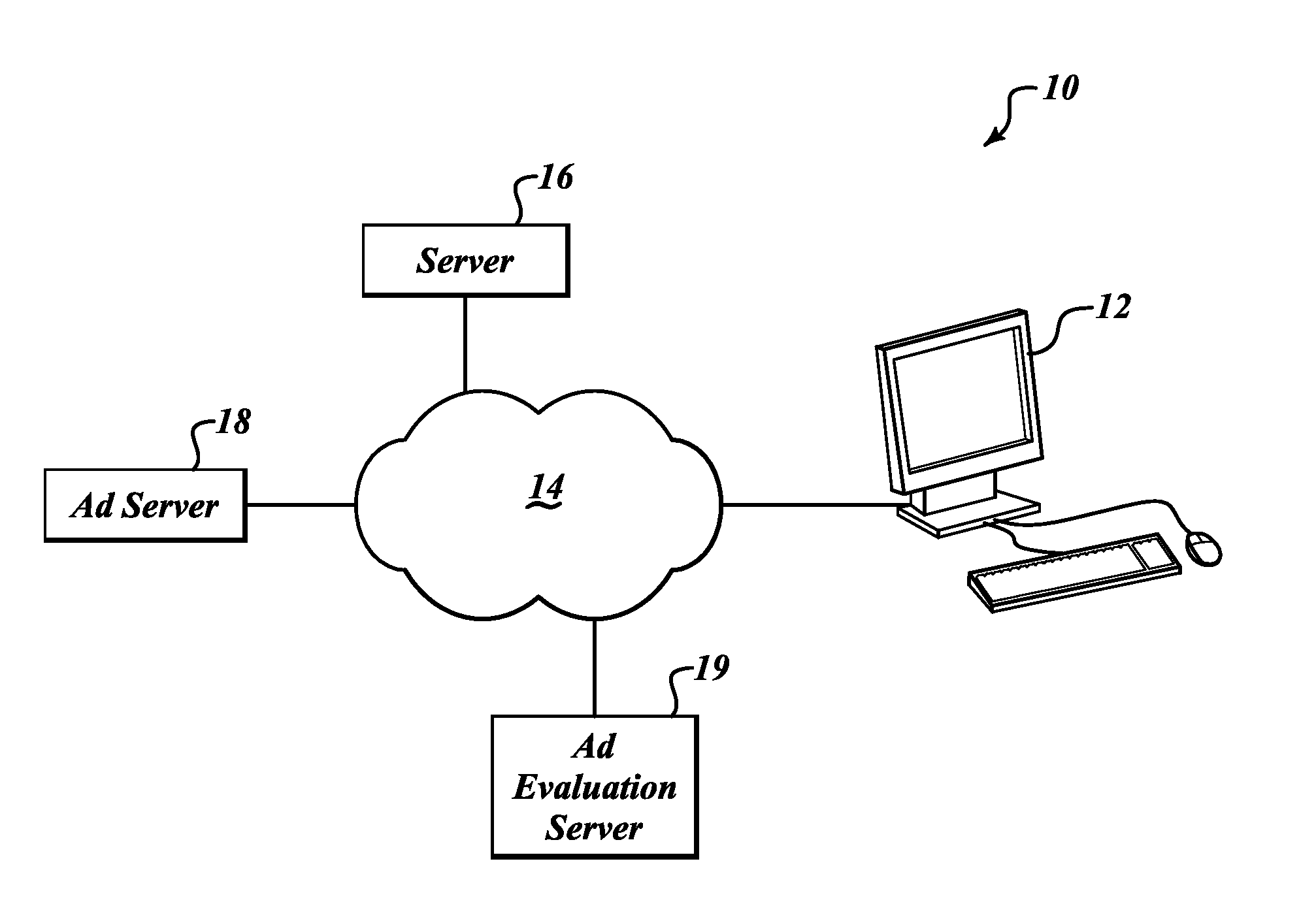
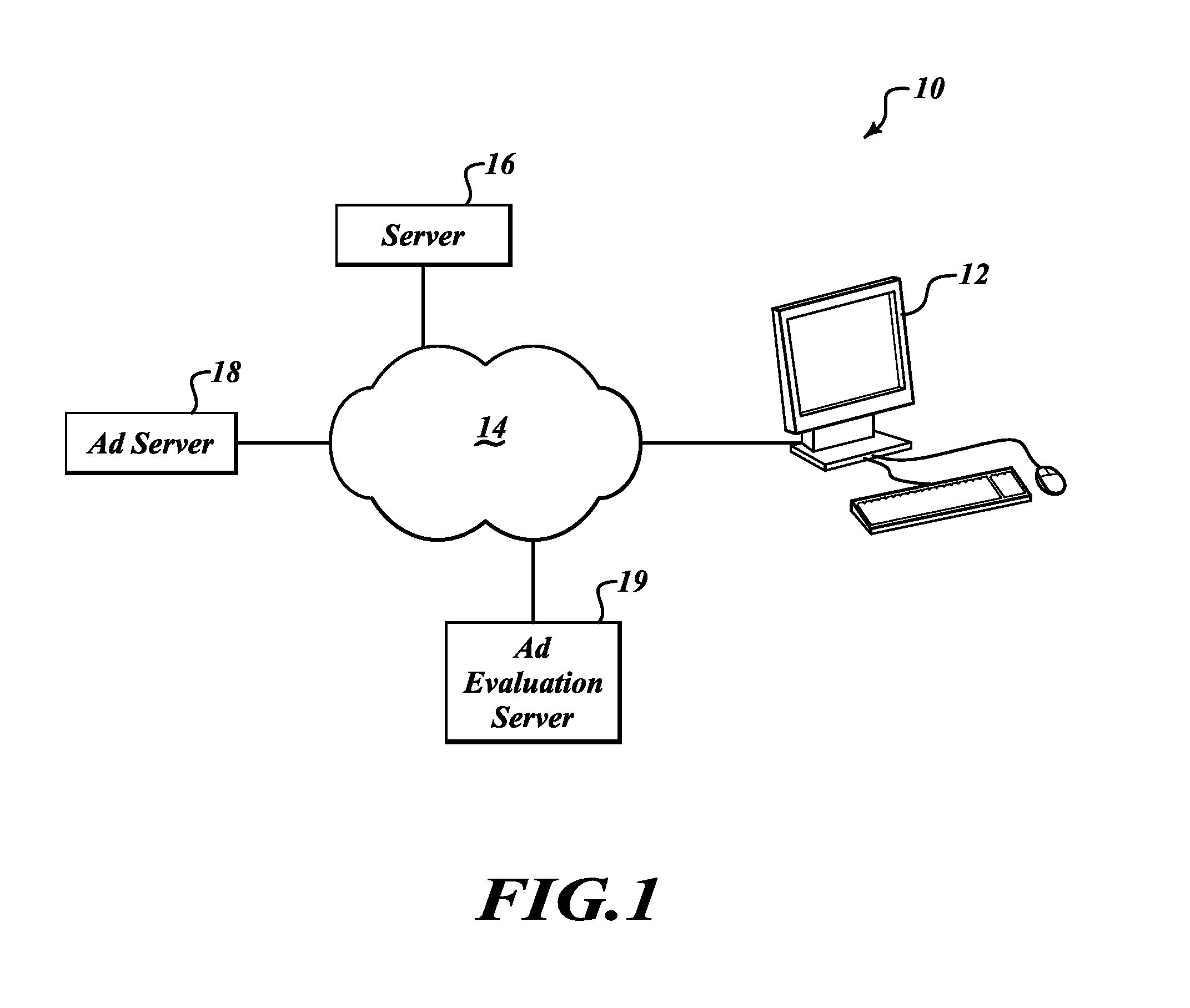
Methods for capturing and reporting metrics regarding ad placement
Systems and methods for recording impression events of Ad content on a webpage. An example method renders on a display of a computer device a webpage accessible over a network. The webpage includes at least one Ad unit. Then Ad tag information associated with the at least one Ad unit and browser viewport information (display location and size information) is retrieved. The occurrence of an Ad Placement event is determined if based on the comparison a predefined percentage of the Ad unit is within the browser viewport. An Ad Placement event timer is begun upon the determination of occurrence of the Ad Placement event. The Ad Placement event timer is stopped if an out-of-view event has occurred based on the Ad tag information and the browser viewport information. An Ad Placement event is then recorded. The recorded Ad Placement event is transmitted to a previously designated server over the network.
Owner:COMSCORE
Viewing and navigating within panoramic images, and applications thereof
ActiveUS7990394B2Cathode-ray tube indicatorsSpecial data processing applicationsThree-dimensional spacePanorama
Owner:GOOGLE LLC
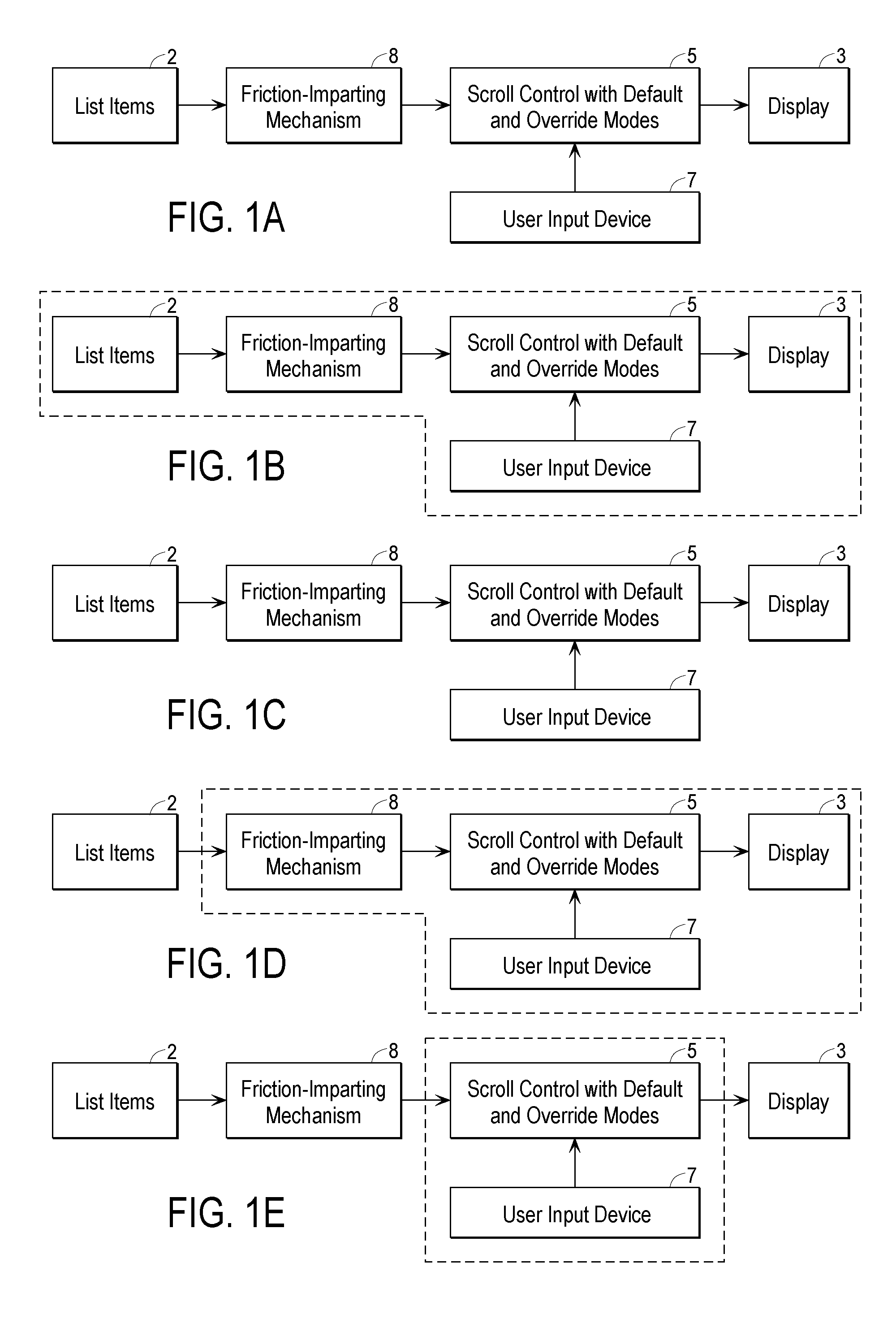
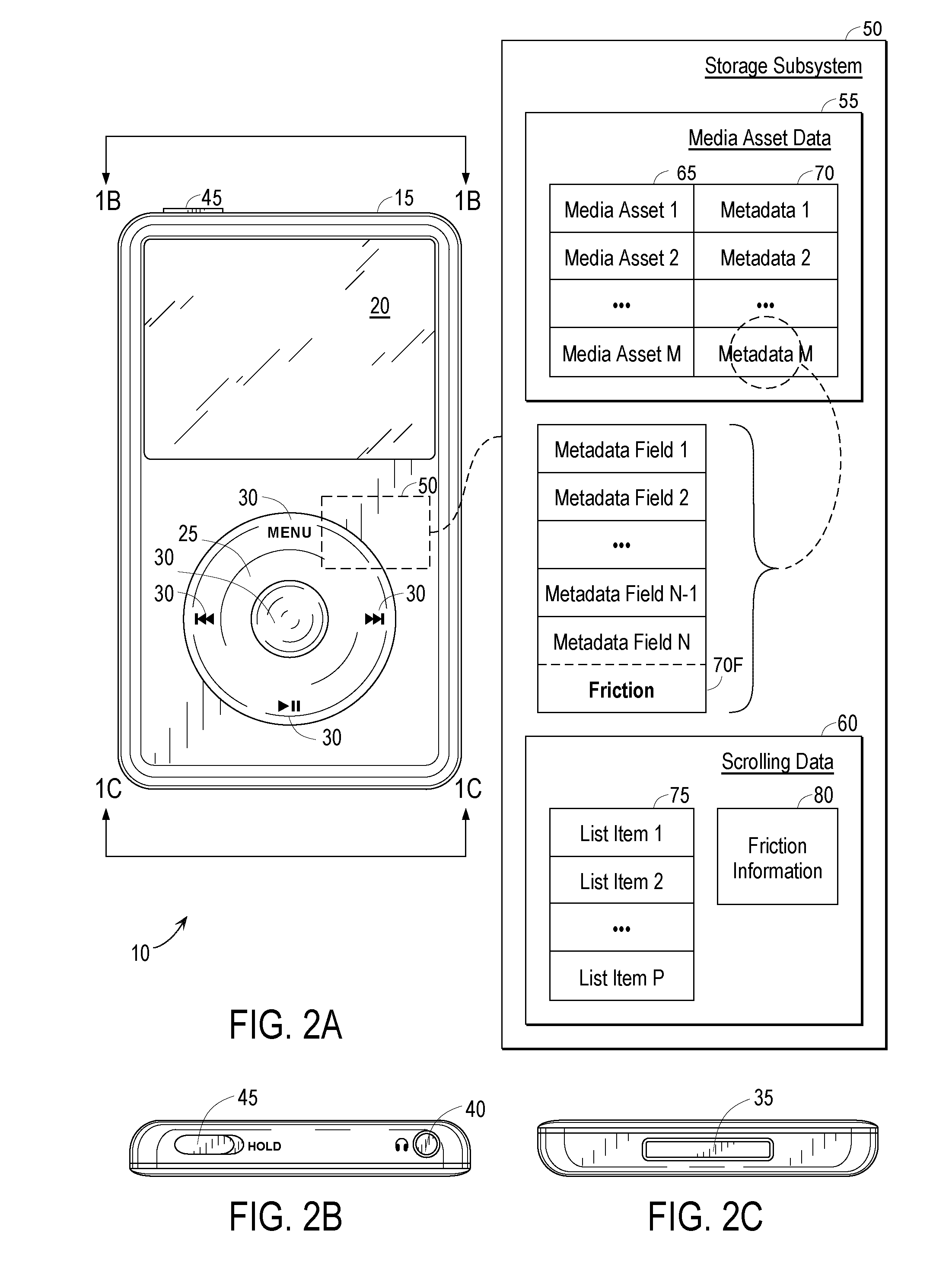
Dynamic Control of List Navigation Based on List Item Properties
InactiveUS20100058240A1Easy to navigateFacilitate scrollingInput/output processes for data processingScrollingMarine navigation
Navigating or scrolling through a list of items is enhanced by assigning a given item a non-null value for a friction property, and slowing the scrolling when the given item nears or enters the viewport, or pausing the scrolling when the given item enters the viewport. Scrolling at speed can be configured to be resumed when the user takes a particular action, or can be configured to resume after a designated elapsed time without user action. At least to the extent that scrolling through the list is accompanied by sequential items being at a cursor position within the viewport, the scrolling can slow down or pause when the given item is within a predetermined number of list items from the cursor position.
Owner:APPLE INC
Efficient rendering of panoramic images, and applications thereof
ActiveUS20080291201A1Easy to handleQuickly renderedCharacter and pattern recognitionCathode-ray tube indicatorsPrecomputationComputer science
A fast renderer for panoramic images is herein disclosed. In an embodiment, a precomputation is made of (a) a region on a surface defined by a first transformation from a viewport to the surface and (b) a second transformation that maps from the precomputed region to the viewport. In order to render the surface on the viewport, the renderer determines what portion of the image intersects with the precomputed region and proceeds to apply the precomputed second transformation to the portion of the image, thereby resulting in a transformed image which can be rendered in the viewport for display.
Owner:GOOGLE LLC
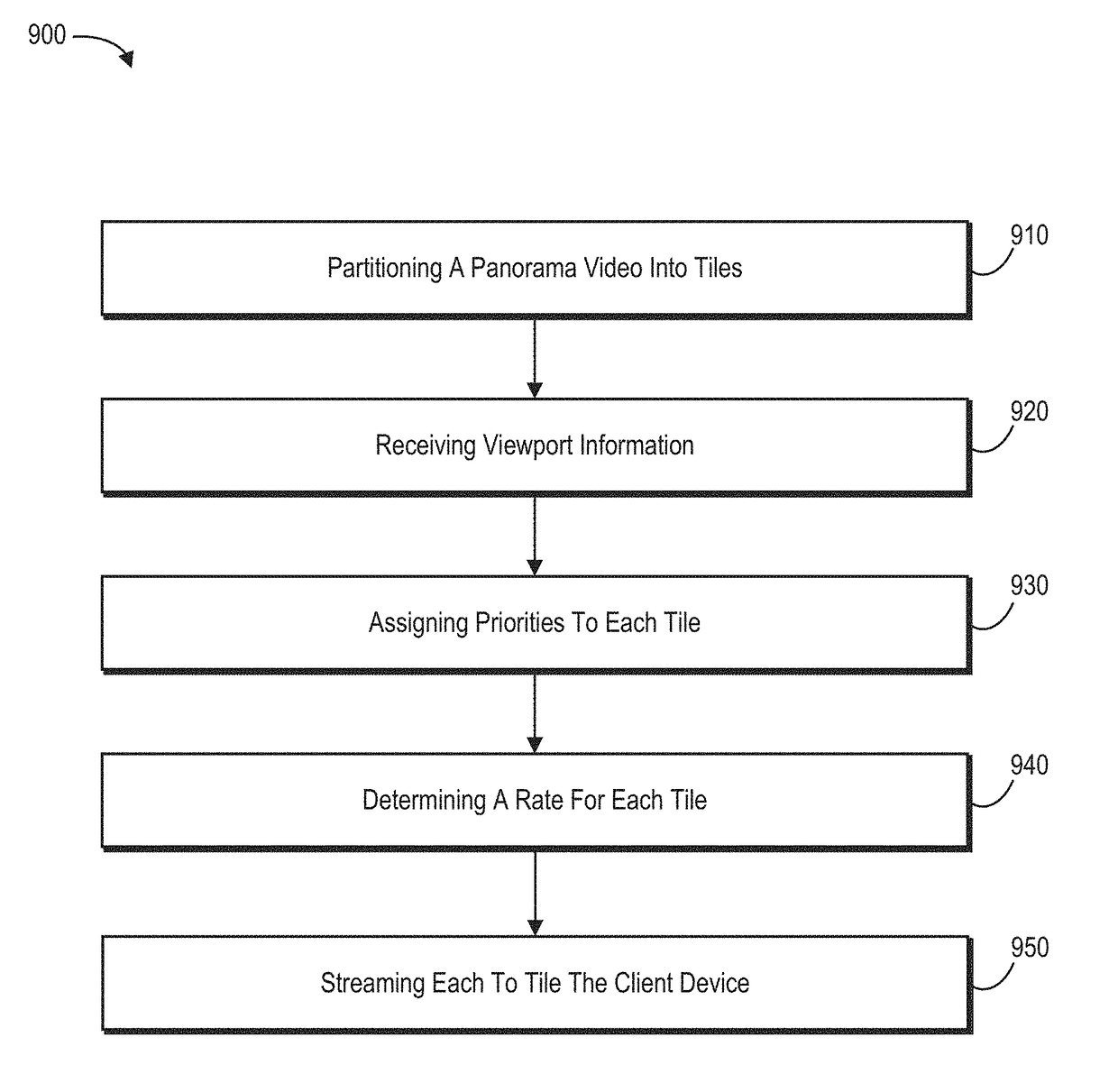
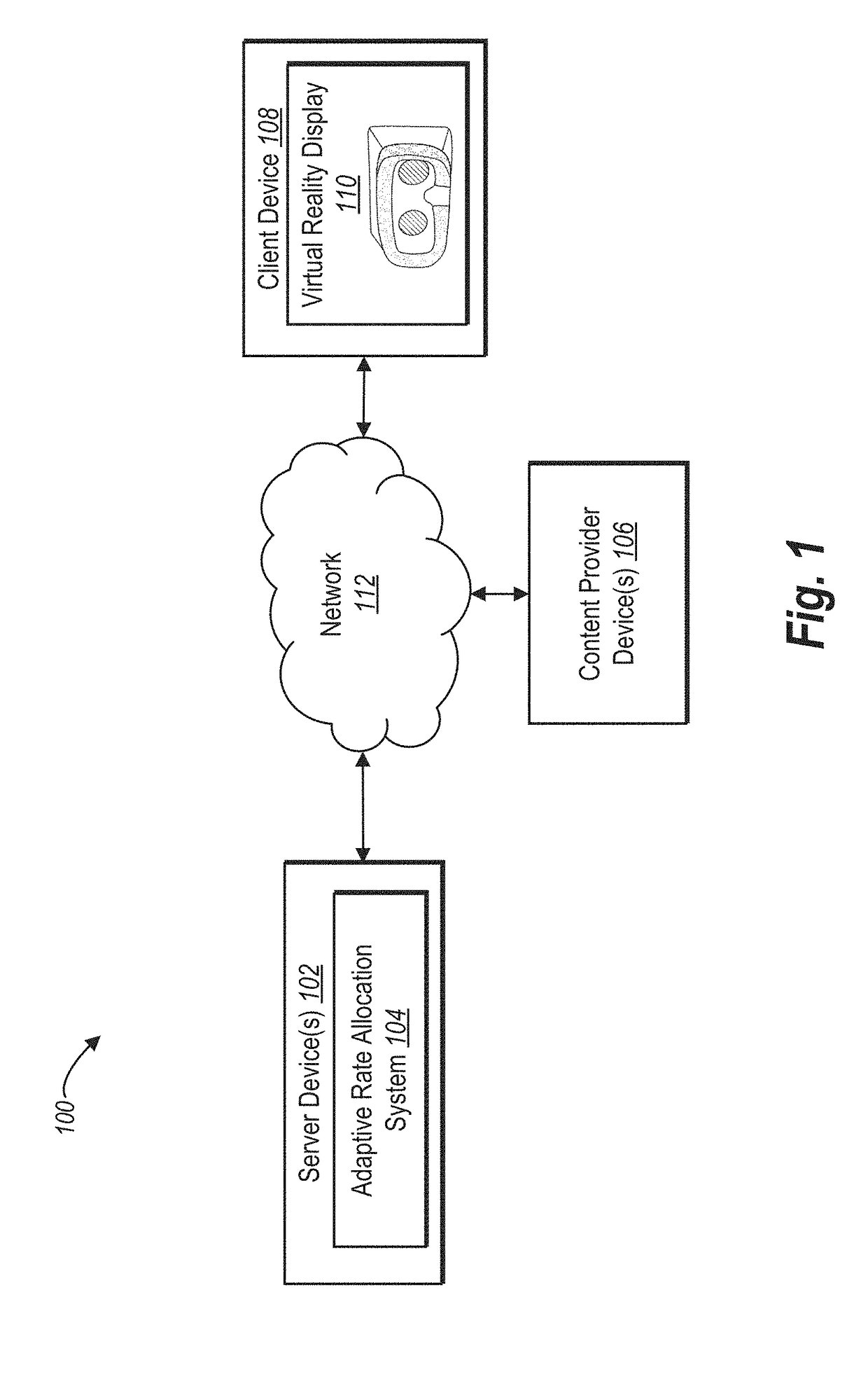
Prioritizing tile-based virtual reality video streaming using adaptive rate allocation
ActiveUS20180160160A1Quality improvementQuality contentImage data processingSelective content distributionVideo qualitySelf adaptive
The present disclosure includes methods and systems for streaming high-performance virtual reality video using adaptive rate allocation. In particular, an adaptive rate allocation system partitions a panorama video into segments or tiles and assigns priorities to each tile or segment based on input (e.g., a viewport of field-of-view) from a user client device. Further, the adaptive rate allocation system streams each tile or segment to the user client device according to the adaptive rate allocation, which maximizes bandwidth efficiency and video quality. In this manner, the adaptive rate allocation system delivers higher quality content to regions in the panorama video where a user is currently looking / most likely to look.
Owner:ADOBE INC
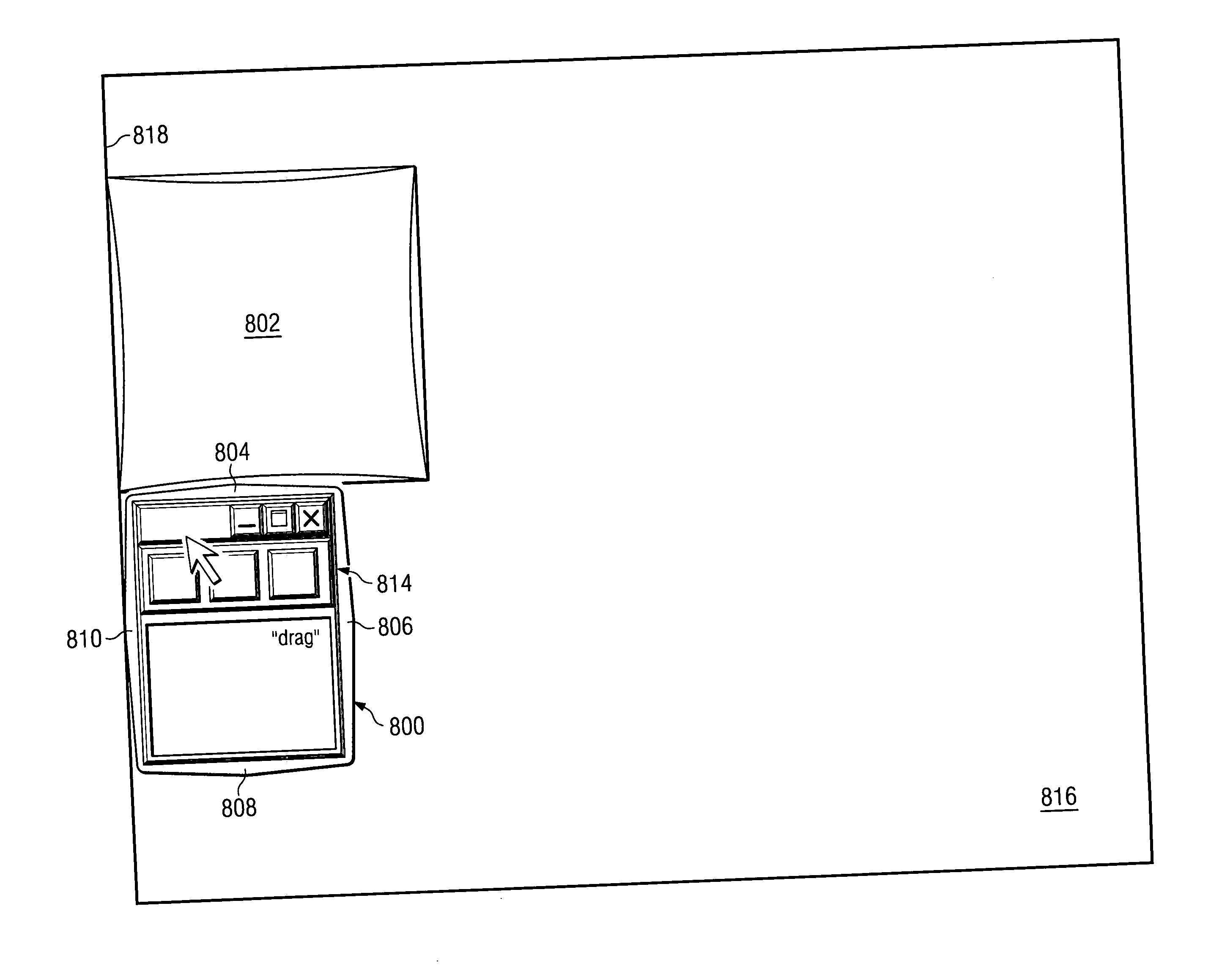
Configuring channels for sharing media
A user interface for sharing media items with others. From a sender's perspective, embodiments of the invention allow for an easy-to-use drag-and-drop technique that is more user-friendly than conventional techniques. From the recipient's perspective, embodiments of the invention allow media items from multiple sources to be aggregated into a single viewport, providing a cohesive and unified approach to media items received from others.
Owner:MICROSOFT TECH LICENSING LLC
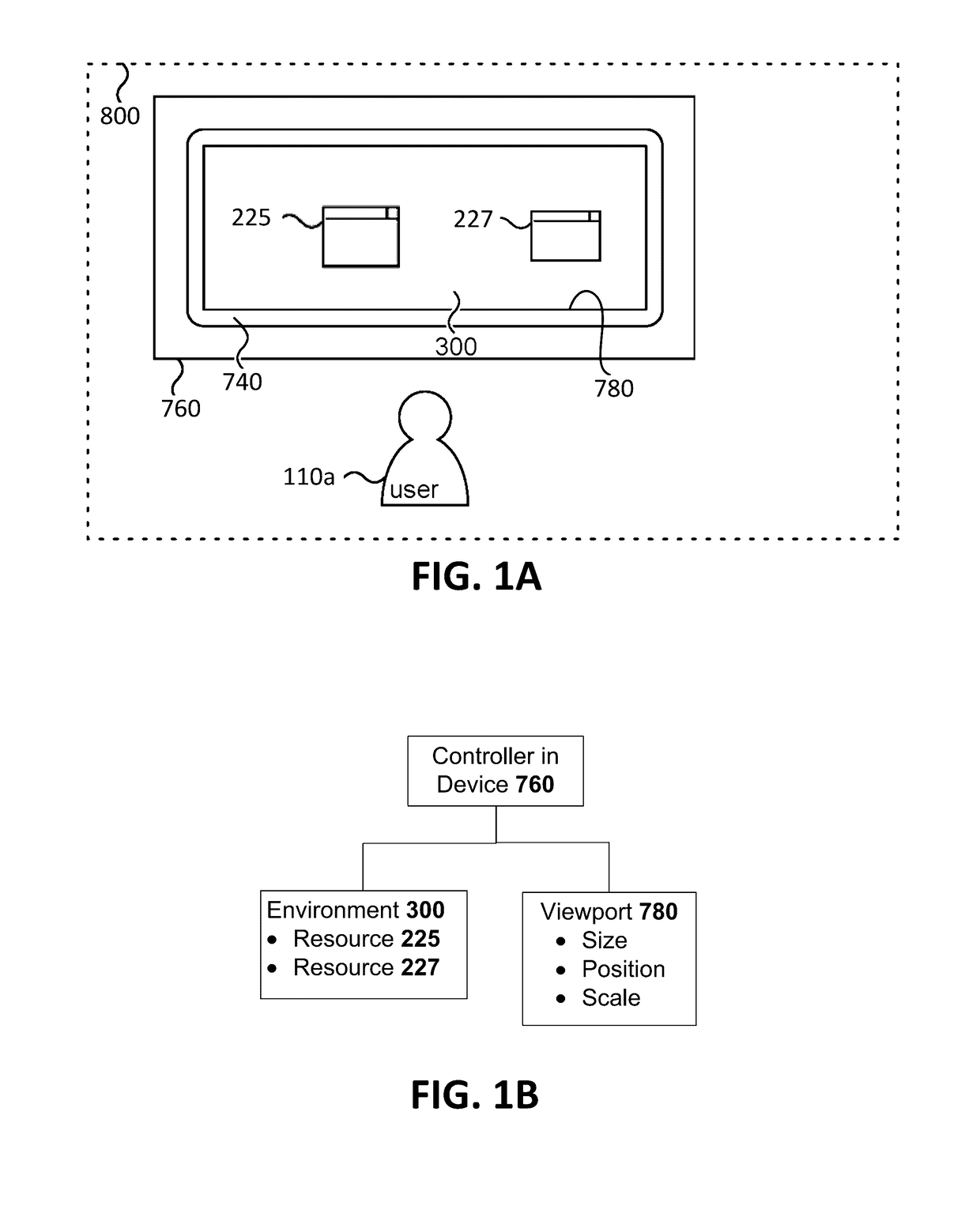
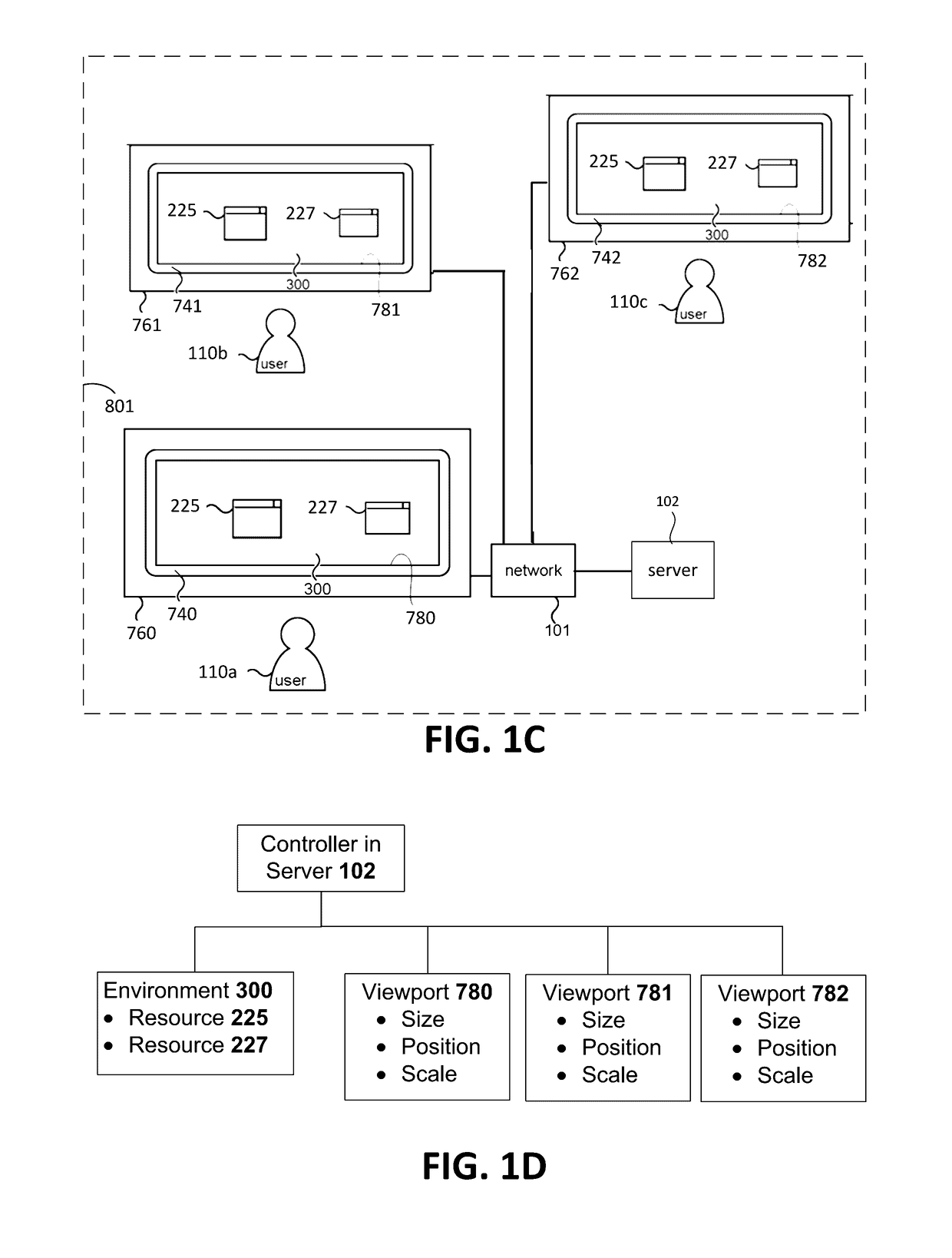
User interaction with desktop environment
Sharing resources by users of computing devices includes providing, at each computing device, a respective viewport to a common desktop environment that has the shared resources. The desktop is independently viewable and independently navigable through each respective viewport. Furthermore, each of the resources is independently viewable and able to be independently acted upon through each respective viewport. One or more resources of each computing device may be added to the desktop environment through the respective viewport of the computing device. A search user interface is provided for text string searching of resources of a respective viewport by a user at the computing device of the respective viewport; and an application launcher view user interface is provided for launching applications, which is viewable by clicking on an open space of the desktop environment as seen through the respective viewport, and by which launchable applications are searchable.
Owner:TILLMAN CHAD DUSTIN
Viewport-based desktop rendering engine
Methods, apparatuses and systems directed, in one implementation, to a system of dynamically spawned, virtual, three-dimensional (3D) viewports which render transparently within the elements of, or on top of, an existing desktop display environment, allowing rendered objects to seamlessly interact and move between different 3-dimensional viewport spaces and the two-dimensional (2D) screen space of the desktop environment. The present invention, in one implementation, renders multiple 3-dimensional viewports and free floating 3-dimensional objects on the client desktop, seamlessly mixed into the normal event and rendering pipeline of the computing device's 2-dimensional screen aligned desktop and windowed environment.
Owner:URBACH JULIAN MICHAEL
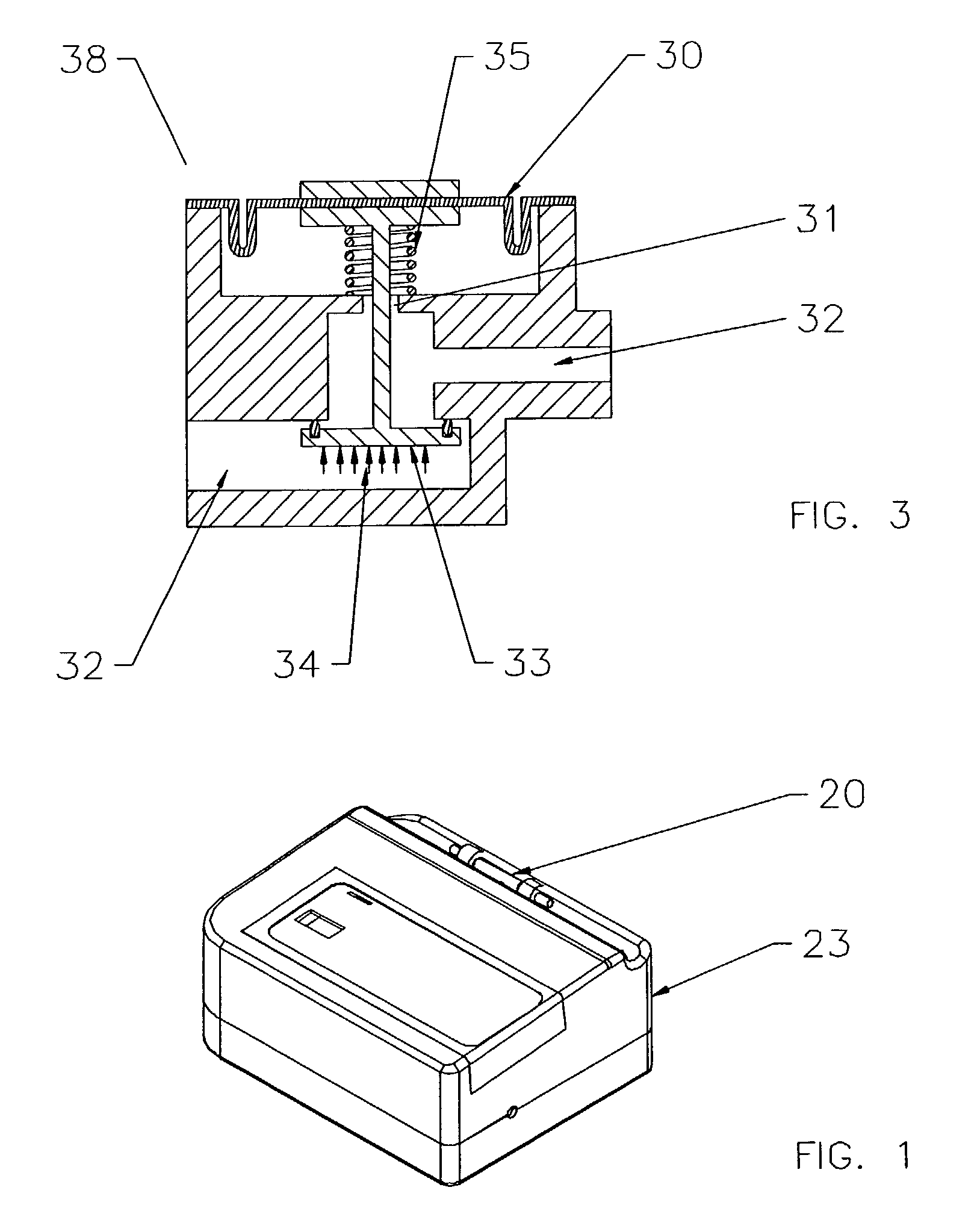
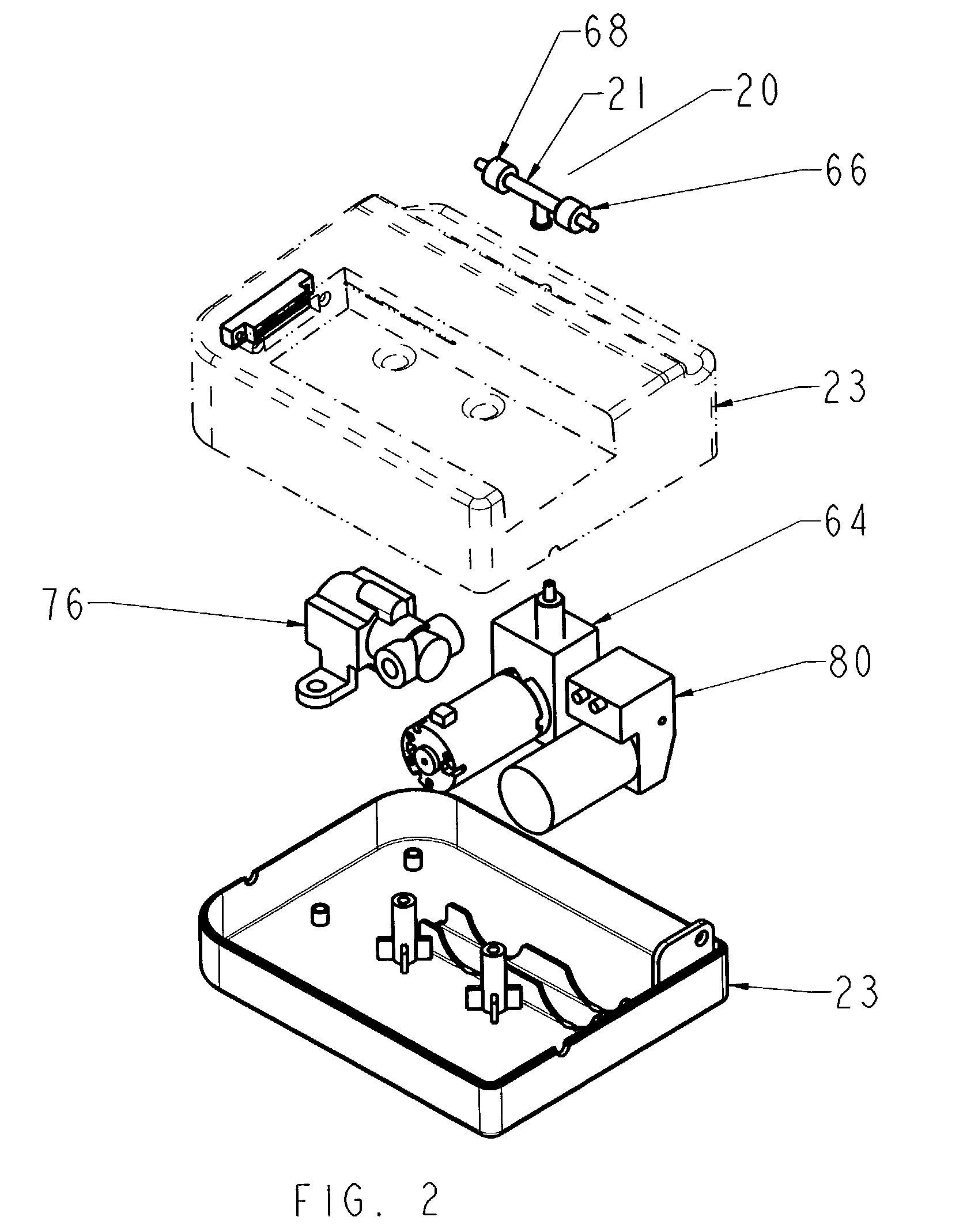
Interventional procedure drive and control system
InactiveUS20040059284A1Sufficiently compactSuppress fluctuationsIntravenous devicesSuction irrigation systemsReciprocating pumpSingle use
A pumping system for use in medical applications where liquids must be infused and aspirated from a mammalian patient, and whose economics are such that it is cost effective to simply dispose of it after a single use. The system features positive displacement pump(s) such as reciprocating pump(s) containing a damping mechanism to dampen out the peaks and valleys in the fluid pressure that is pumped, which is important for preventing cavitation. The system furthermore features a shut-off valve on the extraction side so that certain injected fluids such as contrast medium, are not immediately pumped out of the patient. In a preferred embodiment, the system also features means for independently controlling the fluid pressure / volume on the infusion and extraction sides, self-priming capability, a continuous fluid path, and visual air bubble detection, with viewports located at important points in the fluid path, such as at pumps and valves.
Owner:KENSEY NASH CORP
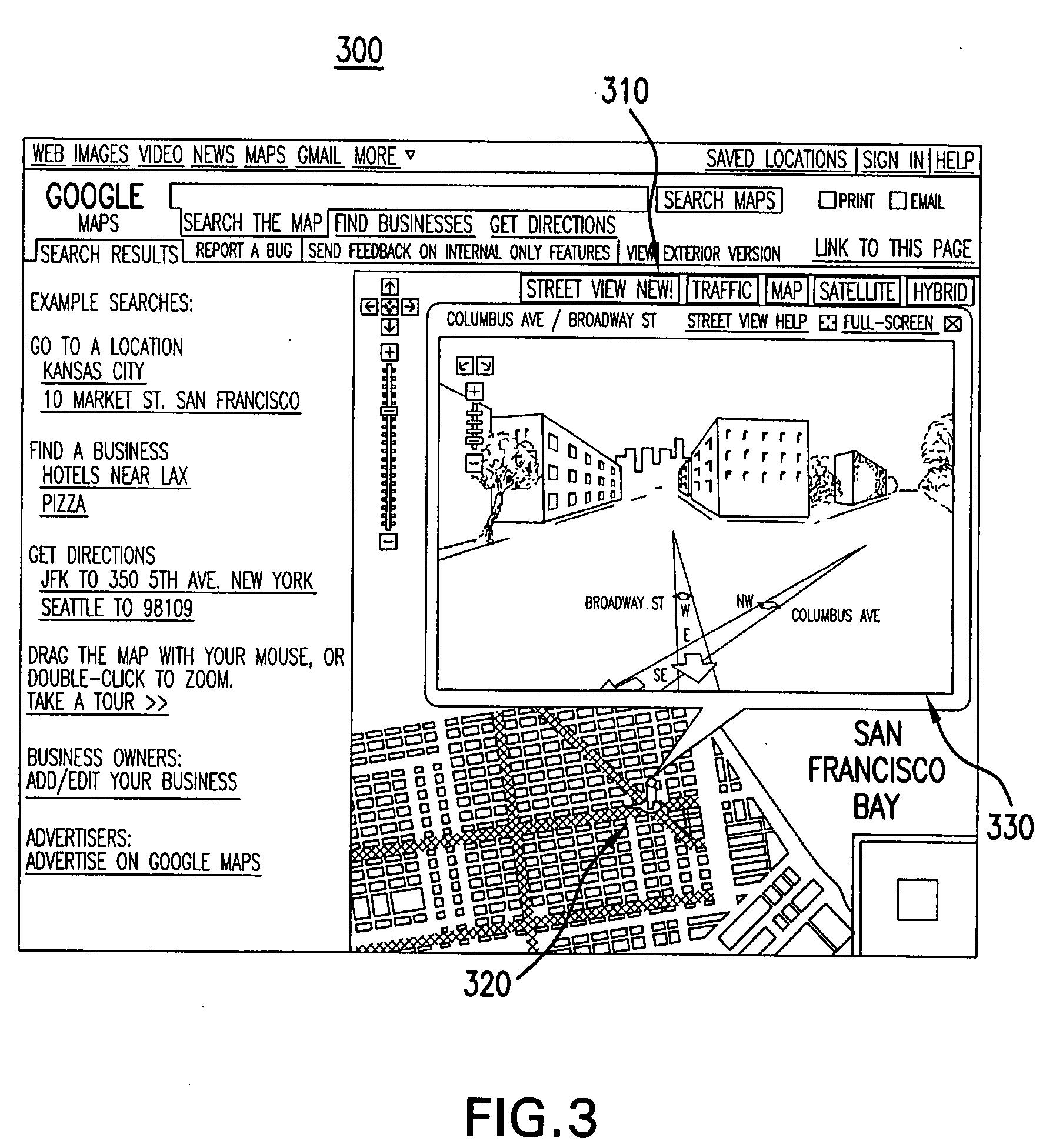
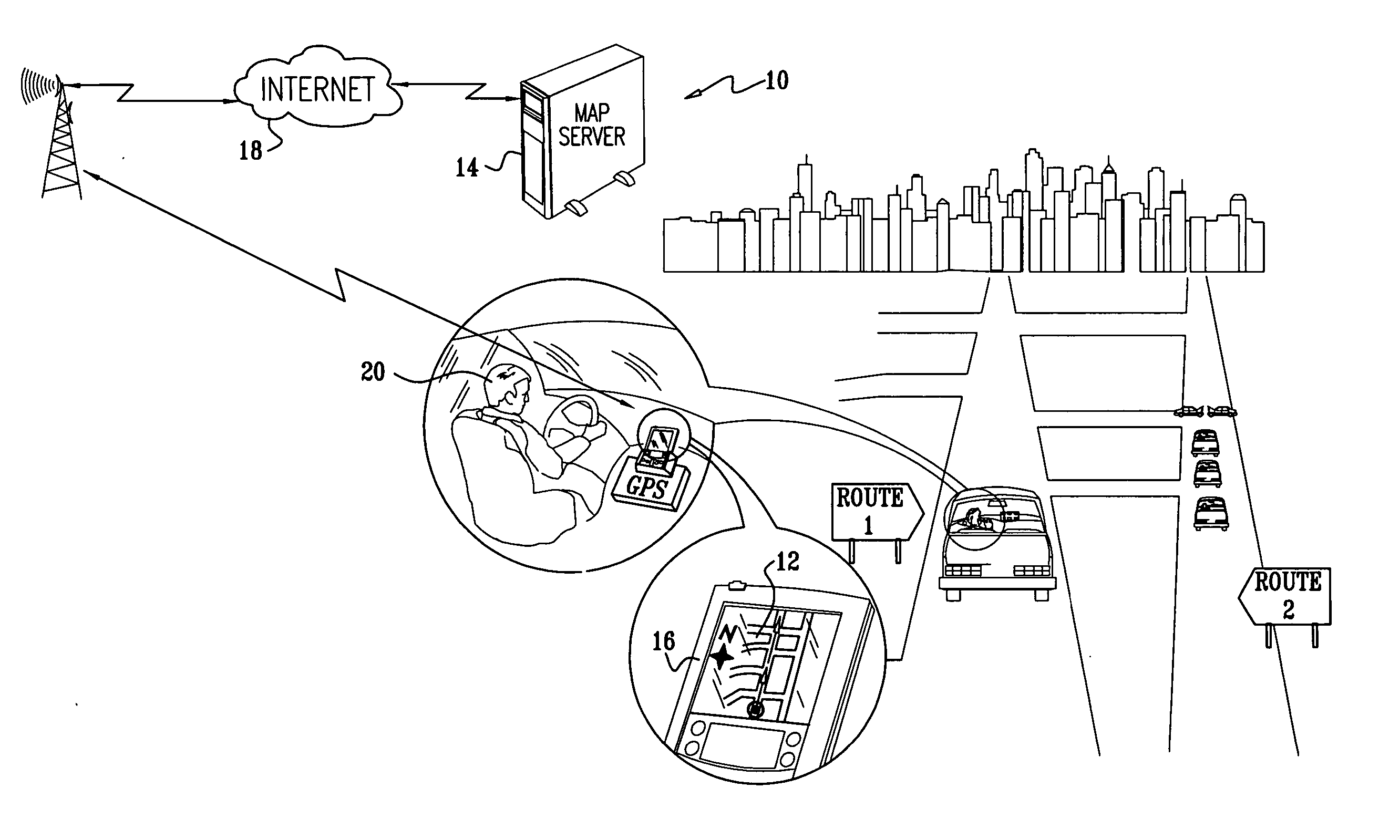
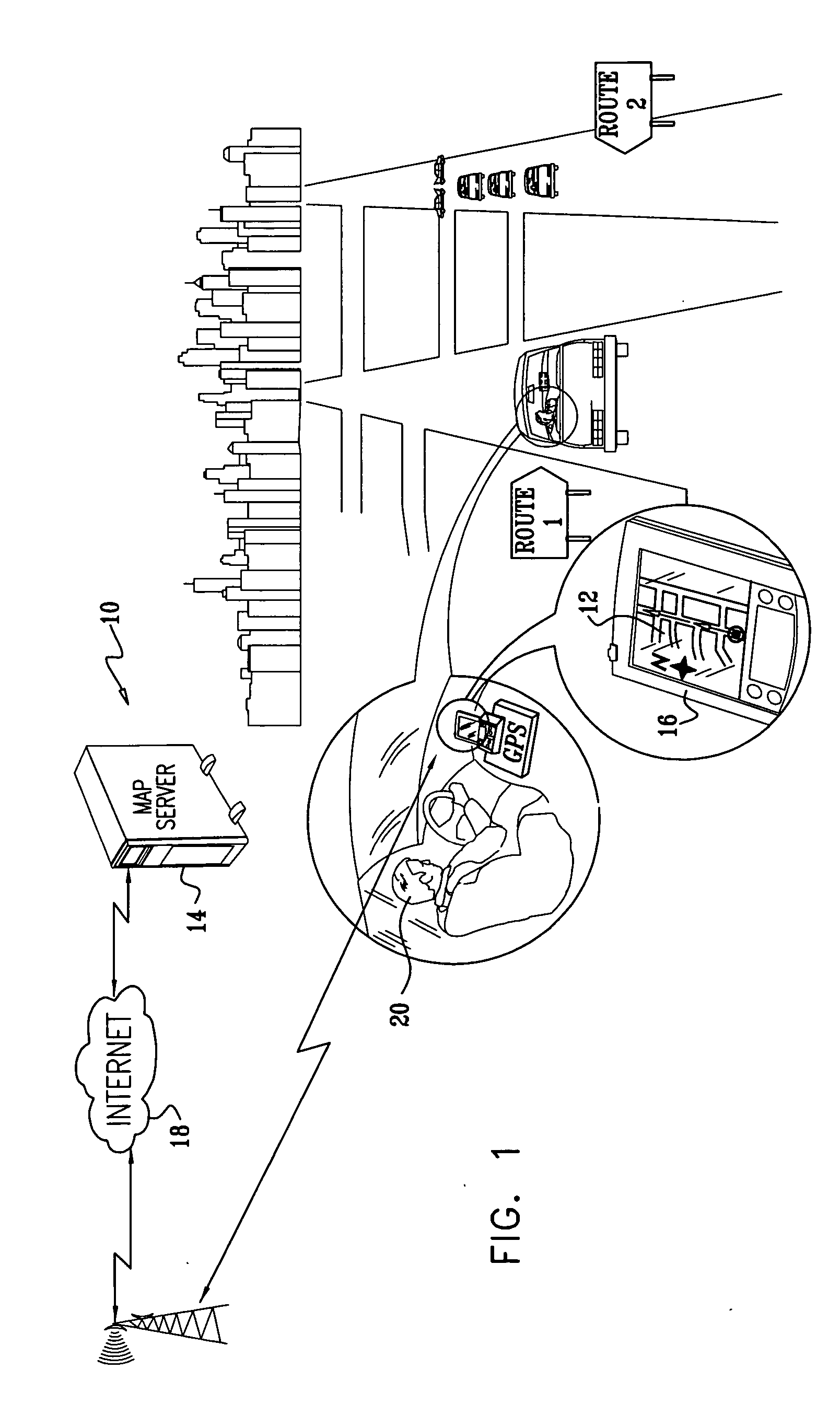
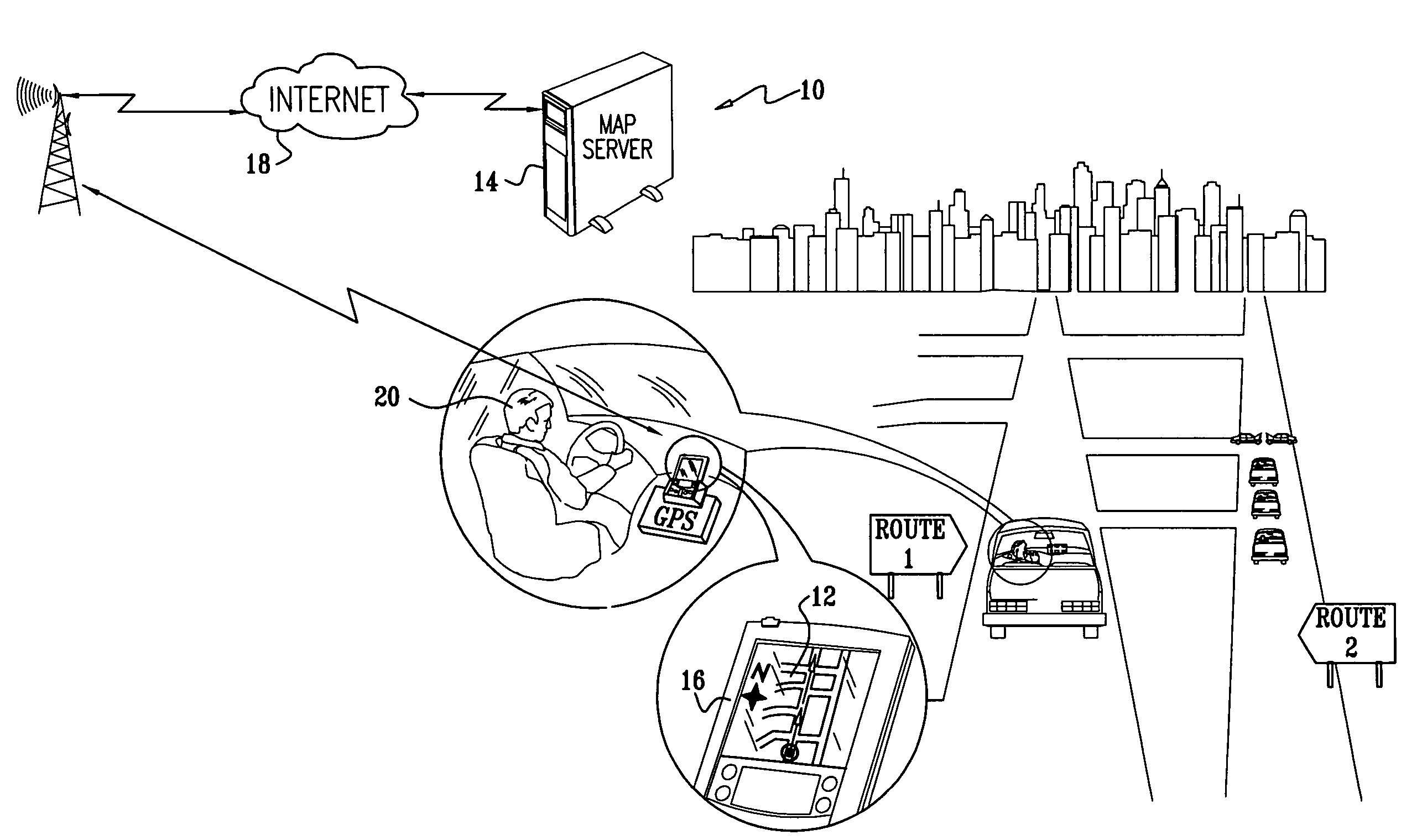
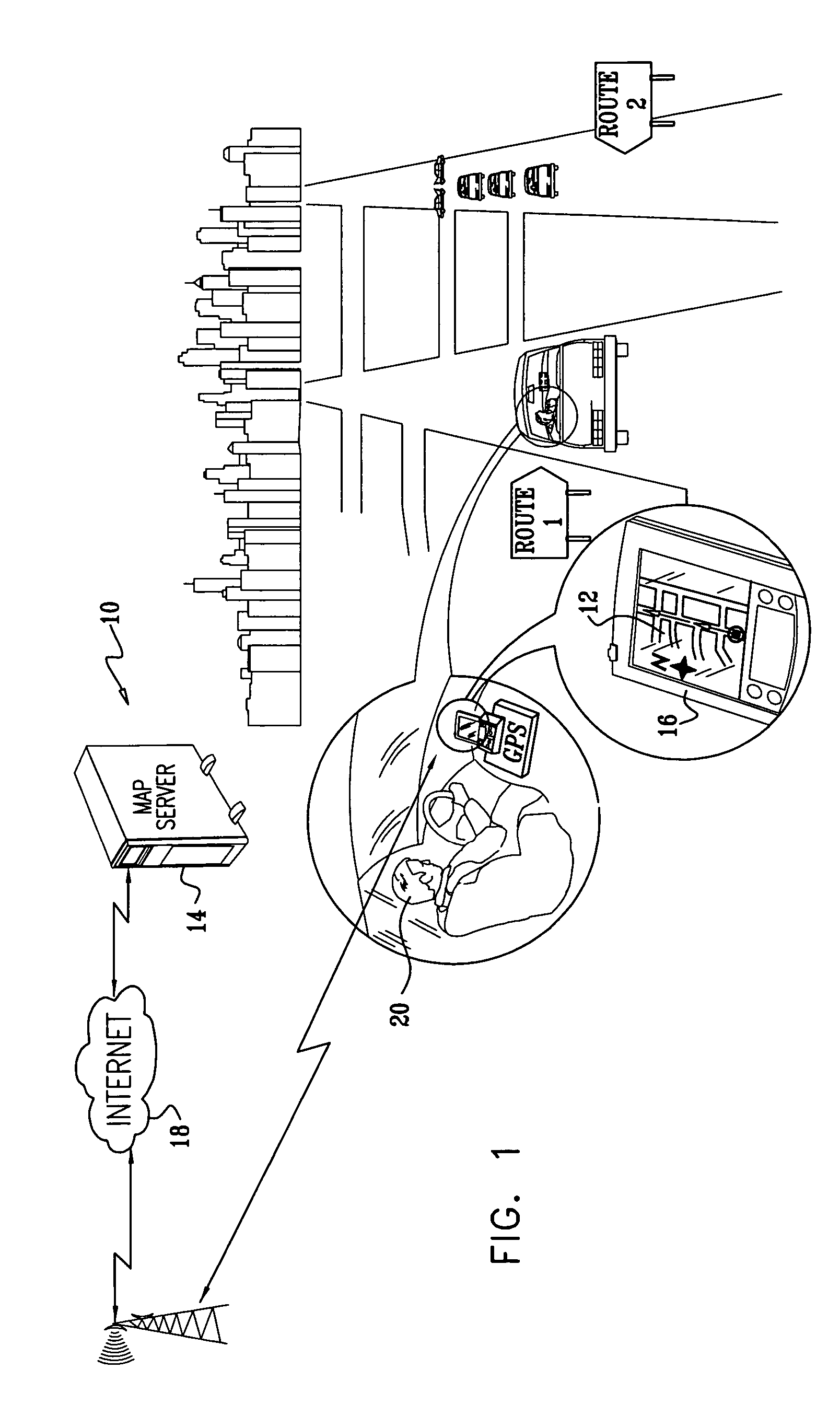
Placement of map labels
InactiveUS20060058949A1Optimize quality functionInstruments for road network navigationRoad vehicles traffic controlGraphicsComputer science
Methods and systems are presented for the automatic optimal placement text or symbol labels corresponding to graphical objects on maps. Using a map server and a thin, typically mobile client, maps are dynamically drawn and displayed at the client. Optimized labeling of map objects is achieved by dividing the task into pipelined subtasks, some being performed off-line, and others being performed in real time, responsively to changing client requests, and changes in the map viewport. Optimization of candidate label positions is accomplished using simulated annealing.
Owner:TAHOE RES LTD
Rapid computation of local eye vectors in a fixed point lighting unit
InactiveUS6014144ADigital computer detailsElectric digital data processingFixation pointSpecular reflection
A rapid method for calculating a local eye vector in a fixed point lighting unit. For a given triangle primitive which is to be projected into a given viewport in screen space coordinates, the local eye vector corresponds to a given eye position and a first vertex of the given triangle primitive. (A different local eye vector is calculated for each vertex of the given triangle primitive). The method first comprises generating a view vector matrix which corresponds to the given eye position and corner coordinates of the given viewport, where the corner coordinates are expressed in screen space coordinates. The view vector matrix is usable to map screen space coordinates to an eye vector space which corresponds to the given viewport. The method next includes receiving a first set of coordinates (in screen space) which correspond to the first vertex. The first set of coordinates are then scaled to a numeric range which is representable by the fixed point lighting unit. Next, the first set of coordinates are transformed using the view vector matrix, which produces a non-normalized local eye vector within the eye vector space for the given viewport. The non-normalized local eye vector is normalized to form a normalized local eye vector. The normalized local eye vector is then usable to perform subsequent lighting computations such as computation of specular reflection values for infinite light sources, producing more realistic lighting effects than if an infinite eye vector were used. These more realistic lighting effects do not come at decreased performance, however, as the local eye vector may be calculated rapidly using this method.
Owner:ORACLE INT CORP
Dynamic client-server video tiling streaming
ActiveUS20080181498A1Character and pattern recognitionCathode-ray tube indicatorsDisplay deviceClient-side
A system and a method for communicating video data associated with content across a network are disclosed. A server partitions the content into a plurality of tiles where each tile includes a subset of the content and index data describing a relationship between a tile and one or more adjacent tiles. Each tile is then encoded as a video frame, for example each tile is encoded according to the H.264 standard. The plurality of tiles are then transmitted to a client which combines the plurality of tiles using the index data to locally recreate the content. The client associates a predetermined viewport tile with a client viewport representing the area of the content that is visible in a client display device to allow viewing of the content while tiles not associated with the client viewport are cached to expedite subsequent retrieval.
Owner:OTELLO CORP ASA
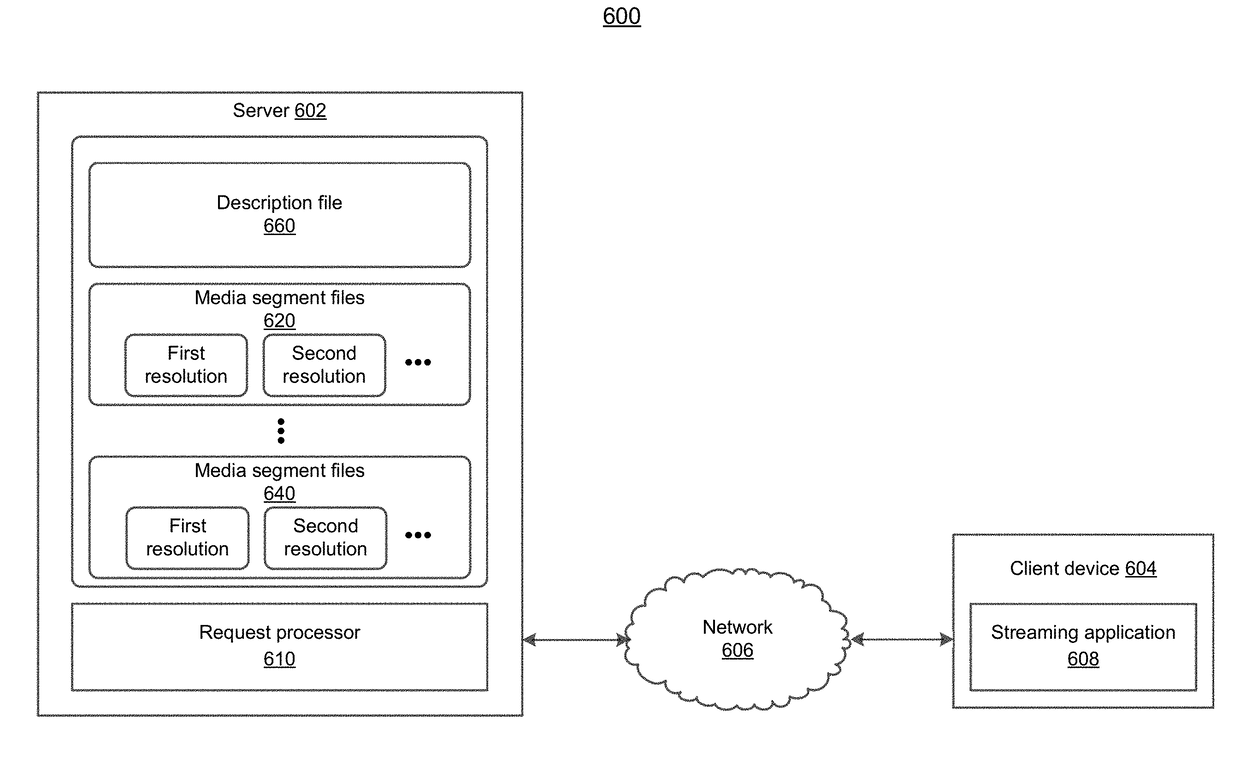
Systems and methods of generating and processing files for partial decoding and most interested regions
Techniques and systems are provided for processing video data. For example, 360-degree video data can be obtained for processing by an encoding device or a decoding device. The 360-degree video data includes pictures divided into motion-constrained tiles. The 360-degree video data can be used to generate a media file including a plurality of tracks. Each of the plurality of tracks contain a set of at least one of the motion-constrained tiles. The set of at least one of the motion-constrained tiles corresponds to at least one of a plurality of viewports of the 360-degree video data. A first tile representation can be generated for the media file. The first tile representation encapsulates a first track of the plurality of tracks, and the first track includes a first set of at least one of the motion-constrained tiles at a first tile location in the pictures of the 360-degree video data. The first set of at least one of the motion-constrained tiles corresponds to a viewport of the 360-degree video data.
Owner:QUALCOMM INC
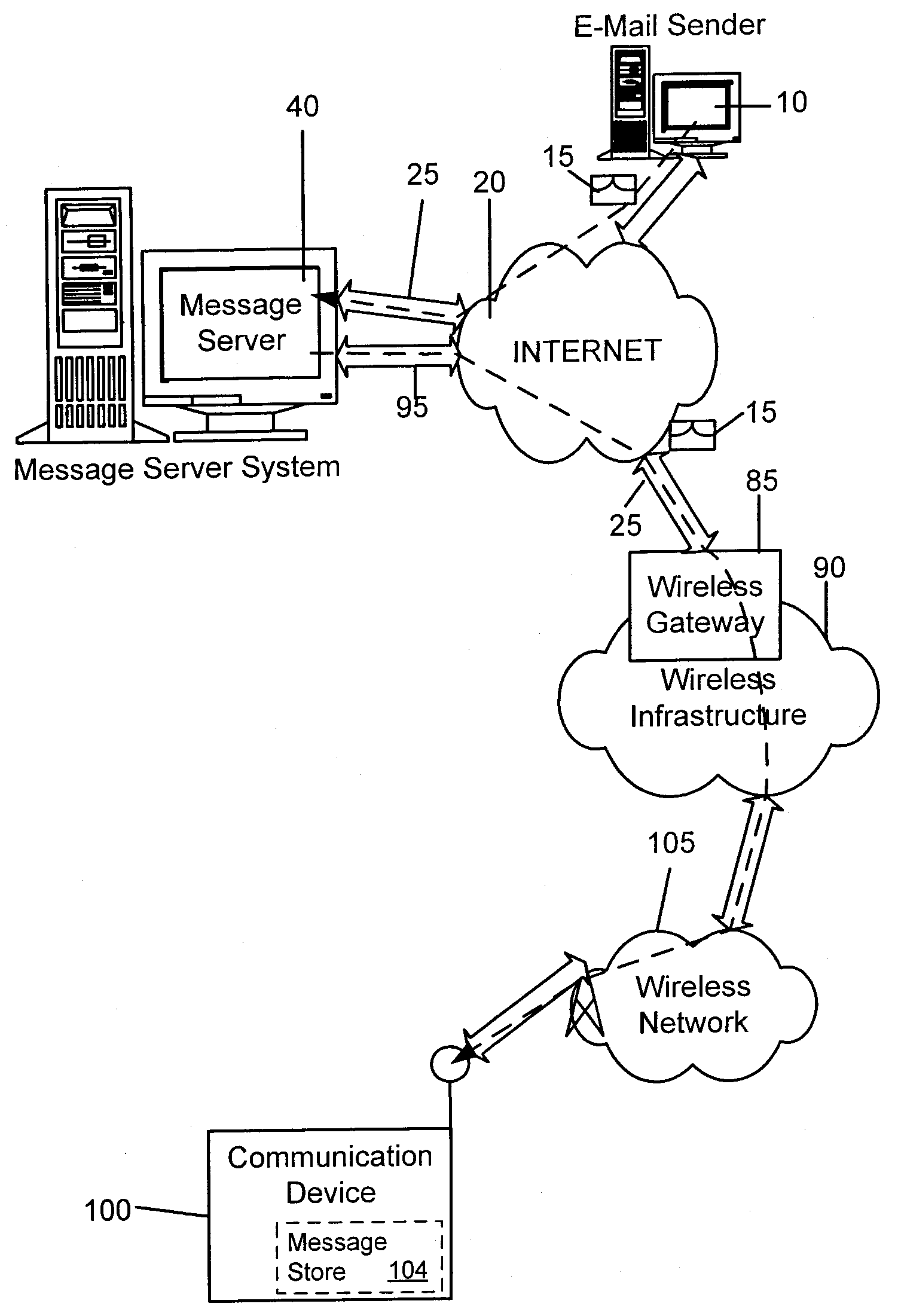
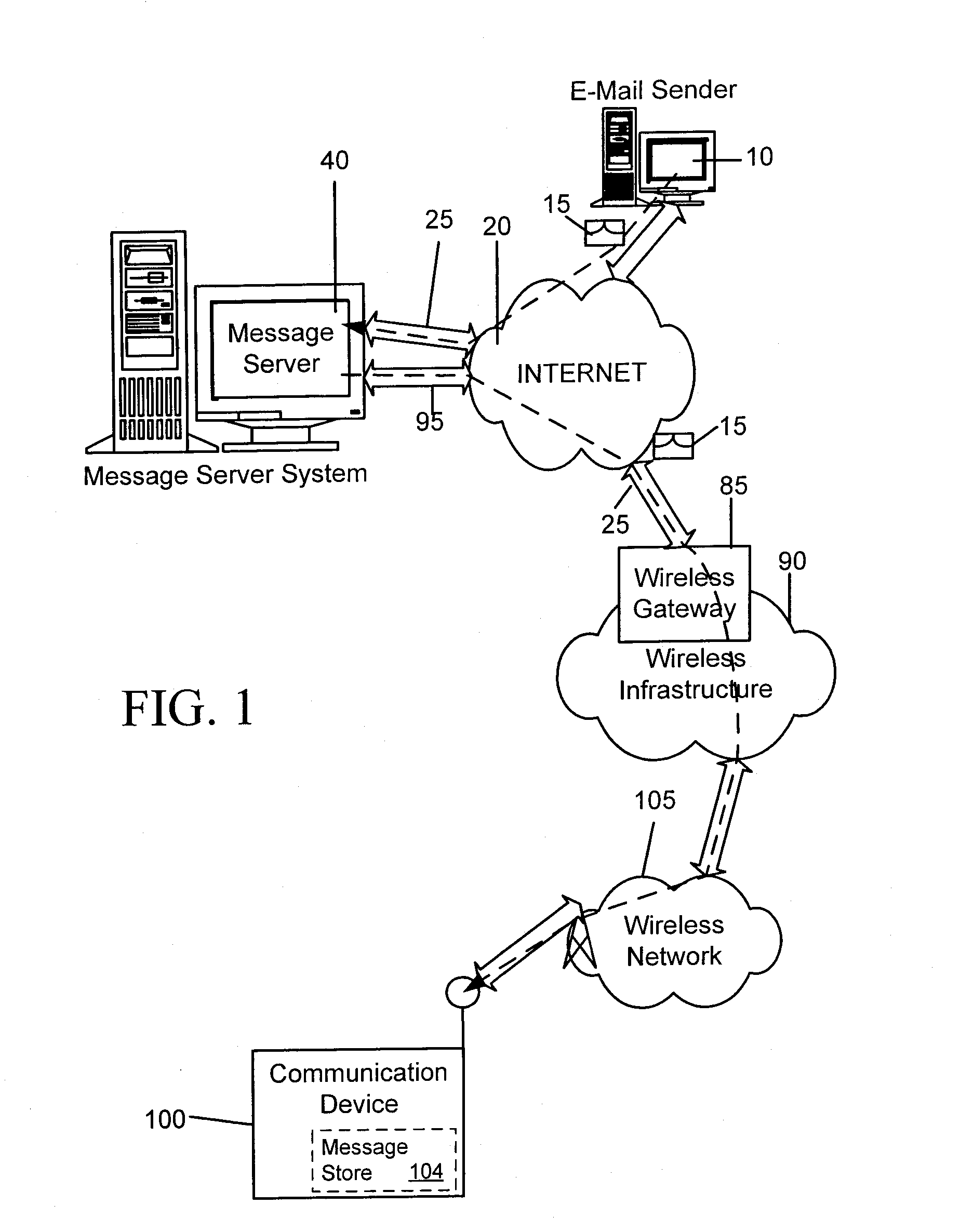
System and method for prioritizing and displaying messages
ActiveUS20080270560A1Multiple digital computer combinationsTransmissionSpeech soundCommunication device
A system for prioritizing and displaying received messages, including e-mail, SMS, IM, multimedia, and voicemail, at a communication device includes means for dynamically associating a priority value with a received message upon detection of an evaluation event, and means for dynamically updating a listing of received messages associated with at least a priority value equal to or greater than a predetermined priority value in a designated priority viewport. The viewport is constantly viewable in a message listing screen and comprises a listing of prioritized messages separate and apart from non-prioritized messages. Evaluation events may include user operation such as reading, deleting, replying, moving, or forwarding the message and similar operations, or a determination that the message has reached a predetermined age.
Owner:BLACKBERRY LTD
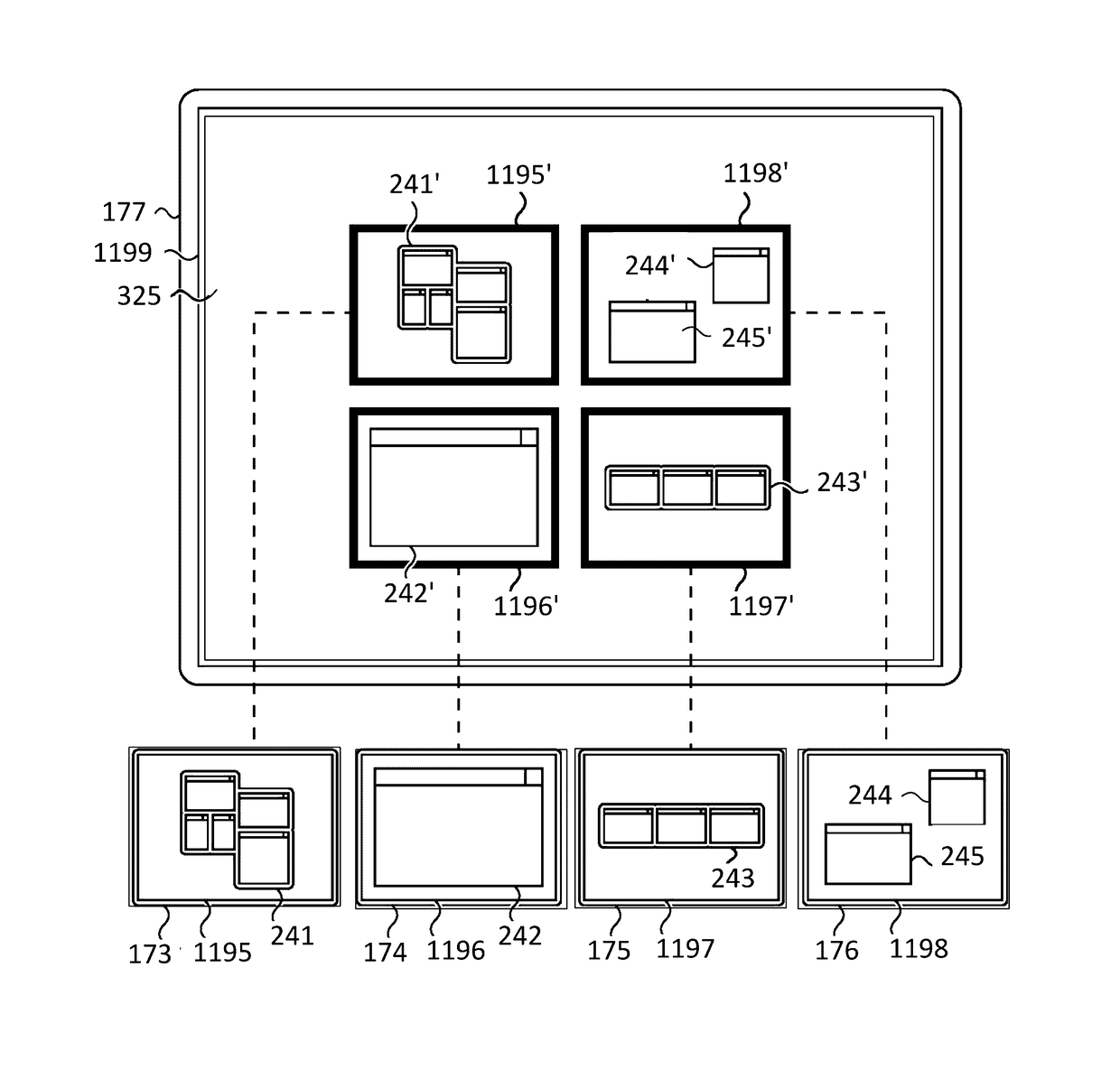
Carousel User Interface For Document Management
InactiveUS20130047079A1Natural language data processingSpecial data processing applicationsDocument representationDocumentation
Methods and systems for managing open documents are disclosed. Document representations are displayed in a carousel display. Each of the representations displays a document viewport portion of content from a corresponding open document. Upon determining a first gesture associated with a selected representation, a full view of the document viewport portion of the open document corresponding to the selected representation is displayed. The content of the open document displayed in the document viewport portion may be adjusted based upon a user action in the open document. Upon determining a second gesture, the full view of the document viewport portion is closed and the adjusted content is displayed as the document viewport portion in the carousel display. A greater portion of the open document than what is visible in the document viewport portion is displayed.
Owner:GOOGLE LLC
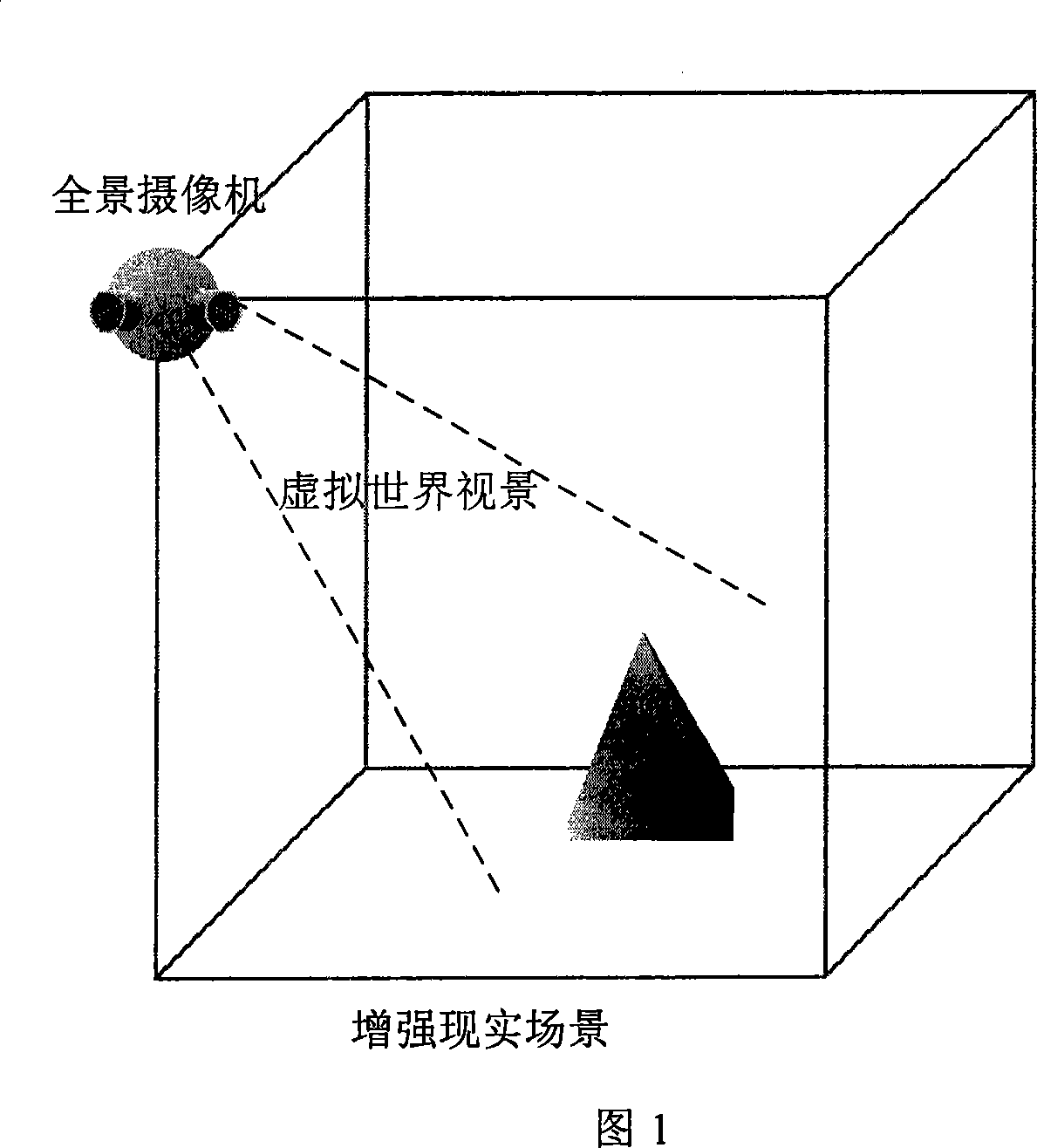
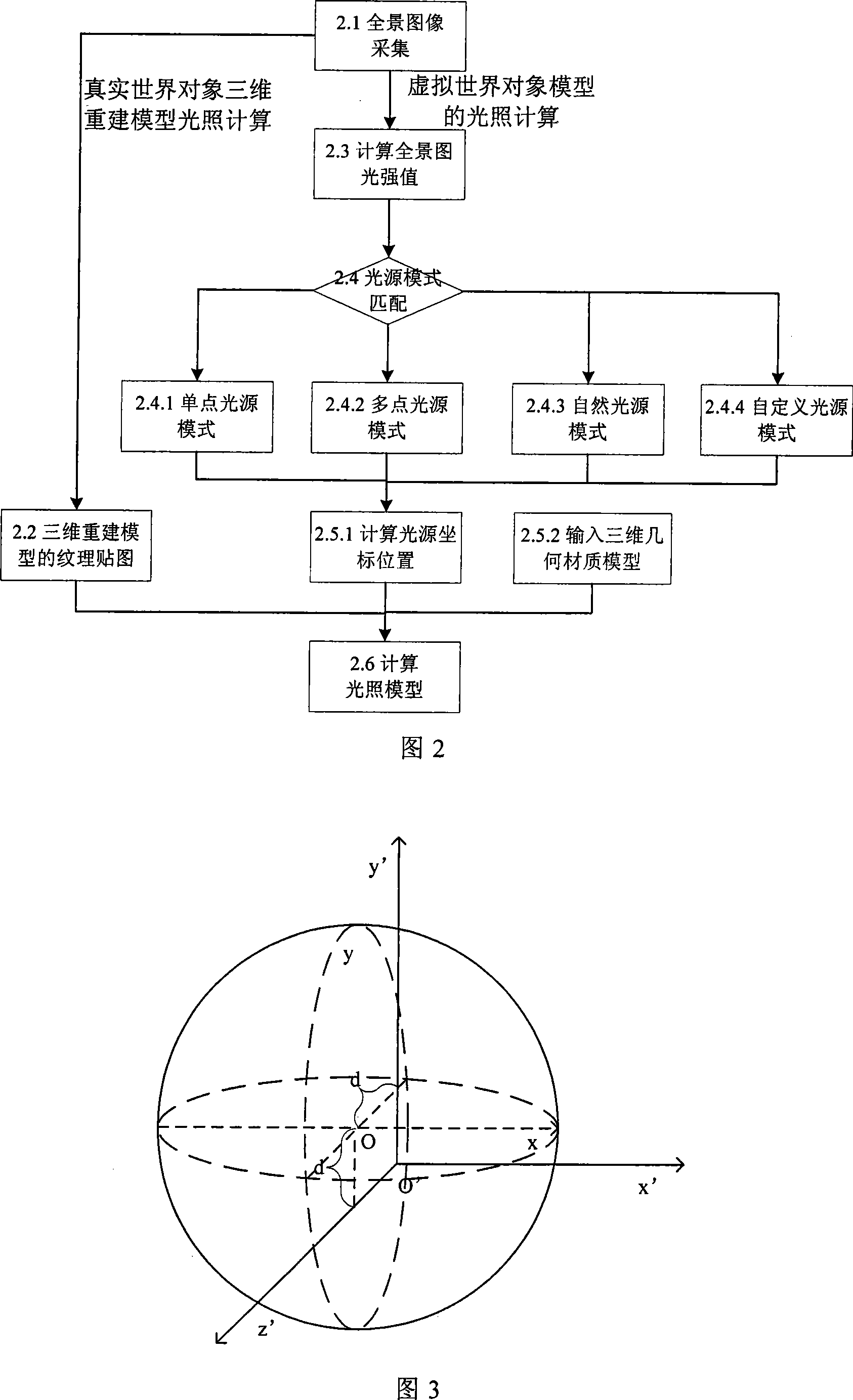
Method for real-time generating reinforced reality surroundings by spherical surface panoramic camera
InactiveCN101246600AReal-time generationEnhance real-time dynamic interaction3D-image renderingOptical propertyPattern matching
The present invention provides a method of generating augmented reality surroundings illumination model by a spherical panoramic camera real time, including: (1) placing the spherical panoramic camera in the augmented reality surroundings, placing in the viewport of the virtual worlds, real-time collecting panoramic picture; (2) processing the texture map having optical property aimed at the real world object after being collected panoramic picture of the step 1; (3) calculating collected panoramagram light intensity value aimed at the virtual world object after being collected the panoramic picture of the step 1, processing illumination model pattern matching, generating virtual world illumination model by the calculation; (4) calculating the illumination model of the augmented reality site under the condition of interactive local impact of the consideration reconstruction model and the virtual object model. The invention real-time generates illumination model in the complex photoenvironment, having advantage of support augmented reality site real time interactive.
Owner:BEIHANG UNIV
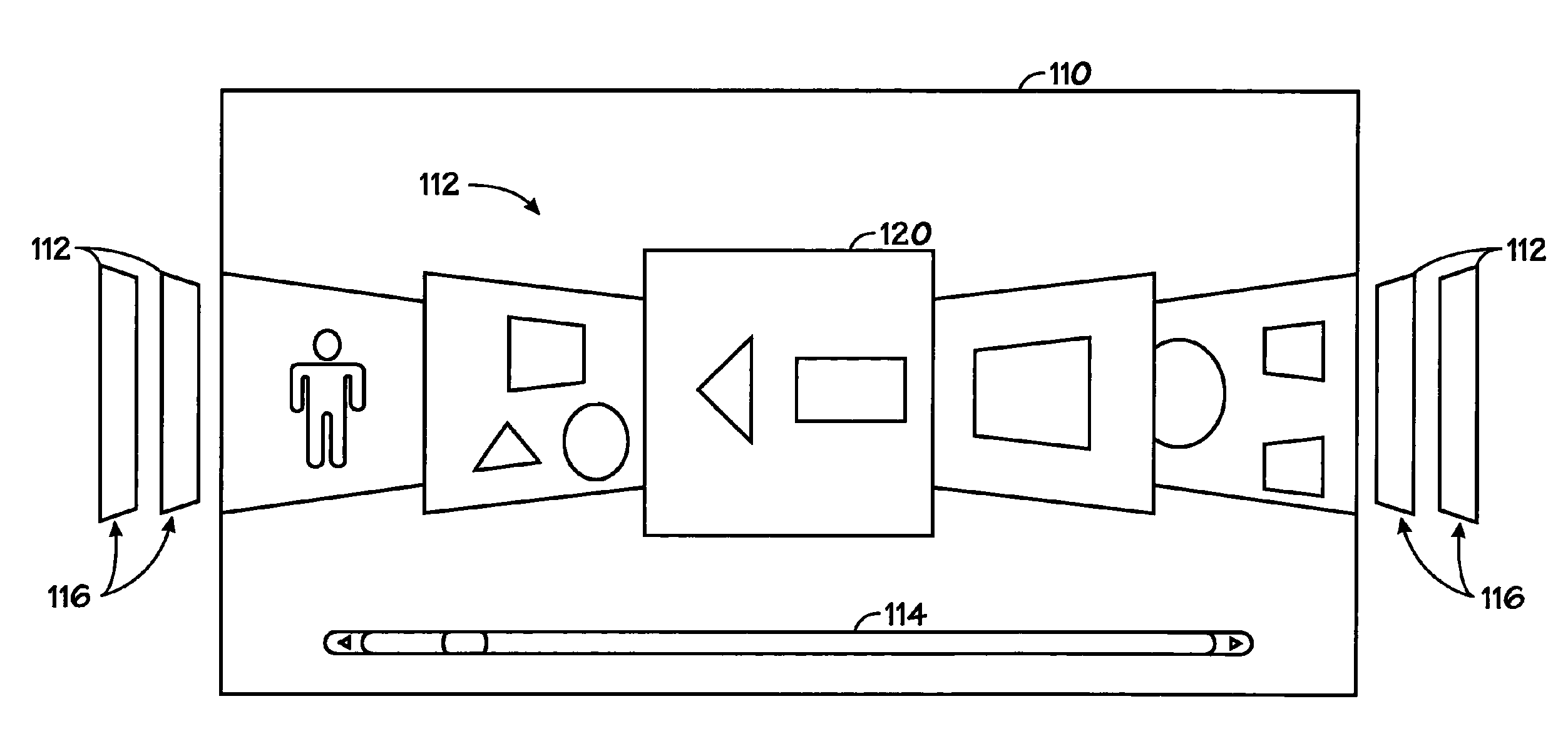
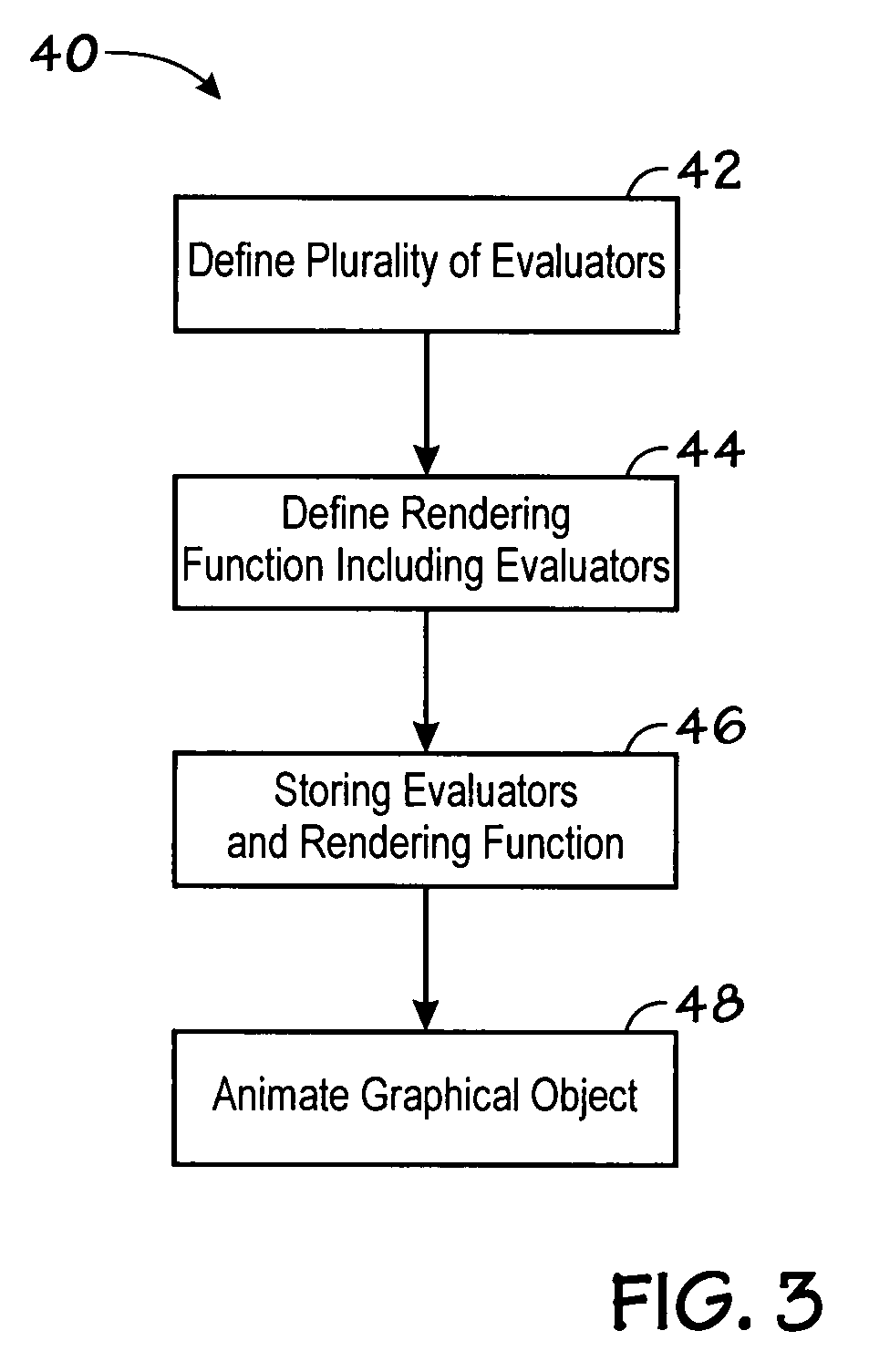
Animation of graphical objects
ActiveUS7941758B2Smooth animationInput/output for user-computer interactionCathode-ray tube indicatorsGraphicsVirtual destination
A method for animating graphical objects is provided. In one embodiment, the method includes providing a plurality of graphical objects and displaying a subset of the objects in a viewport. In this embodiment, the method may also include calculating a virtual destination for one of the graphical objects based on a received user input, and moving the graphical object to the virtual destination over a period of time. Various additional methods, machine-readable media, and devices for animating graphical objects and controlling operational characteristics of a device are also provided.
Owner:APPLE INC
Using Image Content to Facilitate Navigation in Panoramic Image Data
ActiveUS20090213112A1Easy to navigateGeometric image transformationCharacter and pattern recognitionImaging dataMarine navigation
The present invention relates to using image content to facilitate navigation in panoramic image data. In an embodiment, a computer-implemented method for navigating in panoramic image data includes: (1) determining an intersection of a ray and a virtual model, wherein the ray extends from a camera viewport of an image and the virtual model comprises a plurality of facade planes; (2) retrieving a panoramic image; (3) orienting the panoramic image to the intersection; and (4) displaying the oriented panoramic image.
Owner:GOOGLE LLC +1
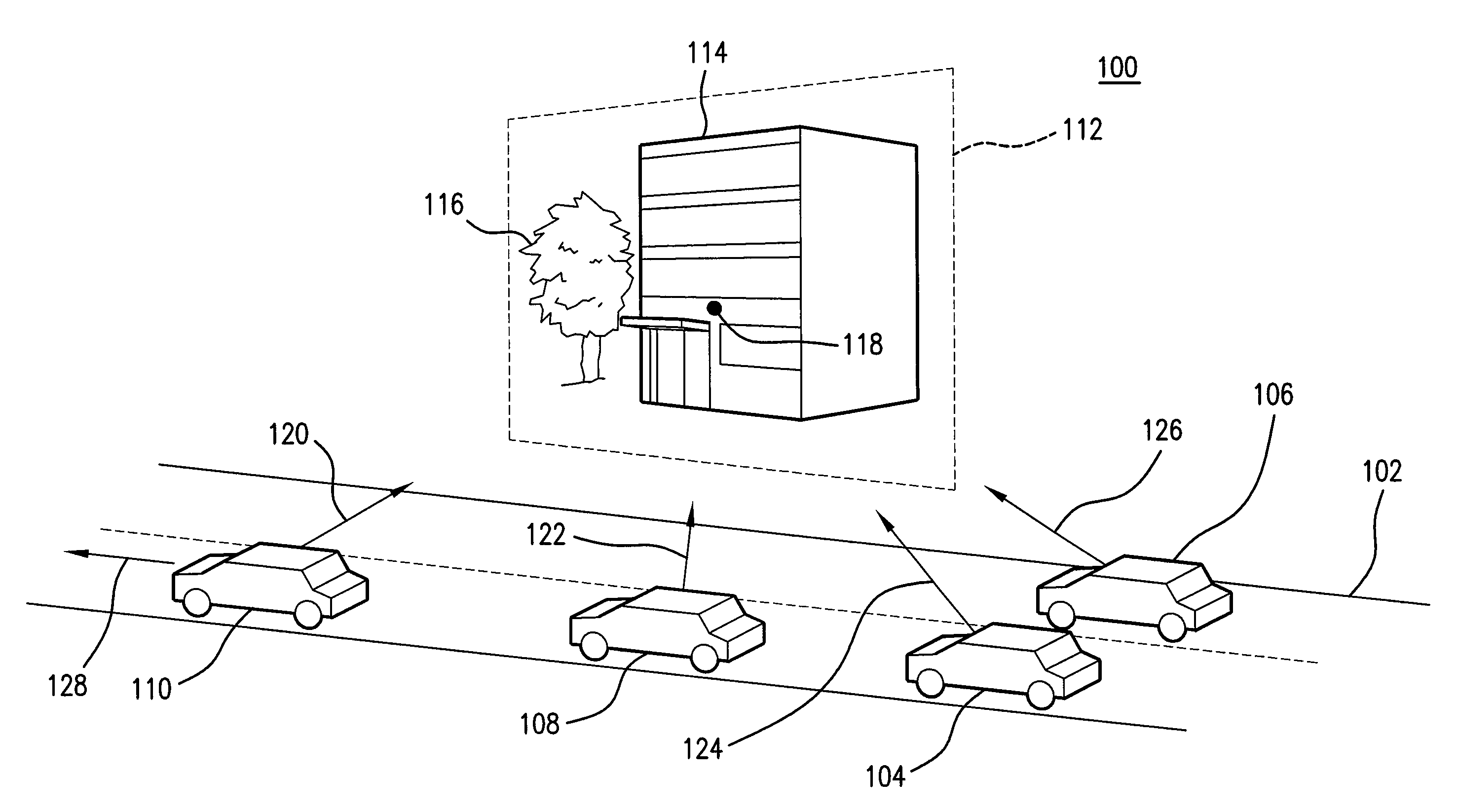
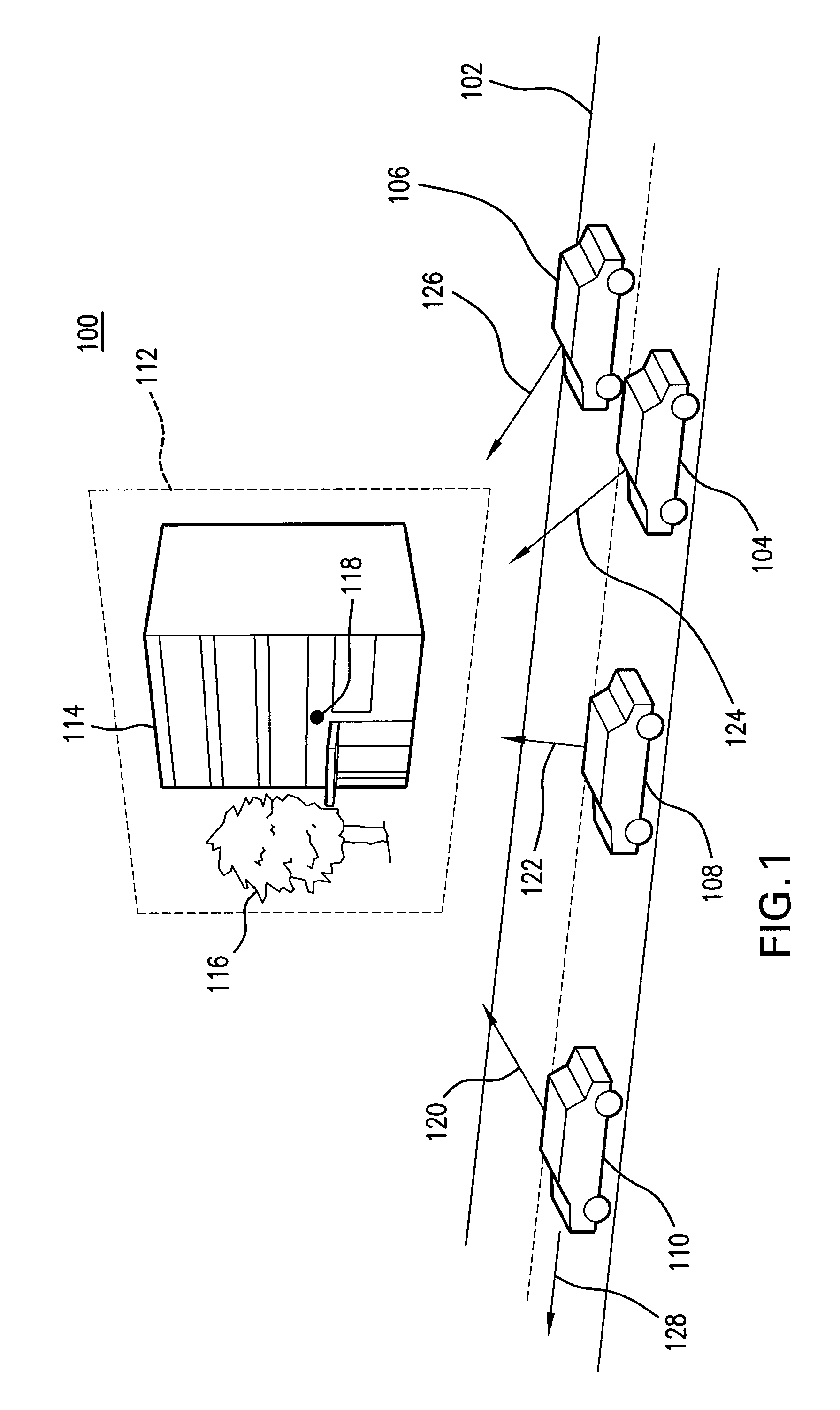
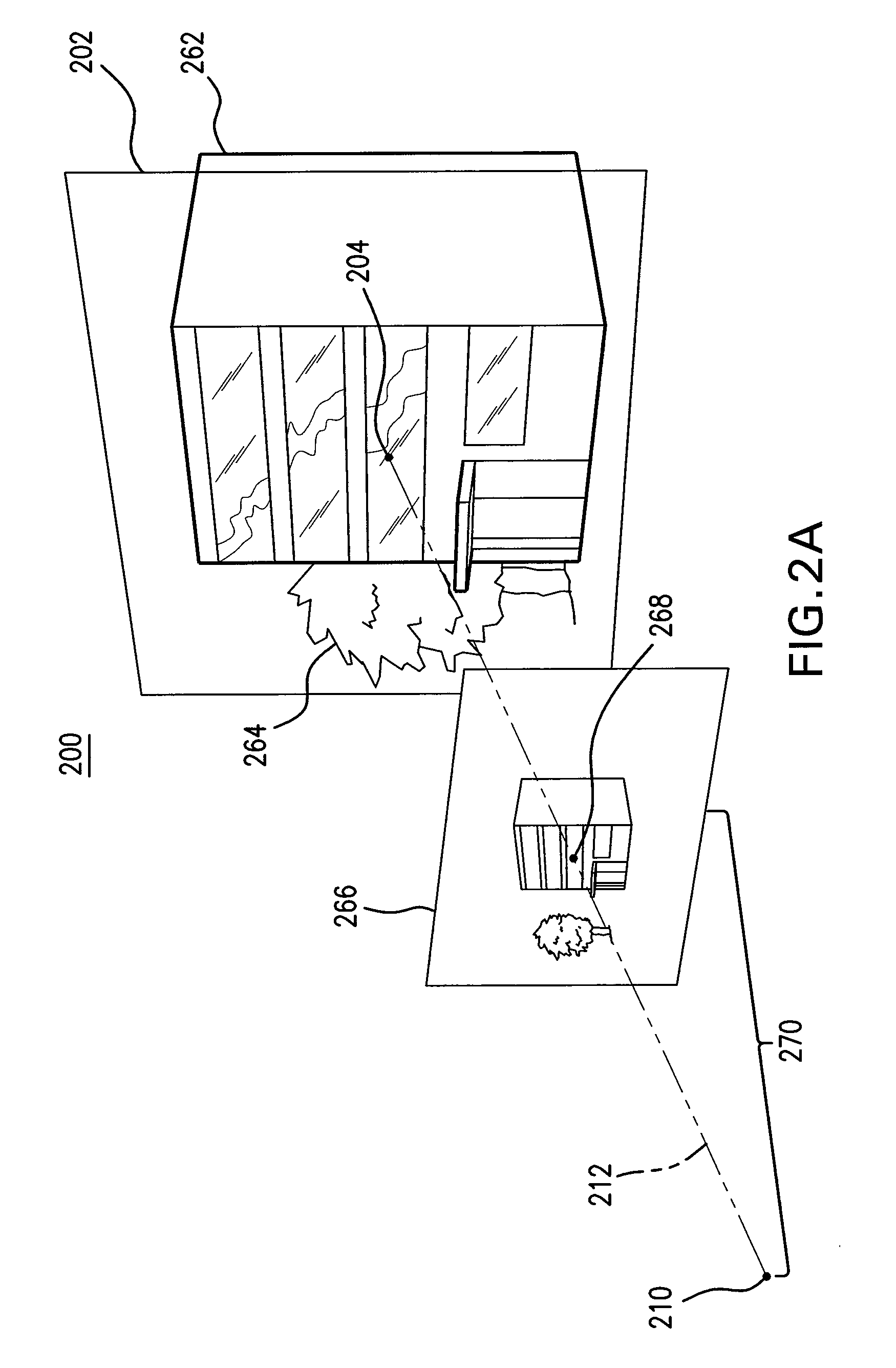
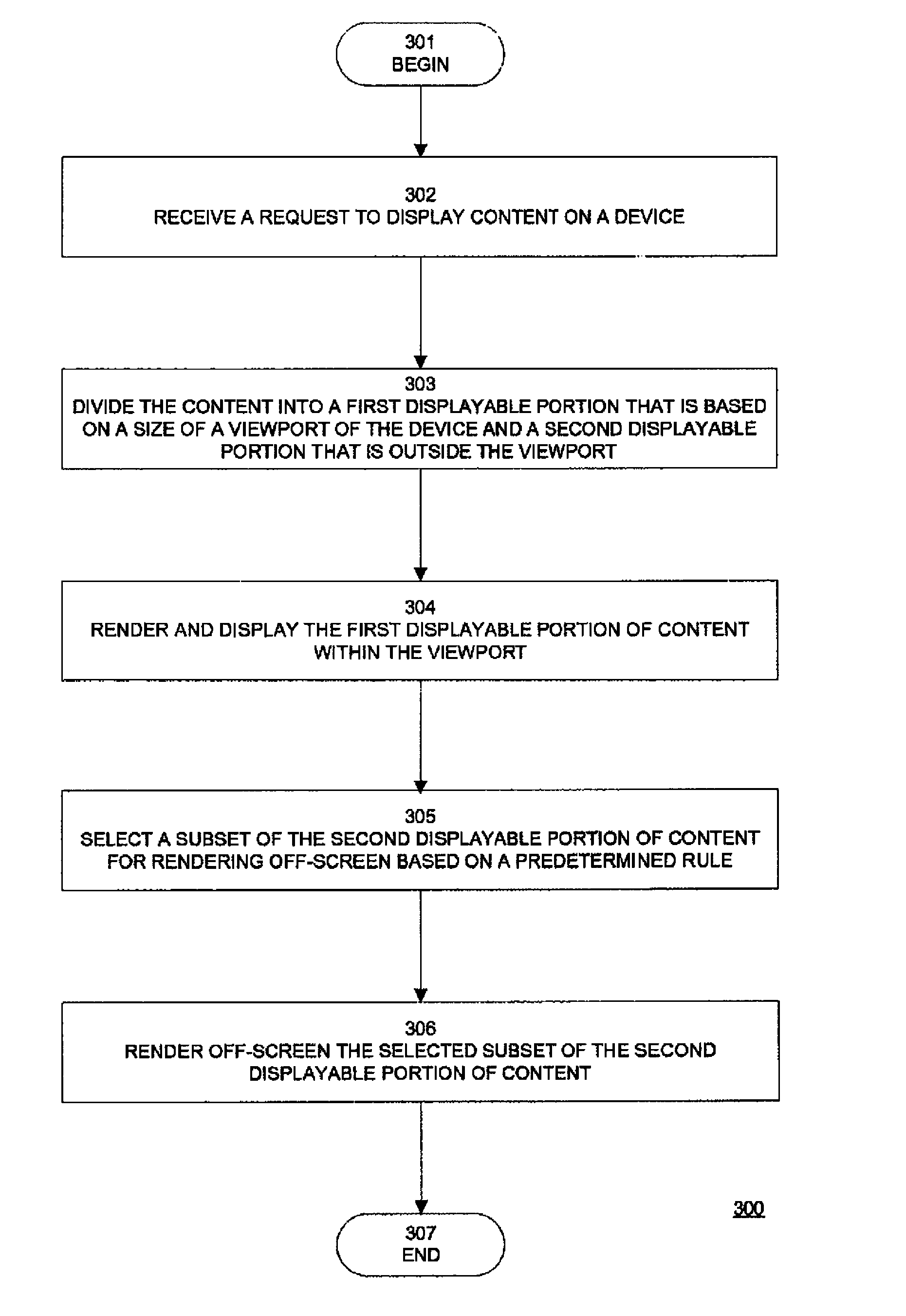
Selective rendering of off-screen content
ActiveUS8314809B1Digital data information retrievalCathode-ray tube indicatorsGraphicsGraphical user interface
Computer-implemented methods for selectively pre-rendering off-screen content for display before the content comes on-screen on a device are provided. In one aspect, a method includes receiving a request to display content on a device and dividing the content into a first displayable portion that is based on a size of a viewport of the device and a second displayable portion that is outside the viewport. The method also includes rendering and displaying the first displayable portion of content within the viewport, and selecting a subset of the second displayable portion of content for rendering off-screen based on a predetermined rule. Systems, graphical user interfaces, and machine-readable media are also provided.
Owner:GOOGLE LLC
Method and apparatus for viewpoint collaboration
InactiveUS20050060656A1Special service provision for substationInput/output processes for data processingGraphicsViewpoints
A method, apparatus, and computer instructions for managing messages. A viewport is displayed on a display in association with a chat window in which the viewport defines an area on the display. The image is defined as graphical data in the area defined by the viewport to form a selected image in response to a user input to select an image. A marker is placed in a text message in the chat window in which the marker is associated with the selected image.
Owner:SNAP INC
Configuring channels for sharing media
A user interface for sharing media items with others. From a sender's perspective, embodiments of the invention allow for an easy-to-use drag-and-drop technique that is more user-friendly than conventional techniques. From the recipient's perspective, embodiments of the invention allow media items from multiple sources to be aggregated into a single viewport, providing a cohesive and unified approach to media items received from others.
Owner:MICROSOFT TECH LICENSING LLC
Placement of map labels
InactiveUS7414637B2Instruments for road network navigationRoad vehicles traffic controlGraphicsClient-side
Methods and systems are presented for the automatic optimal placement text or symbol labels corresponding to graphical objects on maps. Using a map server and a thin, typically mobile client, maps are dynamically drawn and displayed at the client. Optimized labeling of map objects is achieved by dividing the task into pipelined subtasks, some being performed off-line, and others being performed in real time, responsively to changing client requests, and changes in the map viewport. Optimization of candidate label positions is accomplished using simulated annealing.
Owner:TAHOE RES LTD
Features
- R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
Why Patsnap Eureka
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com