Patents
Literature
528 results about "Screen space" patented technology
Efficacy Topic
Property
Owner
Technical Advancement
Application Domain
Technology Topic
Technology Field Word
Patent Country/Region
Patent Type
Patent Status
Application Year
Inventor
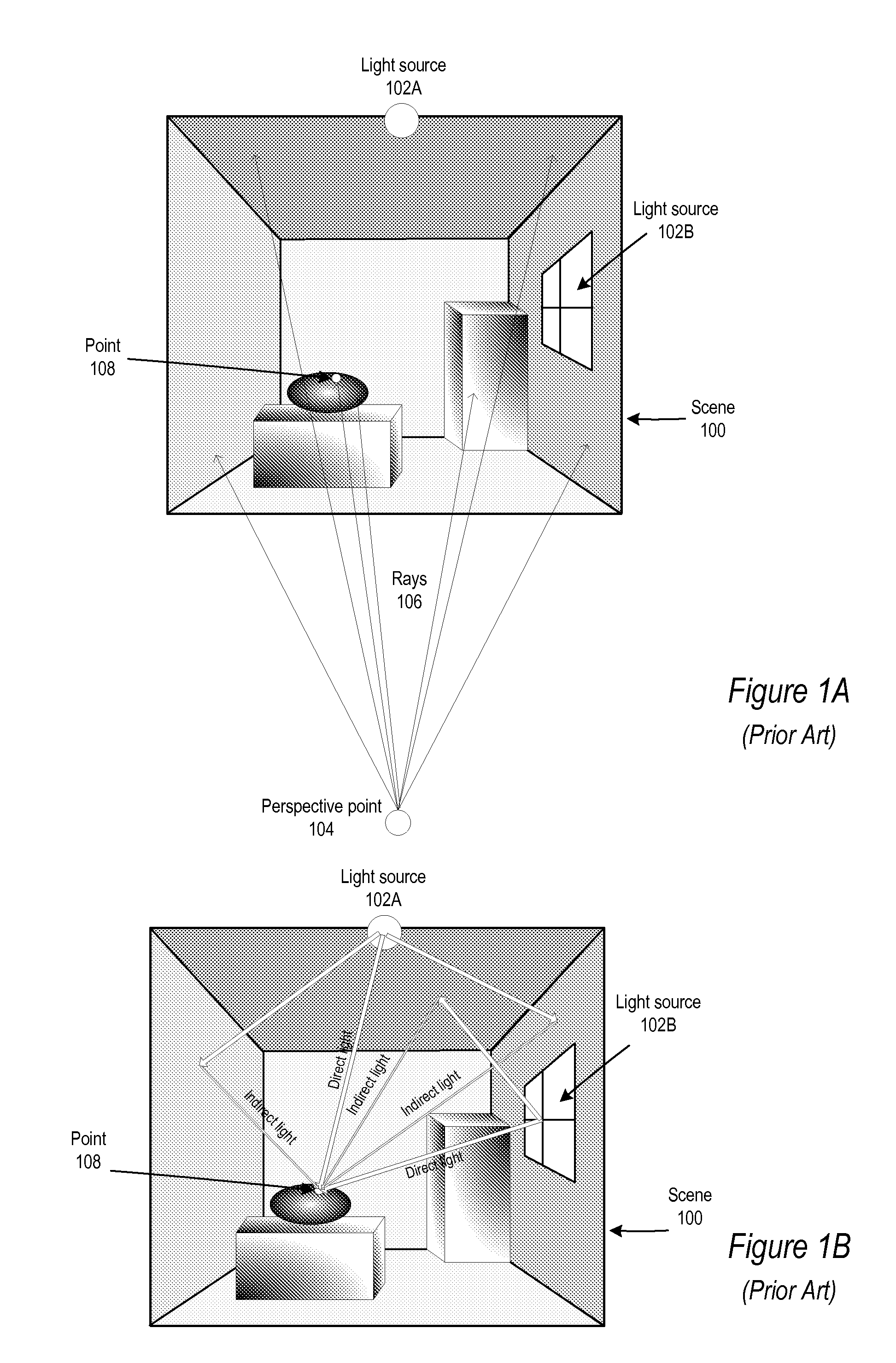
Screen Space Reflection is an effect which is enabled by default that alters the appearance of objects on the surface of Materials.
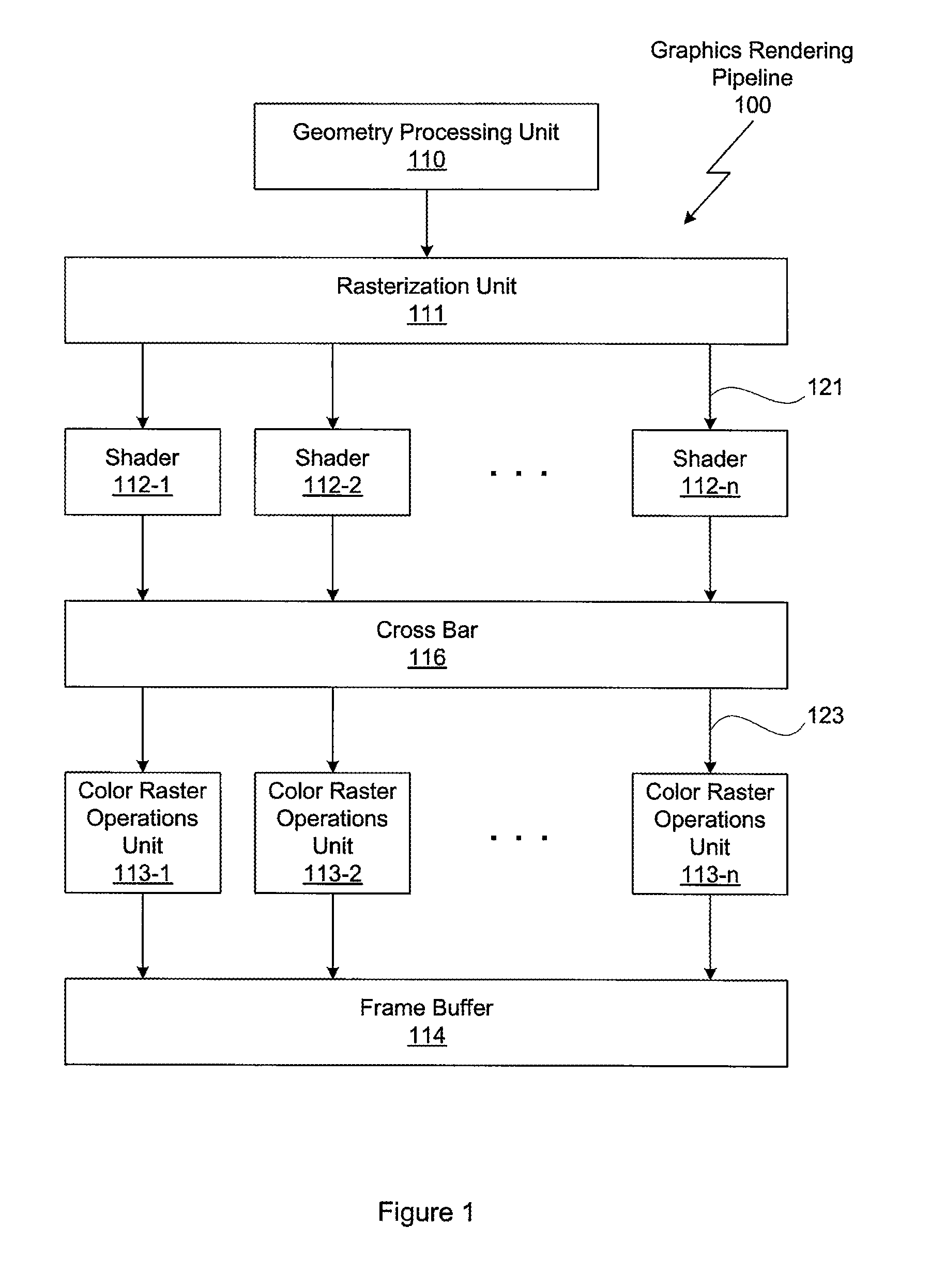
Rendering pipeline
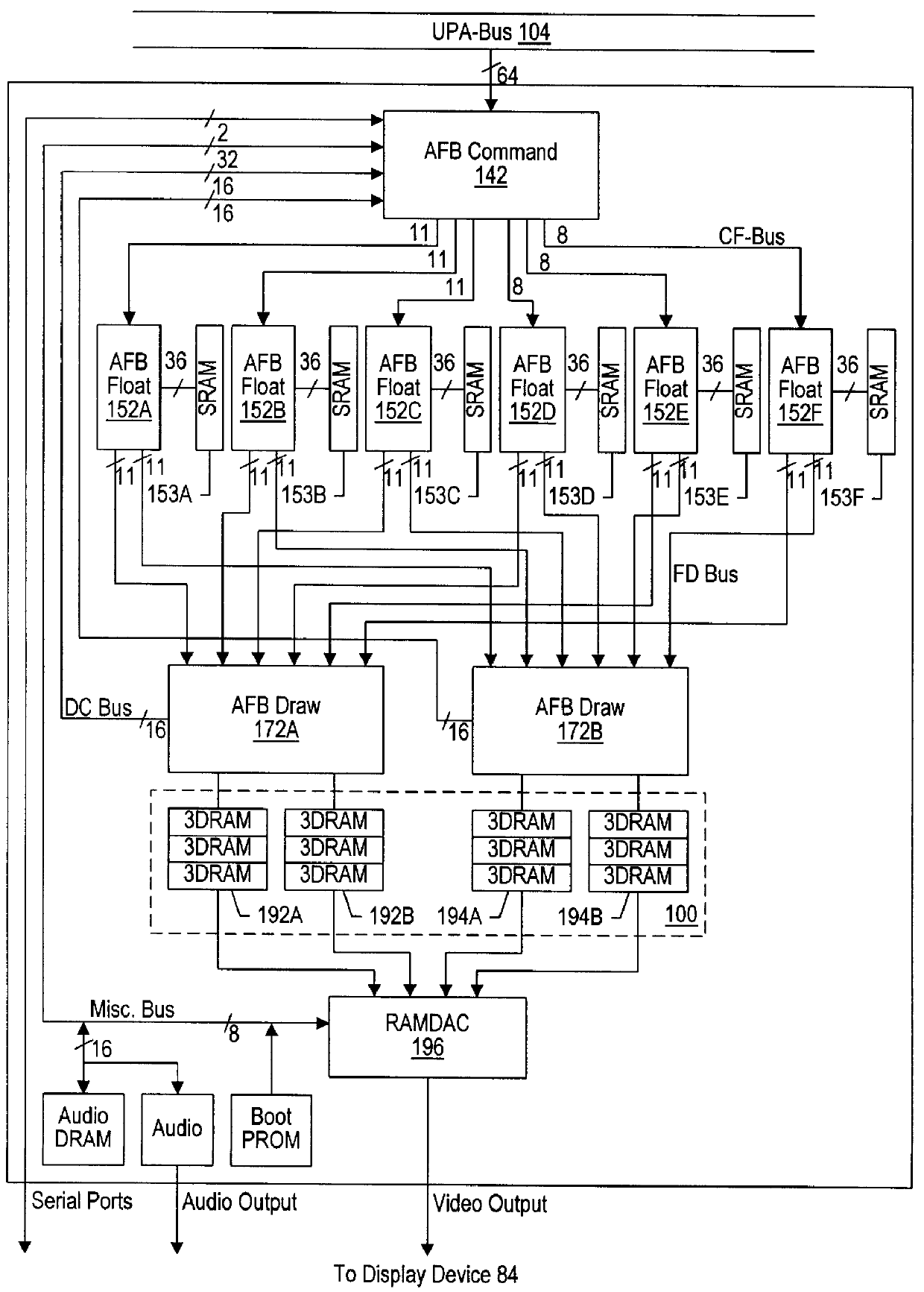
InactiveUS7170515B1EfficientlyReduce memory bandwidth3D-image rendering3D modellingComputational scienceVisibility
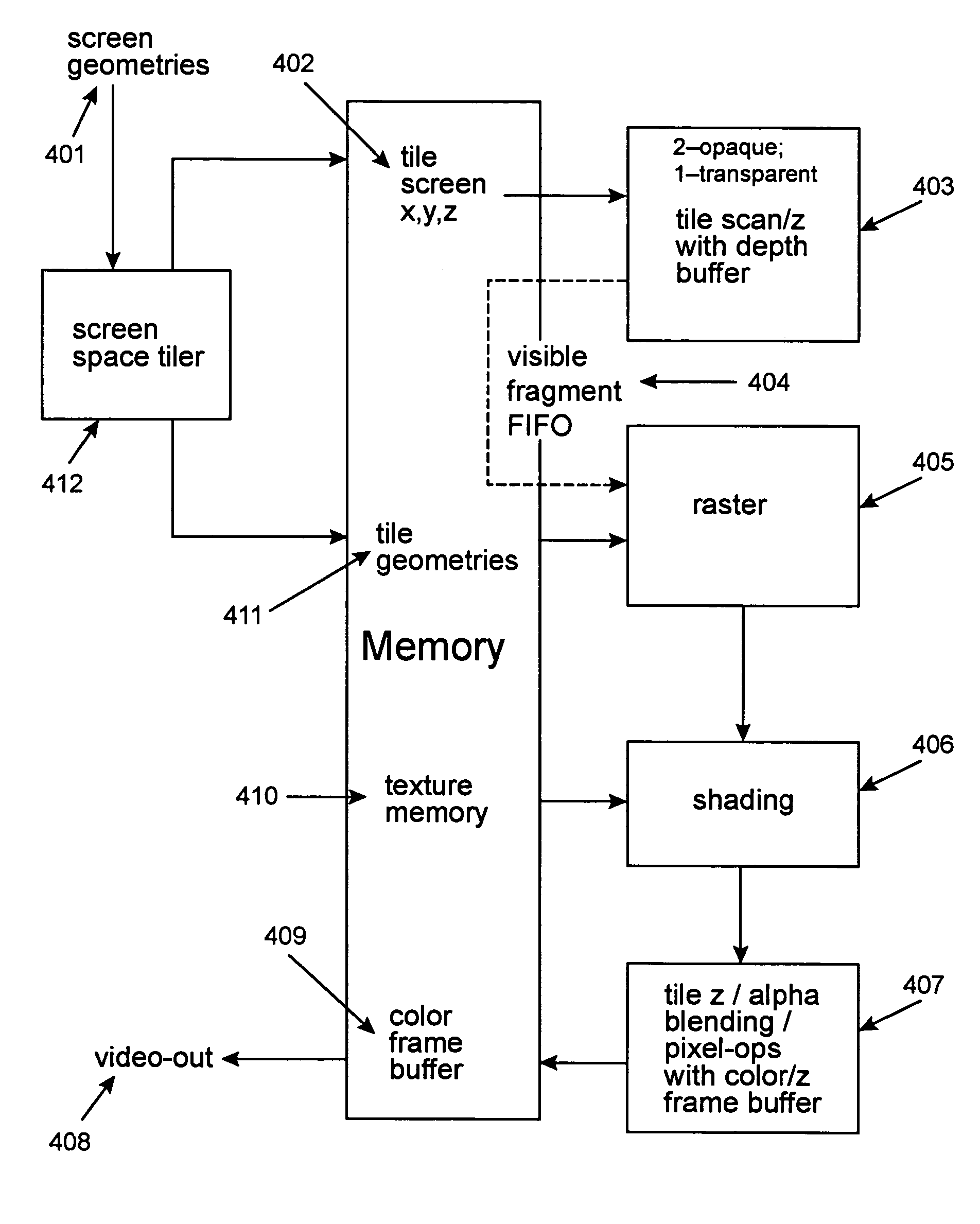
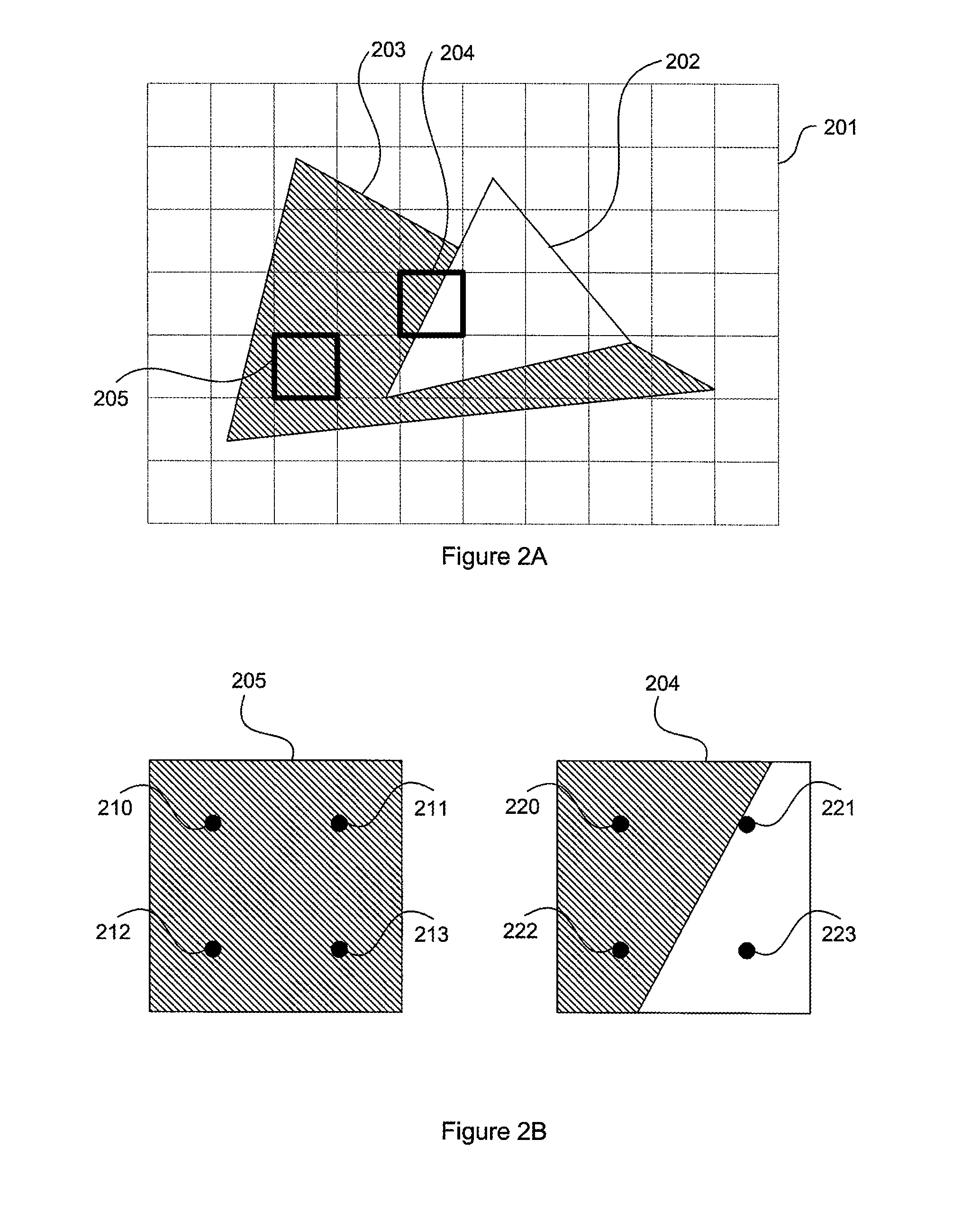
A rendering pipeline system for a computer environment uses screen space tiling (SST) to eliminate the memory bandwidth bottleneck due to frame buffer access and performs screen space tiling efficiently, while avoiding the breaking up of primitives. The system also reduces the buffering size required by SST. High quality, full-scene anti-aliasing is easily achieved because only the on-chip multi-sample memory corresponding to a single tile of the screen is needed. The invention uses a double-z scheme that decouples the scan conversion / depth-buffer processing from the more general rasterization and shading processing through a scan / z engine. The scan / z engine externally appears as a fragment generator but internally resolves visibility and allows the rest of the rendering pipeline to perform setup for only visible primitives and shade only visible fragments. The resulting reduced raster / shading requirements can lead to reduced hardware costs because one can process all parameters with generic parameter computing units instead of with dedicated parameter computing units. The invention processes both opaque and transparent geometries.
Owner:NVIDIA CORP
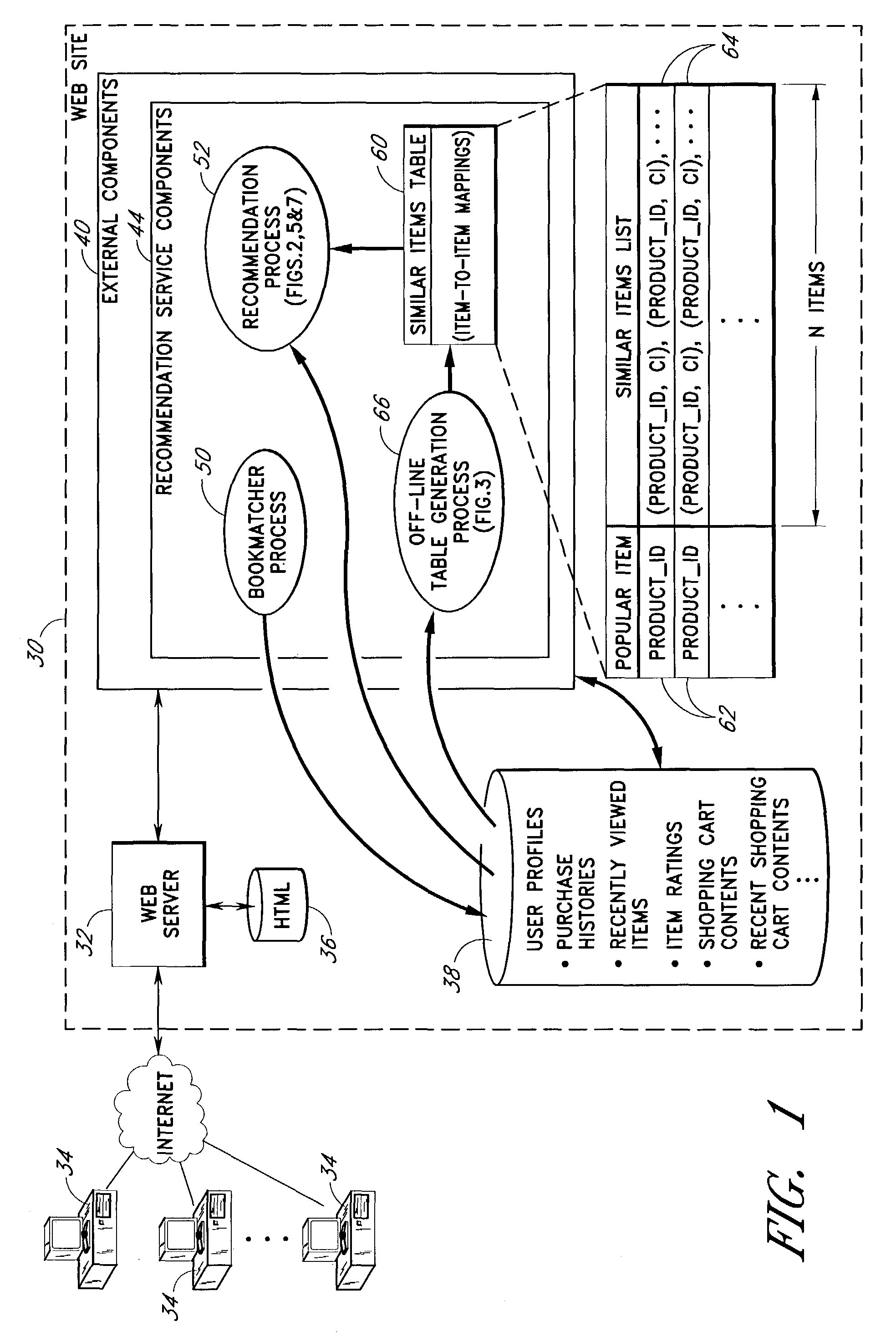
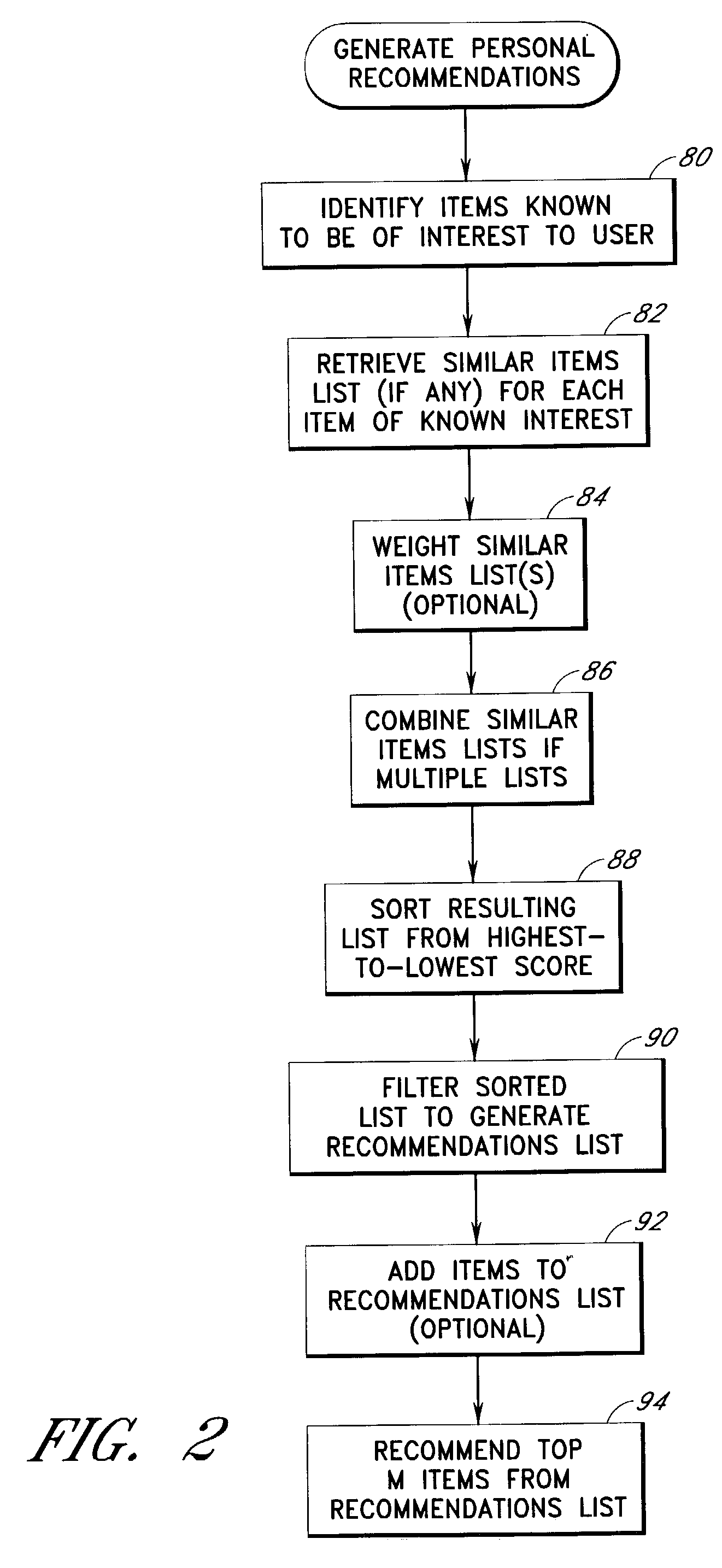
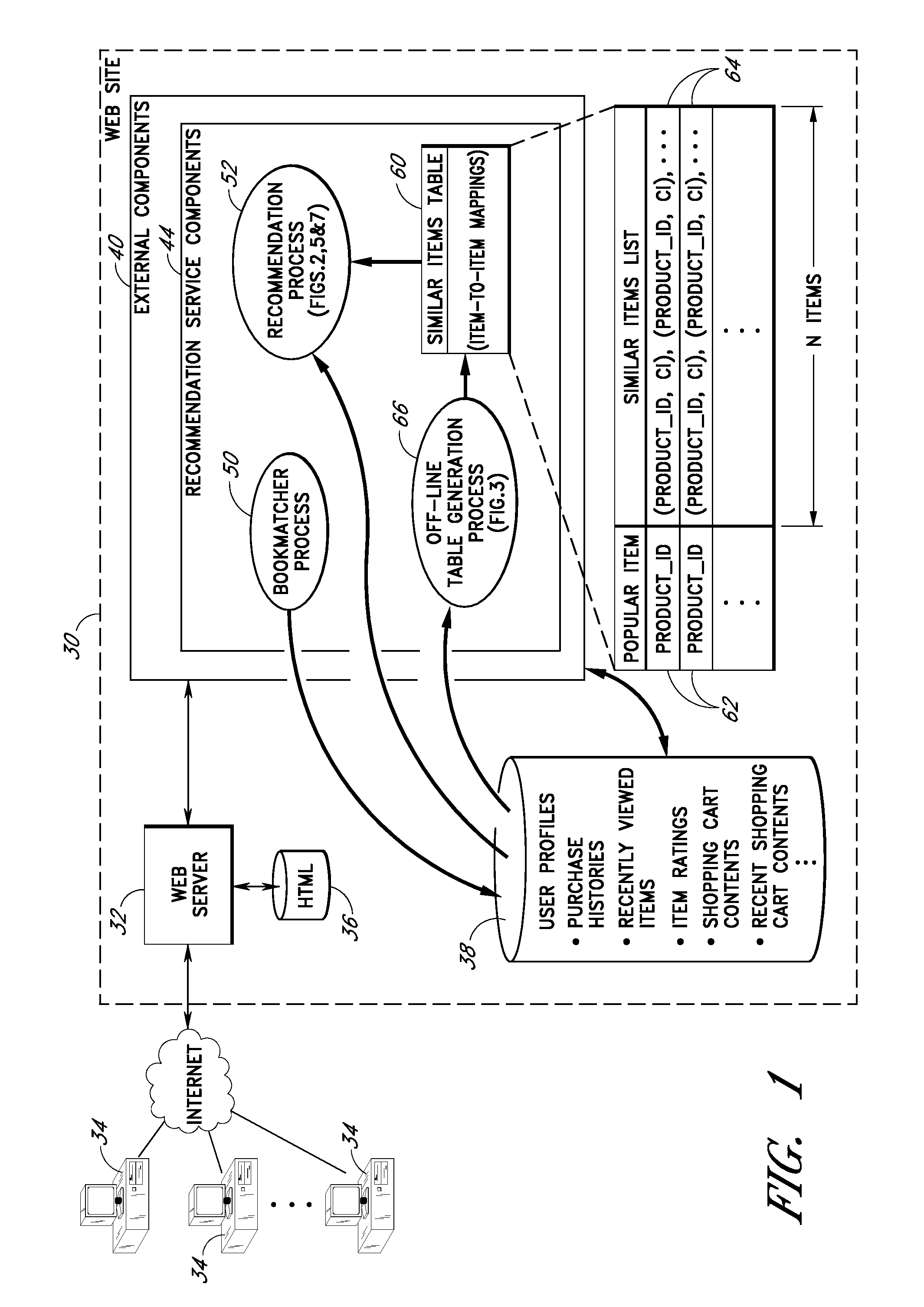
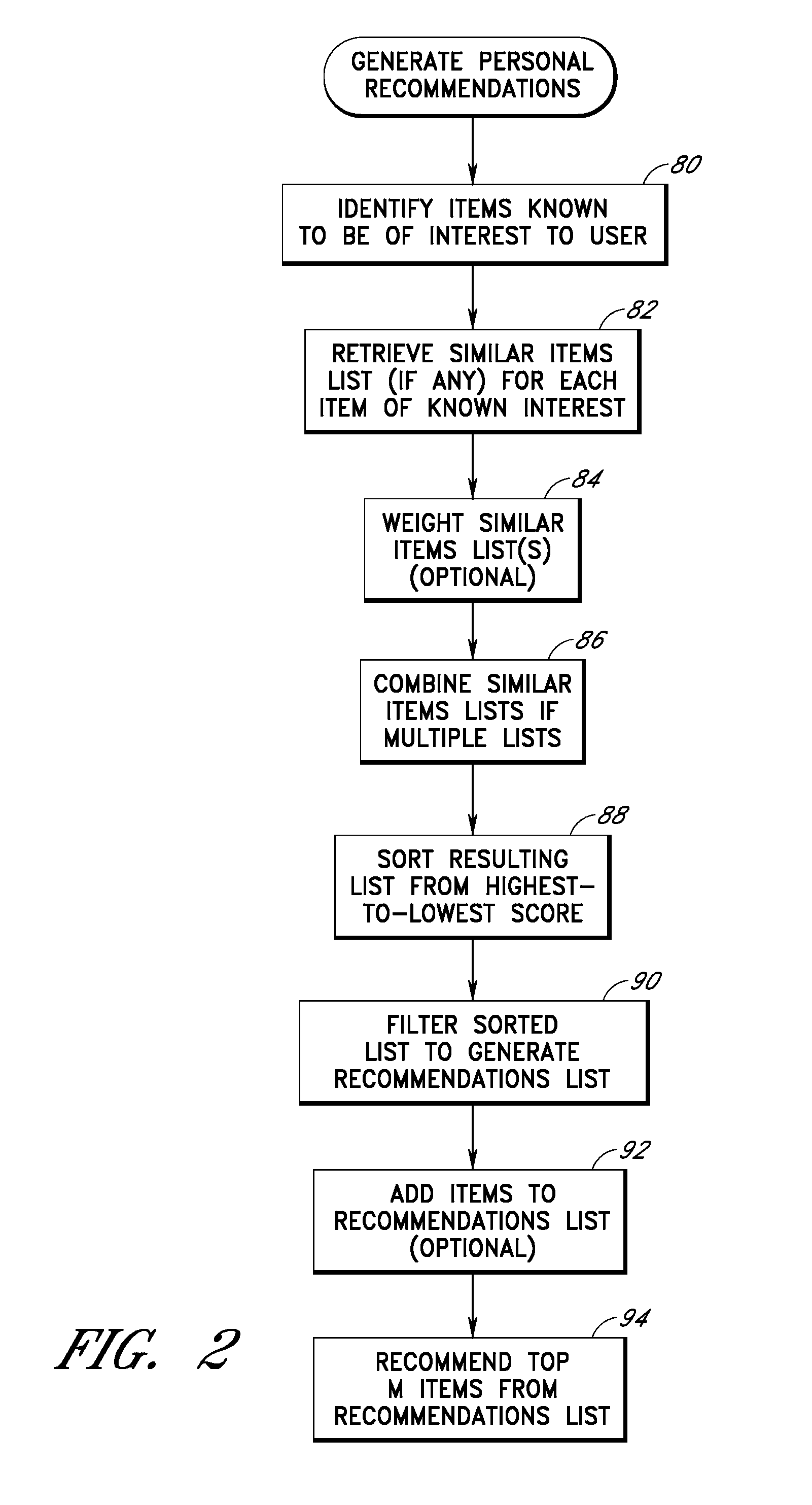
User interface and methods for recommending items to users
ActiveUS7720723B2Good user interfaceWithout sacrificing breadthAdvertisementsGeneration processScreen space
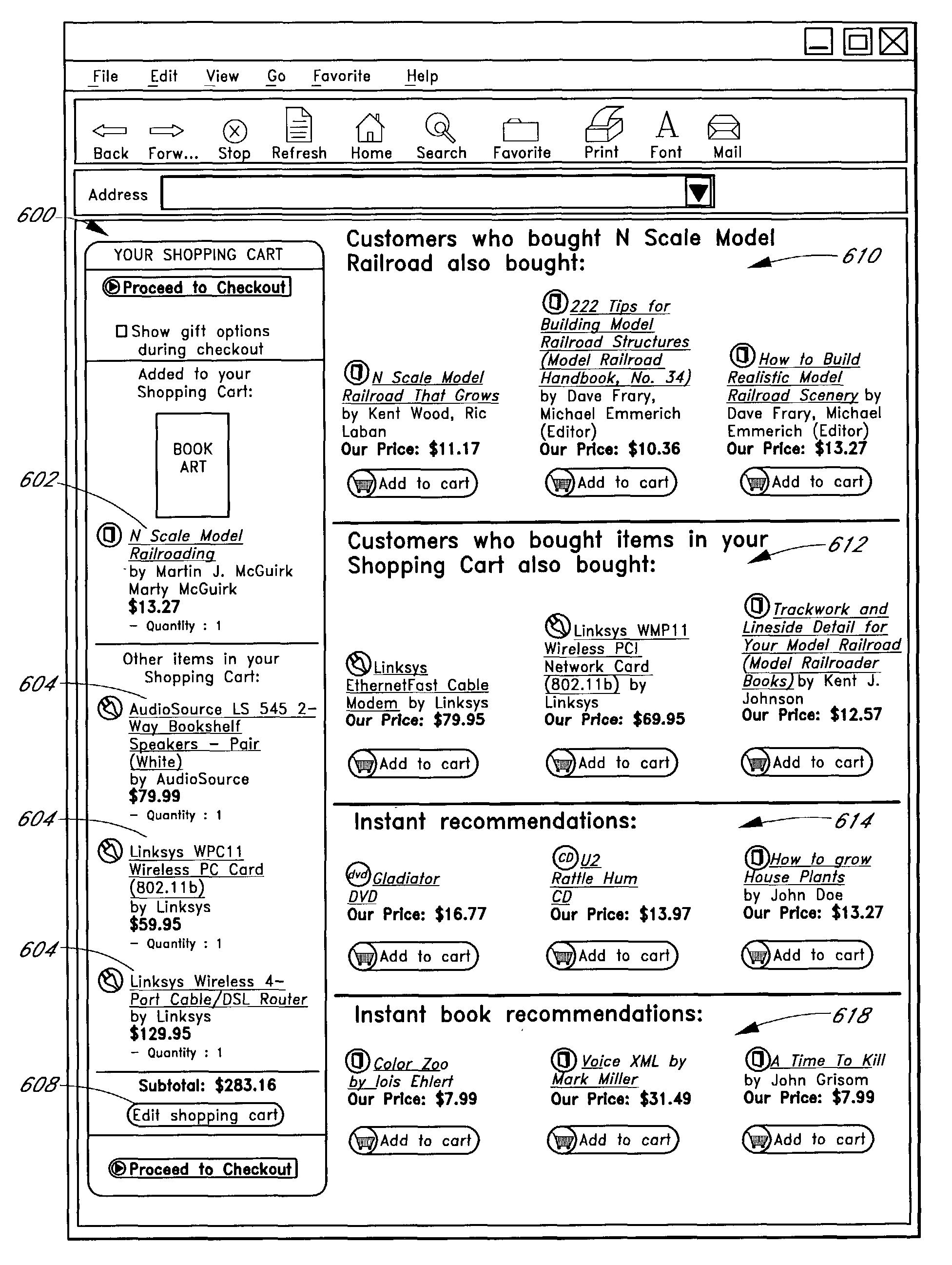
An improved user interface and method are provided for presenting recommendations to a user when the user adds an item to a shopping cart. In response to the shopping cart add event, a page generation process generates and returns a page that includes a recommendations portion and a condensed view of the shopping cart. The recommendations portion preferably includes multiple recommendation sections, each of which displays a different respective set of recommended items selected according to a different respective recommendation or selection algorithm (e.g., recommendations based on shopping cart contents, recommendations based on purchase history, etc.). The condensed shopping cart view preferably lacks controls for editing the shopping cart, and lacks certain types of product information, making more screen real estate available for the display of the recommendations content. A link to a full shopping cart page allows the user to edit the shopping cart and view expanded product descriptions.
Owner:AMAZON TECH INC
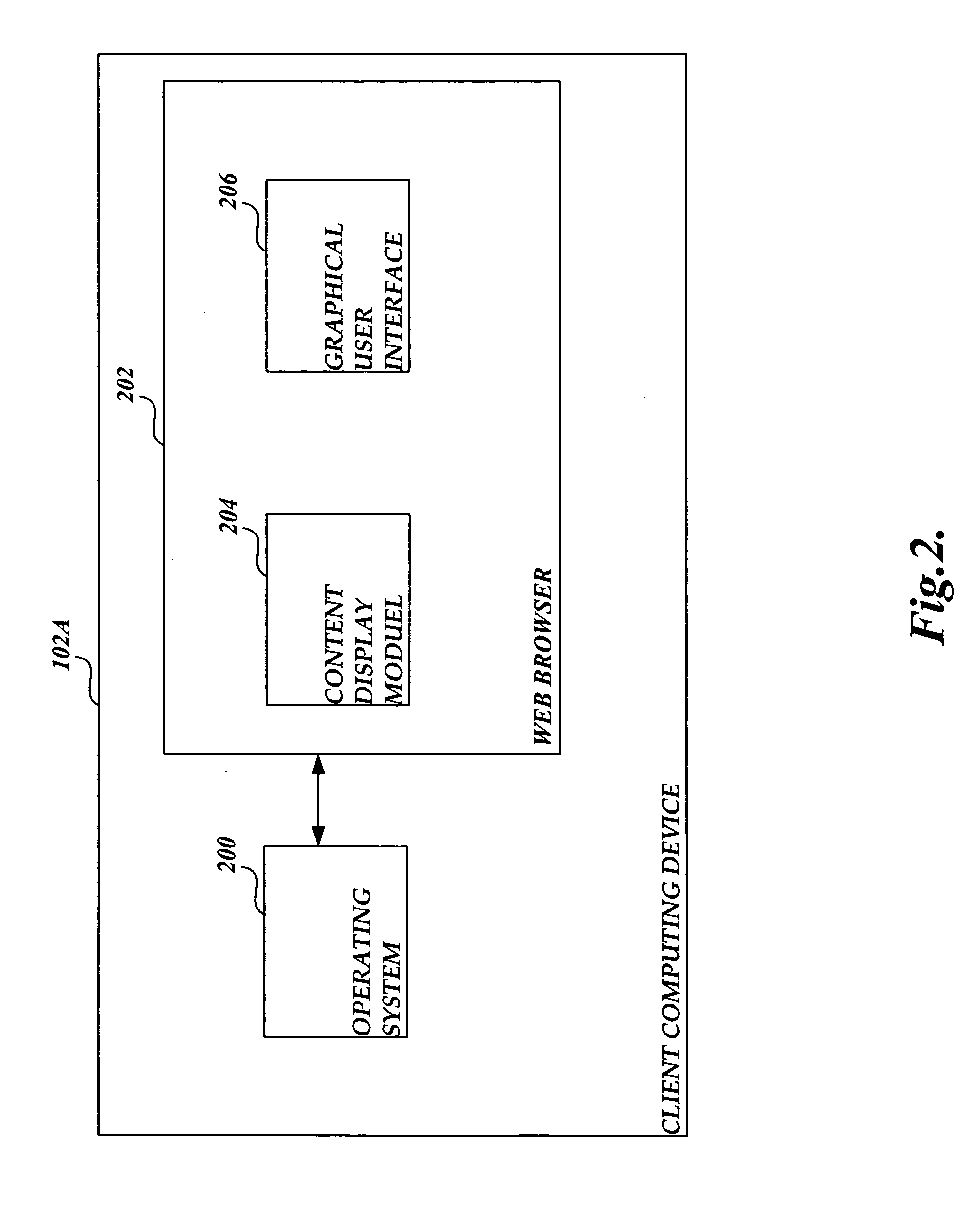
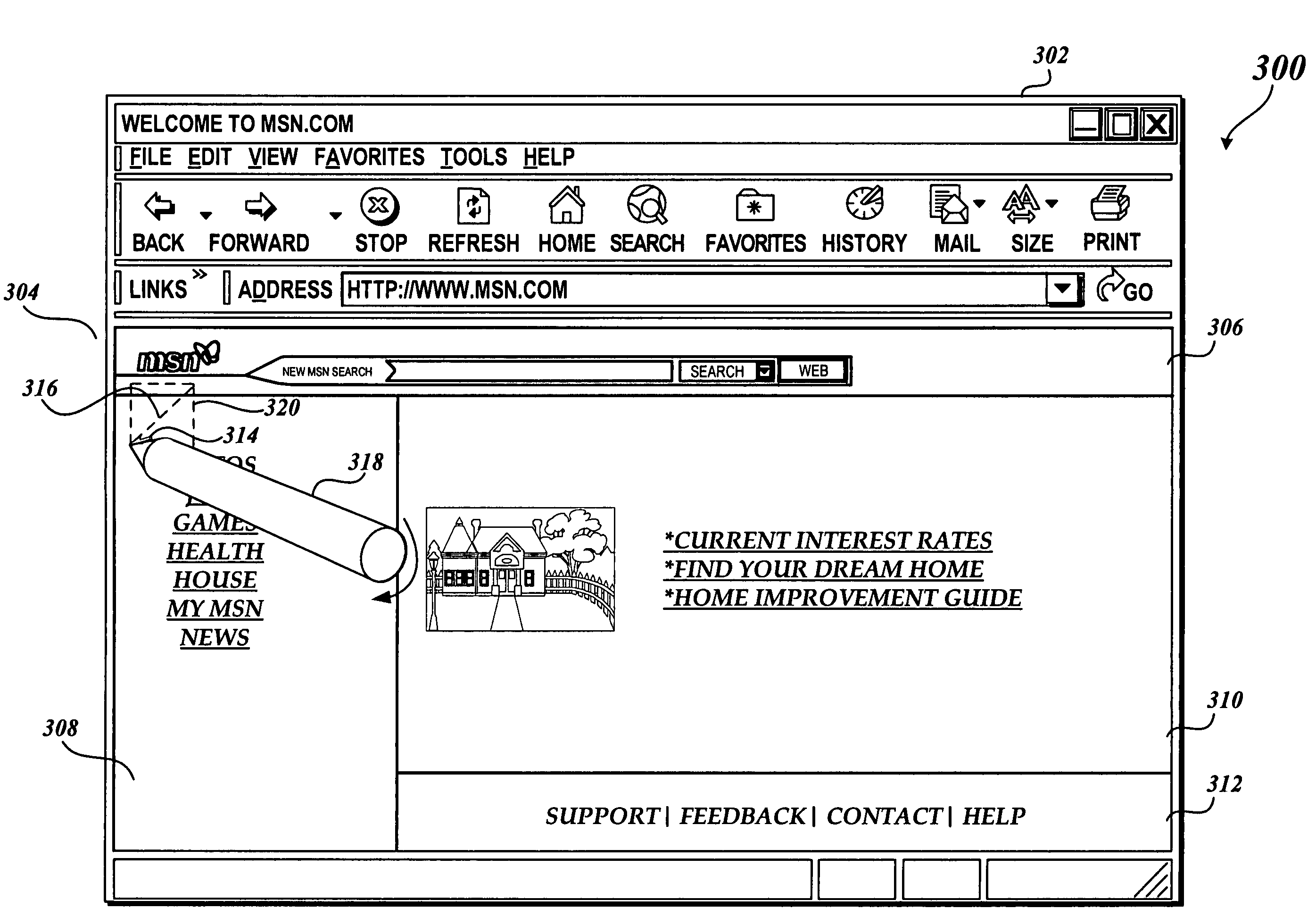
System and method of displaying content on small screen computing devices
InactiveUS20060036955A1Simple interfaceEasy to viewDigital data information retrievalSpecial data processing applicationsSmall form factorMagnification
Embodiments of the present invention provide a system, method, and computer-readable medium for viewing Web pages on small form factor computing devices. More specifically, the present invention layers Web browsing in a system where a Web page is first displayed in an overview mode at a predetermined magnification. From a Web page displayed in overview mode, the user may issue adaptive viewing commands that cause relevant content to be displayed using additional screen space.
Owner:MICROSOFT TECH LICENSING LLC
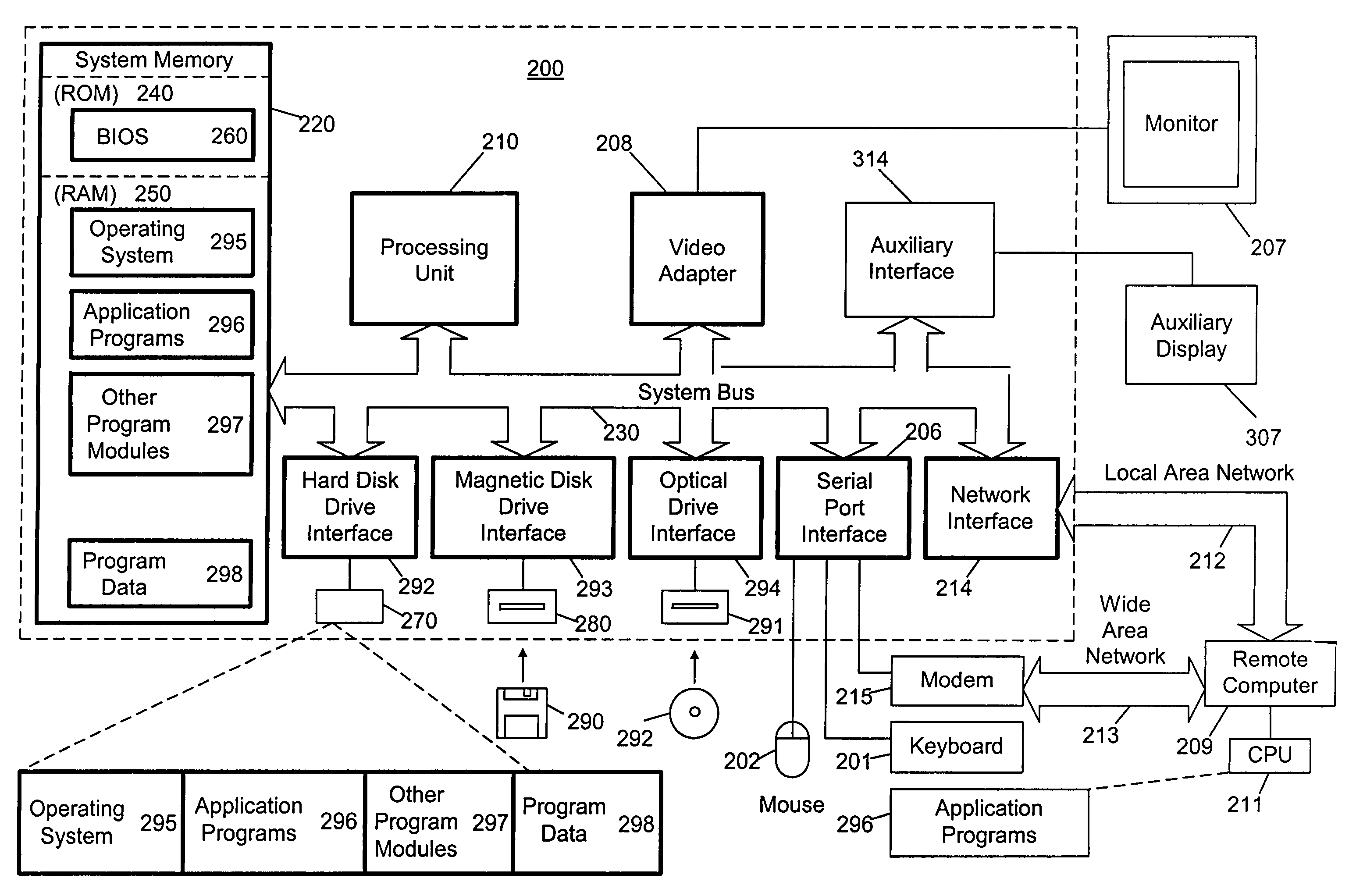
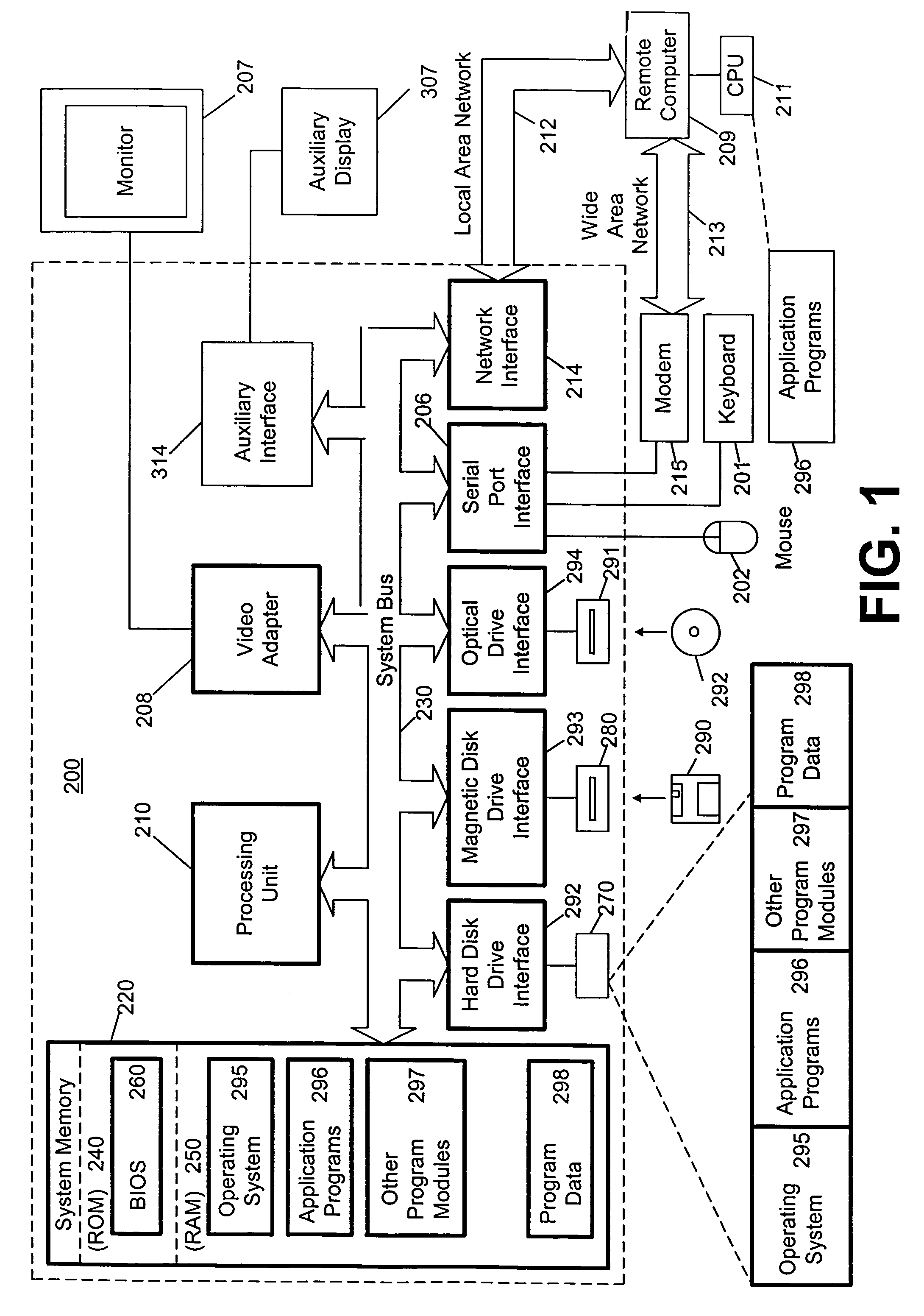
Auxiliary display unit for a computer system
InactiveUS7030837B1Digital data processing detailsDigital computer detailsComputerized systemApplication software
A host computer is provided with a main display unit and an auxiliary display unit. The host computer can free up screen space on the main display screen by routing certain types of display information to the auxiliary display unit for display. Display information can range from notification of events such as receipt of email, appointments, system messages, and information from separate applications. The auxiliary display panel may function as a user interface for audio, video, “push information”, MP3 player or become the hardware equivalent of a multimedia player. The auxiliary display panel may be integrated together with the host computer in the same physical structure or may be part of a standalone display unit that is wired or wirelessly coupled to the host computer.
Owner:MICROSOFT TECH LICENSING LLC
User interface and methods for recommending items to users
ActiveUS20100191619A1Without sacrificing breadthQuick buildMarketingInput/output processes for data processingGeneration processUser interface
Improved user interfaces and methods are provided for presenting item recommendations to a user when the user selects an item to add to an electronic shopping cart. In response to the user's selection, a page generation process generates and returns a page that includes a condensed shopping cart portion and a recommendations portion. The condensed shopping cart portion displays the contents of the shopping cart, but omits some of the item information and / or controls provided on a shopping cart page, thereby preserving more screen real estate for the display of item recommendations. The condensed shopping cart portion also includes a link to the shopping cart page.
Owner:AMAZON TECH INC
System and method for asynchronous continuous-level-of-detail texture mapping for large-scale terrain rendering
InactiveUS20070171234A1Character and pattern recognitionCathode-ray tube indicatorsLevel of detailMulti resolution
A multi-resolution texture mapping system suitable for large scale terrain rendering using commodity graphics processing units (GPU). The GPU vertex and fragment shaders are used to implement the clip-mapping functionality. The terrain texture is represented by a combination of a mip-map and a multi-level clip-map having independent origins and off-set values. The independent clip-map levels may be independently updated. The offset values allow the origins to be associated with a reference point in a scene to be rendered. The desired clip-map level to be used to render a particular fragment may be determined using the base 2 logarithm of the maximum screen-space derivative of the source texture required by the terrain geometry to be drawn. If the desired clip-map level is non-integer and lies between two clip-map levels, appropriate texel data is created by interpolating between the bounding clip-map levels. This interpolation allows a multi-resolution texture mapping to be displayed.
Owner:D& S CONSULTANTS
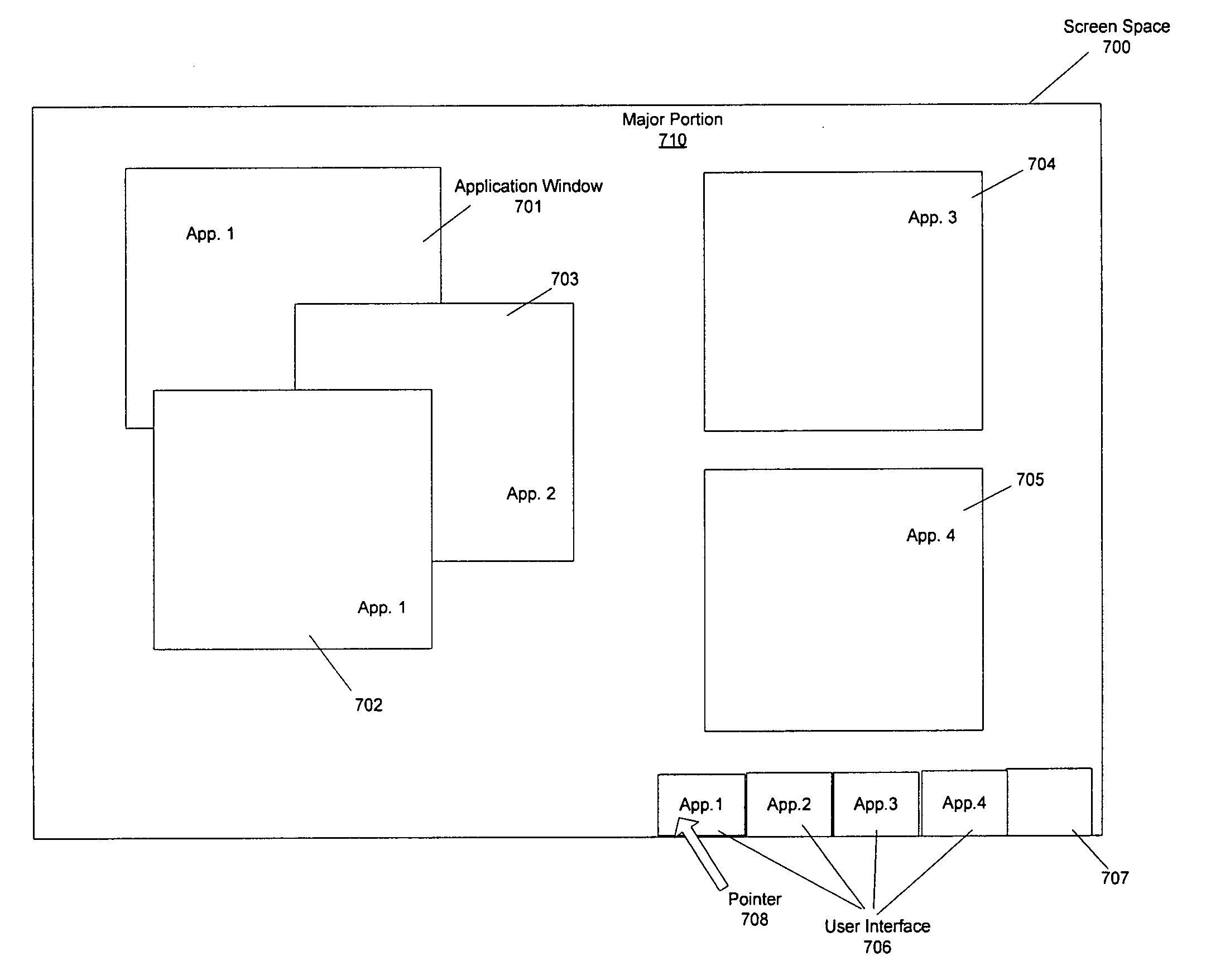
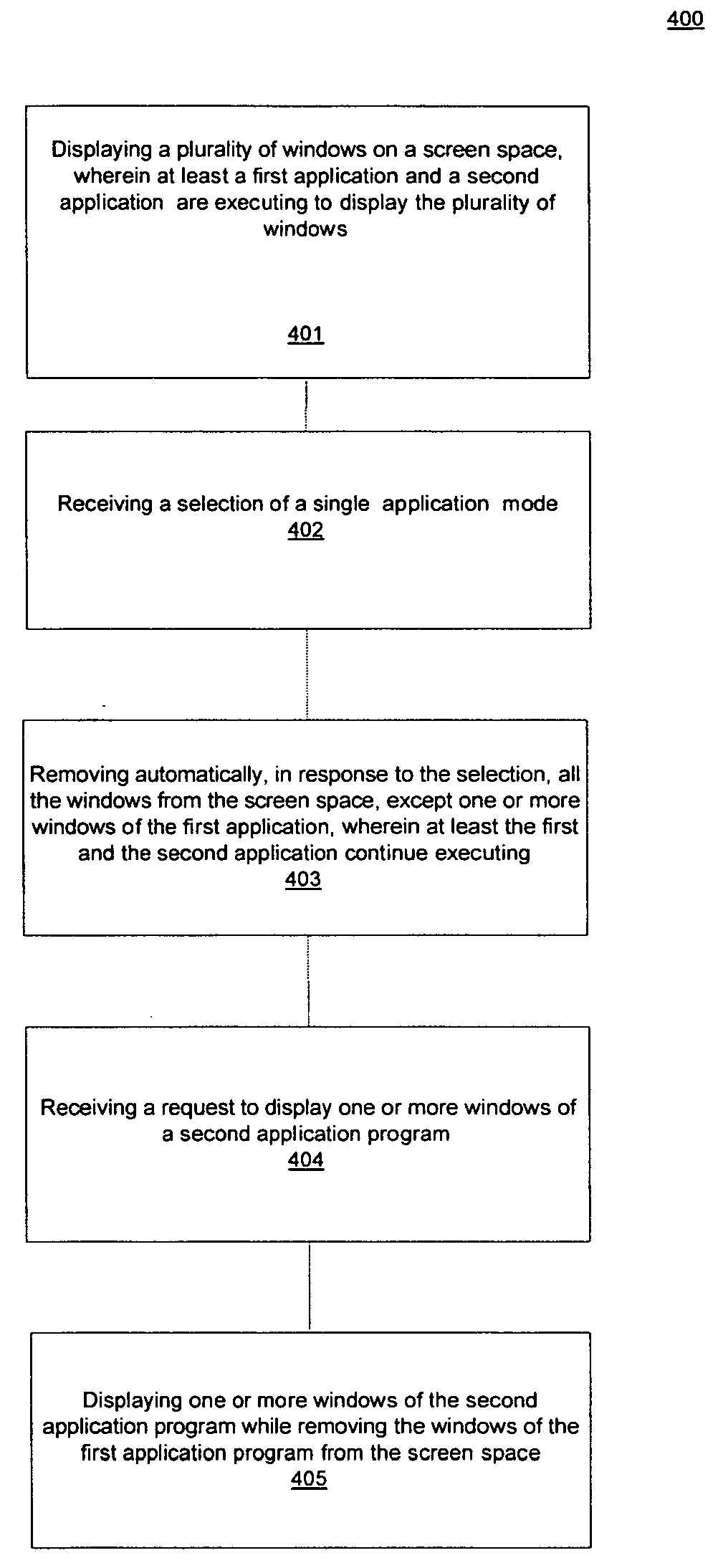
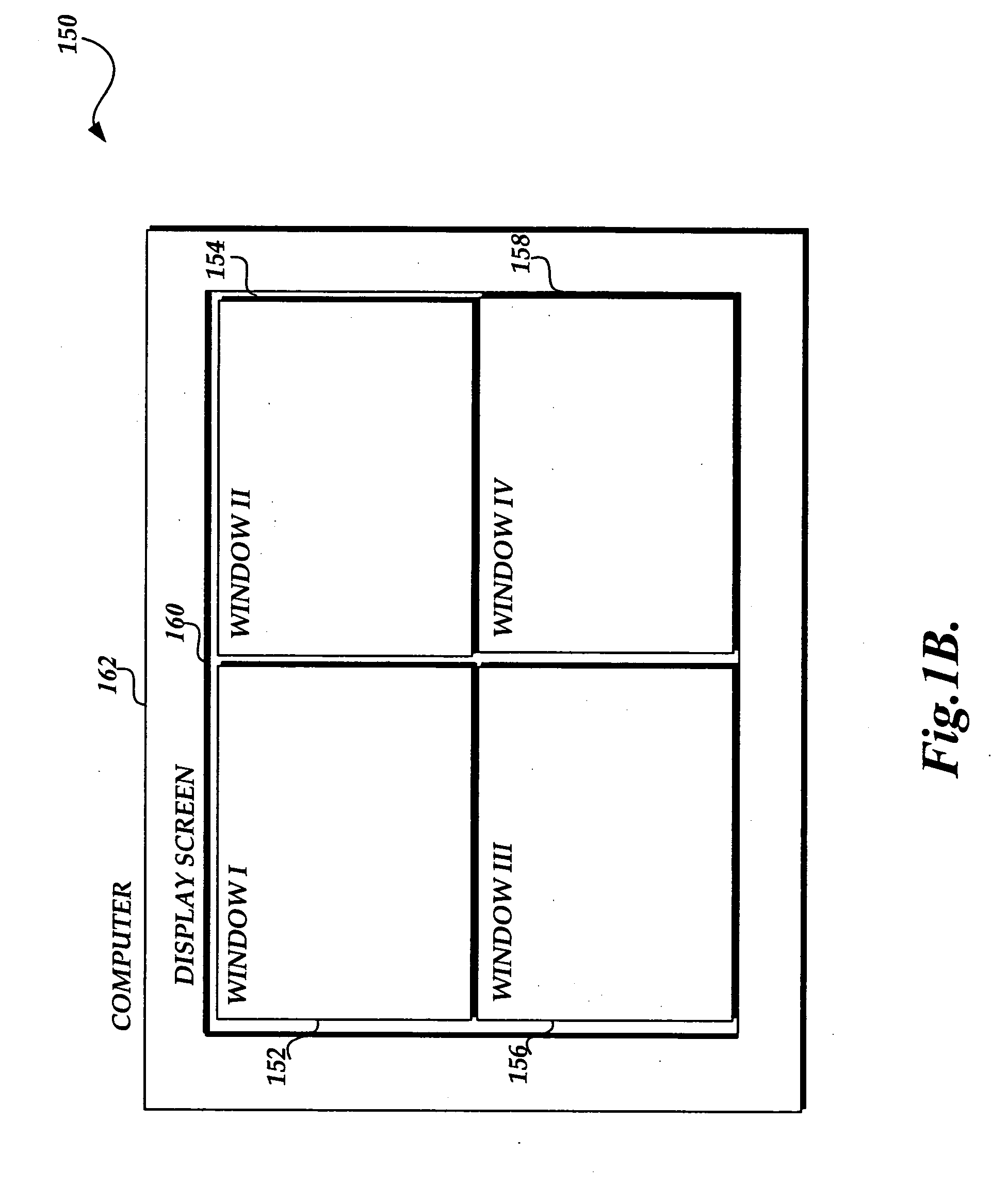
Methods of manipulating a screen space of a display device
ActiveUS20100088635A1Cathode-ray tube indicatorsExecution for user interfacesDisplay deviceApplication software
Methods to manipulate a screen space of a display device are disclosed. A plurality of application windows of a plurality of applications are displayed on a screen space. At least a first application and a second application are executing to display a plurality of windows. A user interface of system level applications may be displayed. A selection of a single application mode is received. In response to the receiving of the selection of the single application mode, all the windows are removed automatically from the screen space, except for a first application window. At least the first and second applications continue being executed. The user interface of the system level applications may continue to be displayed. Next, a request to display a second application window is received. The second application window is displayed while the first application window is removed from the screen space.
Owner:APPLE INC
Methods of manipulating a screen space of a display device
InactiveUS7595810B2Cathode-ray tube indicatorsExecution for user interfacesDisplay deviceMultiple applications
Methods to manipulate a screen space of a display device are disclosed. A plurality of application windows of a plurality of applications are displayed on a screen space. At least a first application and a second application are executing to display a plurality of windows. A user interface of system level applications maybe displayed. A selection of a single application mode is received. In response to the receiving of the selection of the single application mode, all the windows are removed automatically from the screen space, except for a first application window. At least the first and second applications continue being executed. The user interface of the system level applications may continue to be displayed. Next, a request to display a second application window is received. The second application window is displayed while the first application window is removed from the screen space.
Owner:APPLE INC
Arrangement of information into linear form for display on diverse display devices
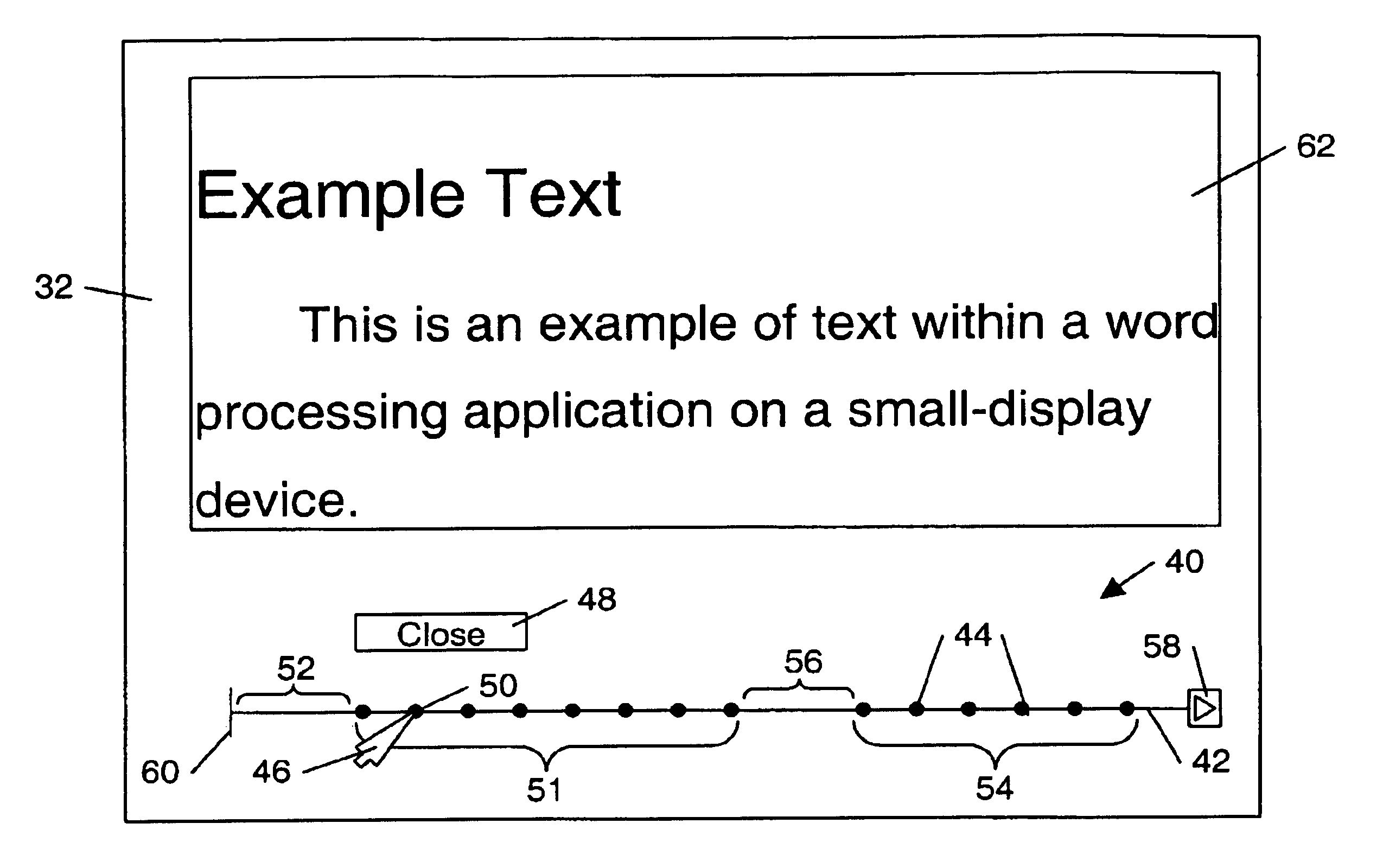
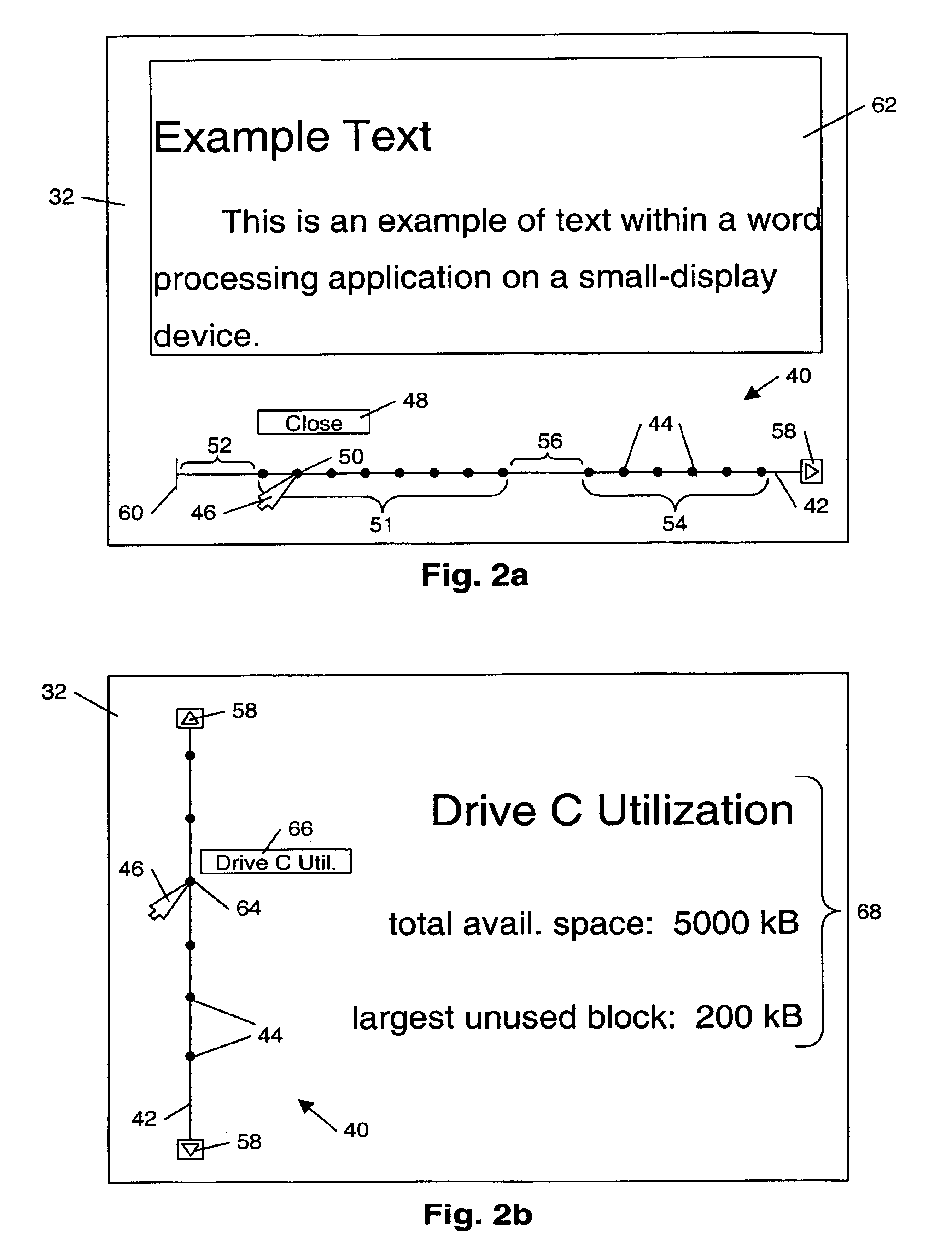
InactiveUS6924797B1Make fastEasy accessDigital output to display deviceGraphicsGraphical user interface
A method of display with a graphical user interface includes arranging selectable navigation points along a line configured on a display screen. In some embodiments, the selectable points correspond to pieces of information to be displayed, such that selection of a selectable point causes the corresponding piece of information to be displayed. The selectable points may be arranged along the line according to a priority sequence of the corresponding pieces of information. In other embodiments, the selectable points correspond to functions useful in using an application program. Selection of a selectable point in this embodiment causes the corresponding function to be executed. The line with selectable navigation points may therefore be used in place of other display tools such as toolbars or pull-down menus, and may allow rapid selection of desired options, commands, or information while using a minimum amount of screen space.
Owner:IBM CORP
Viewport-based desktop rendering engine
Methods, apparatuses and systems directed, in one implementation, to a system of dynamically spawned, virtual, three-dimensional (3D) viewports which render transparently within the elements of, or on top of, an existing desktop display environment, allowing rendered objects to seamlessly interact and move between different 3-dimensional viewport spaces and the two-dimensional (2D) screen space of the desktop environment. The present invention, in one implementation, renders multiple 3-dimensional viewports and free floating 3-dimensional objects on the client desktop, seamlessly mixed into the normal event and rendering pipeline of the computing device's 2-dimensional screen aligned desktop and windowed environment.
Owner:URBACH JULIAN MICHAEL
Rapid computation of local eye vectors in a fixed point lighting unit
InactiveUS6014144ADigital computer detailsElectric digital data processingFixation pointSpecular reflection
A rapid method for calculating a local eye vector in a fixed point lighting unit. For a given triangle primitive which is to be projected into a given viewport in screen space coordinates, the local eye vector corresponds to a given eye position and a first vertex of the given triangle primitive. (A different local eye vector is calculated for each vertex of the given triangle primitive). The method first comprises generating a view vector matrix which corresponds to the given eye position and corner coordinates of the given viewport, where the corner coordinates are expressed in screen space coordinates. The view vector matrix is usable to map screen space coordinates to an eye vector space which corresponds to the given viewport. The method next includes receiving a first set of coordinates (in screen space) which correspond to the first vertex. The first set of coordinates are then scaled to a numeric range which is representable by the fixed point lighting unit. Next, the first set of coordinates are transformed using the view vector matrix, which produces a non-normalized local eye vector within the eye vector space for the given viewport. The non-normalized local eye vector is normalized to form a normalized local eye vector. The normalized local eye vector is then usable to perform subsequent lighting computations such as computation of specular reflection values for infinite light sources, producing more realistic lighting effects than if an infinite eye vector were used. These more realistic lighting effects do not come at decreased performance, however, as the local eye vector may be calculated rapidly using this method.
Owner:ORACLE INT CORP
Methods of manipulating a screen space of a display device
InactiveUS20070226647A1Cathode-ray tube indicatorsExecution for user interfacesDisplay deviceHuman–computer interaction
Methods to manipulate a screen space of a display device are disclosed. A plurality of application windows of a plurality of applications are displayed on a screen space. At least a first application and a second application are executing to display a plurality of windows. A user interface of system level applications maybe displayed. A selection of a single application mode is received. In response to the receiving of the selection of the single application mode, all the windows are removed automatically from the screen space, except for a first application window. At least the first and second applications continue being executed. The user interface of the system level applications may continue to be displayed. Next, a request to display a second application window is received. The second application window is displayed while the first application window is removed from the screen space.
Owner:APPLE INC
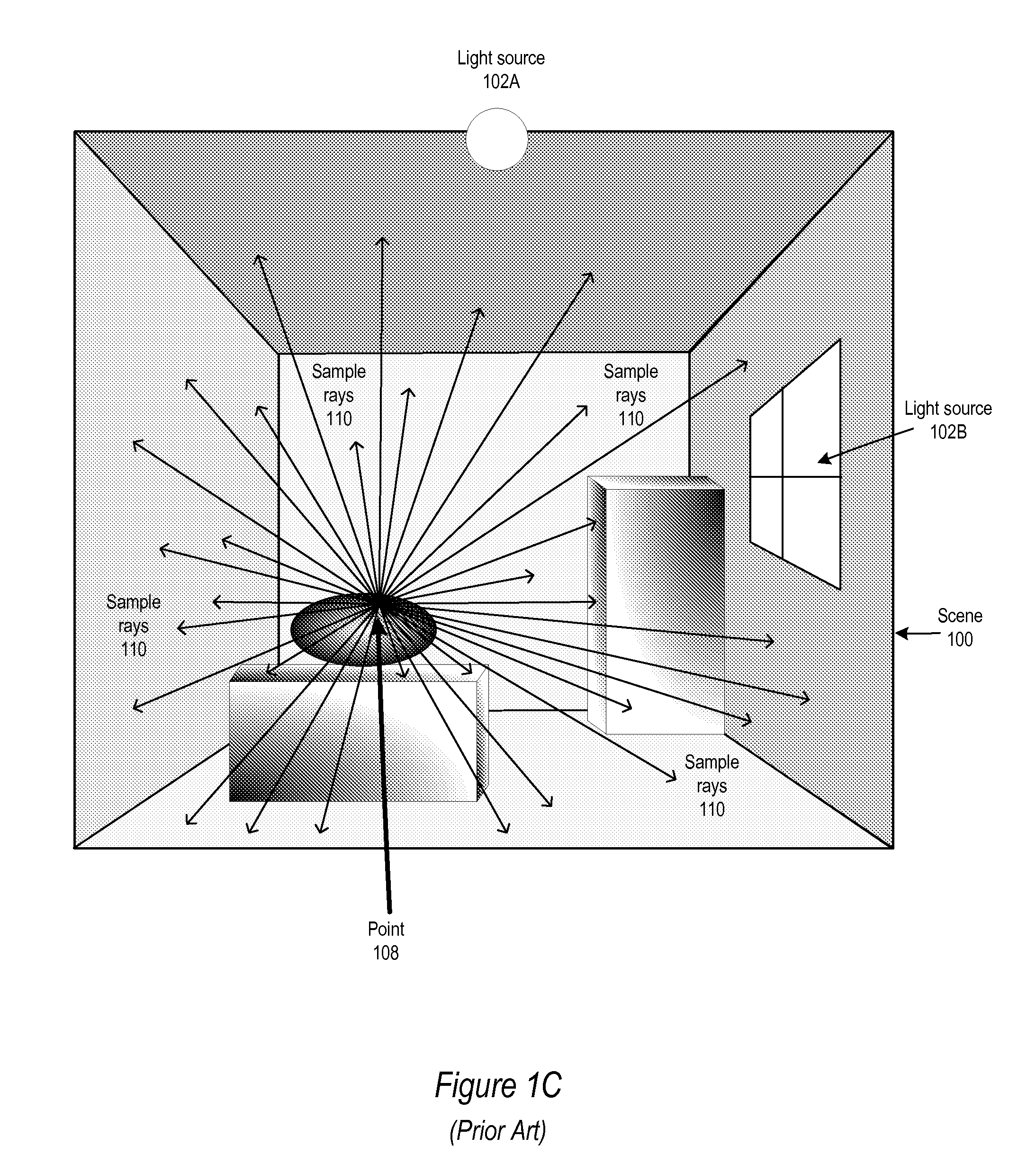
Methods and Apparatus for Diffuse Indirect Illumination Computation using Progressive Interleaved Irradiance Sampling
InactiveUS20130120385A1Quality improvementUniform coverage3D-image renderingDiffuse reflectionBilateral filter
Methods and apparatus for diffuse indirect illumination computation using progressive interleaved irradiance sampling. Embodiments may implement a method that amortizes the cost of computing the irradiance integral for diffuse indirect illumination both temporally and spatially in screen space. For each pixel, only one secondary ray is fired. By carefully arranging different secondary ray directions for different pixels according to a sampling sequence, embodiments may filter the noisy estimate so that each pixel receives a relatively uniform coverage of the integrated hemisphere. Some embodiments may use a bilateral filter so that the geometric discontinuities are respected. The sequence may continue to a higher-level of stratification in each frame. This ensures that the rendering is converging to a noise-free result.
Owner:ADOBE INC
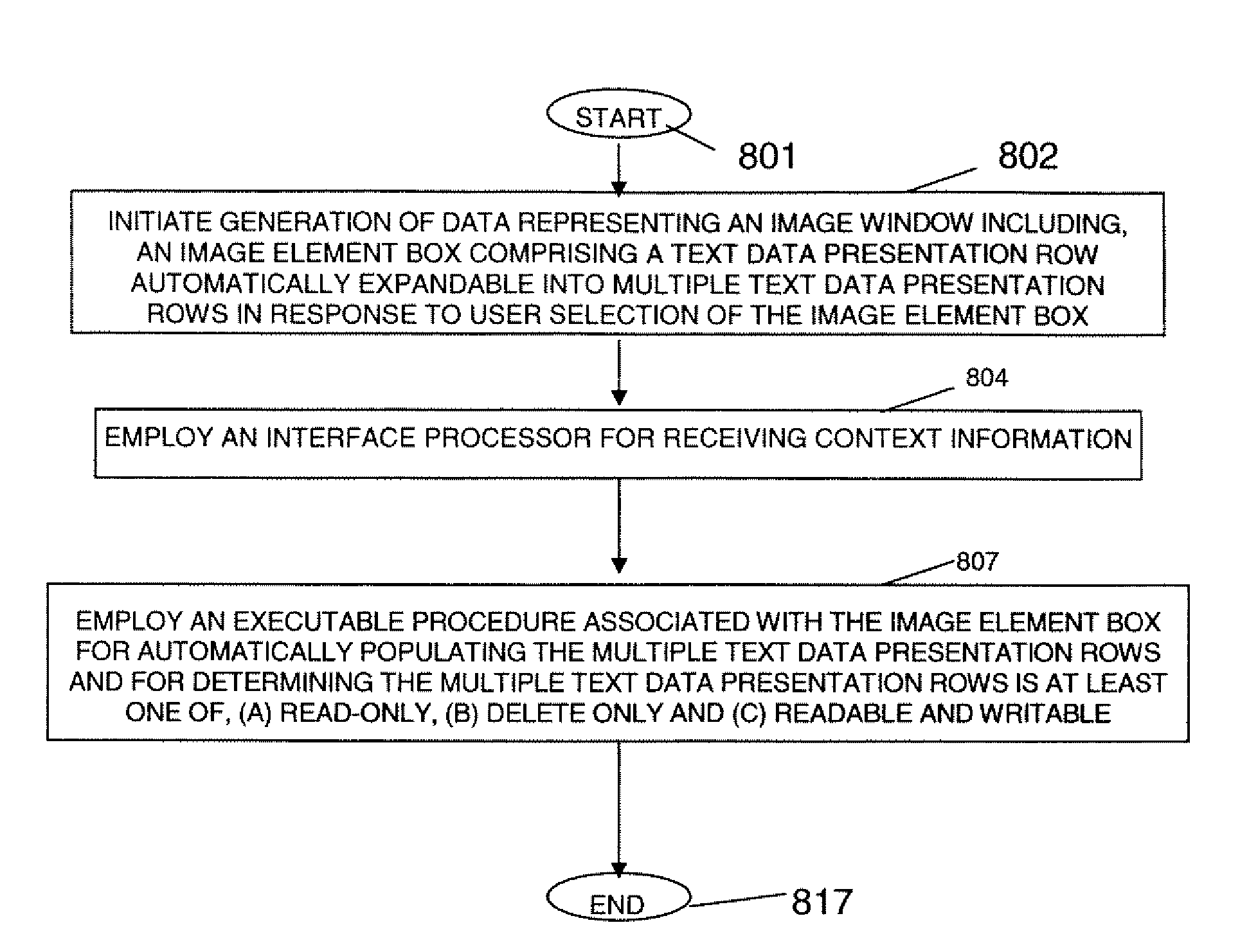
User Interface Image Element Display and Adaptation System
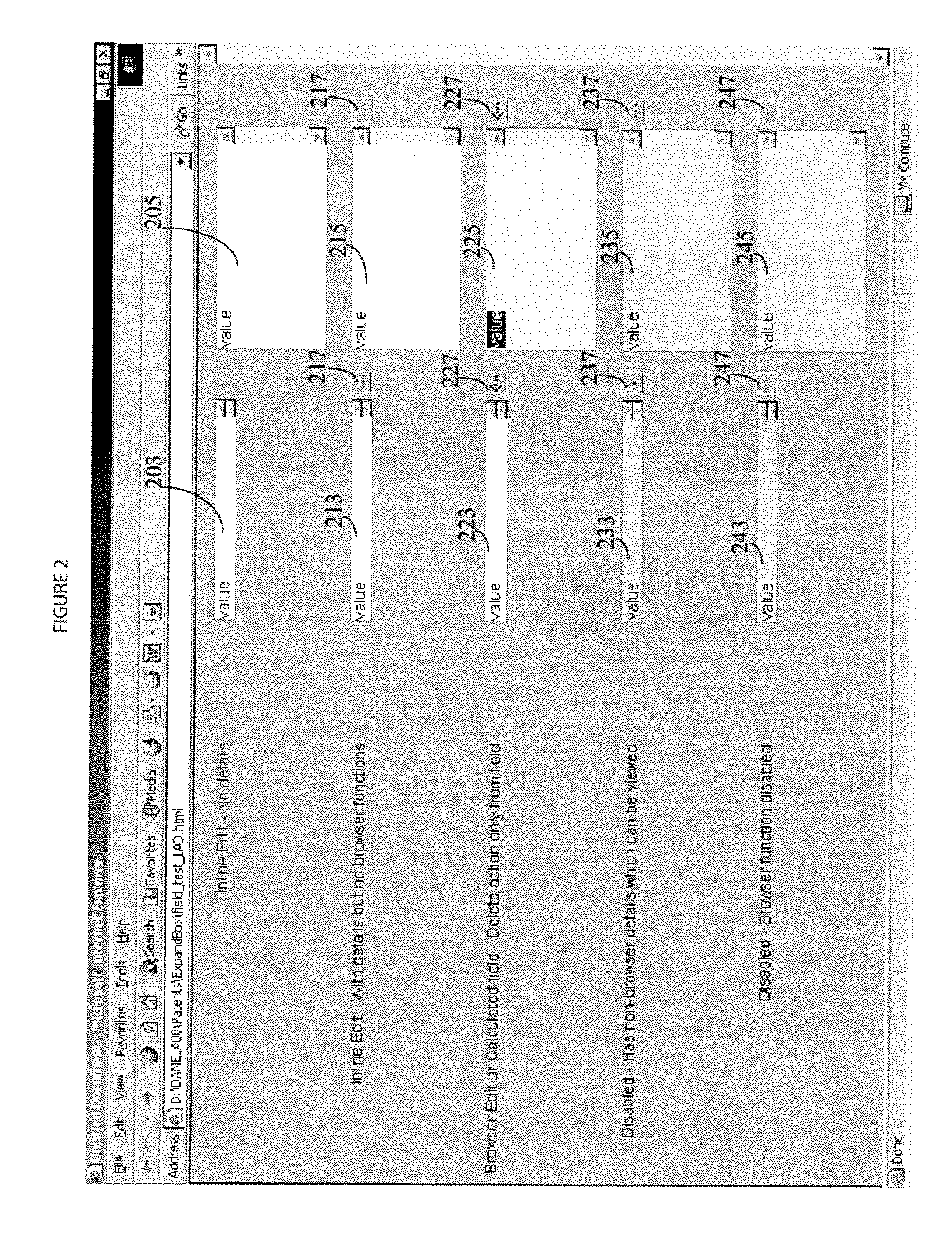
A system provides a single-click expandable data control implemented in a user interface development language as a data entry and viewing element including options enabling or restricting data entry and specifying a related dialog for entry or selection of data for a primary display field. A system provides a single-click expandable data element in HTML, for example, as a data entry and viewing element that is used within a user interface interactive page to allow a single line-height data display using a single mouse click to expand or collapse data, thereby providing a simple means for a user to view or enter larger amounts of data than typically fit within the limited screen space. A user interface system adaptively presents information to a user. The system includes a display processor for initiating generation of data representing an image. The image includes, an image element box comprising a text data presentation row automatically expandable into multiple text data presentation rows in response to user selection of the image element box. An executable procedure associated with the image element box determines whether text in the multiple text data presentation rows is at least one of, (a) delete only, (b) read-only and (c) readable and writable. The executable procedure is in a user interface compatible code language (e.g., HTML, SGML, XML, Visual Basic) and execution of the executable procedure is initiated in response to user selection of the image element box.
Owner:SIEMENS MEDICAL SOLUTIONS USA INC
Managing arbitrary window regions for more effective use of screen space
InactiveUS20050240873A1Easy to manageEasy to useProgram controlMemory systemsScreen spaceRegion of interest
The present invention enables the management of arbitrary regions of a window. A surrogate window is created to contain a region of interest in a source window. A surrogate window may also be shared among multiple devices. A user may interact with the content in a source window or its surrogate window(s). A surrogate window is updated to reflect any content change in the region of interest in the source window. In the case that a user resizes a surrogate window, the entire content of the surrogate window is scaled accordingly so the entire content remains visible.
Owner:MICROSOFT TECH LICENSING LLC
Direction-based system and method of generating commands
InactiveUS7469388B1Simple interfaceEasy to viewDigital data information retrievalCathode-ray tube indicatorsMagnificationBiological activation
Embodiments of the present invention provide a system, method, and computer-readable medium for identifying a command in response to receiving notice of a pointer selection event followed by an associated pointer activation event. Also, the present invention layers Web browsing in a system where a Web page is first displayed in an overview mode at a predetermined magnification. From a Web page displayed in overview mode, the user may issue adaptive viewing commands that cause relevant content to be displayed using additional screen space. The adaptive viewing commands are identified based on the direction the pointer was moved when the pointer selection event occurred.
Owner:MICROSOFT TECH LICENSING LLC
Information visualization system
ActiveUS20070180408A1Simple structureEasy to displaySpecial data processing applicationsInput/output processes for data processingInformation visualizationScreen space
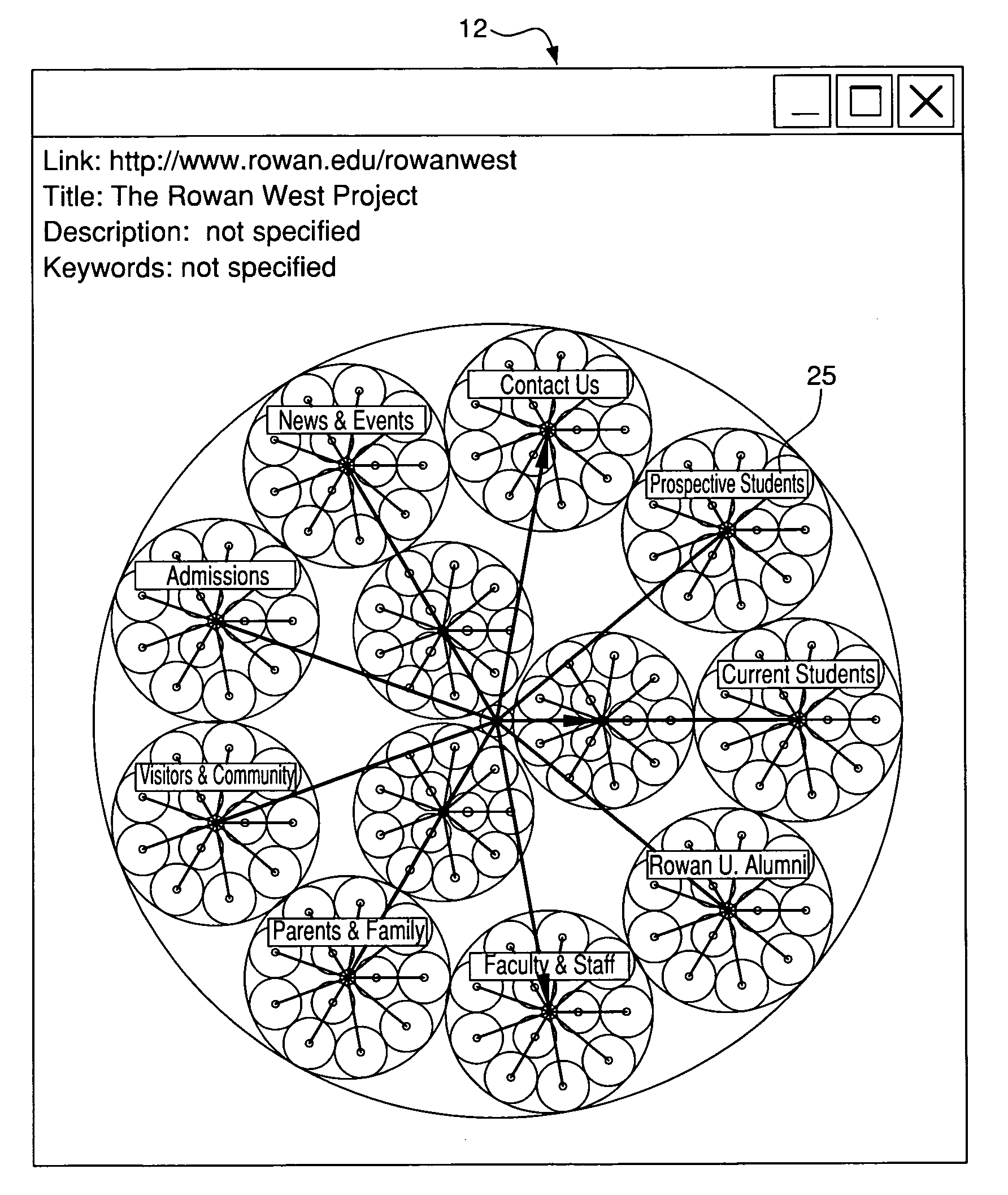
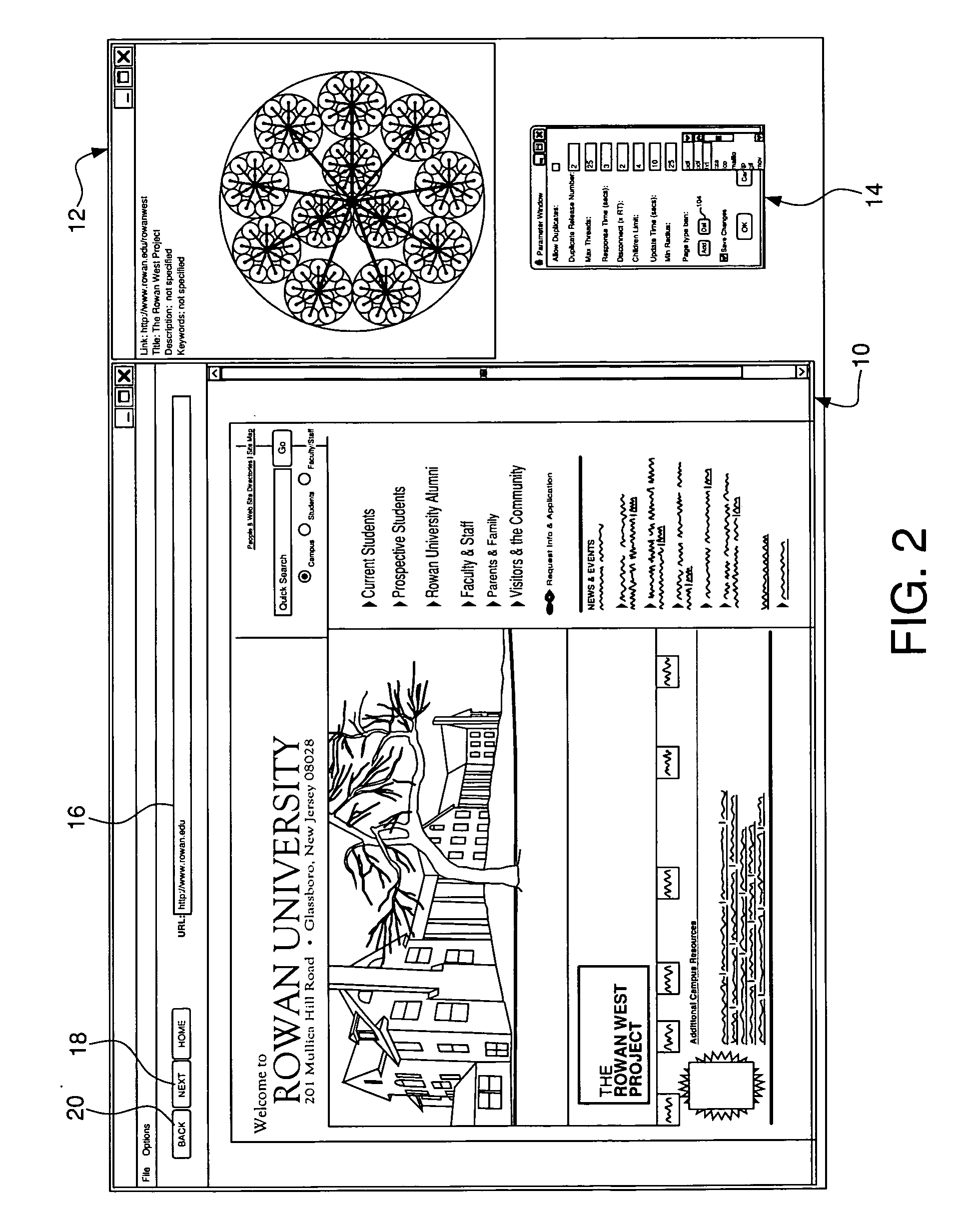
A Web browsing and visualization system and method wherein: (i) Web data is retrieved and displayed in real-time (i.e., Web data is not pre-recorded), (ii) browsing and visualization are synchronized together in the same interface, (iii) a tree-based, rings-type visualization engine, (iv) space-efficient display of visualization, and (v) the amount of resources needed from the host computer is comparatively modest. In addition, the tree-based rings engine used to create the visualization displays the information in a smaller area than previous systems. Thus, the system requires less screen space to display the same amount of information as comparable systems. Alternatively, it can display more information to the user in the same amount of screen space as comparable systems. Moreover, although the present invention is disclosed herein in connection with visualizing Web data, it can be applied to portray any information hierarchy.
Owner:ROWAN UNIVERSITY
Pull and Swipe Navigation
InactiveUS20160041702A1Highlighting on-screen contentInput/output processes for data processingMenu barFeature set
The “Pull and Swipe Navigation” comprises a set of heuristic gesture-based commands overlaid on a smart user interface that optimizes for dynamic content and ease of navigation on touch screen devices.The feature set improves upon existing touch screen user interface design, user experience design, and navigation by freeing up valuable on-screen real estate for relevant content by hiding otherwise static menu bars and icons until required; implementing a set of easy to use and simple to navigate heuristic commands that delineate between menu access and scrolling; making menu bars and icons accessible to the touch at any part of the touch screen, thus solving reach issues particularly for larger devices; and by providing theoretically unlimited real-estate for menu items through over-scrolling.
Owner:WANG NAN
Method and apparatus for controlling virtual object, and touch control device
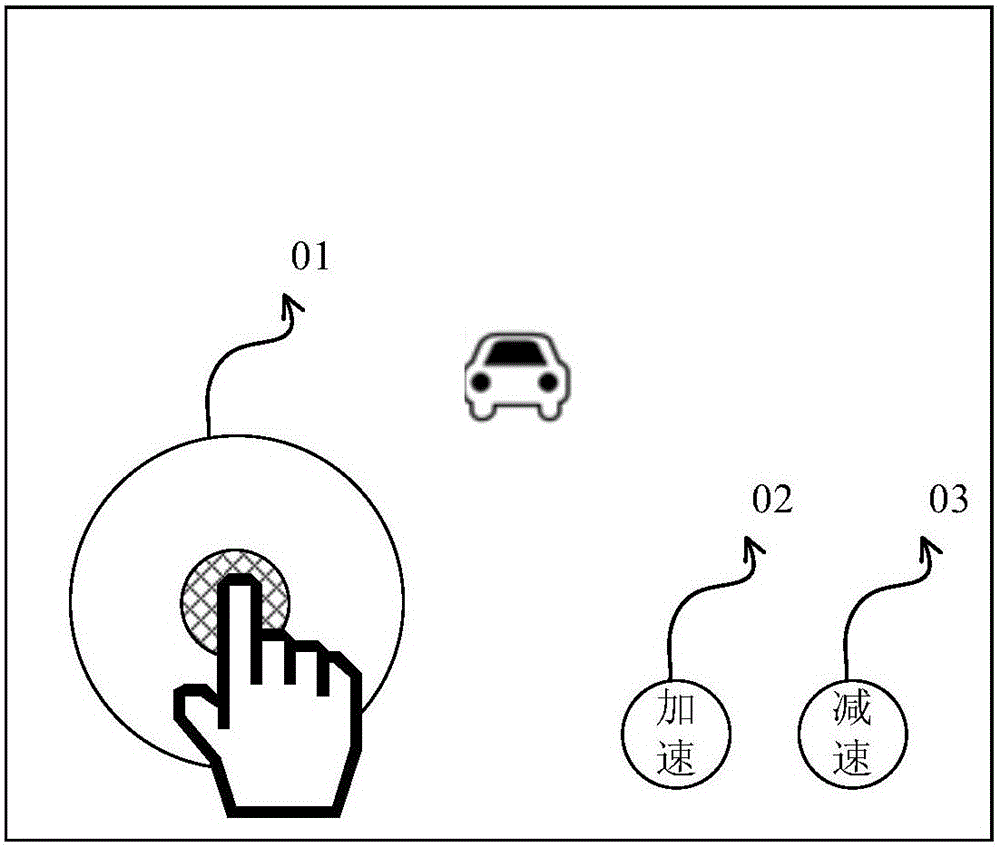
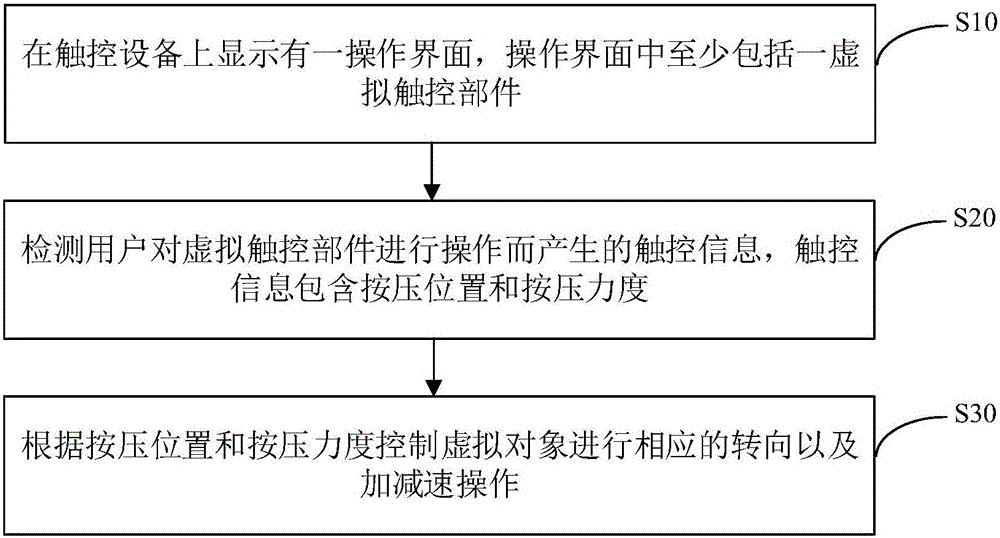
ActiveCN105912162AReduce in quantityDoes not take up spaceInput/output processes for data processingHuman–computer interactionScreen space
The present invention provides a method and apparatus for controlling a virtual object, and a touch control device. The method comprises displaying an operation interface on the touch control device, the operation interface at least comprising a virtual touch control part corresponding to a virtual object and controlling movement of the virtual object; detecting touch control information generated by operation of the virtual touch control part by a user, the touch control information including pressing position and pressing force; and controlling the virtual object to perform corresponding turning and acceleration and deceleration operation according to the pressing position and the pressing force. Through directly integrating the acceleration and deceleration operation with the virtual touch control part controlling the movement direction of the virtual object, the turning, acceleration and deceleration operation of the virtual object can be controlled through operating the virtual touch control part, the operation is visual, rapid and convenient, an acceleration button and a deceleration button are not required to be additionally arranged, screen space is not occupied, and the operation interface is simple and concise.
Owner:NETEASE (HANGZHOU) NETWORK CO LTD
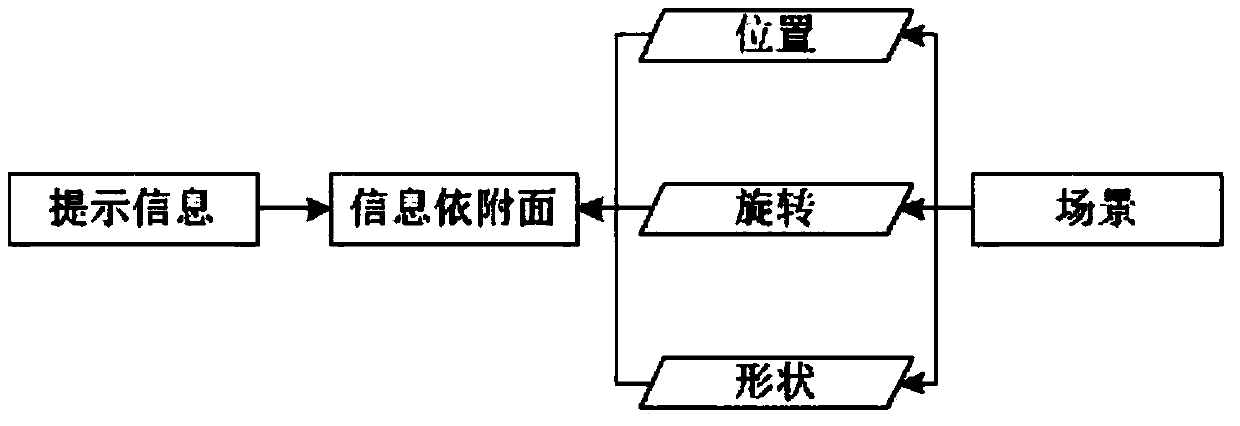
An information labeling method having high fusion degree and oriented to city augmented reality
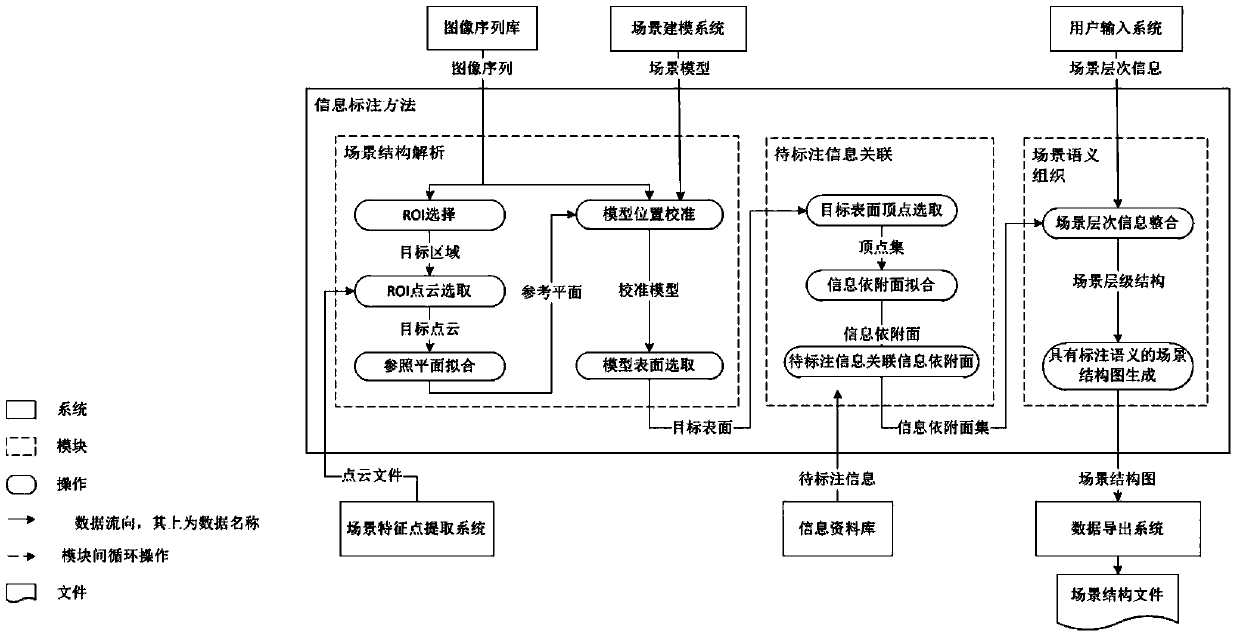
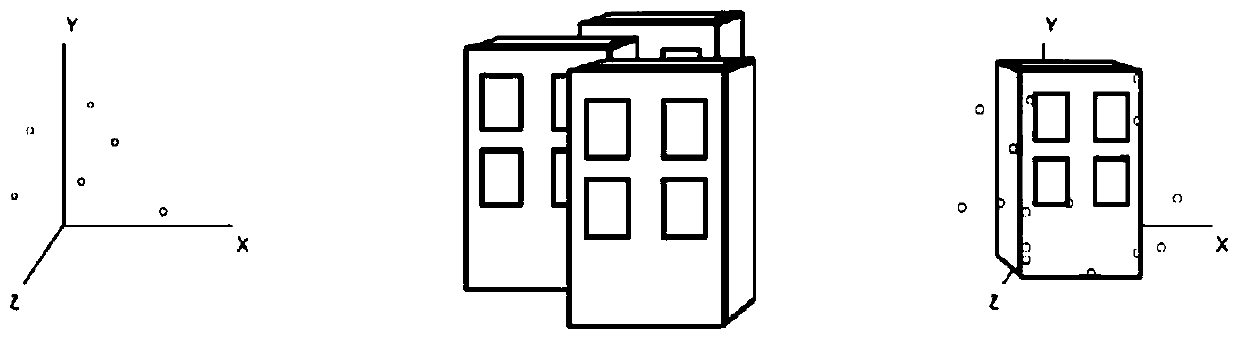
ActiveCN104183014AAchieve a high degree of integrationEasy to understand3D modellingScreen spaceAugmented reality
The invention discloses an information labeling method having high fusion degree and oriented to city augmented reality. The method comprises four steps of establishing a virtual-real fusion scene, generating an information attachment plane, multi-information labeling, and executing scene semantic organization. According to the invention, prompt information is transferred from a screen space to a three-dimensional scene space, a scene structure suited as an information carrier is extracted through analyzing the scene, and the prompt information is associated with the scene structure, finally realizing high fusion of the prompt information and the scene, and achieving the objective of enabling the augmented reality prompt for the city scene to be clearer and easy to understand.
Owner:ZHEJIANG UNIV
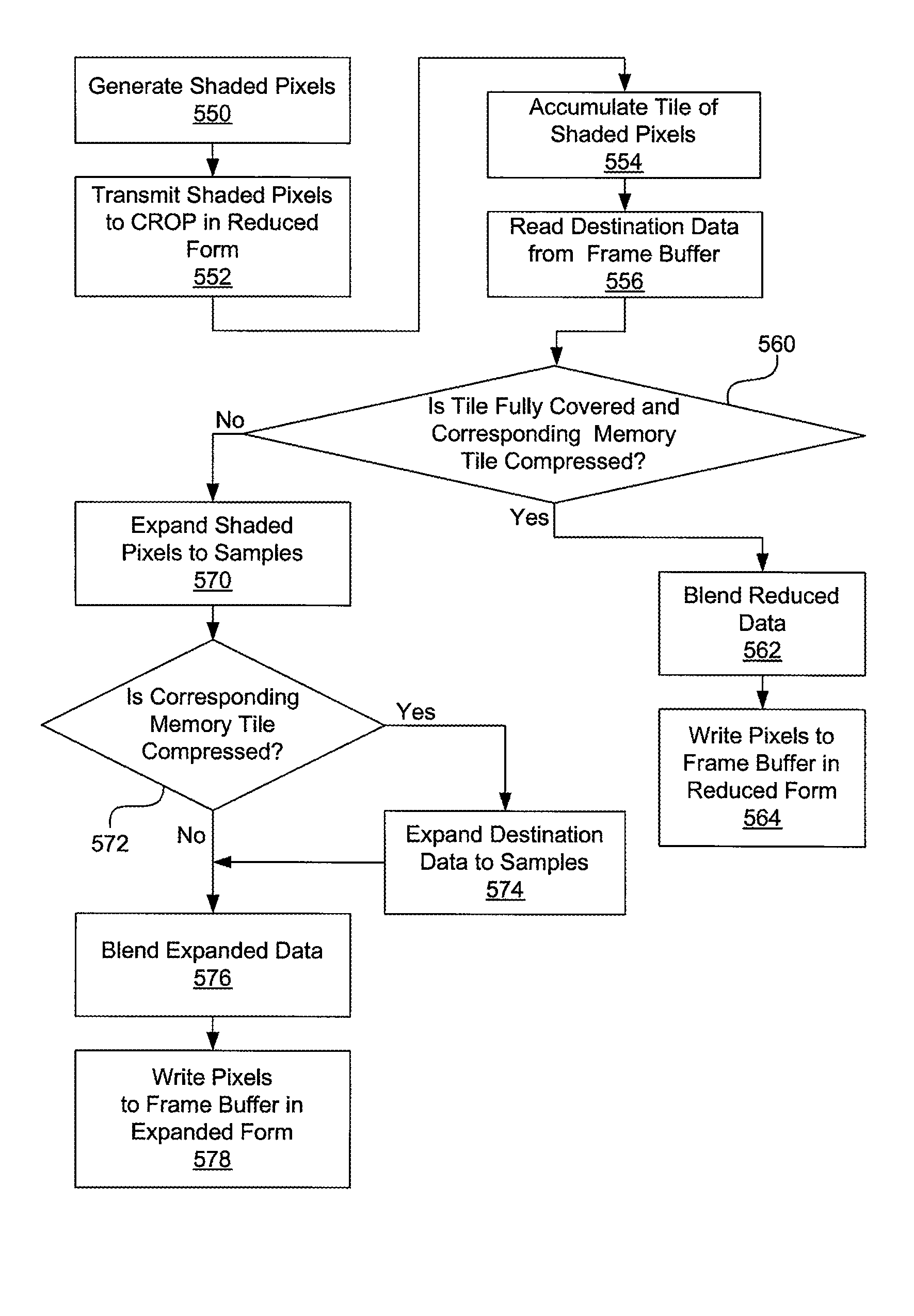
Color-compression using automatic reduction of multi-sampled pixels
ActiveUS8233004B1Reduce the amount of dataSmall sizeImage codingCathode-ray tube indicatorsGraphicsGrating
One embodiment of the present invention sets forth a technique for improving graphics rendering efficiency by processing pixels in a compressed format whenever possible within a multi-sampling graphics pipeline. Each geometric primitive is rasterized into fragments, corresponding to screen space pixels covered at least partially by the geometric primitive. Fragment coverage represents the pixel area covered by the geometric primitive and determines the weighted contribution of a fragment color to the corresponding screen space pixel. Samples associated with a given fragment are called sibling samples and have the same color value. The property of sibling samples having the same color value is exploited to compress and process multiple samples, thereby reducing the size of the associated logic and the amount of data written to and read from the frame buffer.
Owner:NVIDIA CORP
Touch screen apparatus and digital equipment having the same, and command-input method thereof
ActiveUS20080143684A1Enter exactlySafely inputInput/output processes for data processingTouchscreenElectric signal
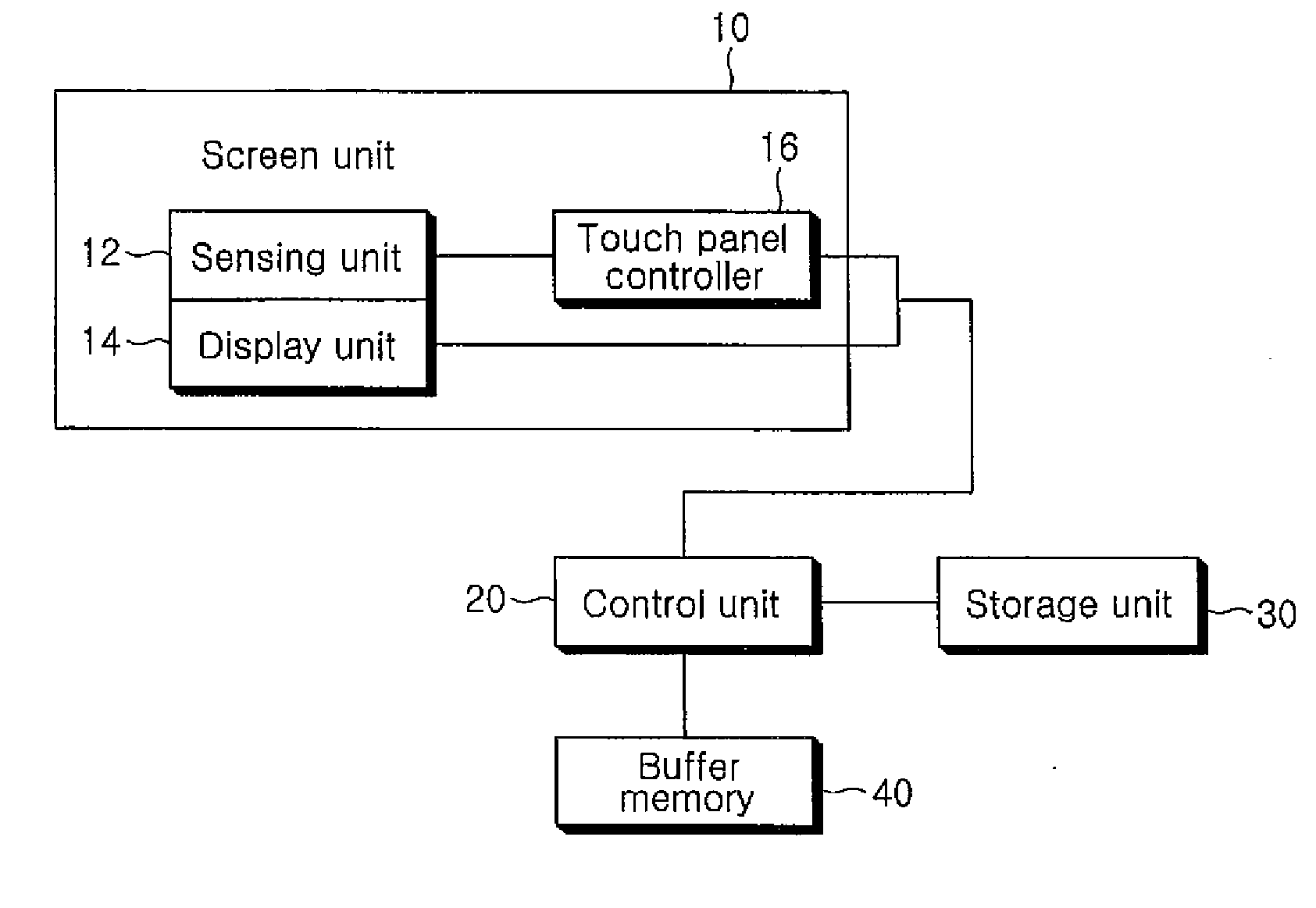
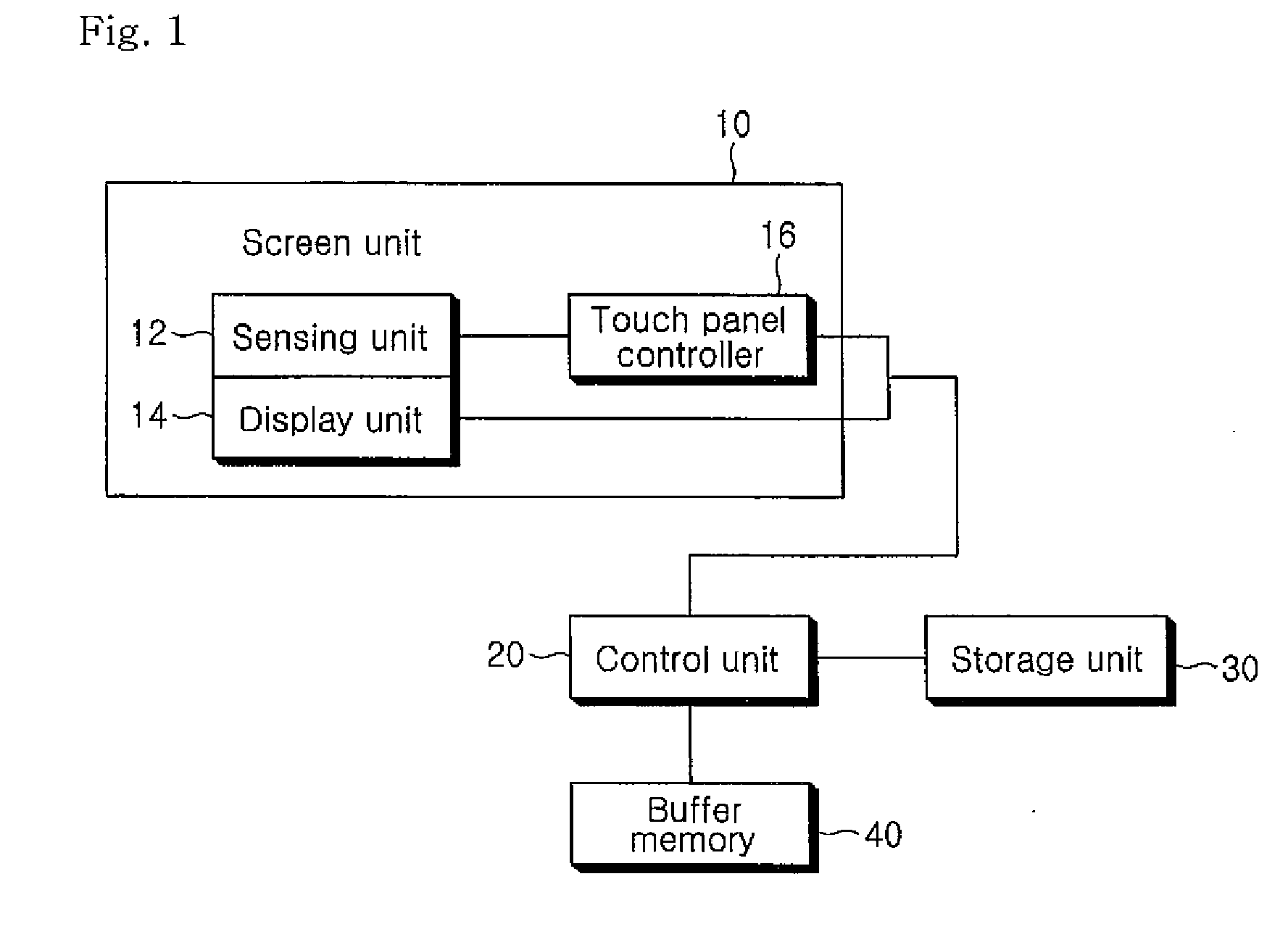
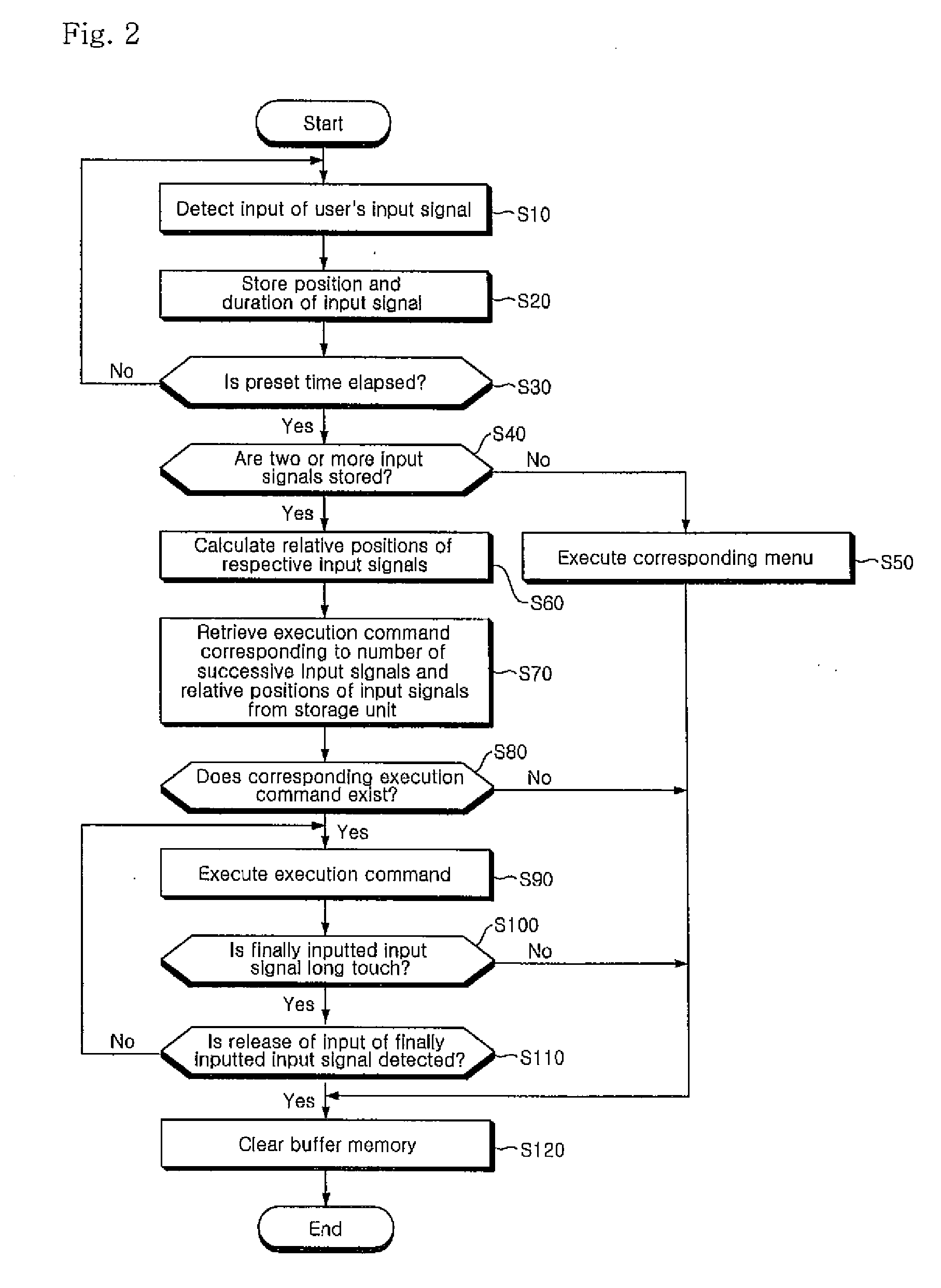
The present invention relates to a touch screen apparatus and a method of inputting a user command through the apparatus. A touch screen apparatus of the present invention comprises an input unit 10 having a sensing unit 12 for recognizing user's touches and converting the touches into electrical signals; a storage unit 30 for storing execution commands corresponding to relative positions of the successive touches; and a control unit 20 for receiving the signals from the sensing unit 12 and executing an execution command retrieved from the storage unit. According to the present invention constructed as such, a variety of execution commands can be inputted without using a pattern of touches rather than an input area narrowly partitioned in a screen space.
Owner:LG ELECTRONICS INC
Reversible user interface component
ActiveUS8860763B2Cathode-ray tube indicatorsInput/output processes for data processingGraphicsDisplay device
Owner:XEROX CORP
Method and system for avoiding overlapped display of bullet screen
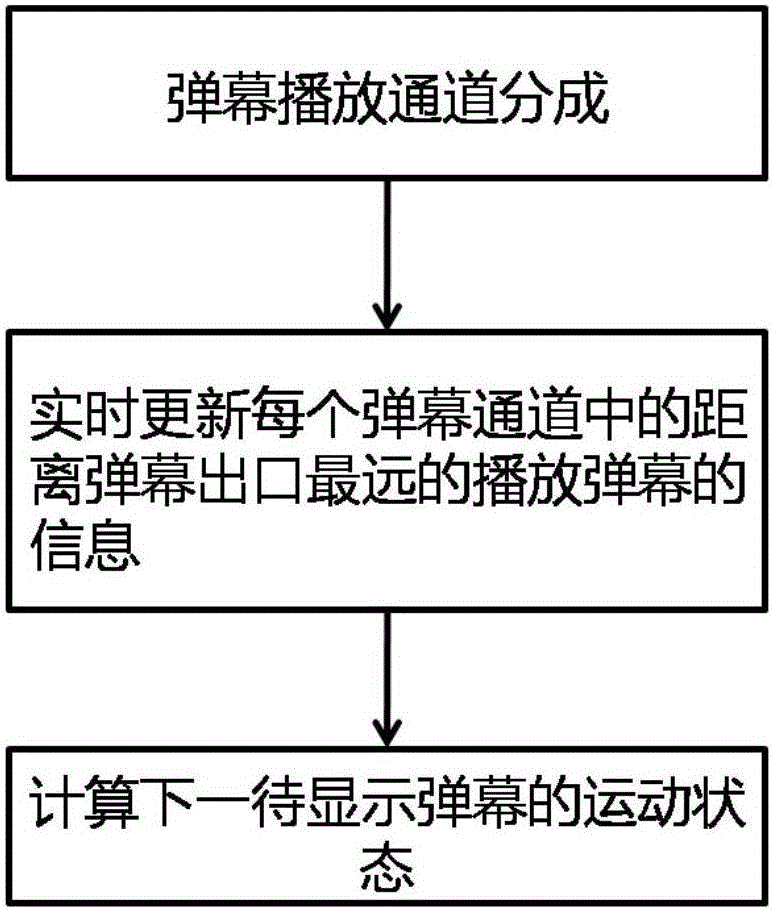
ActiveCN105828164AAvoid overlappingEfficient managementSelective content distributionComputer scienceScreen space
The invention discloses a method and a system for avoiding overlapped display of a bullet screen. The method comprises the following steps: dividing a live streaming display page into n bullet screen playing channels; wherein n meets the following conditions: n X a bullet screen height + (n-1) X a bullet screen spacing <= a live streaming display page; real-time updating information which plays a bullet screen and is the utmost distal from an exit of the bullet screens in each bullet screen playing channel; analyzing the information so as to calculate the motion state of the bullet screen to be displayed next, playing the bullet screen based on the motion state. The method and the system of the invention can explicitly increase efficiency of bullet screen display resources, and explicitly increase interaction experience of bullet screen users.
Owner:WUHAN DOUYU NETWORK TECH CO LTD
Semi-transparency in size-constrained user interface
InactiveUS20050166158A1Miniaturization exerciseIncrease the screening areaCathode-ray tube indicatorsInput/output processes for data processingInterface designUsability
The present invention provides a method that increases screen space of a computing device by using semi-transparent functional areas that overlap non-functional content areas on the screen. This method allows for relatively large functional targets on the screen—thus mitigating the usability problems associated with tiny buttons and other images—while also allowing the underlying content on the screen to be clearly visible. A main design feature of this invention is that two functional areas are never allowed to overlap. An overlap condition would cause user confusion as to which layer is active. Instead, the interface is designed to foreground functionality in all instances.
Owner:IBM CORP
Computer Input and Output Peripheral Device
InactiveUS20120092253A1More interactiveMinimizing/maximizing overviewDigital data processing detailsCathode-ray tube indicatorsDirect touchDisplay device
The peripheral input and output device embeds a touch-screen display onto a mouse. Users interact with the display of the mouse using direct touch, whilst also performing regular cursor-based mouse interactions. The resulting device has many unique capabilities, in particular for interacting with auxiliary windows, such as toolbars, palettes, pop-ups and dialog-boxes. By migrating these windows onto a peripheral computer mouse challenges such as screen real-estate use and window management can be alleviated.
Owner:IRANI POURANG +2
Auxiliary display unit for a computer system
InactiveUS20060119537A1Digital data processing detailsCathode-ray tube indicatorsAudio frequencyUser interface
A host computer is provided with a main display unit and an auxiliary display unit. The host computer can free up screen space on the main display screen by routing certain types of display information to the auxiliary display unit for display. Display information can range from notification of events such as receipt of email, appointments, system messages, and information from separate applications. The auxiliary display panel may function as a user interface for audio, video, “push information”, MP3 player or become the hardware equivalent of a multimedia player. The auxiliary display panel may be integrated together with the host computer in the same physical structure or may be part of a standalone display unit that is wired or wirelessly coupled to the host computer.
Owner:MICROSOFT TECH LICENSING LLC
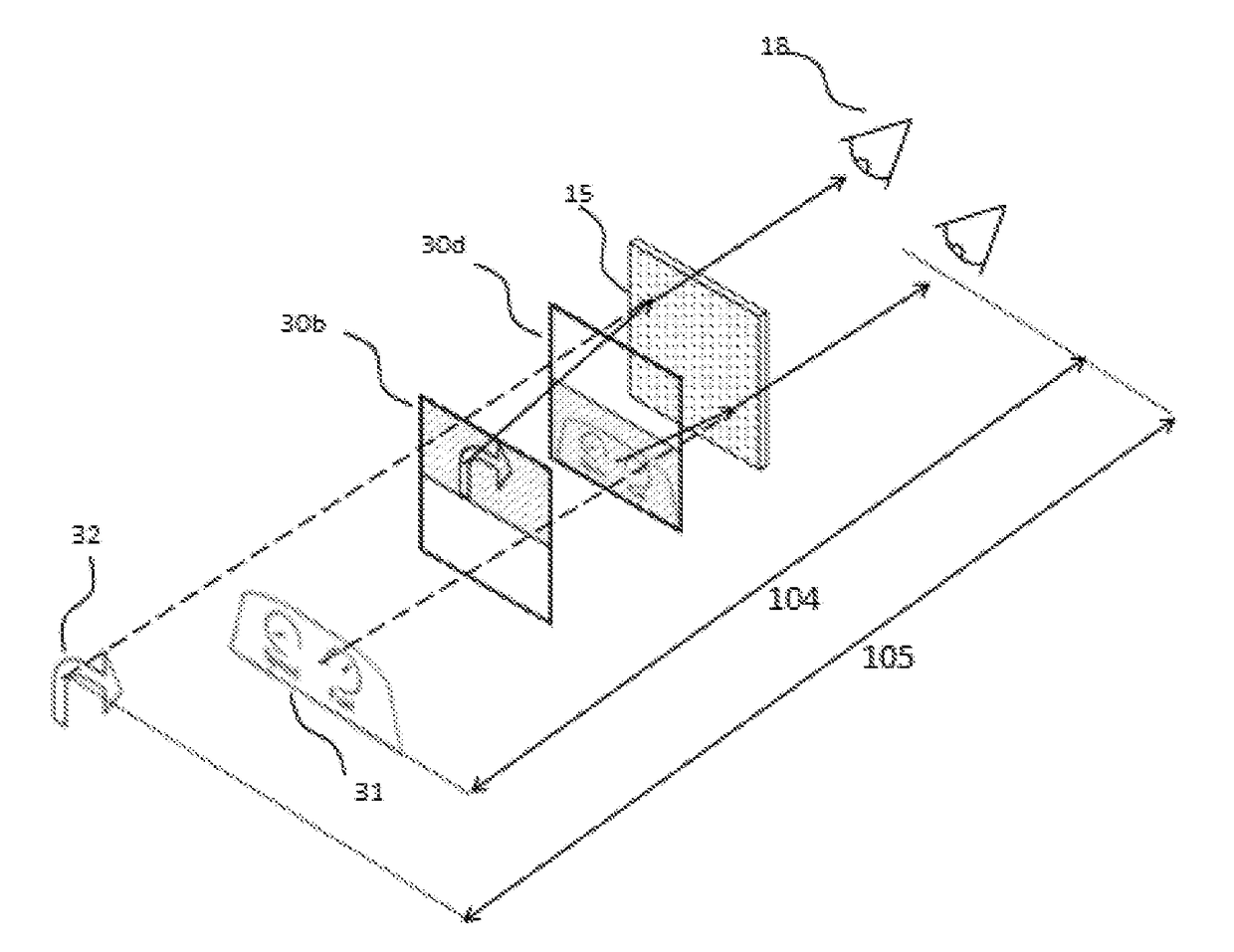
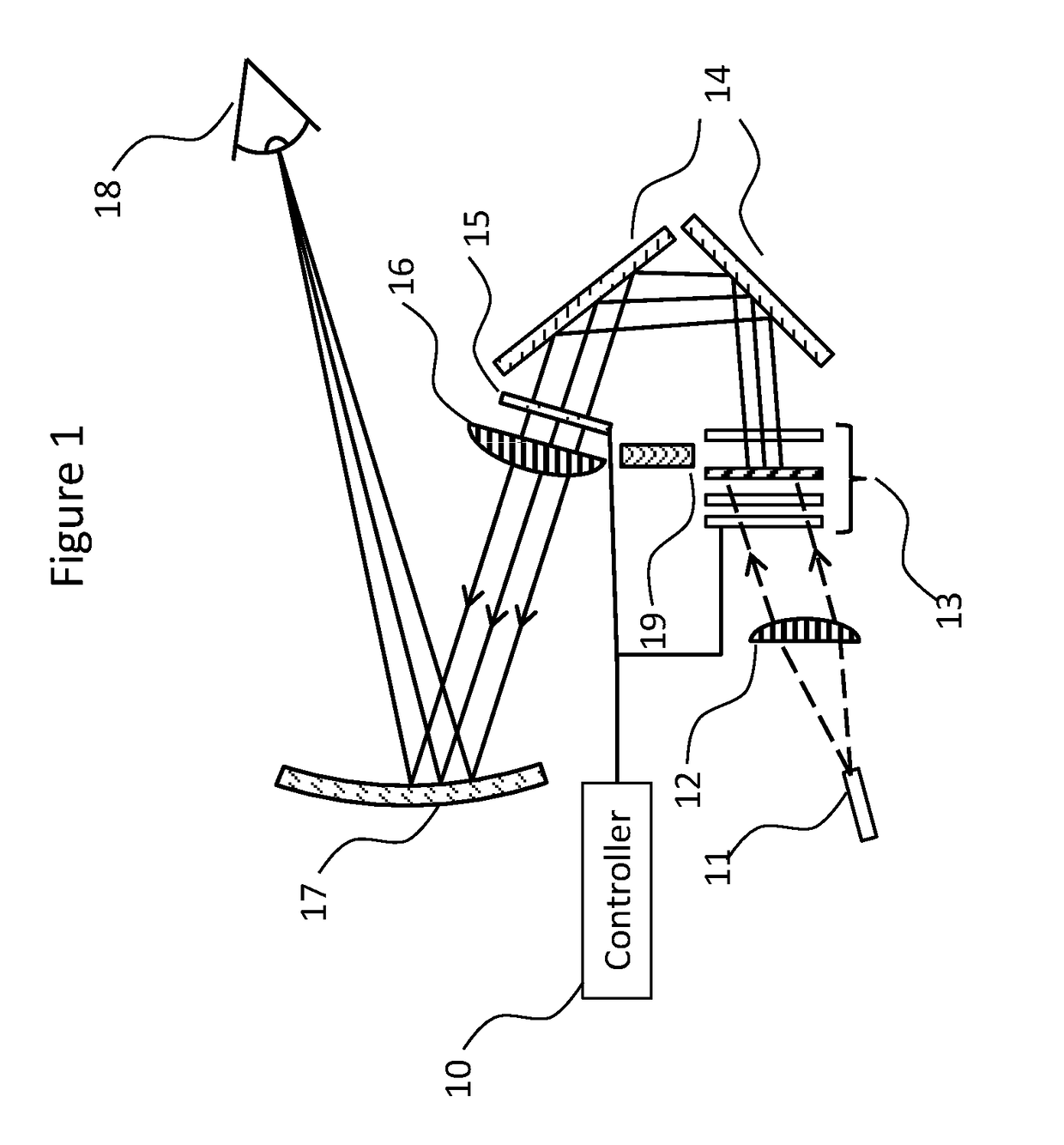
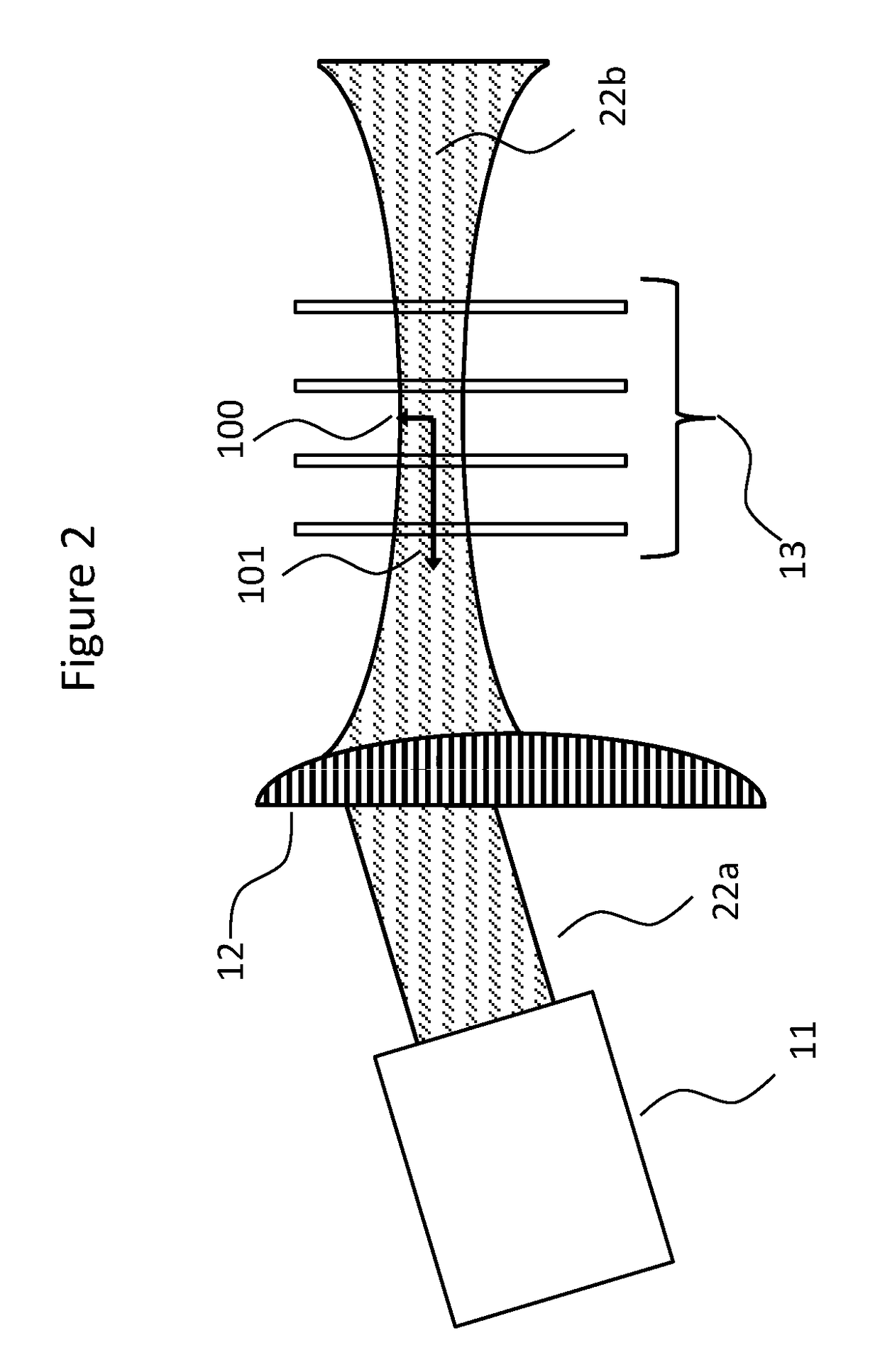
Automotive head up display
A head-up-display (HUD) system includes at least one scanning laser projector operative to generate laser light, and a stacked array of multiple-switchable screens arranged relative to the projector to receive laser light generated by the projector, each screen of the stacked array of multiple-switchable screens spaced apart from one another and operative to switch between a transparent state and a diffusive state. A controller is operatively coupled to the stacked array of multiple-switchable screens, the controller configured to time sequentially switch each screen of the array from a transparent state to a diffusive state, wherein only one screen is switched to the diffusive state at any given time. An output of the projector is arranged at an angle or a distance from imaging optics succeeding the array of screens to prevent a specular beam emitted by the at least one scanning laser projector from intercepting the imaging optics succeeding the array of screens when all screens are in the transparent state.
Owner:SHARP KK
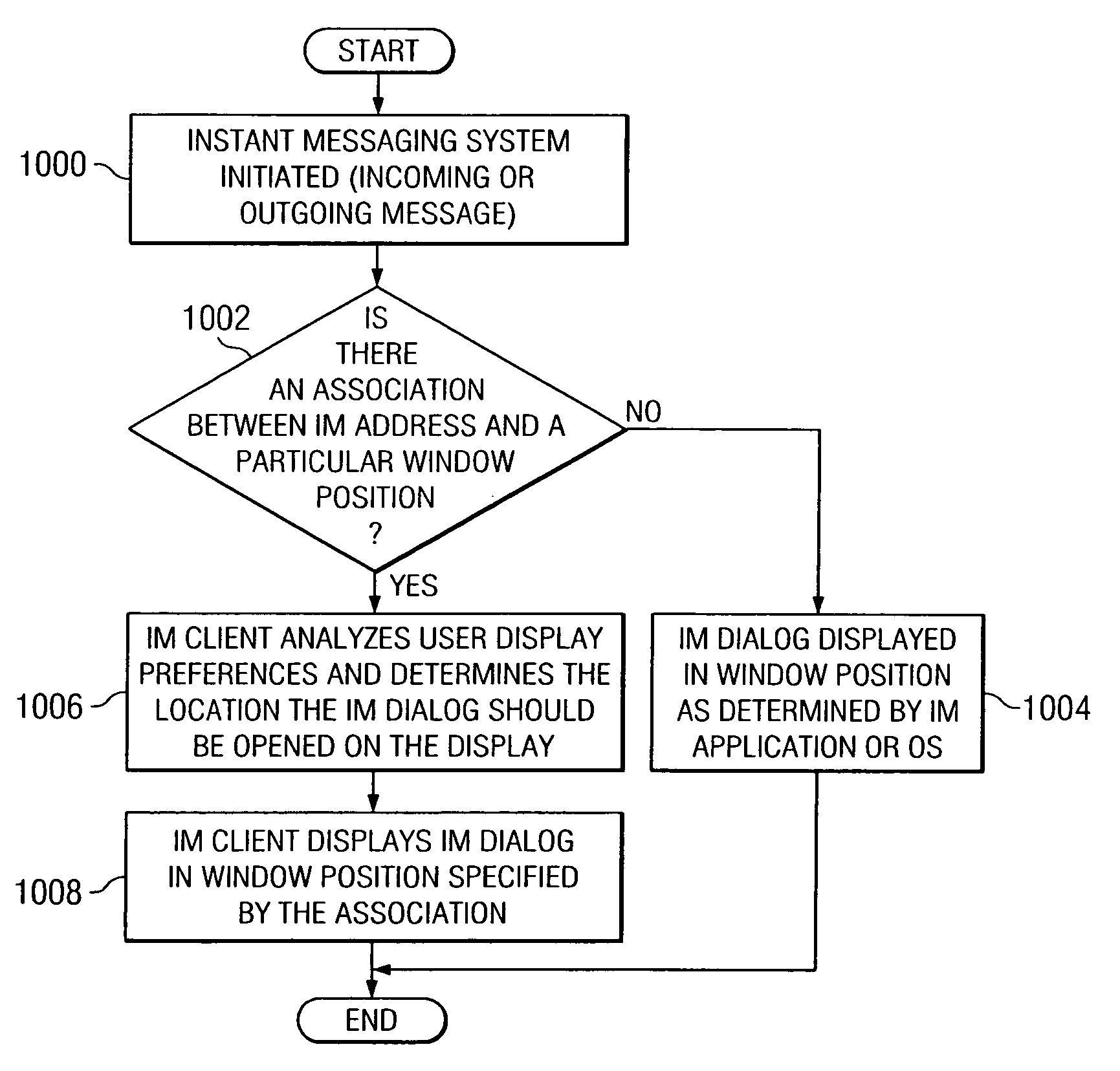
Associating an instant message dialog with screen real estate and role based positioning
InactiveUS20060031322A1Multiple digital computer combinationsData switching networksDisplay deviceMessage passing
A method, apparatus, and computer instructions for allowing areas of a display to be associated with particular instant messaging users. The present invention provides a menu option to allow a user to select whether to have instant messaging dialog windows open up in the same position as the current window, or alternatively, to have the dialog windows from a specific person open up in a specified location on the display. Thus, the instant messaging software may allow window positions to be associated and “saved” with particular users. A user may create roles or add individual people to a preferences list to allow for different instant messaging window preferences for each role or person. In this manner, a user may specify areas of the display in which an instant messaging dialog window may open according to the various roles.
Owner:IBM CORP
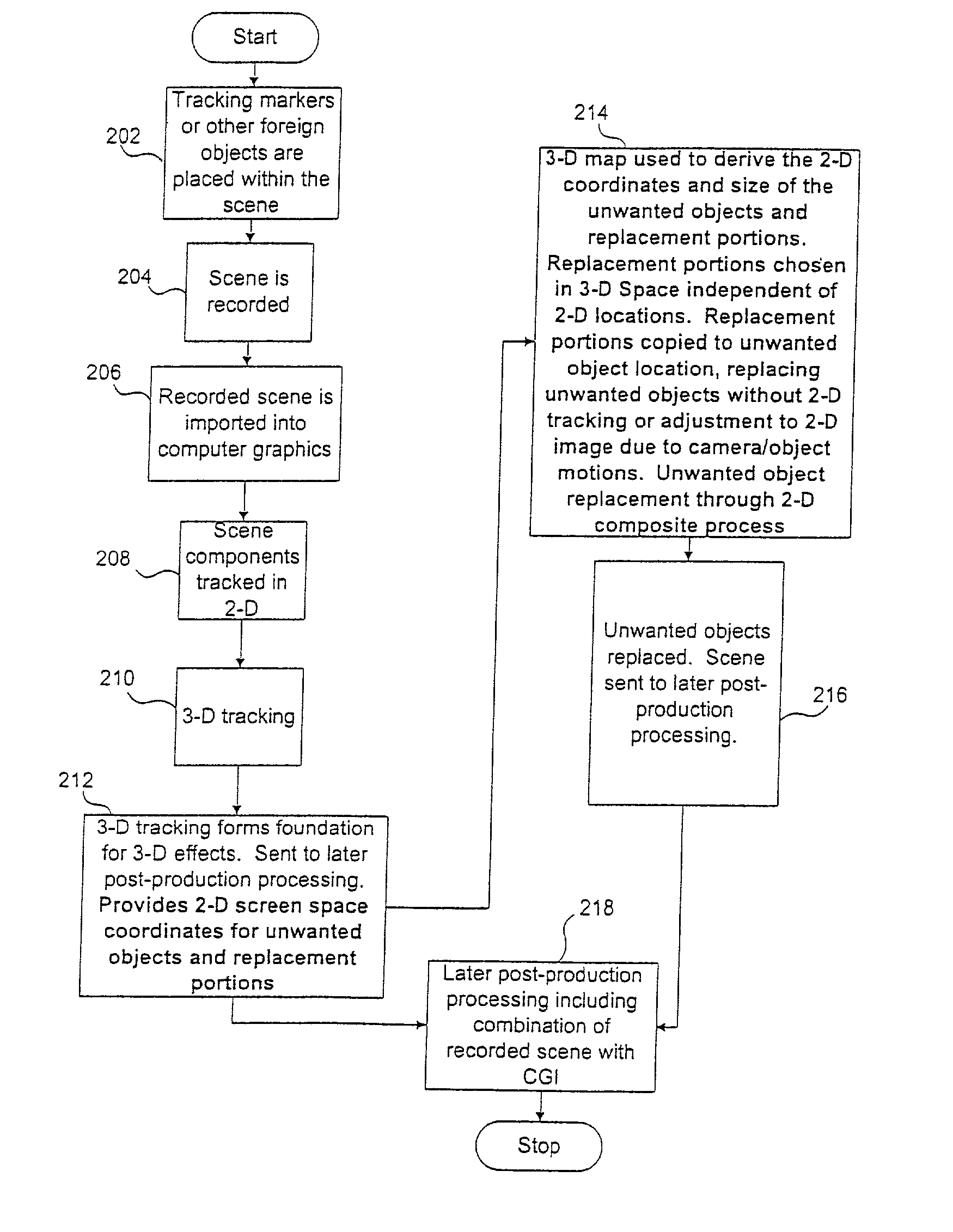
System and process for geometry replacement
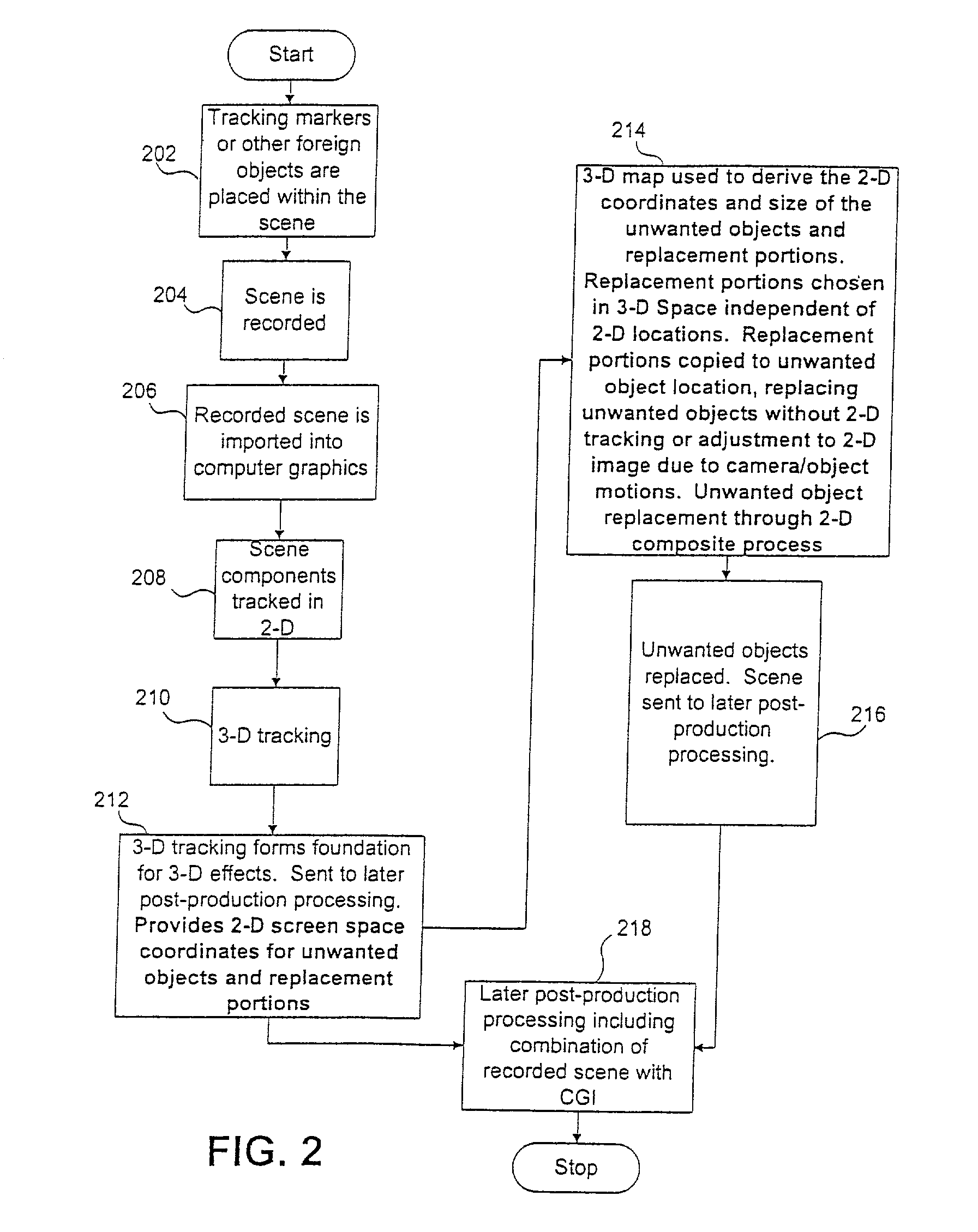
InactiveUS20030076321A1Simplifying post-production processAccurate replacementImage analysis3D-image renderingGraphicsComposite application
A system and process for replacing unwanted geometry (for example, tracking markers) in a recorded scene with new geometry. A 3-D matchmove process creates a 3-D map. The 3-D map is used to determine the 3-D coordinates of objects within the recorded scene. The 3-D coordinates of the tracking markers (and / or other objects) and the replacement portions are converted by a conversion means to 2D screen space coordinates of pixels that make up both the tracking markers (and / or other objects) and the replacement portions. A list comprising the 2D screen space pixel coordinates is then exported from the conversion means into a compositing application which reads the list of 2D pixel coordinates and makes the desired replacement automatically from frame-to-frame. Tracking markers (and / or other unwanted objects) are replaced with replacement portions with suitable characteristics.
Owner:SONY CORP
Features
- R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
Why Patsnap Eureka
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com