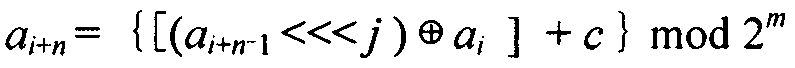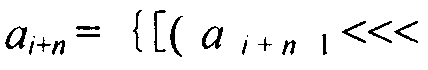Patents
Literature
35 results about "Key schedule" patented technology
Efficacy Topic
Property
Owner
Technical Advancement
Application Domain
Technology Topic
Technology Field Word
Patent Country/Region
Patent Type
Patent Status
Application Year
Inventor
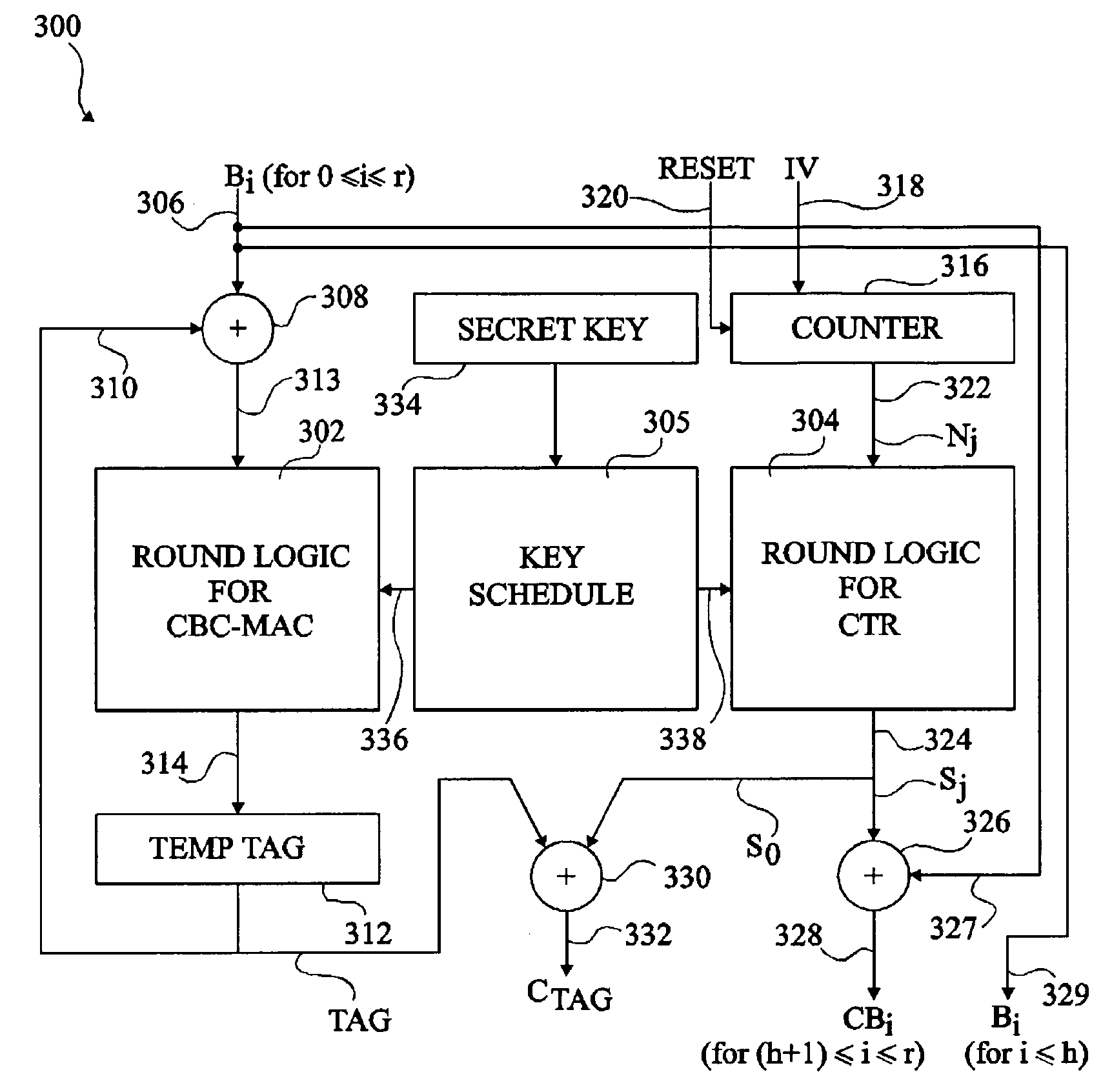
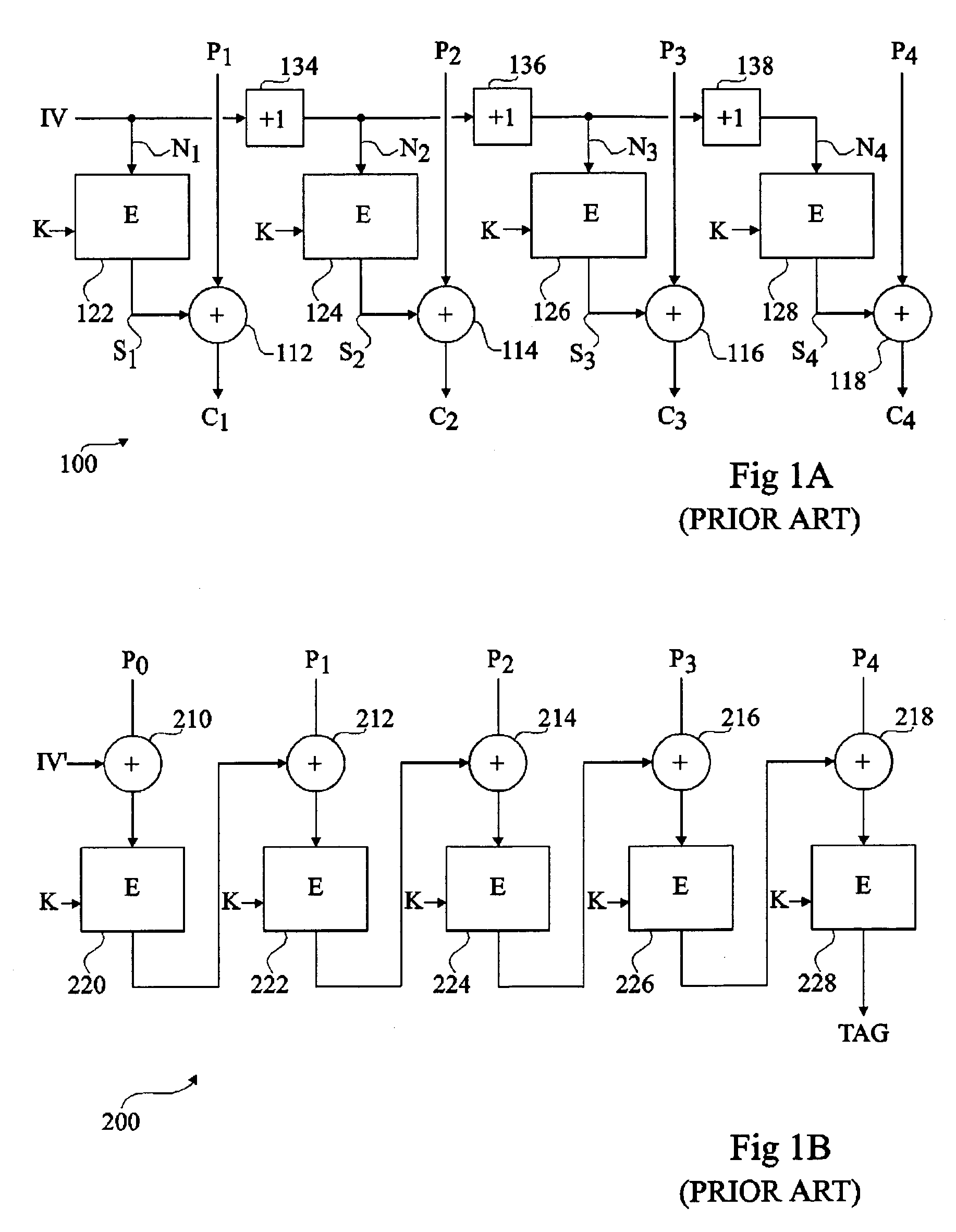
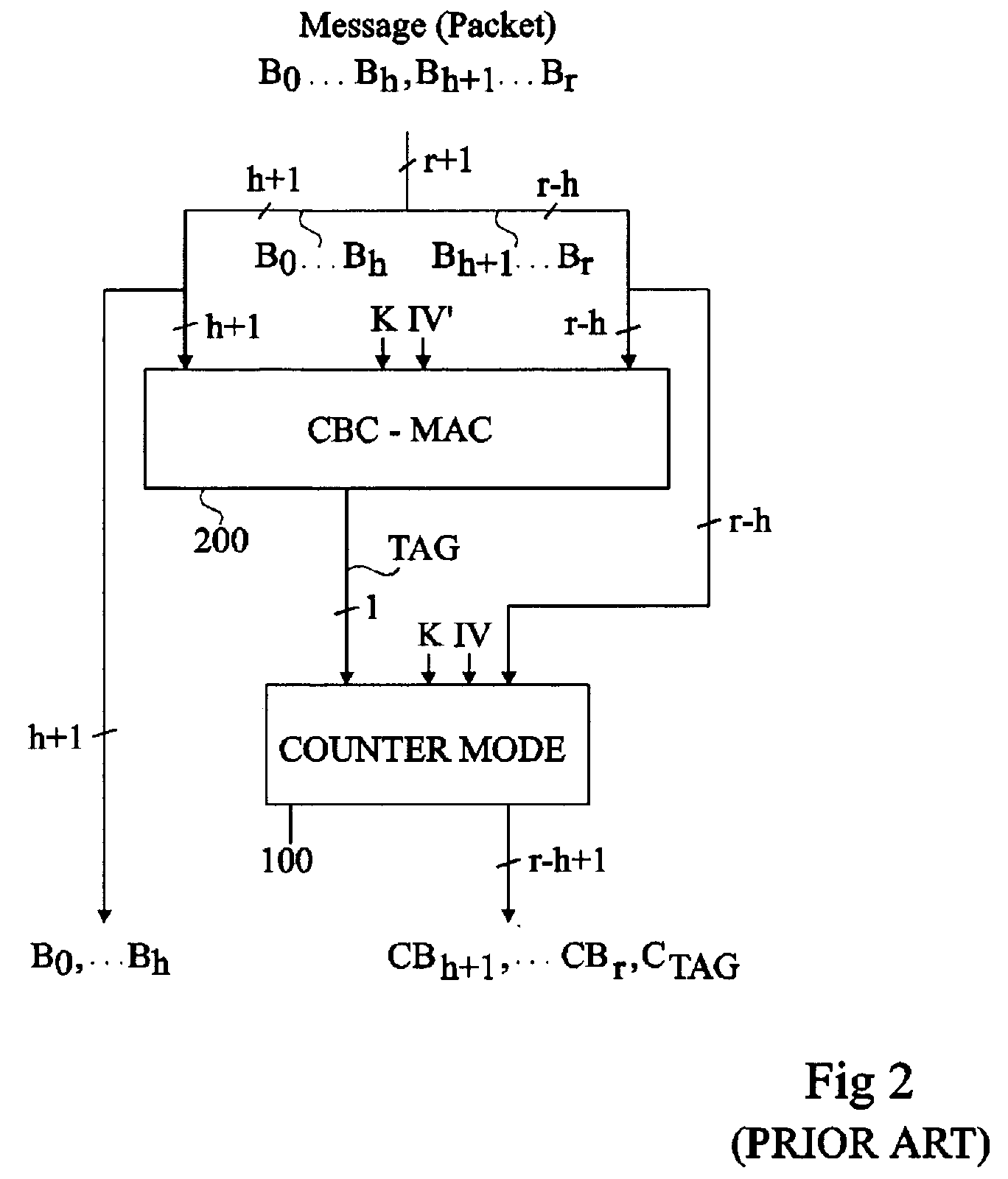
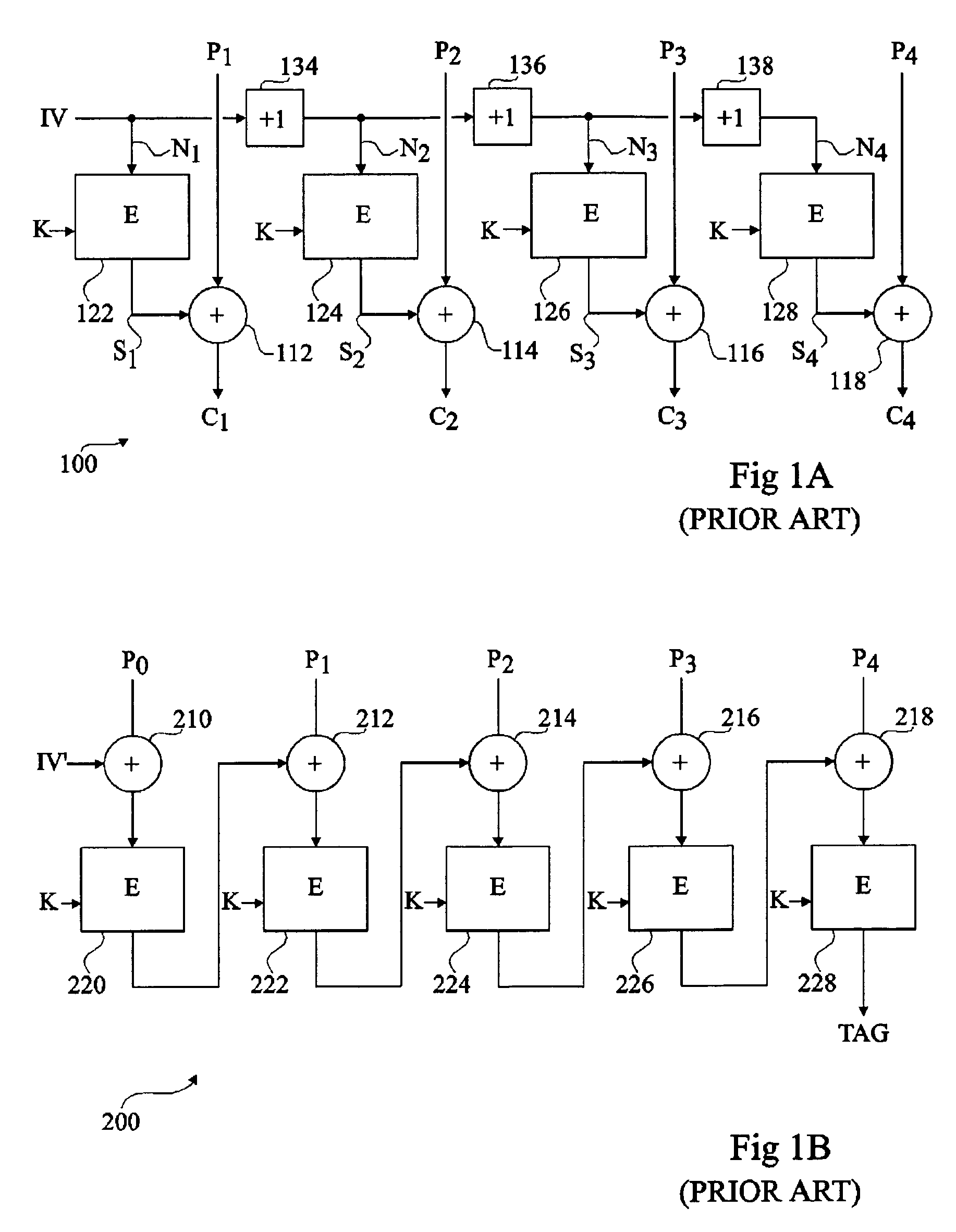
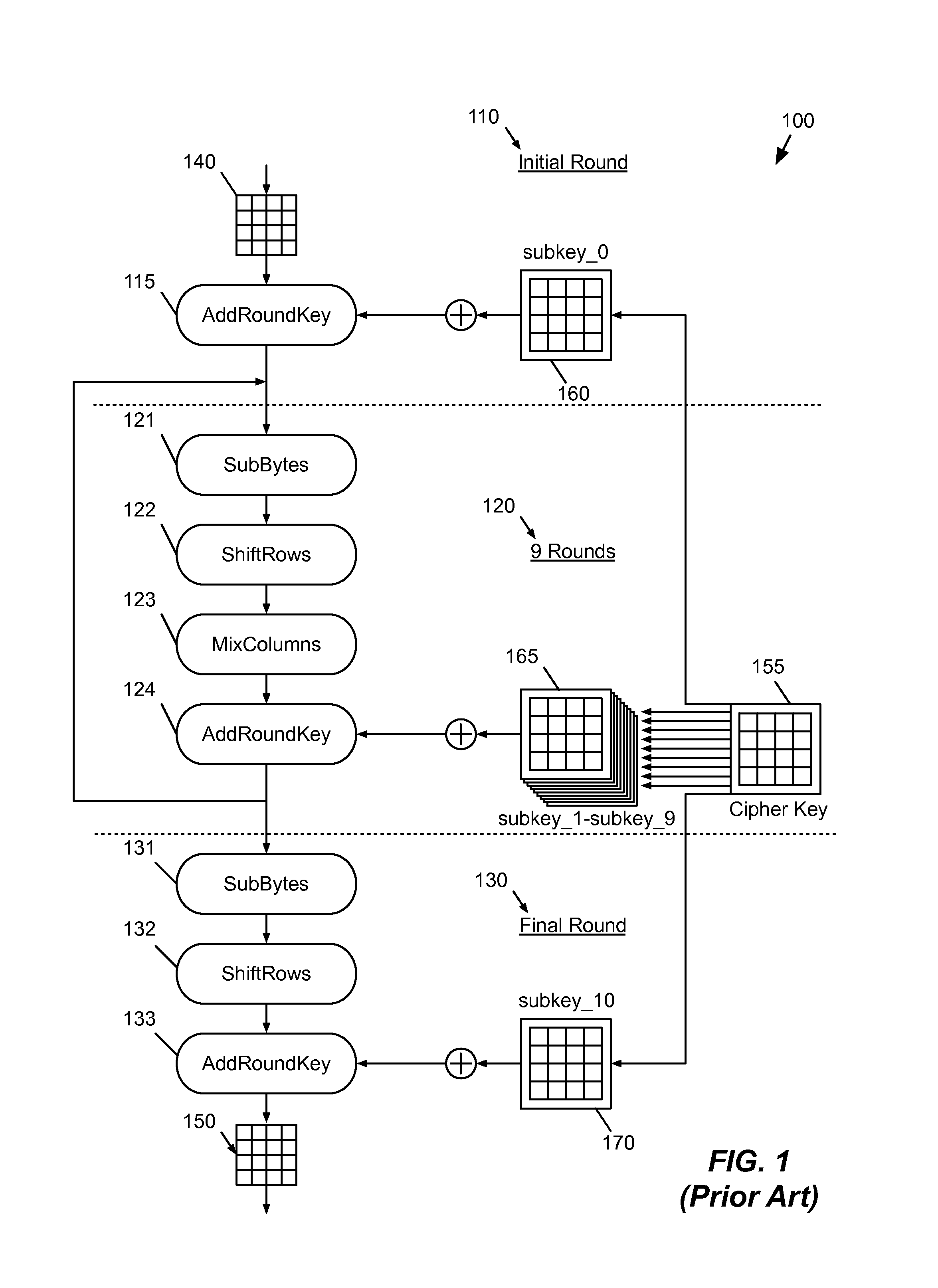
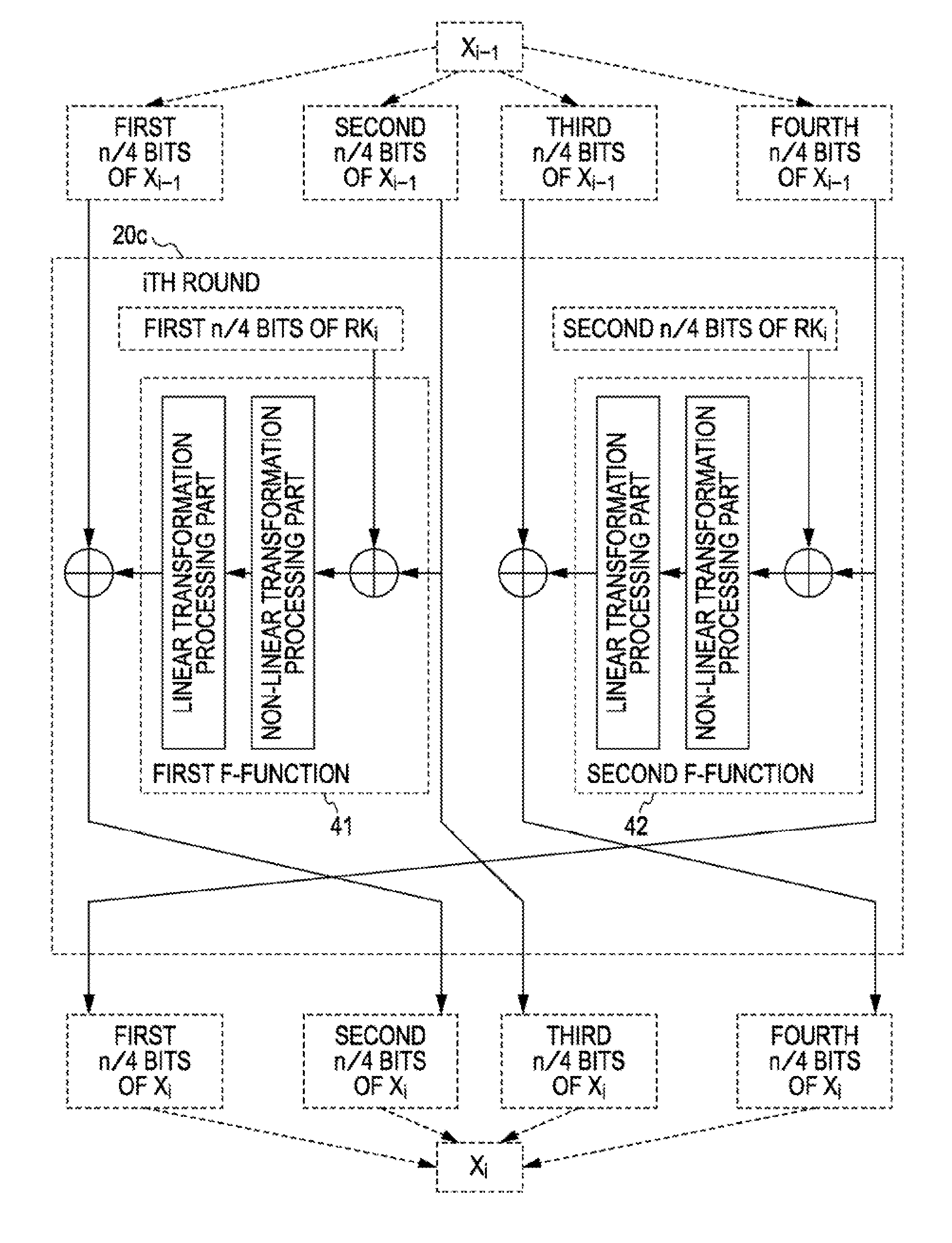
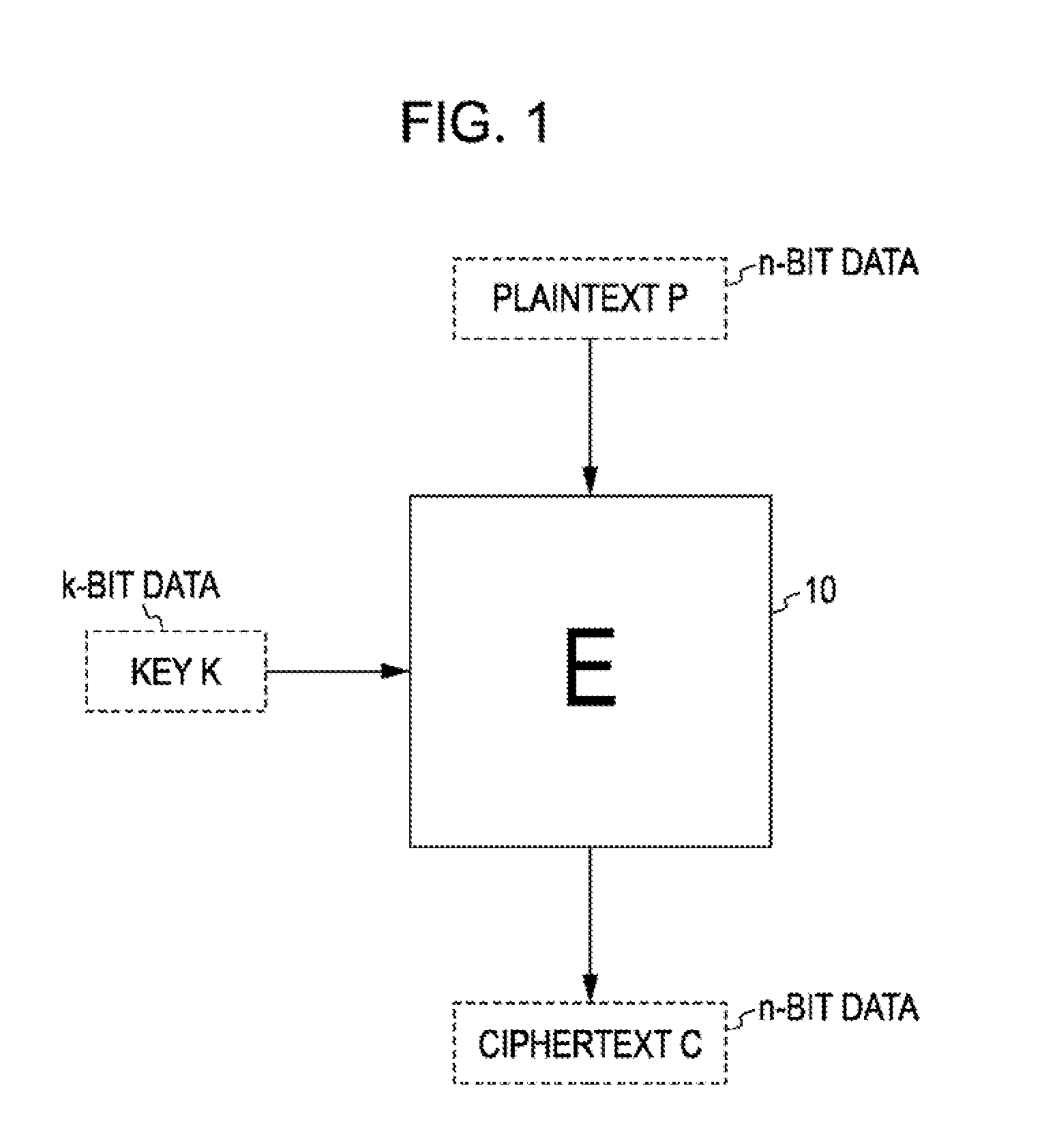
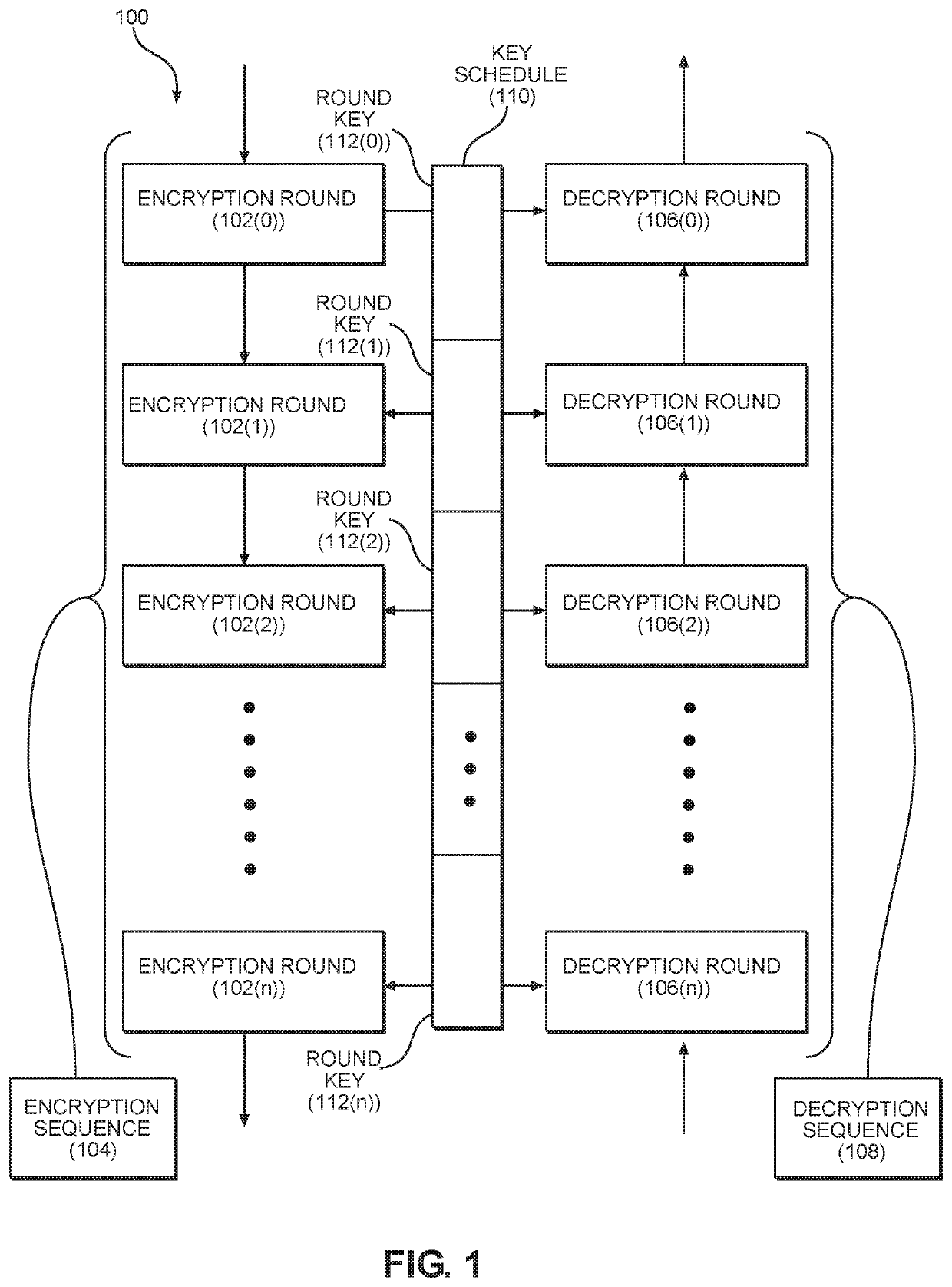
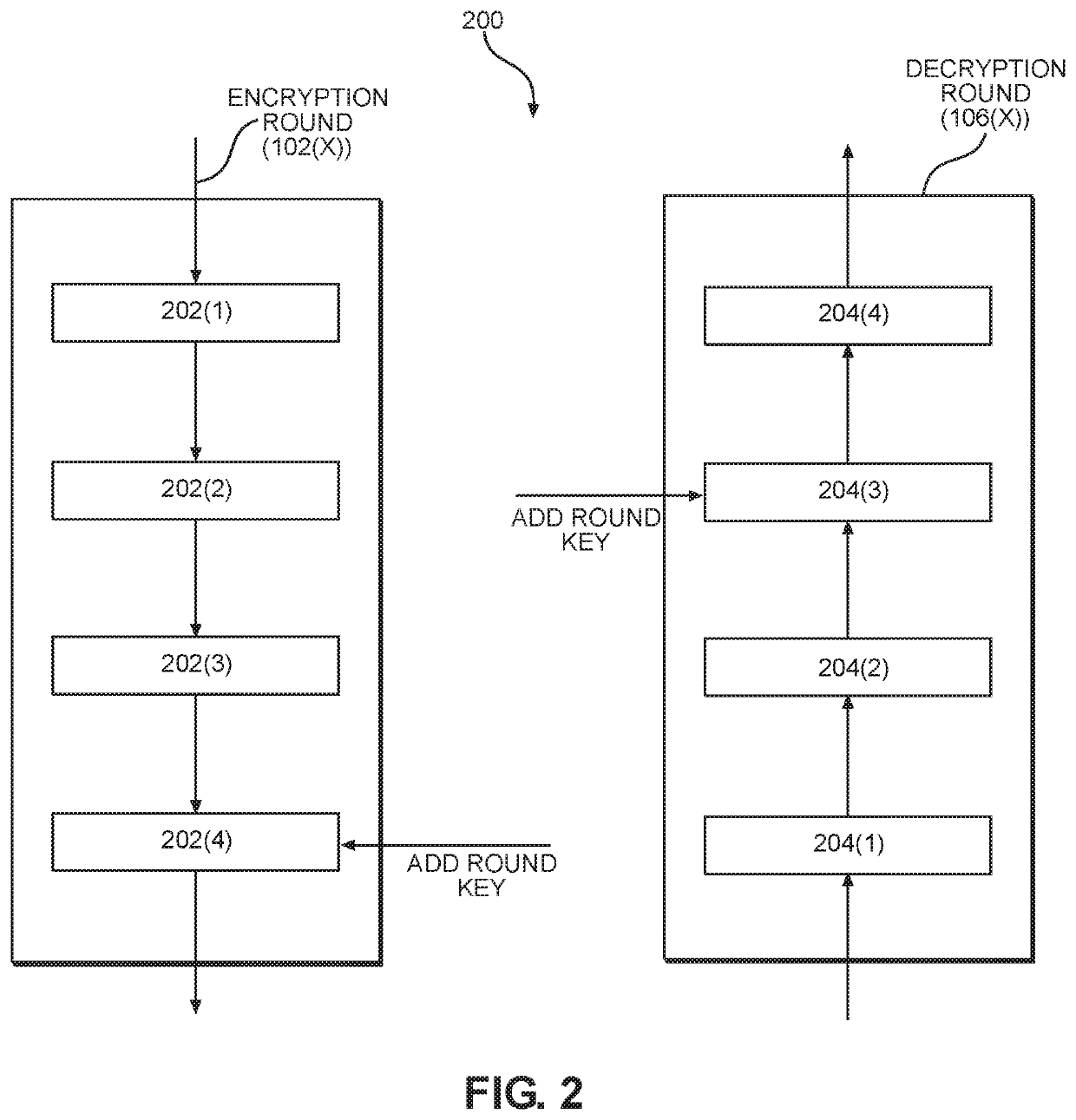
In cryptography, the so-called product ciphers are a certain kind of cipher, where the (de-)ciphering of data is typically done as an iteration of rounds. The setup for each round is generally the same, except for round-specific fixed values called a round constant, and round-specific data derived from the cipher key called a round key. A key schedule is an algorithm that calculates all the round keys from the key.
Identity authentication method and system
ActiveCN104579694AFull assurance of authenticityDynamicUser identity/authority verificationCommunications securityPassword
The invention discloses an identity authentication method and an identity authentication system. The method comprises the following steps: fixed identity identification information, a key schedule and a dynamic identity function are exchanged between a server and a client; a first random number is transmitted to the server and first response information transmitted by the client and second random number are received; the hash values of the first random number, the first dynamic identity information and the fixed client identity identification information as original texts are calculated and compared with the first response information, if the same hash values are present, the authentication is qualified; second response information is calculated and transmitted to the client, so that the hash values of the second random number, the second dynamic identity information and the fixed server identity identification information as the original texts are calculated by the client and compared with the second response information; if the same hash values are present, the authentication is qualified. The method is characterized in that the dynamic identity information is flexible and changeable, the information can be prevented from being revealed, the password encoding difficulty is increased and the security of the identity authentication is improved. Besides the method further comprises the following steps of key negotiation, heartbeat authentication and key schedule update, and thus the communication security and the periodic identity authentication are ensured.
Owner:ZHEJIANG UNIV
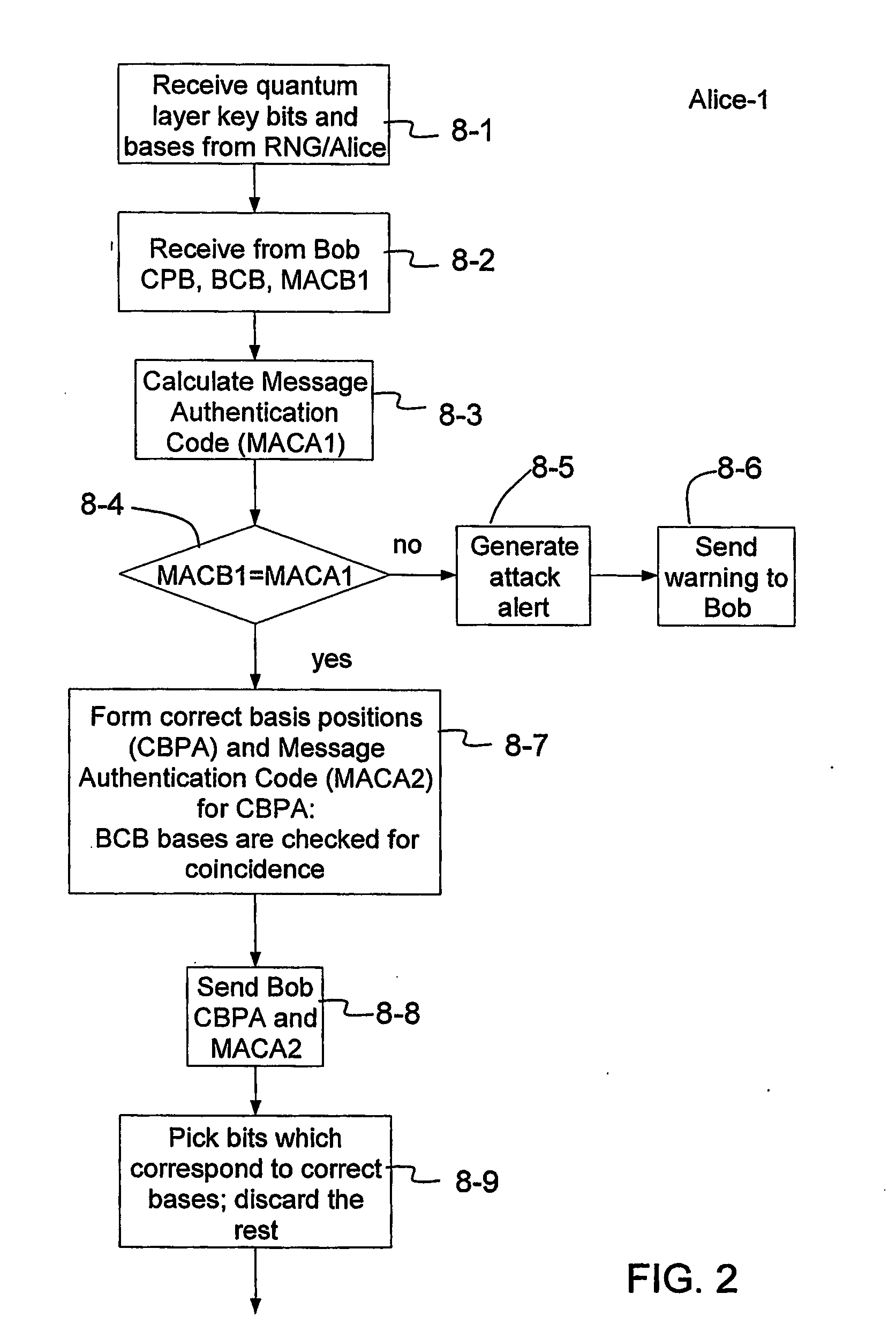
Key expansion for qkd
InactiveUS20060059343A1Key distribution for secure communicationSynchronisation information channelsKey exchangeKey schedule
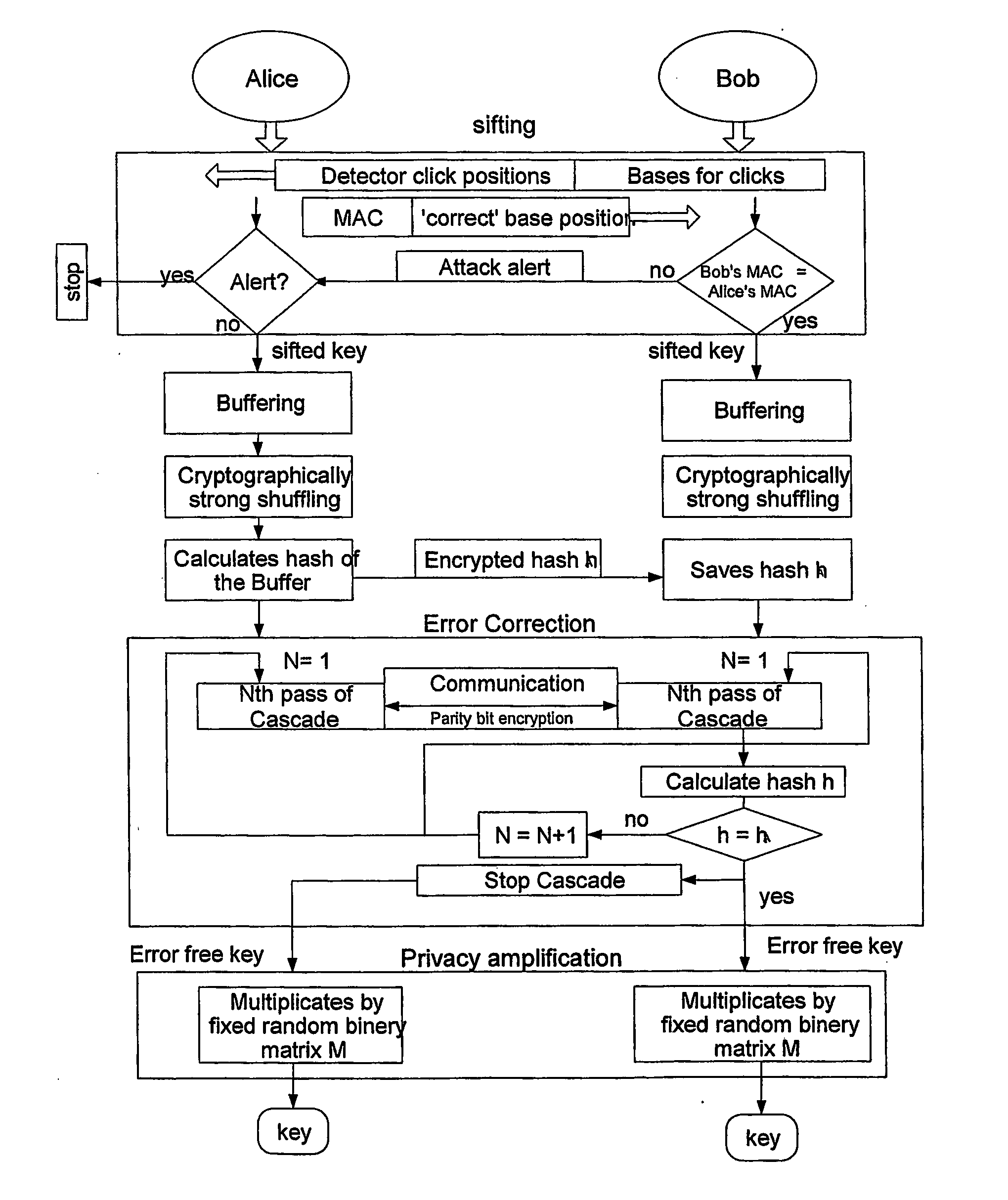
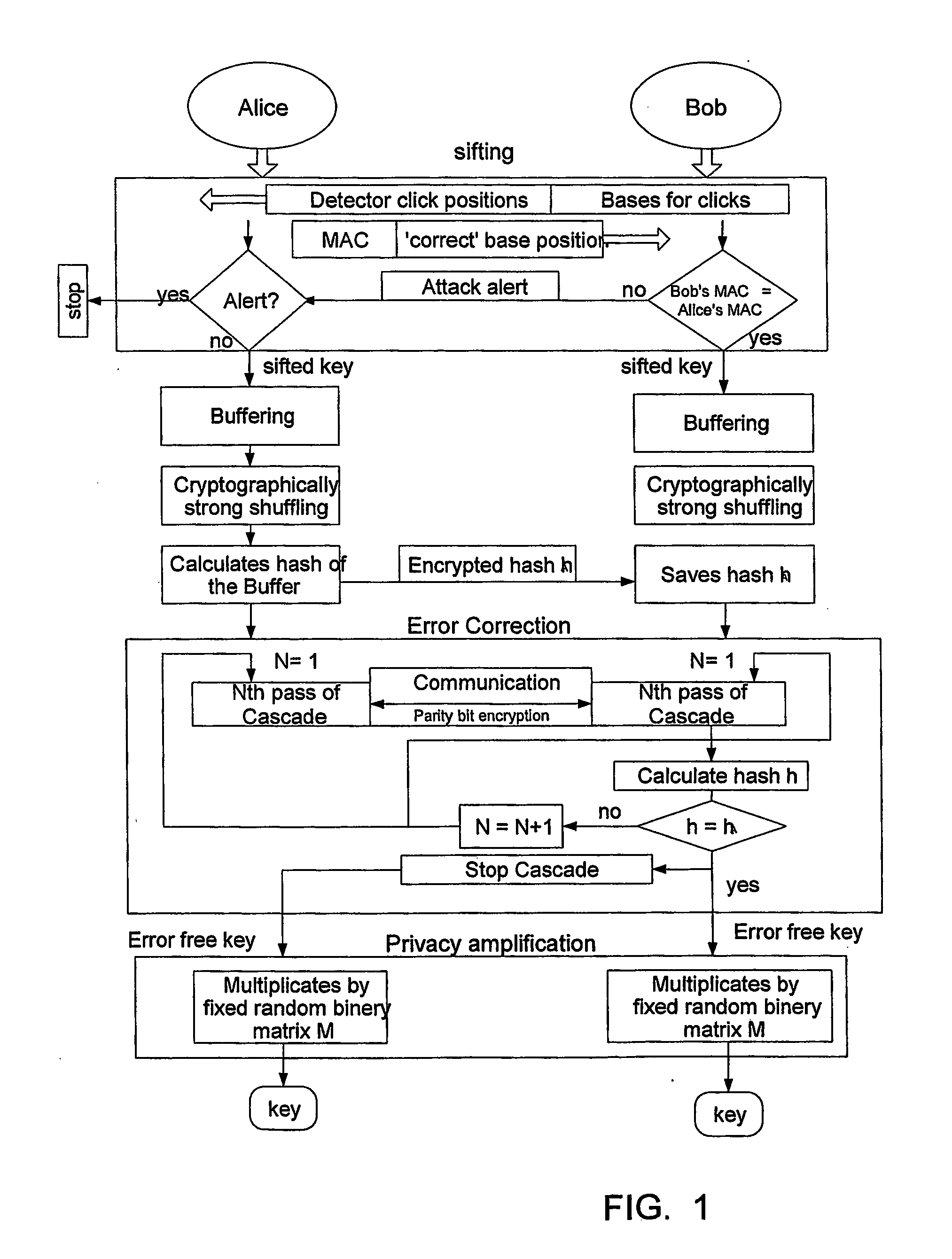
A method of encrypting information using an encryption pad based on keys exchanged between quantum key distribution (QKD) stations is disclosed. The method includes establishing raw keys between two stations using QKD, processing the keys to establish a plurality of matching privacy amplified keys at each station and buffering the keys in a shared key schedule. The method also includes the option of expanding one or more of the keys in the shared key schedule using a stream cipher to create a supply of expanded keys that serve as pads for one-time-pad encryption.
Owner:MAGIQ TECH INC
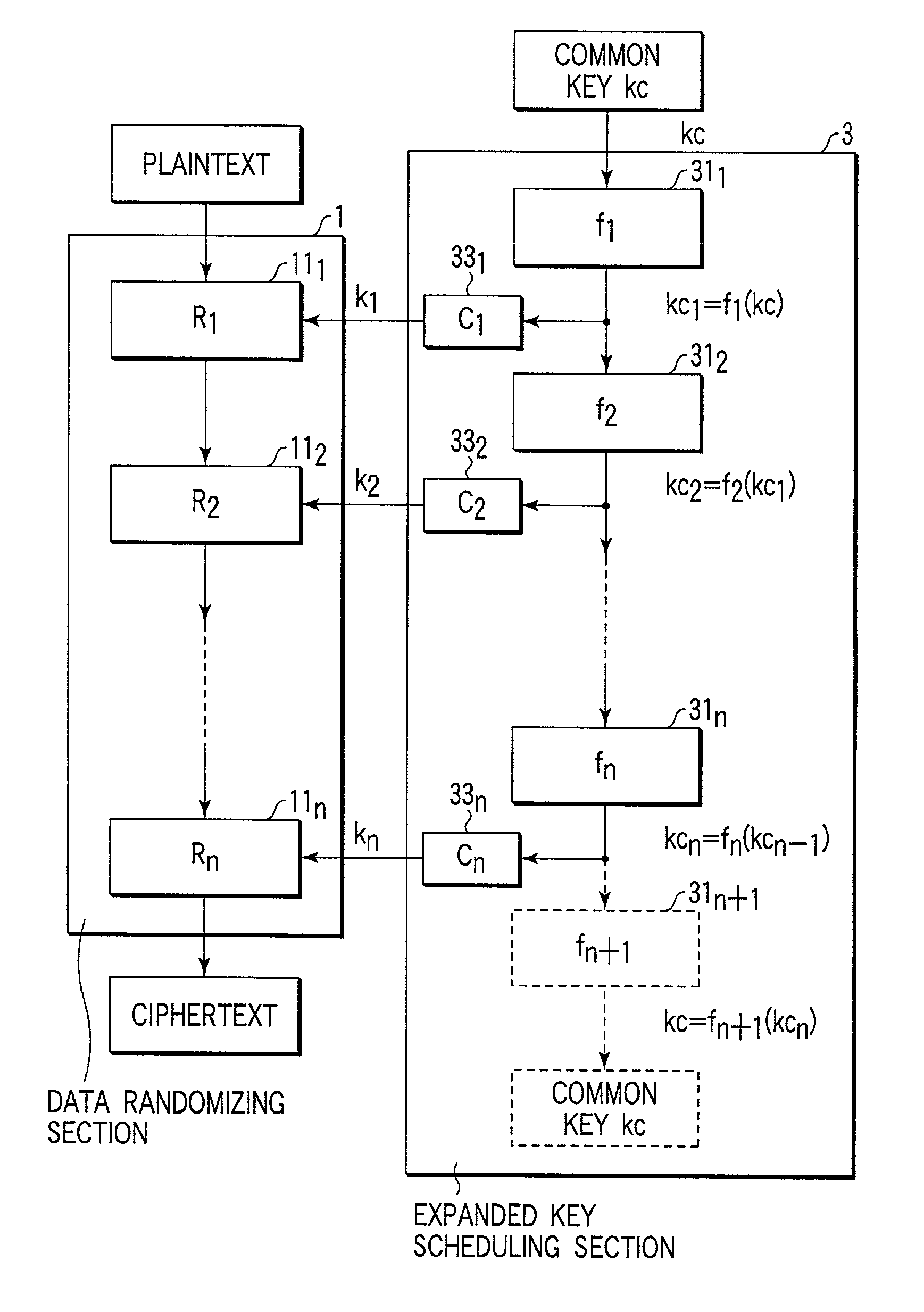
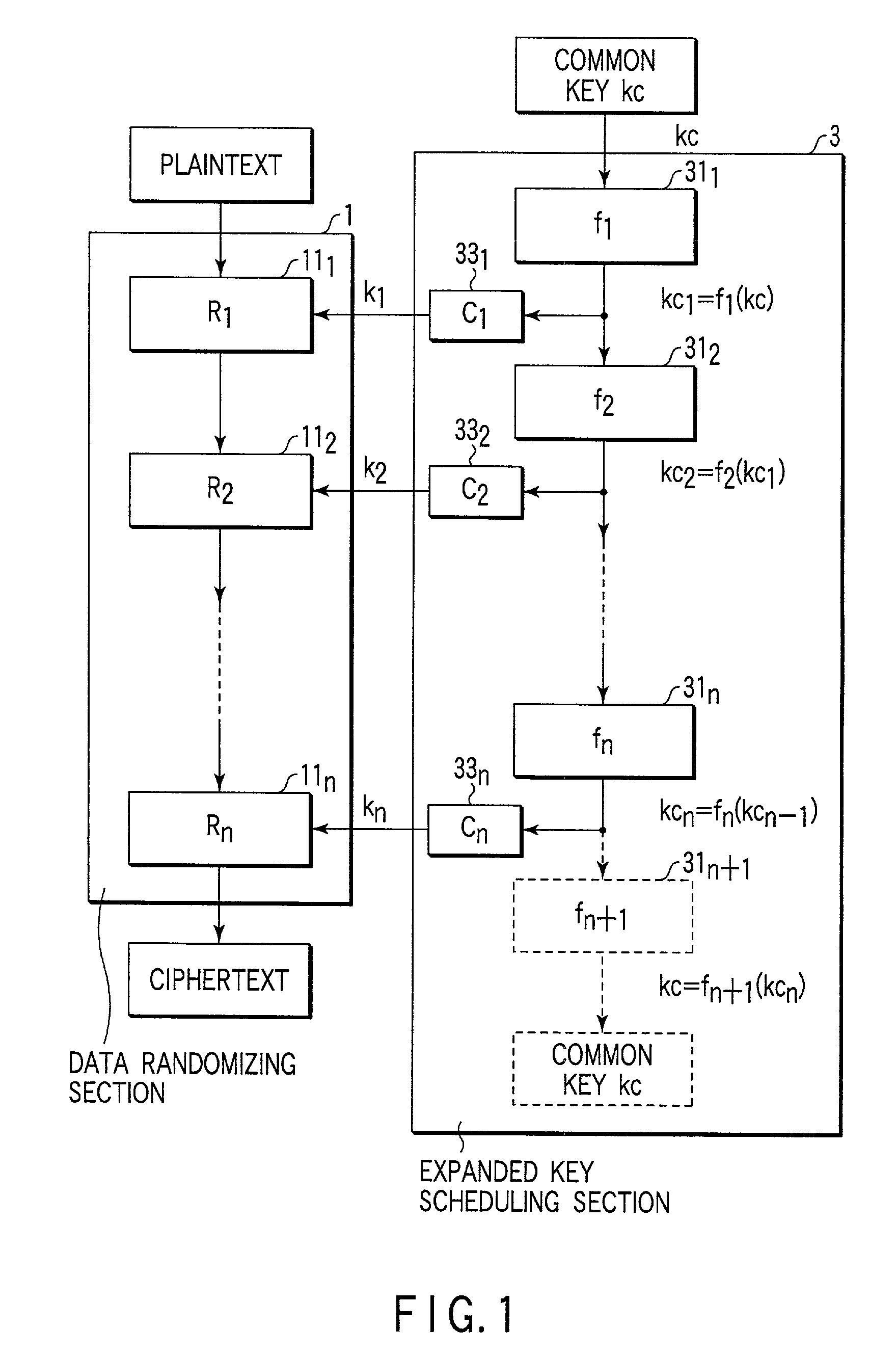
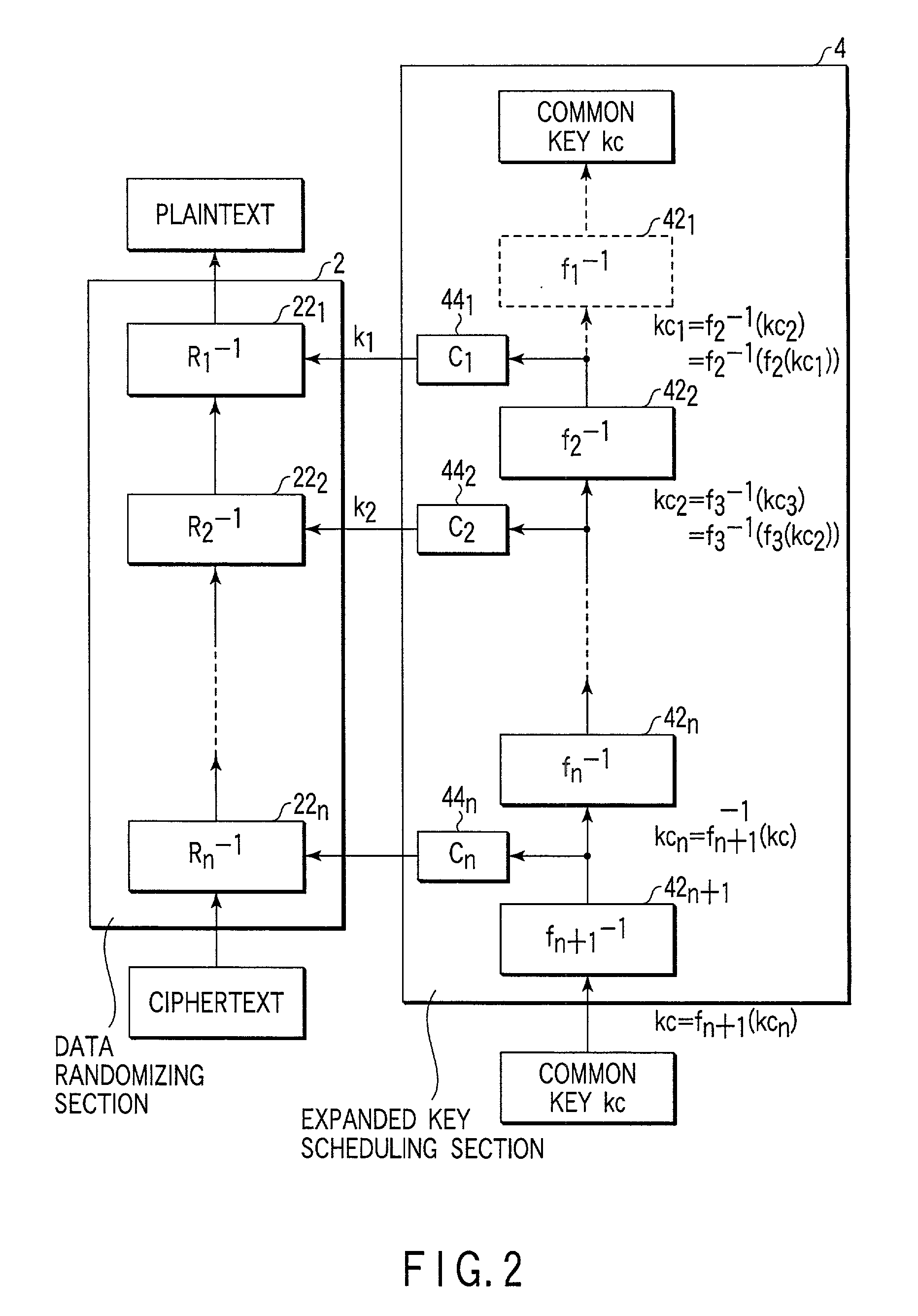
Encryption apparatus, decryption apparatus, expanded key generating apparatus and method therefor, and recording medium
InactiveUS7194090B2Avoids and reduces delay timeEncryption apparatus with shift registers/memoriesSecret communicationComputer hardwareKey schedule
Expanded key schedule circuit for common key encryption system in which expanded keys are used in a predetermined order in data randomizing process for encryption and in a reversed order in data randomizing process for decryption, comprises round processing circuits connected in series. The round processing circuits subject the common key or sub key of a previous stage to a round function to output a sub key. The sub key of the last stage is equal to the common key. The expanded keys are generated from the sub keys.
Owner:KK TOSHIBA
Methods and devices for a chained encryption mode
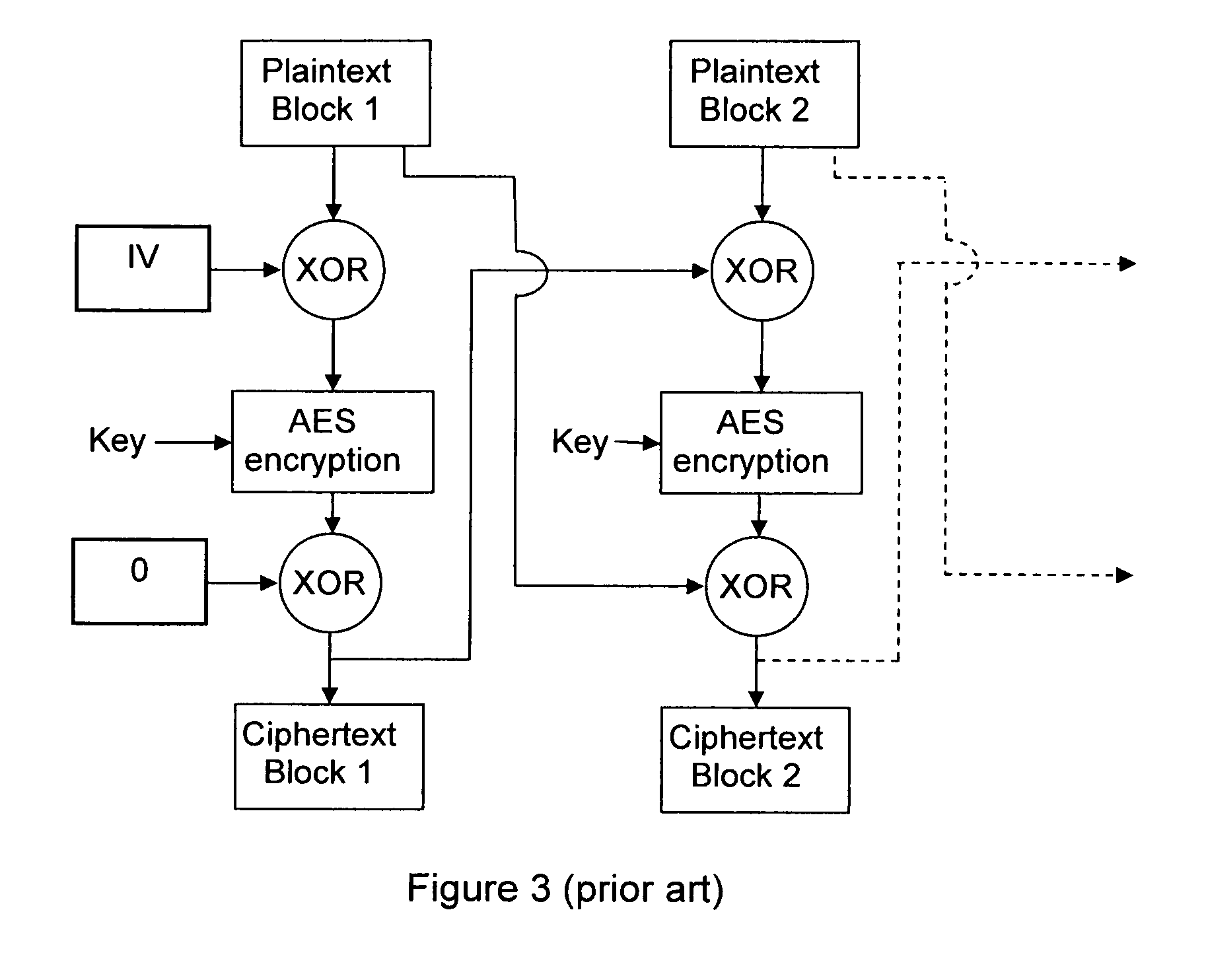
InactiveUS8259934B2Data stream serial/continuous modificationSecret communicationPlaintextComputer hardware
Owner:THOMSON LICENSING SA
Methods and devices for a chained encryption mode
InactiveUS20100150344A1Data stream serial/continuous modificationMultiple keys/algorithms usageComputer hardwarePlaintext
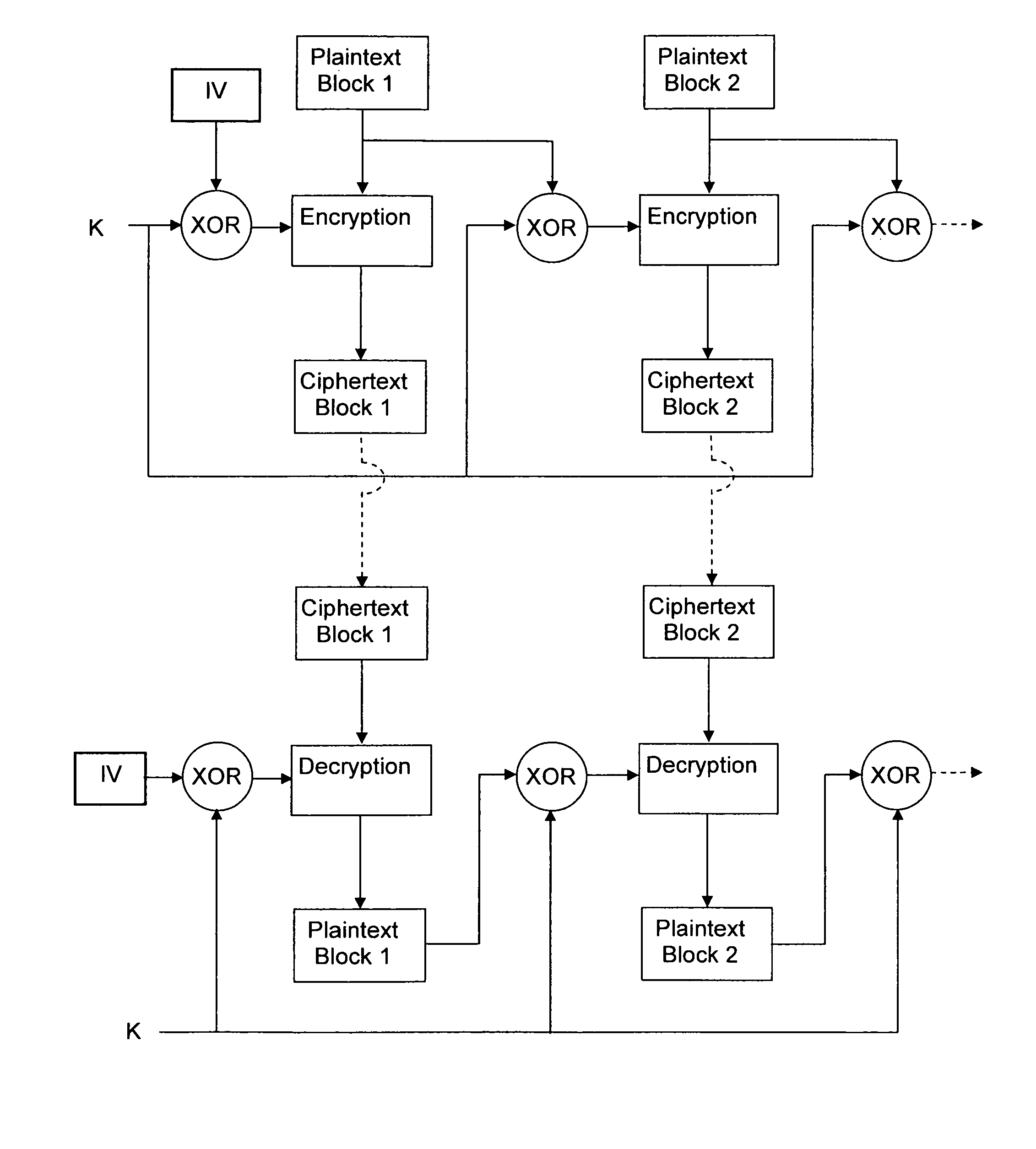
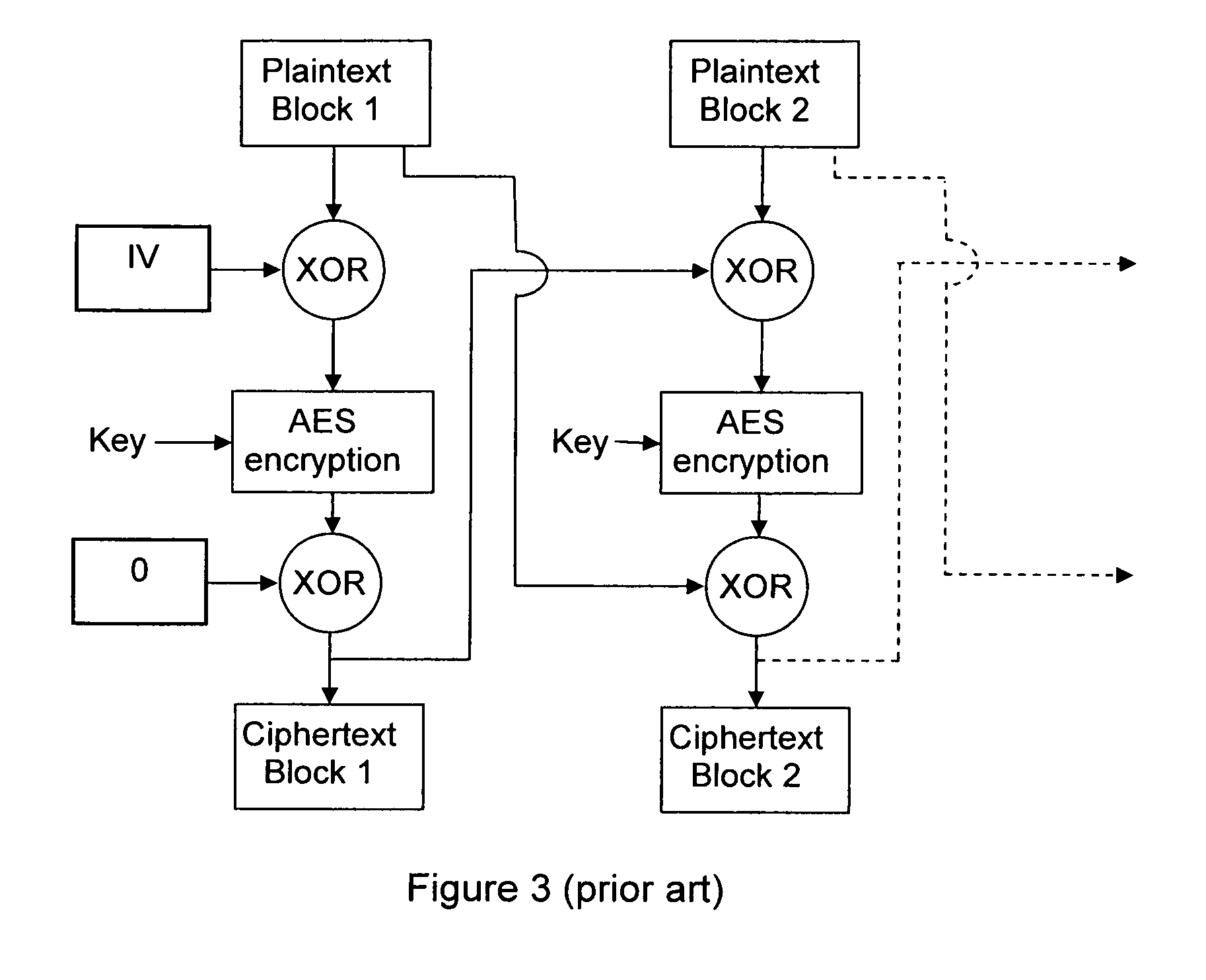
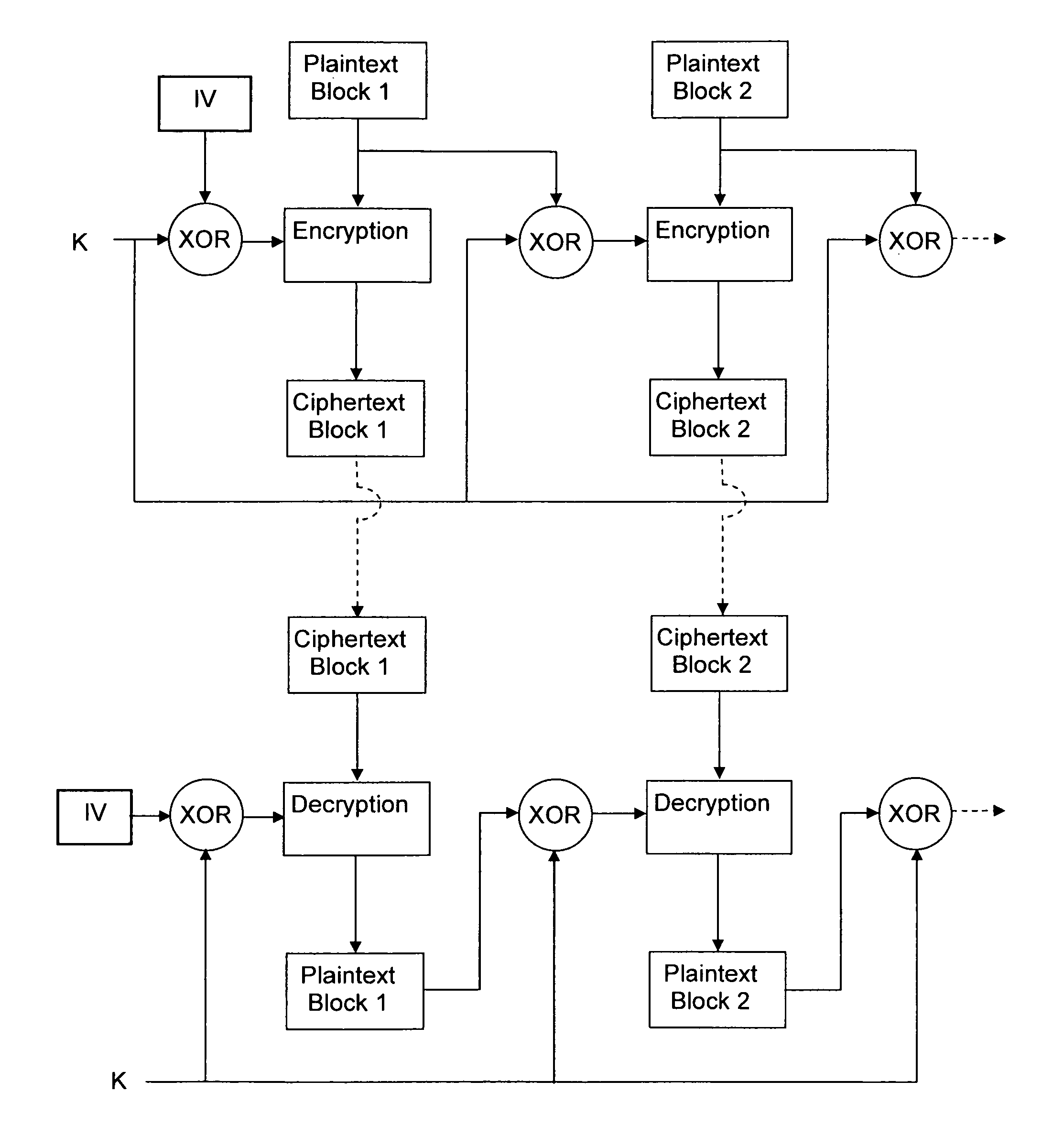
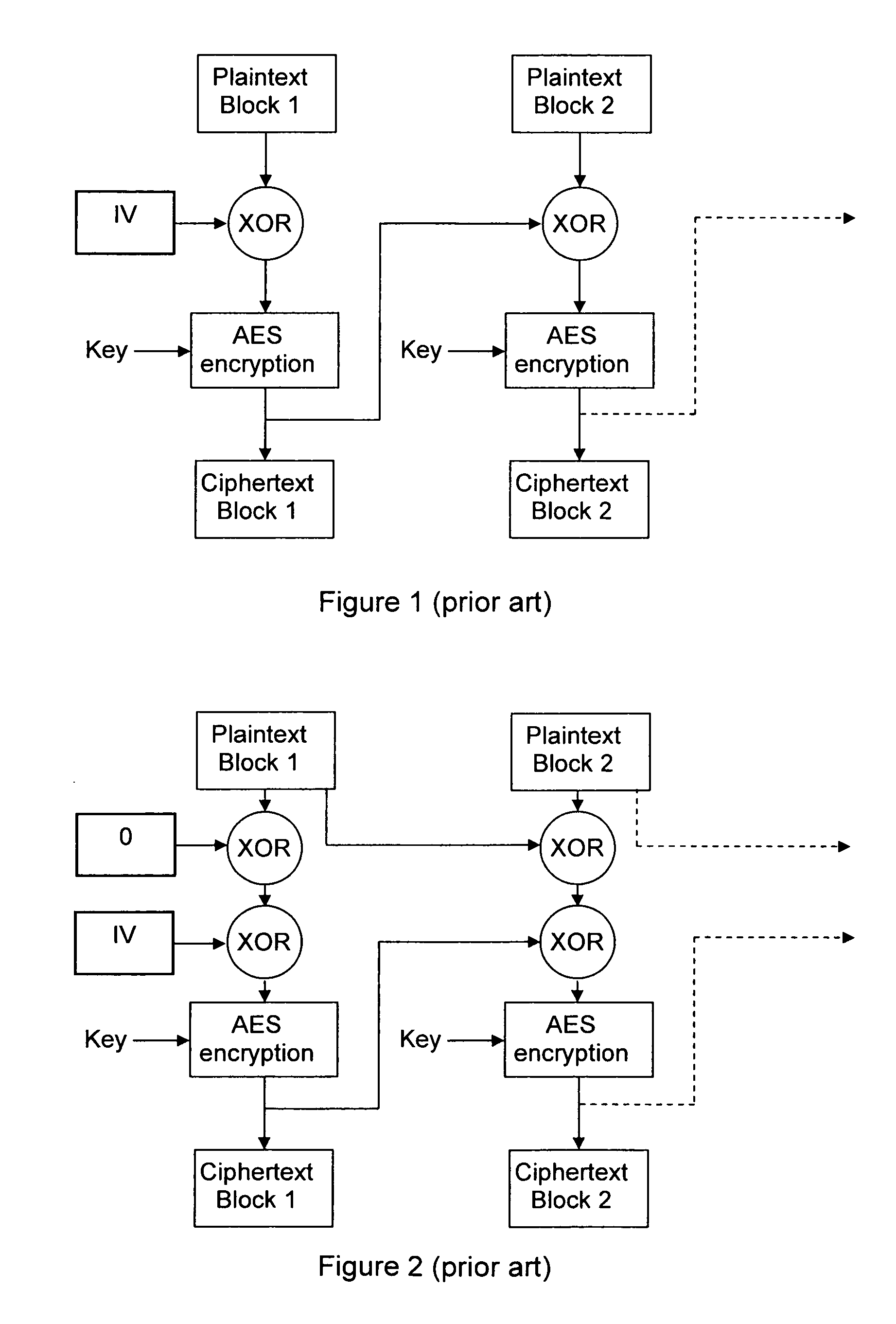
An encryption chaining mode takes plaintext block N, generates encryption key N by combining, preferably by XOR, encryption key N−1 and plaintext block N−1 and encrypts plaintext block N using an encryption algorithm with encryption key N to output ciphertext block N. Encryption key for the first plaintext block is generated by XOR-ing a random Initialization vector and a random initialization key K. In a preferred embodiment, initialization key K is subkeys resulting from a key schedule algorithm and encryption key N−1 is only one of the subkeys. Encryption key for the first plaintext block is generated by XOR-ing a random Initialization vector and one subkey resulting from a key schedule algorithm. Also provided is a corresponding decryption method, an encryption device, a decryption device.
Owner:THOMSON LICENSING SA
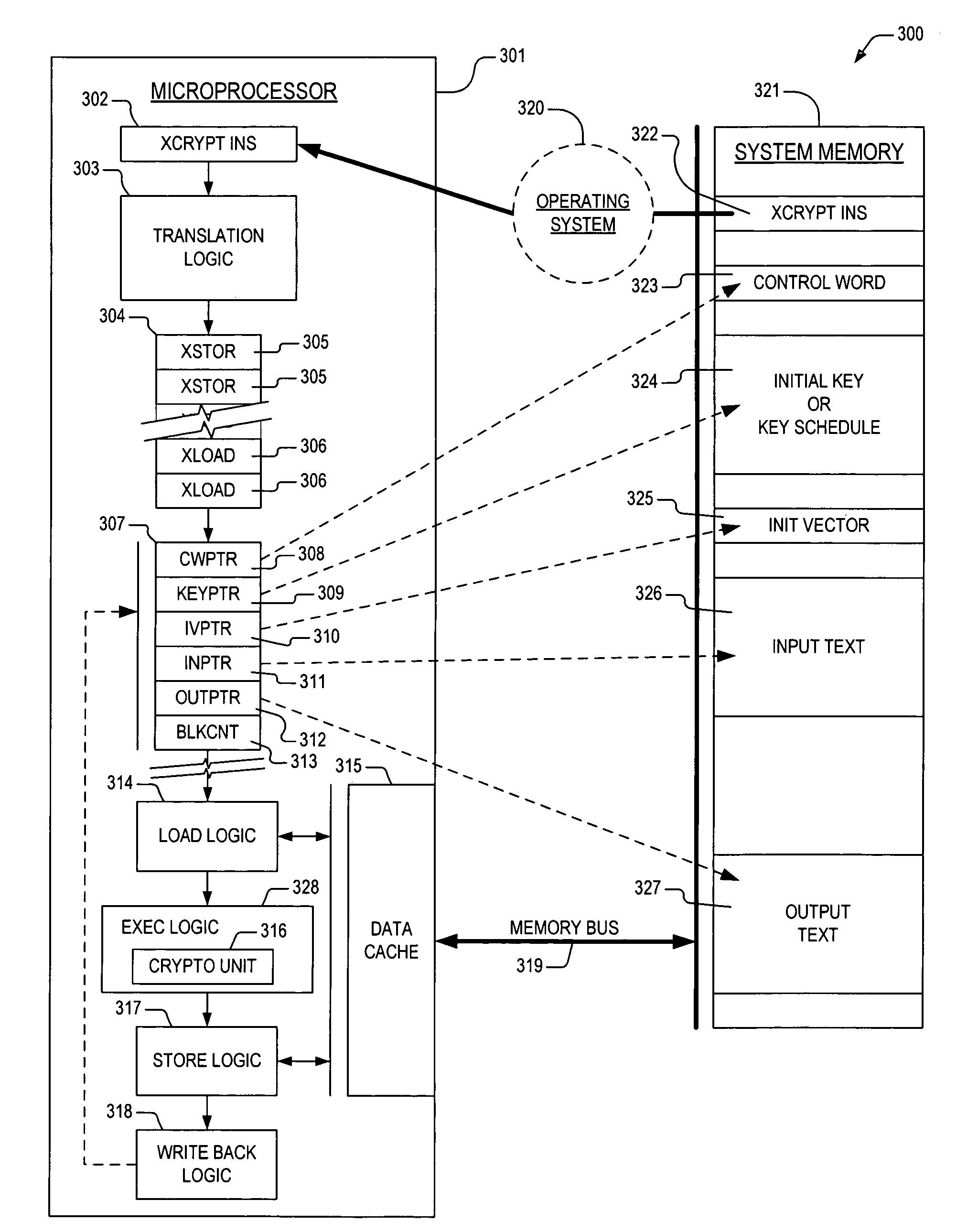
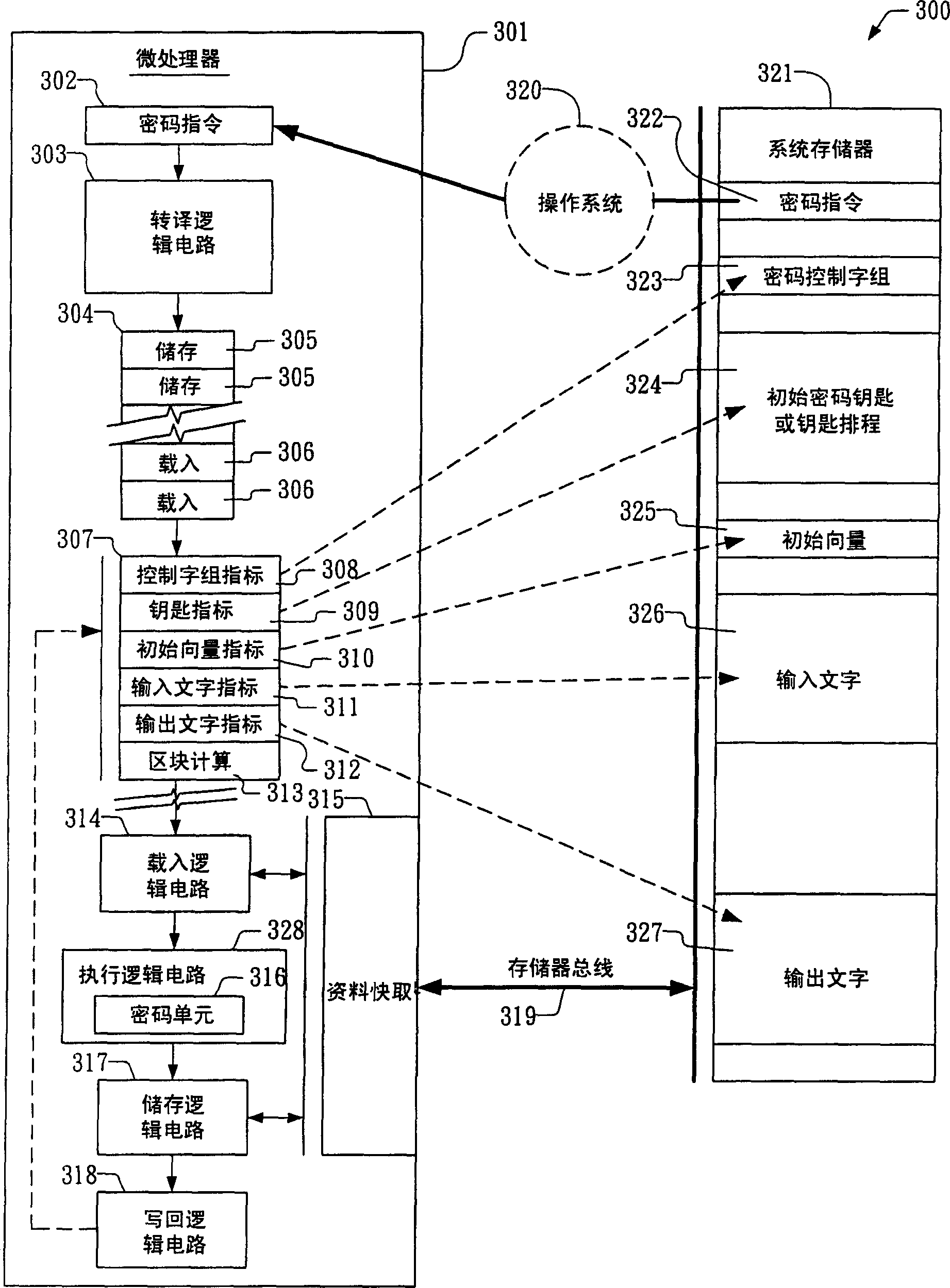
Apparatus and method for generating a cryptographic key schedule in a microprocessor
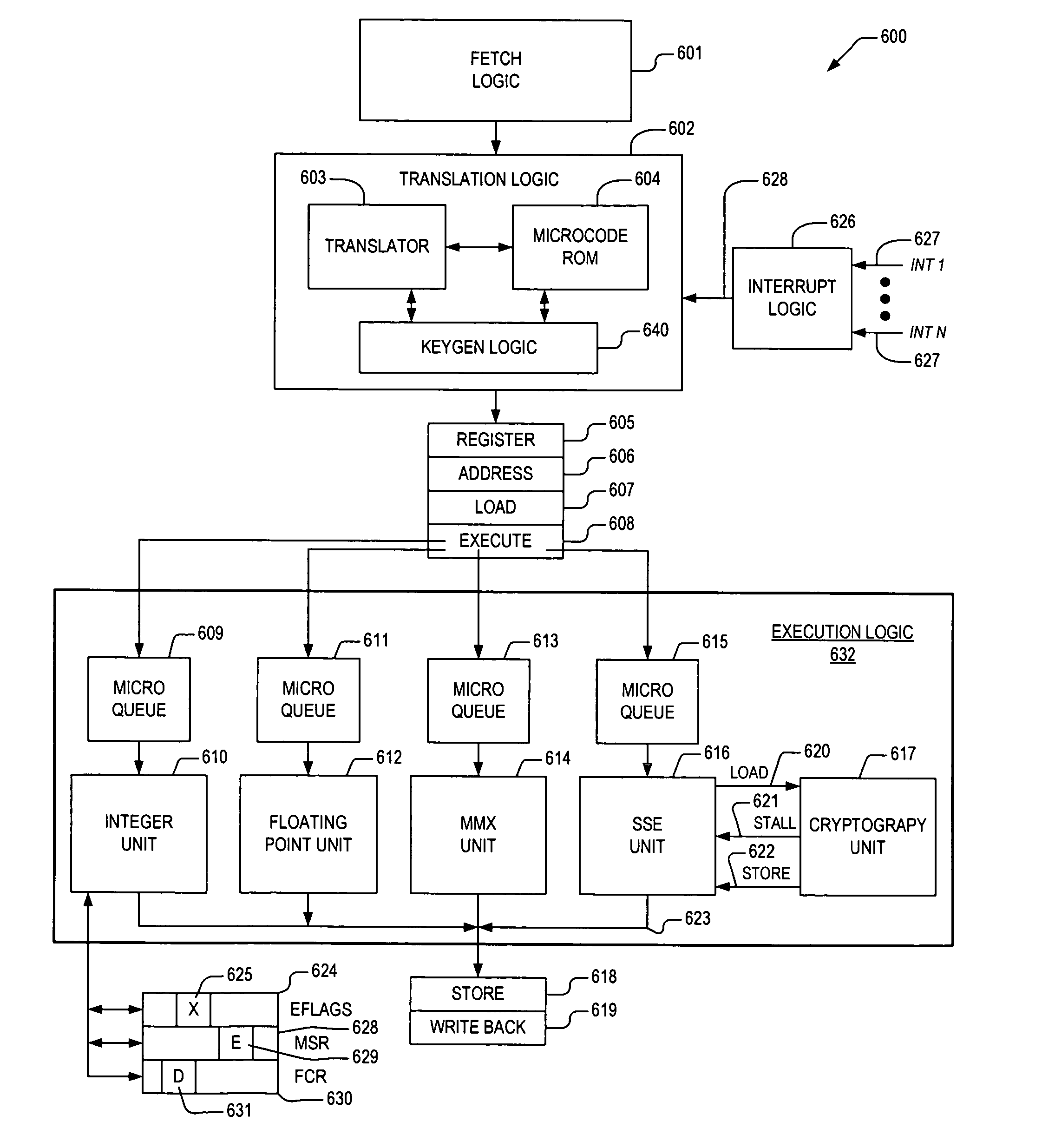
ActiveUS7539876B2Good techniqueKey distribution for secure communicationSynchronising transmission/receiving encryption devicesKey scheduleKey generation
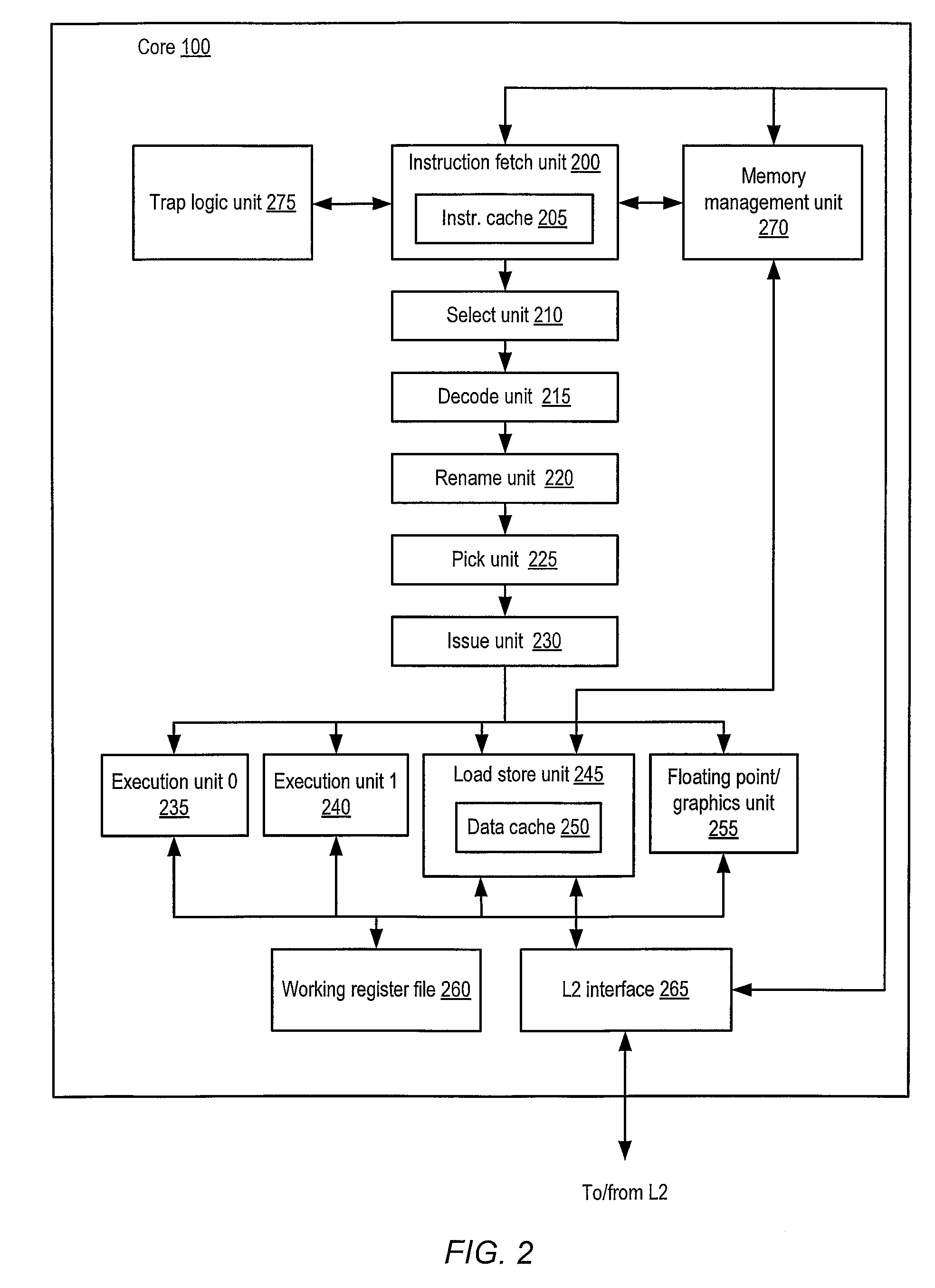
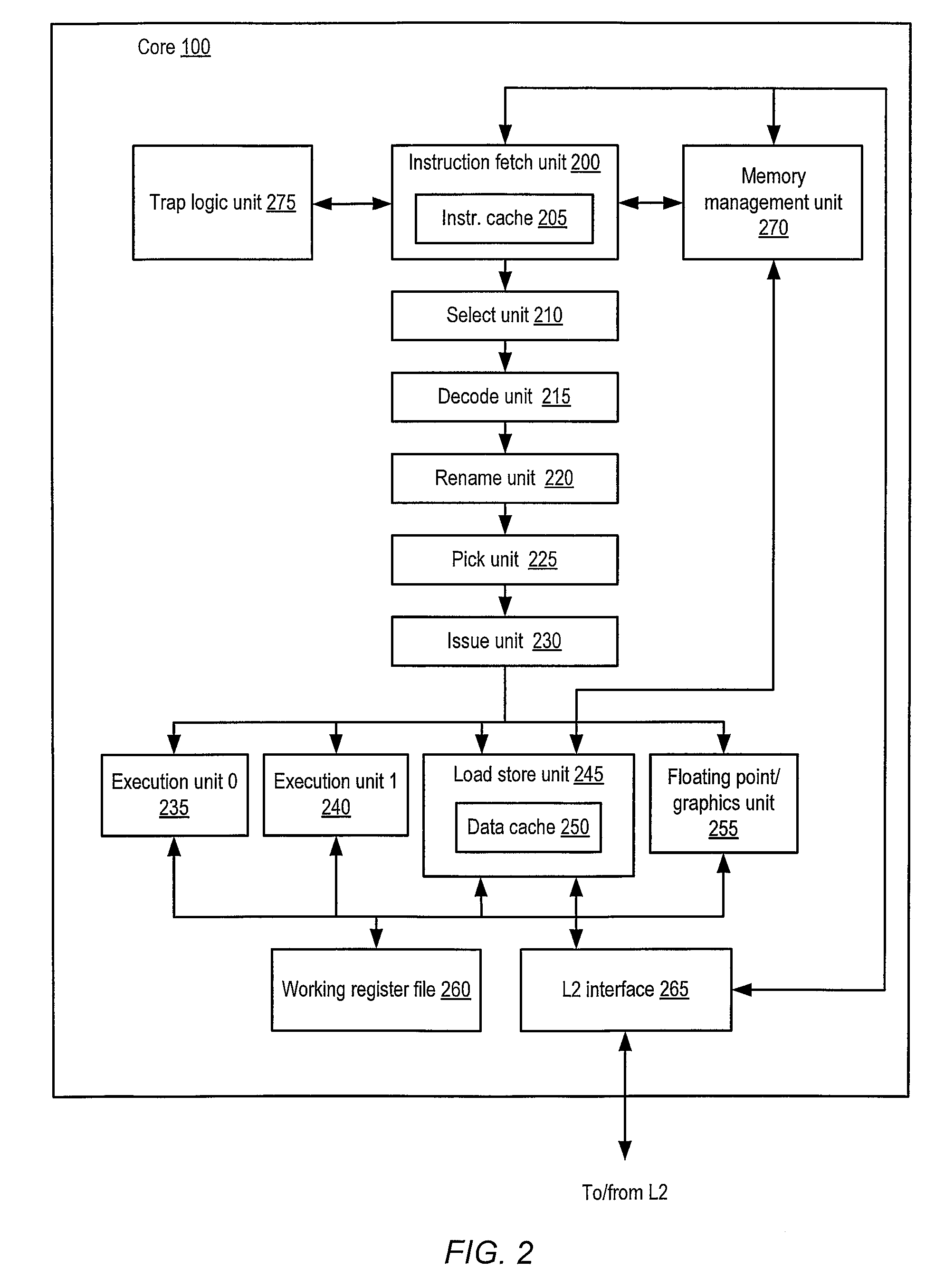
An apparatus and method for performing cryptographic operations. In one embodiment, an apparatus is provided for performing cryptographic operations. The apparatus includes fetch logic, keygen logic, and execution logic. The fetch logic is disposed within a microprocessor and receives cryptographic instruction single atomic cryptographic instruction as part of an instruction flow executing on the microprocessor. The cryptographic instruction single atomic cryptographic instruction prescribes one of the cryptographic operations, and also prescribes that a provided cryptographic key be expanded into a corresponding key schedule for employment during execution of the one of the cryptographic operations. The keygen logic is disposed within the microprocessor and is operatively coupled to the single atomic cryptographic instruction. The keygen logic directs the microprocessor to expand the provided cryptographic key into the corresponding key schedule. The execution logic is coupled to the keygen logic. The execution logic is disposed within the microprocessor and expands the provided cryptographic key into the corresponding key schedule.
Owner:VIA TECH INC
AES encryption circuitry with CCM
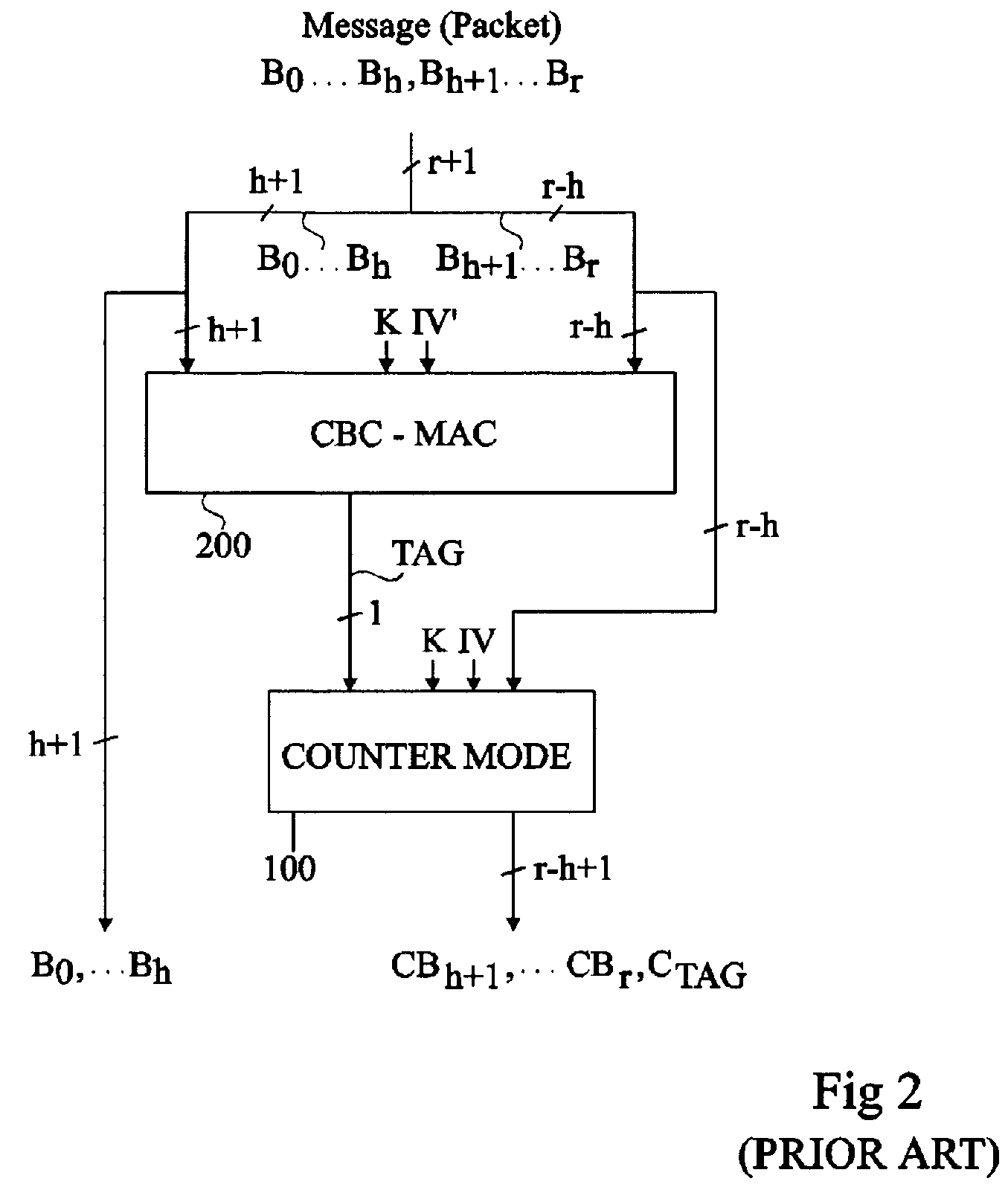
ActiveUS20070286415A1User identity/authority verificationSecret communicationData streamKey schedule
Circuitry for encrypting at least a part of an input data flow and generating a tag based on the input data flow with the same ciphering algorithm and the same key including a first ciphering branch arranged to encrypt the at least part of the input data; a second ciphering branch arranged to generate the tag; and a single key schedule unit arranged to receive the key, to generate at least one sub-key based on the key and to provide the at least one sub-key to the first and second ciphering branches.
Owner:STMICROELECTRONICS SRL
Apparatus and method for providing configurable cryptographic key size
ActiveCN1655496AKey distribution for secure communicationSynchronising transmission/receiving encryption devicesComputer hardwareKey size
The present invention provides an apparatus and method for performing cryptographic operations. In one embodiment, an apparatus is provided for performing cryptographic operations. The apparatus includes a cryptographic instruction, keygen logic, and execution logic. The cryptographic instruction is received by a computing device as part of an instruction flow executing on the computing device. The cryptographic instruction prescribes one of the cryptographic operations, and also prescribes that a provided cryptographic key be expanded into a corresponding key schedule for employment during execution of the one of the cryptographic operations. The keygen logic is operatively coupled to the cryptographic instruction. The keygen logic directs the computing device to expand the provided cryptographic key into the corresponding key schedule. The execution logic is coupled to the keygen logic. The execution logic expands the provided cryptographic key into the corresponding key schedule.
Owner:VIA TECH INC
AES encryption circuitry with CCM
Owner:STMICROELECTRONICS SRL
Differential power analysis resistant encryption and decryption functions
ActiveUS9331848B1Encryption apparatus with shift registers/memoriesCryptographic attack countermeasuresPower analysisPlaintext
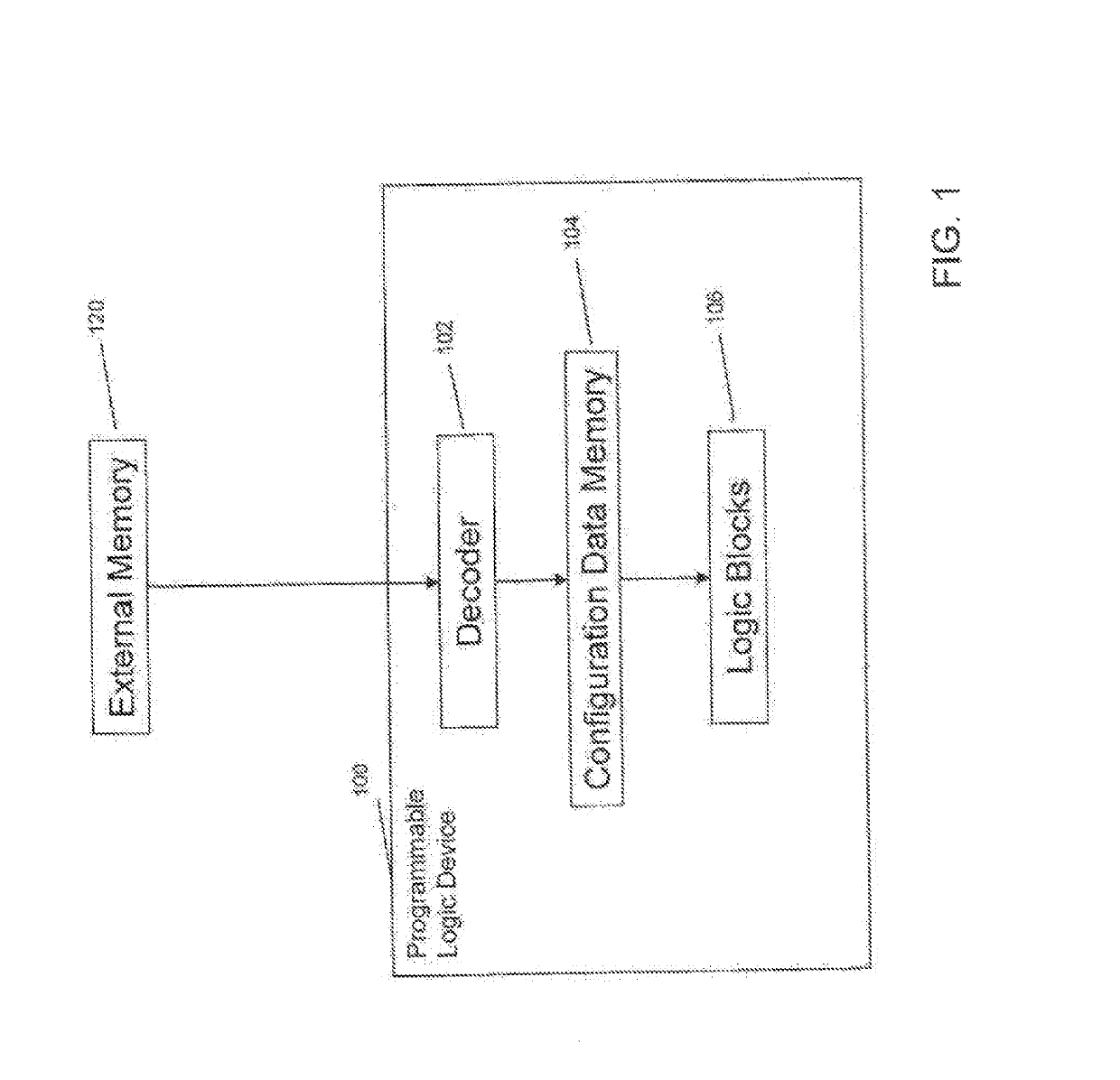
Circuits, methods, and systems are provided for securing an integrated circuit device against Differential Power Analysis (DPA) attacks. Plaintext (e.g., configuration data for a programmable device) may be encrypted in an encryption system using a cryptographic algorithm. Ciphertext may be decrypted in a decryption system using the cryptographic algorithm. The encryption and / or decryption systems may obfuscate the plaintext, the ciphertext, and / or the substitution tables used by the cryptographic algorithm. The encryption and / or decryption systems may also generate cryptographic key schedules by using different keys for encrypting / decrypting different blocks and / or by expanding round keys between encryption / decryption blocks. These techniques may help mitigate or altogether eliminate the vulnerability of cryptographic elements revealing power consumption information to learn the value of secret information, e.g., through DPA.
Owner:ALTERA CORP
Communication encryption method and device
InactiveUS8767957B1Sufficient performanceSmall memory footprintSecret communicationProgram controlMicrocontrollerTransceiver
An encryption method and device employing a modified low-resource AES algorithm. The algorithm in one embodiment has a 128-bit key and a 16-bit data type, along with optimization functions including function inlining, memory move reduction via multiple transformations on a given state during a given iteration of a main loop of the algorithm, pointer-based accessing of the state from a transformation function, and a global key schedule. Another embodiment of the invention is a low-power secure communication device comprising a ZigBee-compliant transceiver having a maximum over-the-air data rate of 250 kbps, and a 16-bit RISC encryption processor configured to implement an AES algorithm adapted to encrypt data at a faster rate than 250 kbps. The AES algorithm only requires about 5000 bytes of ROM and about 250 bytes of RAM. The disclosed implementation of AES in a high-level language (C in this case) is believed to be the first software-based solution for 16-bit microcontrollers capable of matching the communication rate of 250 kbps specified by the Zigbee protocol, while also minimizing RAM and ROM usage.
Owner:PURDUE RES FOUND INC
Apparatus and method for implementing instruction support for the data encryption standard (DES) algorithm
ActiveUS8654970B2Unauthorized memory use protectionHardware monitoringComputer hardwareInformation processing
A processor including instruction support for implementing the Data Encryption Standard (DES) block cipher algorithm may issue, for execution, programmer-selectable instructions from a defined instruction set architecture (ISA). The processor may include a cryptographic unit that may receive instructions for execution. The instructions include one or more DES instructions defined within the ISA. In addition, the DES instructions may be executable by the cryptographic unit to implement portions of an DES cipher that is compliant with Federal Information Processing Standards Publication 46-3 (FIPS 46-3). In response to receiving a DES key expansion instruction defined within the ISA, the cryptographic unit may generate one or more expanded cipher keys of the DES cipher key schedule from an input key.
Owner:ORACLE INT CORP
Apparatus and method for implementing instruction support for the data encryption standard (DES) algorithm
ActiveUS20100246814A1Encryption apparatus with shift registers/memoriesInternal/peripheral component protectionInformation processingComputer hardware
A processor including instruction support for implementing the Data Encryption Standard (DES) block cipher algorithm may issue, for execution, programmer-selectable instructions from a defined instruction set architecture (ISA). The processor may include a cryptographic unit that may receive instructions for execution. The instructions include one or more DES instructions defined within the ISA. In addition, the DES instructions may be executable by the cryptographic unit to implement portions of an DES cipher that is compliant with Federal Information Processing Standards Publication 46-3 (FIPS 46-3). In response to receiving a DES key expansion instruction defined within the ISA, the cryptographic unit may generate one or more expanded cipher keys of the DES cipher key schedule from an input key.
Owner:ORACLE INT CORP
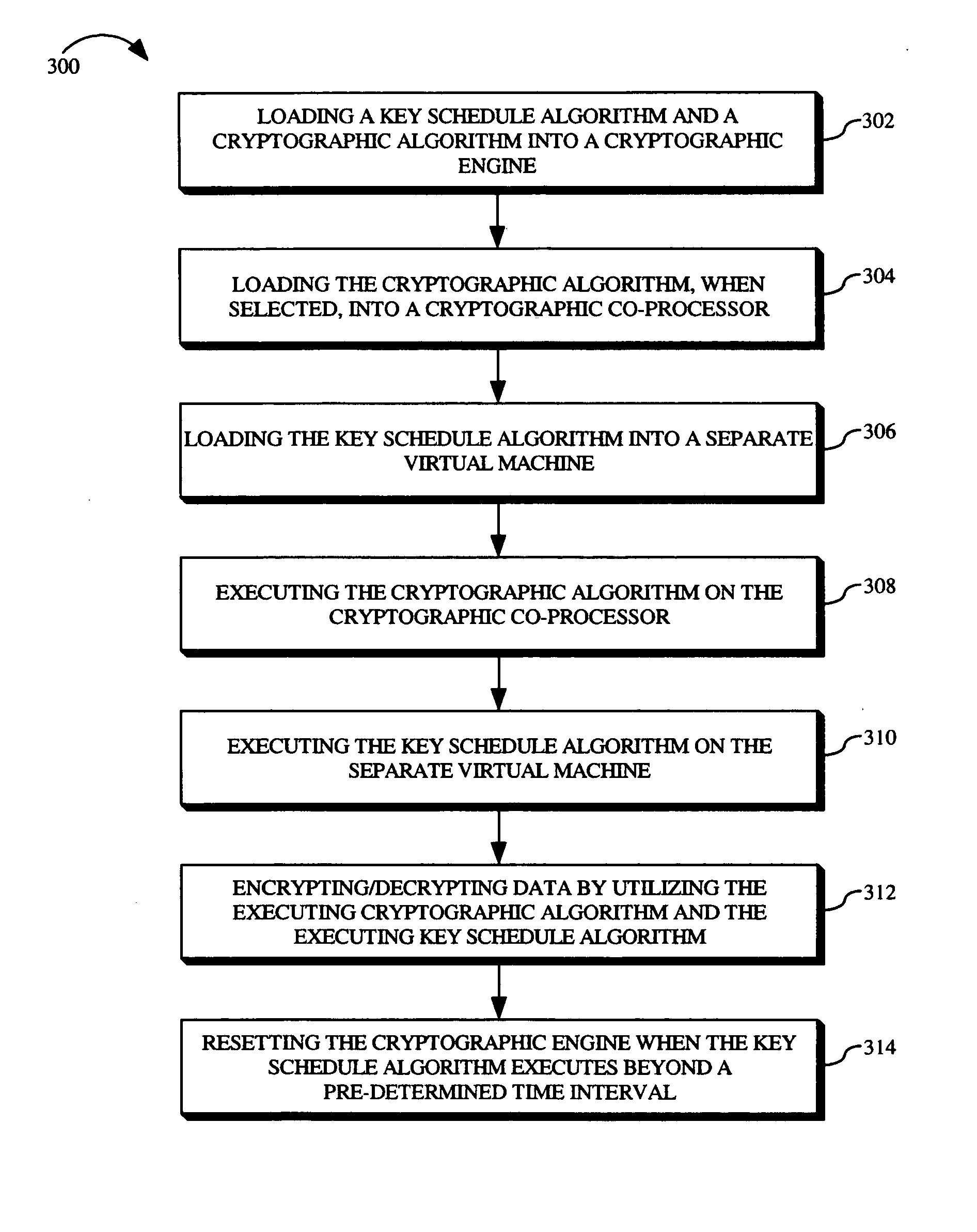
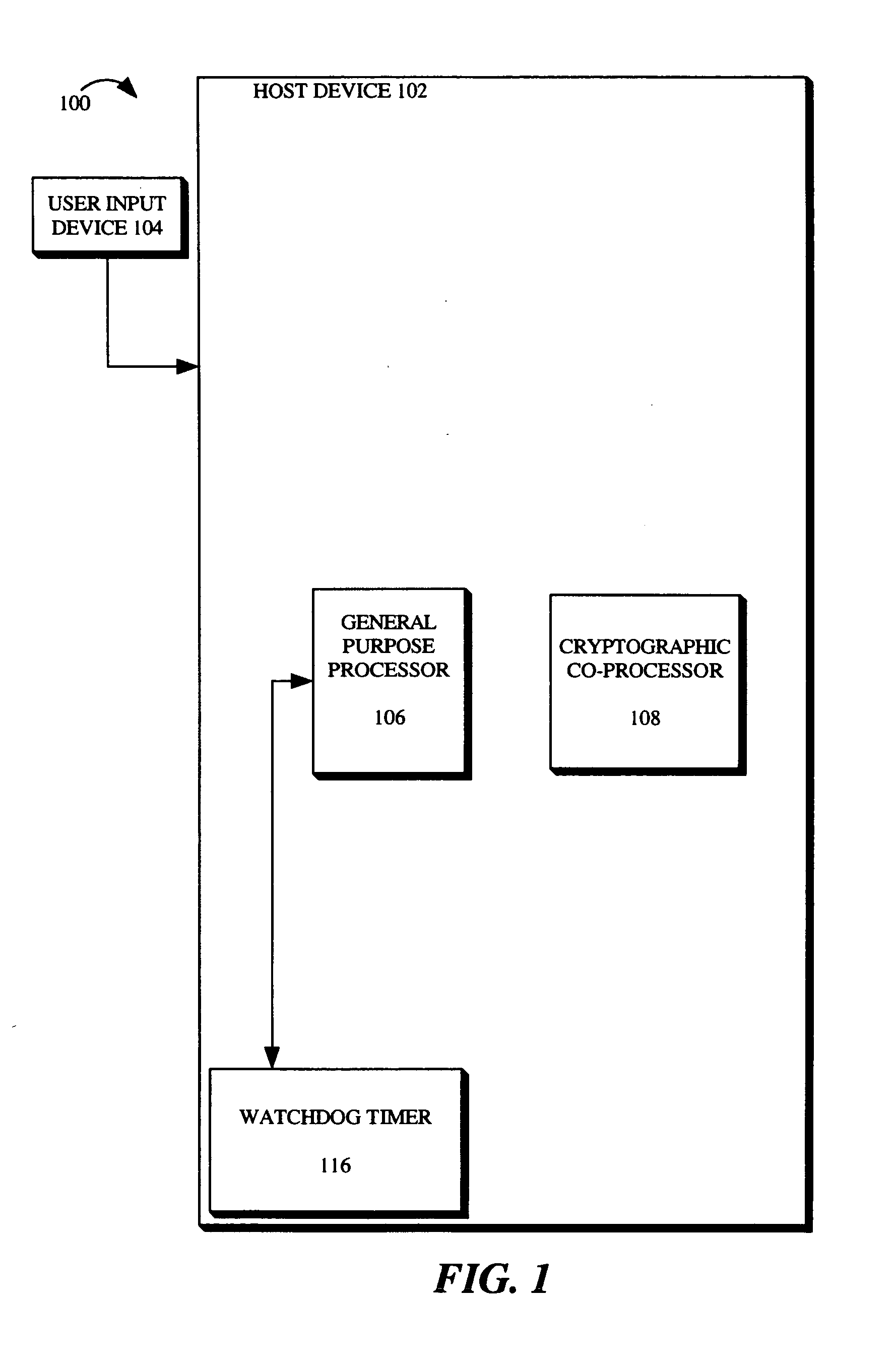
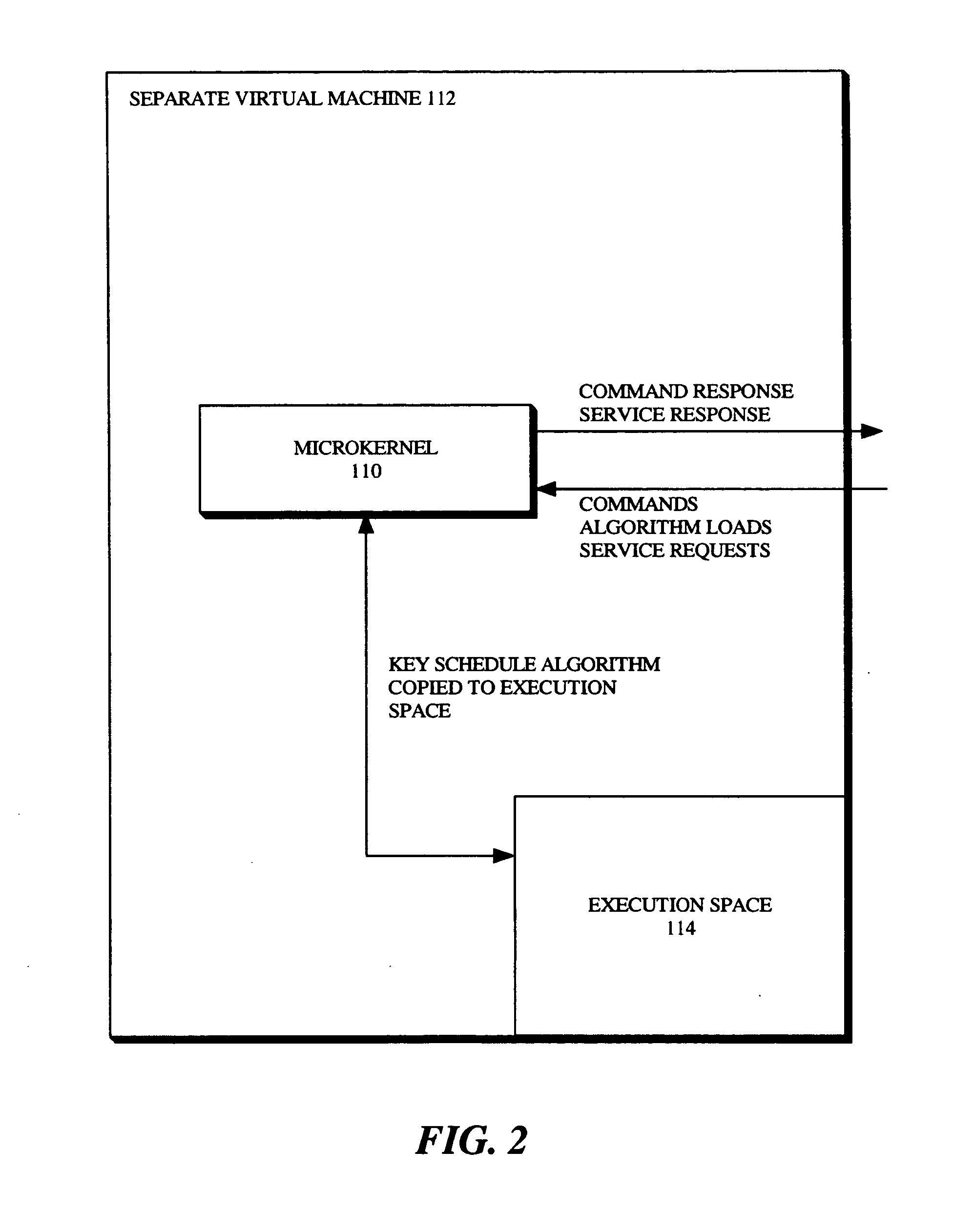
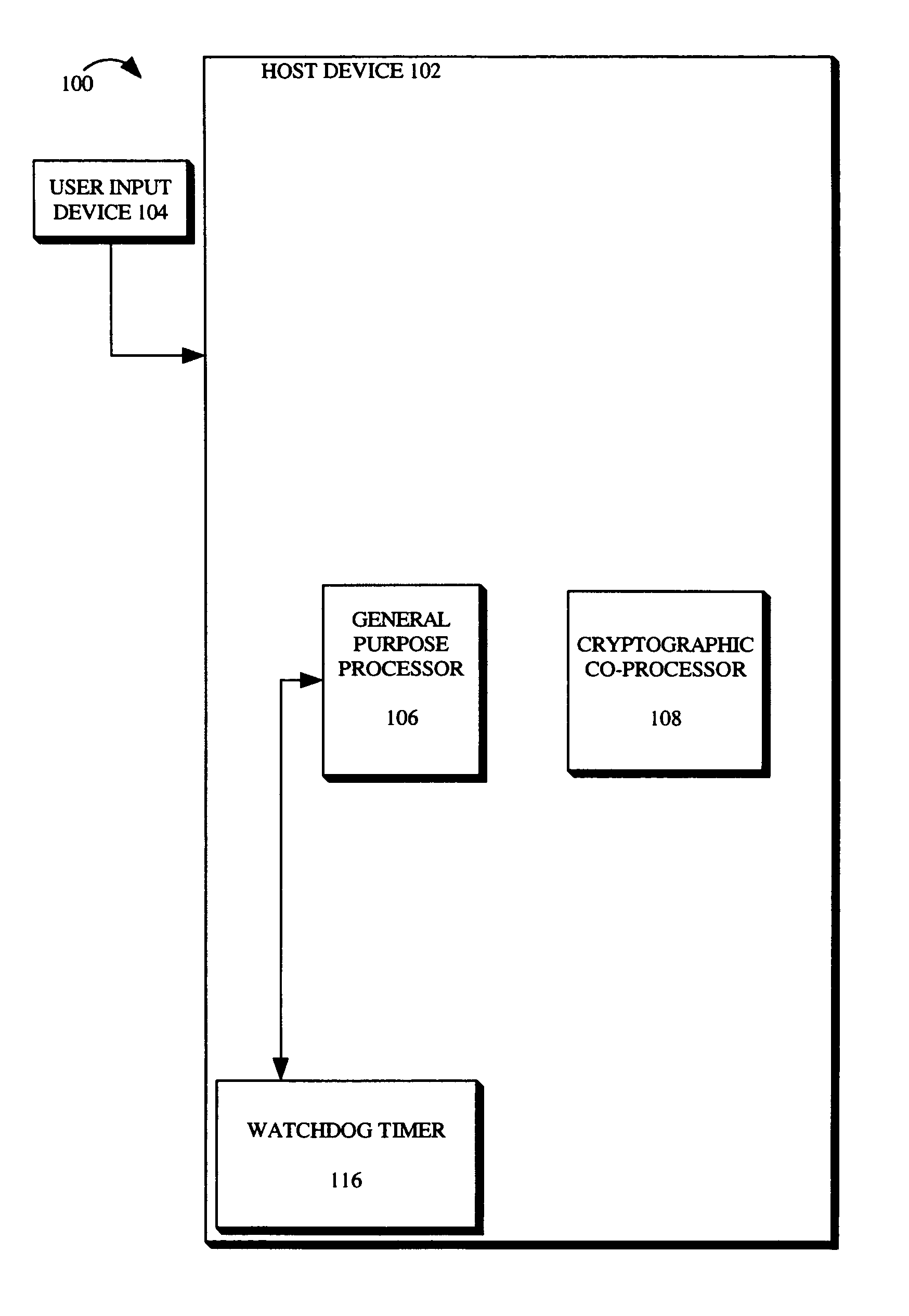
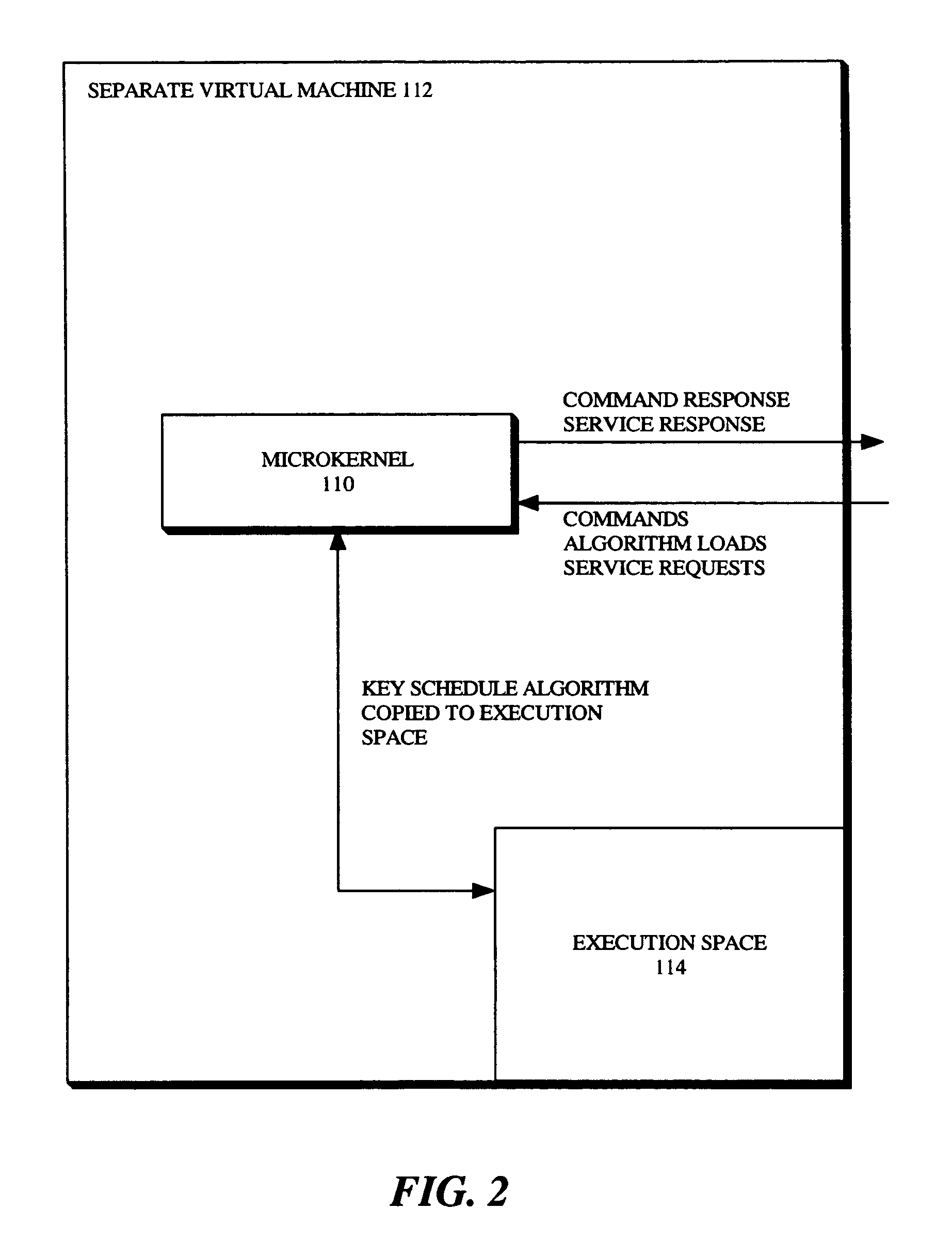
System and method for secure and flexible key schedule generation
The present invention is a method for secure and flexible key schedule generation, which includes loading a key schedule algorithm and a cryptographic algorithm into a cryptographic engine. The method further includes loading the cryptographic algorithm, when selected, into a cryptographic co-processor. The method further includes loading the key schedule algorithm into a separate virtual machine.
Owner:ROCKWELL COLLINS INC
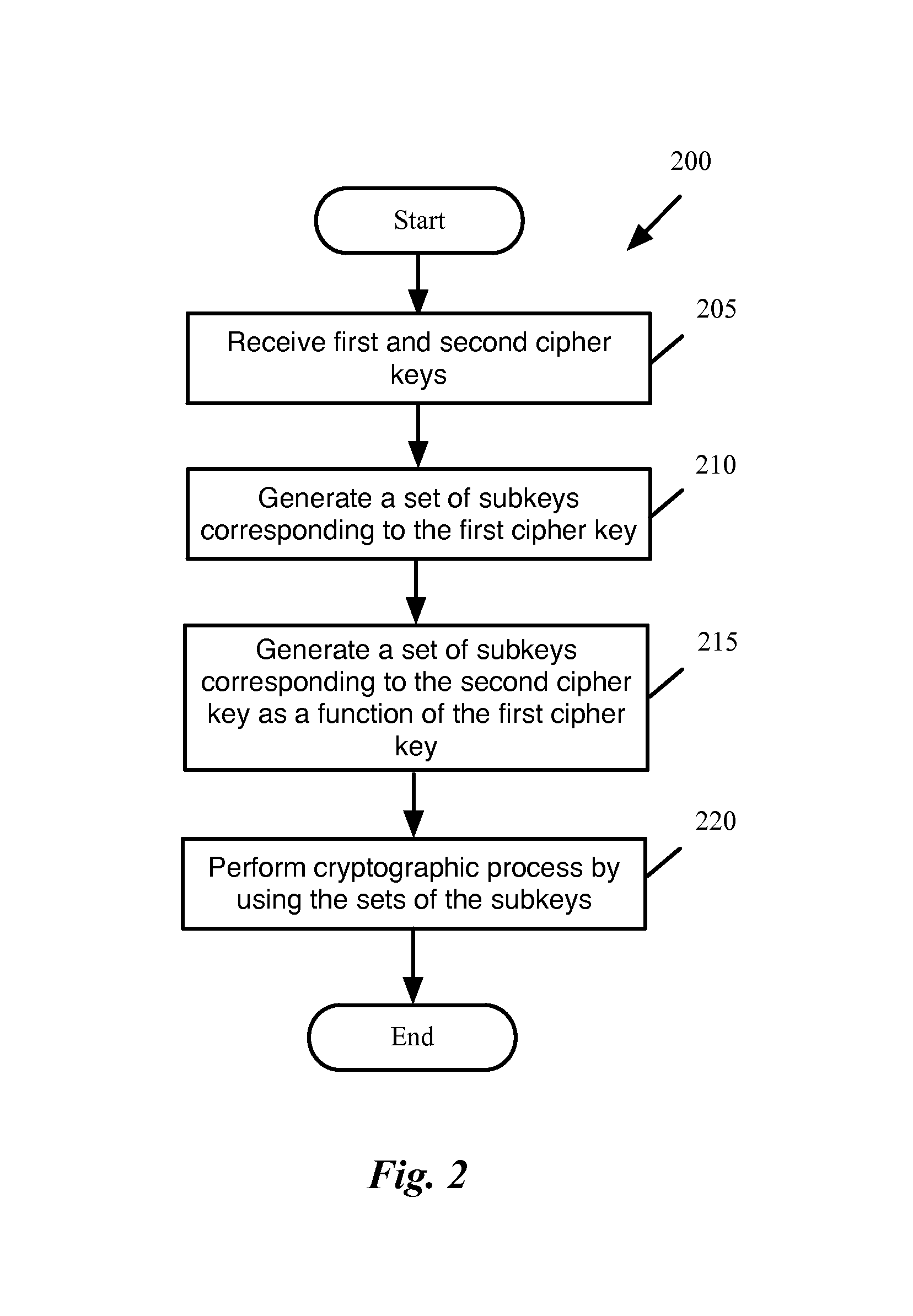
Computing key-schedules of the AES for use in white boxes
ActiveUS20160261405A1Multiple keys/algorithms usageEncryption apparatus with shift registers/memoriesComputer hardwareKey schedule
Some embodiments provide a method for performing a cryptographic process. The method receives first and second cipher keys. The method generates a set of subkeys corresponding to each of the first and second cipher keys. The set of subkeys for the first cipher key is dependent on the first cipher key and the second cipher key. The method performs the cryptographic process by using the generated sets of subkeys.
Owner:APPLE INC
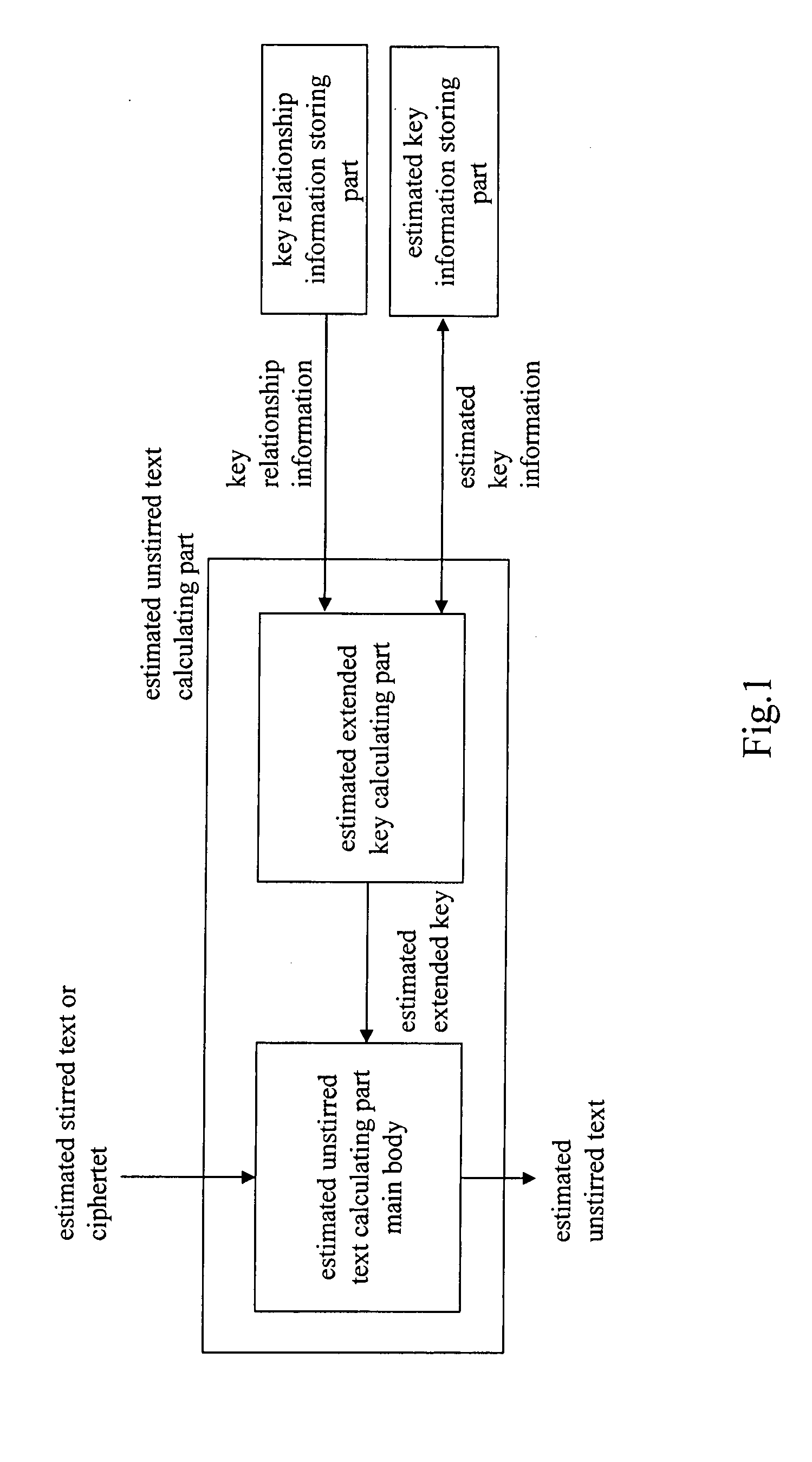
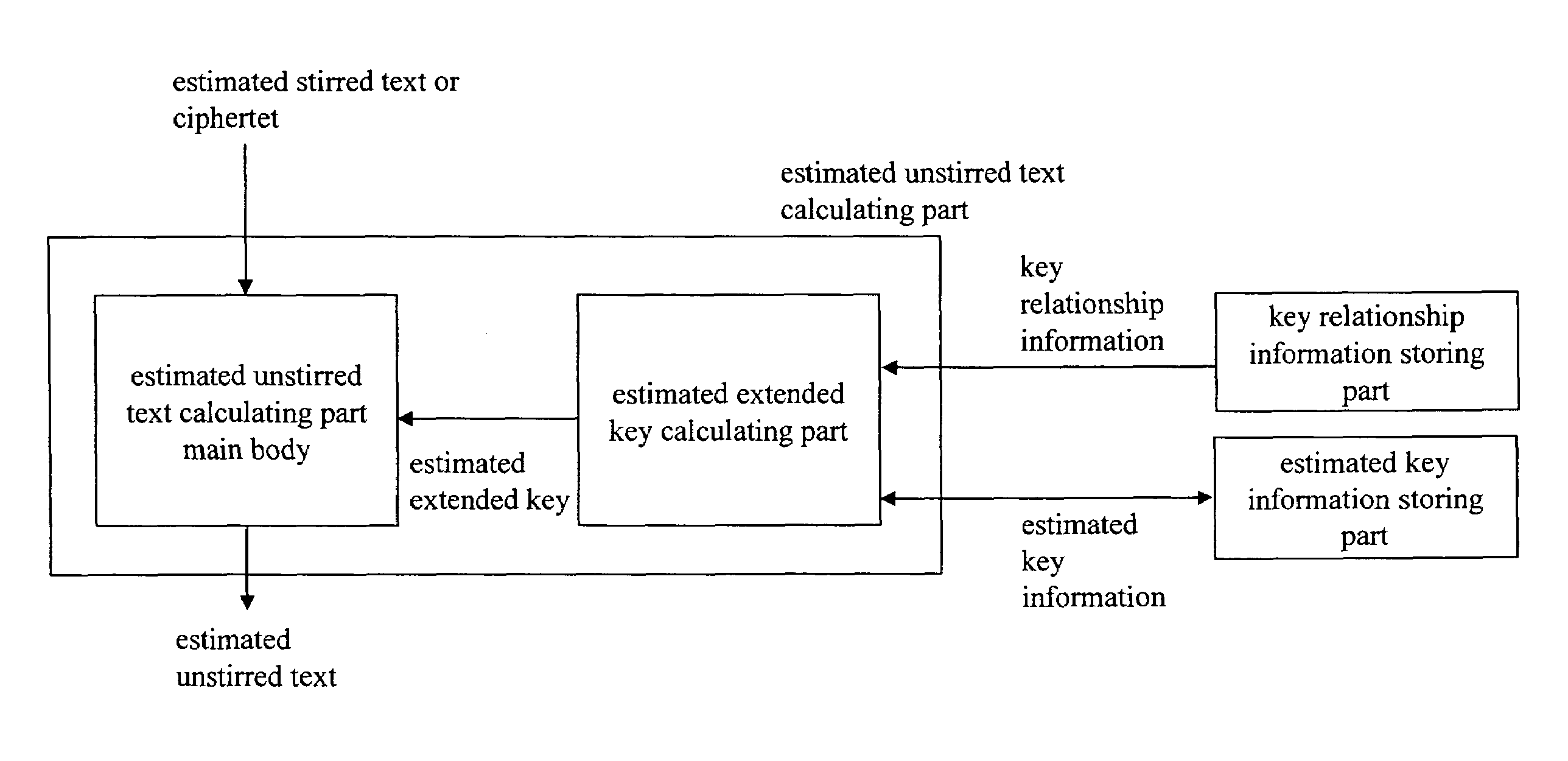
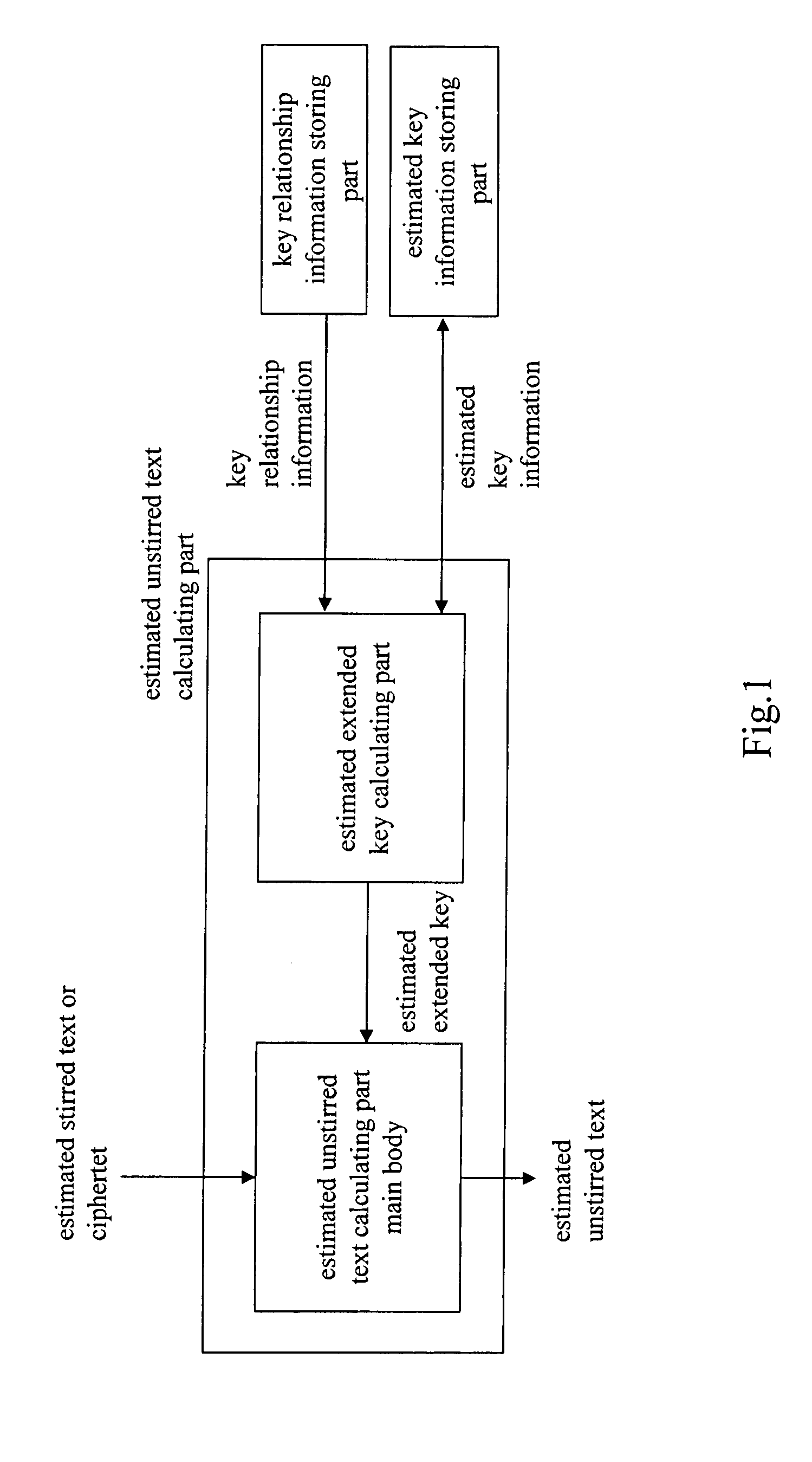
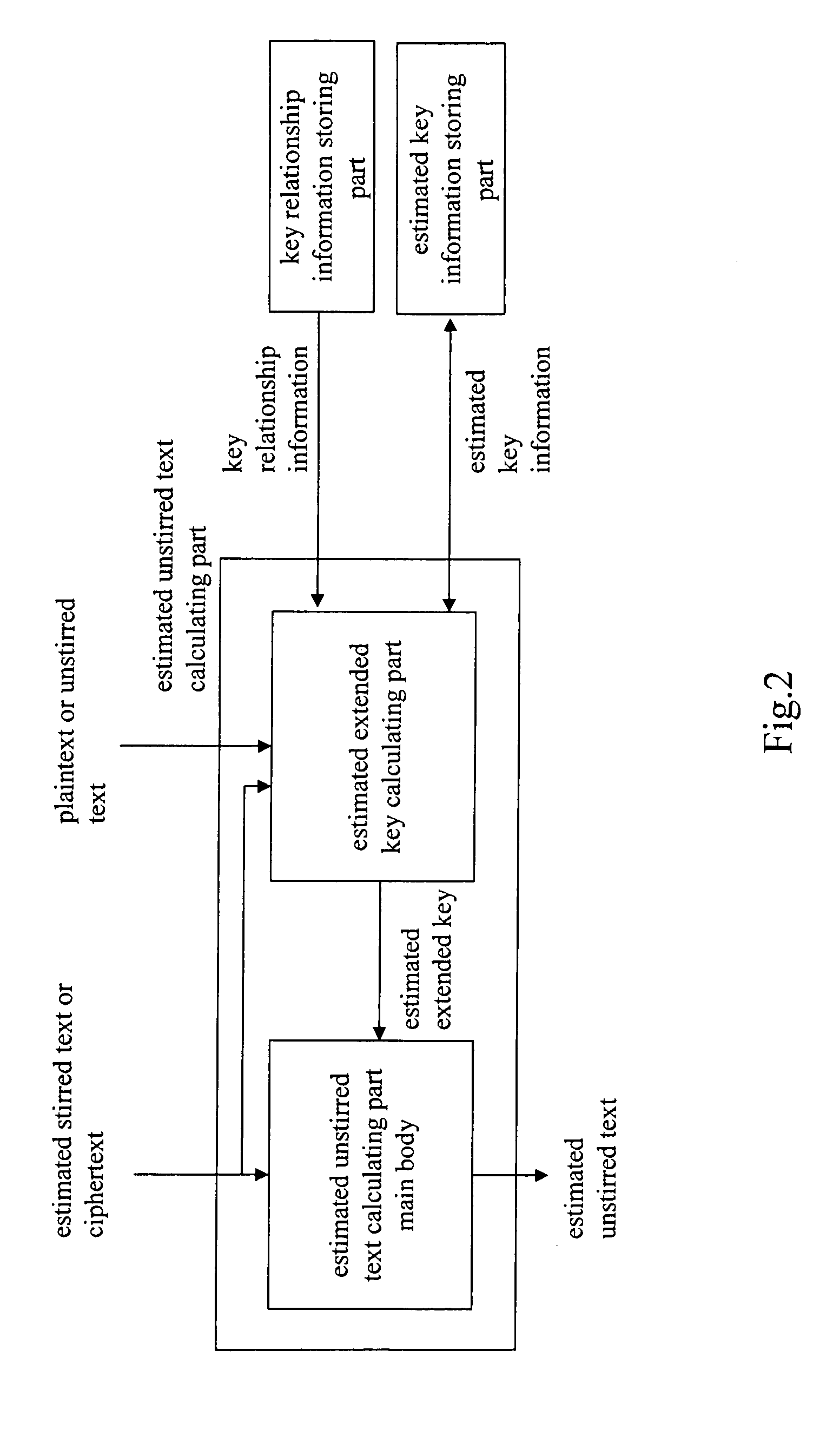
Cipher strength evaluation apparatus
InactiveUS20050157879A1Improve bindingLow difficulty of decryptionKey distribution for secure communicationMemory loss protectionCiphertextKey schedule
An object is to evaluate the strength in consideration of the relationship held between keys, to allow the detection of a weak key condition to lower the difficulty in decrypting ciphertext, and to detect a weak key based on the weak key condition. Based on the relationship between keys in a key schedule and based on estimated keys, a certain estimated extended key can be calculated by utilizing the relationship between the estimated extended key in the key schedule and an estimated extended key having been calculated, and cost information required for calculation is outputted to allow the verification of a weak key condition. A weak key can be detected based on the weak key condition, and the difficulty in decrypting ciphertext can be increased without modifying an encryption apparatus.
Owner:NAT INST OF INFORMATION & COMM TECH
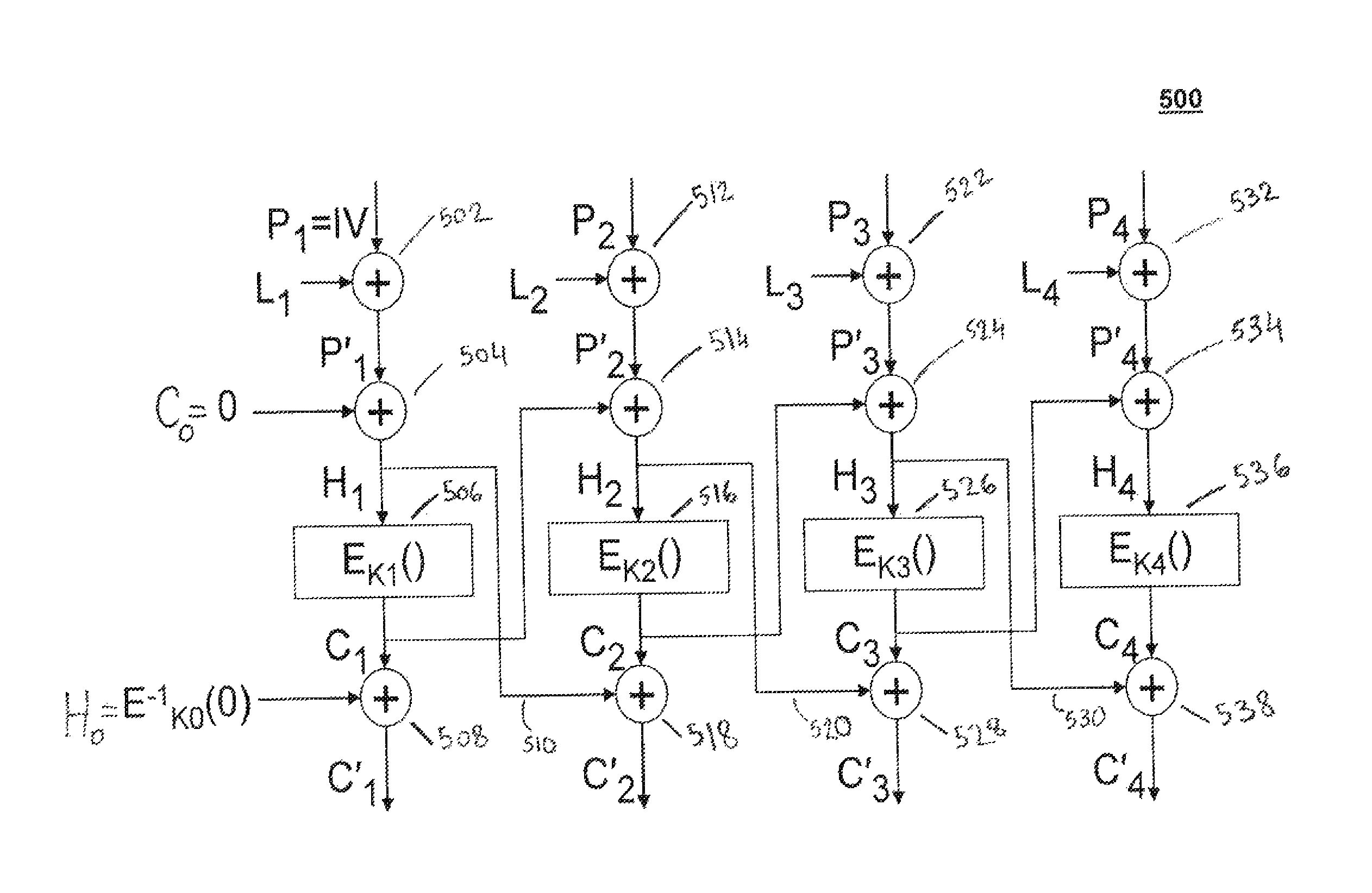
Method and device for digital data blocks encryption and decryption
ActiveUS20150263858A1Minimizing calculation processing capabilityAcceptable security levelMultiple keys/algorithms usagePublic key for secure communicationPlaintextDigital data
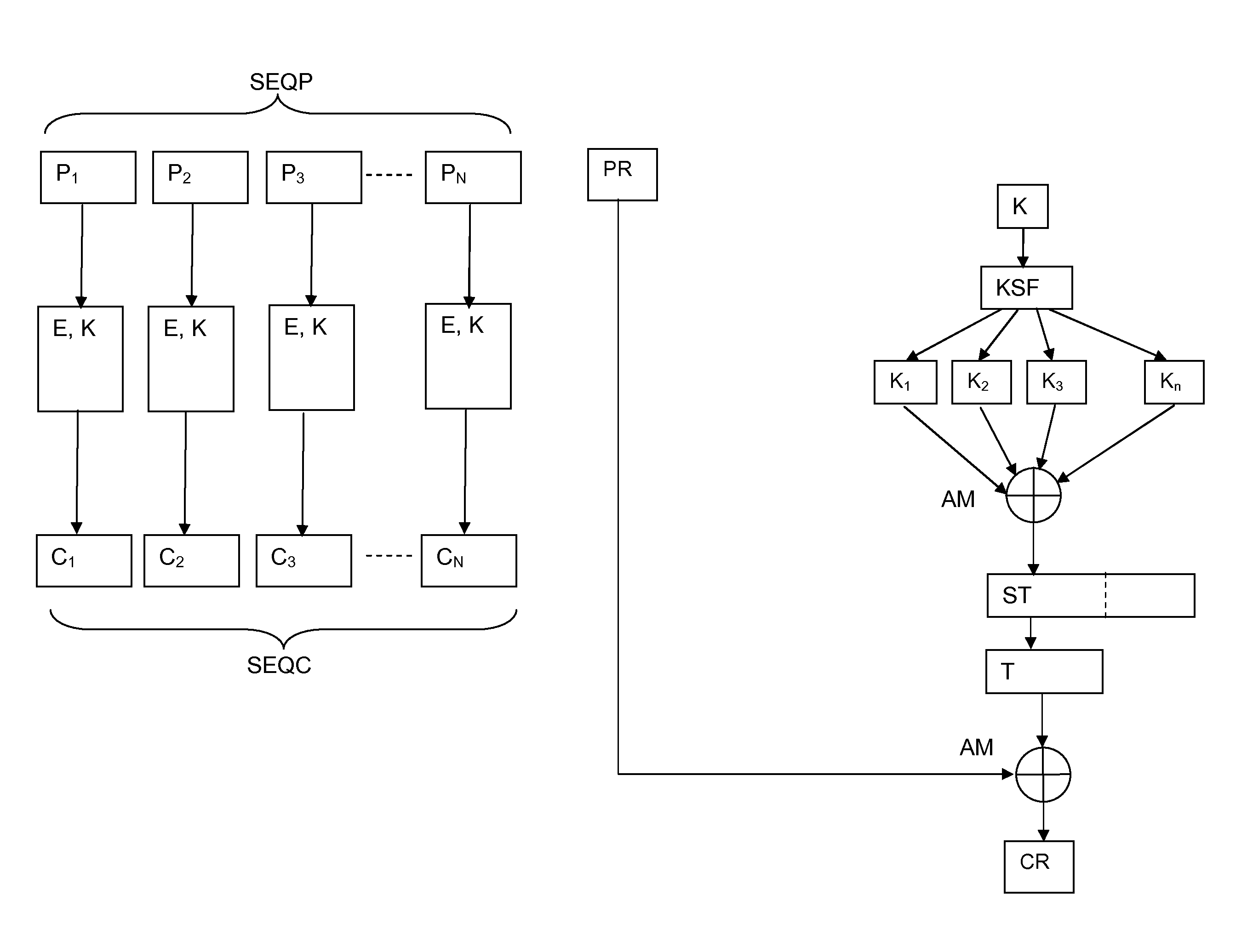
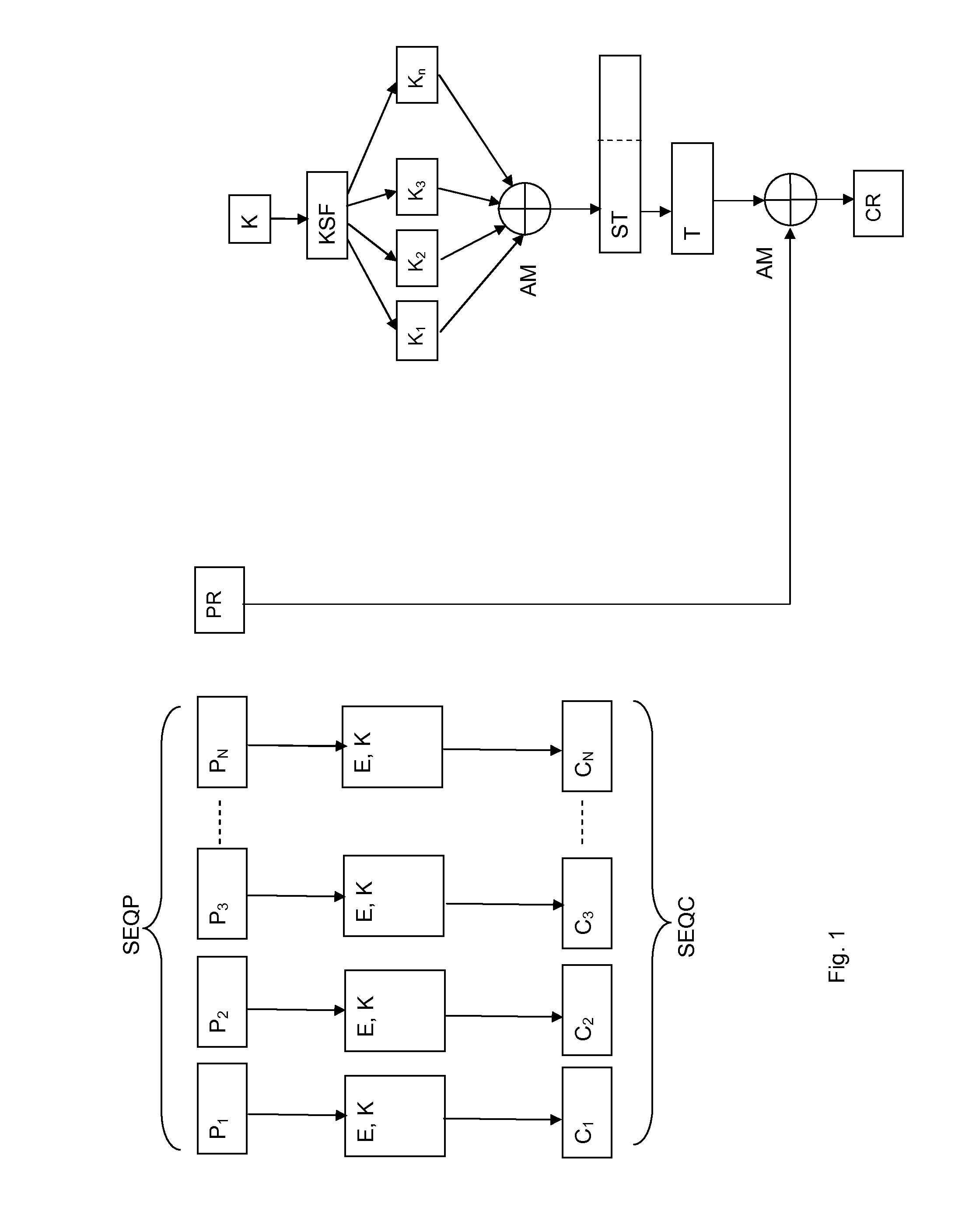
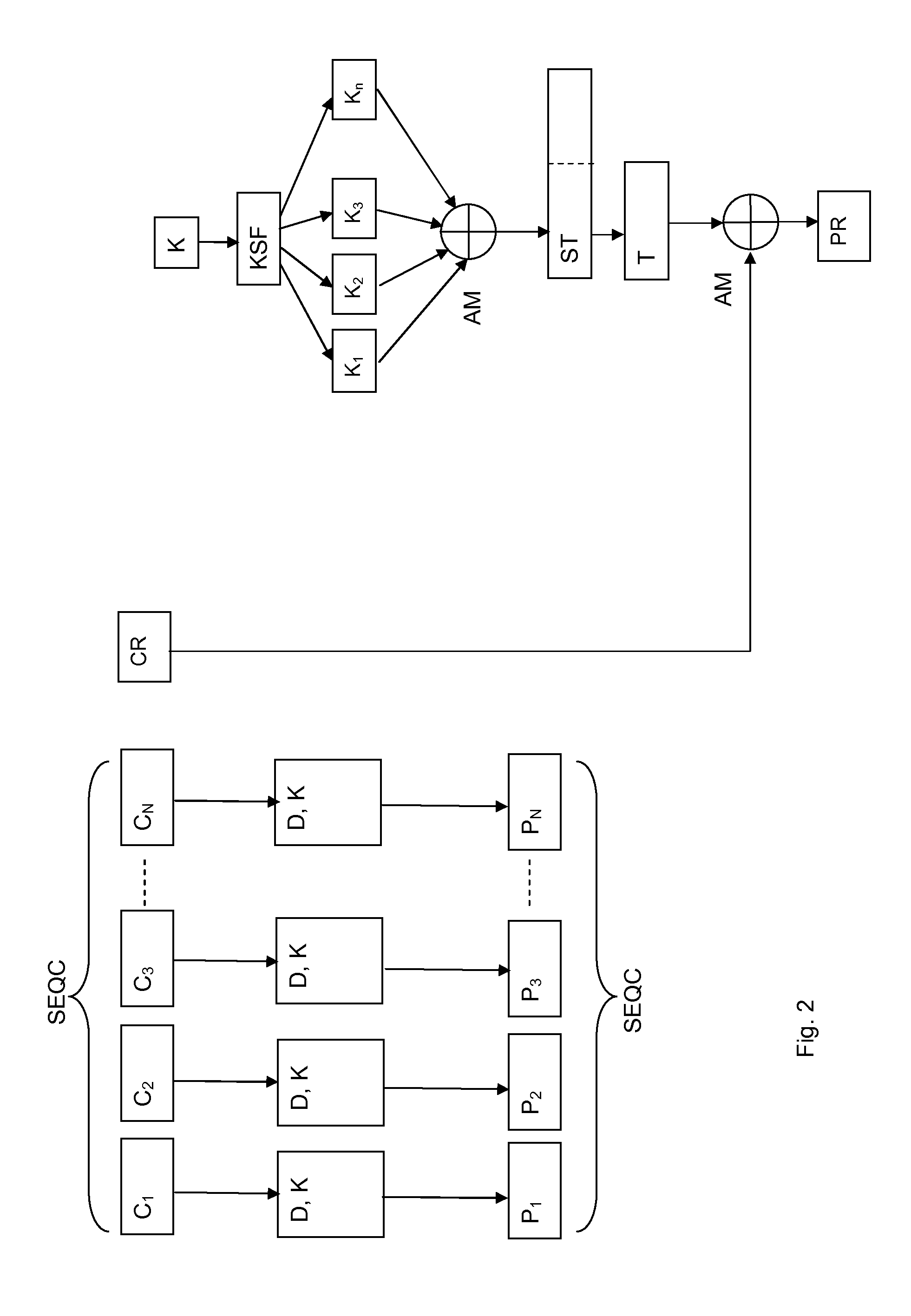
Method and System for encrypting plaintext digital data divided into a sequence comprising successive plaintext blocks of a same length of bits each and a residual plaintext block having a length of bits lower than the length of one of the successive plaintext blocks. The successive plaintext blocks are ciphered with the main encryption key by using a ciphering algorithm based on a cipher block chaining mode to obtain a sequence of successive ciphered blocks having the same length as the successive plaintext blocks. A set of round keys having a same length, are generated by applying a key schedule function on a string obtained by adding the last ciphered block to the main encryption key. The round keys of the set are added together to obtain a resulting string having a length equal to the length of a block of the sequence. The residual plaintext block is then added to the most left bits of the resulting string forming a string) having a length equal to the length of the residual block to obtain a residual ciphered block. The method and the system apply also to decipher a sequence of successive ciphered blocks followed by a residual ciphered block.
Owner:NAGRAVISION SA
System and method for secure and flexible key schedule generation
The present invention is a method for secure and flexible key schedule generation, which includes loading a key schedule algorithm and a cryptographic algorithm into a cryptographic engine. The method further includes loading the cryptographic algorithm, when selected, into a cryptographic co-processor. The method further includes loading the key schedule algorithm into a separate virtual machine.
Owner:ROCKWELL COLLINS INC
Apparatus for encrypting/decrypting real-time input stream
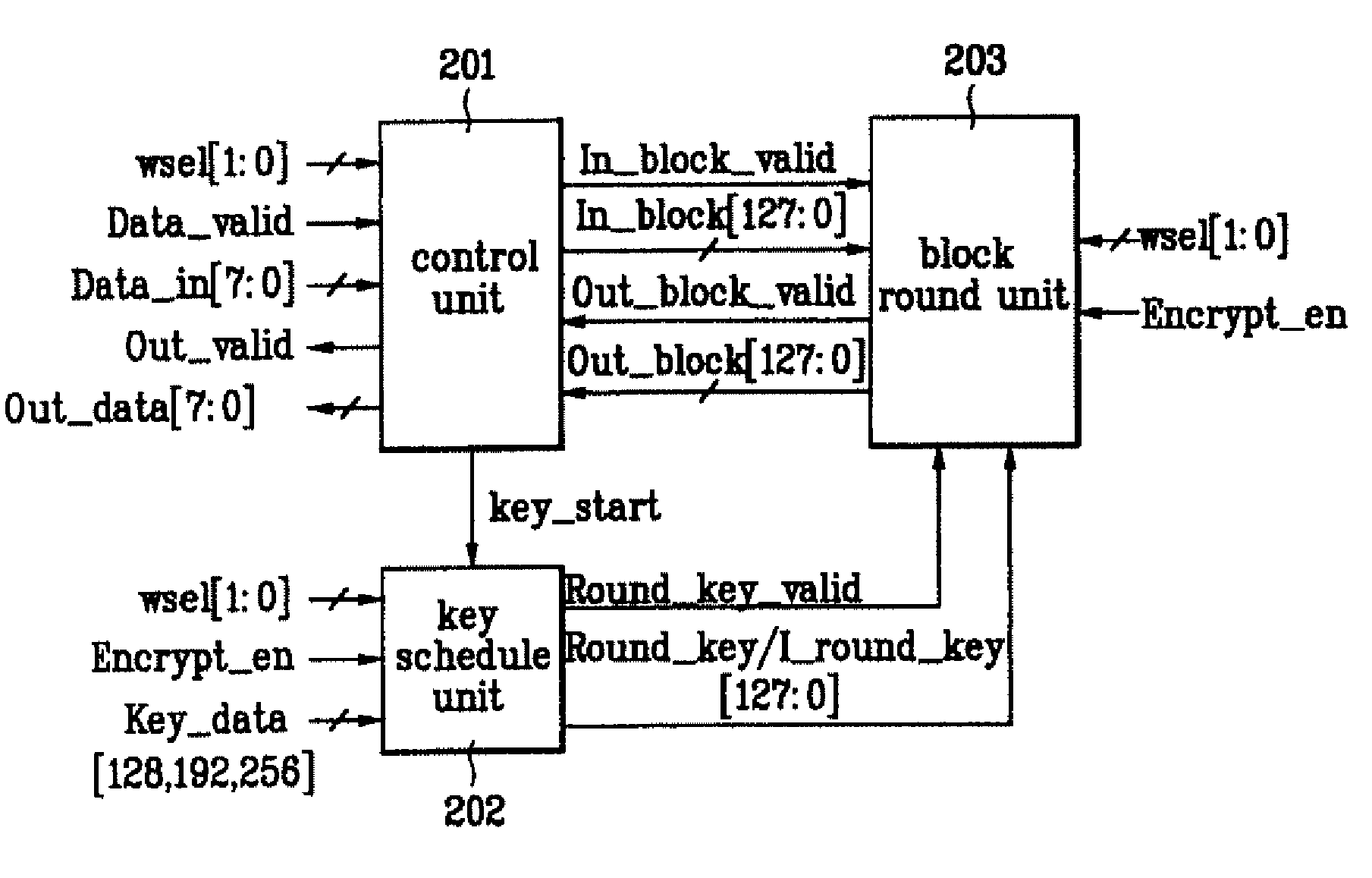
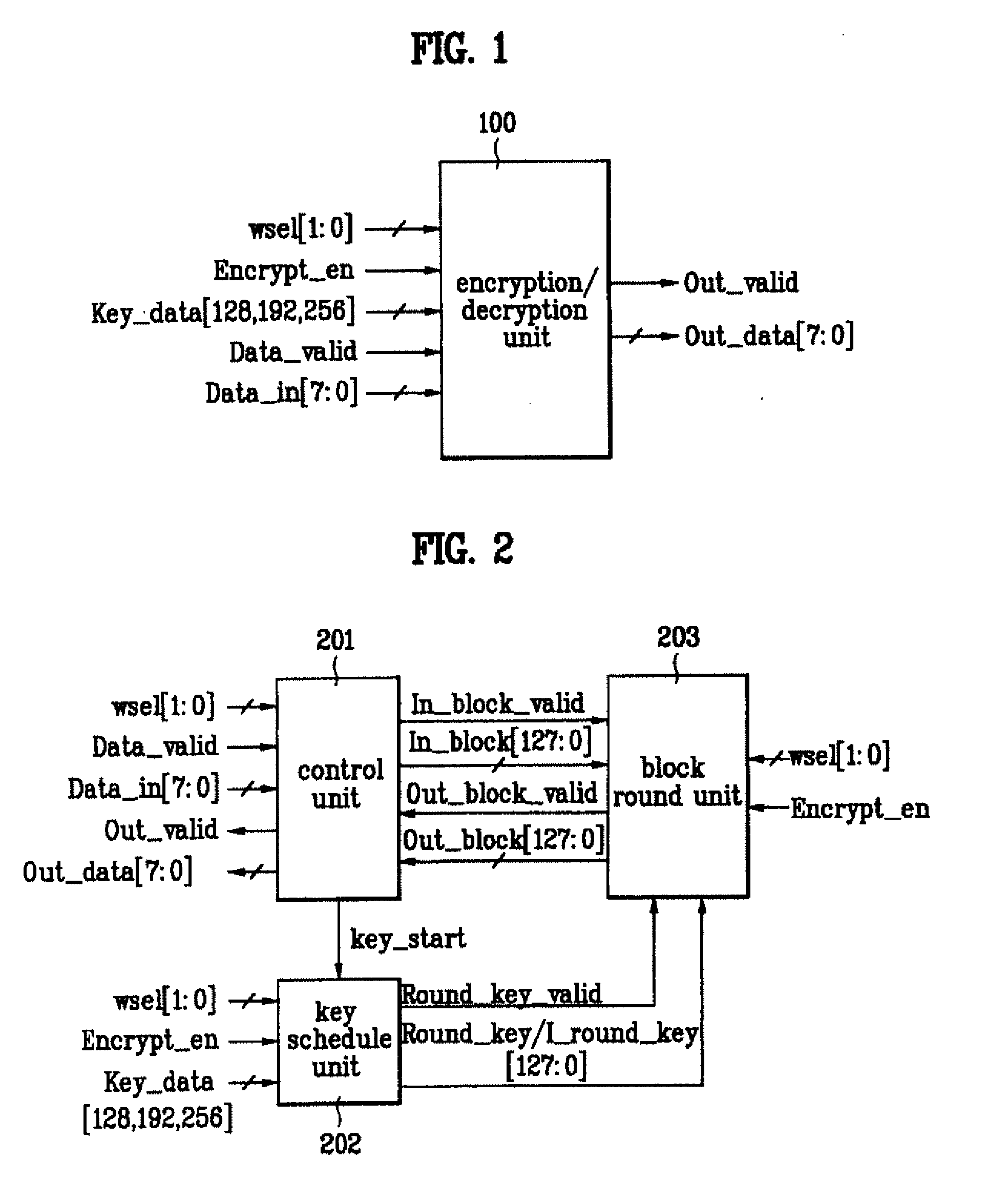
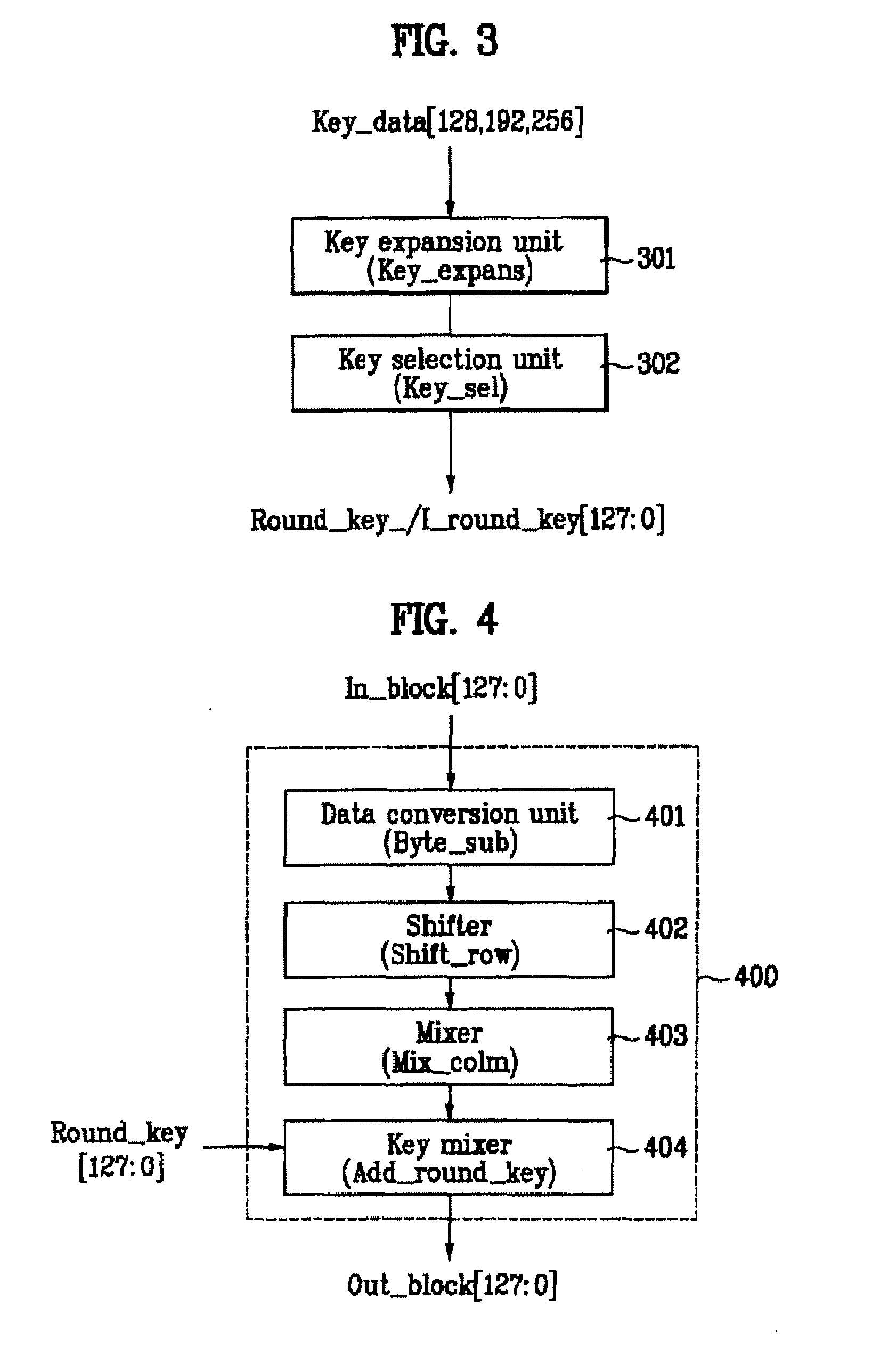
InactiveUS20080137866A1Simple hardware structureData stream serial/continuous modificationComputer hardwareKey schedule
Owner:LG ELECTRONICS INC
Apparatus and method for providing user-generated key schedule in a microprocessor cryptographic engine
ActiveUS8060755B2Good techniqueEncryption apparatus with shift registers/memoriesUser identity/authority verificationKey scheduleExecution unit
An apparatus and method for performing cryptographic operations within microprocessor. The apparatus includes an instruction register having a cryptographic instruction disposed therein, a keygen unit, and an execution unit. The cryptographic instruction is received by a microprocessor as part of an instruction flow executing on the microprocessor. The cryptographic instruction prescribes one of the cryptographic operations, and also prescribes that a user-generated key schedule be employed when executing the one of the cryptographic operations. The keygen unit is operatively coupled to the instruction register. The keygen unit directs the microprocessor to load the user-generated key schedule. The execution unit is operatively coupled to the keygen unit. The execution unit employs the user-generated key schedule to execute the one of the cryptographic operations. The execution unit includes a cryptography unit.
Owner:VIA TECH INC
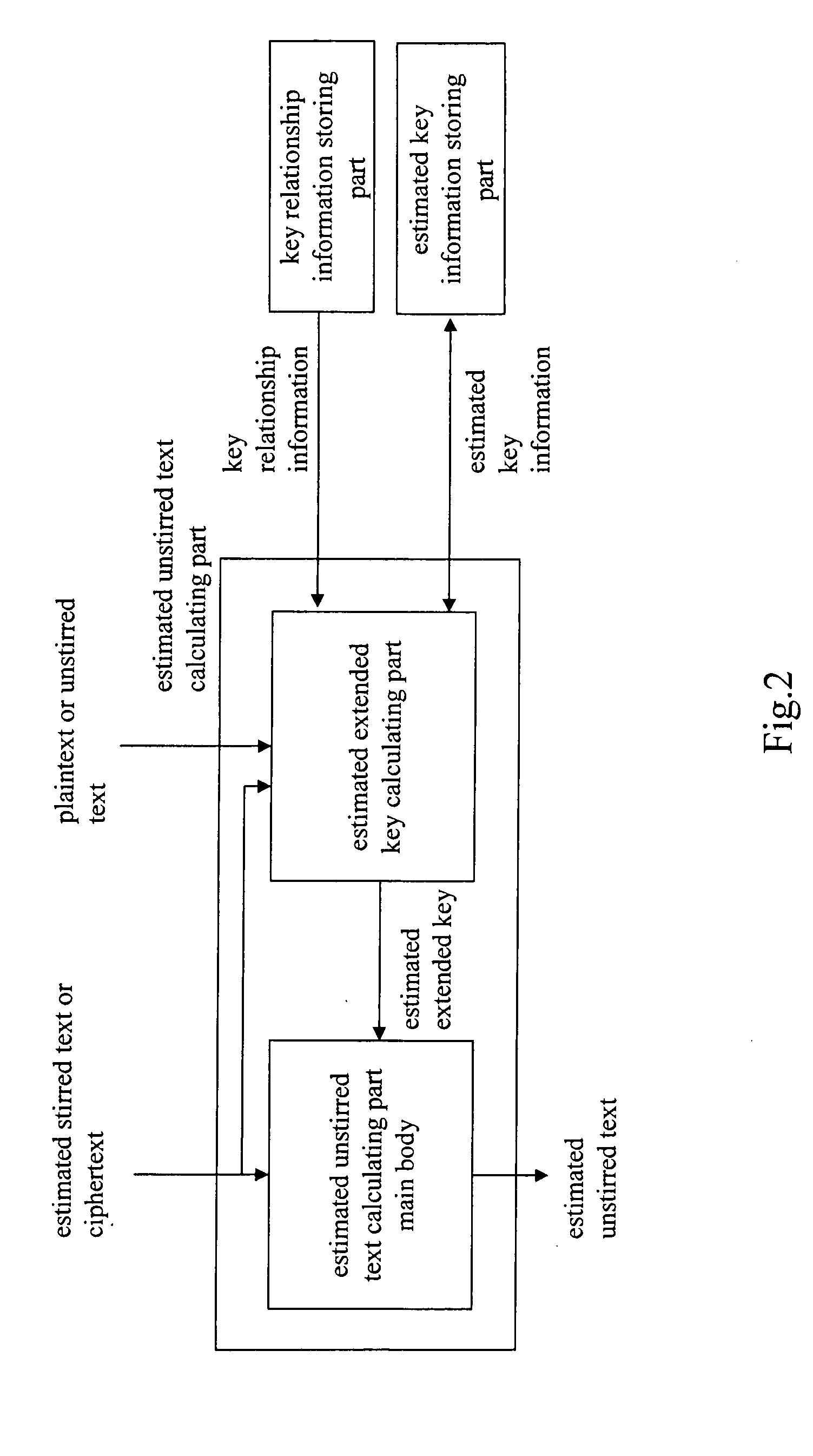
Cipher strength evaluation apparatus
InactiveUS7460665B2Reduce calculationLess complexKey distribution for secure communicationMemory loss protectionCiphertextKey schedule
An object is to evaluate the strength in consideration of the relationship held between keys, to allow the detection of a weak key condition to lower the difficulty in decrypting ciphertext, and to detect a weak key based on the weak key condition. Based on the relationship between keys in a key schedule and based on estimated keys, a certain estimated extended key can be calculated by utilizing the relationship between the estimated extended key in the key schedule and an estimated extended key having been calculated, and cost information required for calculation is outputted to allow the verification of a weak key condition. A weak key can be detected based on the weak key condition, and the difficulty in decrypting ciphertext can be increased without modifying an encryption apparatus.
Owner:NAT INST OF INFORMATION & COMM TECH
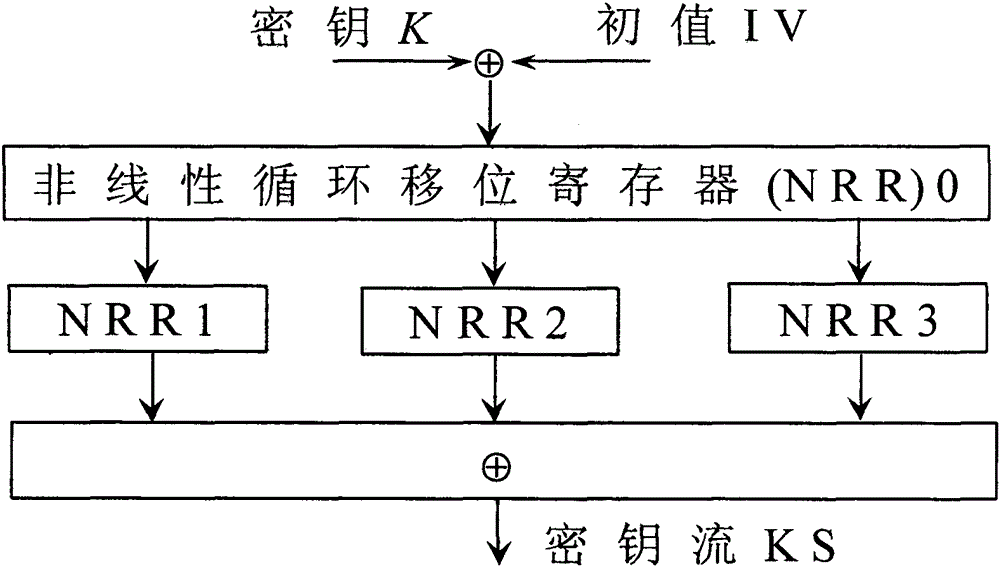
Lightweight stream cipher LSNRR based on non-linear cyclic shift register
InactiveCN105162579ALong cycleImprove securityEncryption apparatus with shift registers/memoriesNonlinear feedback shift registerKey schedule
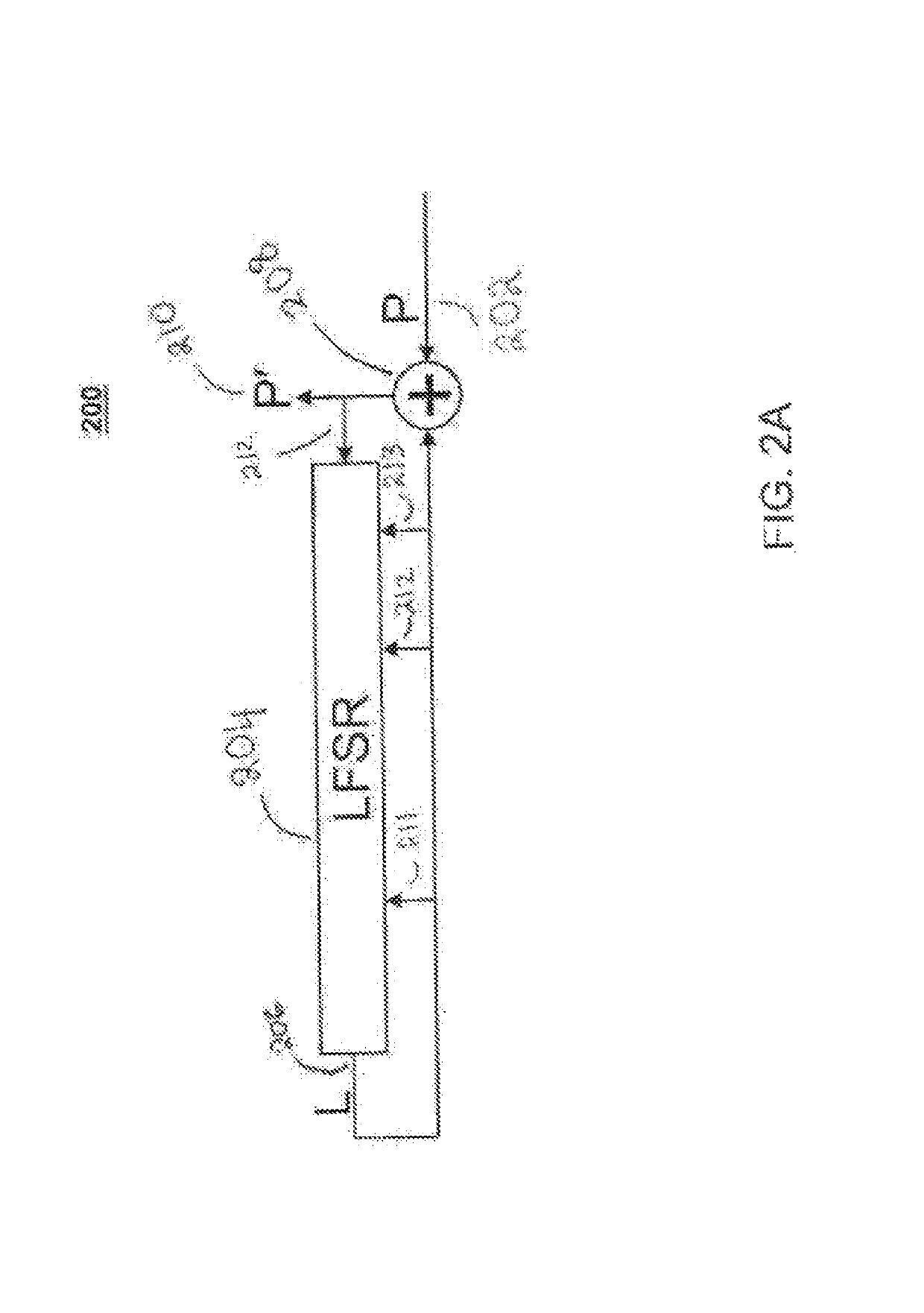
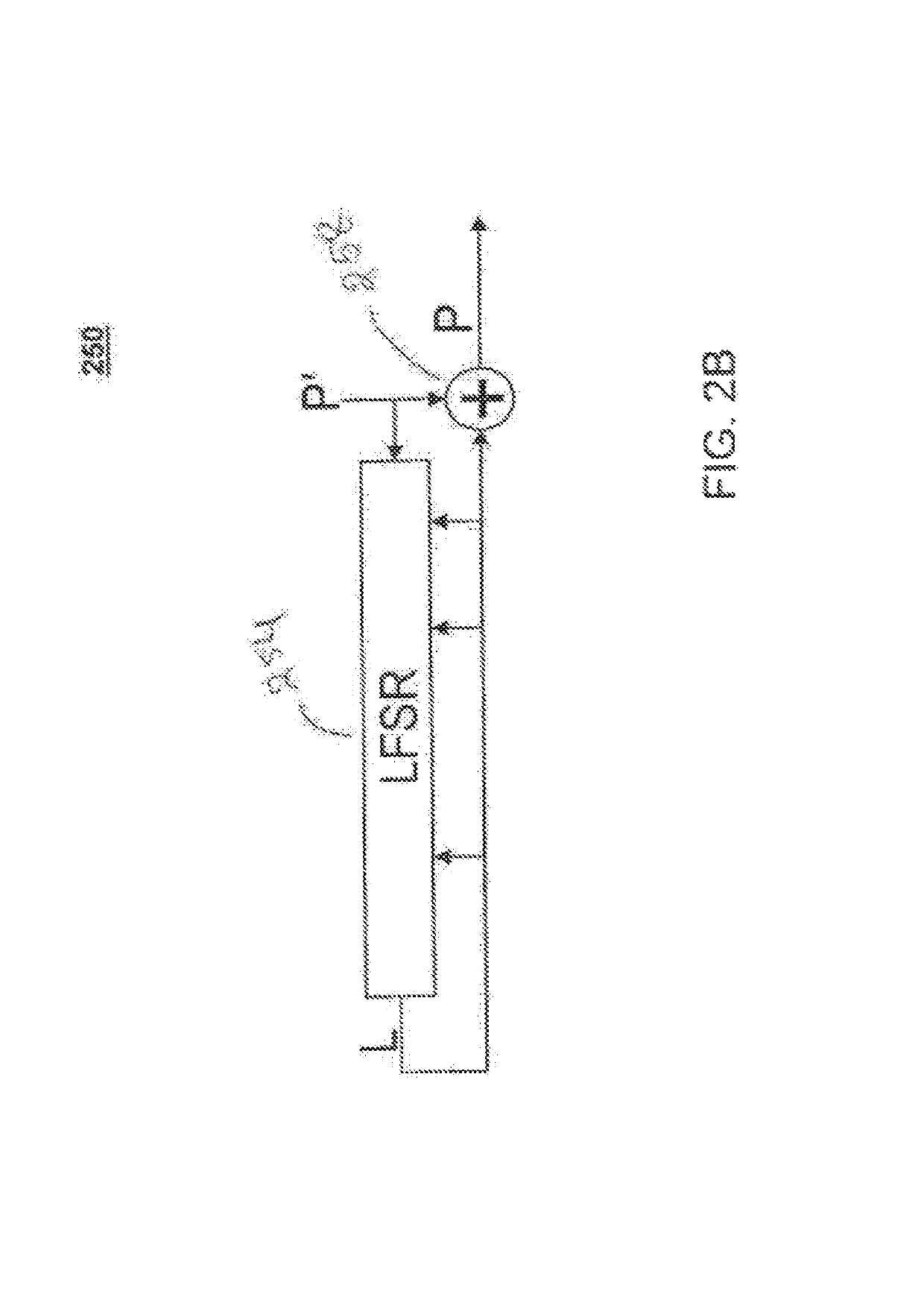
Shift registers are cipher components used for generating pseudo random sequences in the field of secret communication, comprising linear feedback shift registers LFSRs, non-linear feedback shift registers NLFSRs, and so on, wherein the maximum period T of the shift register is not greater than 2n. The feedback mode of an n-level non-linear cyclic shift register NRR refers to the following formula, in the formula, i>=0, n>=2, word length m is determined by the number of bits of a platform; <<<j represents ring shift left with j bits; a symbol referring to the description represents modular addition; c is an odd number within the range from 1 to 2<m>-1; initial values a<0>-a<n-1>of n inputted words are unlimited, and each word is an arbitrary m-digit number. When the word length is m bits, the period of the n-level non-linear cyclic shift register NRR is greater than (2<m>)<n>, i.e., the security of the n-level non-linear cyclic shift register NRR is better than the security of a traditional (non-)linear feedback shift register (N)LFSR, and the efficiency of the n-level non-linear cyclic shift register NRR is also better than the efficiency of a common (non-)linear feedback shift register (N)LFSR. The lightweight stream cipher LSNRR is designed through four non-linear cyclic shift registers NRRs, wherein the first NRR is used for secret key schedule, and modular addition is performed for outputs of the other three NRRs to generate a secret key stream of the LSNRR. The efficiency of the LSNRR is better than the efficiency of a common symmetric cipher, thus the LSNRR is suitable for the a resource-constrained environment and a resource-unconstrained environment, and is mainly used for data encryption and decryption.
Owner:NANJING UNIV OF AERONAUTICS & ASTRONAUTICS
Apparatus for encrypting/decrypting real-time input stream
InactiveUS20080101599A1Simple hardware structureData stream serial/continuous modificationComputer hardwareKey schedule
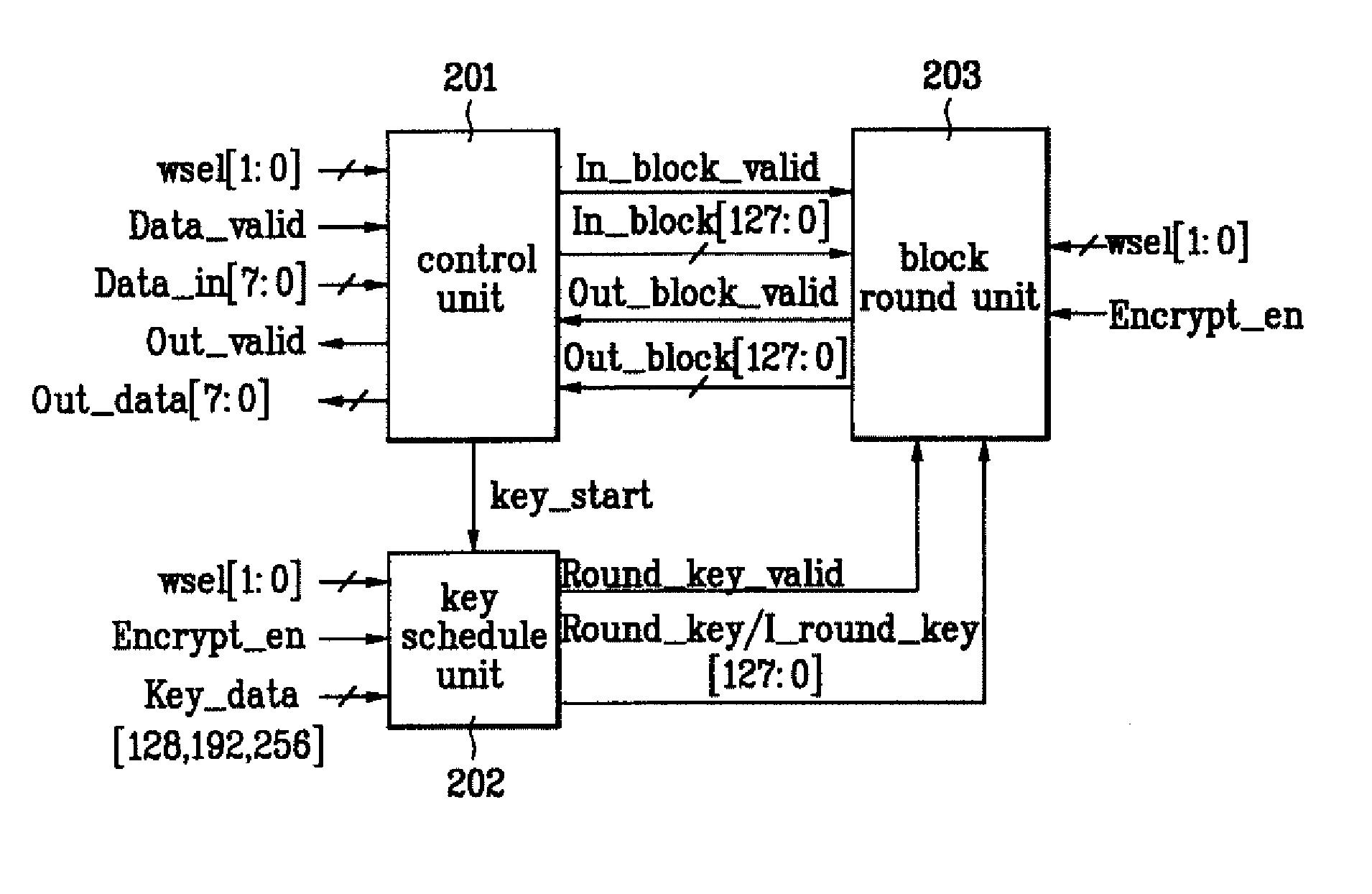
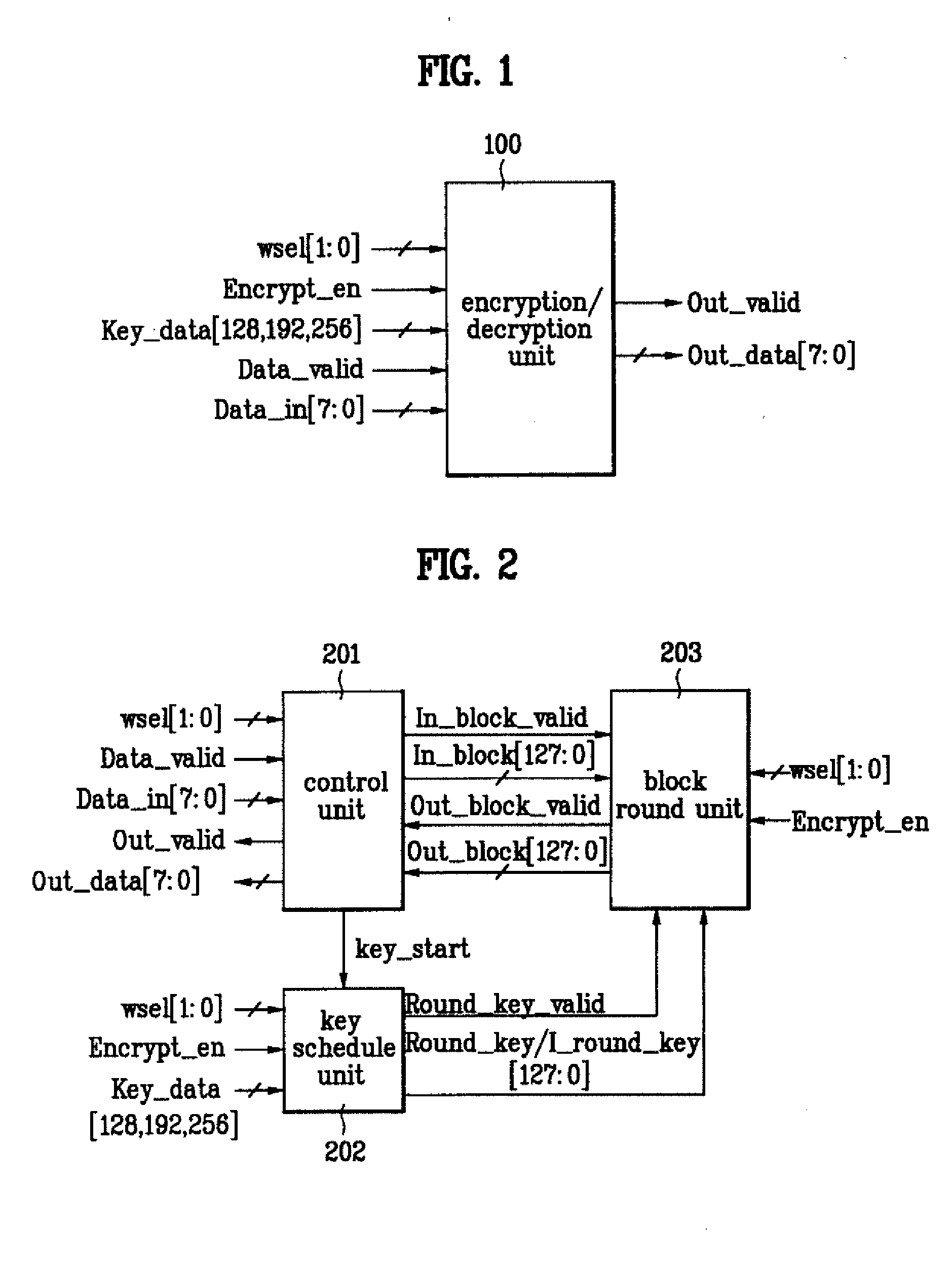
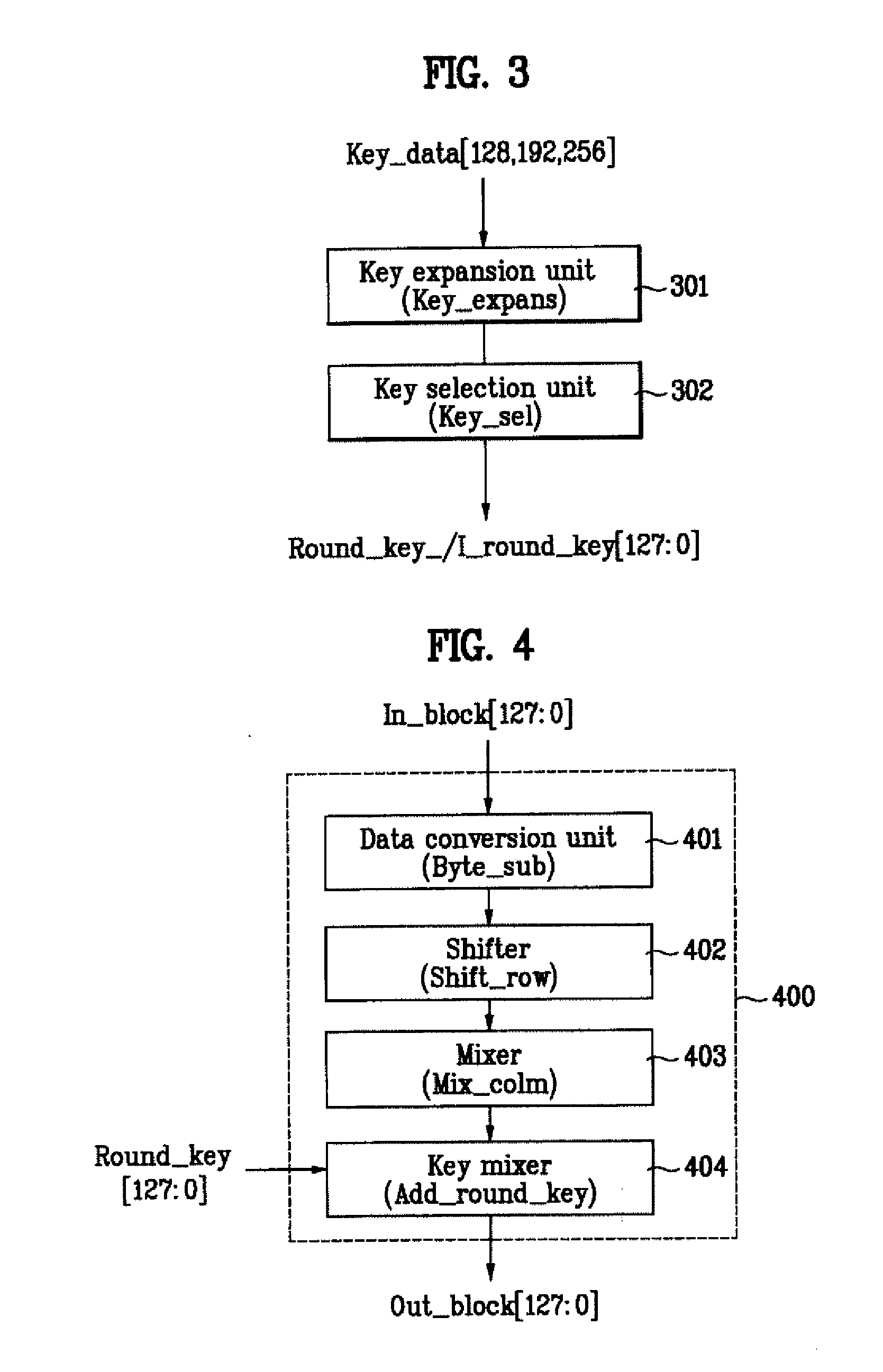
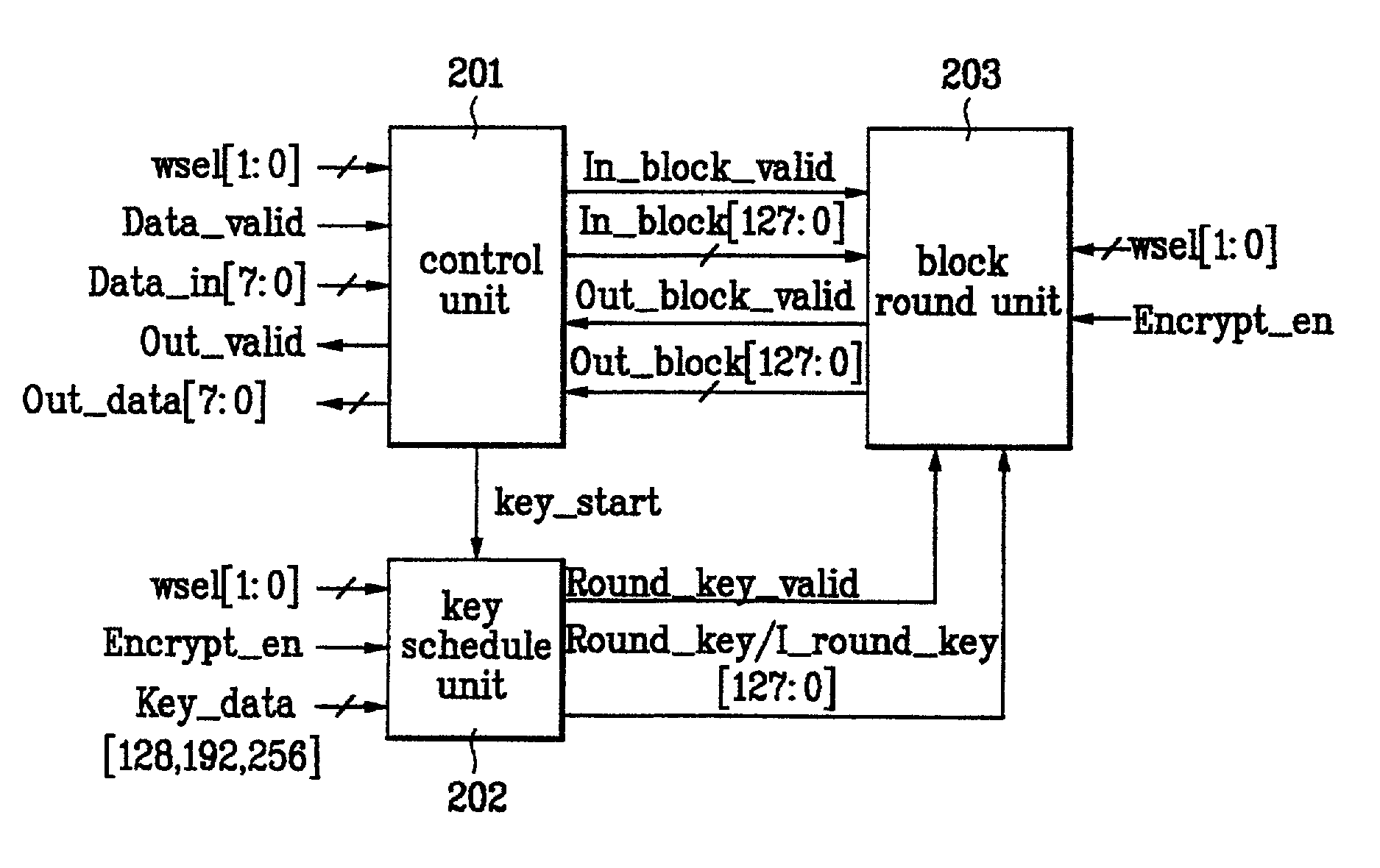
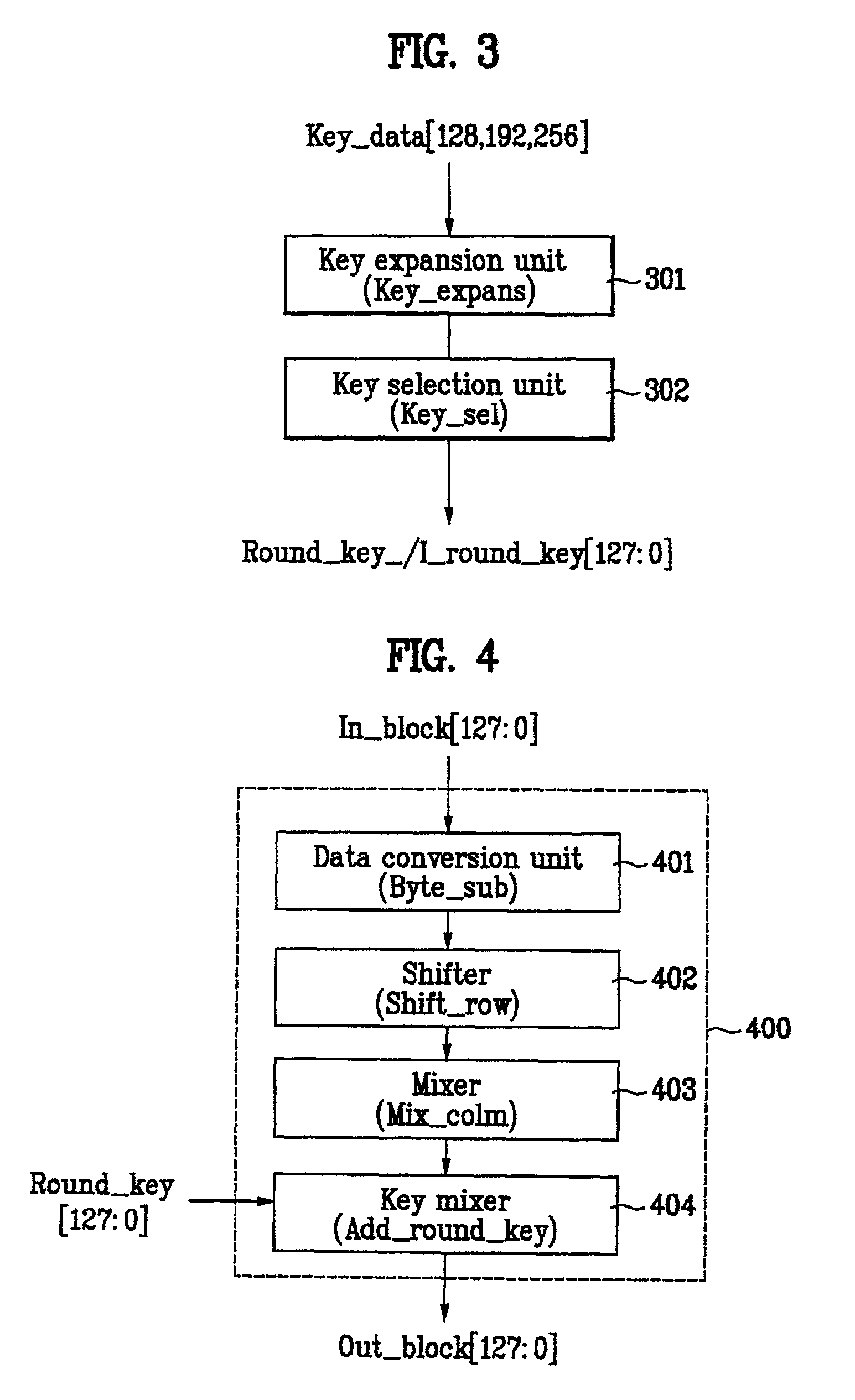
Disclosed is an apparatus for encrypting / decrypting a real-time input stream. The present invention includes a control unit, a key schedule unit, and a block round unit. Accordingly, the present invention realizes the encryption and decryption of AES algorithm in a manner of hardware, thereby enabling to carry out the encryption and decryption of the real-time input stream real-timely. And, the present invention finds the key for encryption or decryption of one block every round when realizing the encryption and decryption of the AES algorithm in a hardware manner, and then outputs the found keys to the block round unit. The present invention reduces the size of the key register required for the encryption / decryption of block data, thereby enabling to reduce a size of hardware as well as cost of product.
Owner:LG ELECTRONICS INC
Differential power analysis resistant encryption and decryption functions
ActiveUS10320554B1Encryption apparatus with shift registers/memoriesSecret communicationPower analysisPlaintext
Circuits, methods, and systems are provided for securing an integrated circuit device against Differential Power Analysis (DPA) attacks. Plaintext (e.g., configuration data for a programmable device) may be encrypted in an encryption system using a cryptographic algorithm. Ciphertext may be decrypted in a decryption system using the cryptographic algorithm. The encryption and / or decryption systems may obfuscate the plaintext, the ciphertext, and / or the substitution tables used by the cryptographic algorithm. The encryption and / or decryption systems may also generate cryptographic key schedules by using different keys for encrypting / decrypting different blocks and / or by expanding round keys between encryption / decryption blocks. These techniques may help mitigate or altogether eliminate the vulnerability of cryptographic elements revealing power consumption information to learn the value of secret information, e.g., through DPA.
Owner:ALTERA CORP
Fast verification device for MAC (Message Authentication Code) of RSSP-II (Railway Signal Security Protocol-II) based on FPGAs (Field Programmable Gate Arrays)
ActiveCN108933788AReduce verification timeImprove throughputEncryption apparatus with shift registers/memoriesUser identity/authority verificationError processingFinite-state machine
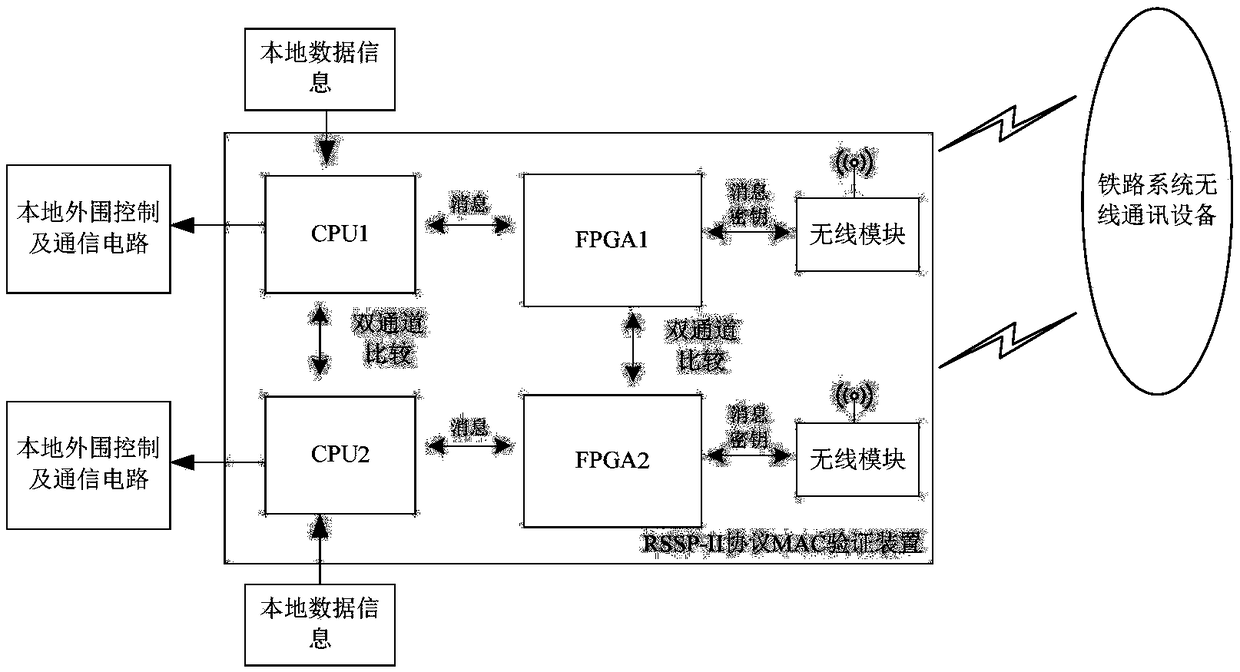
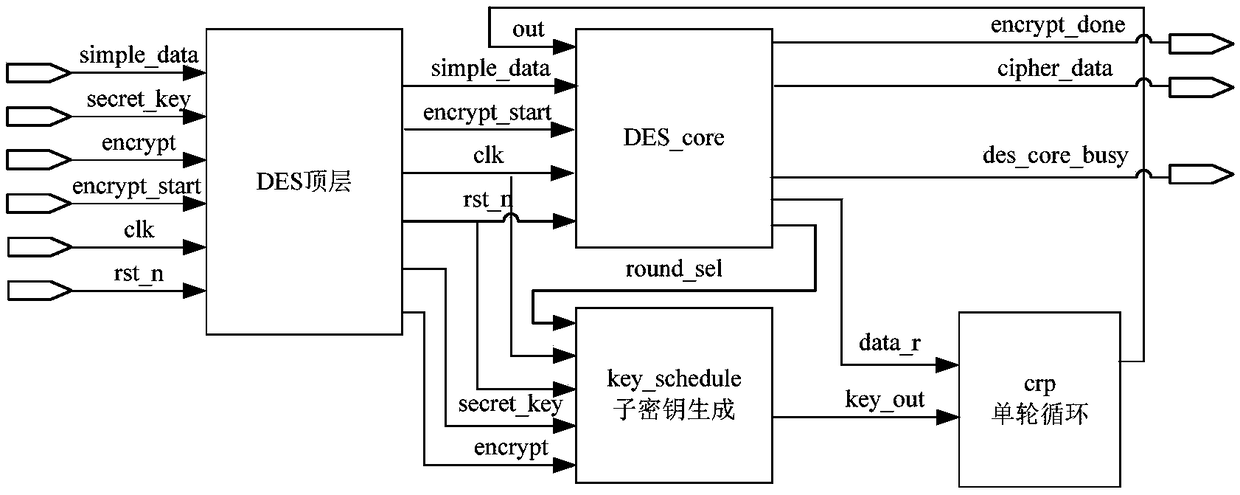
The invention relates to a fast verification method for an MAC (Message Authentication Code) of an RSSP-II (Railway Signal Security Protocol-II) based on FPGAs (Field Programmable Gate Arrays). The FPGA1 and FPGA2 are programmed with the following module through programming language hardware: a data interface module, an MAC scheduling module, a DES module and a dual-channel comparison module, wherein the DES module comprises a DES top module, a DES core module, a Key-schedule sub-key generation module and a crp single-round circulation module; the dual-channel comparison module is used for communication between the two FPGAs, forms a two-out-of-two structure, and sends a dual-channel comparison status flag to a CPU through the data interface module when the two FPGAs are inconsistent in result; and subsequent message transmission is carried out if it passes the dual-channel comparison, otherwise, the process enters an error processing program. The fast verification device adopts the design method of a finite state machine and an assembly line, fully takes the consumption of system resources into account on the basis of ensuring the processing speed and achieves the balance betweenspeed and area. The fast verification device effectively reduces the CPU resource occupation of the RSSP-II for high-speed railway train-ground wireless security communication, greatly improves the data throughout, shortens the train-ground authentication delay and has higher security and reliability.
Owner:SOUTHWEST JIAOTONG UNIV
Key recovery mechanism for cryptographic systems
ActiveCN102334307AEncryption apparatus with shift registers/memoriesCoding/ciphering apparatusComputer hardwareProcessor register
A cryptographic system can include a register containing a key and a processor coupled to the register. The processor can be operable for performing a first encrypting operation, where the encrypting operation includes computing a key schedule using the register as a workspace. At the end of the first encrypting operation, the key is recovered from the register for use in a second encrypting operation.
Owner:RAMBUS INC
Flash starting treatment method and system of mobile terminal
ActiveCN106791474AShorten the durationSave powerTelevision system detailsColor television detailsKey scheduleDelayed time
The invention discloses a flash starting treatment method and system of a mobile terminal. The method comprises the following steps: current stored flash delay time is acquired when the mobile terminal is capable of flashing and photographing and the behavior of users pressing camera key is detected, wherein the flash delay time is the average value of time difference between pressing camera key scheduled times before current camera key is pressed currently and acquiring images. When the waiting time of the mobile terminal exceeds the flash delay time, flash is automatically started. According to the method, when starting flash and photographing, the mobile terminal automatically records the flash starting time. The mobile terminal photographs again and automatically starts flash according to current stored routine flash starting time so that to lower total flash starting time and save electric quantity when flash light is opened.
Owner:HUIZHOU TCL MOBILE COMM CO LTD
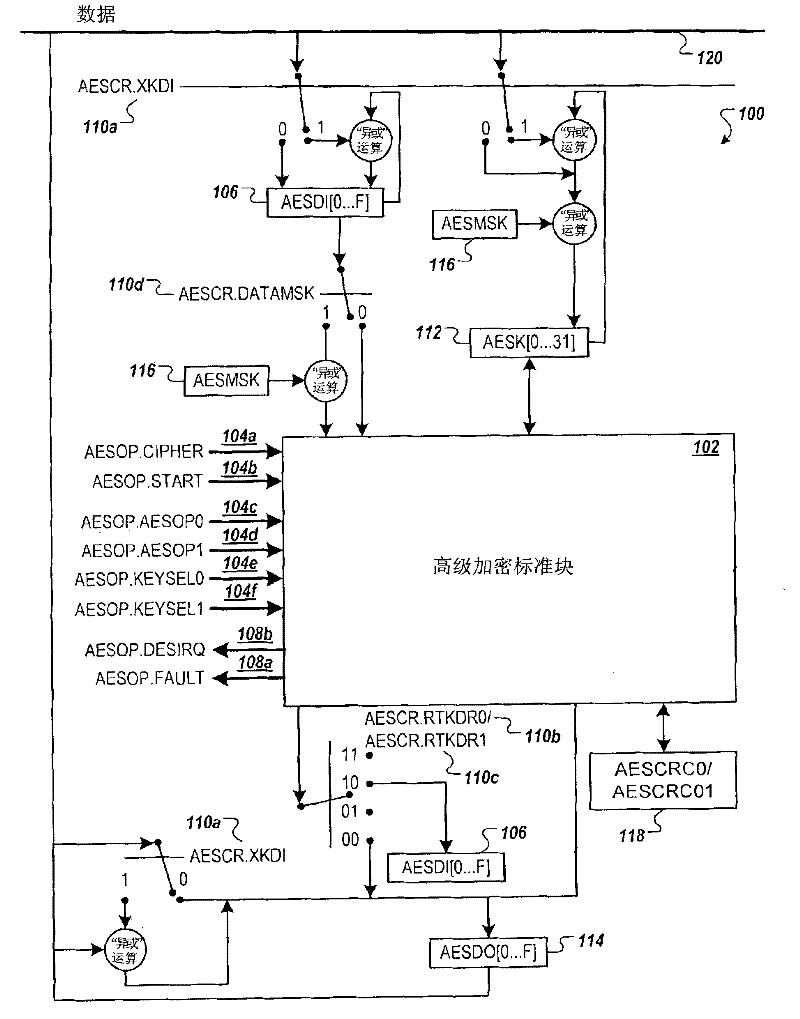
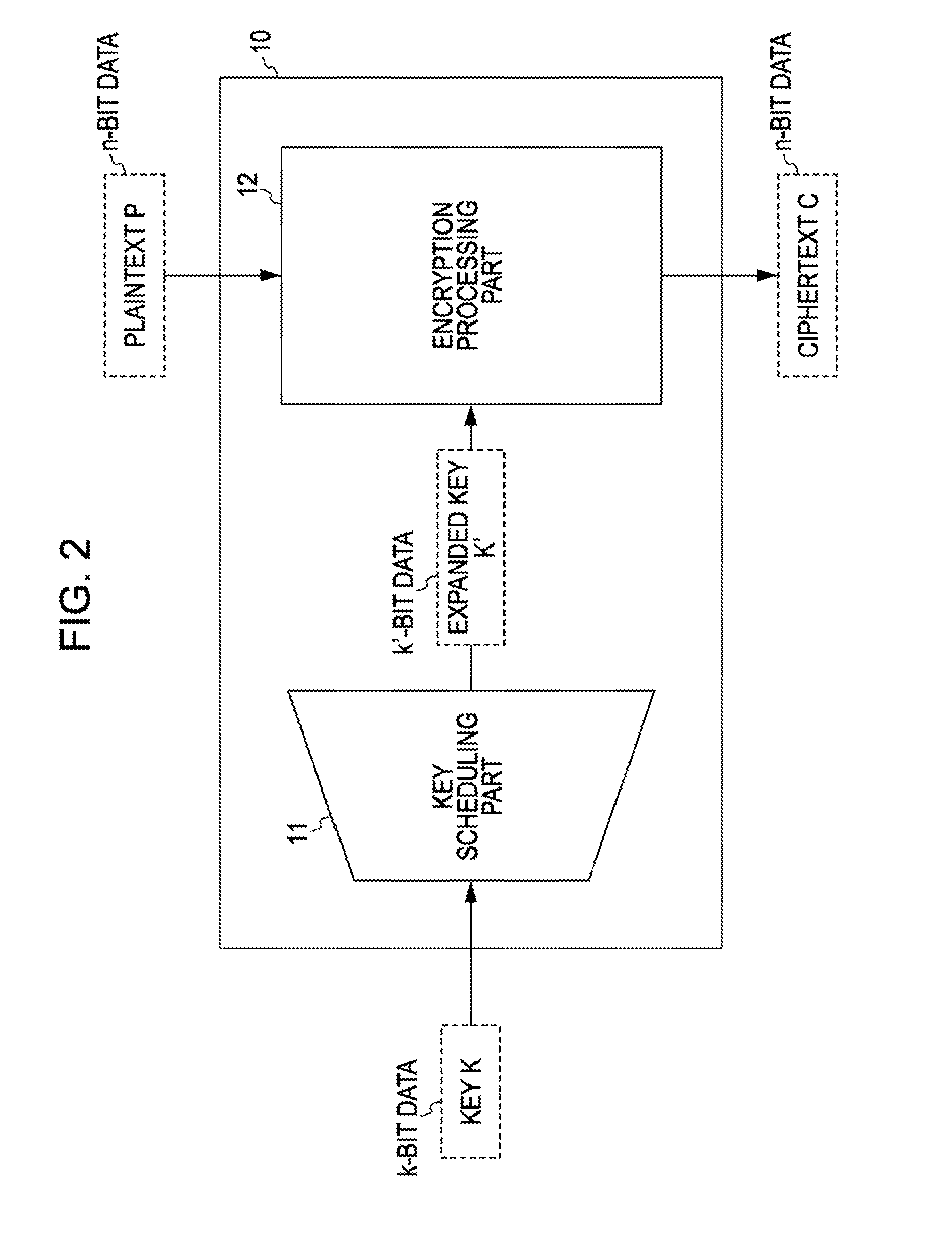
Encryption processing apparatus, encryption processing method, and computer program
InactiveUS8290148B2Great difficulty of cryptanalysisDifficult to analyzeComputer security arrangementsSecret communicationComputer hardwareData transformation
An encryption processing apparatus for performing common-key blockcipher processing, the encryption processing apparatus includes an encryption processing part that performs data transformation in which a round function is iterated for a plurality of rounds; and a key scheduling part that generates round keys used to execute the round function. The key scheduling part is configured to repeatedly apply an xs times multiplication over an extension field GF(2m), generated by an m-th order irreducible polynomial f(x) defined over GF(2), to an m-bit intermediate key generated by transformation of a secret key to generate a plurality of different round intermediate keys serving as data for generating a plurality of different round keys.
Owner:SONY CORP
Apparatus for encrypting/decrypting real-time input stream
ActiveUS7783036B2Simple hardware structureData stream serial/continuous modificationSecret communicationComputer hardwareKey schedule
Disclosed is an apparatus for encrypting / decrypting a real-time input stream. The present invention includes a control unit, a key schedule unit, and a block round unit. Accordingly, the present invention realizes the encryption and decryption of AES algorithm in a manner of hardware, thereby enabling to carry out the encryption and decryption of the real-time input stream real-timely. And, the present invention finds the key for encryption or decryption of one block every round when realizing the encryption and decryption of the AES algorithm in a hardware manner, and then outputs the found keys to the block round unit. The present invention reduces the size of the key register required for the encryption / decryption of block data, thereby enabling to reduce a size of hardware as well as cost of product.
Owner:LG ELECTRONICS INC
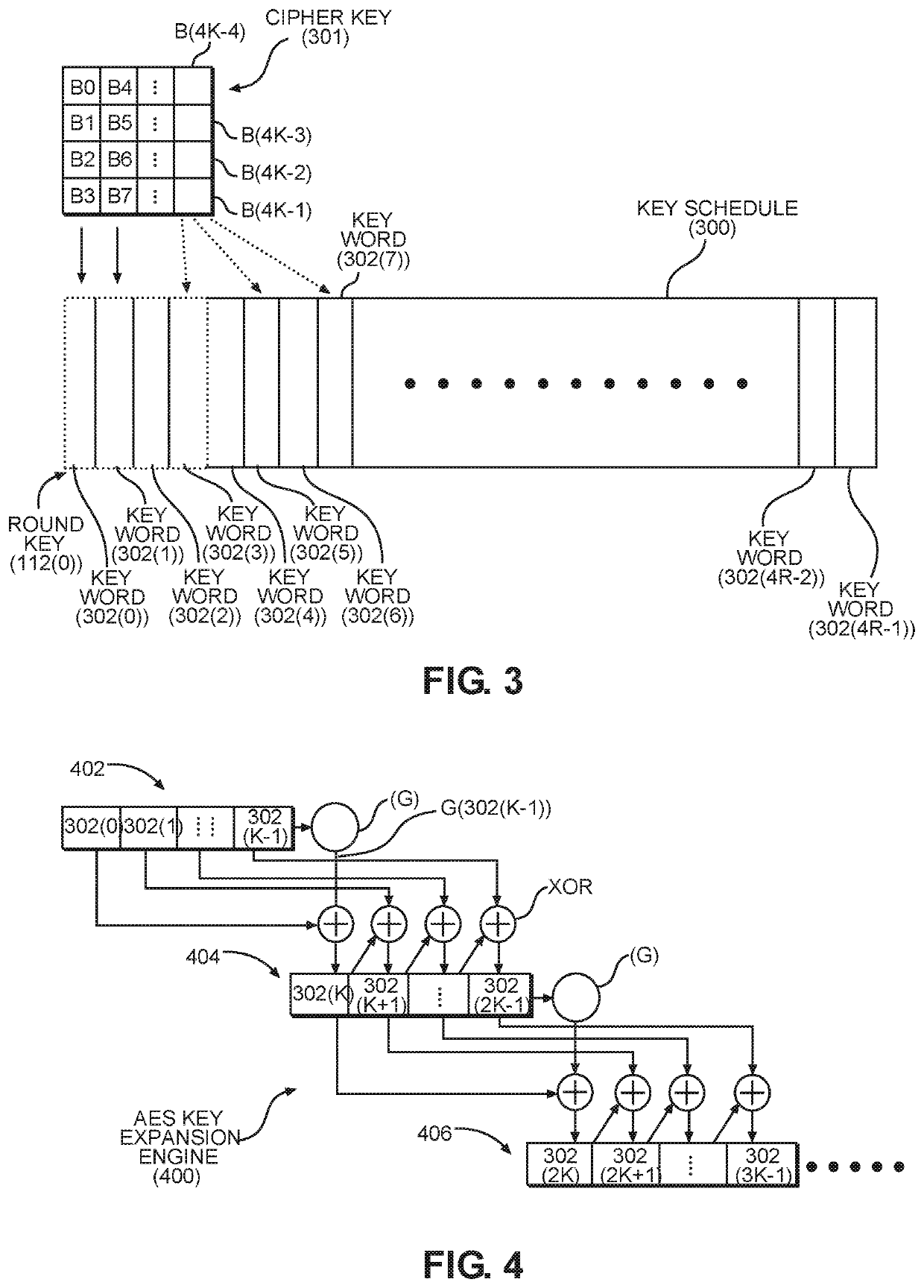
Iterative cipher key-schedule cache for caching round keys used in an iterative encryption/decryption system and related methods
InactiveUS20210091928A1Key distribution for secure communicationEncryption apparatus with shift registers/memoriesData transformationKey schedule
A key-schedule cache stores at least one key schedule based on a cipher key for data transformation using a block cipher. To obtain the round key for a data transformation, a key-word set, which may be a cipher key, including at least one round key is received in a round key control-circuit. The round key control-circuit determines whether the plurality of key words is already stored in the key-schedule cache and also determines whether the next round key, based on the key-word set, is also stored in the key-schedule cache. If the next round key is stored in the key-schedule cache, the round key control-circuit reads the next round key from the key-schedule cache and supplies the next round key to a next round key output. The round key control-circuit may also generate the next round key.
Owner:QUALCOMM INC
Features
- R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
Why Patsnap Eureka
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com