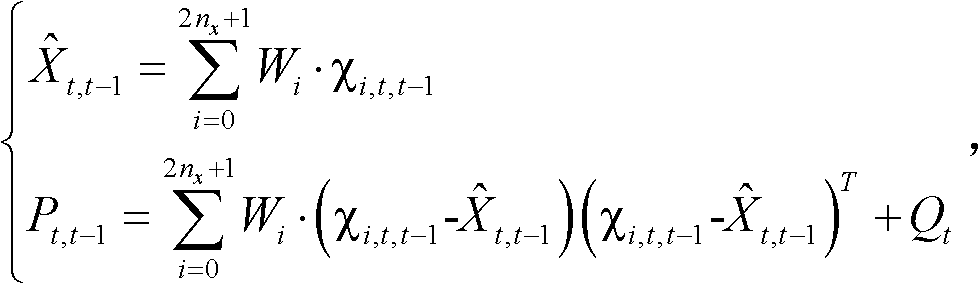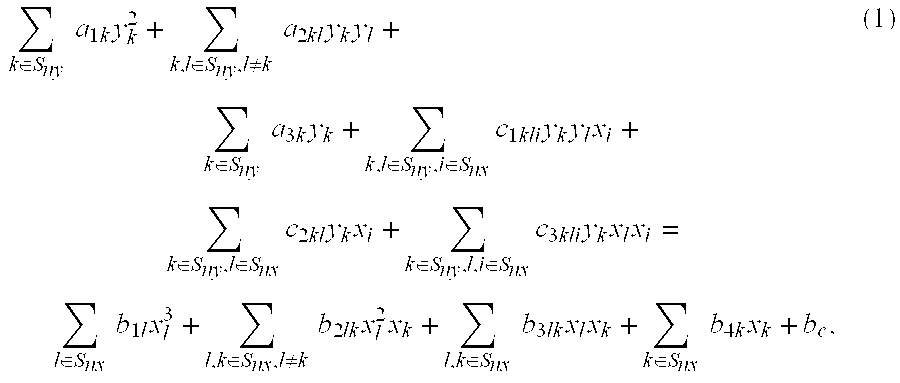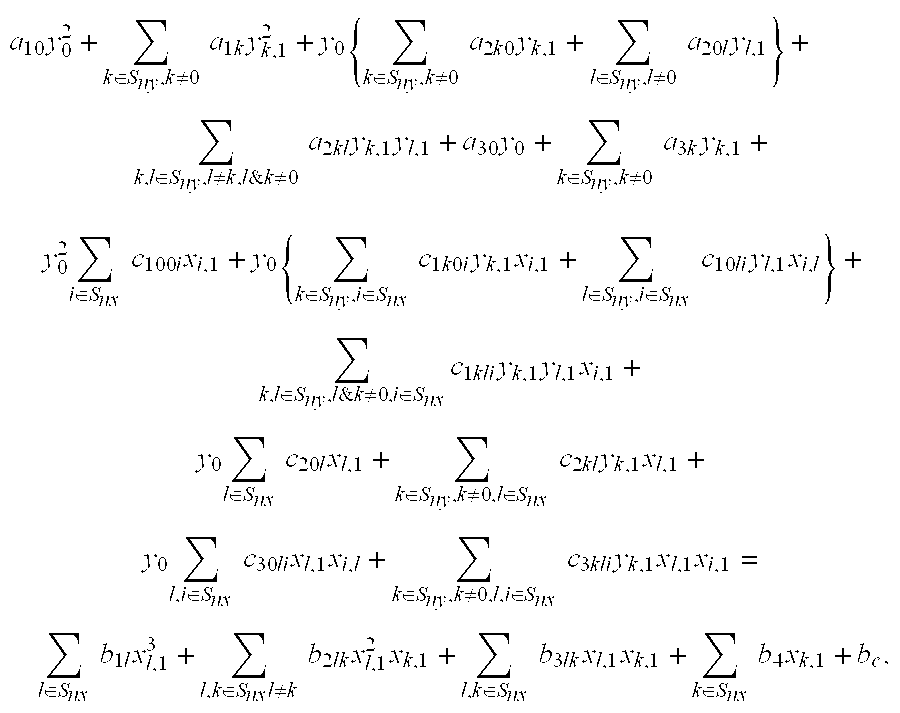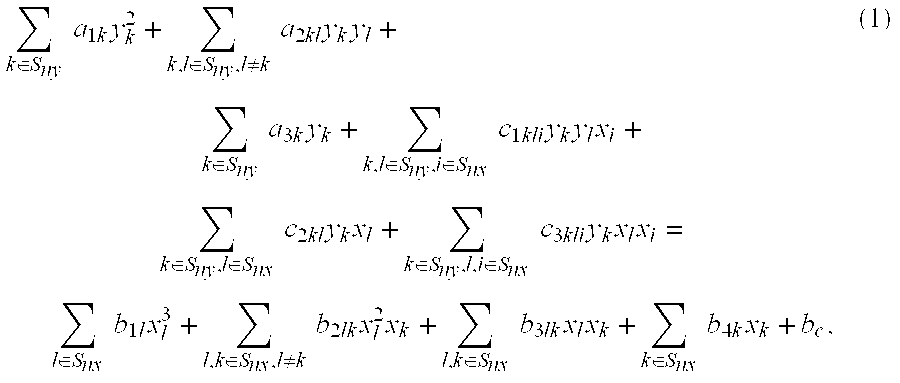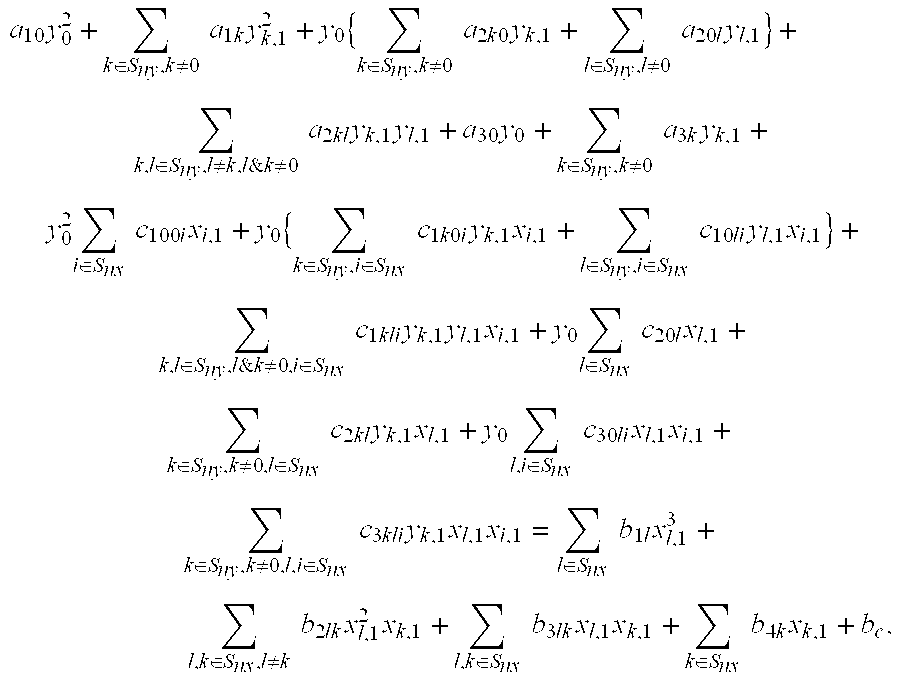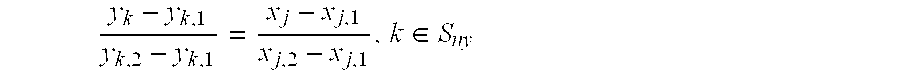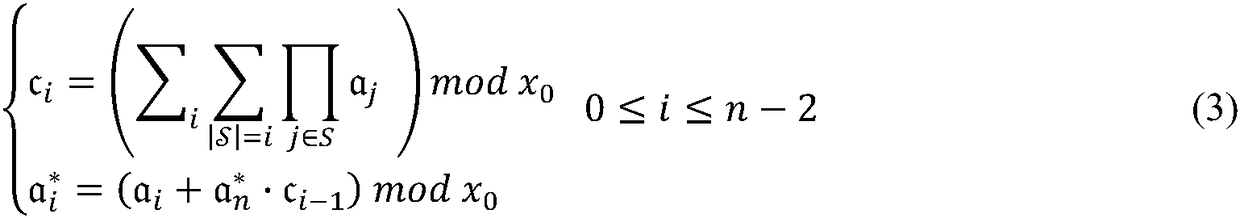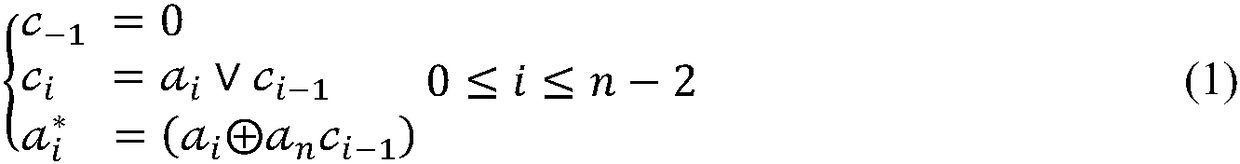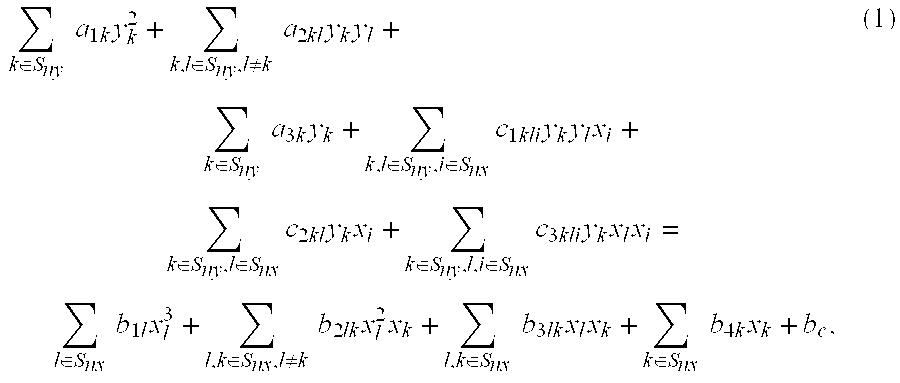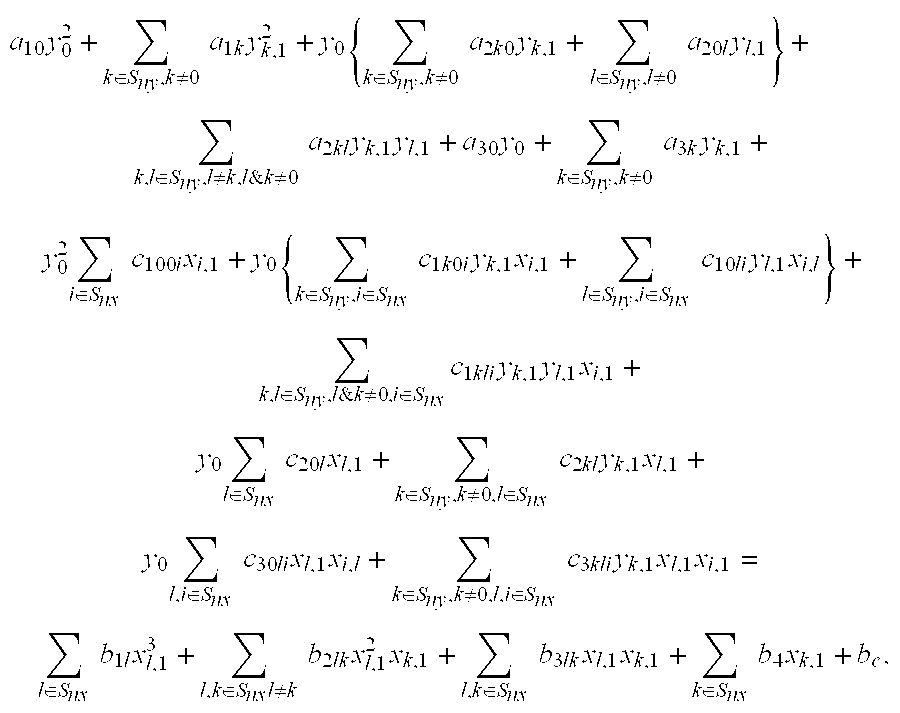Patents
Literature
47 results about "Posynomial" patented technology
Efficacy Topic
Property
Owner
Technical Advancement
Application Domain
Technology Topic
Technology Field Word
Patent Country/Region
Patent Type
Patent Status
Application Year
Inventor
A posynomial, also known as a posinomial in some literature, is a function of the form f(x₁,x₂,…,xₙ)=∑ₖ₌₁ᴷcₖx₁ᵃ₁ₖ⋯xₙᵃₙₖ where all the coordinates xᵢ and coefficients cₖ are positive real numbers, and the exponents aᵢₖ are real numbers. Posynomials are closed under addition, multiplication, and nonnegative scaling. For example, f(x₁,x₂,x₃)=2.7x₁²x₂⁻¹/³x₃⁰·⁷+2x₁⁻⁴x₃²/⁵ is a posynomial. Posynomials are not the same as polynomials in several independent variables.
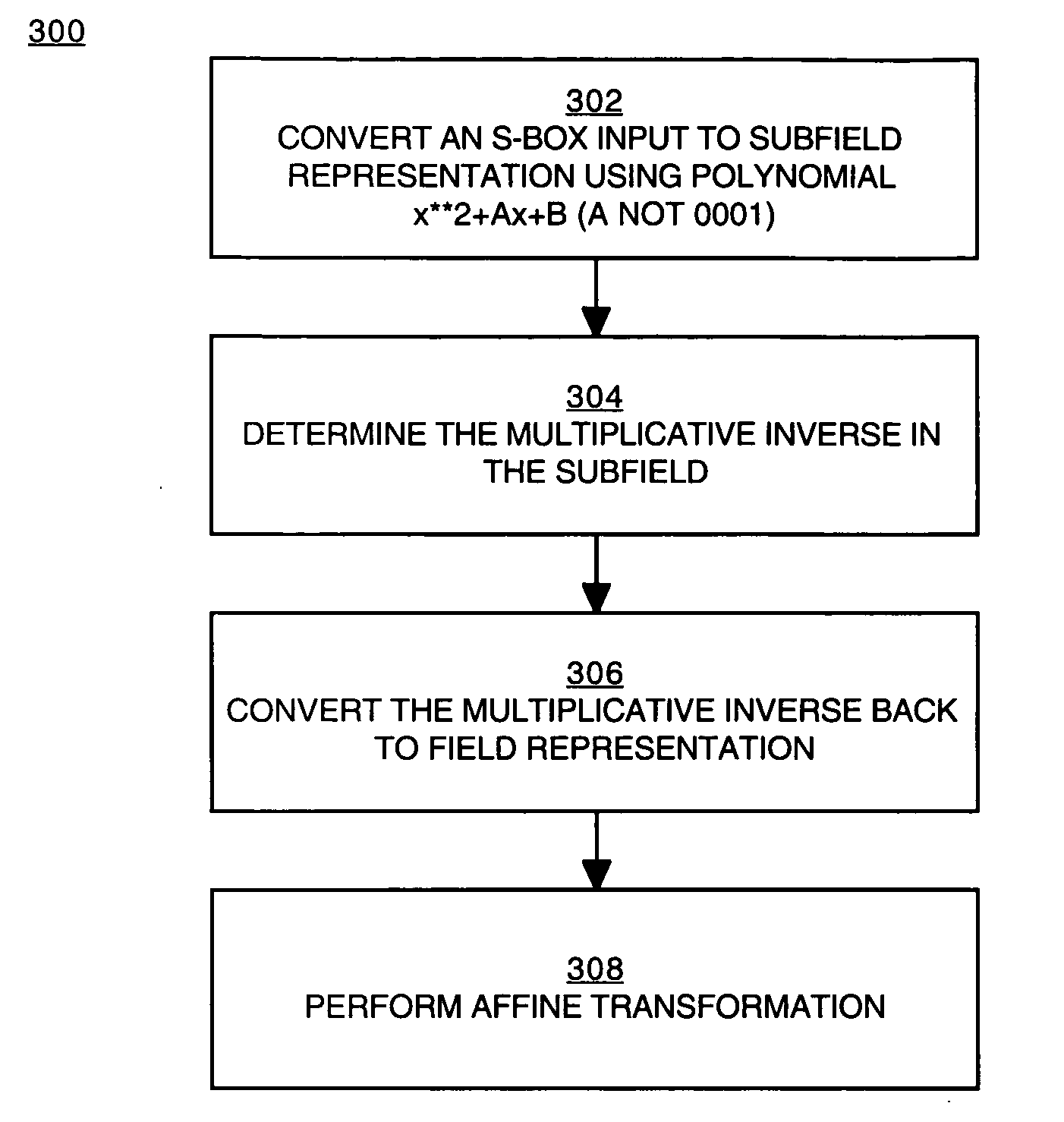
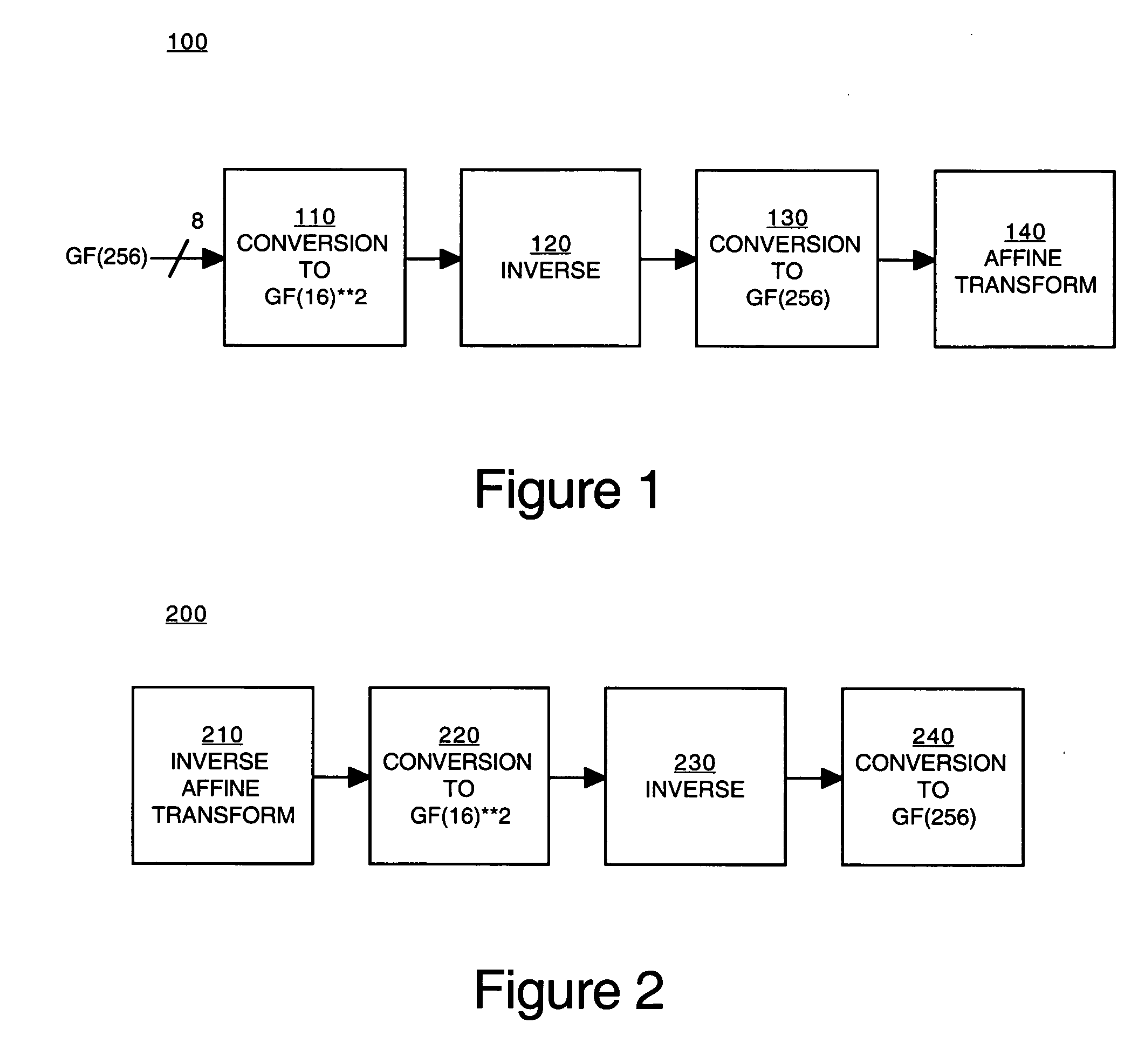
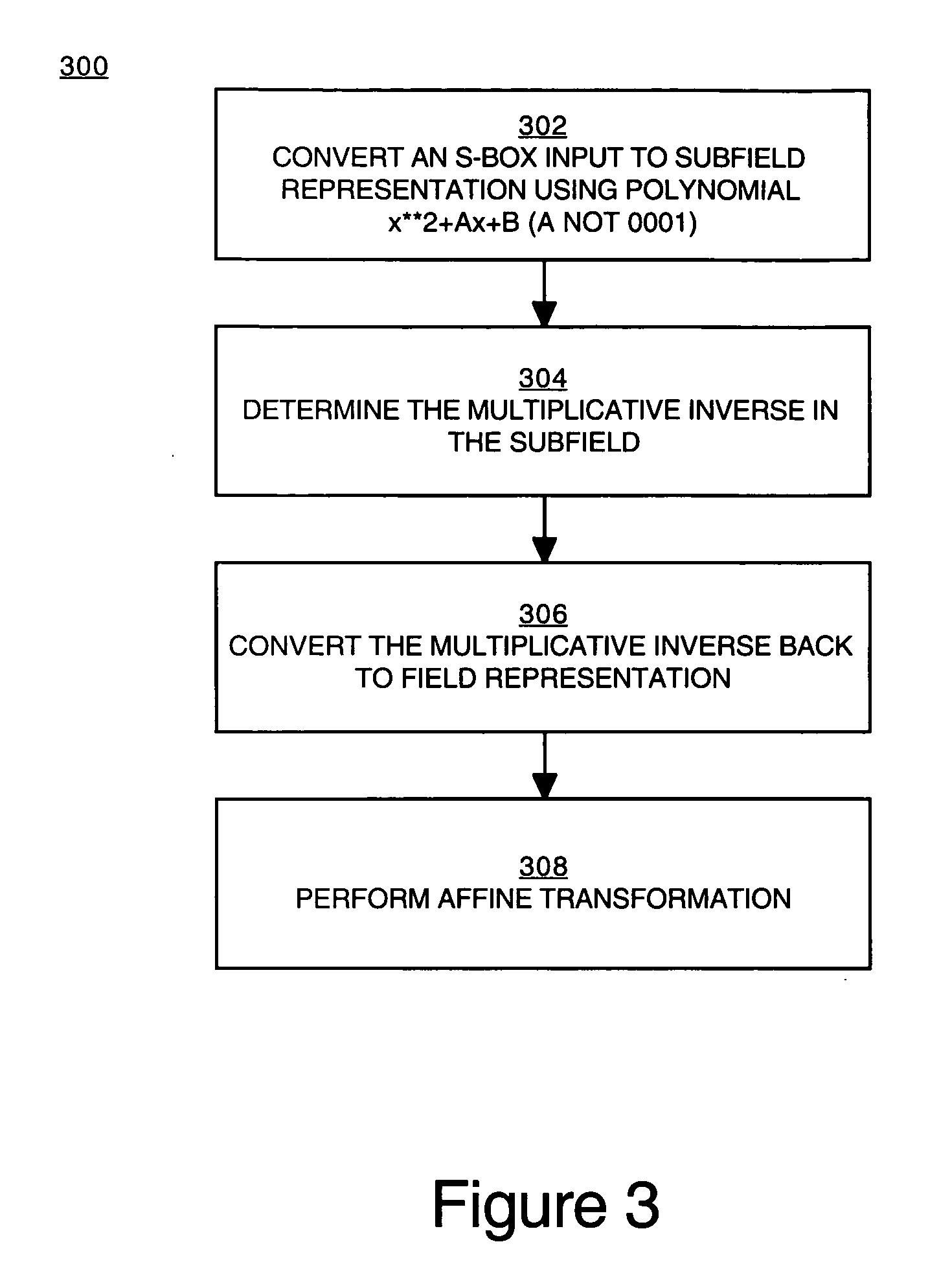
Implementation of a switch-box using a subfield method
InactiveUS20060093136A1Improve S-box implementationLess silicon areaEncryption apparatus with shift registers/memoriesDigital data processing detailsS-boxSwitch box
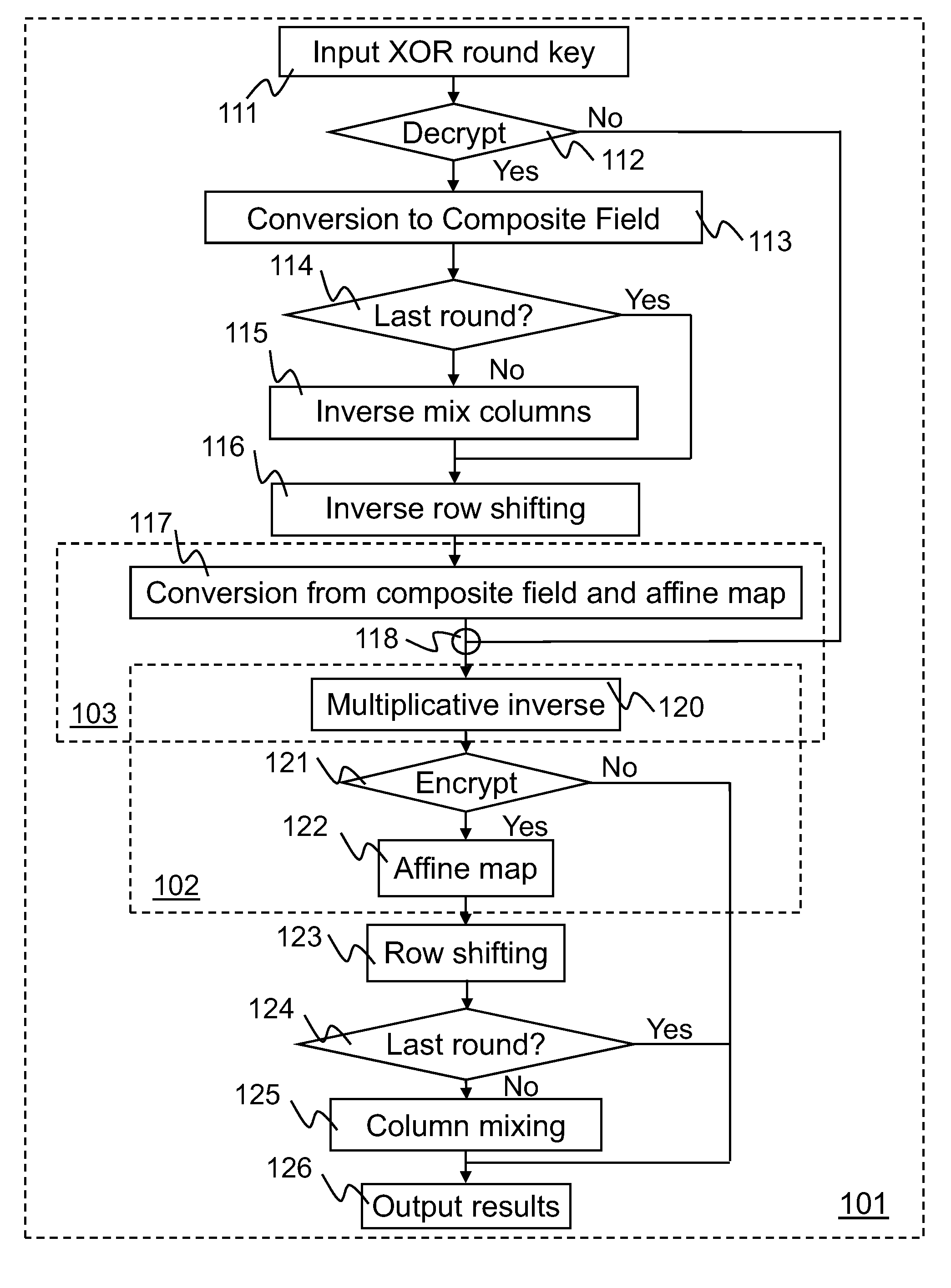
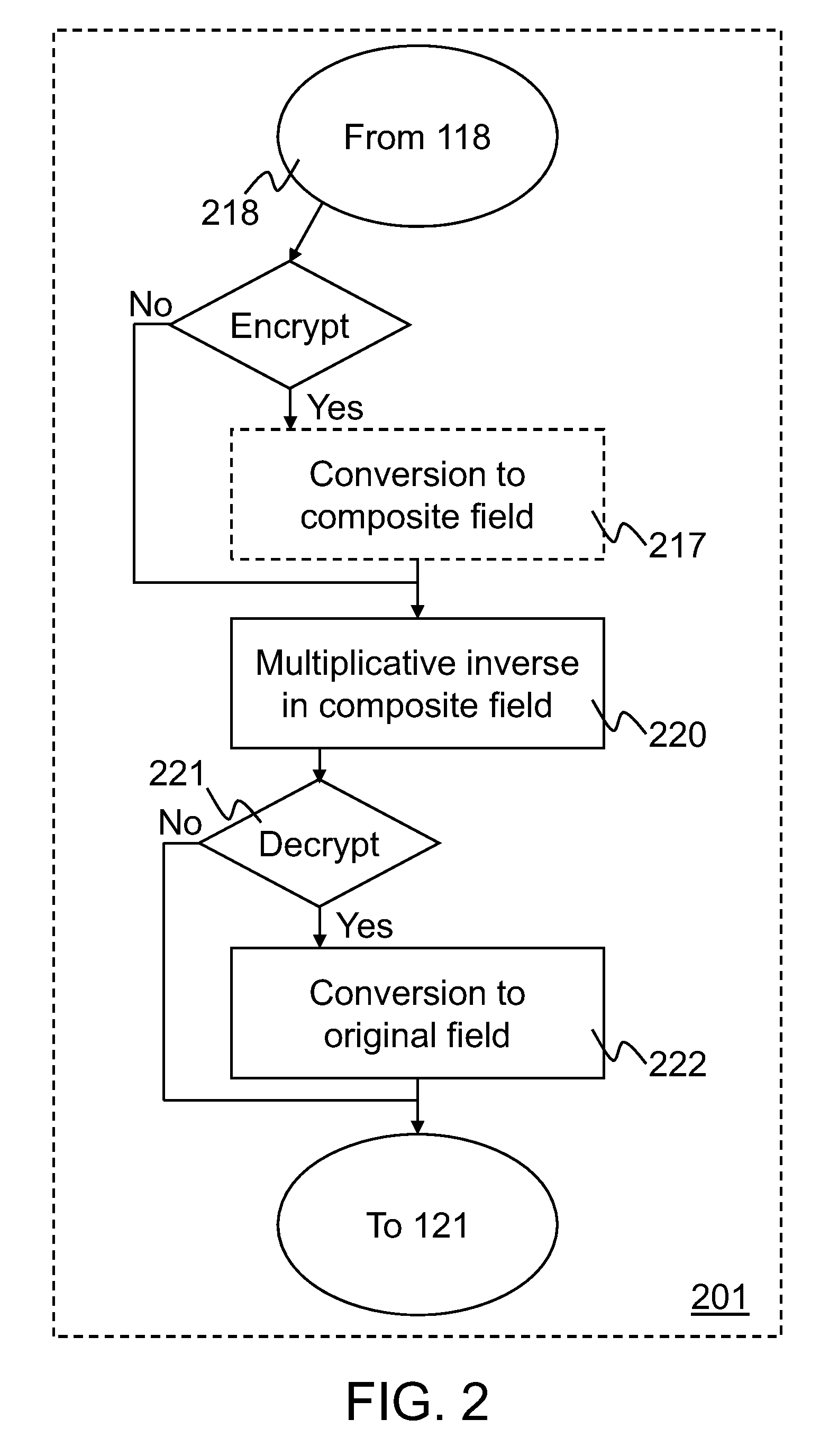
Methods and systems for implementing a switch box (S-box) in a cryptographic application are described. An input to the S-box is converted from a Galois field representation GF(N2) to a Galois subfield representation GF(N)2. The input is converted using a generating polynomial of the form x2+Ax+B, where A and B are elements in GF(N) and where A has a value other than unity. The multiplicative inverse of the Galois subfield representation GF(N)2 is determined. The multiplicative inverse is converted back to the Galois field representation GF(N2). An affine transformation of the multiplicative inverse is then performed.
Owner:CISCO TECH INC
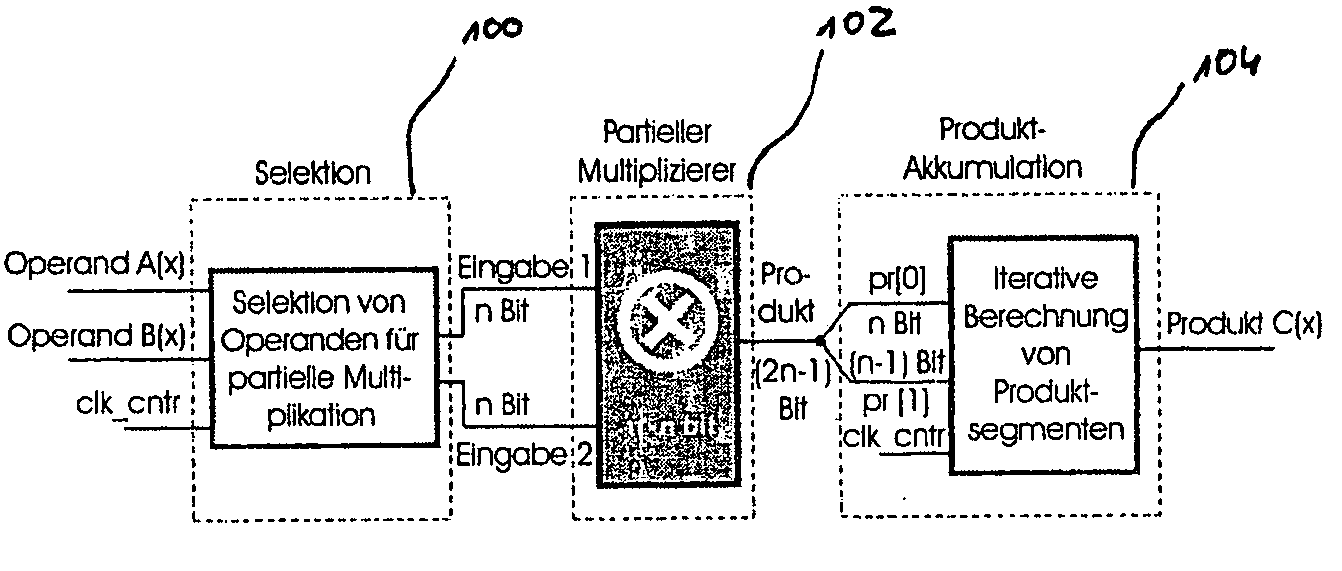
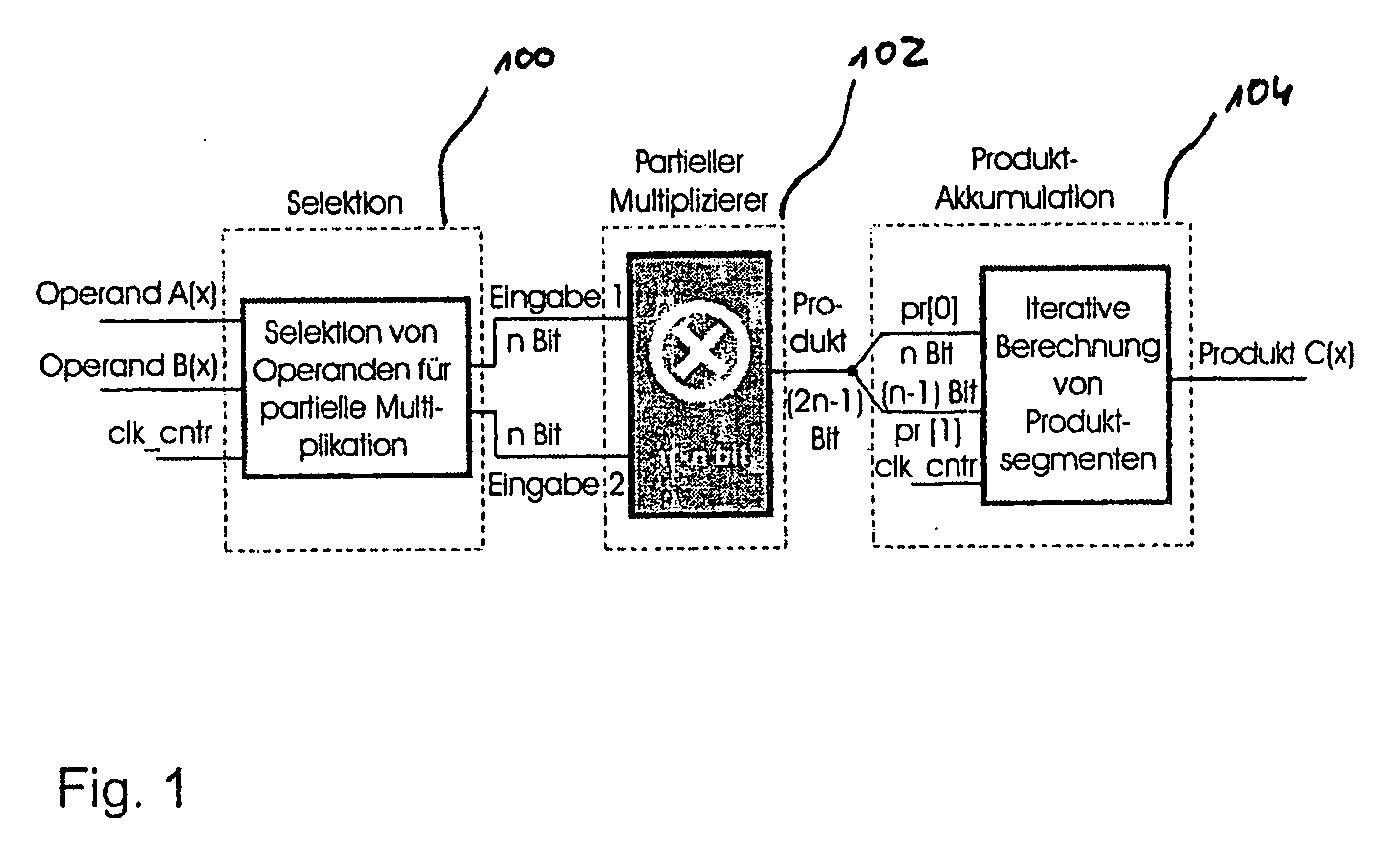
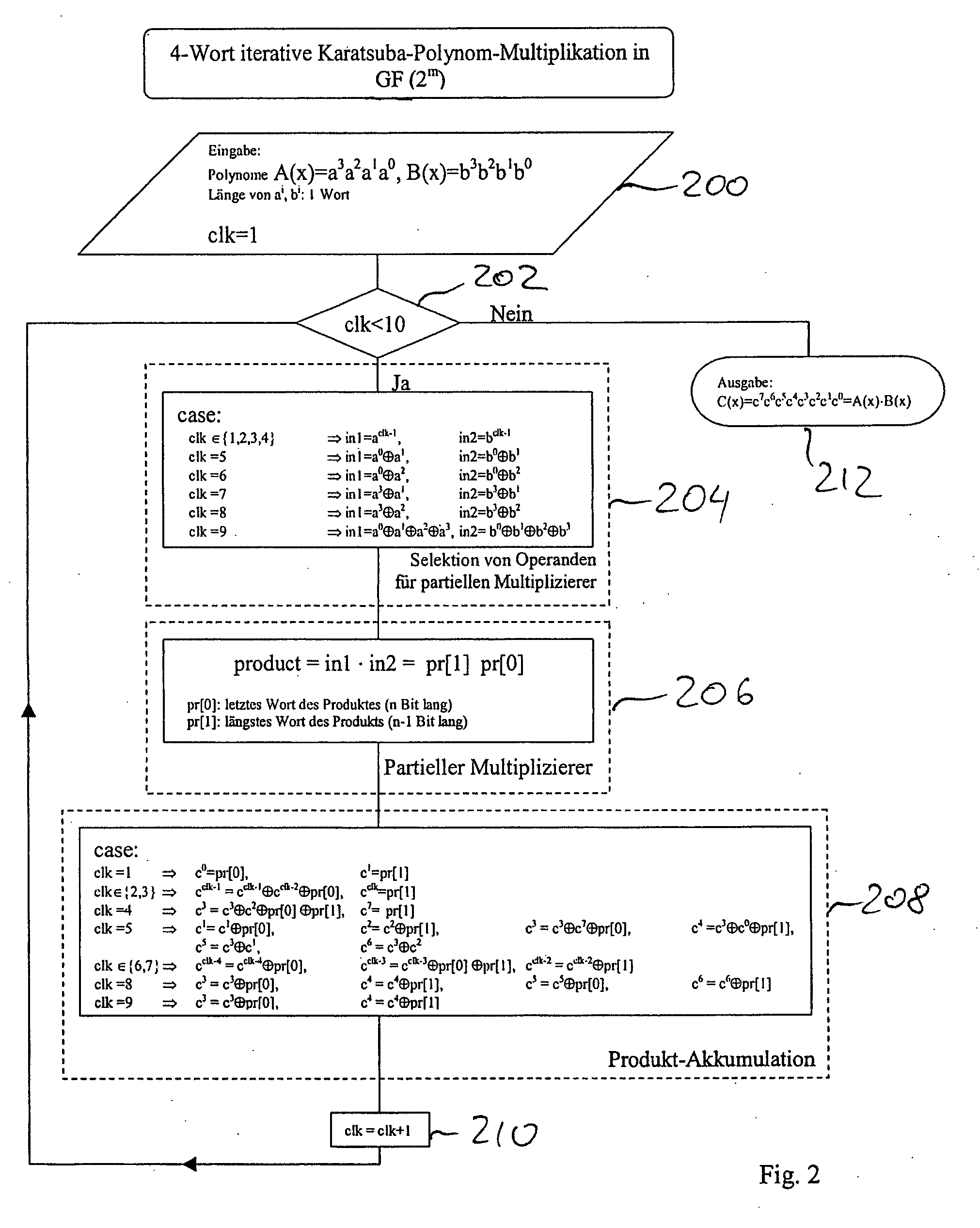
Method and Apparatus for Calculating a Polynomial Multiplication, In Particular for Elliptic Curve Cryptography
ActiveUS20090136022A1Easy to operateEnergy efficient ICTPublic key for secure communicationComputer hardwarePosynomial
Safeguarding communication channels is required in particular in wireless networks. The use of encryption mechanisms in the form of software is limited by the required calculation and energy capacities of mobile terminals. Costs are of significance when using hardware solutions for cryptographic operations. The present invention provides an approach which simultaneously tackles all those points. It concerns a hardware accelerator for polynomial multiplication in extended Galois fields (GF), wherein the per se known Karatsuba method is iteratively applied in accordance with the invention. When using the invention the area requirement can be reduced for example from 6.2 mm2 to 2.1 mm2. The solution according to the invention also reduces the energy consumption in comparison with solutions in accordance with the state of the art by 30%.
Owner:IHP GMBH - INNOVATIONS FOR HIGH PERFORMANCE MICROELECTRONICS INST FOR INNOVATIVE MIKROLEKEKTRONIK
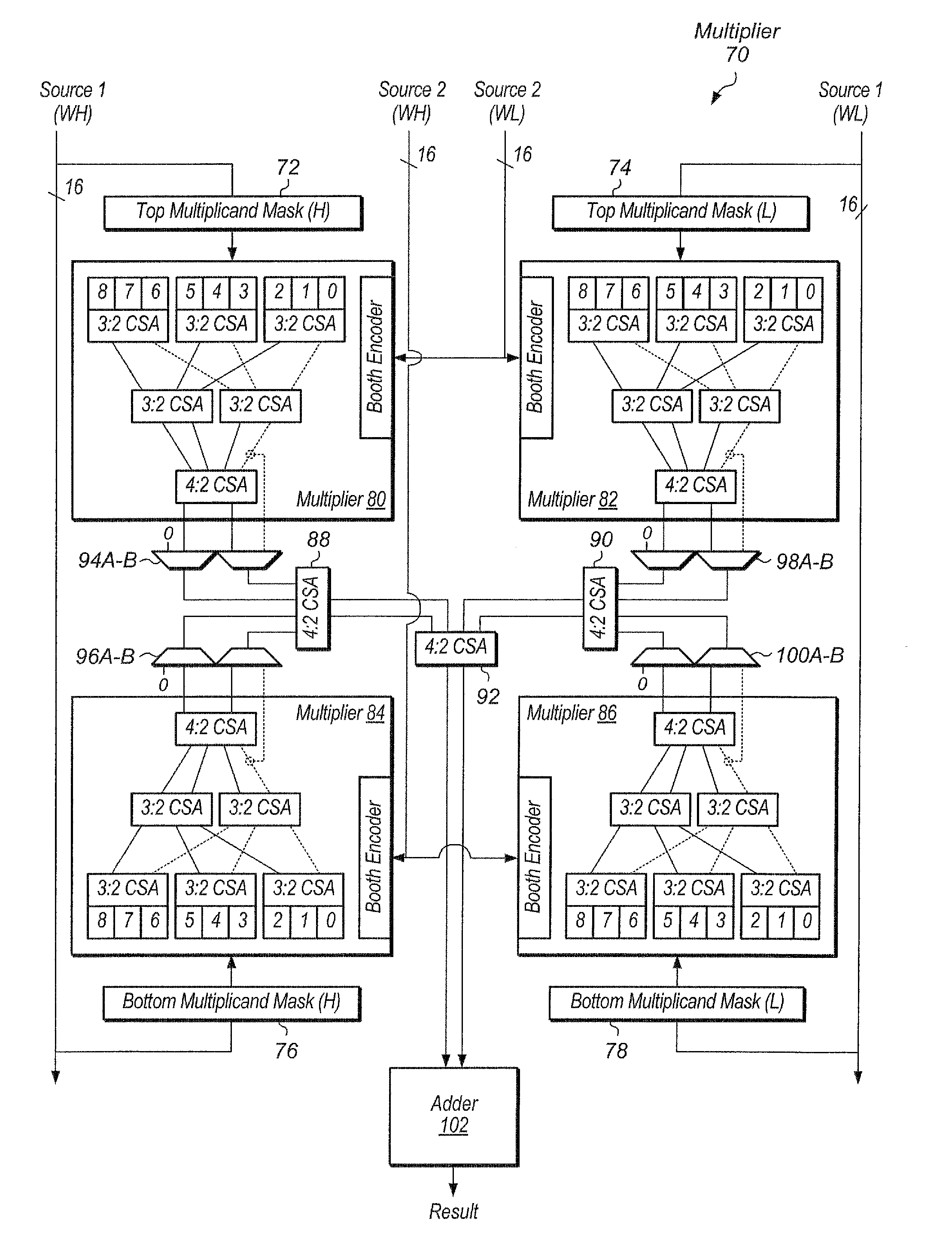
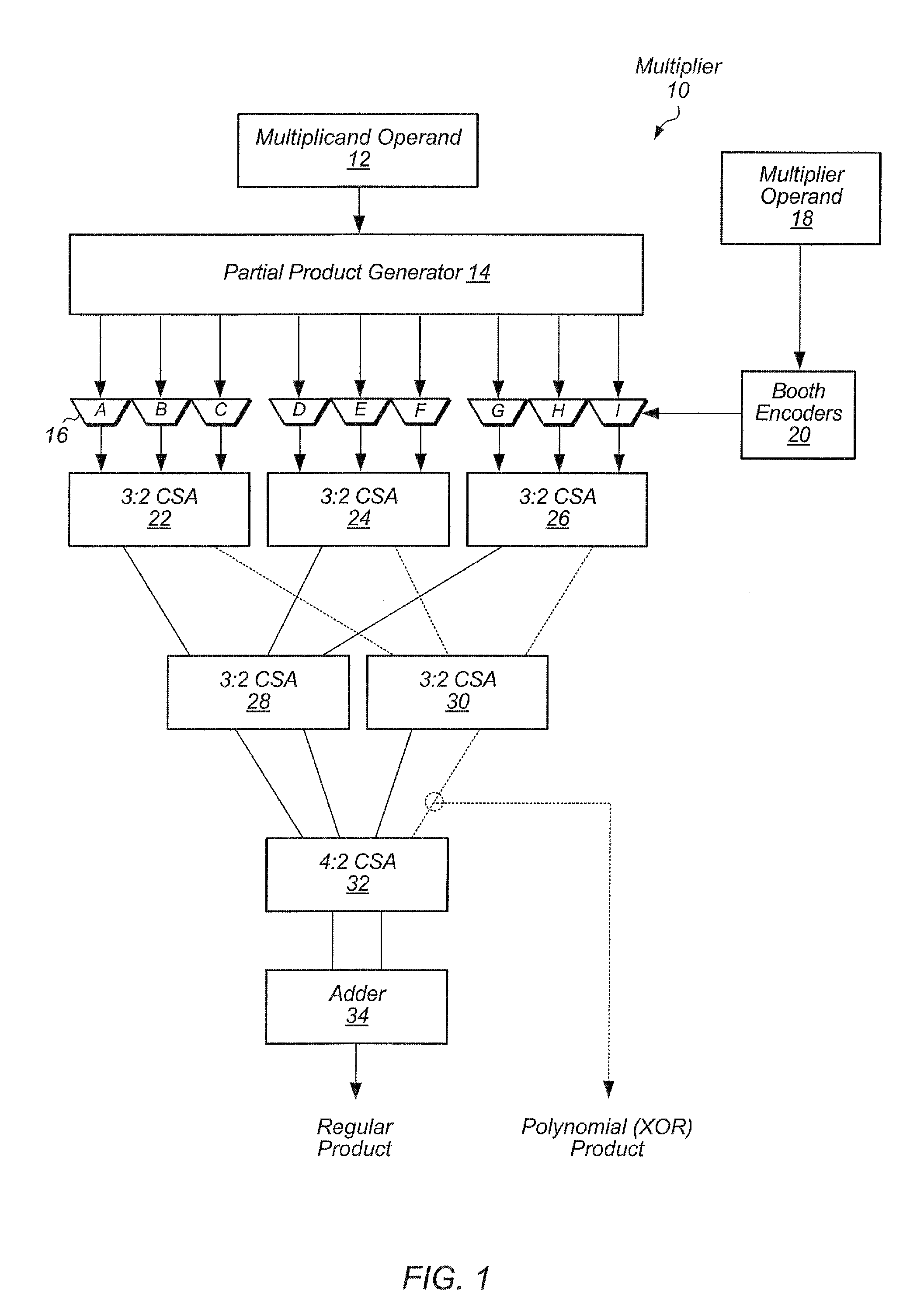
Shared integer, floating point, polynomial, and vector multiplier
ActiveUS20130138711A1Computations using contact-making devicesComputation using non-contact making devicesBinary multiplierTheoretical computer science
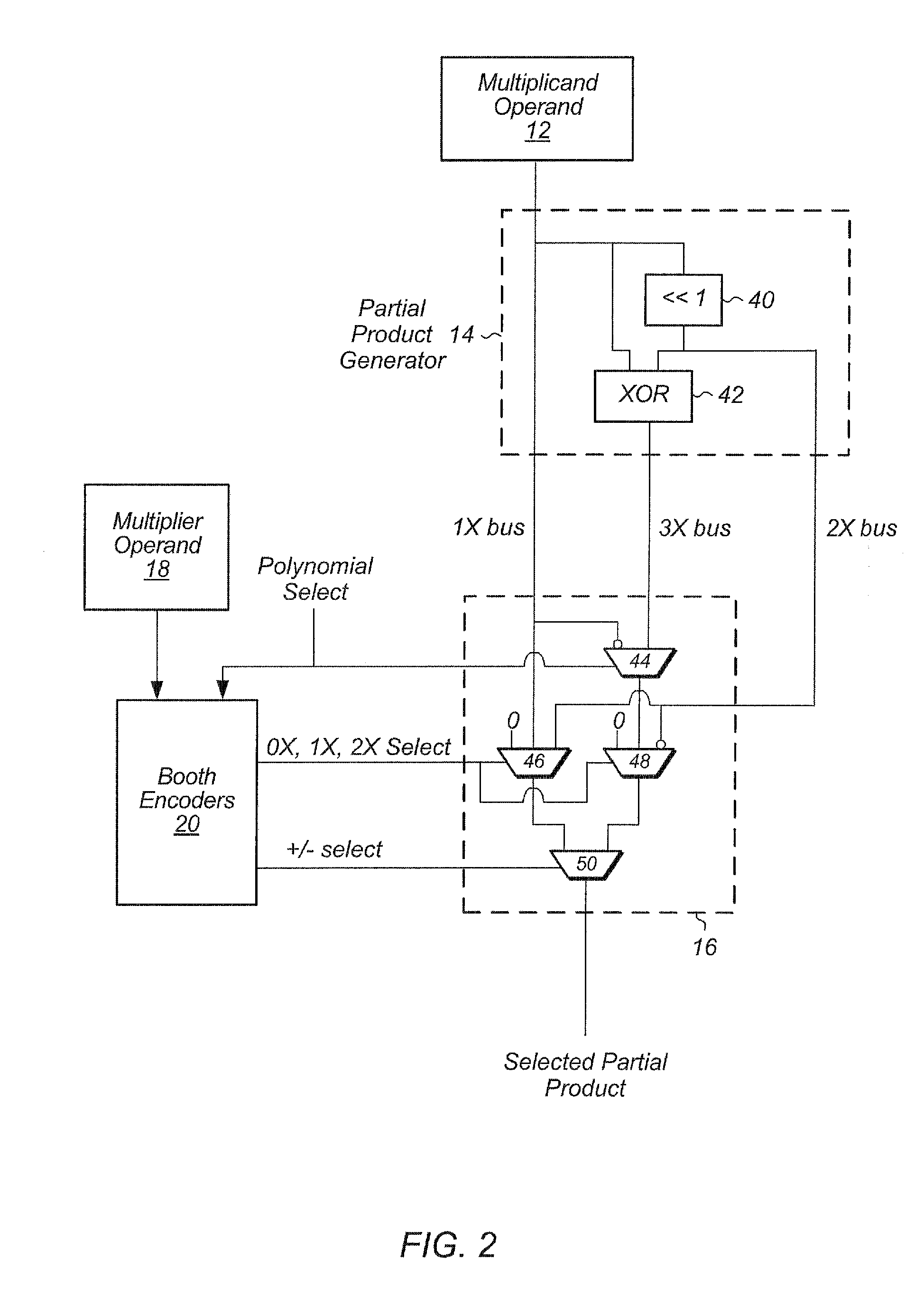
A multiplier for performing multiple types of multiplication including integer, floating point, vector, and polynomial multiplication. The multiplier includes a modified booth encoder within the multiplier and unified circuitry to perform the various types of multiplication. A carry save adder tree is modified to route sum outputs to one part of the tree and to route carry outputs to another part of the tree. The carry save adder tree is also organized into multiple carry save adder trees to perform vector multiplication.
Owner:APPLE INC
Sigmoid function fitting hardware circuit based on Remez approximating algorithm
ActiveCN104484703ASatisfy consumptionIncrease the number ofPhysical realisationResource consumptionSigmoid function
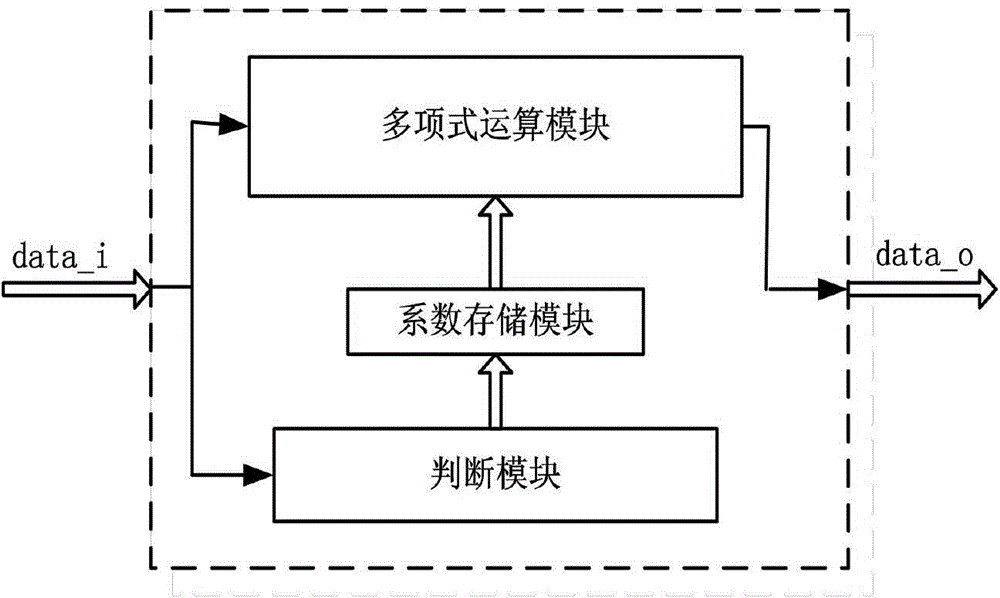
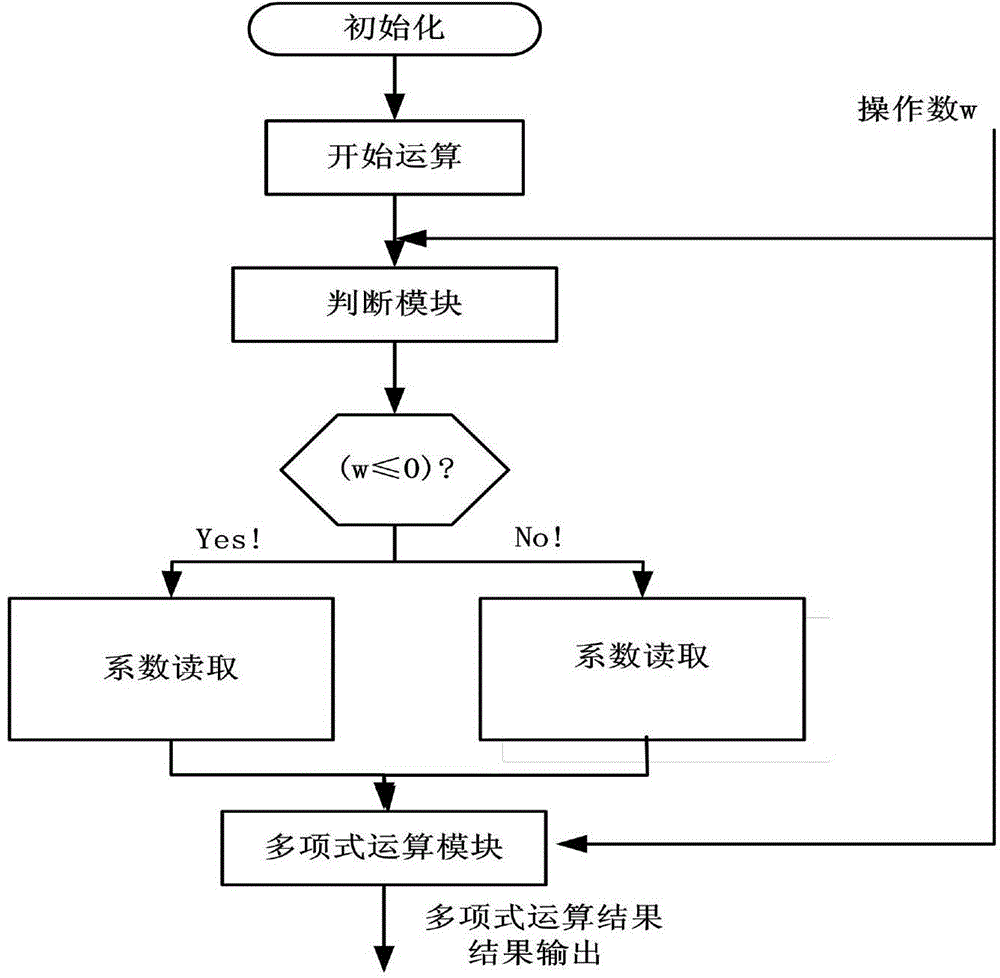
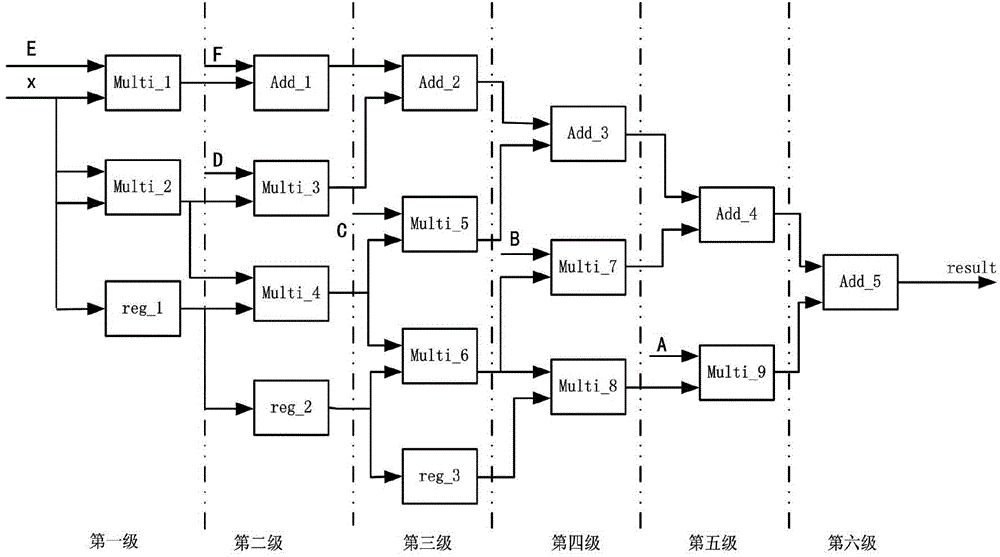
The invention discloses a sigmoid function fitting hardware circuit based on a Remez approximating algorithm. A sigmoid function fitting method is characterized by including the following steps that (1), the order of a fitting polynomial is determined; (2), a fitting interval of a sigmoid function is obtained; (3), a piecewise interval is obtained; (4), the fitting polynomial is obtained; (5), a coefficient storing module is designed; (6), a polynomial calculation module is designed; (7), a judgment module is designed; (8), the fitting hardware circuit is obtained; (9), a fitting execution interval where operands are located is judged; (10), a coefficient of the fitting polynomial is read; (11), fitting calculation is carried out in the polynomial calculation module. On the basis of reducing hardware resource consumption, the calculation accuracy is improved, the calculation speed is increased, and the flexibility of a calculation structure is promoted.
Owner:黄山市开发投资集团有限公司
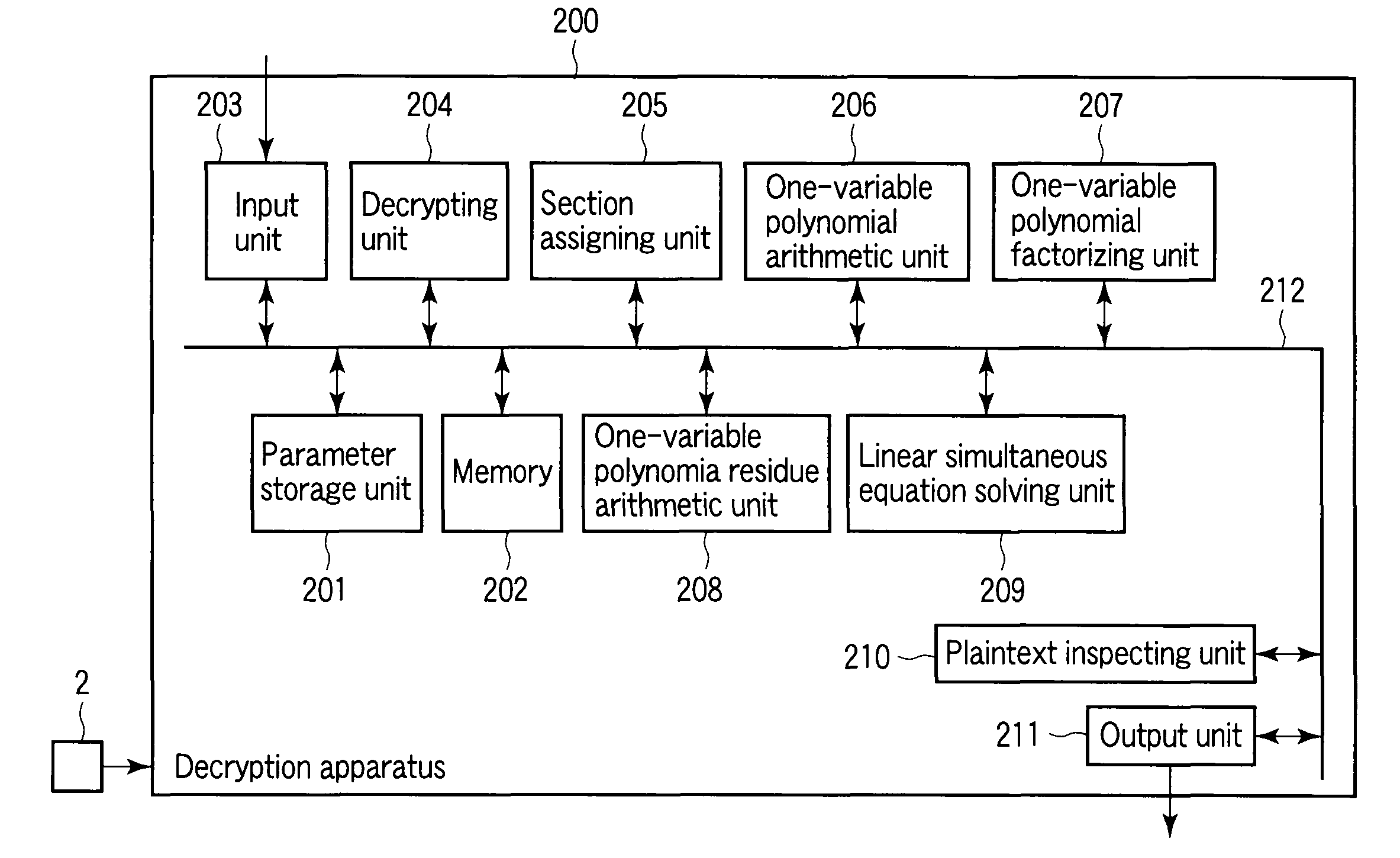
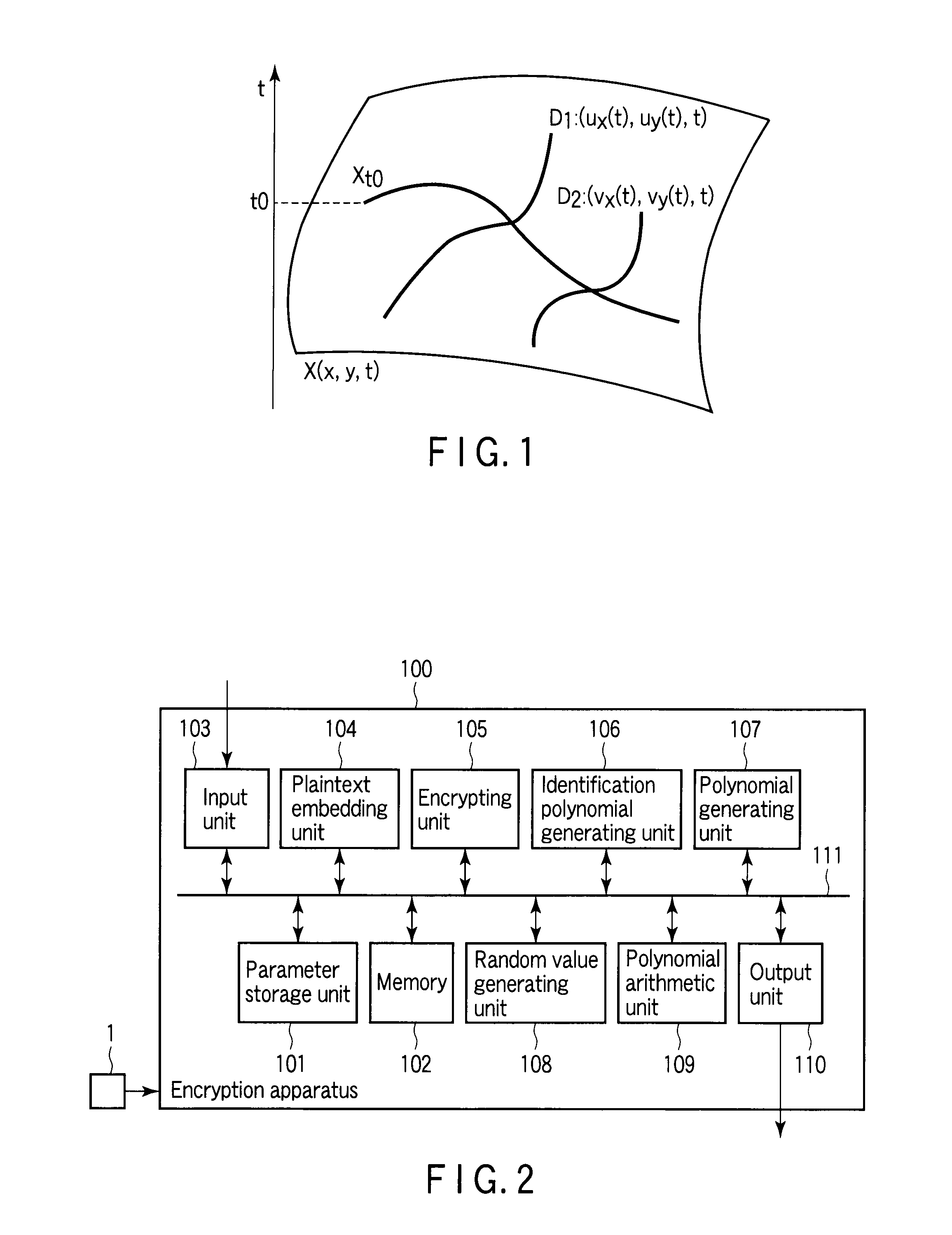
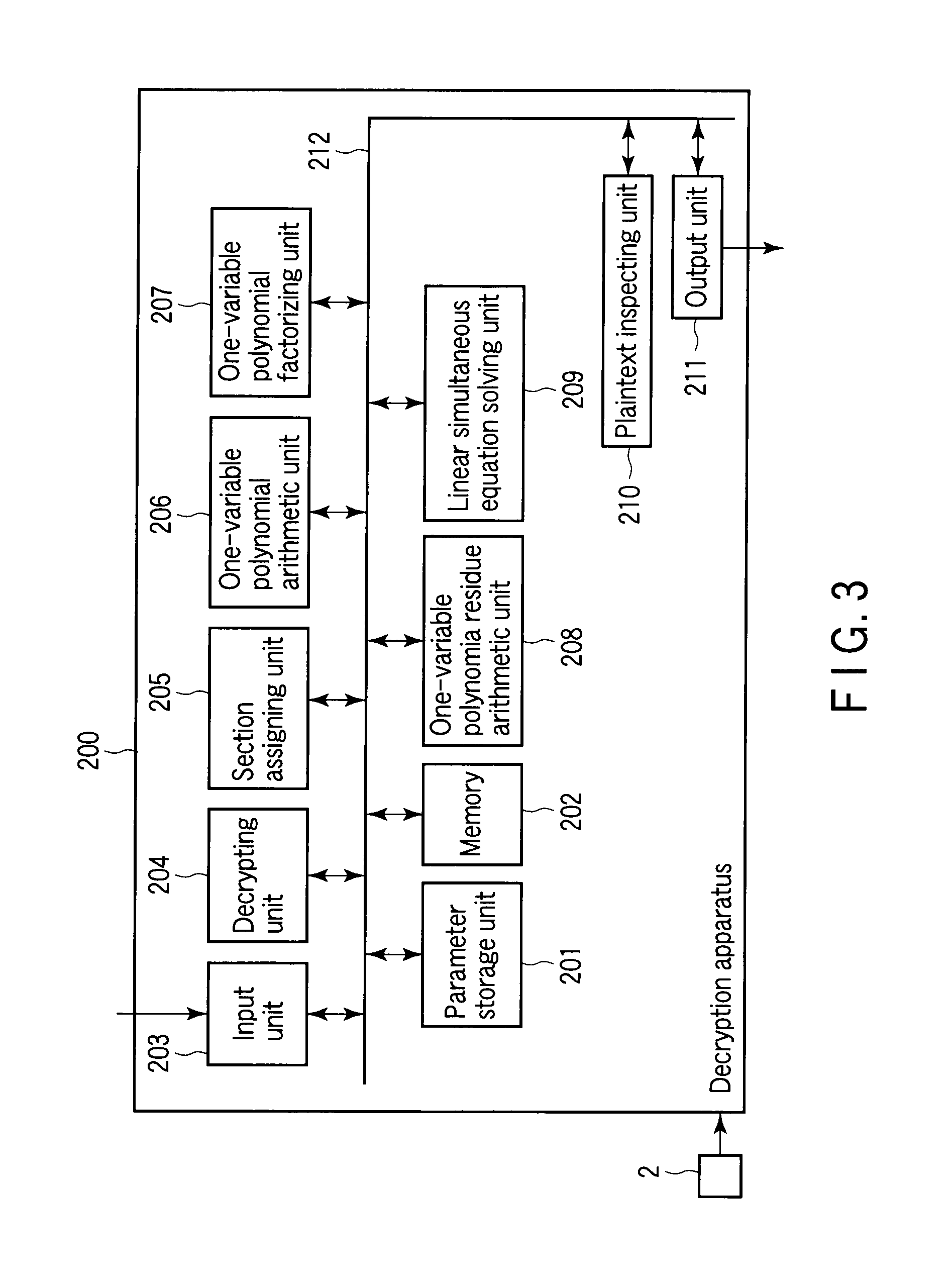
Encryption apparatus, decryption apparatus, and method
InactiveUS20070110232A1Public key for secure communicationUser identity/authority verificationPlaintextComputer hardware
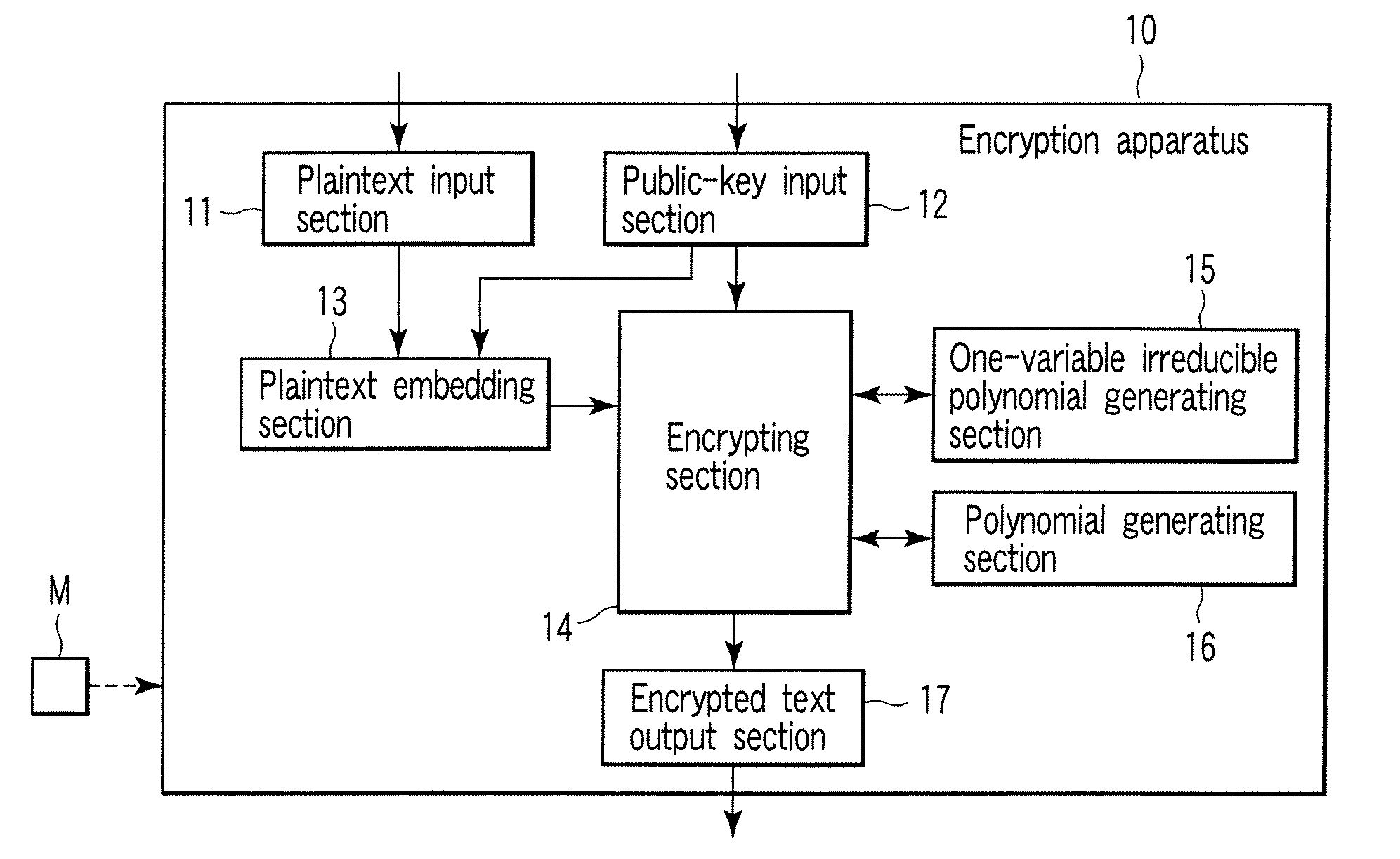
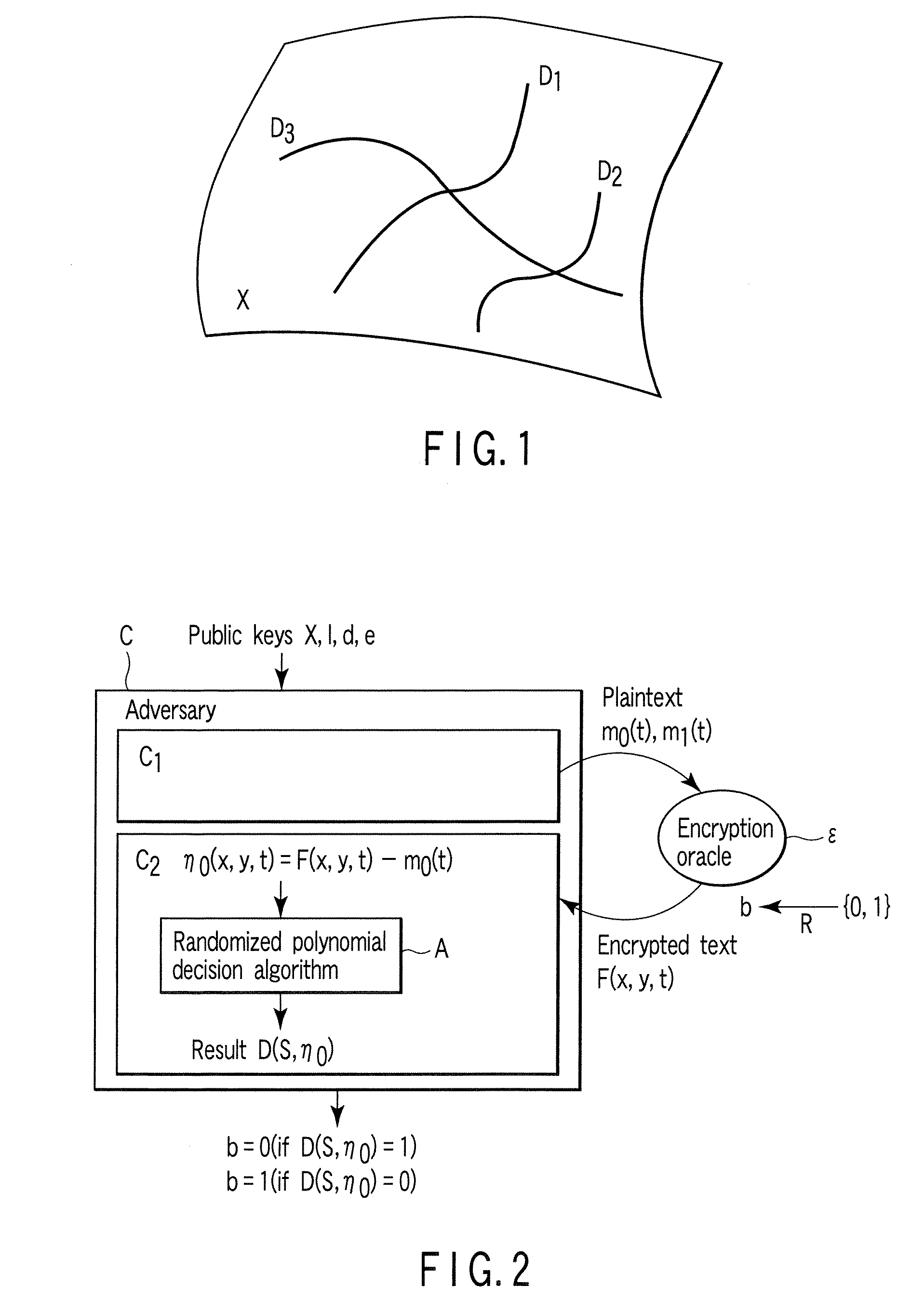
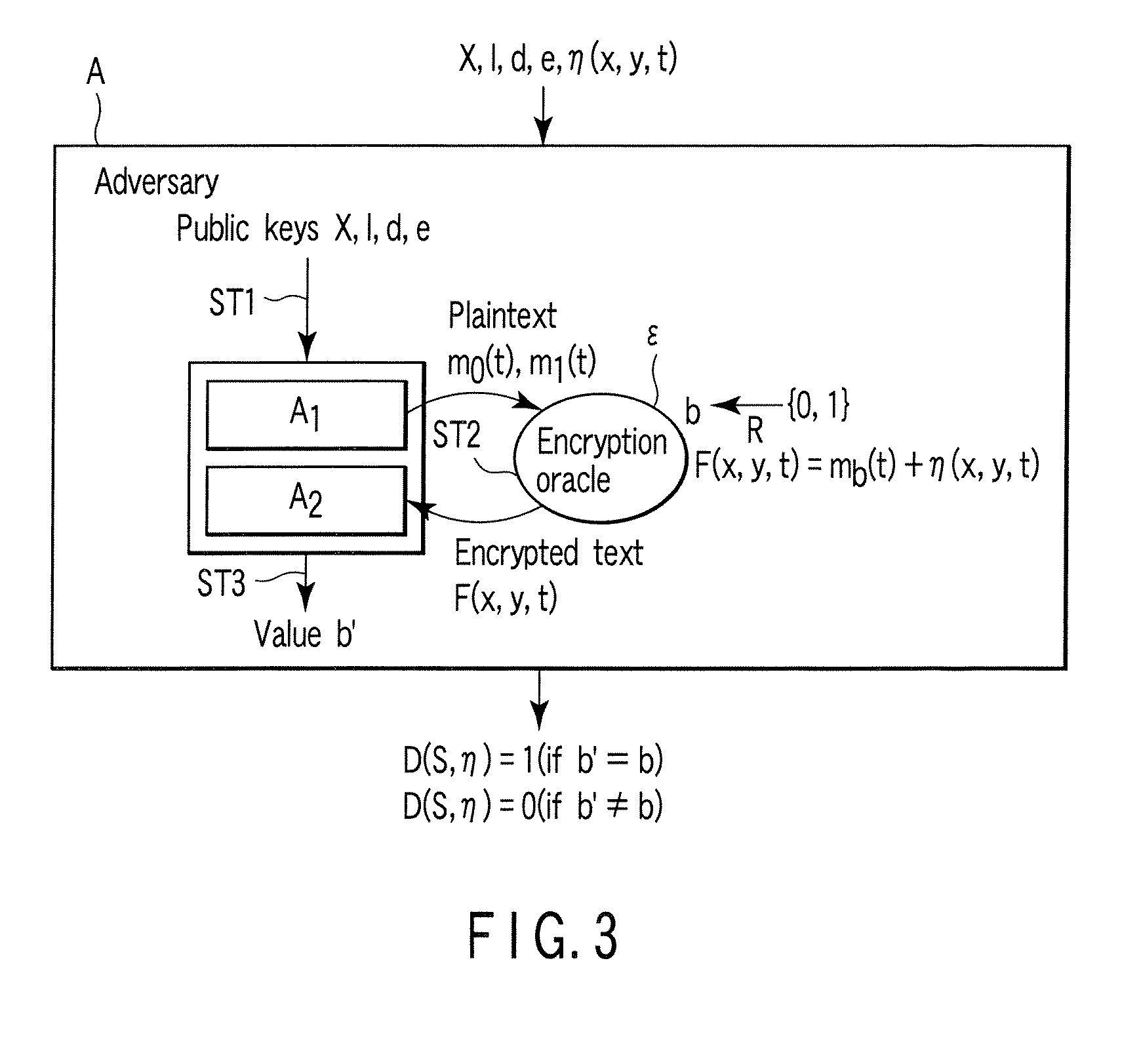
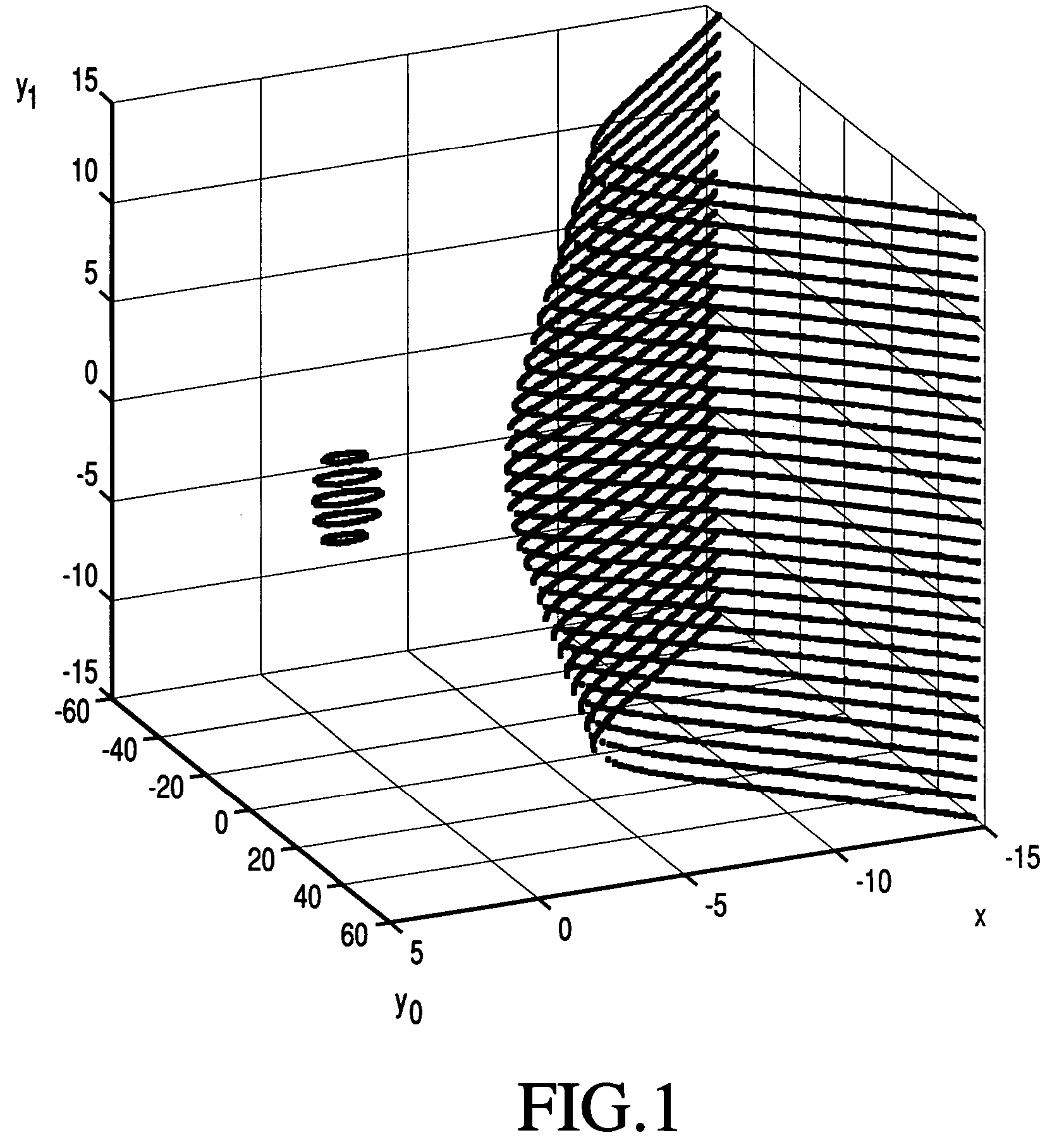
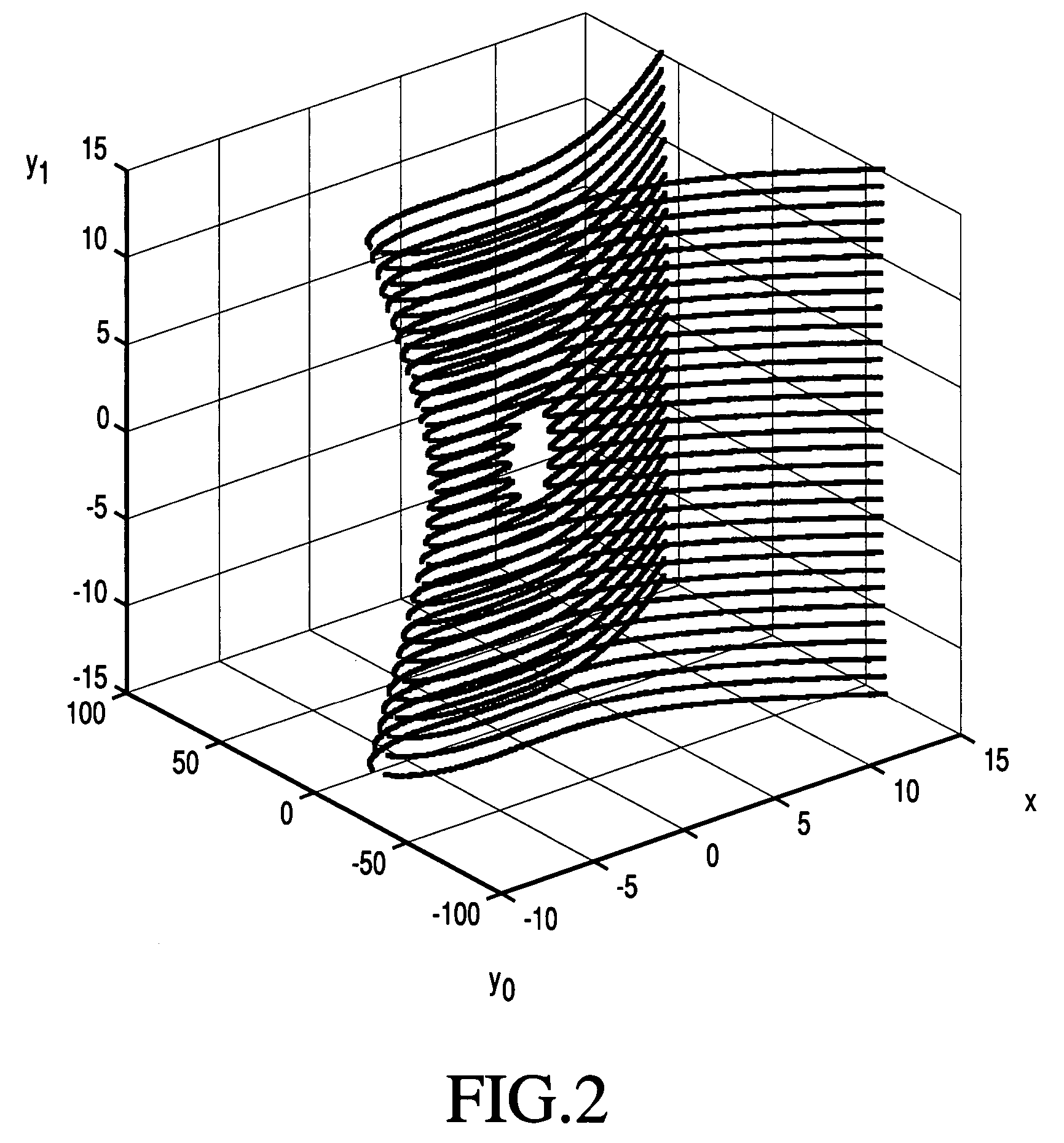
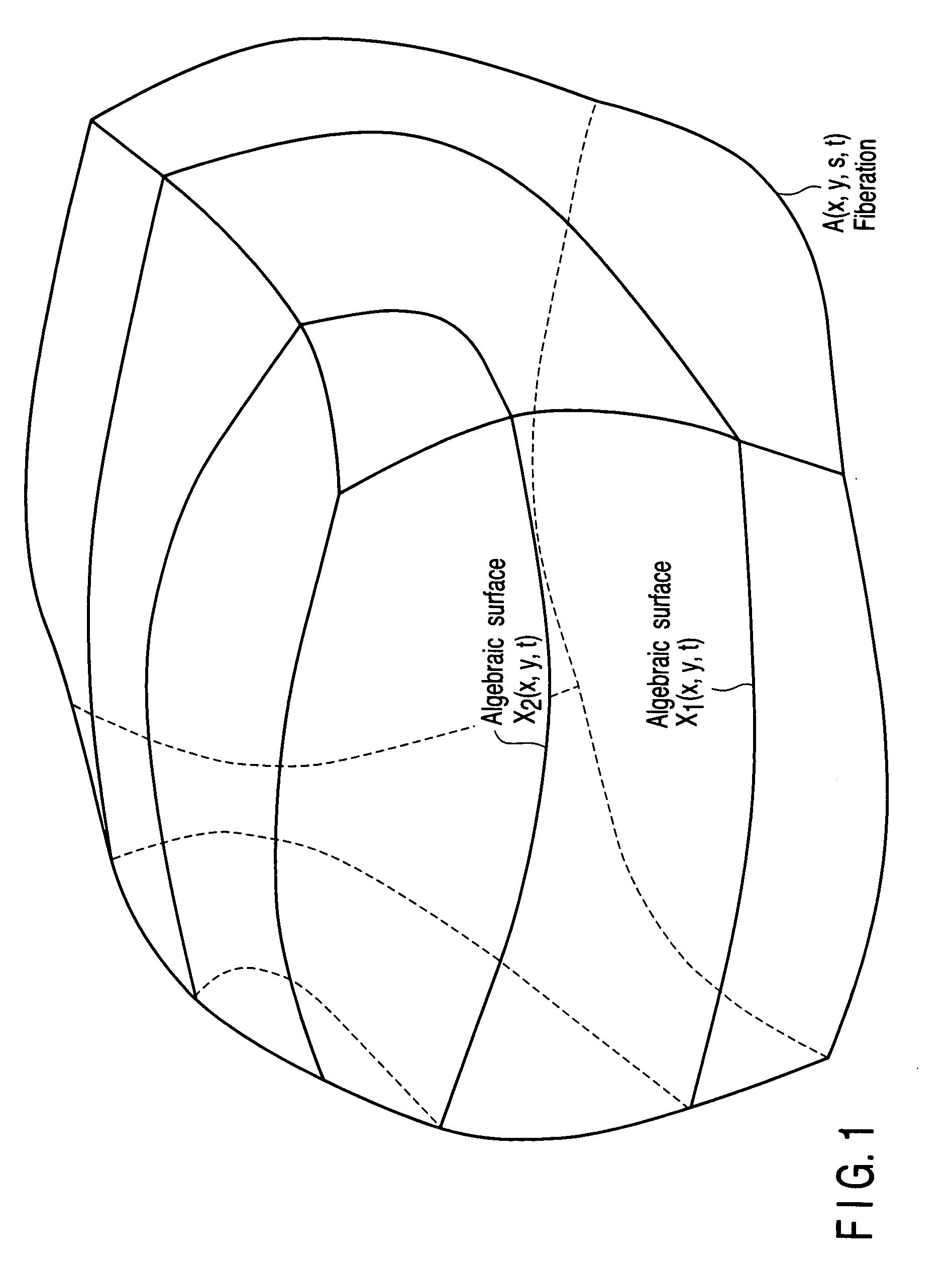
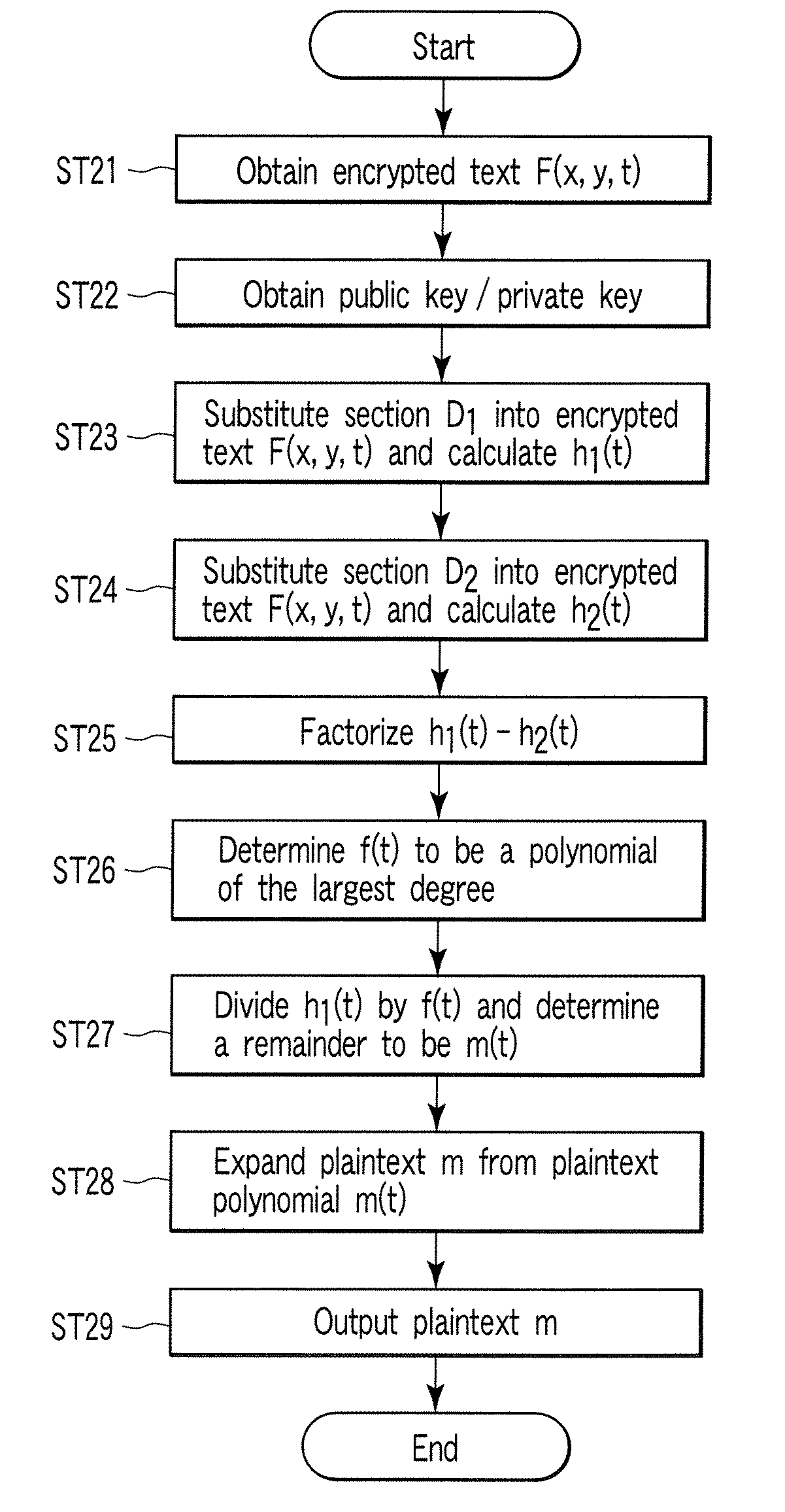
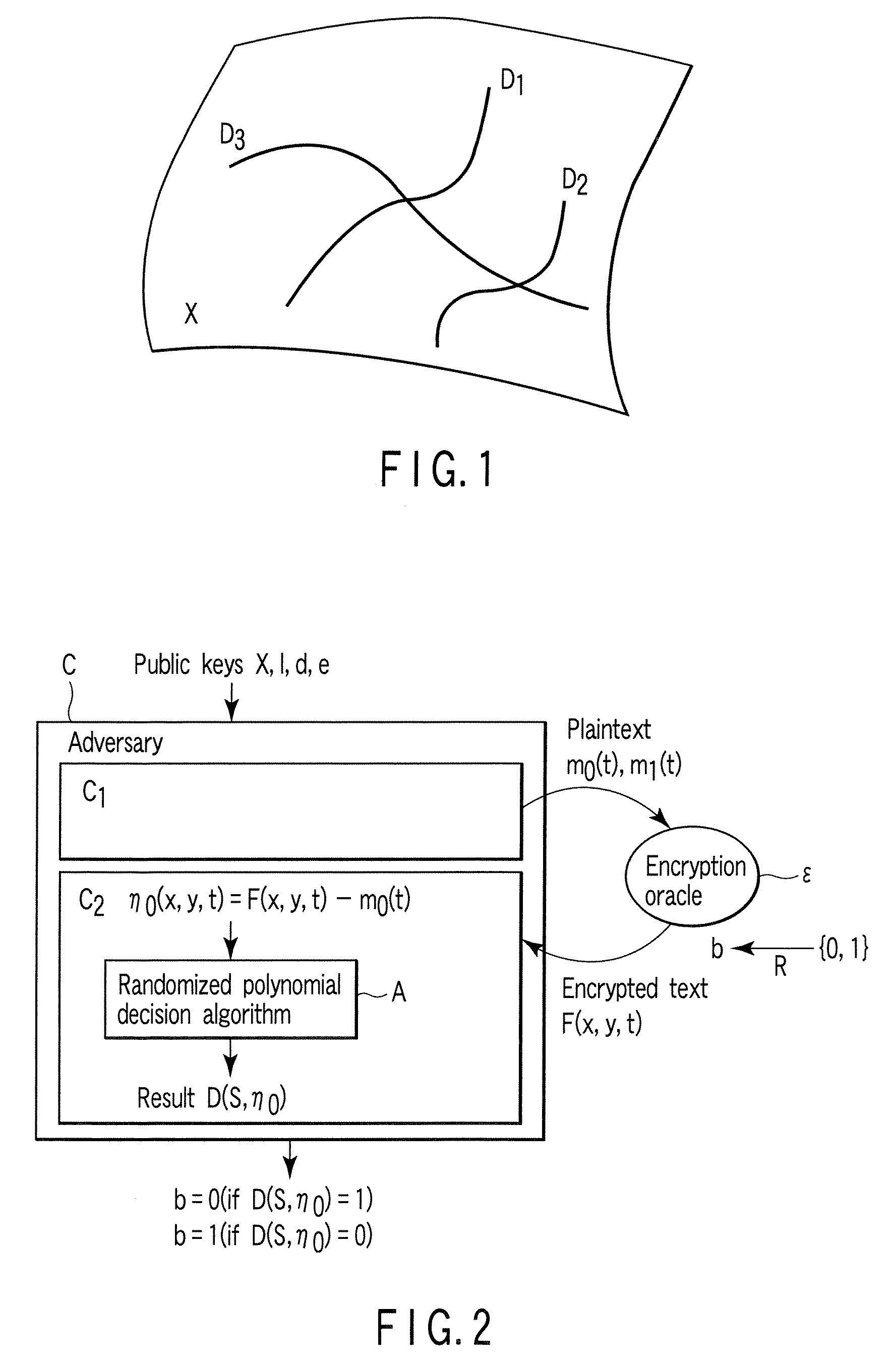
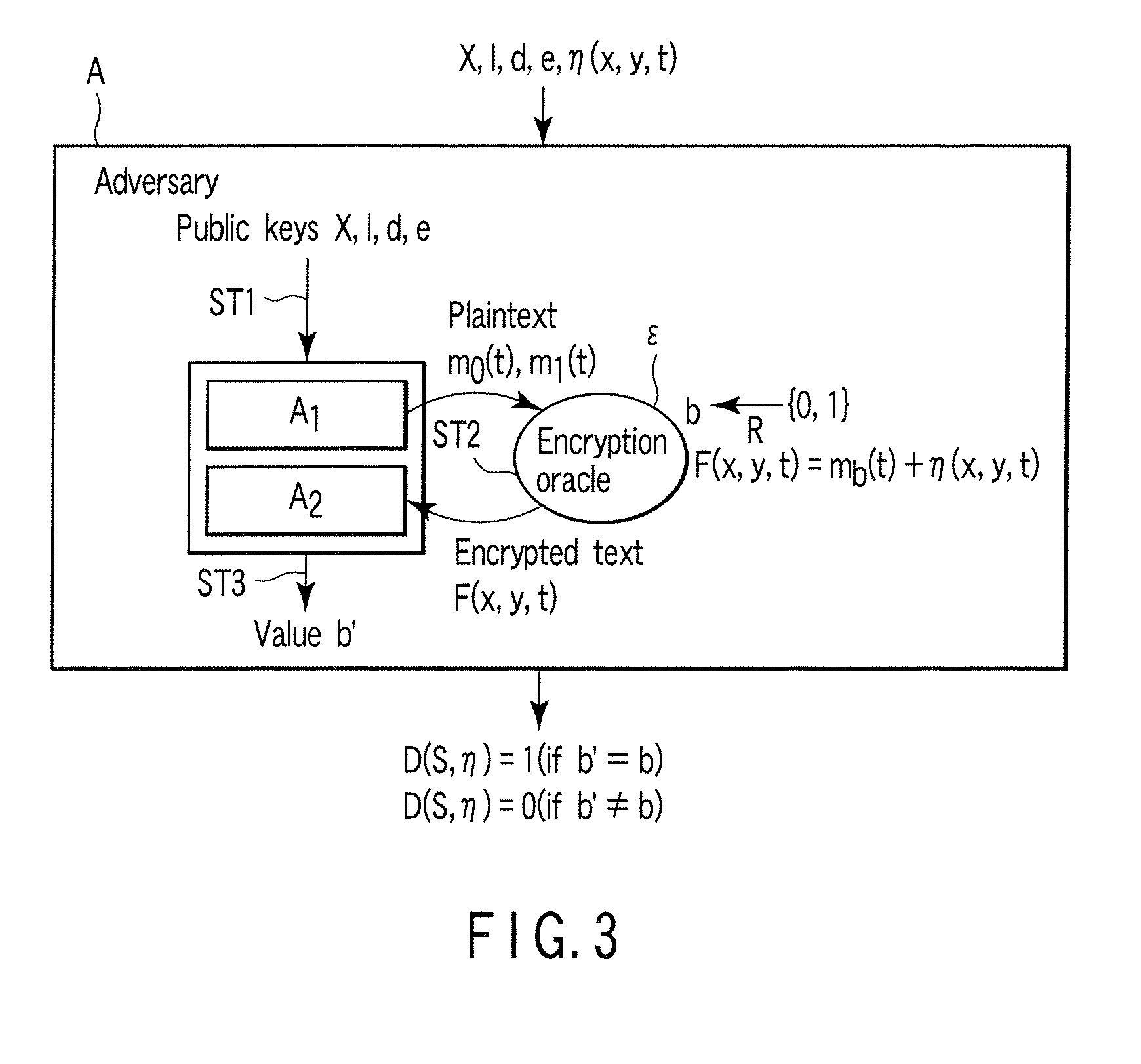
A method whereby an encryption apparatus encrypts a message on the basis of a fibration X(x, y, t) serving as a public key when private keys are two or more sections corresponding to fibration X(x, y, t)=0 of an algebraic surface X, the method comprises embedding plaintext M obtained by concatenating the message to a random number as the coefficients of plaintext polynomial M(t) of degree l−1 or less, and generating encrypted text F=Epk(M, p, q, f, X) from the plaintext polynomial M(t) by an encrypting process of performing operations including at least one of addition, subtraction, and multiplication of random polynomials p(x, y, t), q(x, y, t), a random irreducible polynomial f(t) of degree l or more, and the fibration X(x, y, t) with respect to the plaintext polynomial M(t).
Owner:KK TOSHIBA
Elliptic polynomial cryptography with multi y-coordinates embedding
InactiveUS7483534B2Increase the number ofData augmentationPublic key for secure communicationDigital data processing detailsComputation complexityCountermeasure
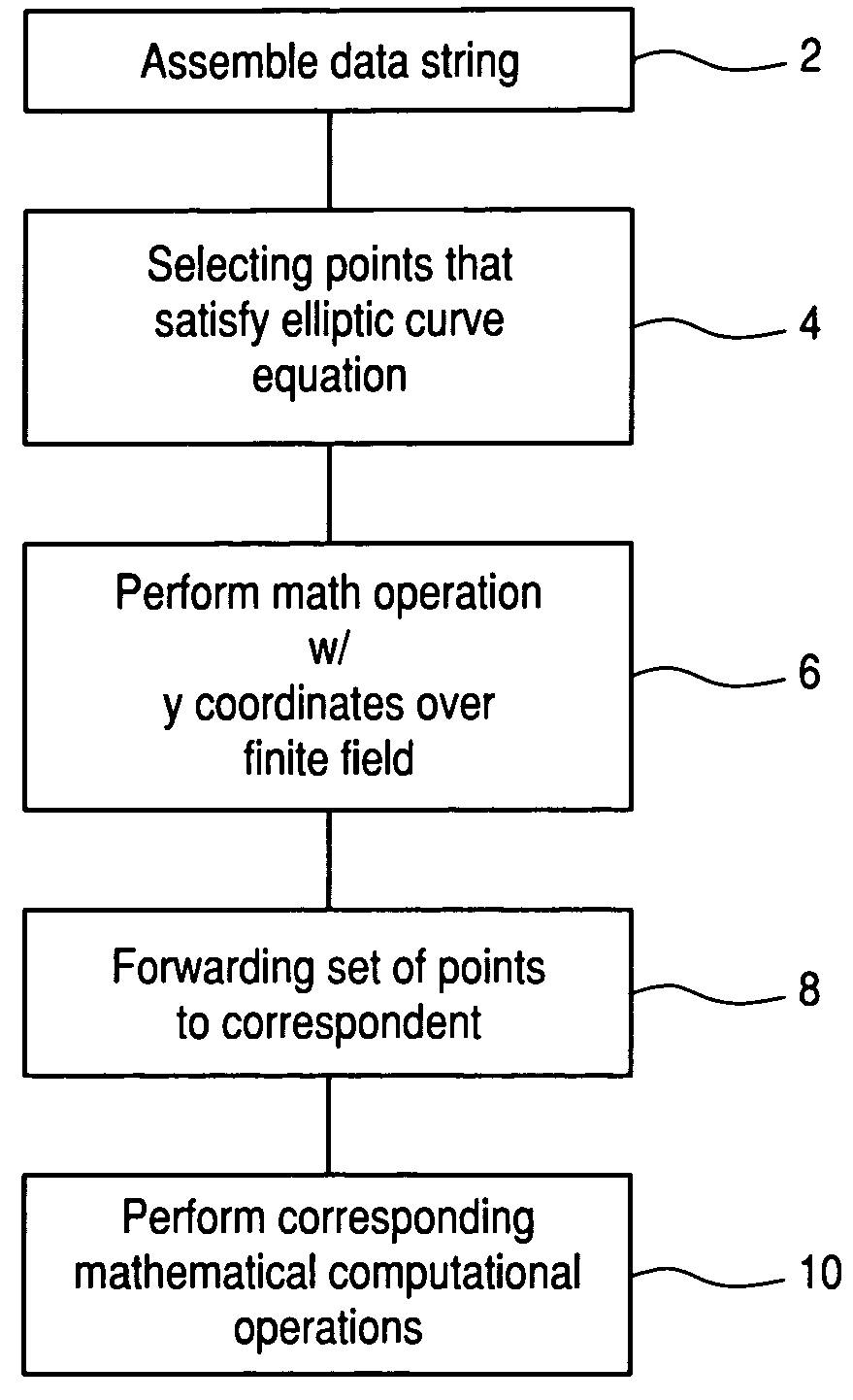
Given a set of elliptic points that satisfy an elliptic polynomial equation defined over a finite field, F, which requires N-bits to represent its elements, a new method of cryptographic encryption and decryption is presented which uses more than one quadratic variable that are termed y-coordinates to obtain an elliptic polynomial equation with multi y-coordinates instead of one y-coordinate. The additional y-coordinates are used to embed extra message data bits. A ny-fold increase in the number of embedded message data bits in a single elliptic point can be achieved with the improved method when using ny additional y-coordinates. The reason is that the number of points that satisfy an elliptic polynomial equation defined over F(p) and which can be used in the corresponding cryptosystem is increased by a factor of (#F)ny, where # denotes the size of a field. The use of the additional y-coordinates can be used to reduce computational complexity. Alternatively, this can be used to increase security by making the bit positions where data bits are embedded known only to the sender and receiver. Also, it can be used as a countermeasure by randomizing the bit positions where data bits are embedded.
Owner:KING FAHD UNIVERSITY OF PETROLEUM AND MINERALS
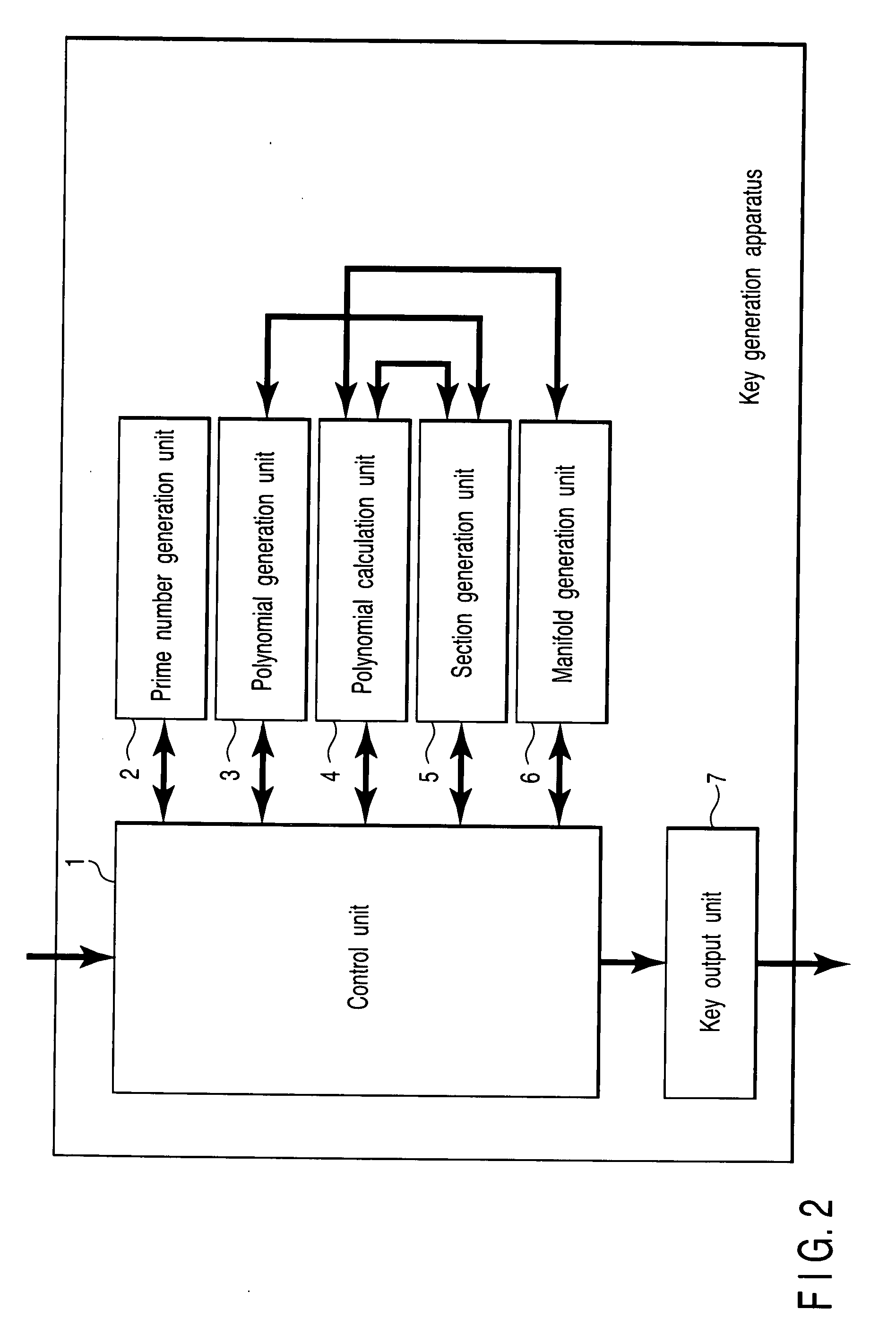
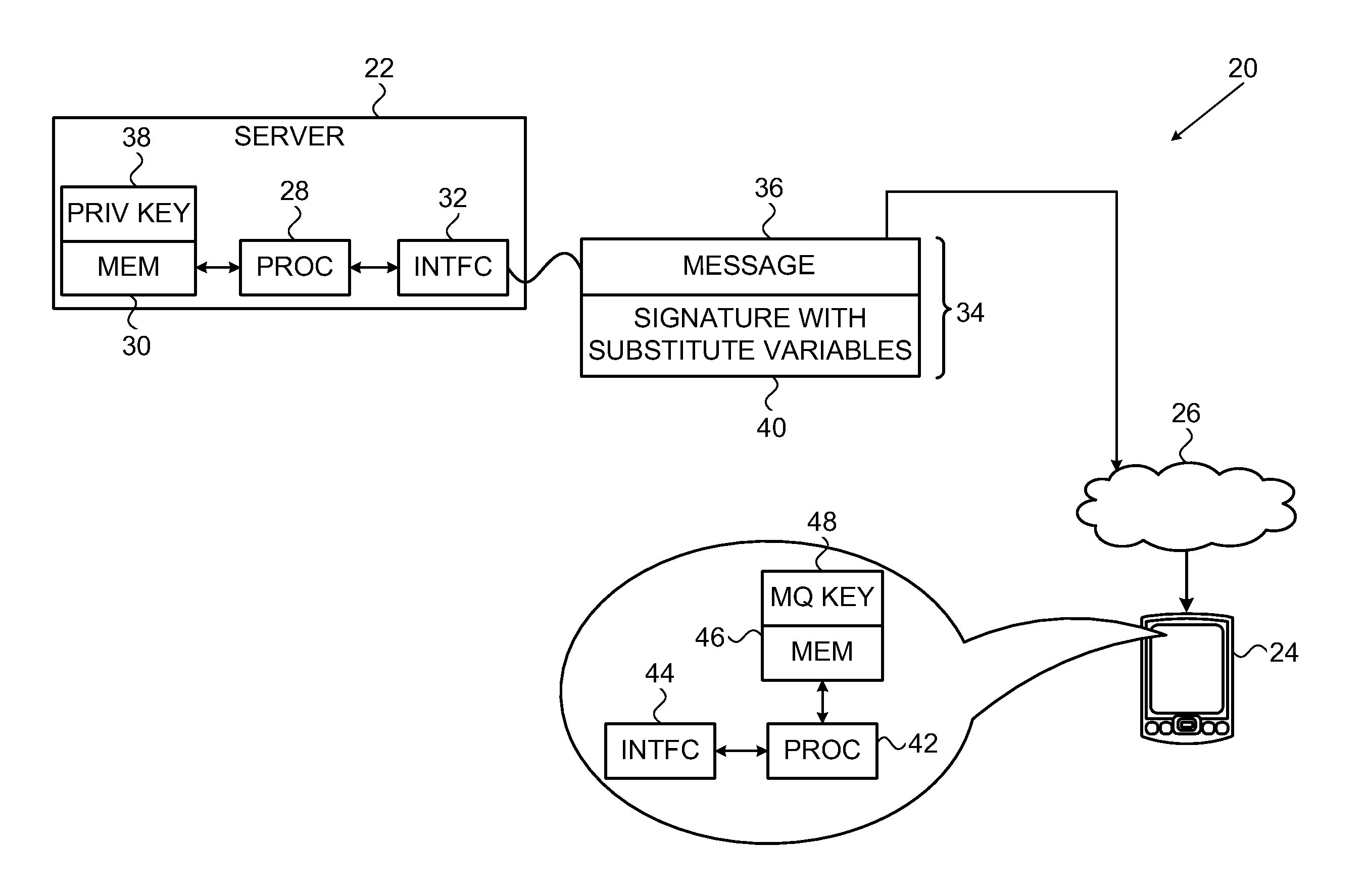
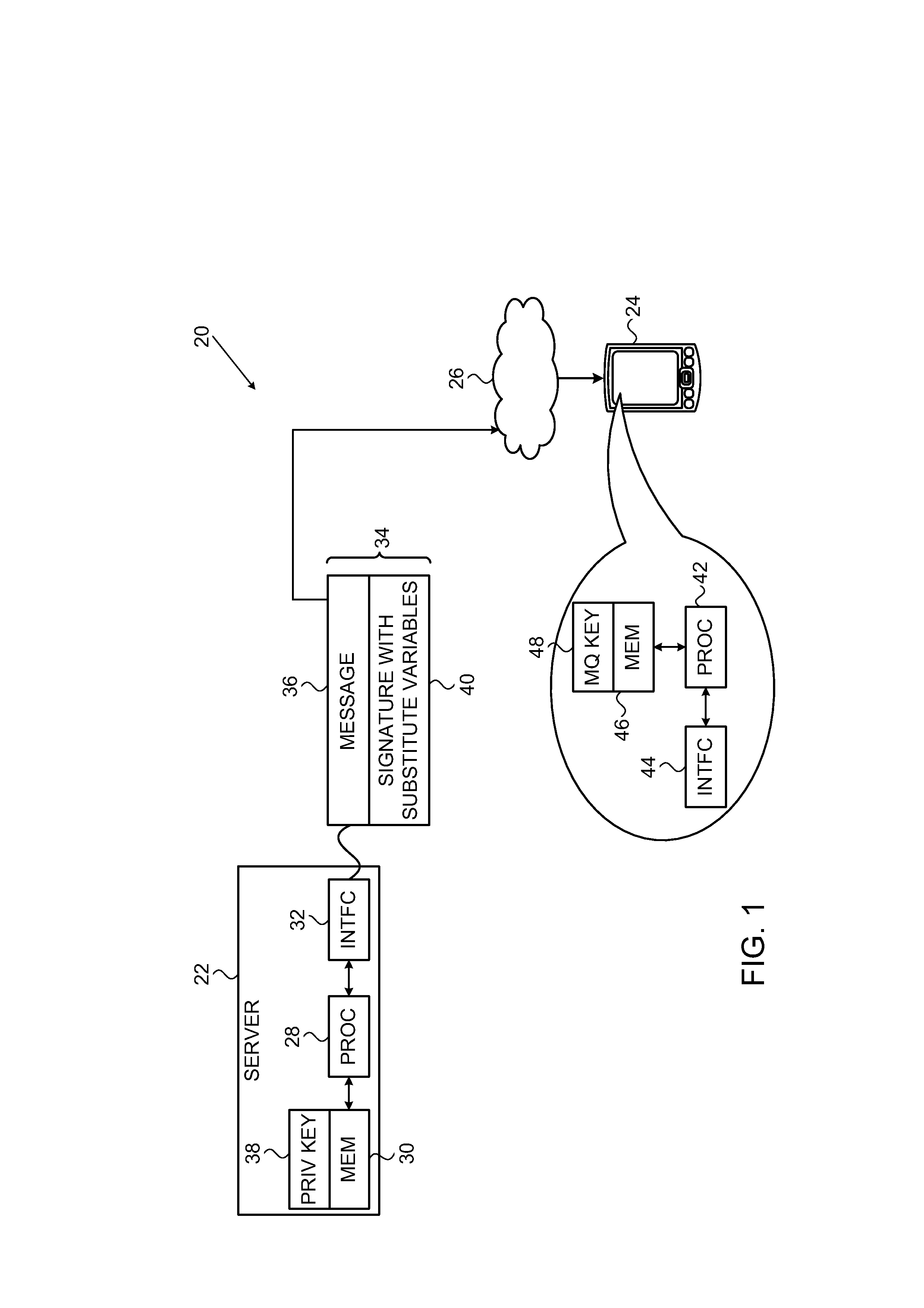
Digital signature generation apparatus, digital signature verification apparatus, and key generation apparatus
InactiveUS20080037776A1Public key for secure communicationUser identity/authority verificationDigital signatureTheoretical computer science
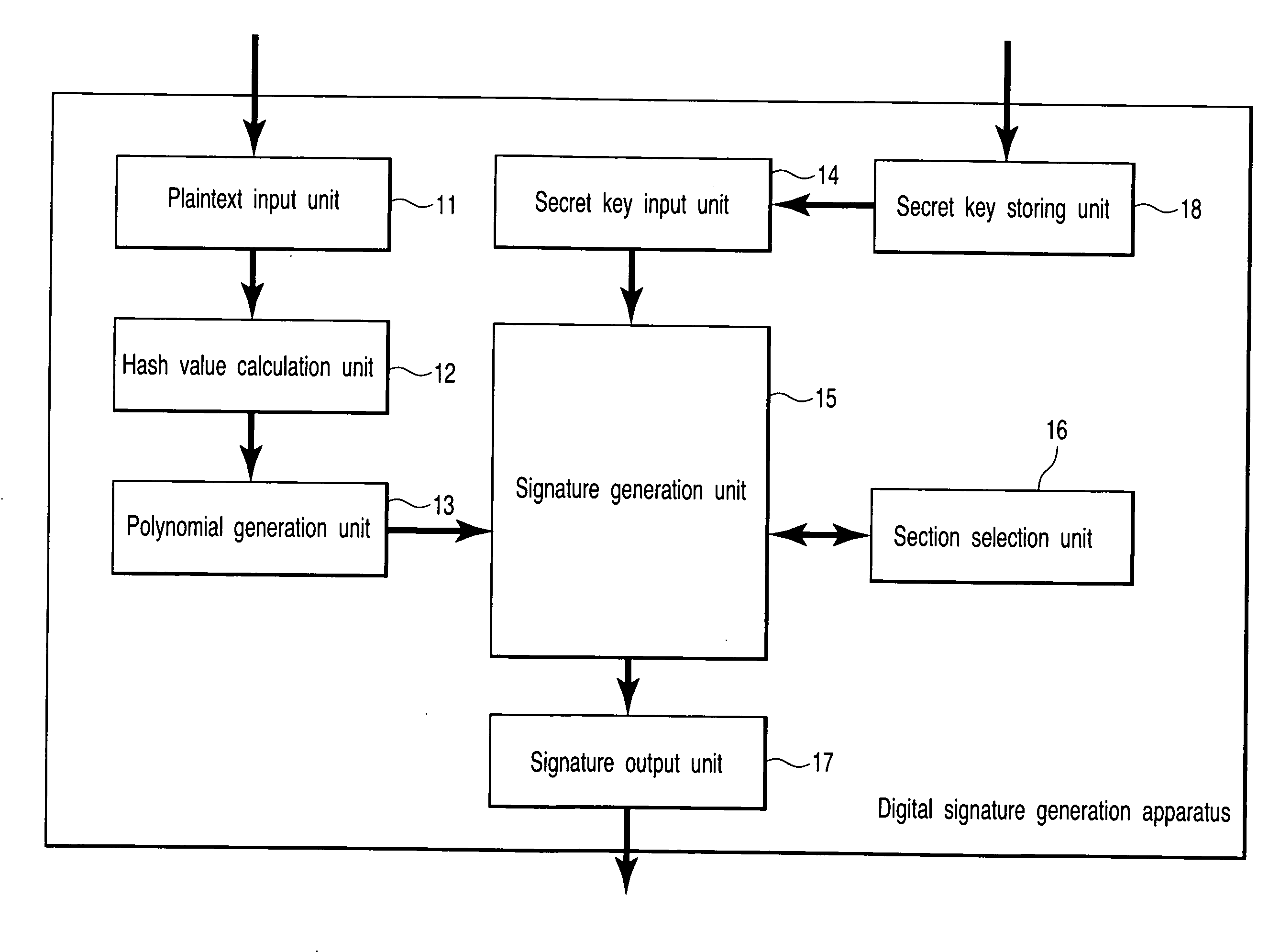
A digital signature generation apparatus includes memory to store finite field Fq and section D(ux(s, t), uy(s, t), s, t) as secret key, section being one of surfaces of three-dimensional manifold A(x, y, s, t) which is expressed by x-coordinate, y-coordinate, parameter s, and parameter t and is defined on finite field Fq, x-coordinate and y-coordinate of section being expressed by functions of parameter s and parameter t, calculates hash value of message m, generates hash value polynomial by embedding hash value in 1-variable polynomial h(t) defined on finite field Fq, and generates digital signature Ds(Ux(t), Uy(t), t) which is curve on section, the x-coordinate and y-coordinate of curve being expressed by functions of parameter t, by substituting hash value polynomial in parameter s of section.
Owner:KK TOSHIBA
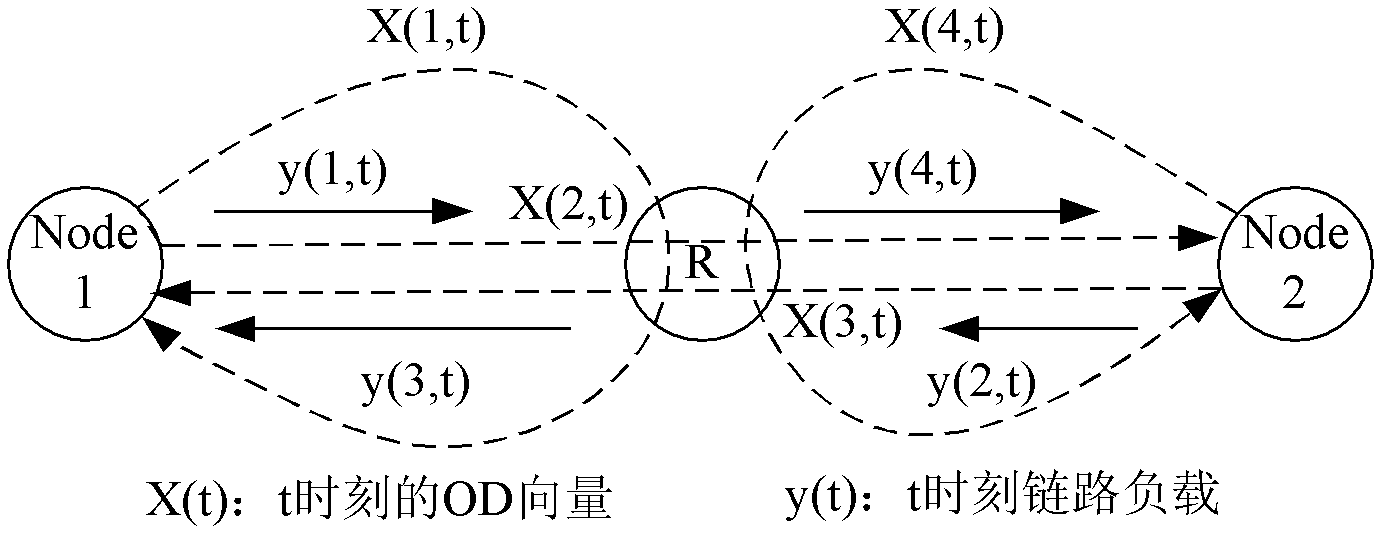
Network flow estimating method
InactiveCN102325090AConform to the real characteristicsHigh precisionData switching networksComputation complexityNormal density
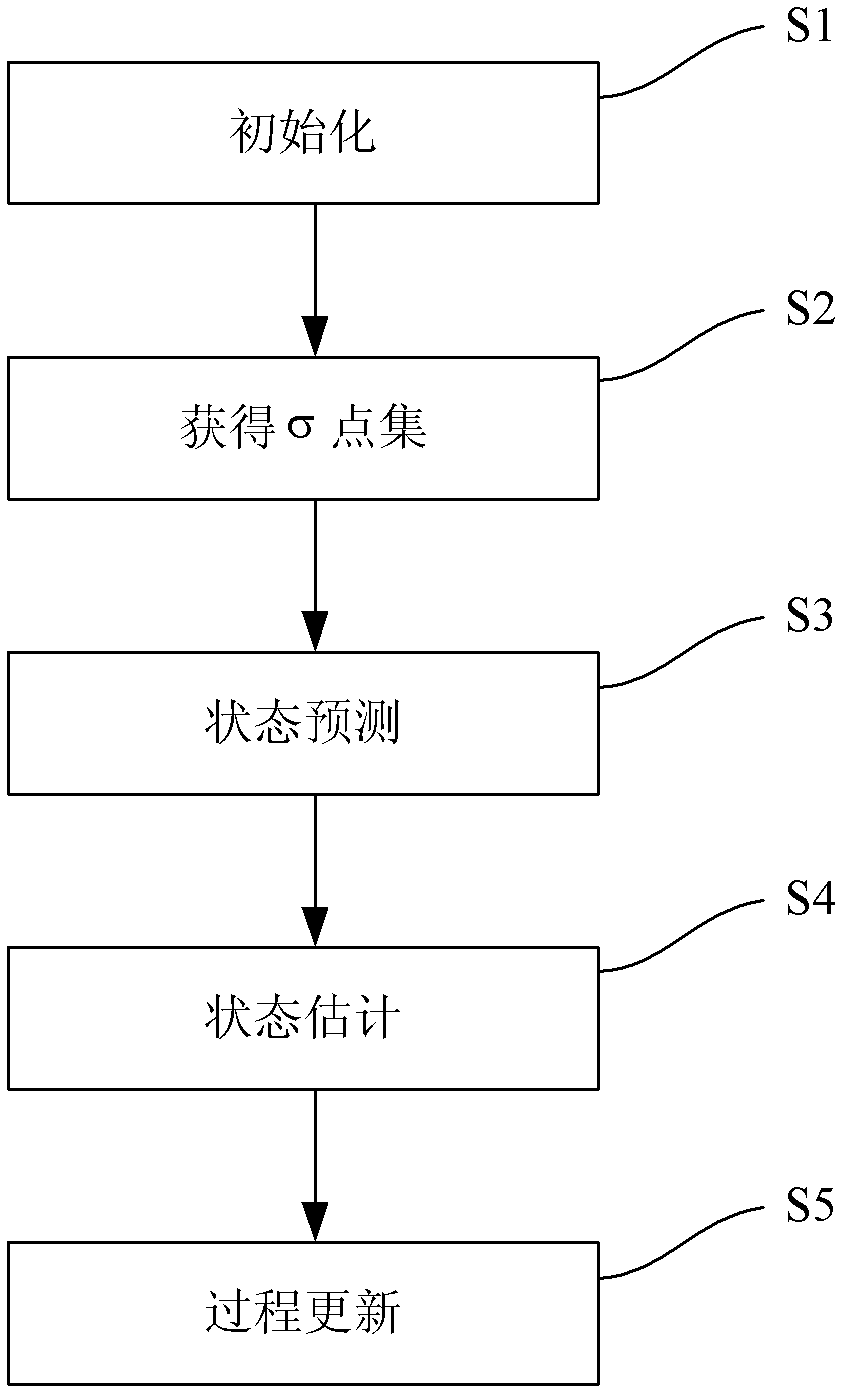
The invention discloses a network flow estimating method which concretely comprises the steps of initializing, obtaining a sigma point set, predicting the state, estimating the state and updating the process. In the method, the flow matrix estimating problem is modeled into a nonlinear system which more meets the OD (Origin-Destination) flow real characteristic; the sigma point set obtained by UT (Unscented Transformation) is subjected to nonlinear transformation; the coefficient of the system sate equation needed by nonlinear transformation is obtained concretely by Chebyshev polynomial fitting instead of approximately obtaining the system state equation by the traditional local linearization; accordingly, the state equation of the system does not need to meet the available linear function approximating condition; a symmetrical sampling policy is adopted for the UT; the particle point set approaches the probability density function distribution of a nonlinear function to obtain the higher-order approximation of state estimation, the result of OD flow estimation has higher precision, and the calculating complexity of the system is reduced.
Owner:四川智联科创科技有限公司
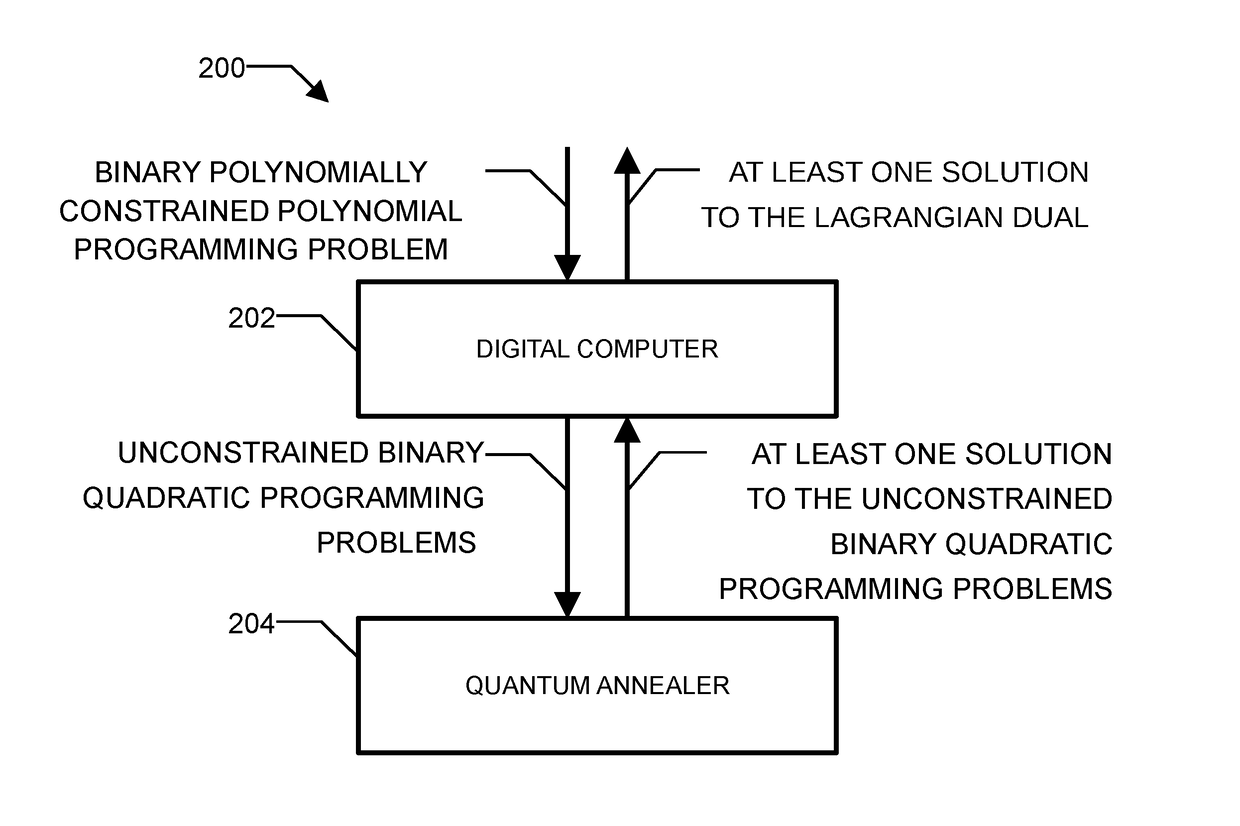
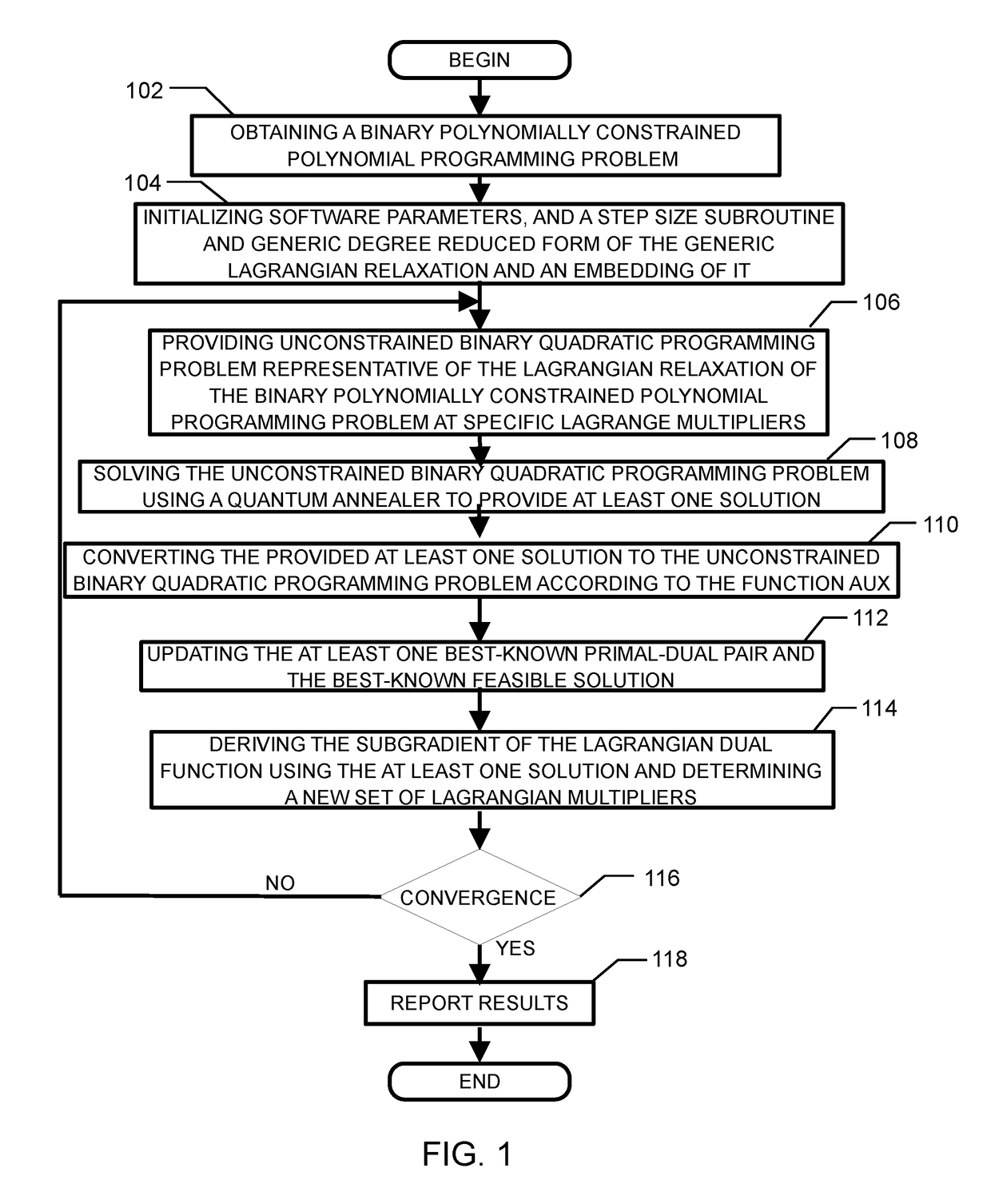
Method and system for solving the lagrangian dual of a binary polynomially constrained polynomial programming problem using a quantum annealer
InactiveUS20170242824A1Less sensitive to errorSpeed up the processQuantum computersComplex mathematical operationsPolynomial programmingPosynomial
A method for solving the Lagrangian dual of a binary polynomially constrained polynomial programming problem comprises obtaining a binary polynomially constrained polynomial programming problem; until a convergence is detected, iteratively, providing a set of Lagrange multipliers, providing an unconstrained binary quadratic programming problem representative of the Lagrangian relaxation of the binary polynomially constrained polynomial programming problem at these Lagrange multipliers, providing the unconstrained binary quadratic programming problem to a quantum annealer, obtaining from the quantum annealer at least one corresponding solution, using the at least one corresponding solution to generate a new set of Lagrange multipliers; and providing all corresponding best-known primal-dual pairs and best-known feasible solutions after convergence.
Owner:1QB INFORMATION TECHNOLOGIES INC
Cryptographic hash functions using elliptic polynomial cryptography
InactiveUS20100166175A1Readily apparentUser identity/authority verificationDigital computer detailsComputer hardwareCryptographic hash function
The cryptographic hash functions using of elliptic polynomial polynomials are based on the elliptic polynomial discrete logarithm problem, which is well known as a computationally hard problem. The hash functions are based on the elliptic polynomial equation in their generation, where different elliptic polynomials are used for different blocks of the same plain text. Particularly, the hash functions use an elliptic polynomial with more than one independent x-coordinate. More specifically, a set of elliptic polynomial points are used that satisfy an elliptic polynomial equation with more than one independent x-coordinate which is defined over a finite field F.
Owner:KING FAHD UNIVERSITY OF PETROLEUM AND MINERALS
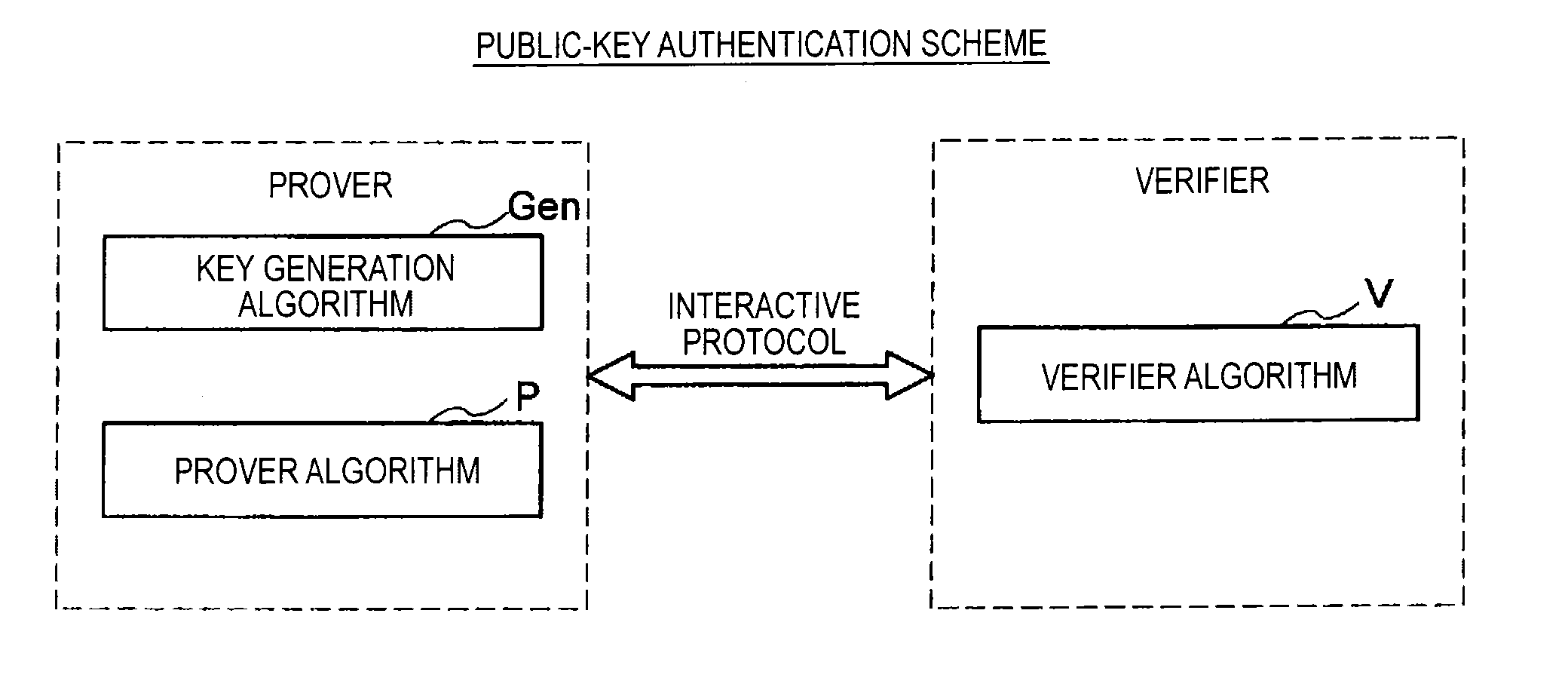
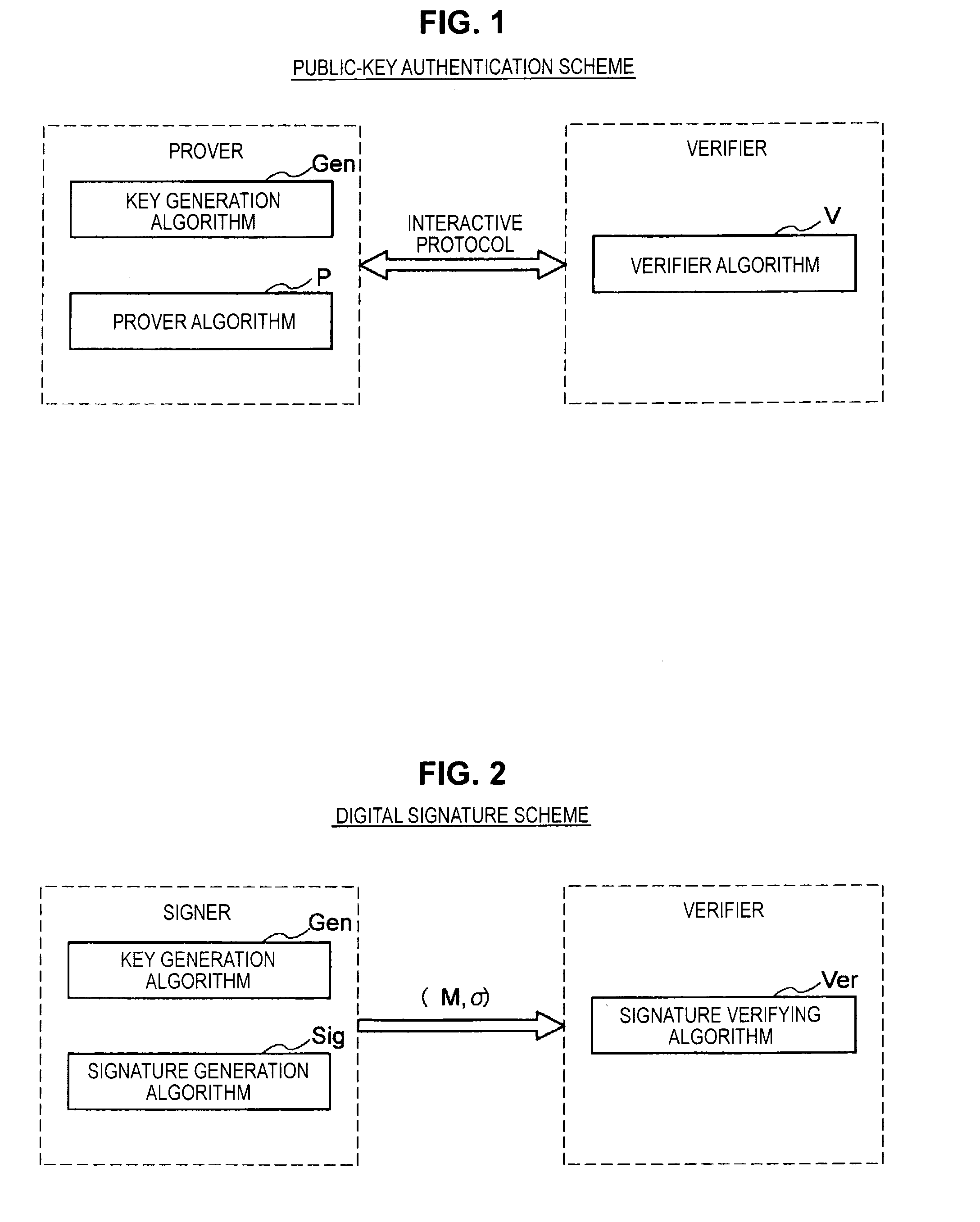
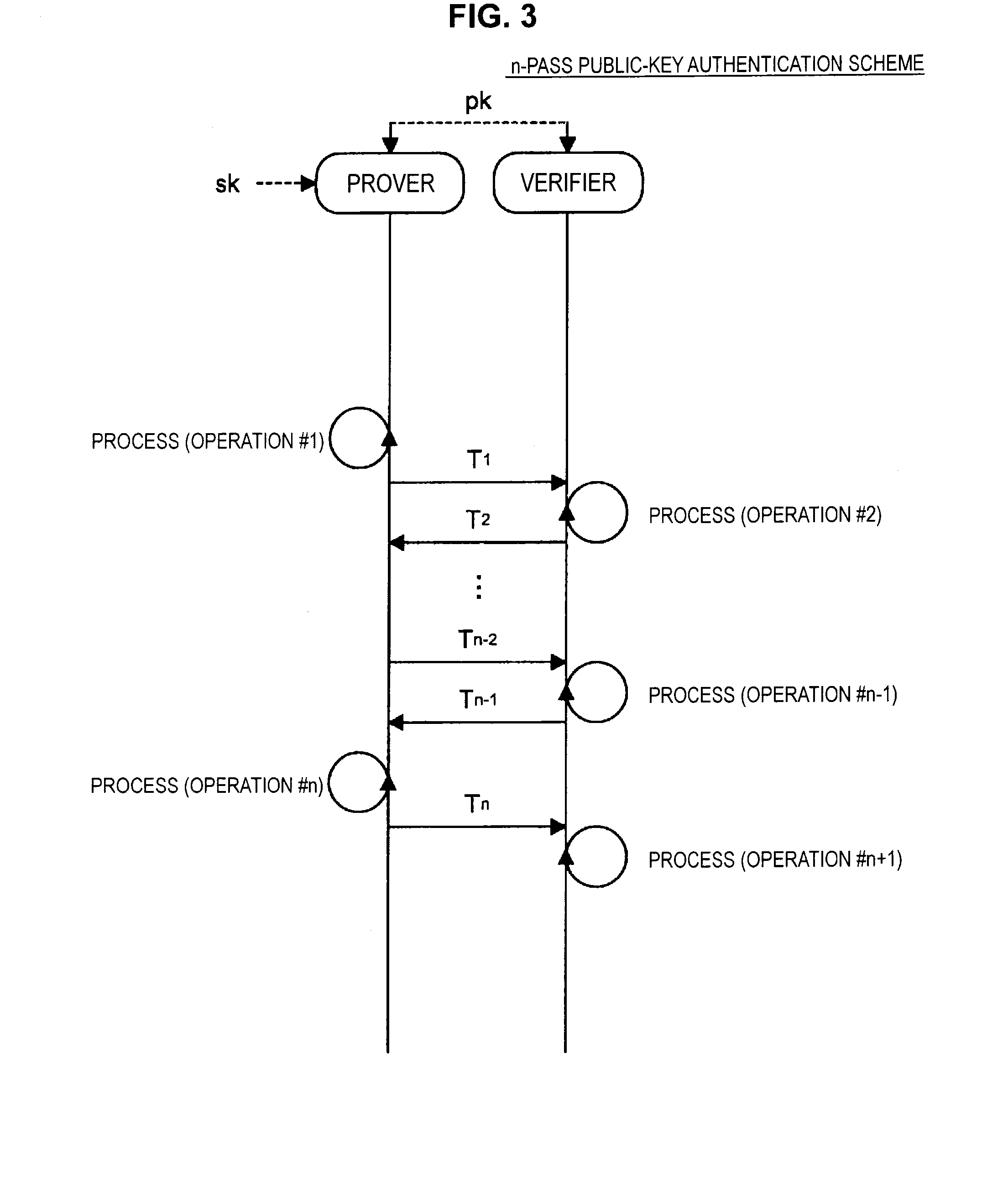
Information processing apparatus, information processing method, and program
ActiveUS20140215222A1Efficient replacementPublic key for secure communicationUser identity/authority verificationInformation processingPublic key authentication
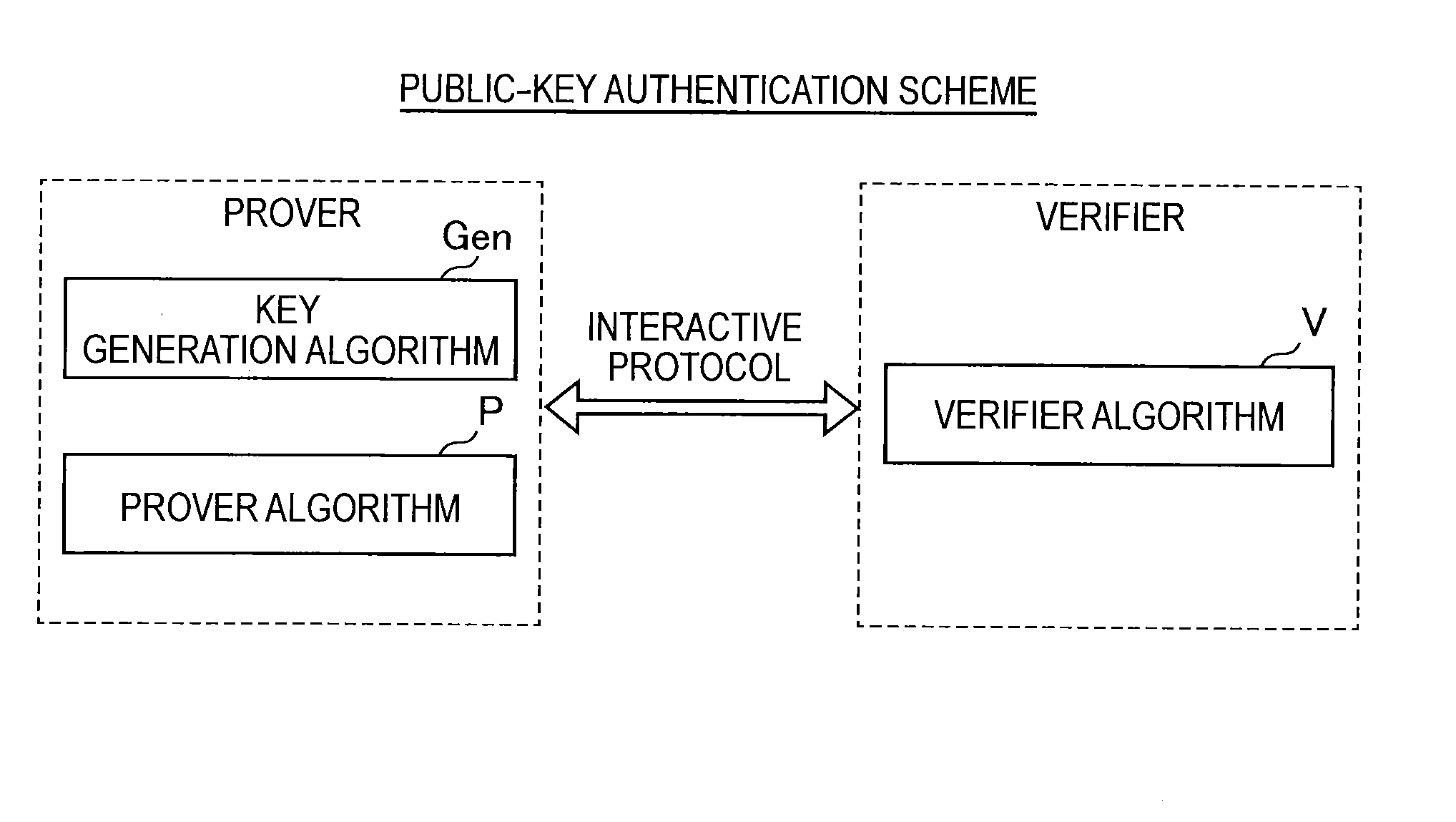
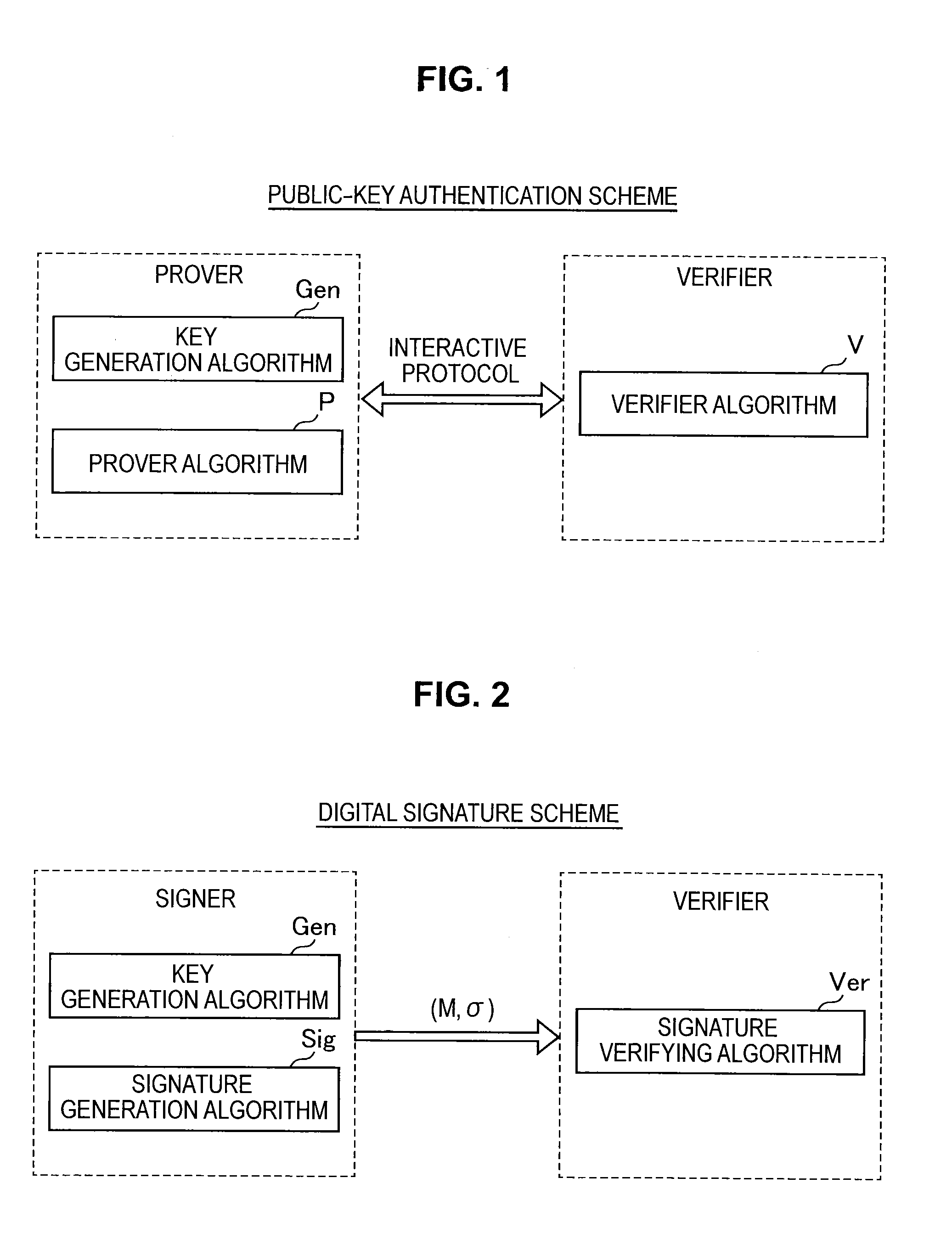
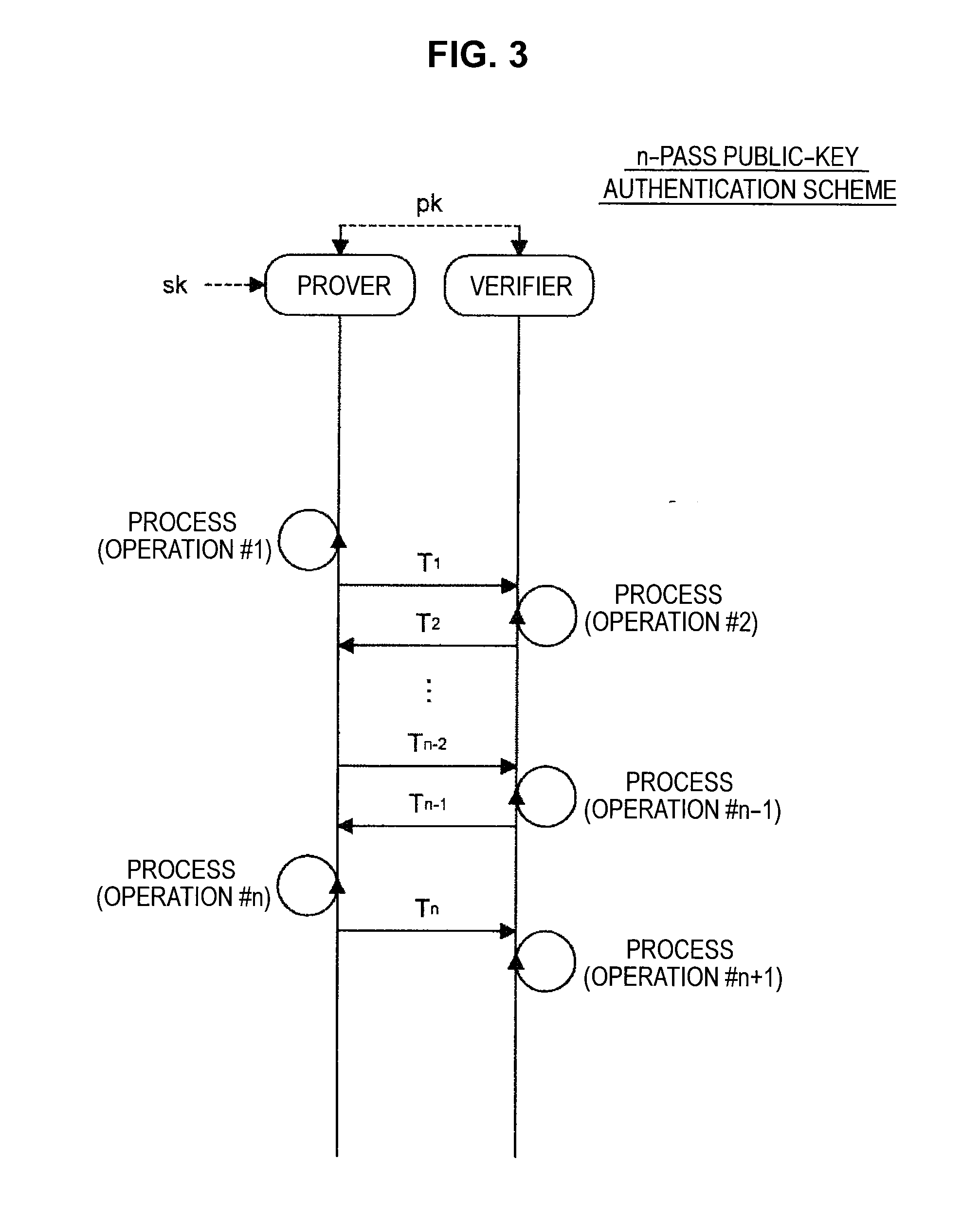
Provided an information processing apparatus including a number generation unit configured to generate numbers used in coefficients of terms included in a pair of multi-order multivariate polynomials F=(f1, . . . , fm), using a predetermined function, from information shared between entities executing an algorithm of a public-key authentication scheme or a digital signature scheme that uses a public key including the pair of multi-order multivariate polynomials F, and an allocation unit configured to allocate the numbers generated by the number generation unit to the coefficients of the multi-order multivariate polynomials for which the pair of multi-order multivariate polynomials F are included in constituent elements.
Owner:SONY CORP
Elliptical polynomial-based message authentication code
InactiveUS20100166176A1Readily apparentEncryption apparatus with shift registers/memoriesUser identity/authority verificationComputer hardwareHash-based message authentication code
The elliptic-polynomial based Message Authentication Code (MAC) provides MAC generation methods based on the elliptic polynomial discrete logarithm problem. It is well known that an elliptic polynomial discrete logarithm problem is a computationally “difficult” or “hard” problem. The methods use both an elliptic polynomial polynomial and its twist, even if the polynomial and its twist are not isomorphic. Since both the polynomial and its twist are used, multiple x- and y-coordinates can be used to embed bit strings into a point that satisfies the elliptic polynomial, and the embedding process is non-iterative, so that the time required to embed the bit string is independent of the bit string content.
Owner:KING FAHD UNIVERSITY OF PETROLEUM AND MINERALS
Integer ciphertext arithmetic operation method based on homomorphic encryption
ActiveCN109412786AImprove algorithm efficiencyReduce frequencyCommunication with homomorphic encryptionAlgorithmNoise reduction
The invention provides an integer ciphertext arithmetic operation method based on homomorphic encryption, which comprises complement homomorphic calculation, addition subtraction homomorphic calculation, multiplication homomorphic calculation and division homomorphic calculation. This invention refers to the rules of complement, addition, subtraction, multiplication and division of binary integersin computer, and transforms this rule into Boolean polynomials containing only logical AND and XOR operations. In multiplication and division, different calculations are made according to the information of special bits to correct the final calculation results. So we modify the form of Boolean polynomials to represent different computational results, that is, Boolean polynomials include all the inputs and mutually exclusive computational branches of this layer. Then Boolean polynomials are transformed into homomorphic polynomials which can be used in ciphertext computation, and the security of homomorphic polynomials is proved, which meets the requirement of semantic security. The multi-bit parallel operation of integer homomorphic arithmetic operation is realized, the algorithm efficiency of homomorphic operation is improved, the frequency of noise reduction operation is reduced, and the operation efficiency is improved.
Owner:SHENYANG AEROSPACE UNIVERSITY
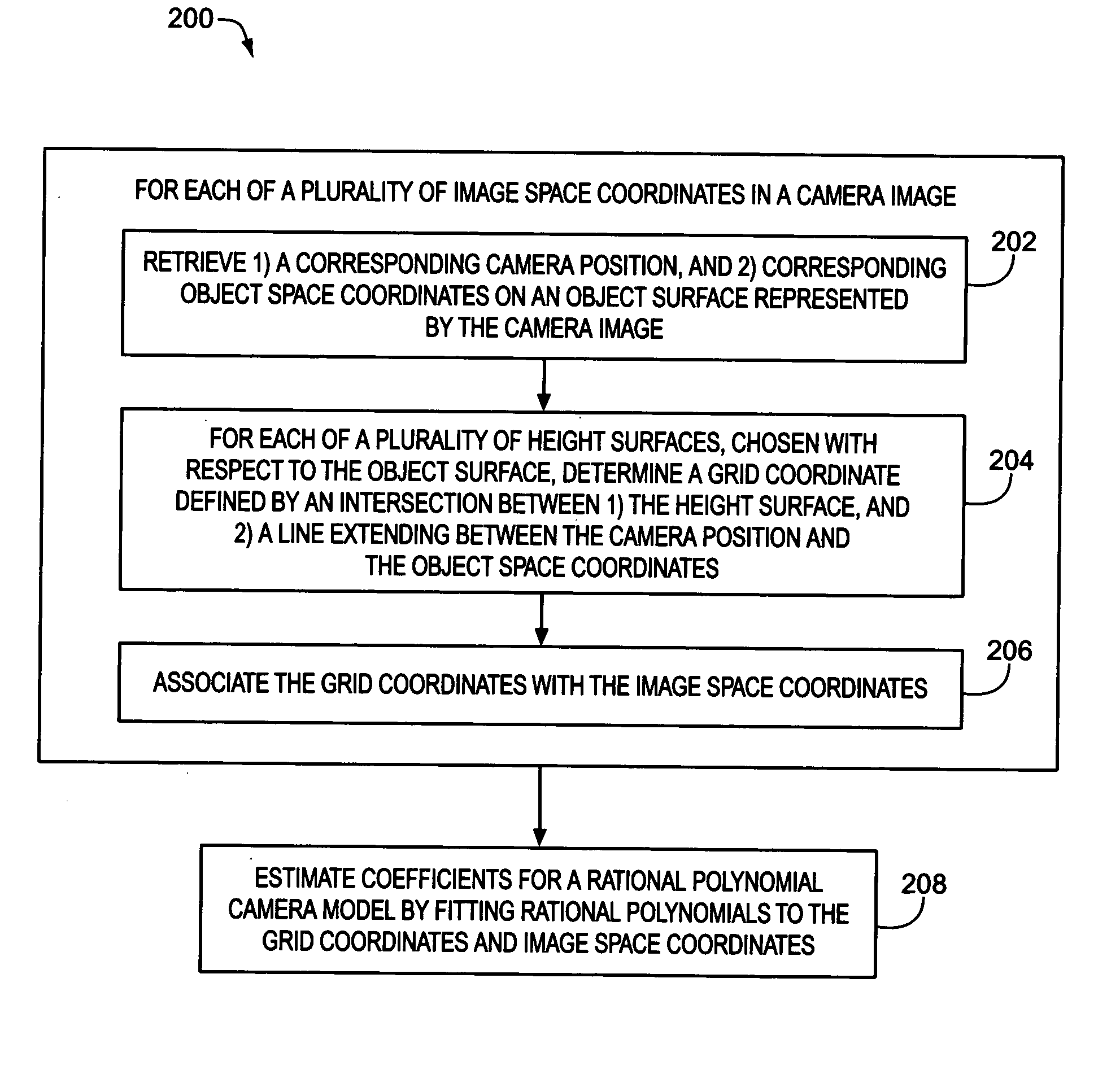
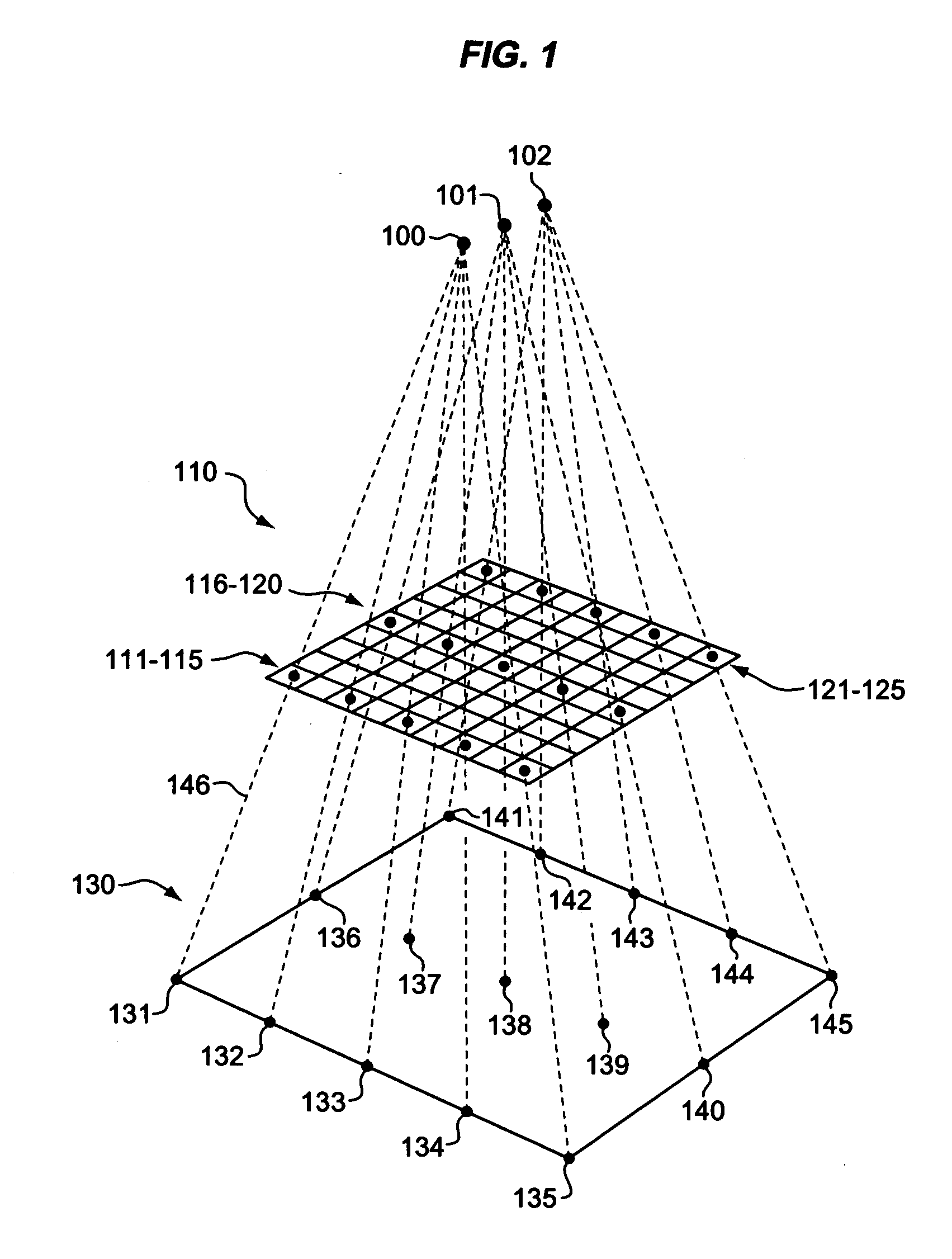
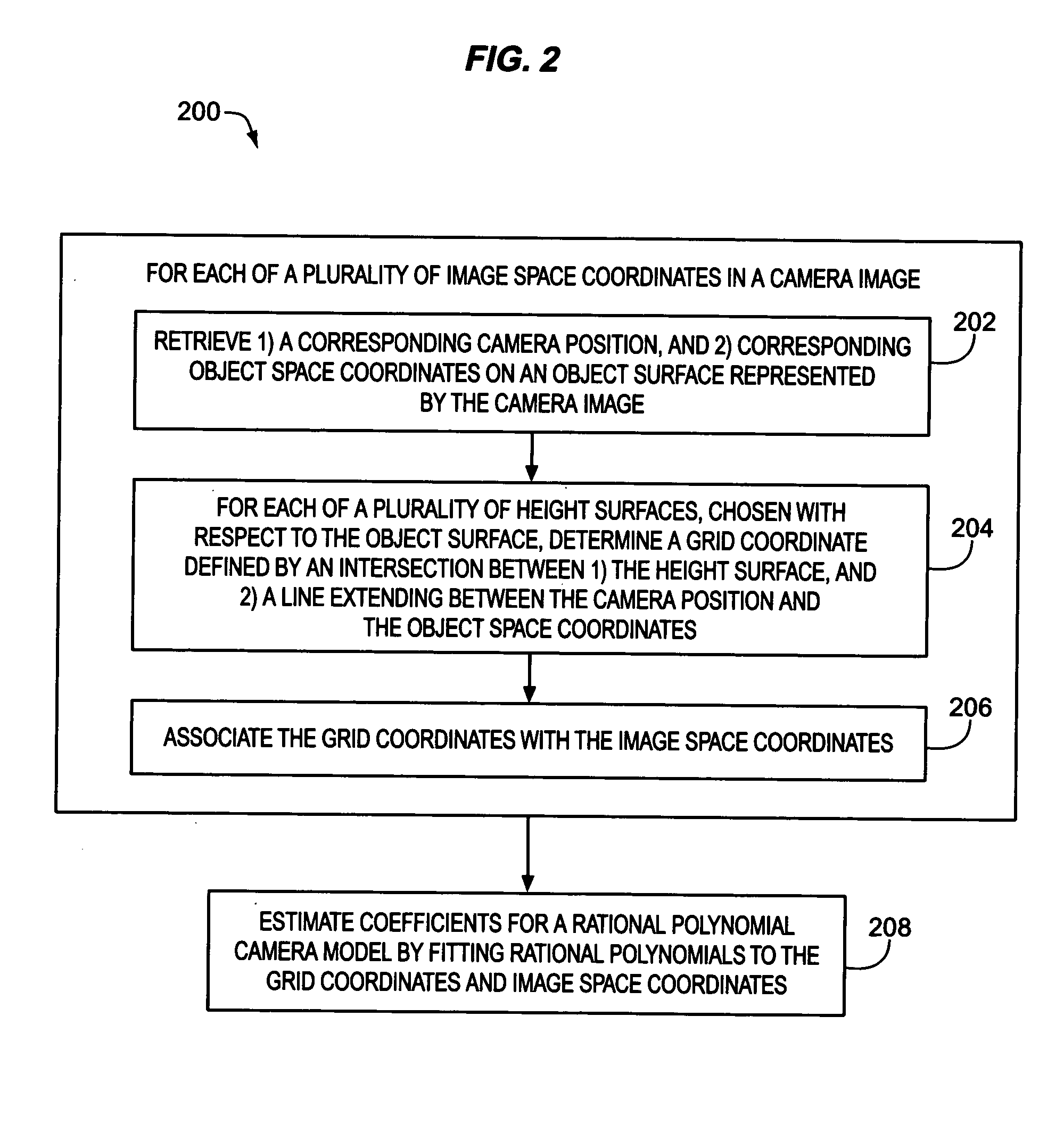
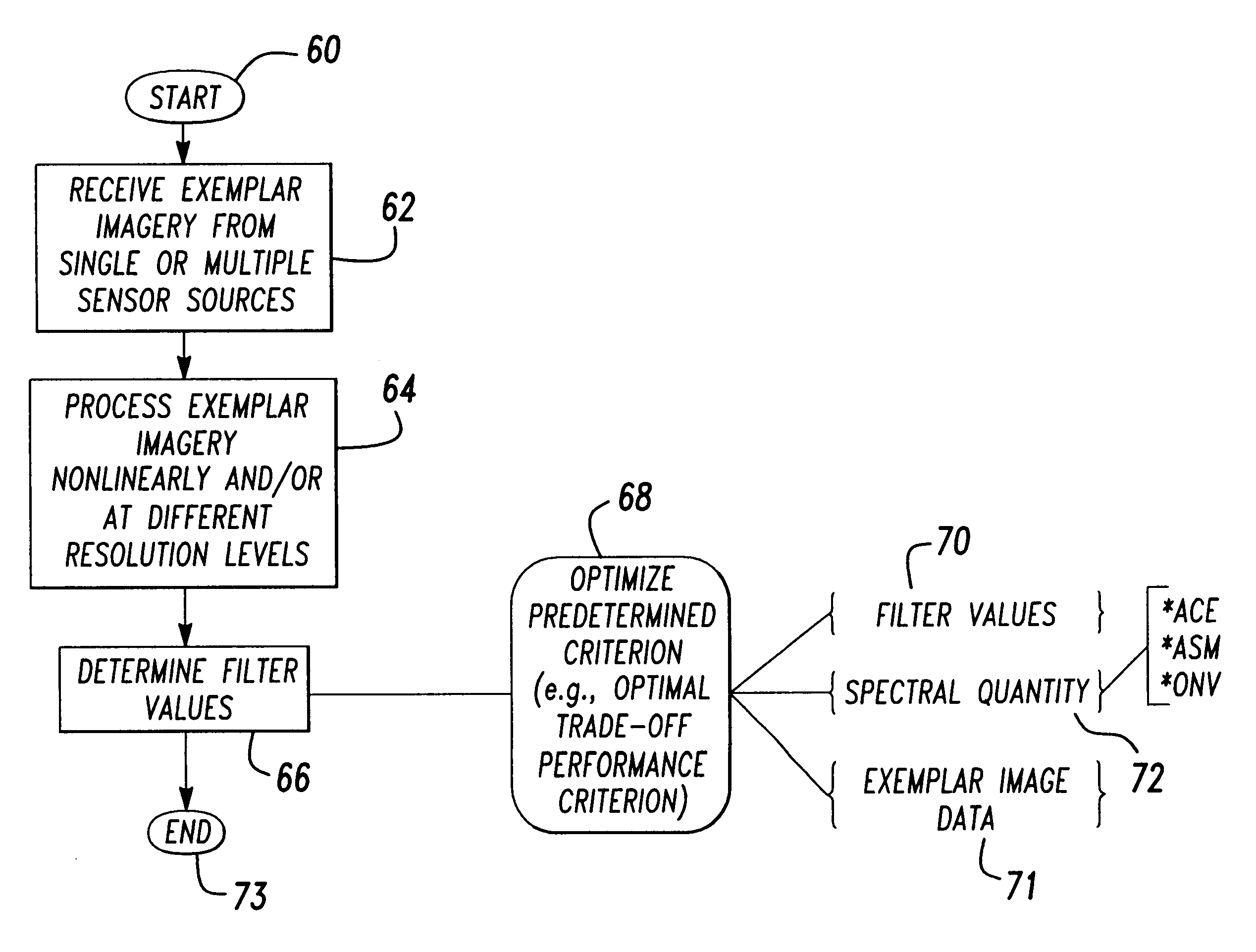
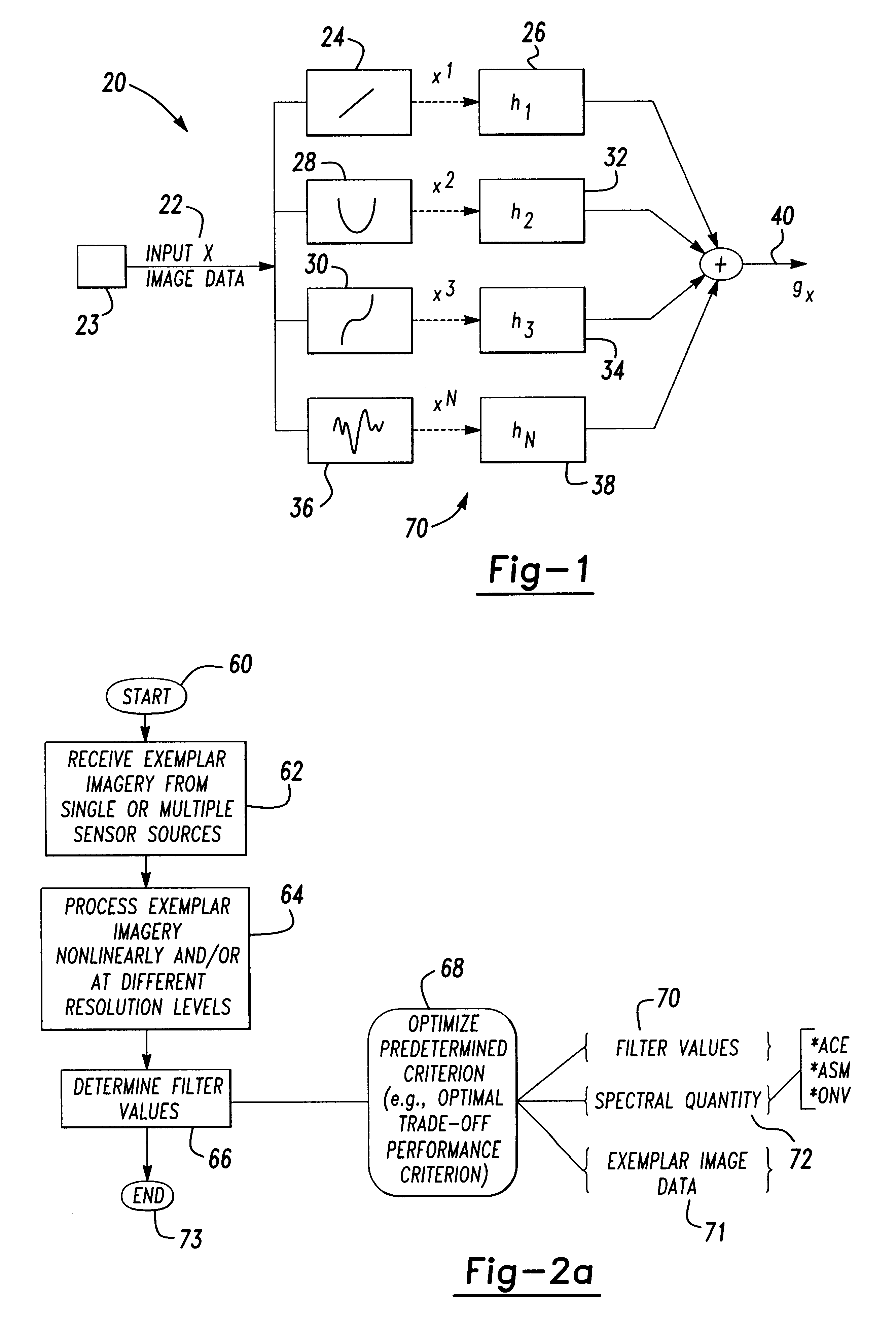
Estimation of coefficients for a rational polynomial camera model
One aspect of the invention is embodied in a number of machine-readable media having stored thereon sequences of instructions which, when executed by a machine, cause the machine to perform a number of actions. The actions include, for each of a plurality of image space coordinates of a camera image, retrieving 1) a corresponding camera position, and 2) corresponding object space coordinates on an object surface that is represented by the camera image. Then, for each of a plurality of height surfaces (chosen with respect to the object surface), a grid coordinate defined by an intersection between the height surface, and a line extending between the camera position and the object space coordinates, is determined. The determined grid coordinates are then associated with their corresponding image space coordinates. Finally, coefficients for a rational polynomial camera model are estimated by fitting rational polynomials to at least the grid coordinates and image space coordinates.
Owner:MAXAR INTELLIGENCE INC
Method and apparatus for efficiently implementing the advanced encryption standard
InactiveUS20090172068A1Instruction analysisComputer security arrangementsS-boxComputer graphics (images)
Implementations of Advanced Encryption Standard (AES) encryption and decryption processes are disclosed. In one embodiment of S-box processing, a block of 16 byte values is converted, each byte value being converted from a polynomial representation in GF(256) to a polynomial representation in GF((22)4). Multiplicative inverse polynomial representations in GF((22)4) are computed for each of the corresponding polynomial representations in GF((22)4). Finally corresponding multiplicative inverse polynomial representations in GF((22)4) are converted and an affine transformation is applied to generate corresponding polynomial representations in GF(256). In an alternative embodiment of S-box processing, powers of the polynomial representations are computed and multiplied together in GF(256) to generate multiplicative inverse polynomial representations in GF(256). In an embodiment of inverse-columns-mixing, the 16 byte values are converted from a polynomial representation in GF(256) to a polynomial representation in GF((24)2). A four-by-four matrix is applied to the transformed polynomial representation in GF((24)2) to implement the inverse-columns-mixing.
Owner:INTEL CORP
Encryption apparatus, decryption apparatus, and method
InactiveUS7773747B2Multiple keys/algorithms usagePublic key for secure communicationComputer hardwarePlaintext
A method whereby an encryption apparatus encrypts a message on the basis of a fibration X(x, y, t) serving as a public key when private keys are two or more sections corresponding to fibration X(x, y, t)=0 of an algebraic surface X, the method comprises embedding plaintext M obtained by concatenating the message to a random number as the coefficients of plaintext polynomial M(t) of degree l−1 or less, and generating encrypted text F=Epk(M, p, q, f, X) from the plaintext polynomial M(t) by an encrypting process of performing operations including at least one of addition, subtraction, and multiplication of random polynomials p(x, y, t), q(x, y, t), a random irreducible polynomial f(t) of degree l or more, and the fibration X(x, y, t) with respect to the plaintext polynomial M(t).
Owner:KK TOSHIBA
Key sharing device and system for configuration thereof
ActiveUS20160254909A1Simple methodKey distribution for secure communicationPublic key for secure communicationKey sizePosynomial
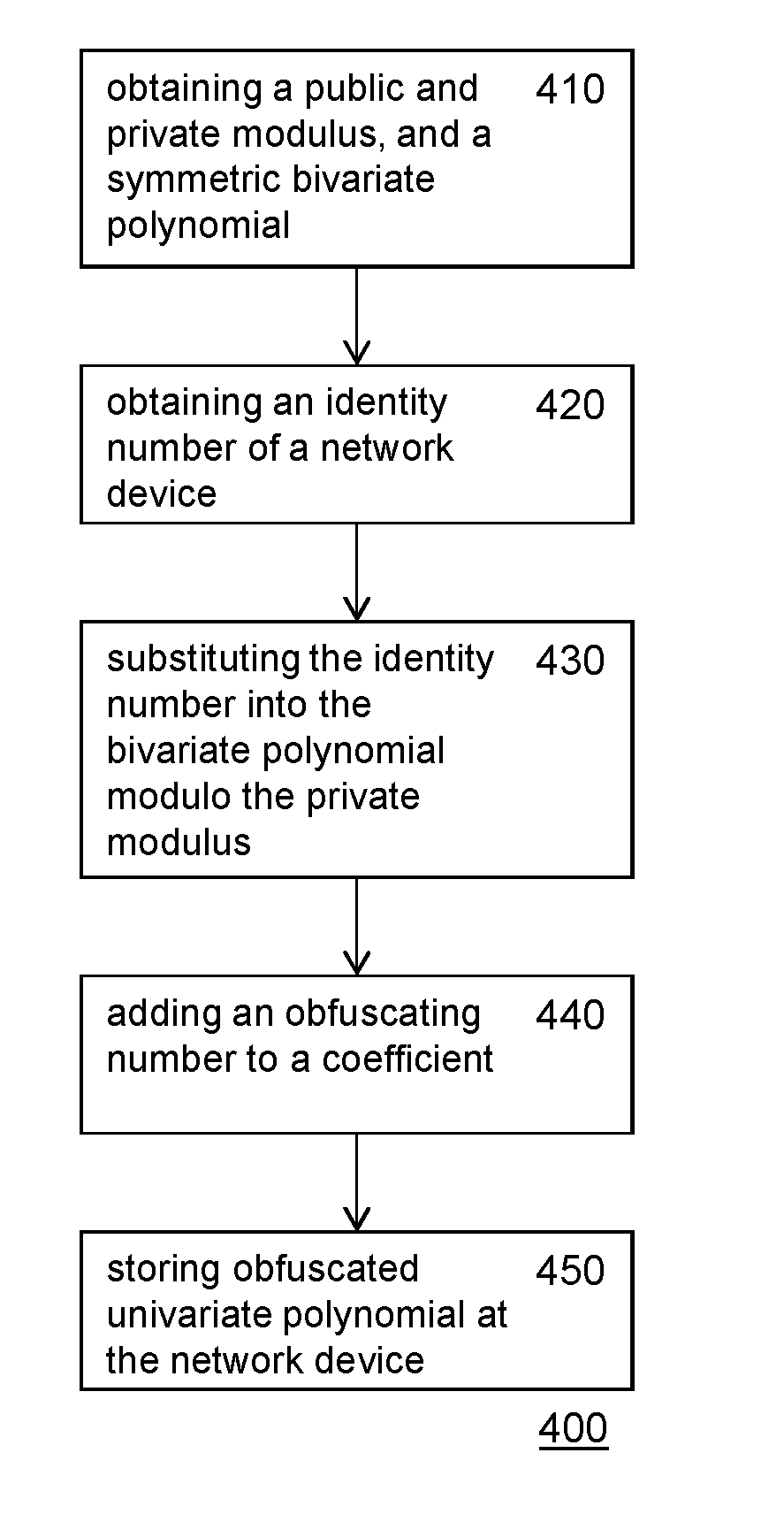
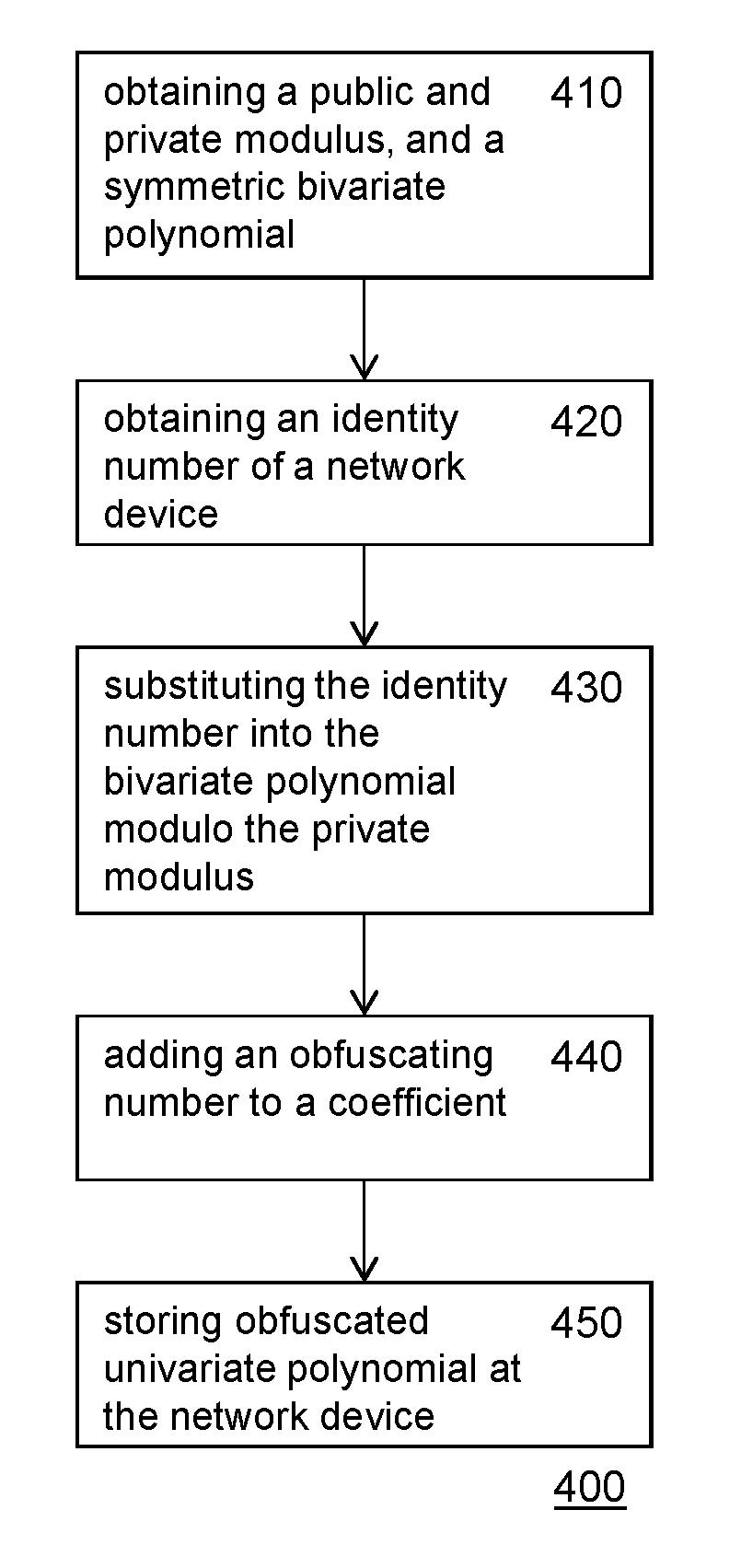
A method of configuring a network device for key sharing and a method for a first network device to determine a shared key are provided. The method of configuring uses a private private modulus, and a modulus (p1) a public modulus (N), and a bivariate polynomial (f1) having integer coefficients, the binary representation of the public modulus and the binary representation of the private modulus are the same in at least key length (b) consecutive bits. Local key material for a network device is generated by substituting an identity number into the bivariate polynomial and reducing modulo the private modulus the result of the substitution to obtain a univariate polynomial. Security may be increased by adding (440) one or more obfuscating numbers to coefficients of the univariate polynomial to obtain an obfuscated univariate polynomial. In a use phase, the network device determines a shared cryptographic key, by substituting (530) the identity number of another network device into the univariate polynomial and reducing modulo the public modulus and reducing modulo a key modulus.
Owner:KONINKLIJKE PHILIPS ELECTRONICS NV
Encryption apparatus, decryption apparatus, key generation apparatus, and program
InactiveUS20100329447A1Eliminate weakness causedSecret communicationSecuring communicationPlaintextComputer hardware
An encryption apparatus includes a plaintext embedding unit that embeds a message m as a coefficient of a three-variable plaintext polynomial m(x,y,t), an identification polynomial generating unit that generates a three-variable identification polynomial f(x,y,t), a polynomial generating unit that randomly generates three-variable polynomials r1(x,y,t), r2(x,y,t), s1(x,y,t), and s2(x,y,t), and an encrypting unit that generates encrypted texts F1 and F2 by performing an arithmetic operation with respect to these three-variable polynomials.
Owner:KK TOSHIBA
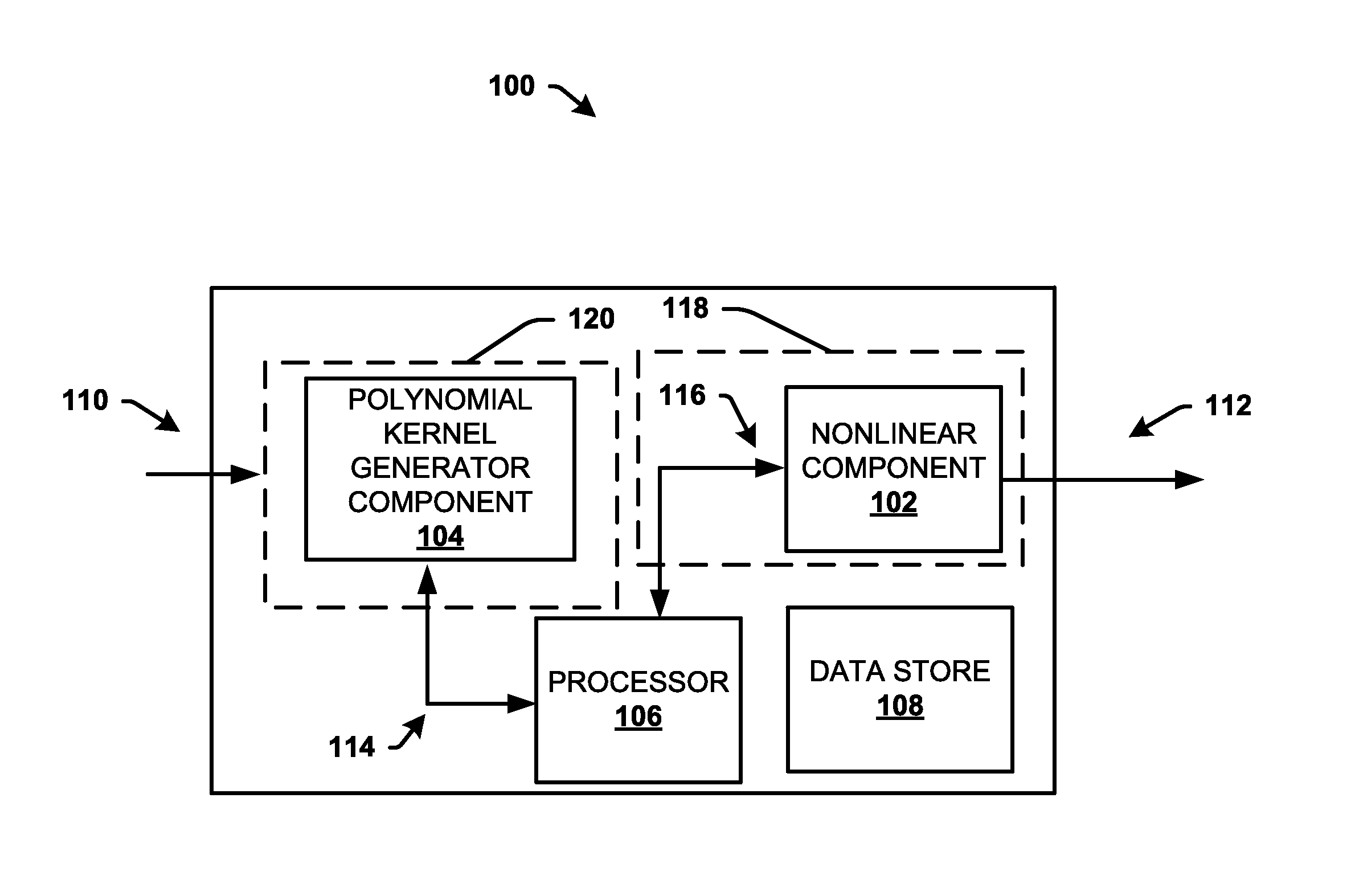
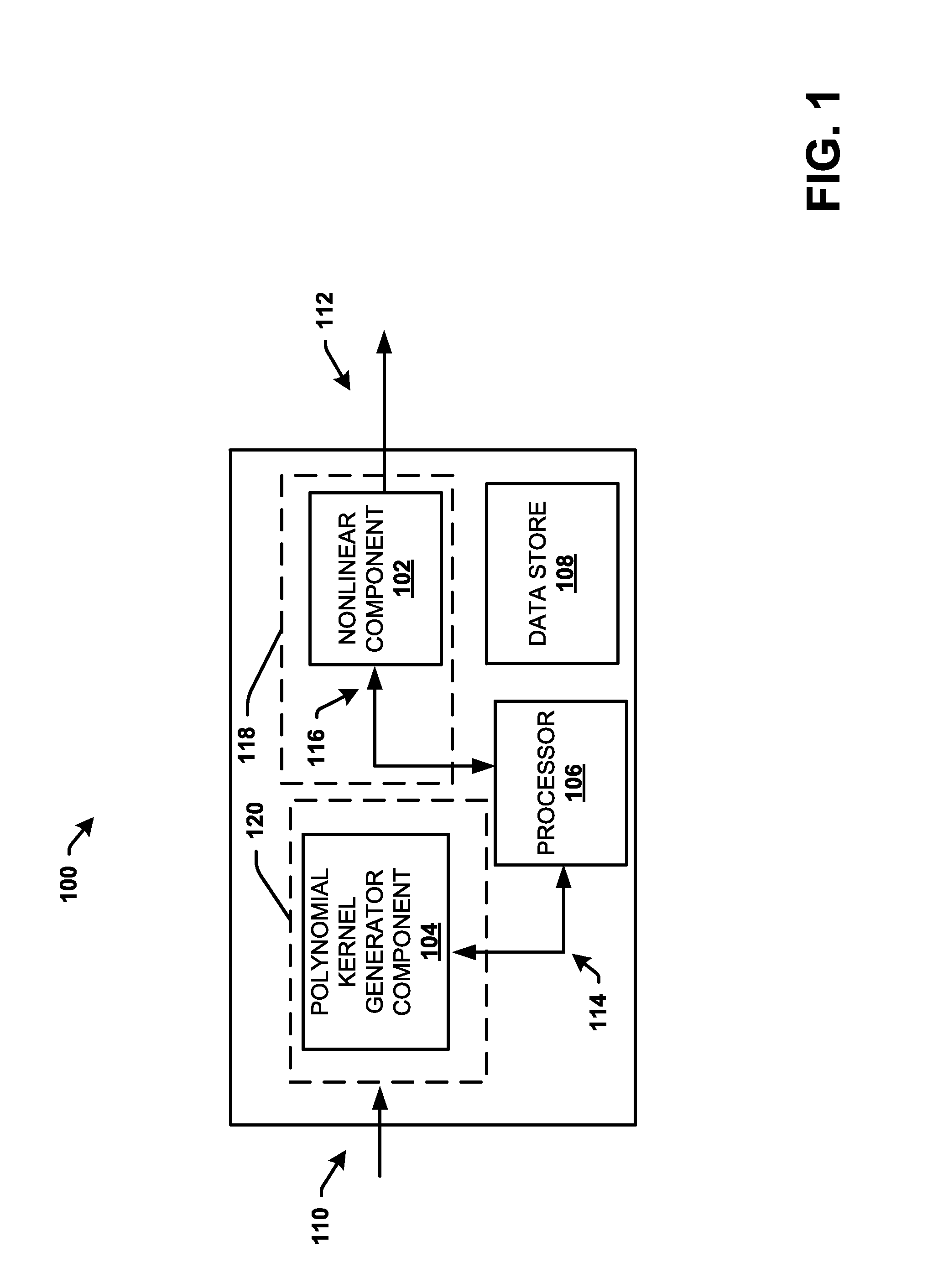
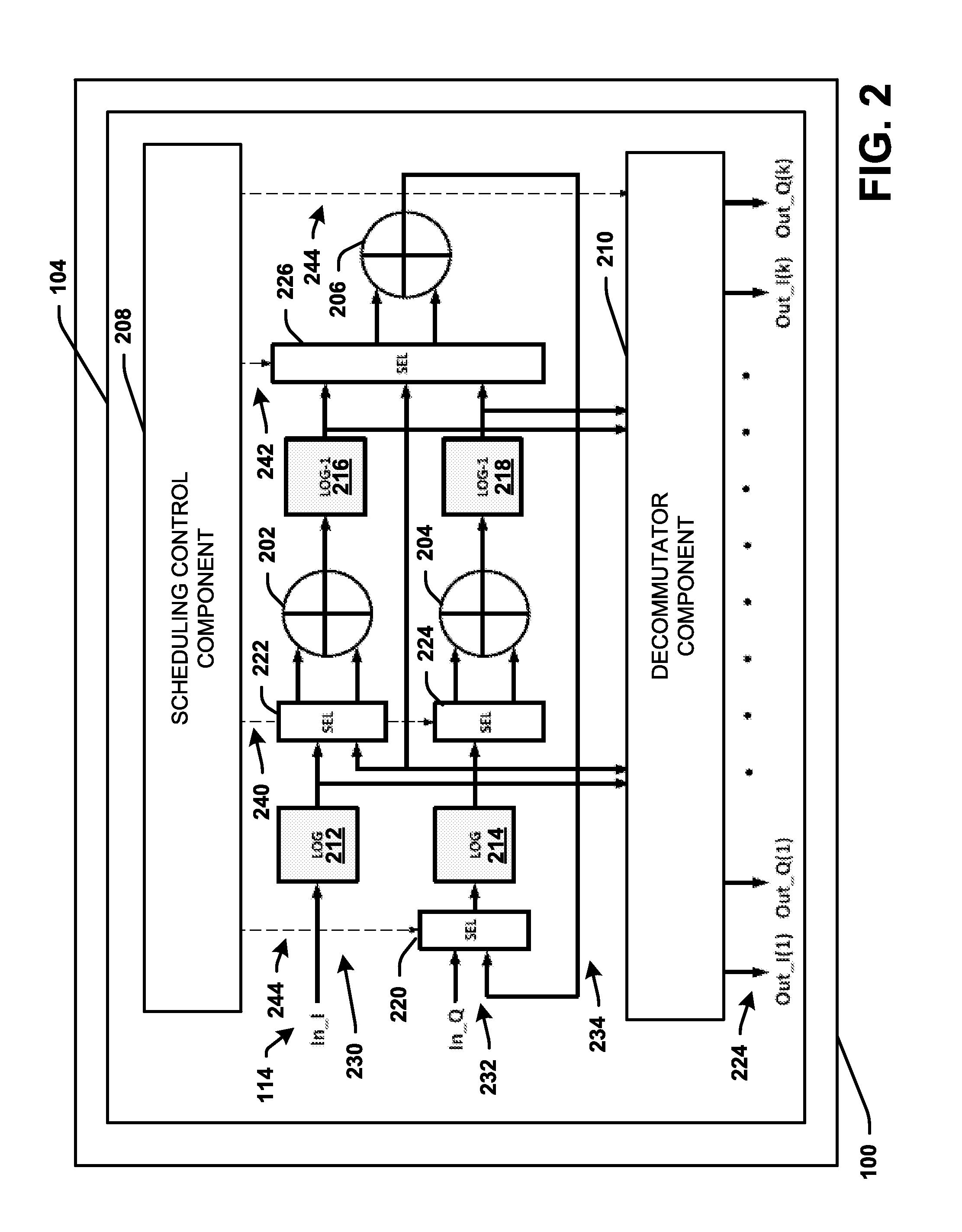
Energy efficient polynomial kernel generation in full-duplex radio communication
ActiveUS20160380653A1Reduce non-linearityBaseband systemsDuplex signal operationNonlinear modellingPosynomial
A polynomial kernel generator is configured to mitigate nonlinearity in a receiver path from a transmitter path comprising a nonlinear component in a communication device or system. The polynomial kernel generator operates to generate polynomial kernels that can be utilized to model the nonlinearity as a function of a piecewise polynomial approximation applied to a nonlinear function of the nonlinearity. The polynomial kernel generator generates kernels in a multiplier less architecture with polynomial computations in a log domain using a fixed number of adders.
Owner:APPLE INC
Cryptographic hash functions using elliptic polynomial cryptography
InactiveUS8165287B2User identity/authority verificationDigital computer detailsComputer hardwareCryptographic hash function
The cryptographic hash functions using of elliptic polynomial polynomials are based on the elliptic polynomial discrete logarithm problem, which is well known as a computationally hard problem. The hash functions are based on the elliptic polynomial equation in their generation, where different elliptic polynomials are used for different blocks of the same plain text. Particularly, the hash functions use an elliptic polynomial with more than one independent x-coordinate. More specifically, a set of elliptic polynomial points are used that satisfy an elliptic polynomial equation with more than one independent x-coordinate which is defined over a finite field F.
Owner:KING FAHD UNIVERSITY OF PETROLEUM AND MINERALS
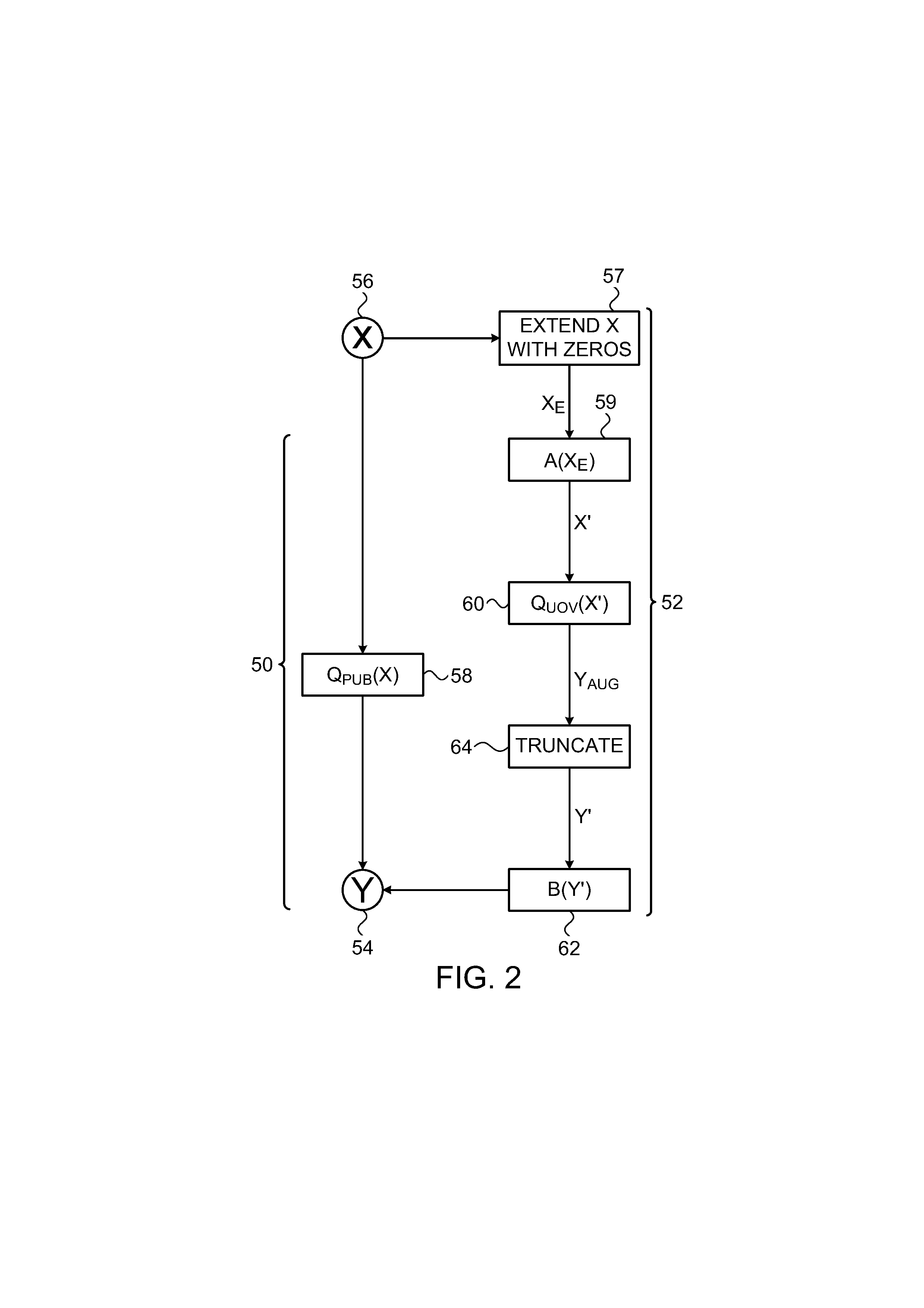
Attack-Resistant Multivariate Signature Scheme
InactiveUS20130177151A1Public key for secure communicationUser identity/authority verificationDigital signatureTheoretical computer science
A cryptographic method, apparatus, and system, including selecting a first multivariate polynomial mapping, which includes first multivariate polynomial equations over first variables in a finite field, defining a second multivariate polynomial mapping, which includes at least some of the first multivariate polynomial equations and further includes second multivariate polynomial equations over the first variables together with second variables in the finite field, generating a public key based on the second multivariate polynomial mapping, and digitally signing a message, using a processor, with a digital signature that is verifiable using the public key and is generated by solving the first multivariate polynomial mapping to find respective first values of the first variables, solving a set of linear equations using the first values to find respective second values of the second variables, and applying a transform to the first and second values so as to generate a vector corresponding to the digital signature, wherein the second values are chosen so that a predefined group of elements of the vector will be zero. Related methods, apparatus, and systems are also described.
Owner:CISCO TECH INC
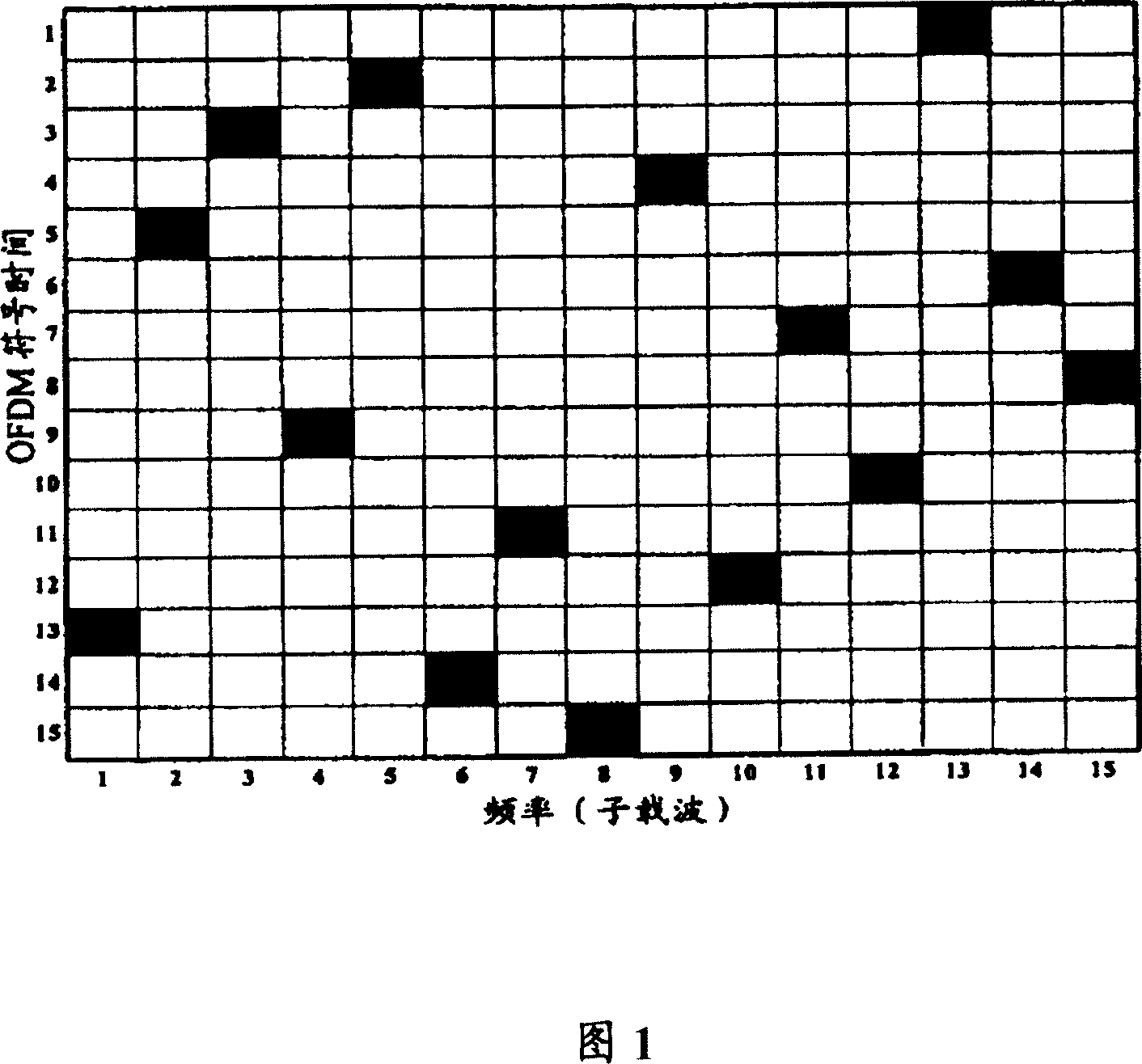
Distribution method of time frequency resource
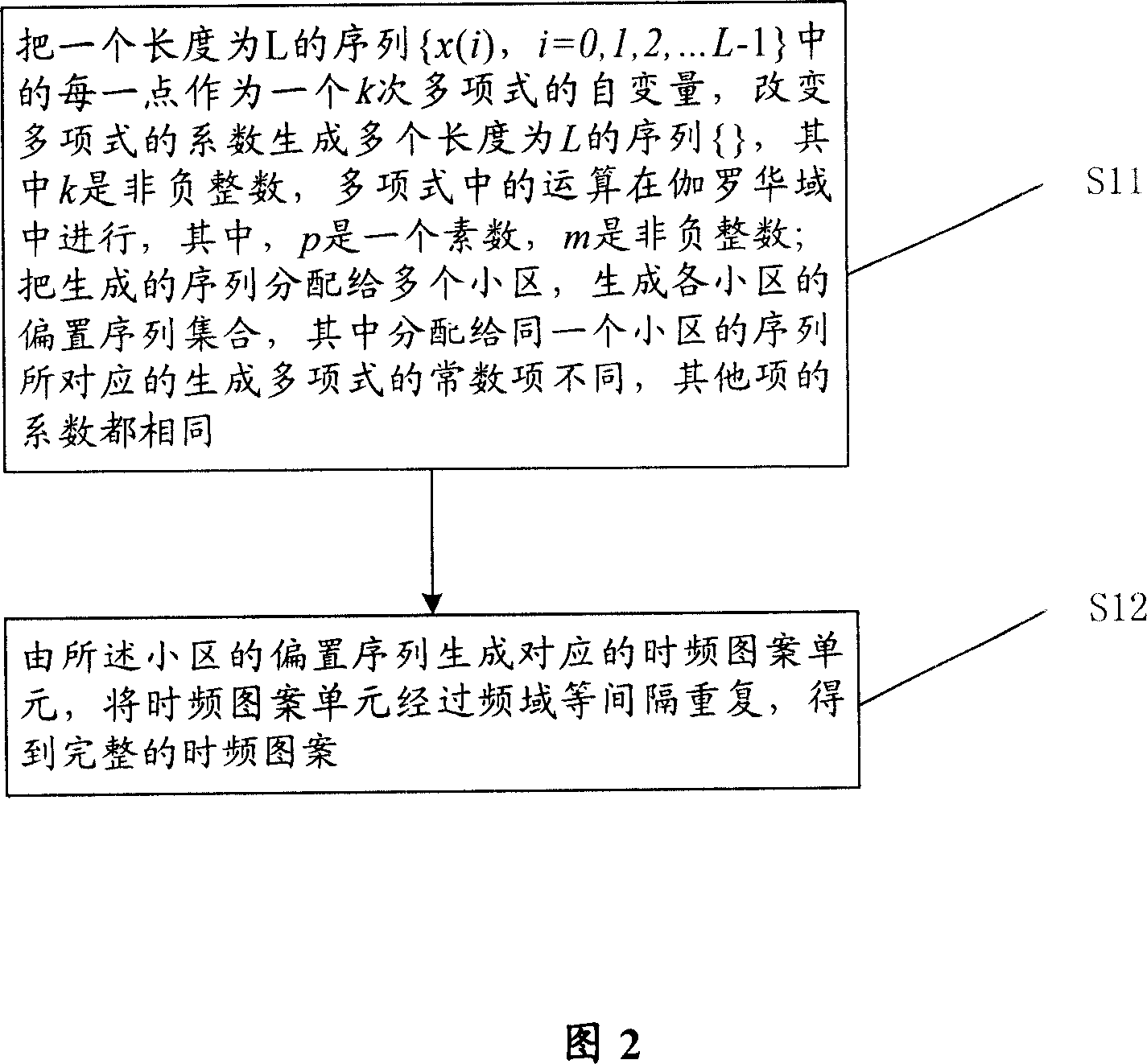
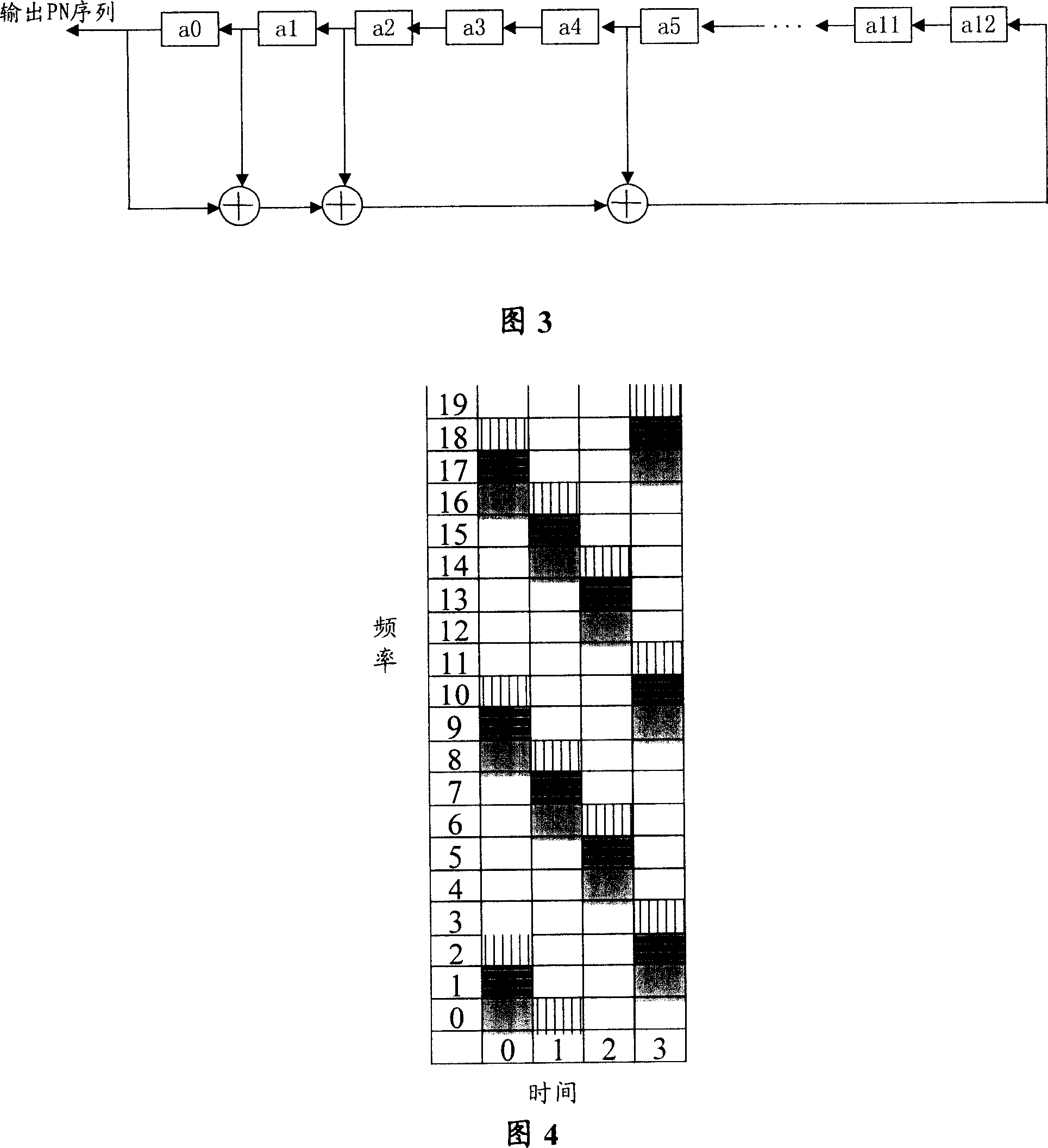
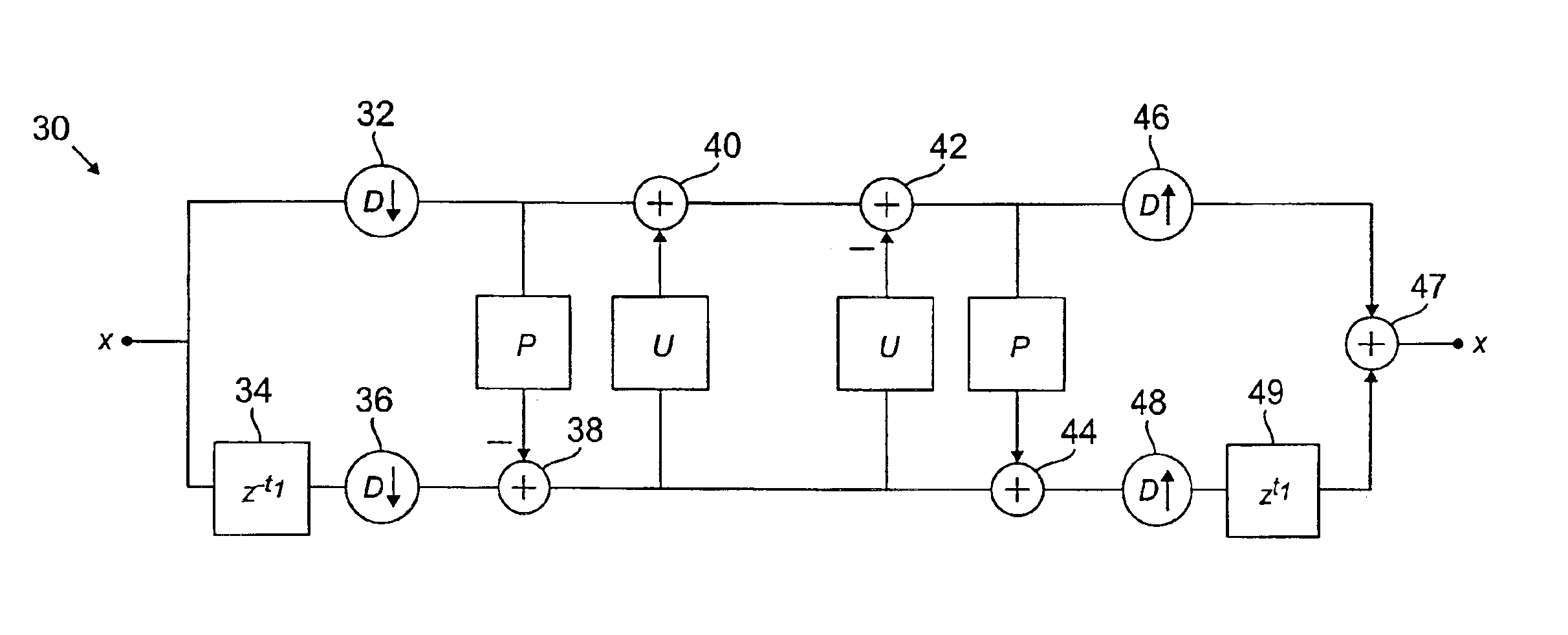
InactiveCN101005346ABig spaceSignal channelsTime-division multiplexing usageDistribution methodPosynomial
The method includes steps: each point in sequence x(i) with length L, i=0, 1, 2,apostrophe L-1 is served as a independent variable of k order polynomial; changing coefficient of polynomial to generate multiple sequence f(i) with length L, where k is nonnegative integer; operation in polynomial is carried out in Galois Field GF(Q), where Q=pm, p as a prime number, and m as nonnegative integer; assigning generated sequences to multiple sectors to set of create biased sequences for each sector; it is different in constant terms of polynomial, and identical to other coefficients of coefficients corresponding to sequence assigned to same sector; creating corresponding time - frequency pattern (TFP) unit from biased sequences of the sector; repeating TFP unit with equal interval in frequency domain so as to obtain integrated TFP. The invention solves issue that current techniques have not considered flattened interference between adjacent common frequency sectors.
Owner:HUAWEI TECH CO LTD
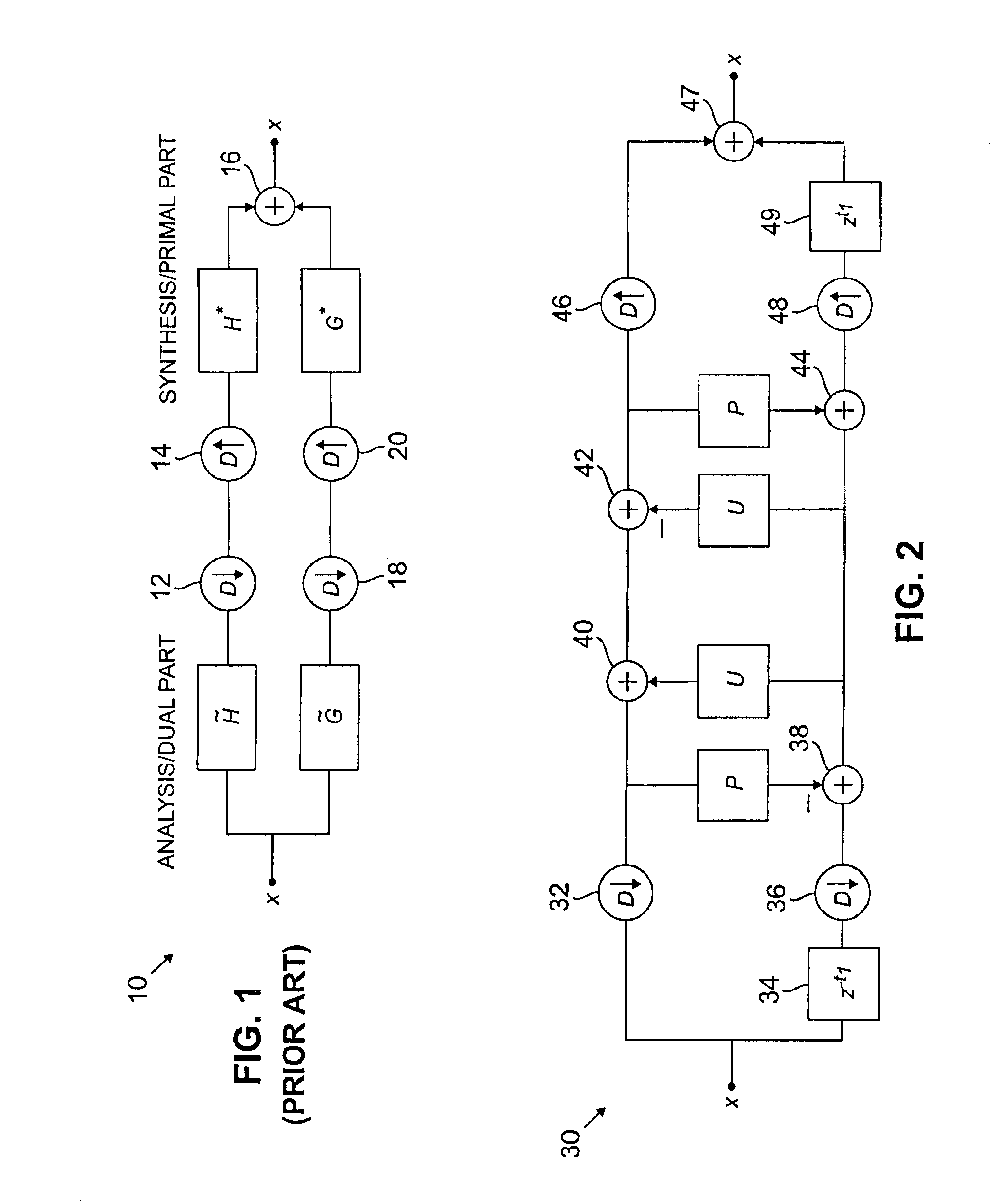
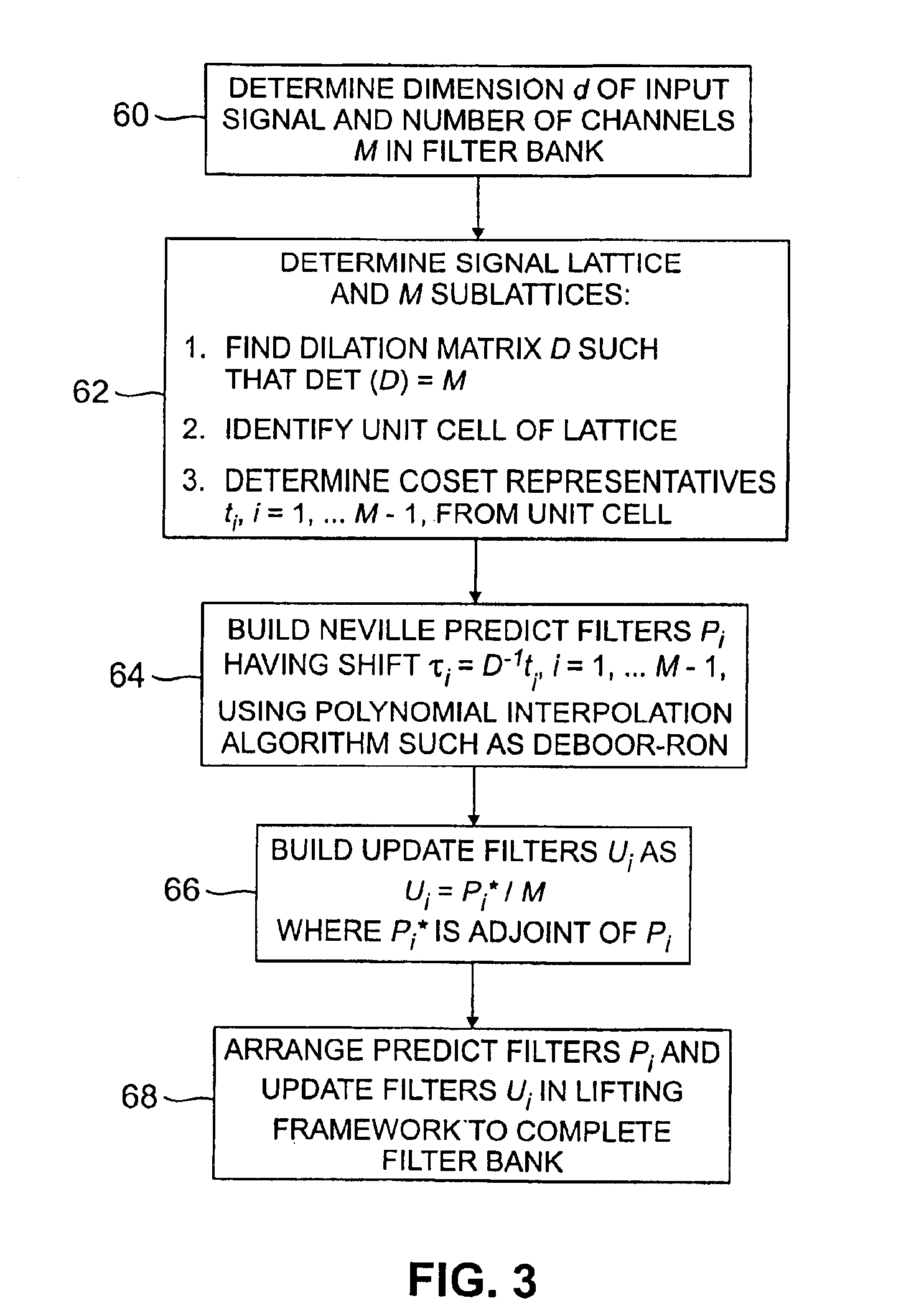
Interpolating filter banks in arbitrary dimensions
InactiveUS6865587B2Geometric image transformationComplex mathematical operationsPosynomialEngineering
Interpolating filter banks are constructed for use with signals which may be represented as a lattice of arbitrary dimension d. The filter banks include M channels, where M is greater than or equal to two. A given filter bank is built by first computing a set of shifts τi as D−1 ti, i=1, 2, . . . M−1, where ti is a set of coset representatives taken from a unit cell of the input signal lattice, and D is a dilation matrix having a determinant equal to M. A polynomial interpolation algorithm is then applied to determine weights for a set of M−1 predict filters Pi having the shifts τi. A corresponding set of update filters Ui are then selected as Ui=P*i / M, where P*i is the adjoint of the predict filter Pi. The resulting predict and update filters are arranged in a lifting structure such that each of the predict and update filters are associated with a pair of the M channels of the filter bank. The input signal applied to the filter bank is downsampled in each of the M channels, and then interpolated using the M−1 predict filters and the M−1 update filters. The downsampled and interpolated signal may be reconstructed using complementary interpolation and upsampling operations.
Owner:LUCENT TECH INC
Information processing apparatus, image processing method, and program
InactiveUS20150010144A1Effective calculationKey distribution for secure communicationPublic key for secure communicationInformation processingPublic key authentication
Provided is an information processing apparatus including a number acquisition unit configured to acquire a number used for a coefficient of each term constituting a set of a multi-order multivariate polynomial F=(f1, . . . , fm), the number generated using a predetermined function from information shared between entities that execute an algorithm of a public-key authentication scheme or a digital signature scheme that uses a public key including the set of the multi-order multivariate polynomial F, and a polynomial calculation unit configured to calculate a multi-order multivariate polynomial for an input value of a variable by allocating the number acquired by the number acquisition unit to coefficients of the multi-order multivariate that includes the set of the multi-order multivariate polynomial F as a structural element. The polynomial calculation unit skips a calculation process for a term in which an input value of at least one variable is 0
Owner:SONY CORP
Key sharing device and system for configuration thereof
ActiveUS9722787B2Improve securityEfficiently implemented in hardwareKey distribution for secure communicationPublic key for secure communicationKey sizePosynomial
A method of configuring a network device for key sharing and a method for a first network device to determine a shared key are provided. The method of configuring uses a private modulus (p1) a public modulus (N), and a bivariate polynomial (f1) having integer coefficients, the binary representation of the public modulus and the binary representation of the private modulus are the same in at least key length (b) consecutive bits. Local key material for a network device is generated by substituting an identity number into the bivariate polynomial and reducing modulo the private modulus the result of the substitution to obtain a univariate polynomial. Security may be increased by adding (440) one or more obfuscating numbers to coefficients of the univariate polynomial to obtain an obfuscated univariate polynomial. In a use phase, the network device determines a shared cryptographic key, by substituting (530) the identity number of another network device into the univariate polynomial and reducing modulo the public modulus and reducing modulo a key modulus.
Owner:KONINK PHILIPS ELECTRONICS NV
Method and apparatus for computing roots of a polynomial equation with interval coefficients
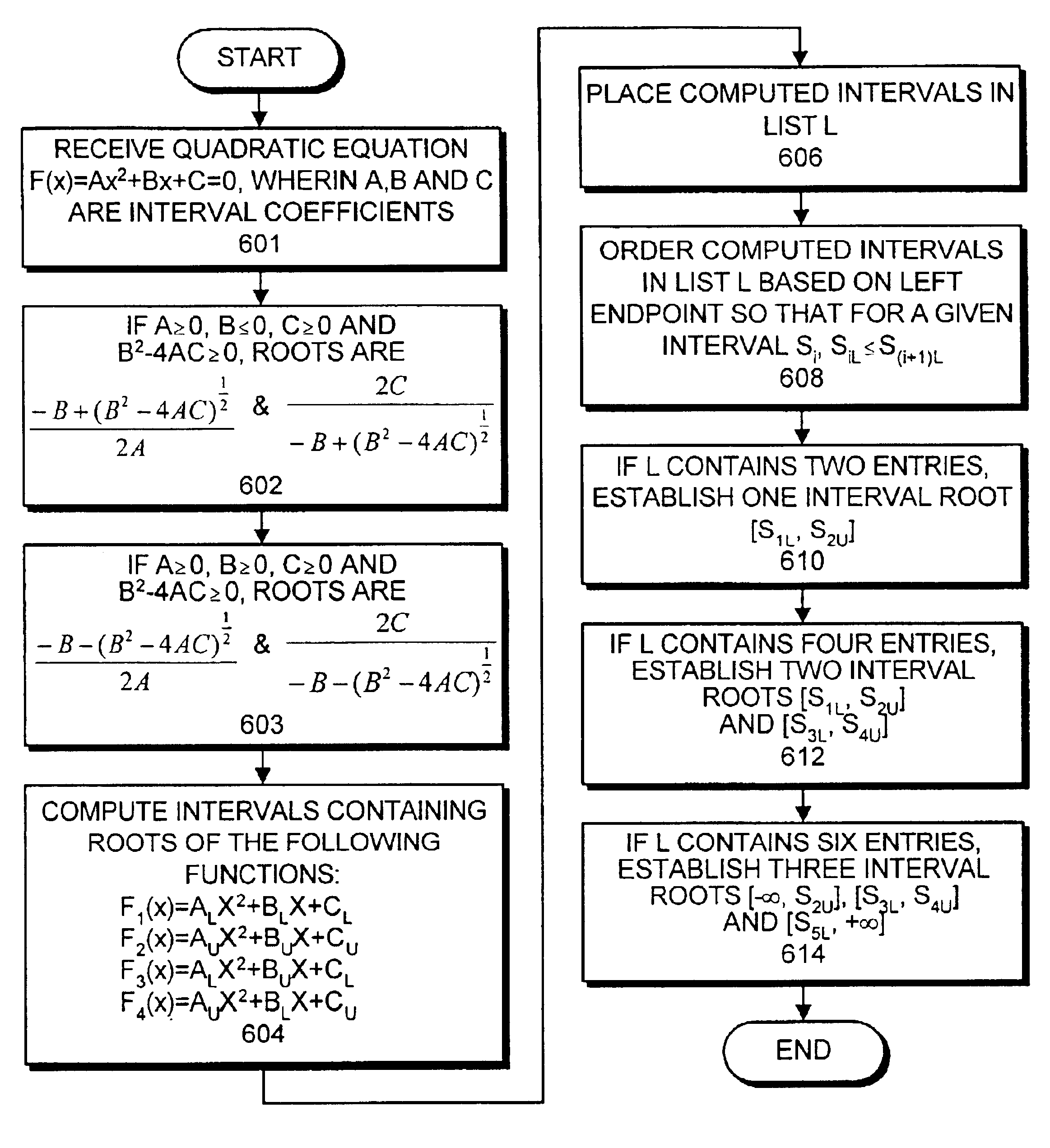
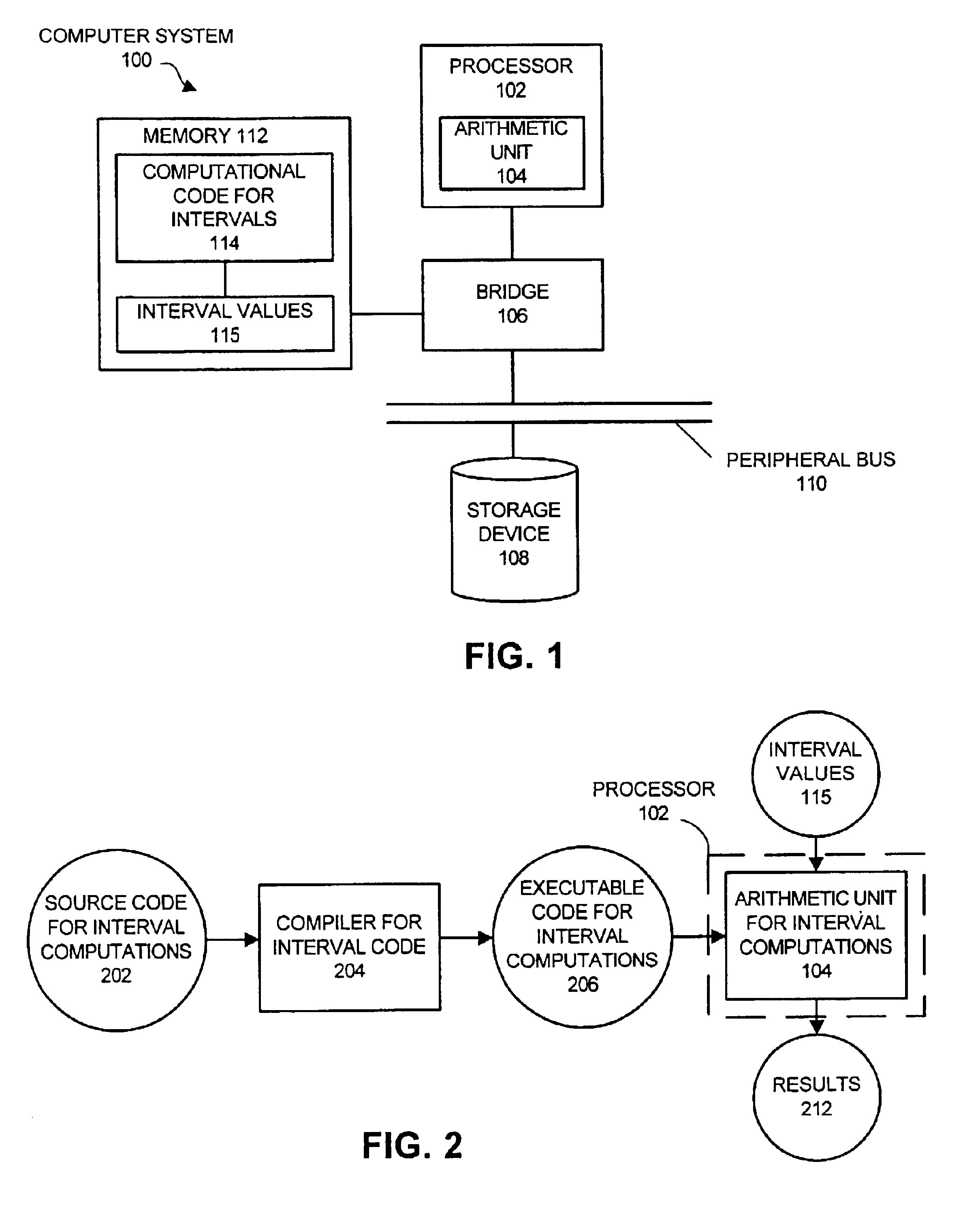
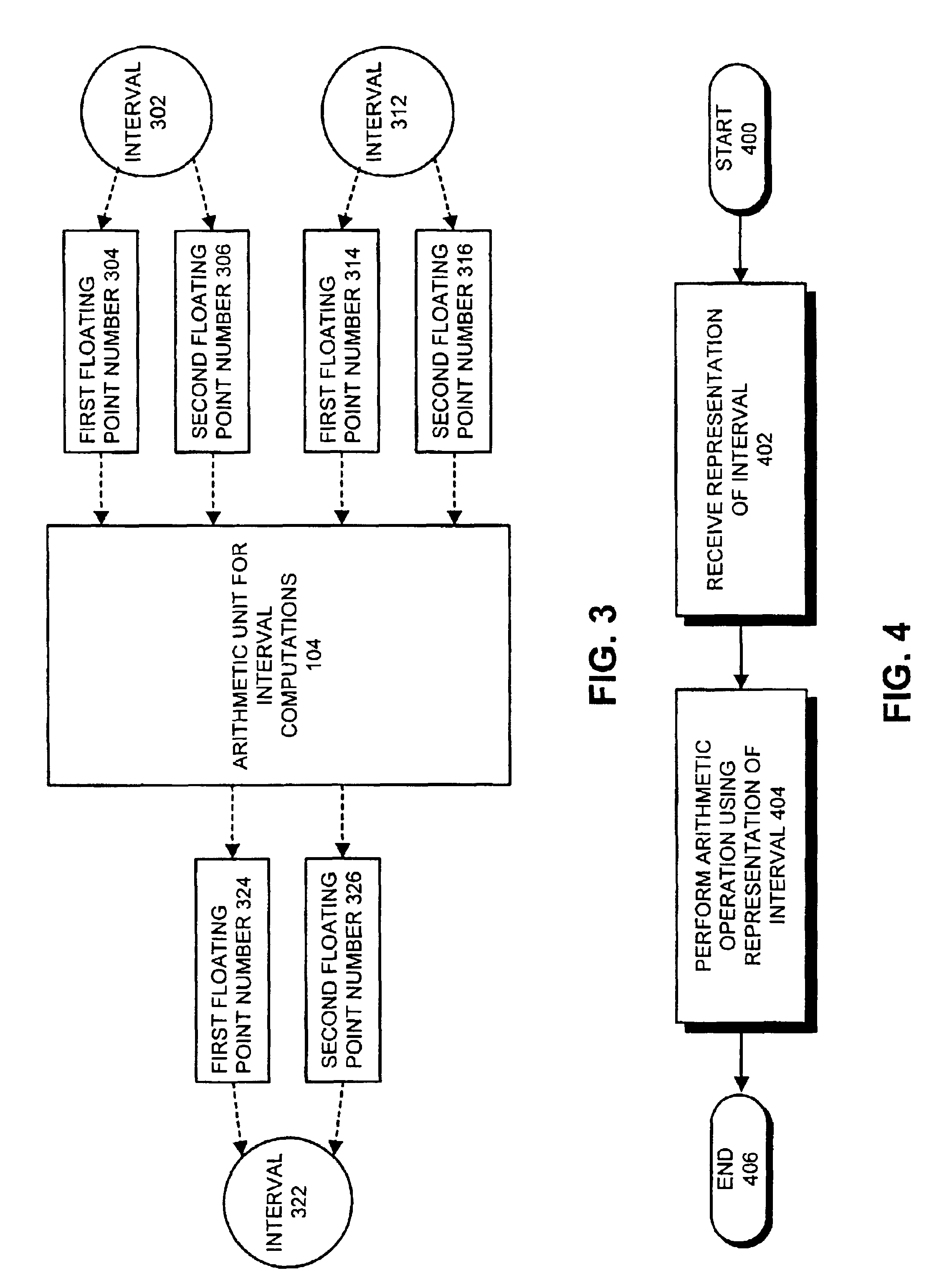
InactiveUS6895422B2Computation using non-contact making devicesComplex mathematical operationsPosynomialInterval coefficients
One embodiment of the present invention provides a system for finding the roots of a polynomial or a quadratic equation with interval coefficients. The system operates by receiving a representation of a polynomial equation, which can be a quadratic equation of the form F(x)=Ax2+Bx+C=0, wherein A=[AL, AU], B=[BL, BU] and C=[CL, CU] are interval coefficients. Next, the system computes intervals containing roots of the functions F1(x), F2(x), F3(x) and F4(x), wherein F1(x)=ALx2+BLx+CL, F2(x)=AUx2+BUx+CU, F3(x)=ALx2+BUx+CL and F4(x)=AUx2+BLx+CU. The system then places the computed intervals into a list, L, and orders the computed intervals in L by their left endpoints, so that for a each entry, Si=[SiL, SiU], SiL≦Si+1,L. Next, the system establishes interval roots for F(x) from the interval entries in list L. In one embodiment of the present invention, establishing interval roots from the list L involves: establishing one interval root, [S1,L, S2U], if L contains two entries, S1 and S2; establishing two interval roots, [S1,L, S2U], and [S3L, S4U], if L contains four entries, S1, S2, S3 and S4; and establishing three interval roots, [−∞, S2U], [S3L, S4U] and [S5L, +∞], if L contains six entries, S1, S2, S3, S4, S5 and S6.
Owner:MICROSYST
Regression using M-estimators and polynomial kernel support vector machines and principal component regression
ActiveUS9658987B2Kernel methodsComplex mathematical operationsSupport vector machinePrincipal component regression
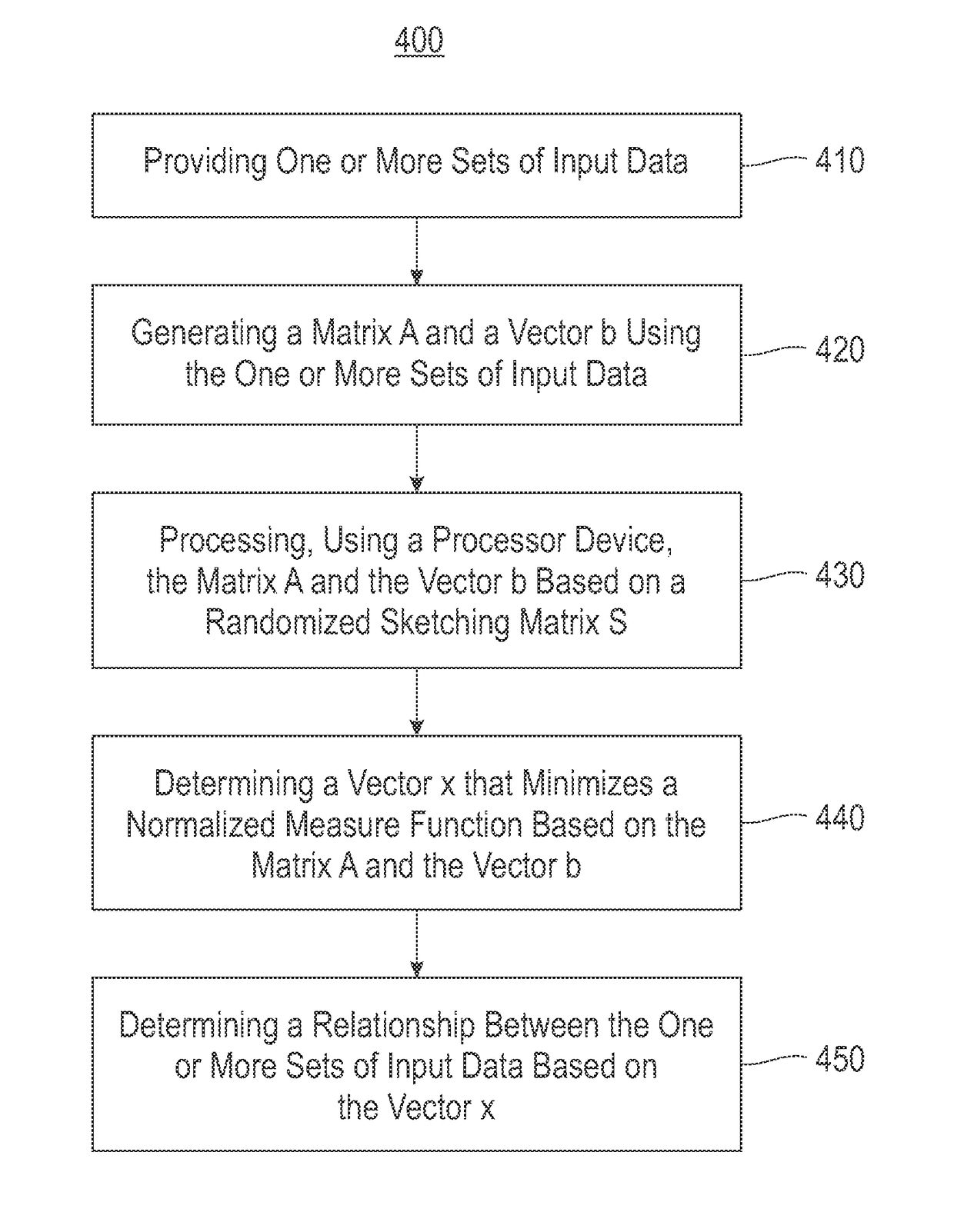
Embodiments of the invention relate to sketching for M-estimators for performing regression. One embodiment includes providing one or more sets of input data. A matrix A and a vector b are generated using the input data. A processor device is used for processing the matrix A and the vector b based on a randomized sketching matrix S. A vector x that minimizes a normalized measure function is determined based on the matrix A and the vector b. A relationship between the input data is determined based on the vector x.
Owner:INT BUSINESS MASCH CORP
Cryptographic method for color images and digital cinema
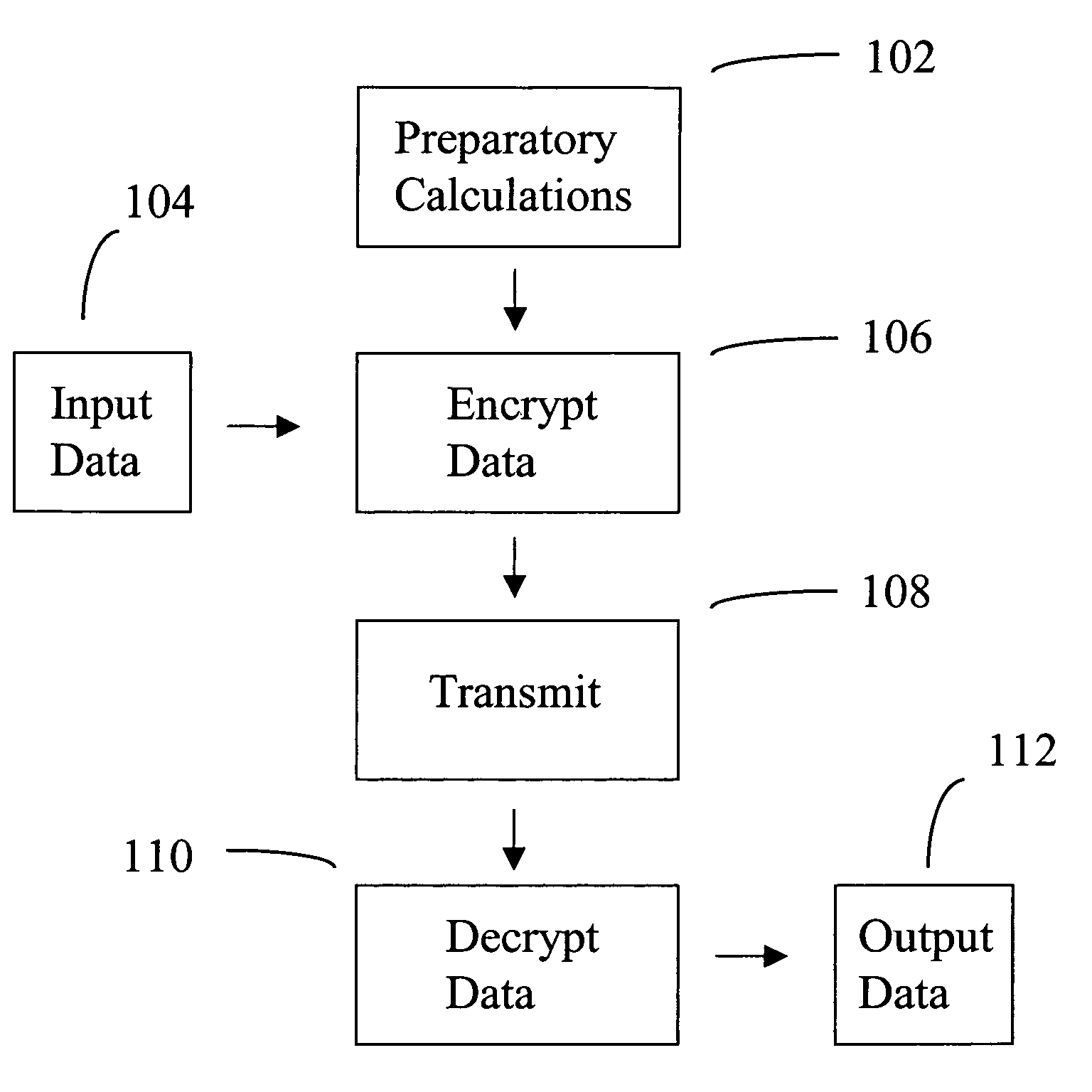
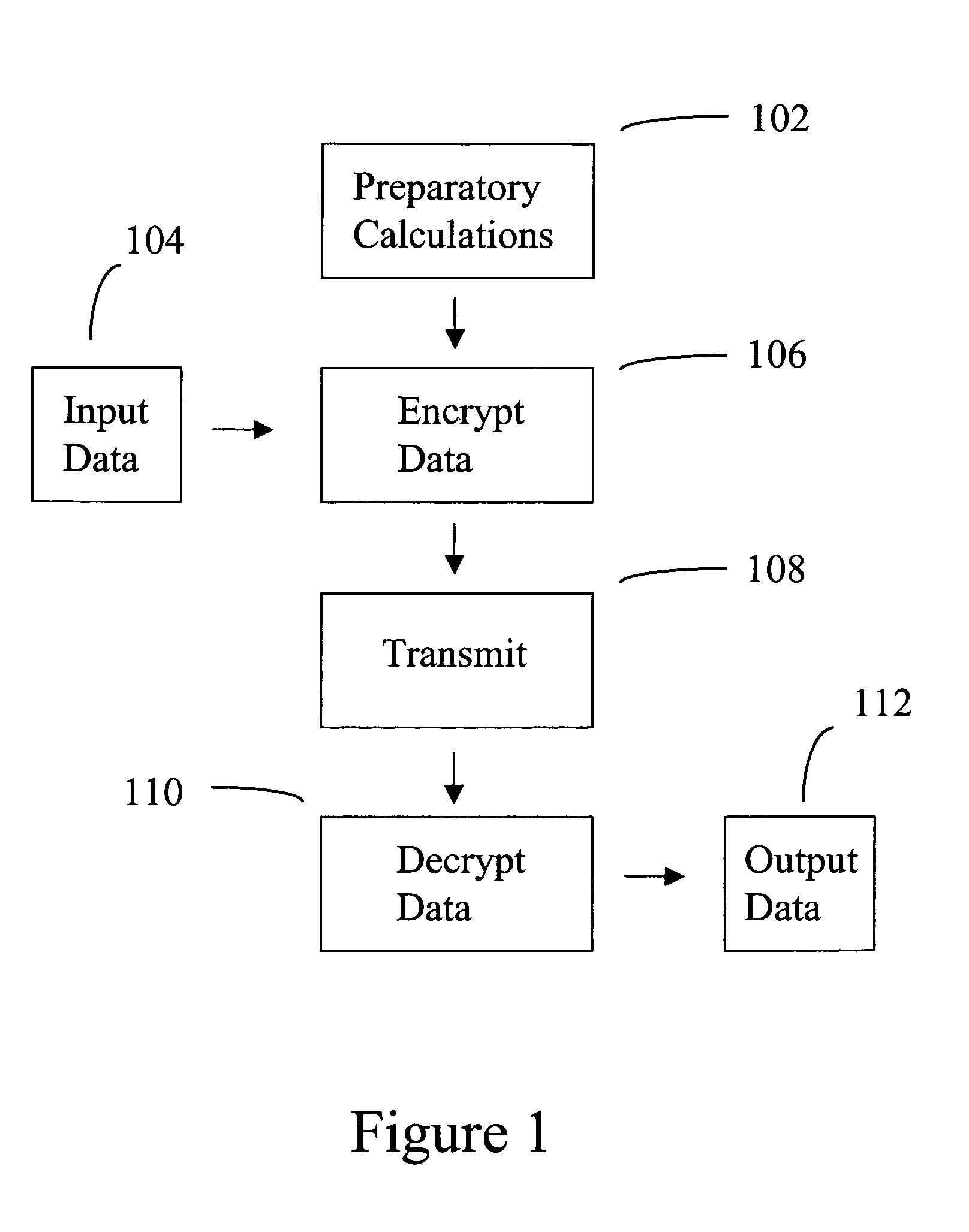
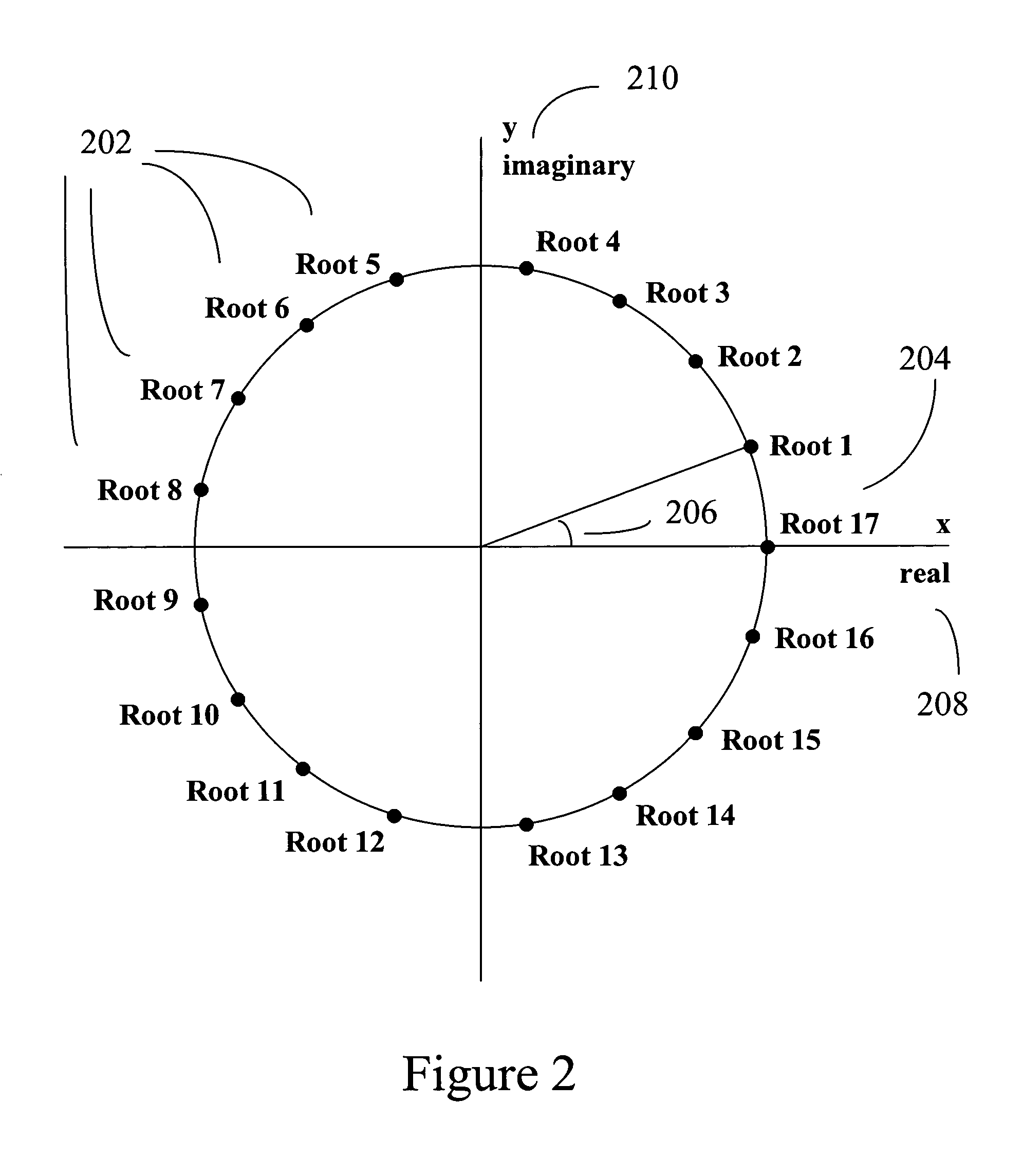
InactiveUS6985585B2Good encryptionEasy to calculatePublic key for secure communicationSecret communicationComputer hardwareColor image
A method for the encryption and decryption of digital images based on cyclotomic polynomials and radiometric expressions comprising the steps of generating an encrypting transform, partitioning the digital images into data blocks, along with encrypting, transmitting, and decrypting the data blocks. Three common radiometric expressions are fundamental metamers, black metamers, and radiometric functions. In one embodiment, the mathematical equation that represents the encrypting transform is a cyclotomic polynomial. In another embodiment, a cyclotomic polynomial is used to calculate the coefficients of the mathematical equation that represents the encrypting transform. In other embodiments, the encrypting transform is generated with a radiometric expression, and the encrypted data blocks are calculated with a radiometric expression.
Owner:AEVUM CORP
Features
- R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
Why Patsnap Eureka
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com