Patents
Literature
82 results about "Minimum cost path" patented technology
Efficacy Topic
Property
Owner
Technical Advancement
Application Domain
Technology Topic
Technology Field Word
Patent Country/Region
Patent Type
Patent Status
Application Year
Inventor
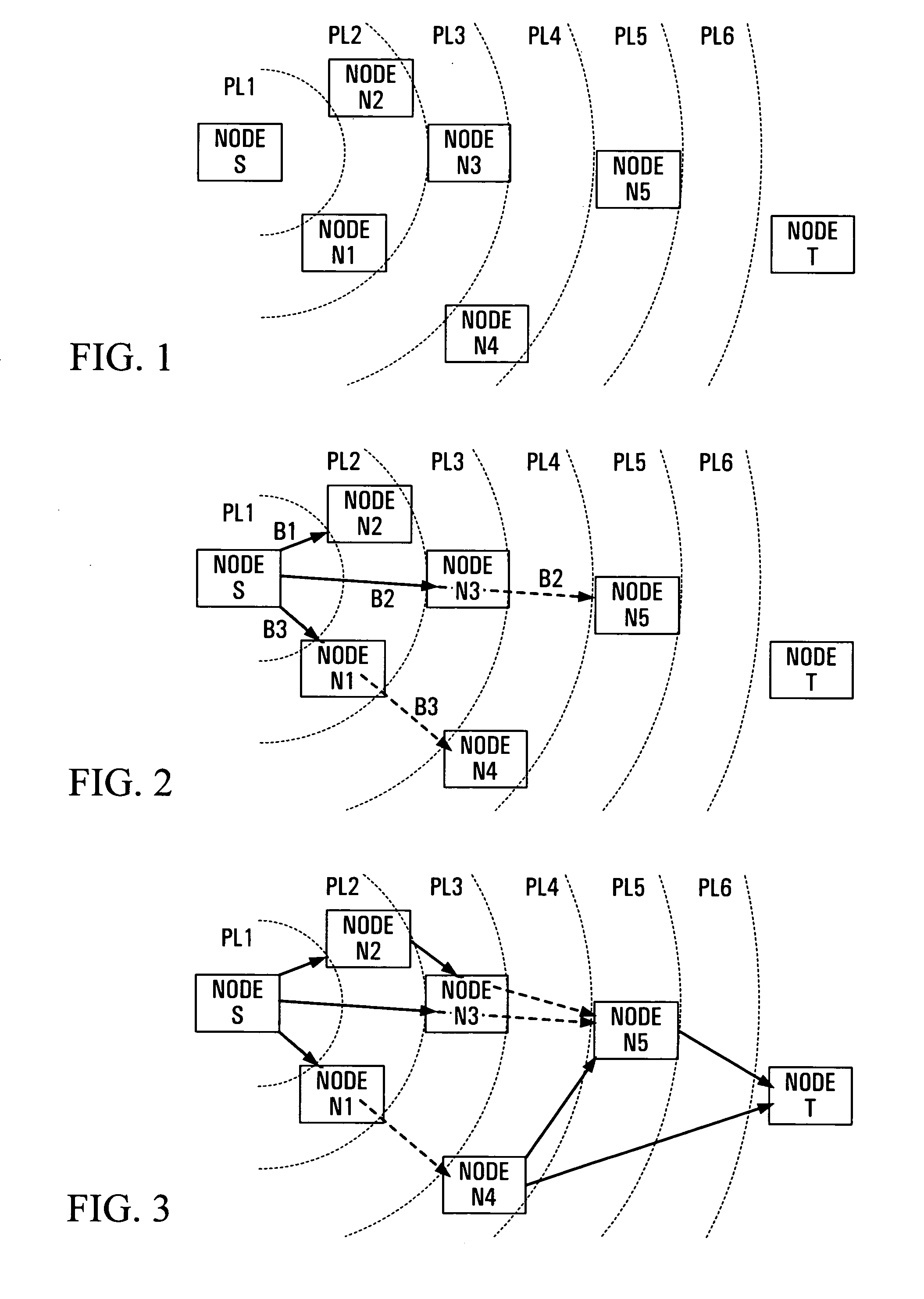
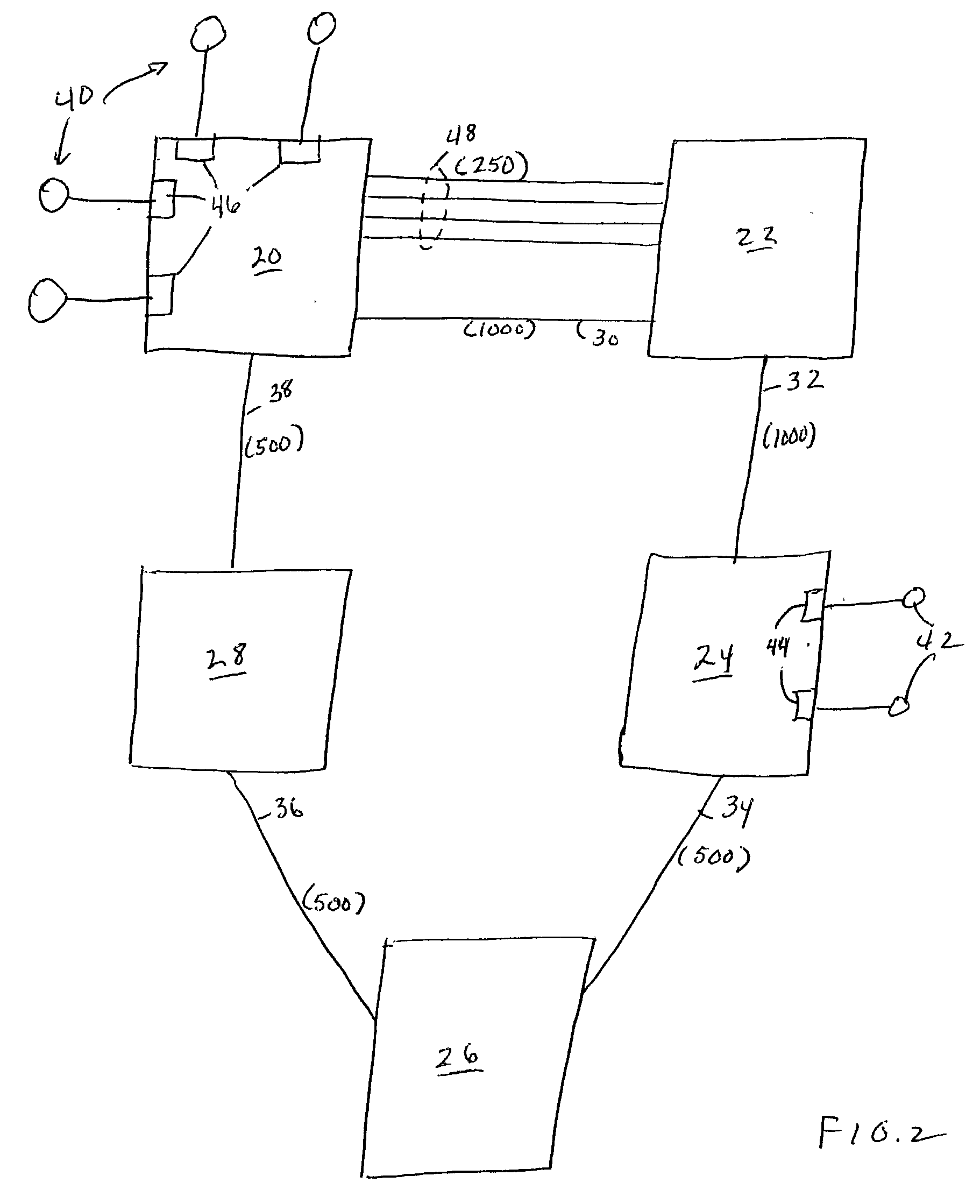
Path selection in wireless networks
ActiveUS7215928B2Low costError prevention/detection by using return channelInterconnection arrangementsWireless mesh networkData rate
In a wireless network, a lowest cost path from a source node to a target node is selected from a plurality of potential paths. The source node sums costs for the links of each potential path. For each link, these costs include a cost of interference, dependent on a number of nodes affected by a signal sent via the respective link. The link costs can also include a cost of transmission, dependent upon a data rate for the respective link, and a cost of coordination for transmissions with other nodes of the network.
Owner:APPLE INC
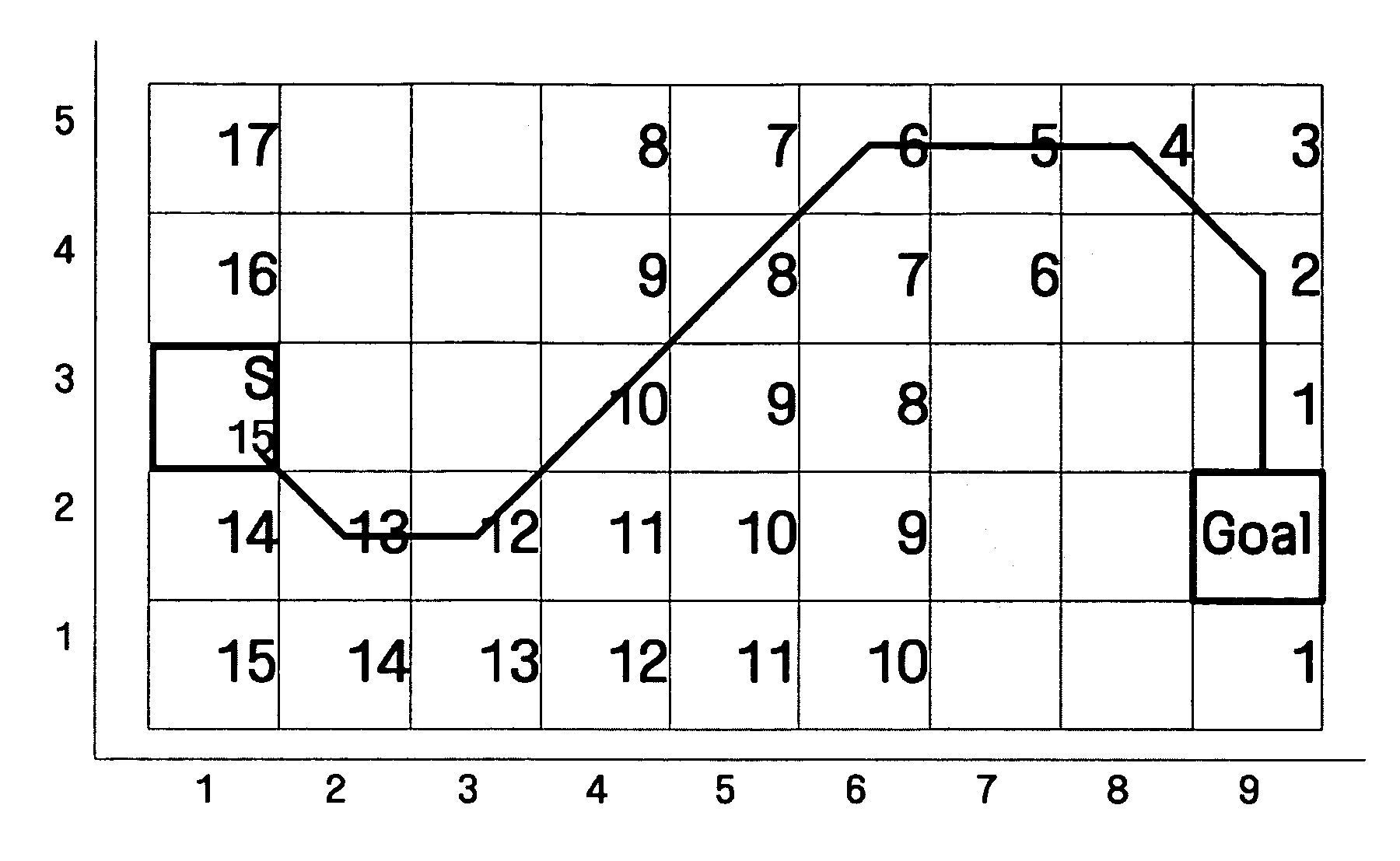
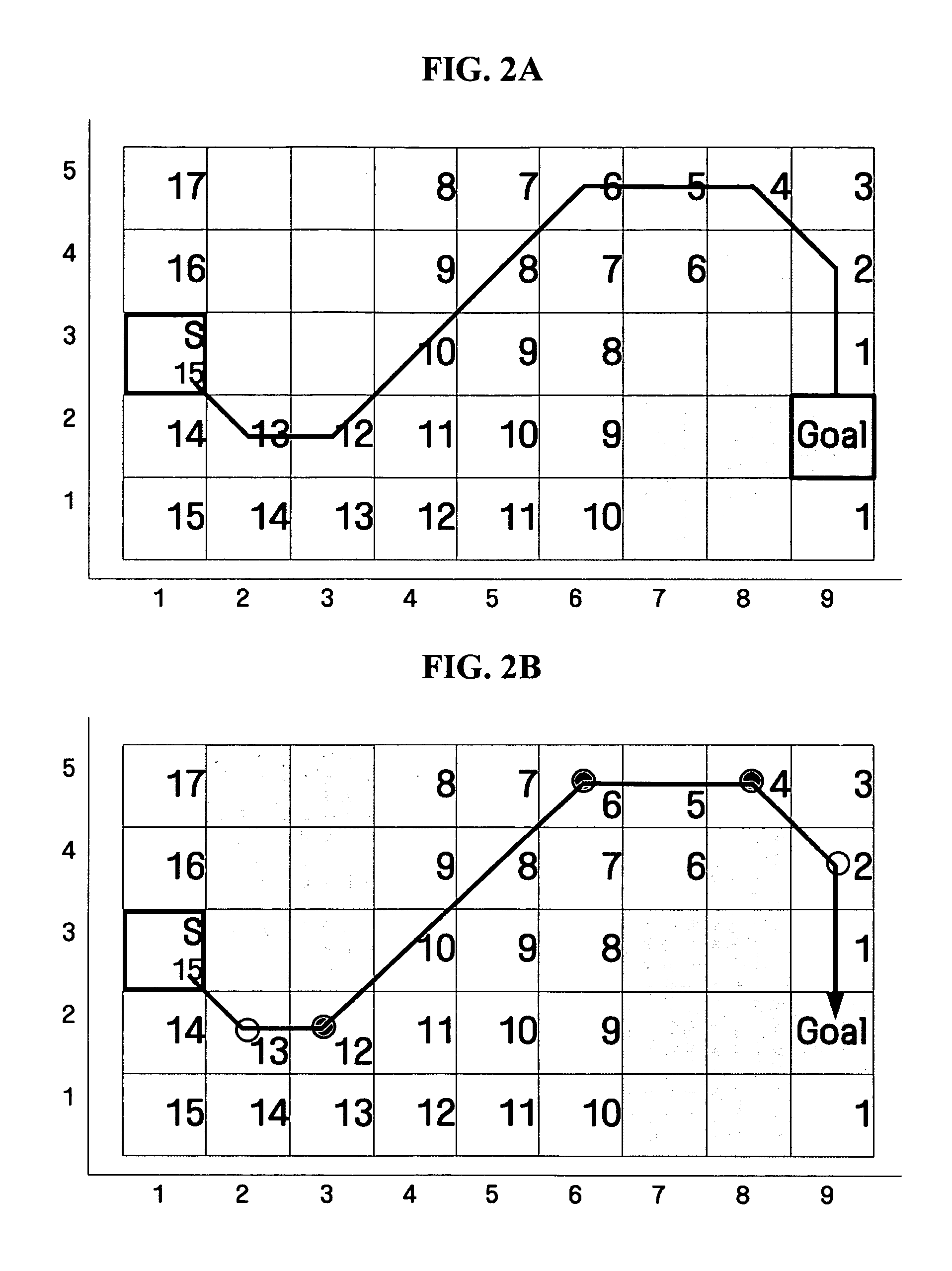
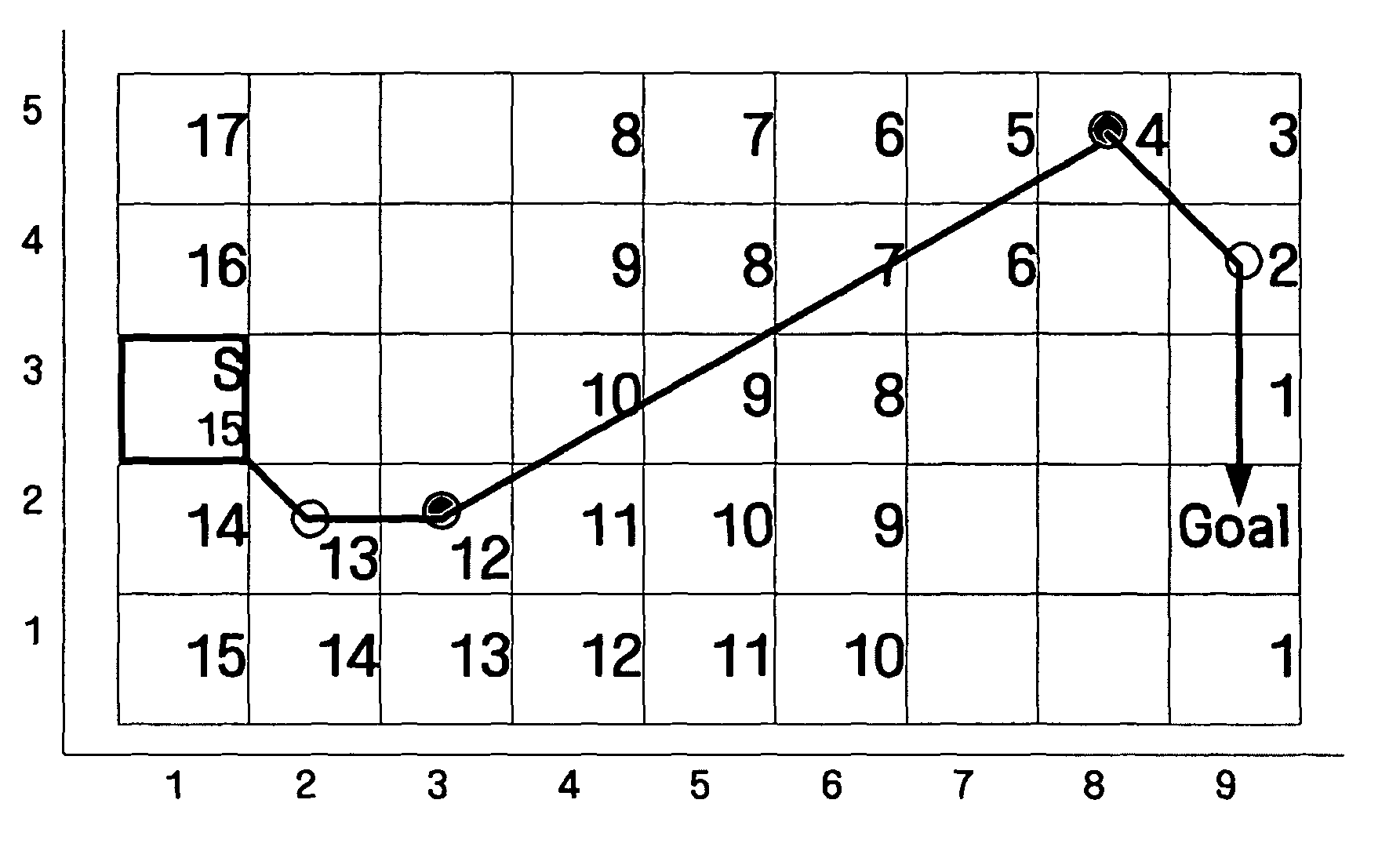
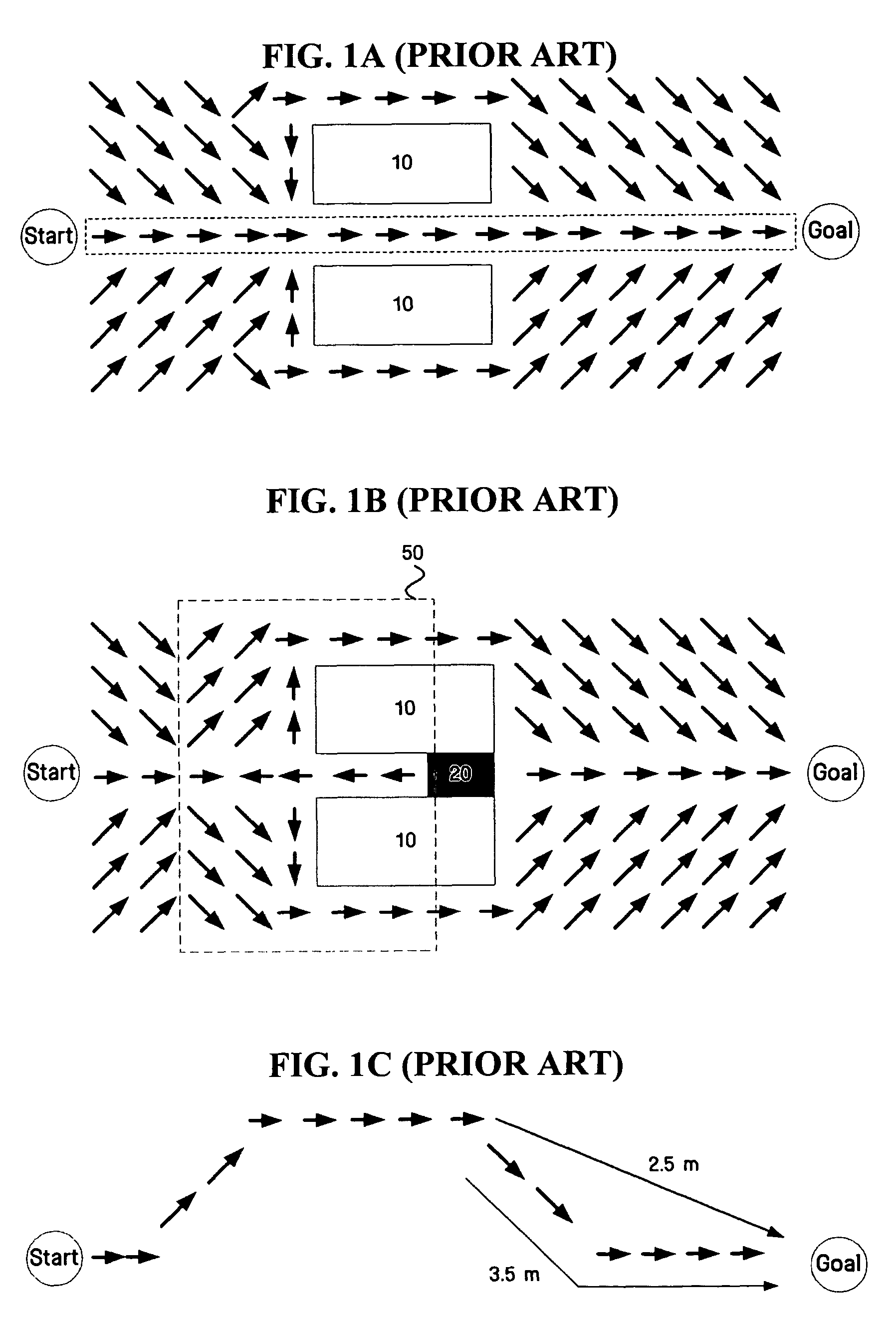
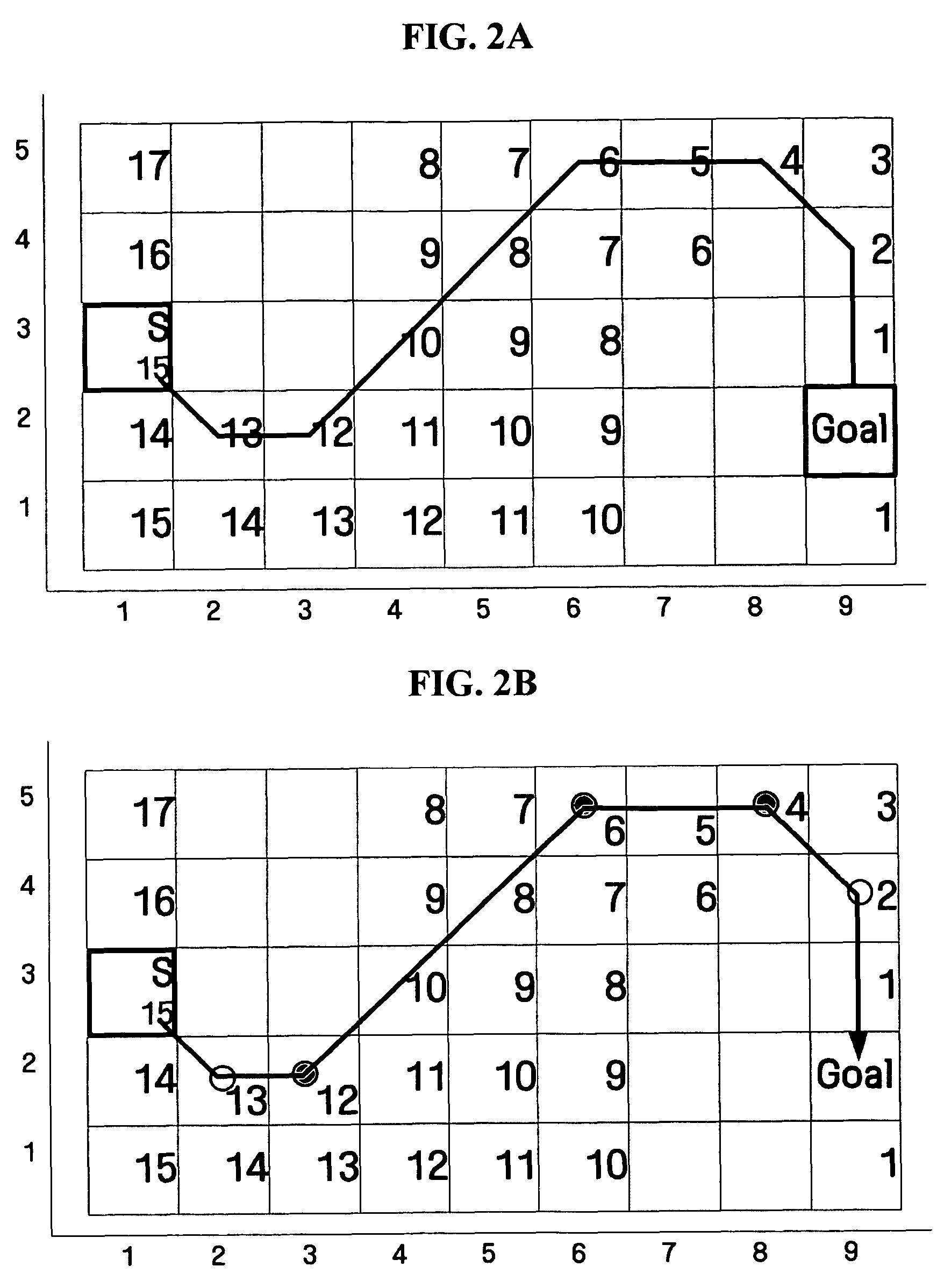
Method and apparatus for moving in minimum cost path using grid map
InactiveUS20060149465A1Instruments for road network navigationNavigational calculation instrumentsShortest distanceMinimum cost path
A method of moving in a minimum cost path using a grid map, and an apparatus to perform the method, the method including calculating a move cost to a goal, from each of a plurality of cells comprises in a space in which a mobile home appliance moves, and planning a movement path to the goal according to the move cost; determining one or more via points at which a direction changes on the movement path; planning the minimum cost path from the movement path by selecting one or more shortest-distance via points from the via points; and moving from a first shortest-distance via point to a second shortest-distance via point.
Owner:SAMSUNG ELECTRONICS CO LTD
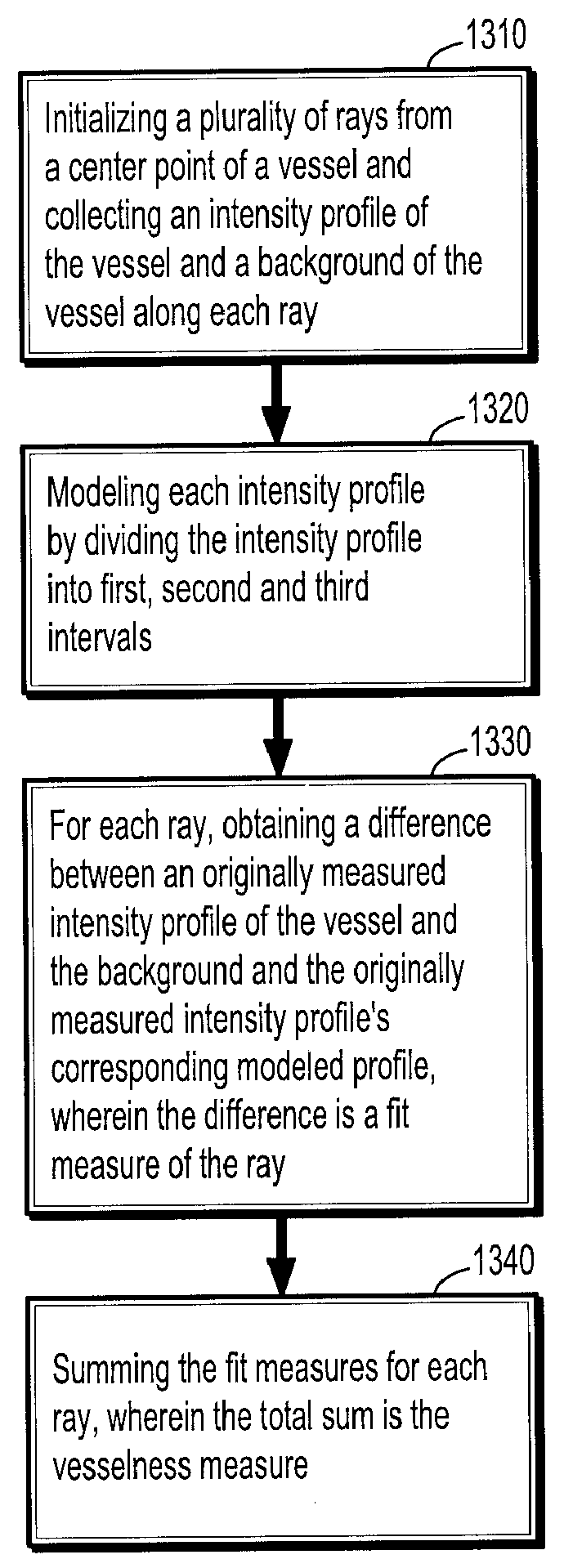
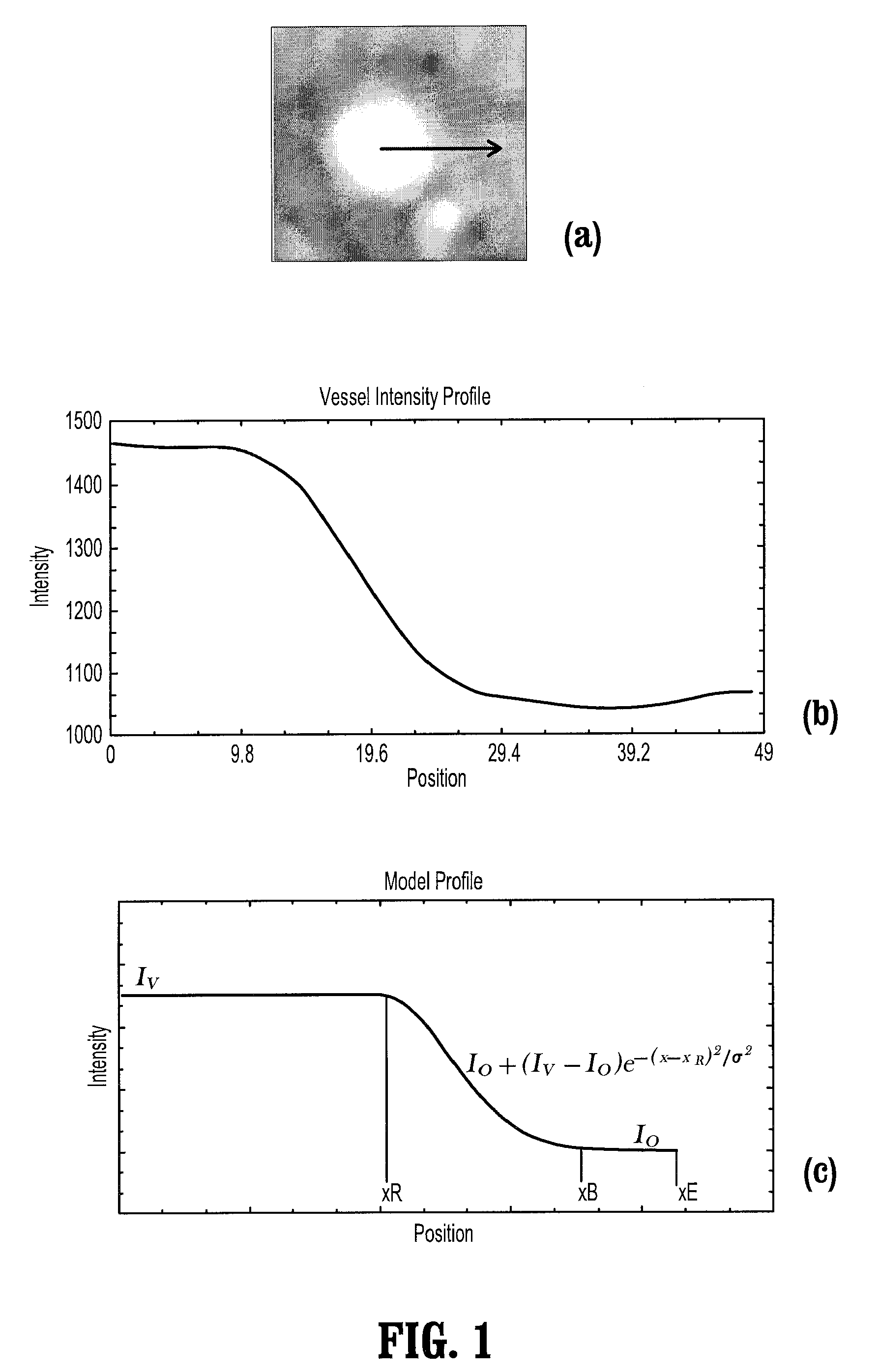
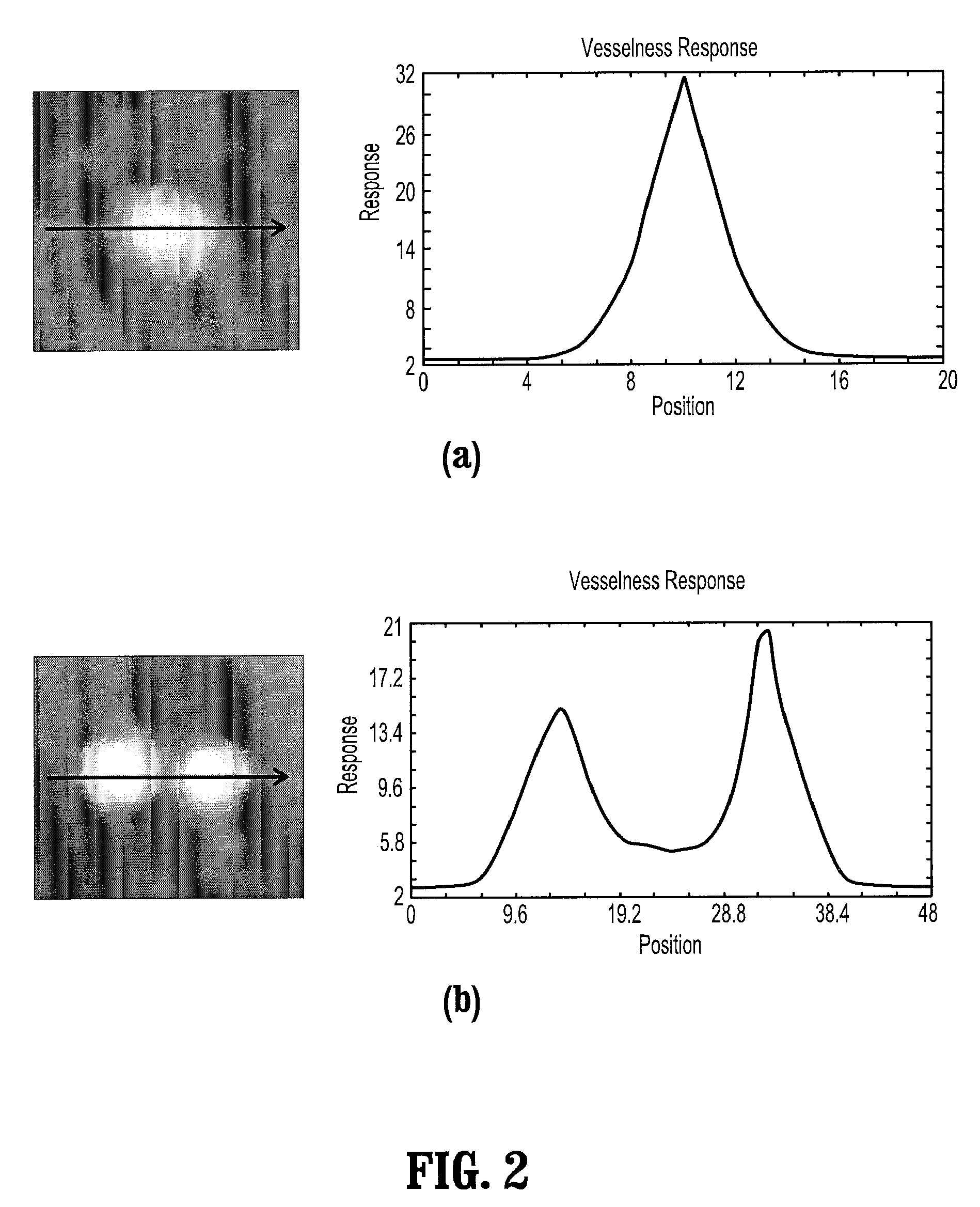
Robust vessel tree modeling
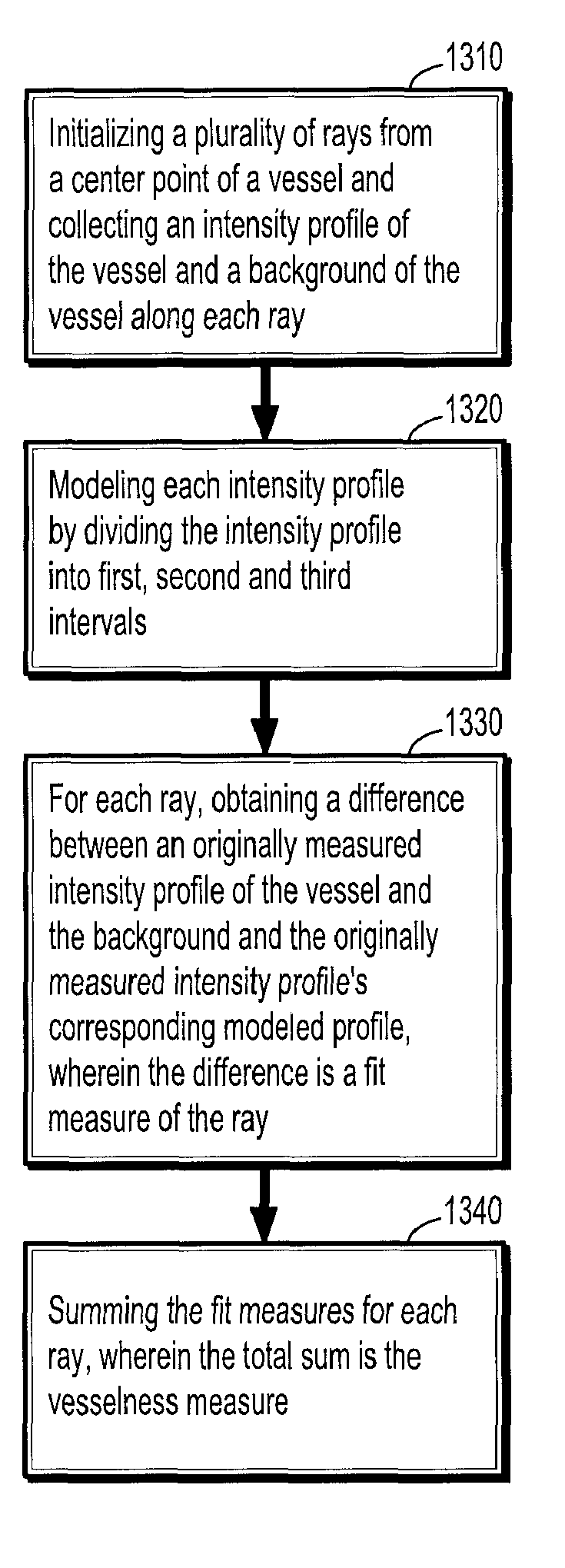
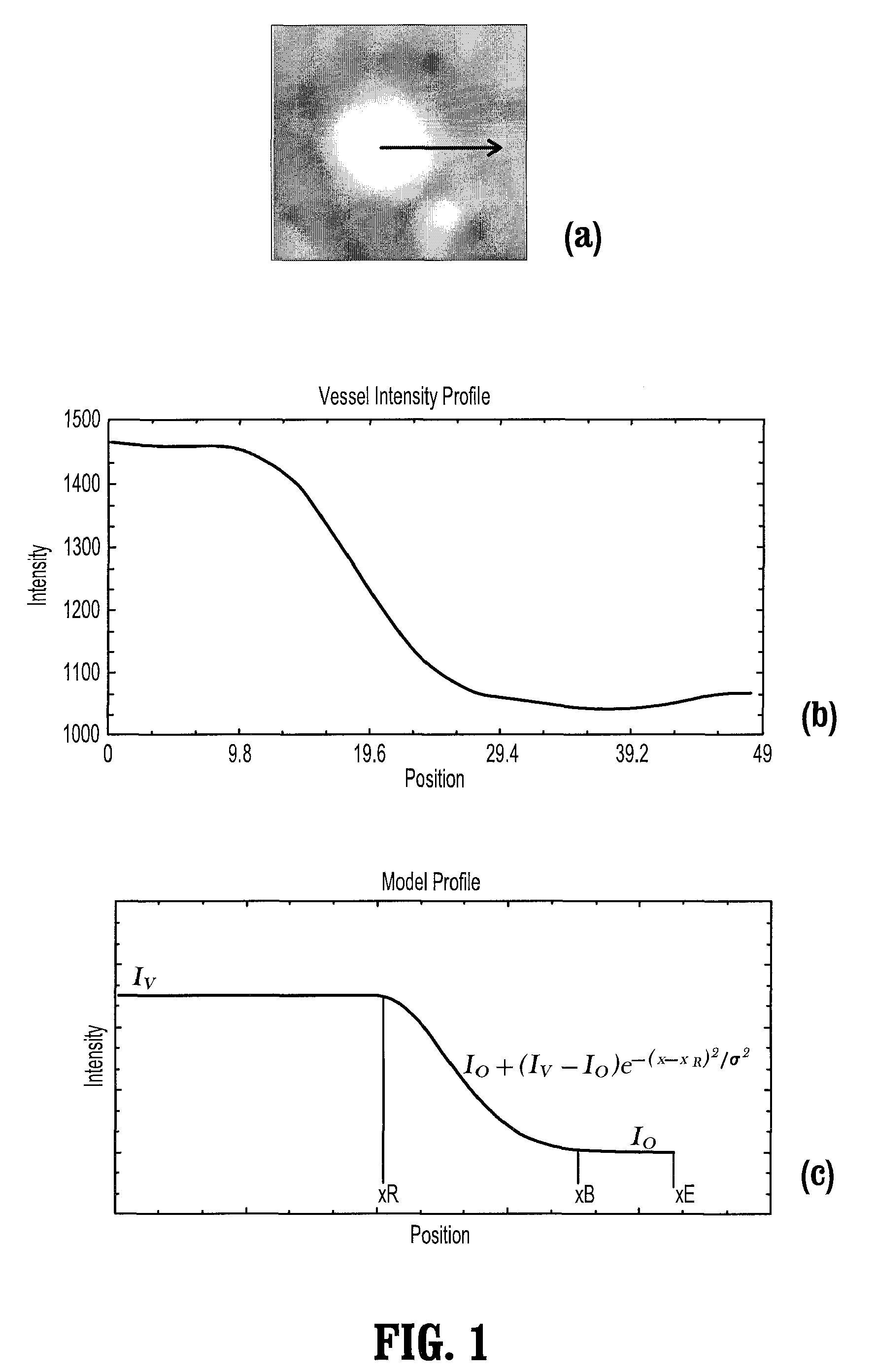
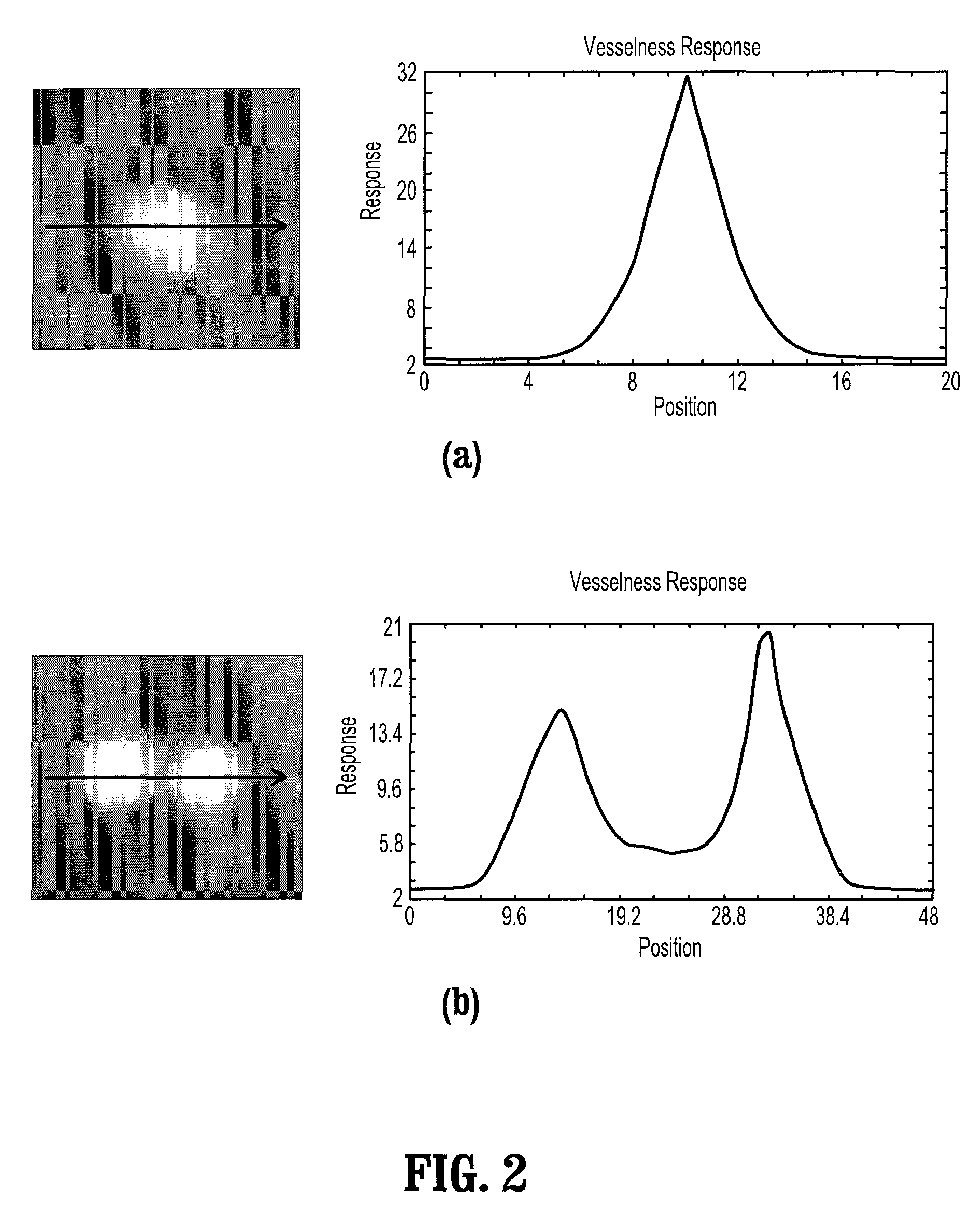
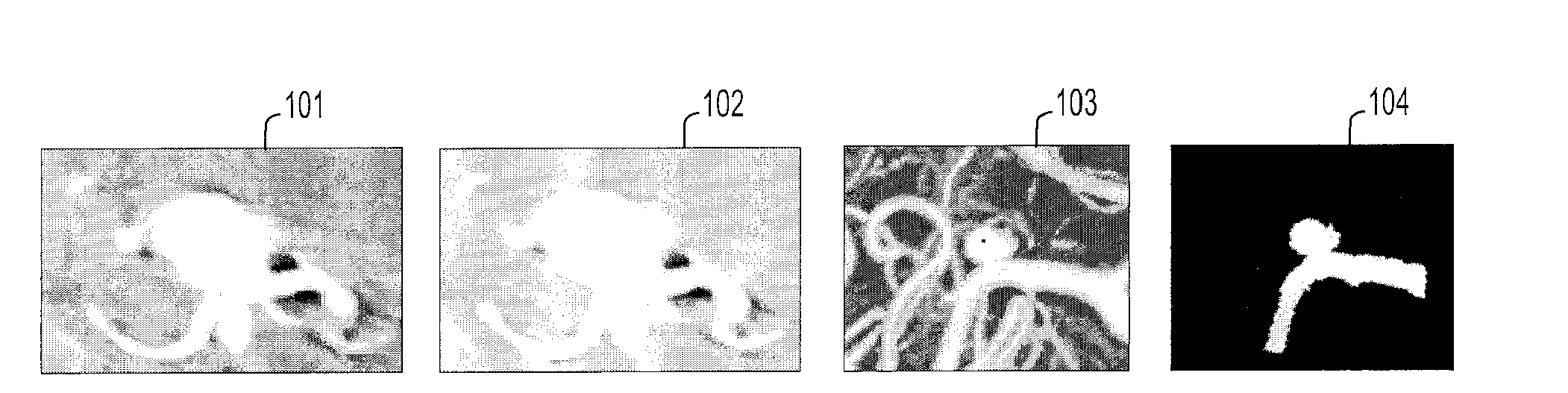
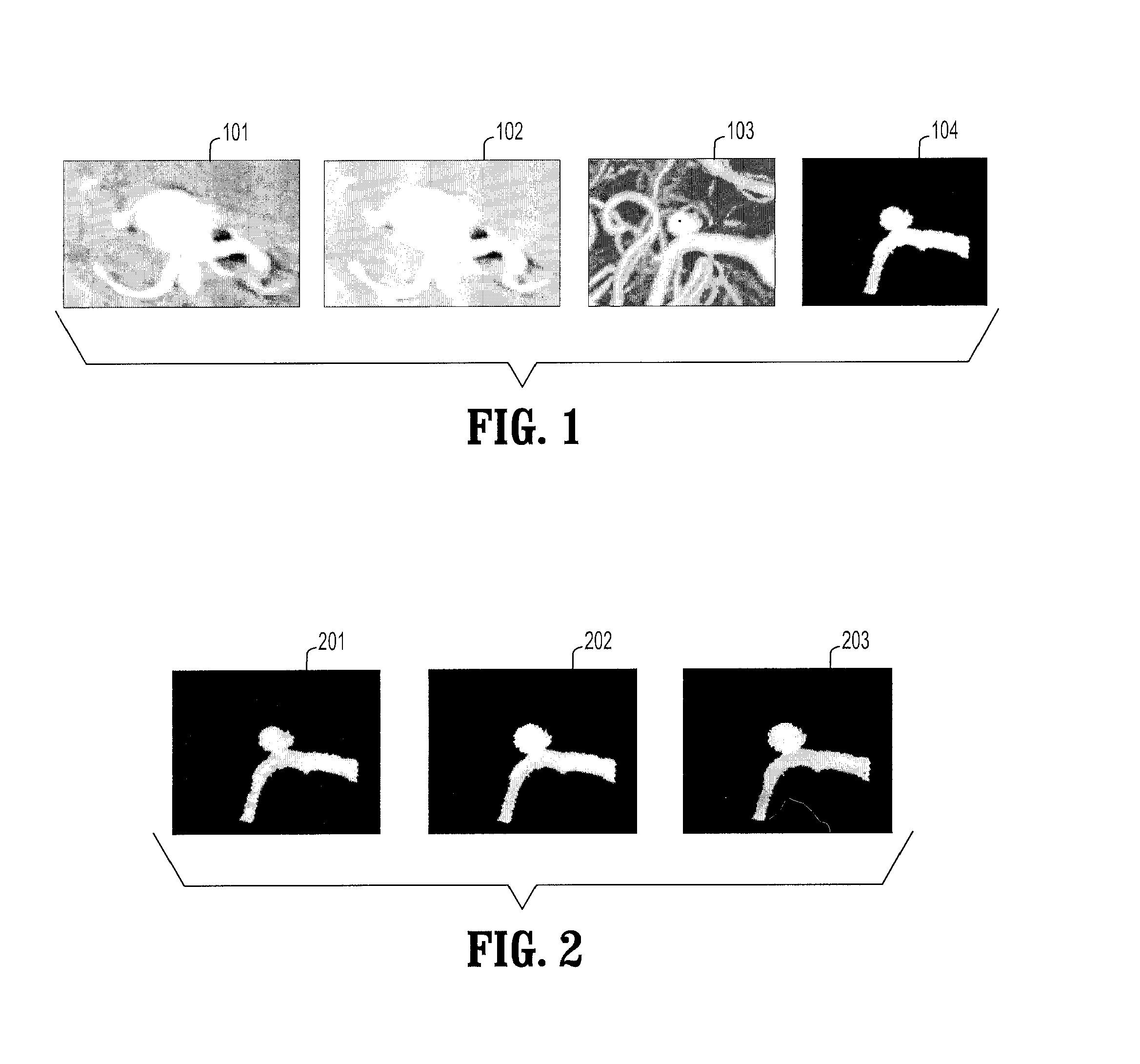
A method for extracting a local center-axis representation of a vessel, includes: placing first and second seed points in an image that includes the vessel, wherein the first and second seed points are placed near a beginning and an end of a centerline of the vessel; representing the image as a discrete graph having nodes and edges, wherein the first seed point is a source node and the second seed point is a goal node; and finding a minimum-cost path between the first and second seed points by computing a cost of edges between the first and second seed points, wherein the cost of each edge is reciprocal to a vesselness measure of the edge.
Owner:SIEMENS HEALTHCARE GMBH +1
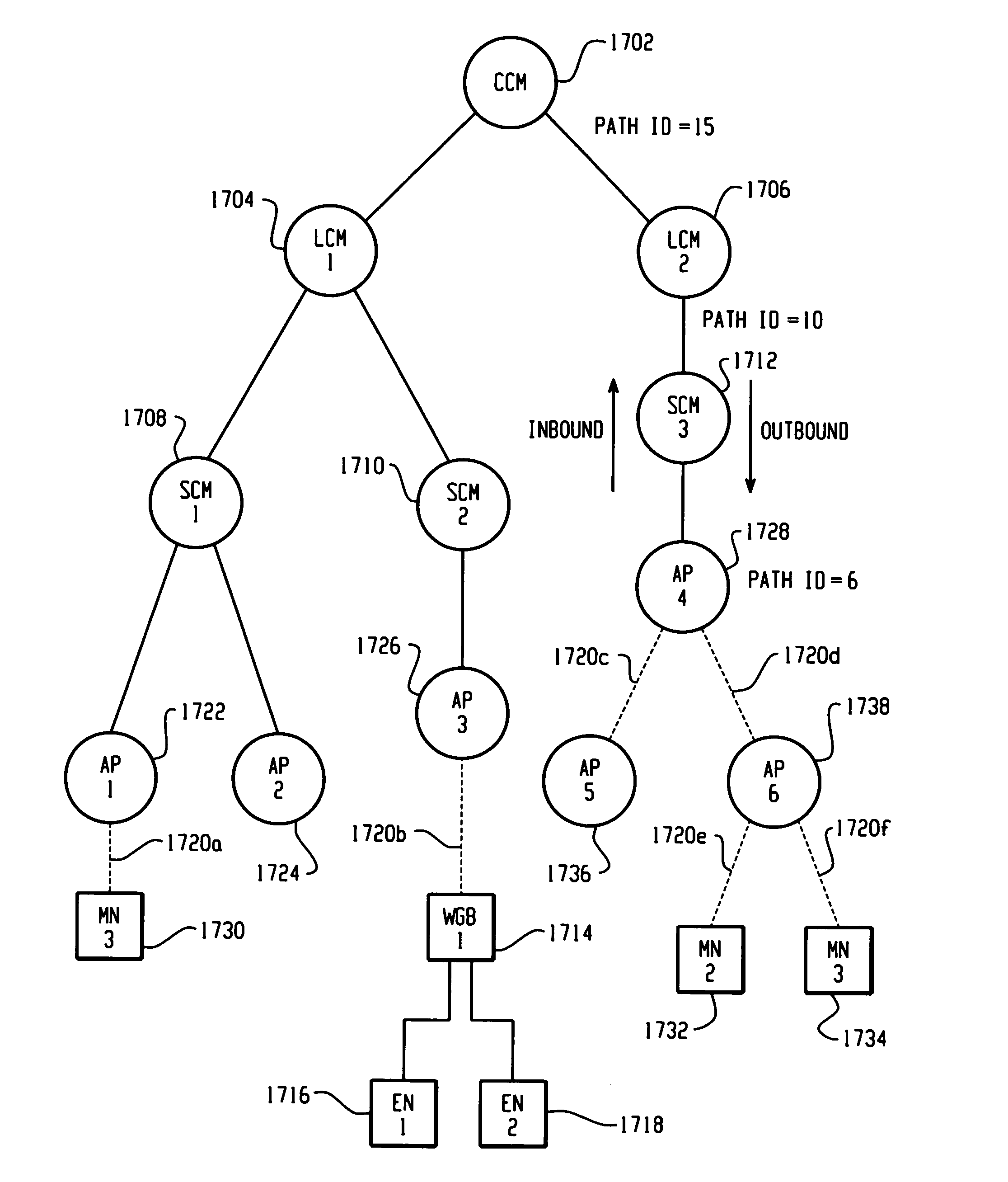
Wireless local area network context control protocol
ActiveUS20050220054A1Easy to optimizeOperational securityNetwork topologiesDigital computer detailsPathPingMobile station
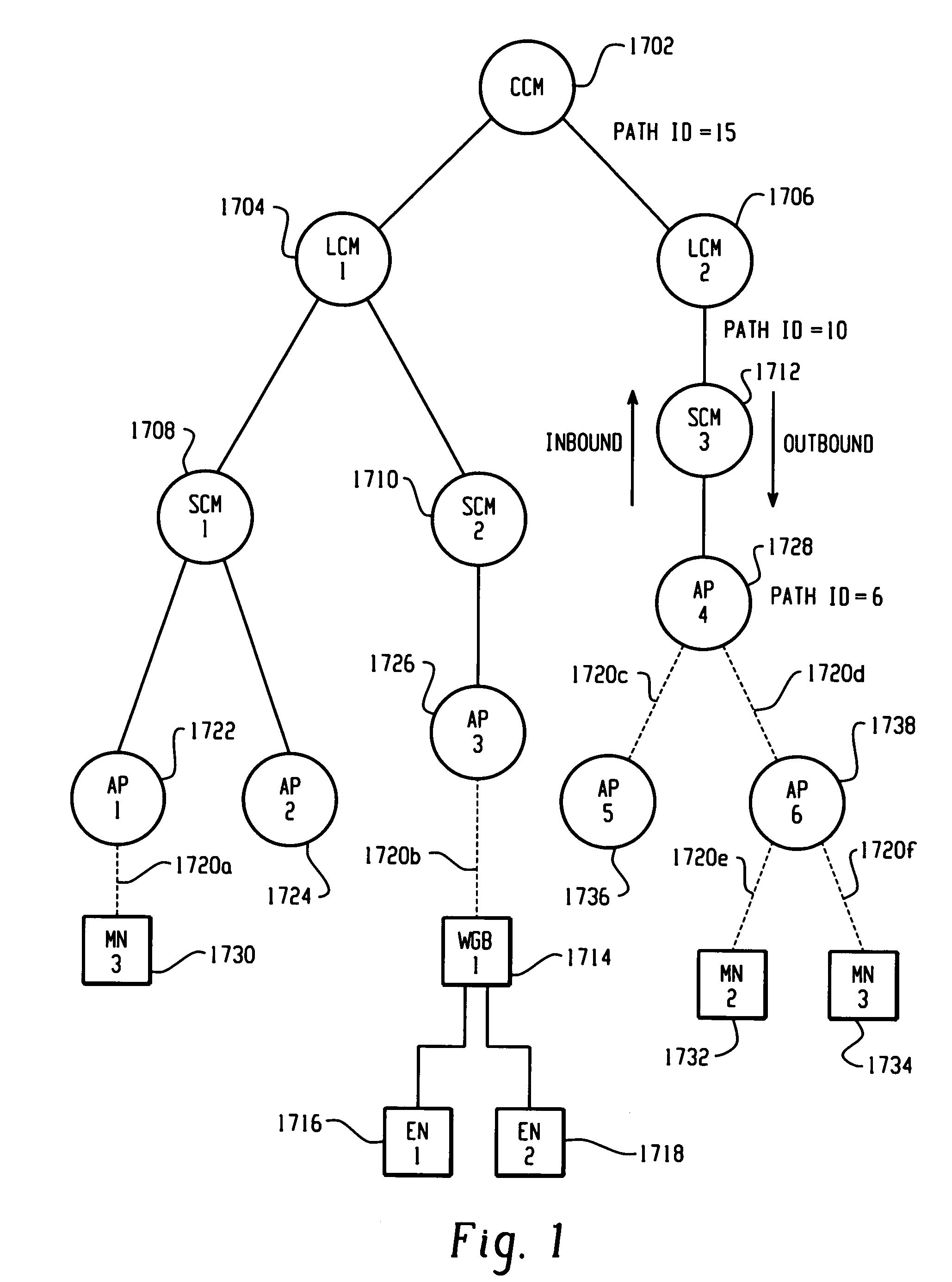
A Wireless LAN Context Control Protocol (WLCCP) is used to establish and manage a wireless network topology and securely manages the “operational context” for mobile stations in a campus network. The WLCCP registration protocol can automatically create and delete links in the network, securely distribute operational context, and reliably establish Layer 2 forwarding paths on wireless links. A single infrastructure node is established as the central control point for each subnet, and enables APs and MNs to select the parent node that provides the “least-cost path” to a backbone LAN. Context messages provide a general-purpose transport for context and management information. WLCCP “Trace” messages facilitate network diagnostic tools. Ethernet or UDP / IP encapsulation can be used for WLCCP messages. Ethernet encapsulation is employed for intra-subnet (e.g. AP-to-AP or AP-to-SCM) WLCCP messages. IP encapsulation is used for inter-subnet WLCCP messages and may also be used for intra-subnet WLCCP messages.
Owner:CISCO TECH INC
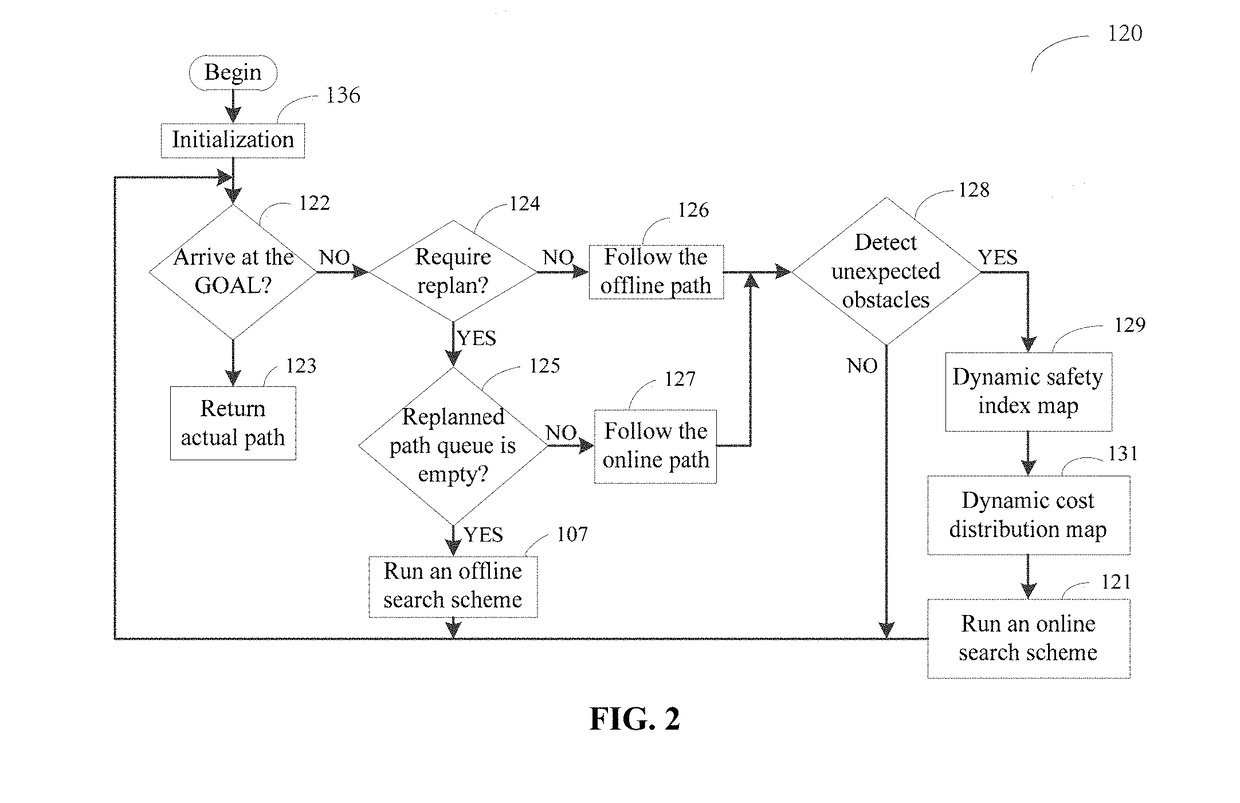
Joint search method for UAV multiobjective path planning in urban low altitude environment
ActiveUS20180308371A1Lower requirementReduce computational complexityRemote controlled aircraftTarget-seeking controlSafety indexPath plan
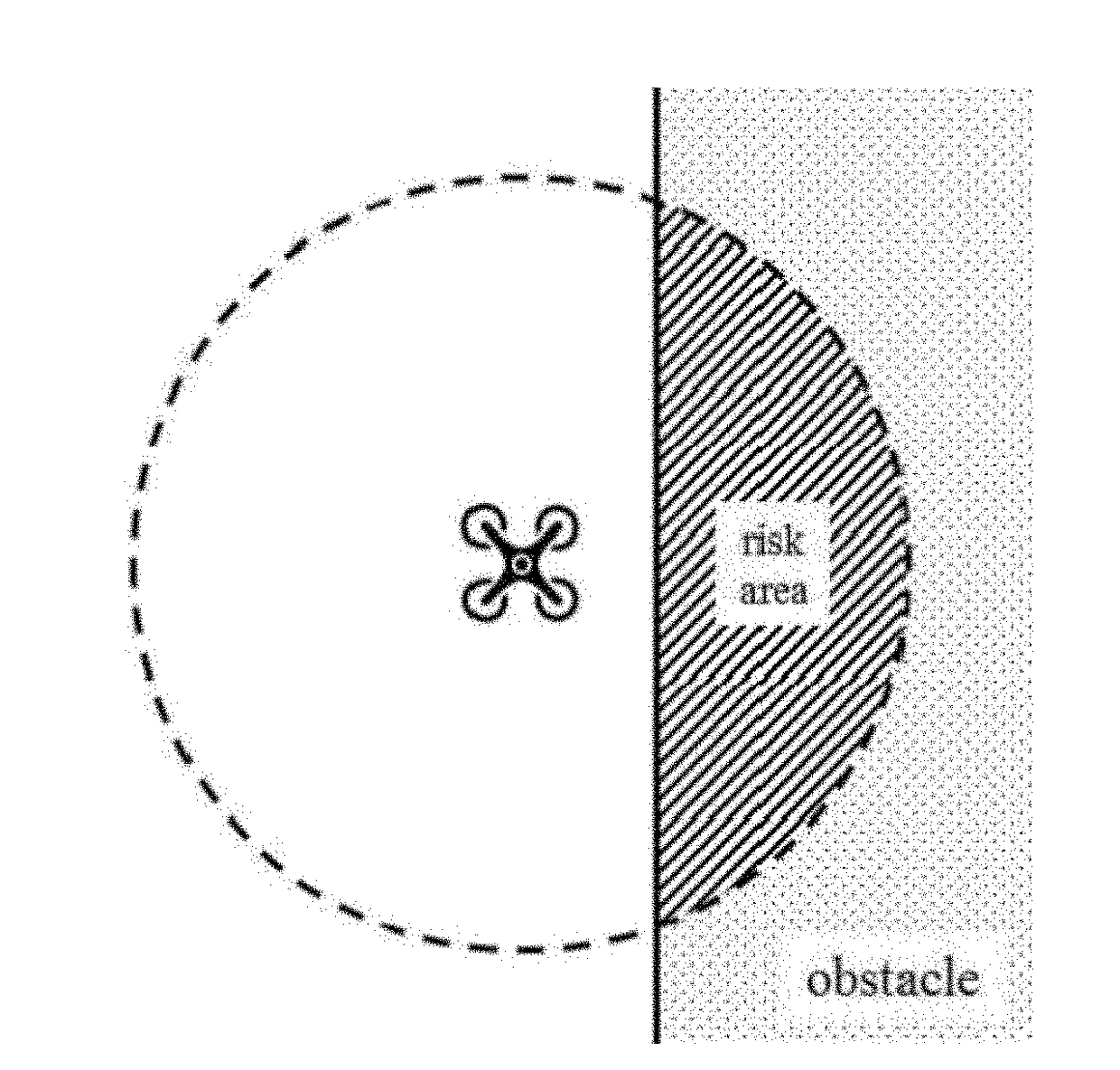
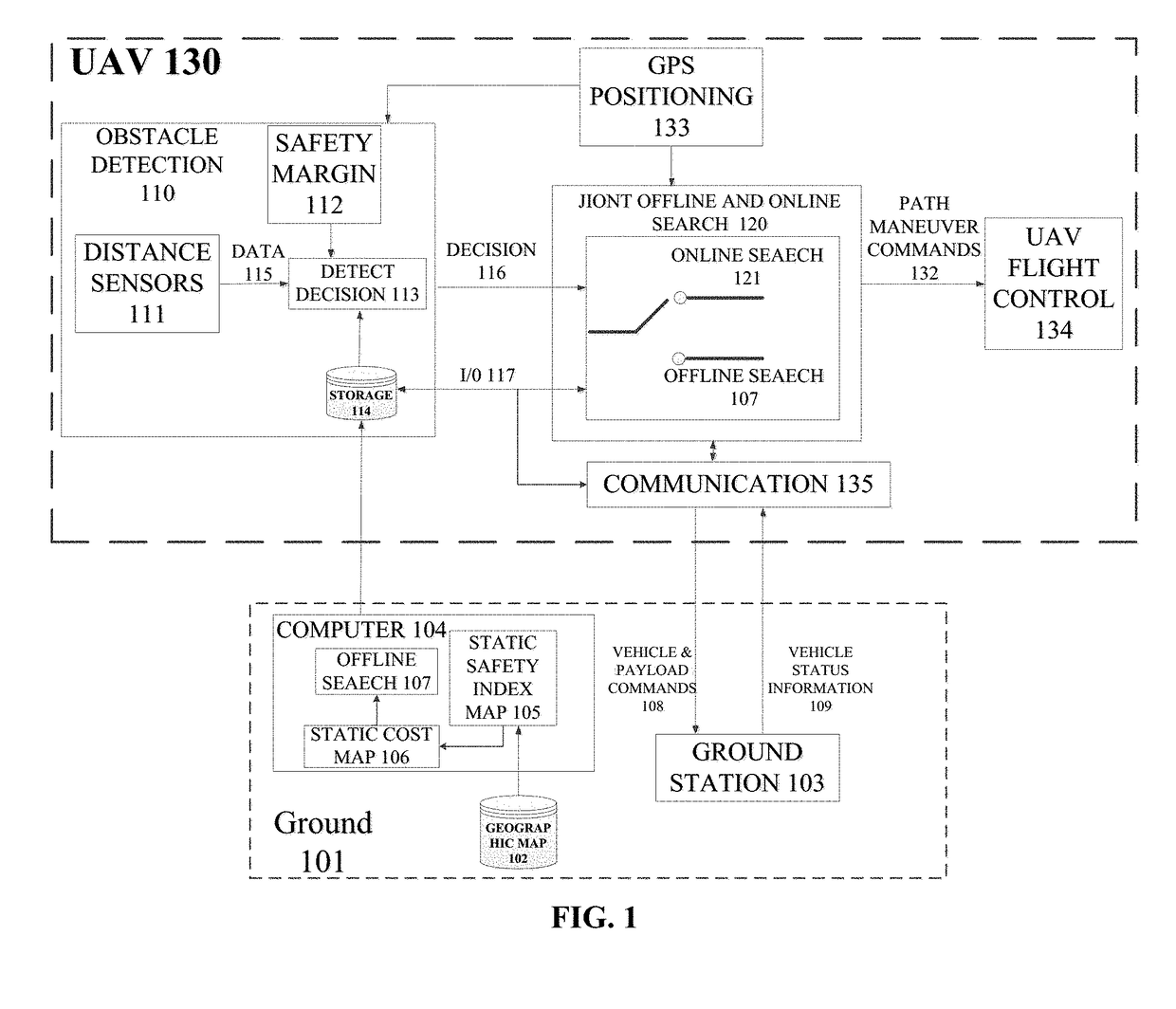
A joint search method for UAV multiobjective path planning in an urban low altitude environment first constructs a static safety index map based on static known obstacles. Meanwhile, based on proactively detected obstacles that are not marked on a geographic map by a UAV, the method constructs online a dynamic safety index map. Second, a multiobjective path planning problem is solved using a joint offline and online search method. Moreover, this method first plans offline the least cost path from a starting point to an end point and then invokes the online search scheme to replan online a changed path when the UAV detects unknown obstacles. Thus, the UAV can avoid dynamic obstacles effectively. The online search scheme has a small search space and can quickly replan a safe path for the UAV, thus satisfying the requirement of UAV on the real-time path planning.
Owner:BEIHANG UNIV
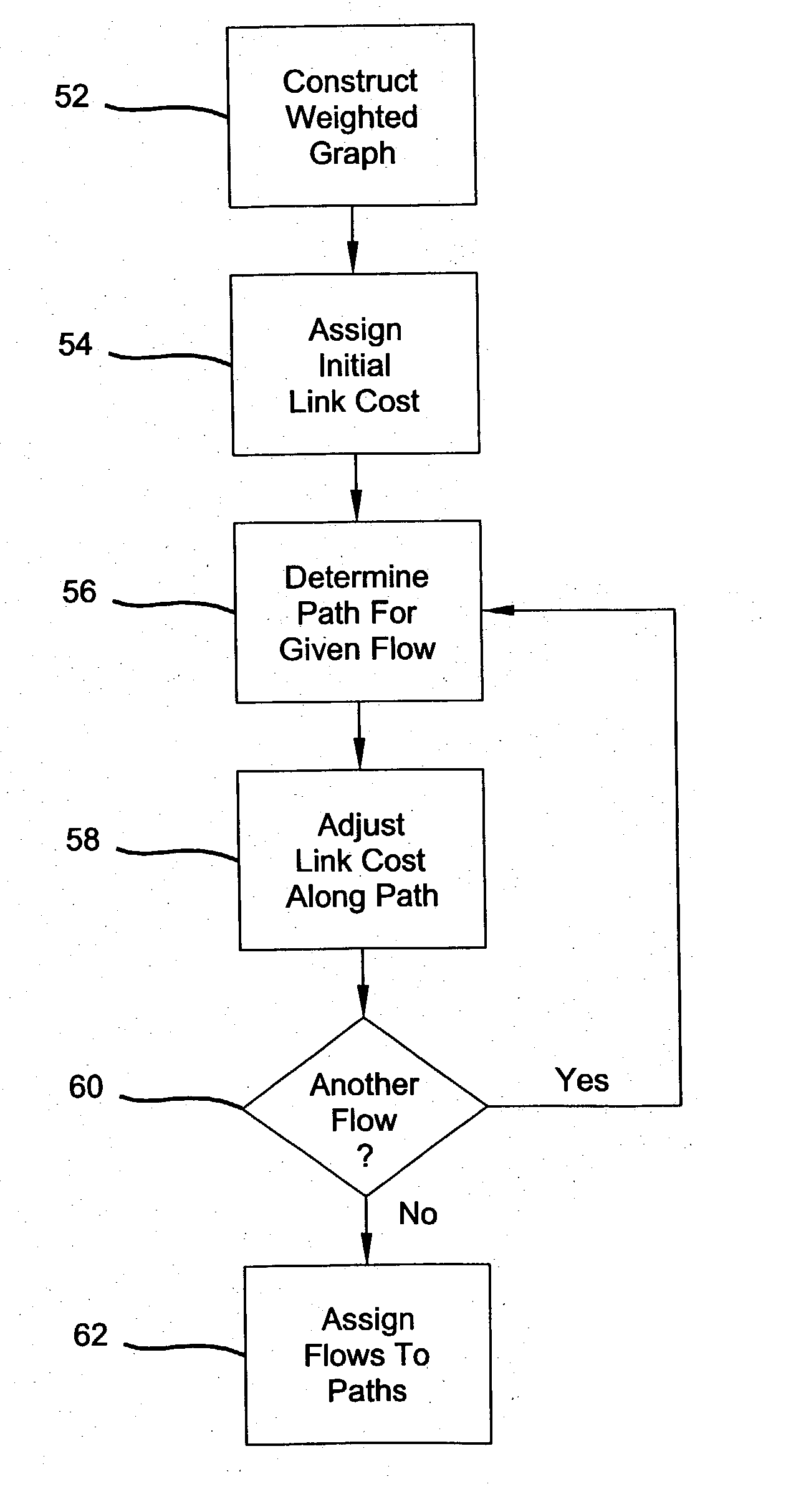
Static dense multicast path and bandwidth management
Improved algorithms are provided for performing path management for a plurality of select data transmission sessions in a multicast network. The algorithms include: constructing a weighted graph which represents topology of the network; assigning load correlated costs to network links; and computing least cost paths for each of the data transmission sessions which accounts for global bandwidth utilization.
Owner:PANASONIC CORP
Static dense multicast path and bandwidth management
Improved algorithms are provided for performing path management for a plurality of select data transmission sessions in a multicast network. The algorithms include: constructing a weighted graph which represents topology of the network; assigning load correlated costs to network links; and computing least cost paths for each of the data transmission sessions which accounts for global bandwidth utilization.
Owner:PANASONIC CORP
Systems and methods for multipath routing
InactiveUS20060133282A1Provides redundancyError preventionTransmission systemsBalancing networkDatapath
A method and system for directing data packets from an origin node to a destination node in a multipath communication network having a plurality of nodes, where each node is connected to at least one other node by links. The apparatus includes a processor for obtaining cost information relating to each link in the network and for determining the least-cost route between the origin node and the destination node based on the cost information relating to each link. The processor establishes a cost margin representing a range of costs above the cost of the least cost route and identifies one or more alternate routes. A data storage device stores the cost information, and a network interface selectively routes the data packets through one or more of the least cost route and the one or more alternate routes falling within the established cost margin thus balancing the network load and providing alternate data paths in case the least-cost path is unavailable.
Owner:AVAYA INC
Robust Vessel Tree Modeling
A method for extracting a local center-axis representation of a vessel, includes: placing first and second seed points in an image that includes the vessel, wherein the first and second seed points are placed near a beginning and an end of a centerline of the vessel; representing the image as a discrete graph having nodes and edges, wherein the first seed point is a source node and the second seed point is a goal node; and finding a minimum-cost path between the first and second seed points by computing a cost of edges between the first and second seed points, wherein the cost of each edge is reciprocal to a vesselness measure of the edge.
Owner:SIEMENS HEATHCARE GMBH +1
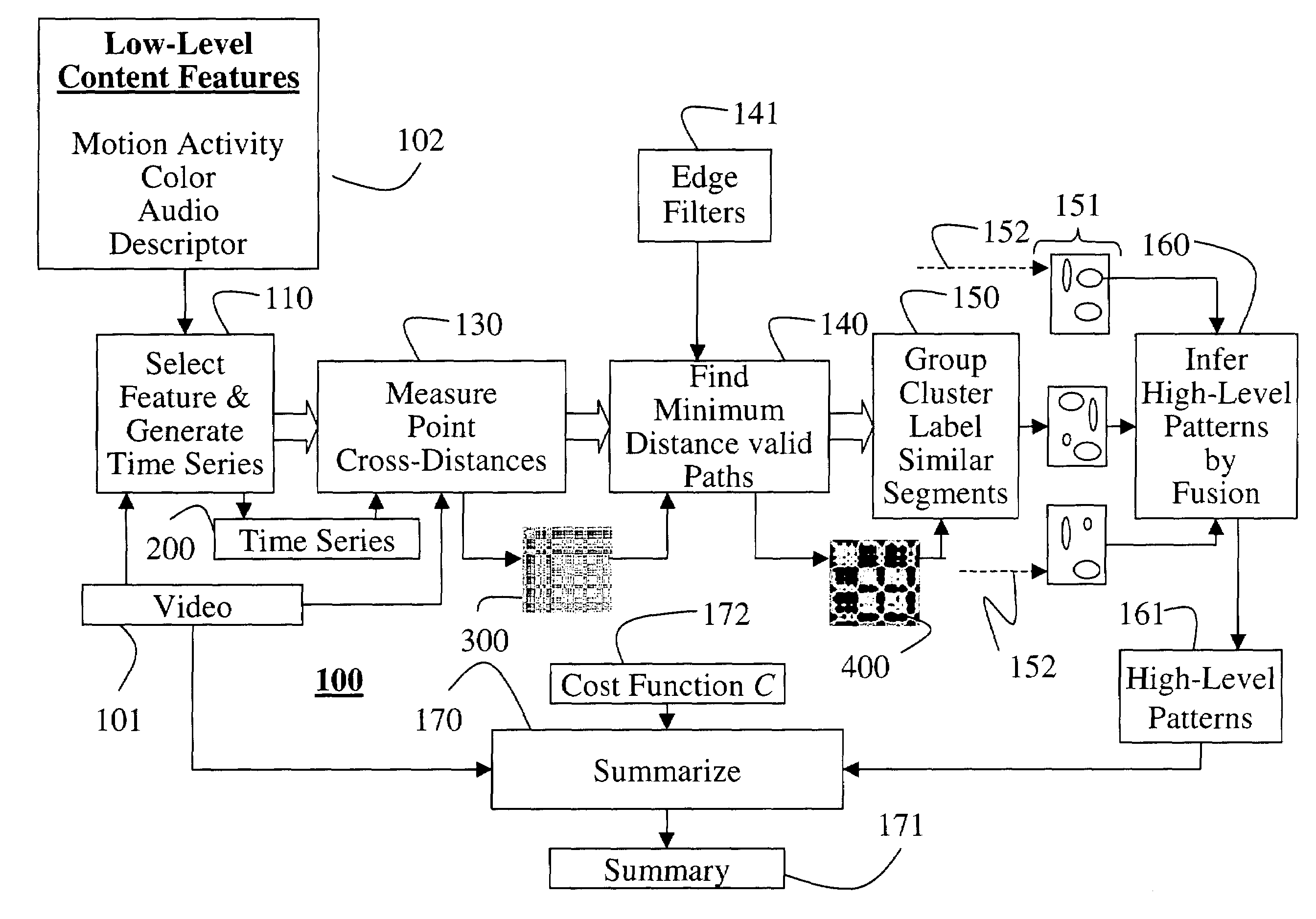
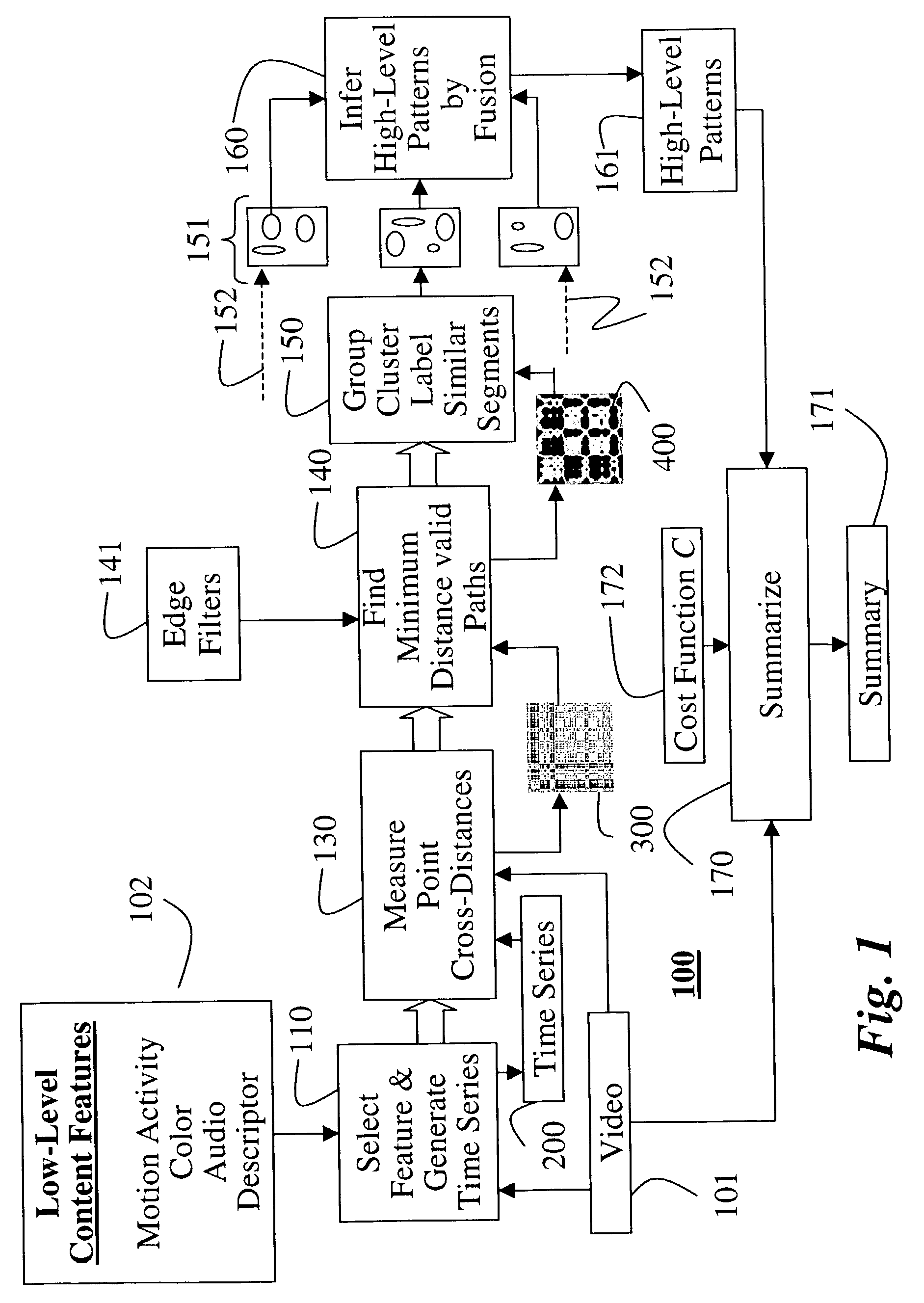
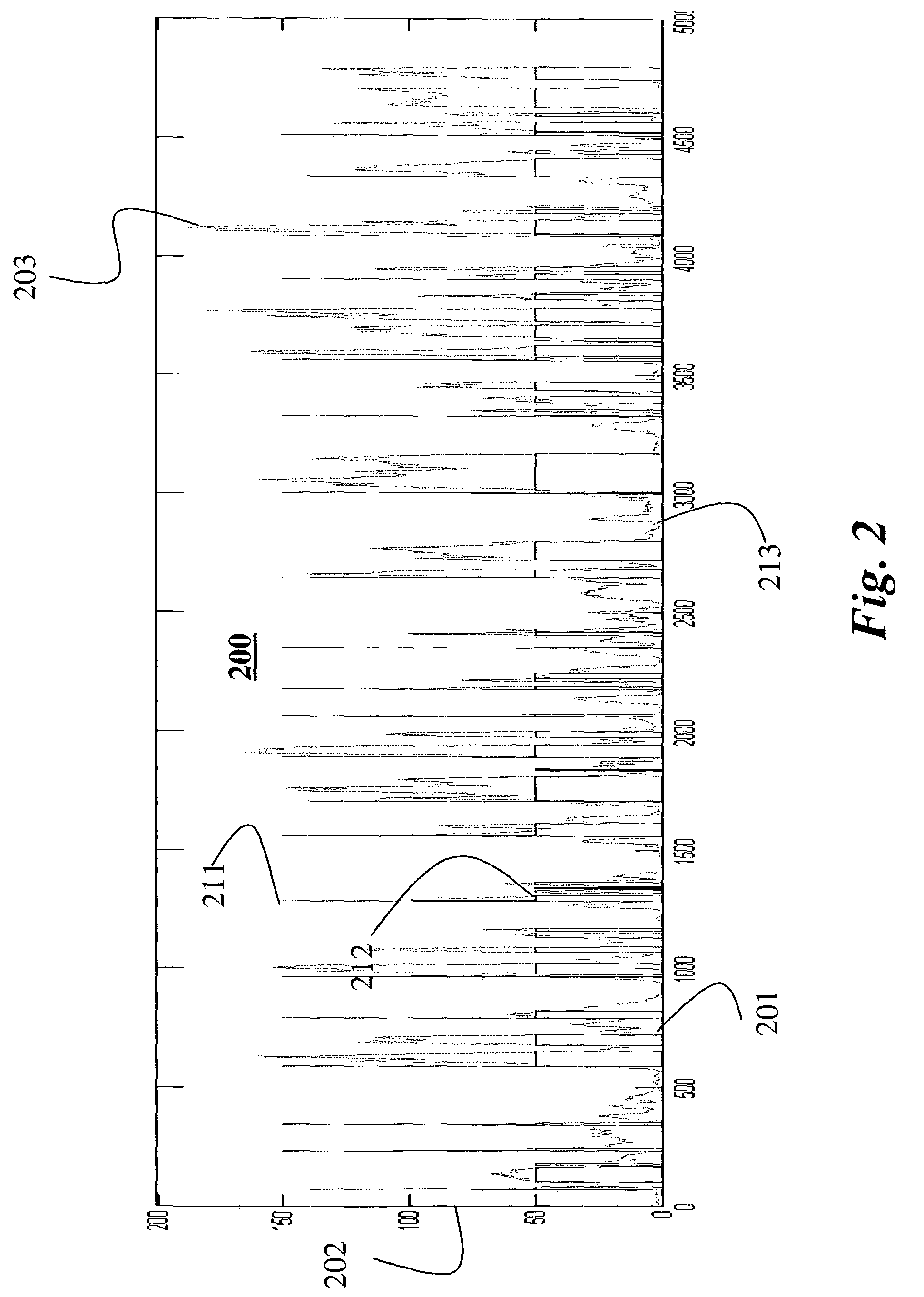
Pattern discovery in multi-dimensional time series using multi-resolution matching
A method discovers patterns in unknown multi-dimensional data. A time-series of the multi-dimensional data is generated and a point cross-distance matrix is constructed by self-correlating the time-series. All minimum cost paths in the point cross-distance matrix are located at multiple time resolutions. The minimum cost paths are then related to temporal sub-sequences in the multi-dimensional data to discover high-level patterns in the unknown multi-dimensional data.
Owner:MITSUBISHI ELECTRIC RES LAB INC
Texture synthesis and transfer for pixel images
InactiveUS6919903B2Texturing/coloringCathode-ray tube indicatorsComputer graphics (images)Texture transfer
The invention provides an image-based method for generating novel visual appearance in a new image. Synthetic texture is stitching together from small patches in existing images. First, we use a least cost path determination to determine the local boundaries between the patches. Second, we perform texture transfer by rendering an arbitrary object with a synthetic texture taken from a different object. More generally, we provide methods for rendering entire images in styles of different images. The method works directly on pixel images, and does not require 3D information.
Owner:MITSUBISHI ELECTRIC INFORMATION TECH CENT AMERICA ITA +1
Method for determining similarities between data sequences using cross-correlation matrices and deformation functions
InactiveUS20050102107A1Character and pattern recognitionBiological testingCross correlation matrixMinimum cost path
A method compares a first data sequence with a second data sequence. A cross-correlation matrix of distances between all possible pairs of values of the first and second data sequences is constructed. A minimum cost path between diagonally opposing corners of the cross-correlation matrix is determined. The minimum cost path is projected onto a transfer function that maps between the first data sequence and the second data sequence. Then, the minimum cost path is projected onto a deformation function that corresponds to a similarity between the first data sequence and the second data sequence.
Owner:MITSUBISHI ELECTRIC RES LAB INC
Load balancing in a network comprising communication paths having different bandwidths
ActiveUS20040024906A1Low costEvenly distributedEnergy efficient ICTDigital computer detailsComputer networkHigh bandwidth
A network comprises a plurality of interconnected switches. At least one pair of switches is interconnected by a trunk formed from a plurality of individual links. A cost value is assigned to the trunk that is equal to the cost of one of the trunk's individual links. As such, a trunk is considered the same as an individual link when shortest path calculations are made. When multiple paths are computed as having the same lowest cost, the system balances load traffic between such lowest cost paths in a way that takes advantage of the higher bandwidth capabilities of trunks.
Owner:AVAGO TECH INT SALES PTE LTD
Method and apparatus for moving in minimum cost path using grid map
InactiveUS7953551B2Instruments for road network navigationNavigational calculation instrumentsShortest distanceMinimum cost path
Owner:SAMSUNG ELECTRONICS CO LTD
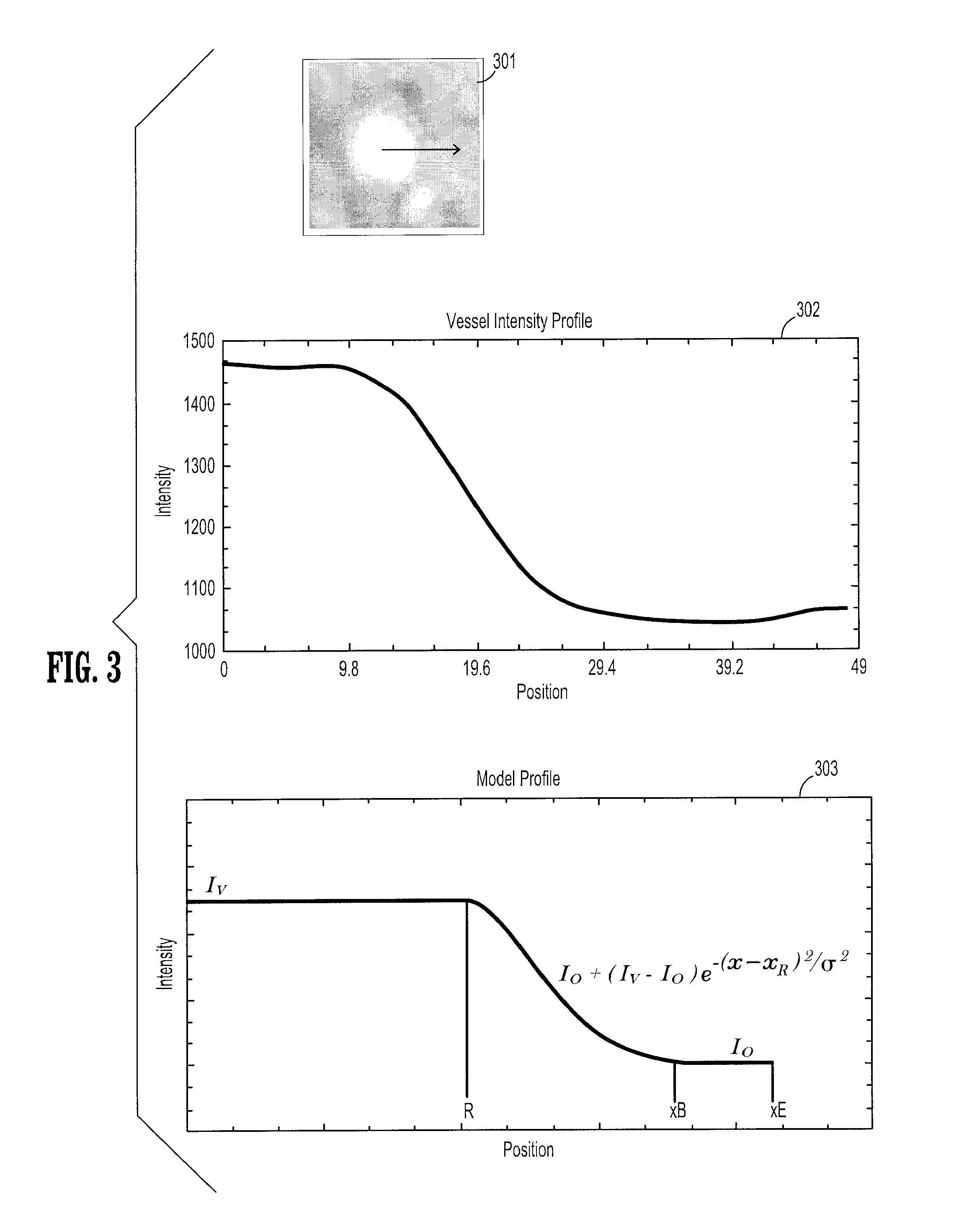
Modeling Cerebral Aneurysms in Medical Images
Methods and systems for modeling cerebral aneurysm and their incoming and outgoing vessels from 3D image data are disclosed. Aneurysms and vessels are segmented from their background using a graph-cuts method. Begin and end of vessels are determined. Construction of a centerline of the incoming and outgoing vessels using a measure of vesselness in calculating a minimum cost path in a graph with nodes being representation of pixels is also disclosed. Vessel surface models are constructed from sub-voxel cross-sectional segmentation. The interpolation of vessels inside an aneurysm based on smooth continuity is disclosed. Selection of endo-vascular stents based on interpolation results is also provided.
Owner:SIEMENS HEALTHCARE GMBH
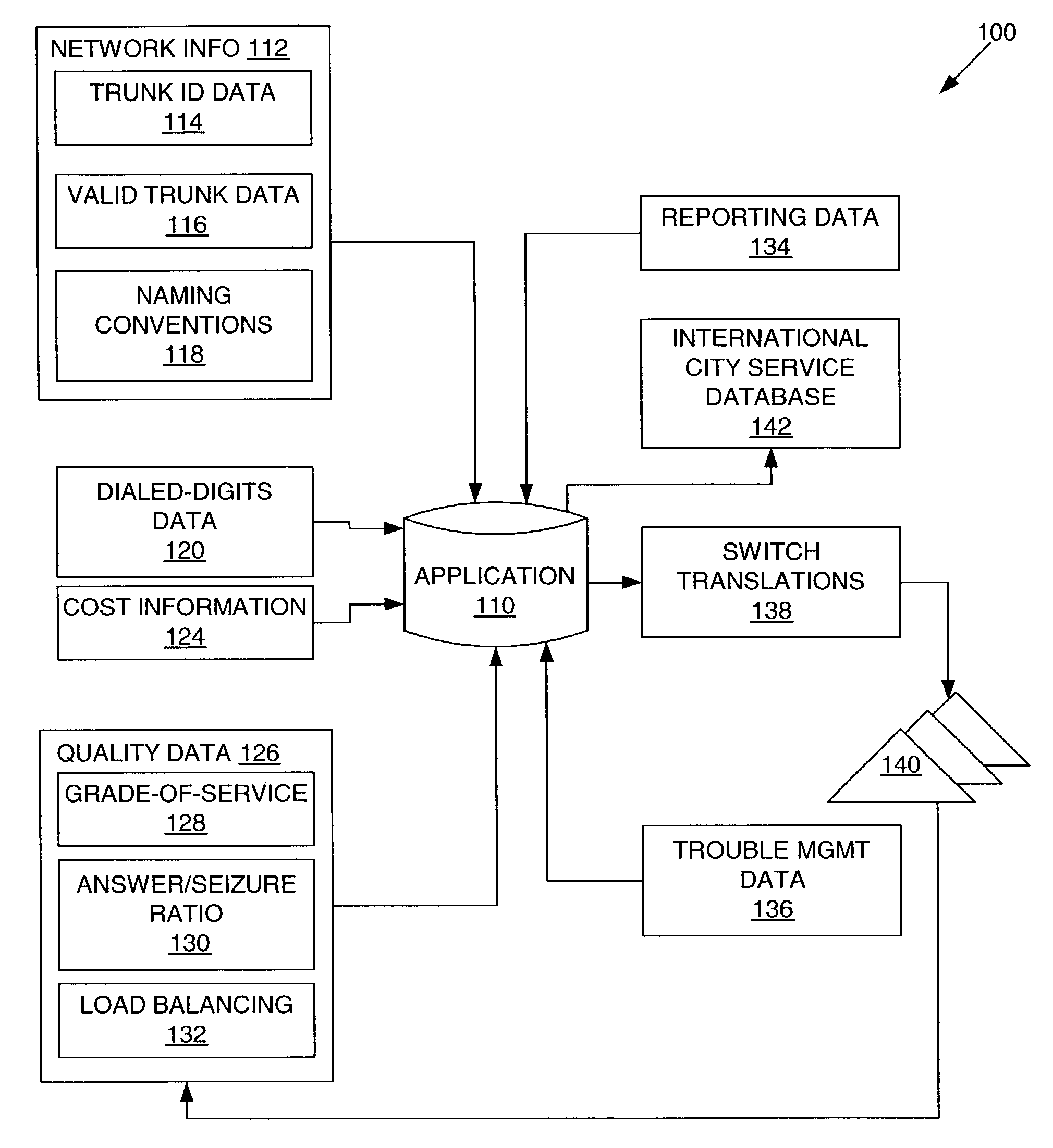
Method and system for determining a least cost path for routing international communications traffic
InactiveUS7352852B1Easily and accurately and efficiently determineFacilitate communicationTelephonic communicationIdentifying VariableTelecommunications network
A method, system, and medium for determining a least-cost, international-routing path to communicate data across a telecommunications network are provided. The path implementation variables can be presented on a user interface or used to automatically generate a switch update transaction that implements the path. The method includes identifying variables that affect the determination of a least-cost path, receiving data values that correspond to the variables, and presenting the data values so that the path can be determined in response to observing the variables. Confidence and route testing can be conducted using the present invention.
Owner:SPRINT CORPORATION
Congestion control method and network nodes
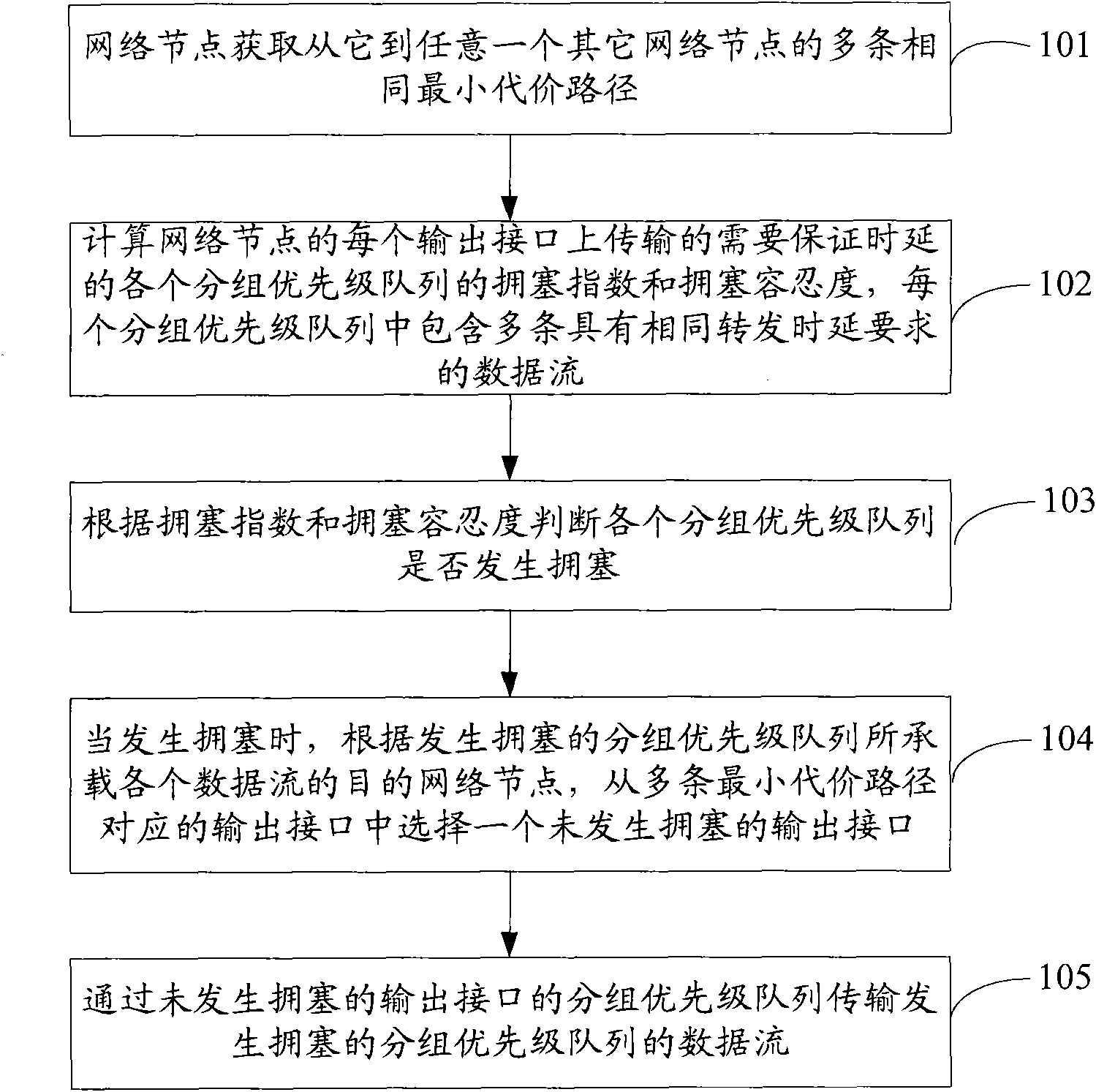
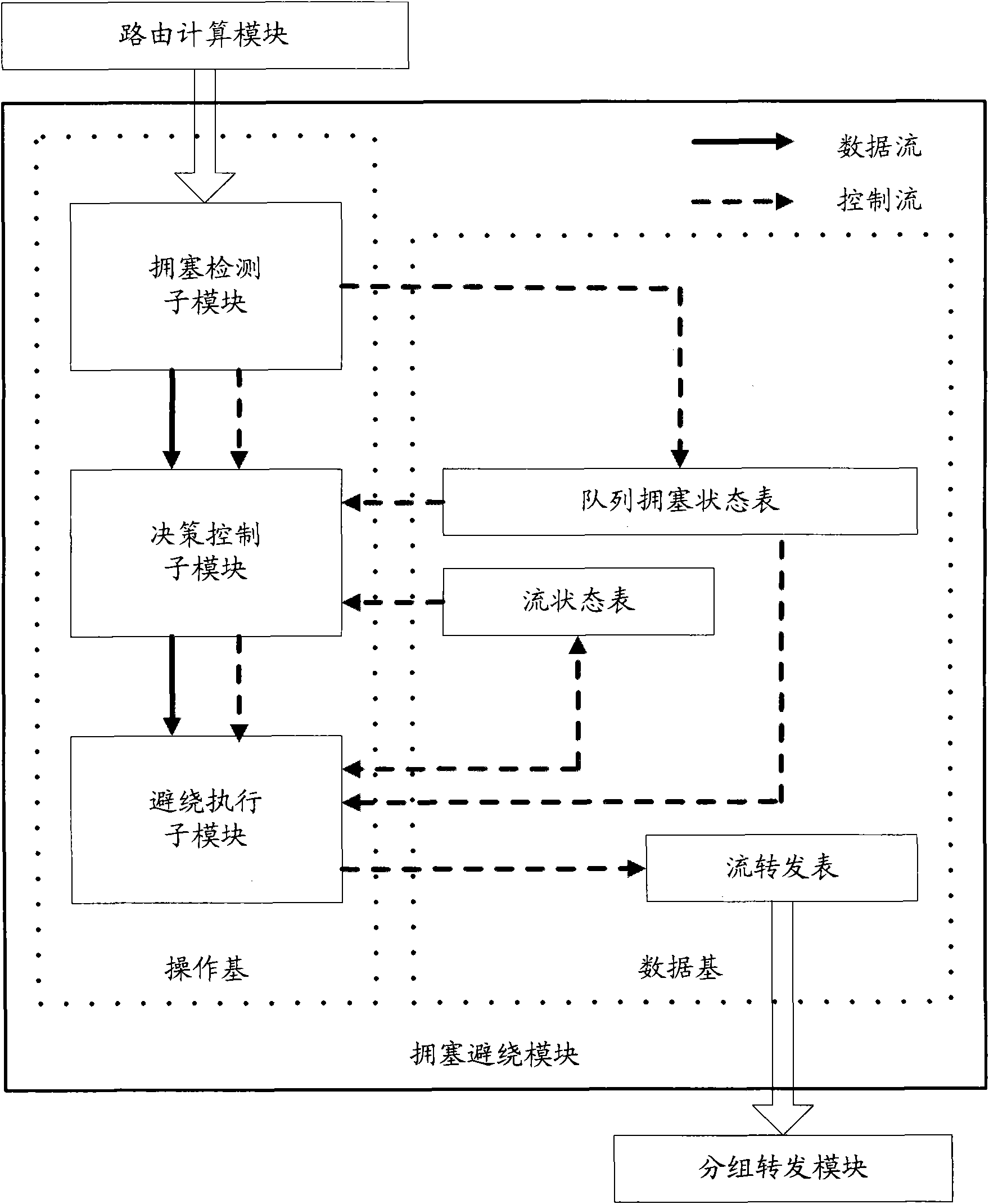
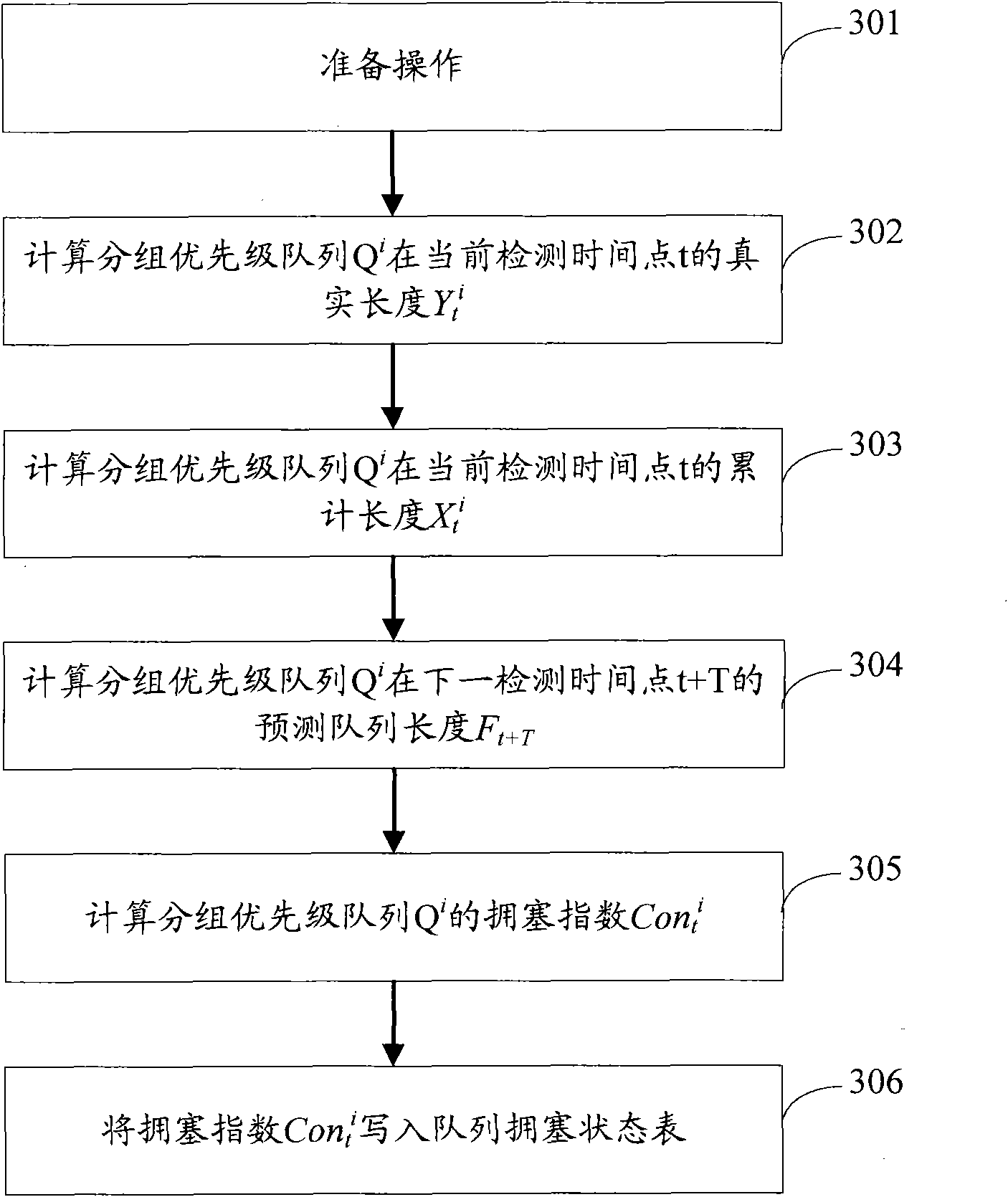
InactiveCN101656674AAccurate transmissionTake advantage ofData switching networksData streamTime delays
The invention discloses a congestion control method and network nodes. The method comprises the following steps: acquiring a plurality of minimum cost paths from one network node to the other networknodes by the network node; computing the congestion index and the congestion tolerability of each grouping priority sequence which is transmitted on each output interface of the network nodes and needs ensuring time delay; judging whether various grouping priority sequences are congested or not according to the congestion index and the congestion tolerability; when the congestion occurs, selectingone output interface which is not congested from output interfaces corresponding to the minimum cost paths according to destination network nodes of various data streams carried by the congested grouping priority sequence; and transmitting the data stream of the congested grouping priority sequence through the grouping priority sequence of the output interface which is not congested. The embodiment of the invention fully utilizes forward resources in the network and ensures that the congested grouping priority sequence correctly transmits.
Owner:THE PLA INFORMATION ENG UNIV
Method for guaranteeing end-to-end QoS in SDN network
The invention discloses a method for guaranteeing the end-to-end QoS in an SDN network, comprising the following steps: (1) for each new data flow arriving at an SDN network, an SDN network controller periodically collects network status information; (2) the SDN network controller calculates the cost of each of all alternative paths for transmitting the new data flow according to the collected network status information, and determines an optimal transmission path; and (3) the SDN network controller packages the information of the optimal transmission path into a flow entry and issues the flow entry to a switch node of the SDN network, and the switch node forwards a received data packet according to the flow entry. According to the invention, an OpenFlow switch queue mechanism is designed, and the queue status of the switch is monitored in real time through the controller. When a new data flow arrives, a minimum-cost path is selected to transmit the data flow according to the transmission delay of the link on the path and the queuing delay of the switch node queue as well as the congestion situation of the current link.
Owner:INST OF INFORMATION ENG CHINESE ACAD OF SCI
Navigation devices and methods carried out thereon
This invention concerns a method of determining a route using map data comprising a plurality of navigable paths, the map data divided into a plurality of regions. The method comprises using at least one processing apparatus to: receive an origin and a destination on the map data and a selection of one of a plurality of cost functions and determine a route from the origin to the destination using the map data and minimum cost data that identifies minimum cost paths between regions of the map data. The minimum cost data identifies more than one minimum cost path between a pair of the regions if different minimum cost paths exist between the pair of regions for different cost functions and determining a route comprises identifying from the minimum cost paths for the pair of regions comprising the origin and destination, the minimum cost path having a lowest cost for the selected cost function.
Owner:TOMTOM INT BV
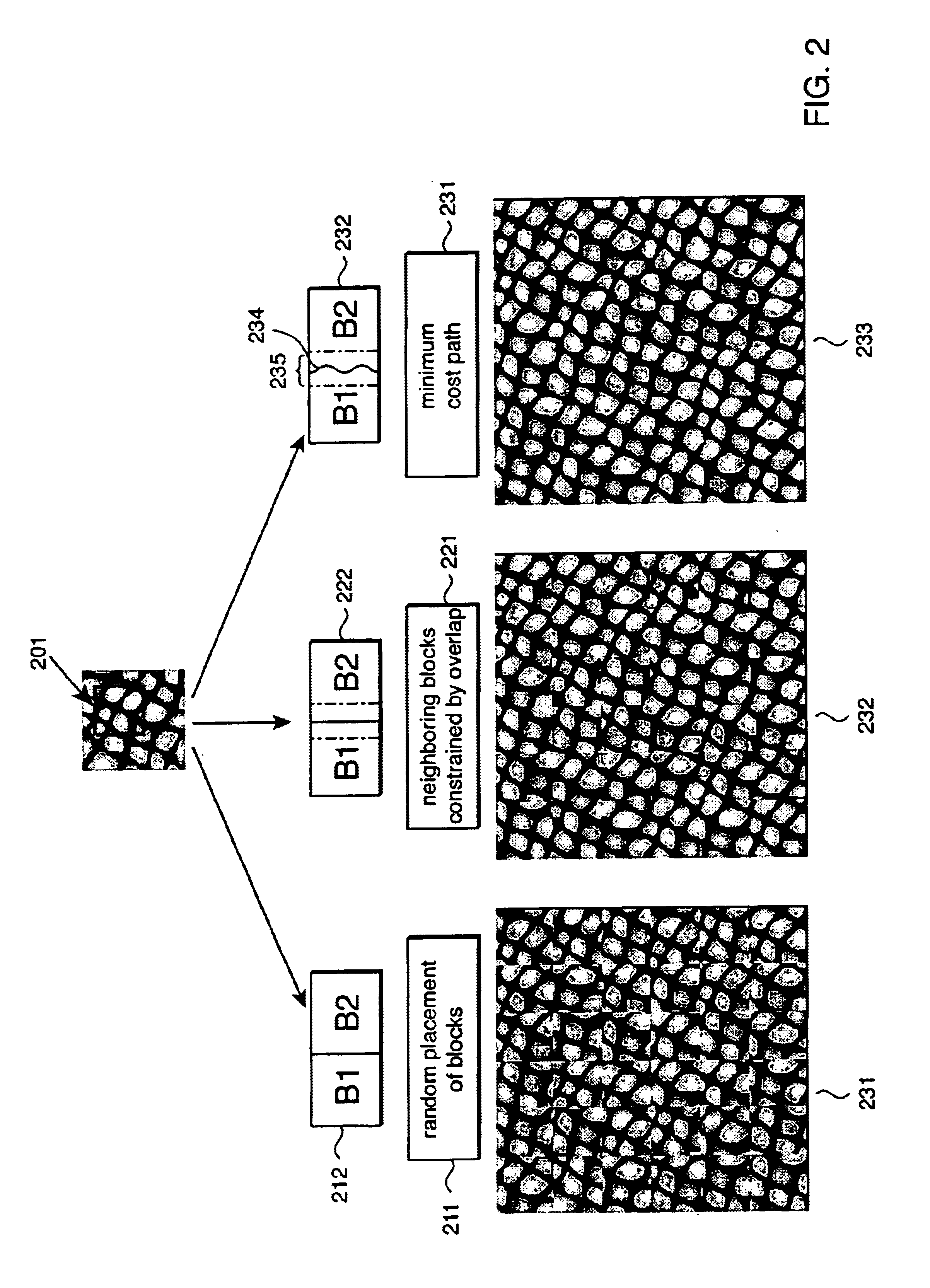
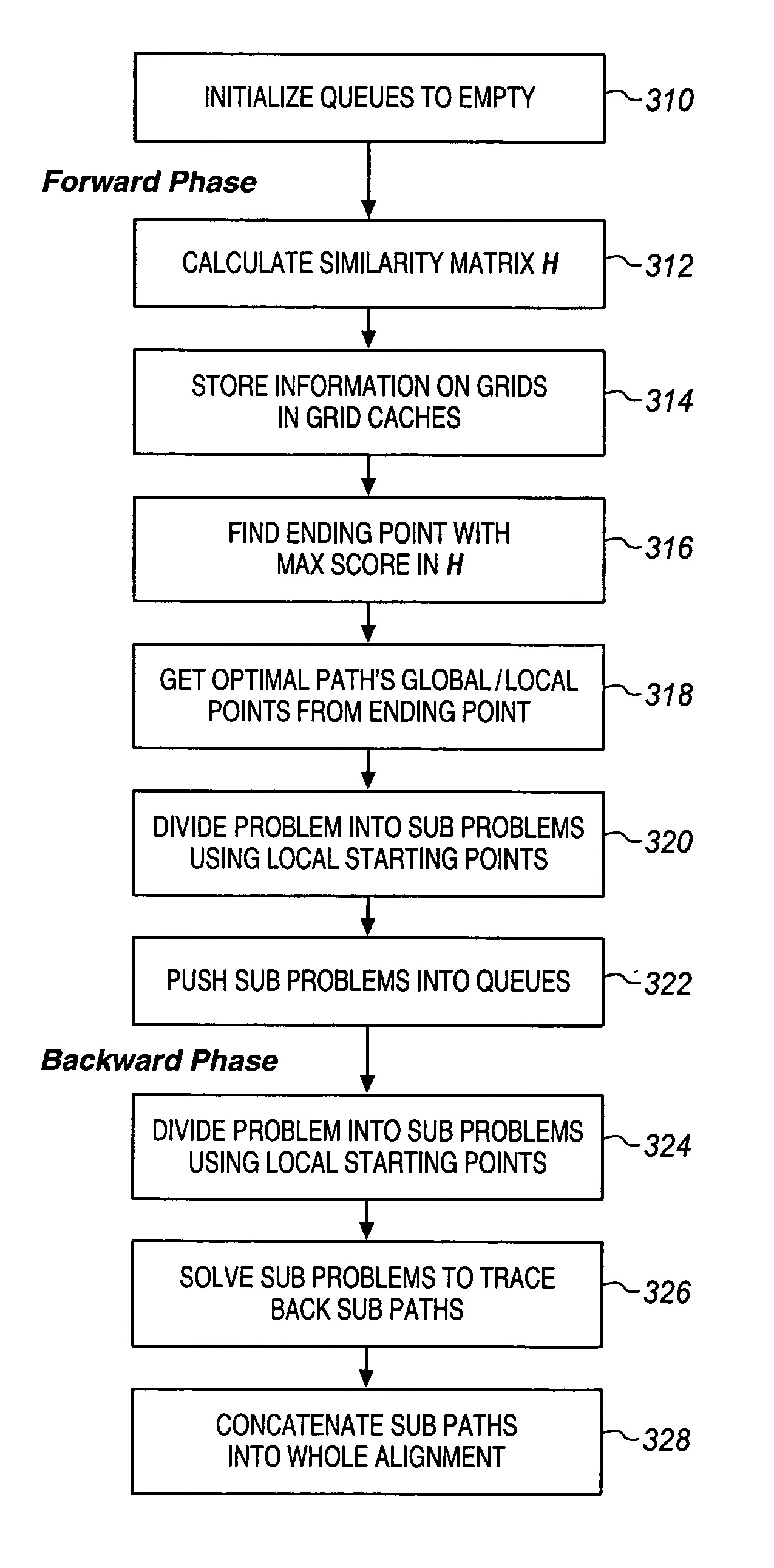
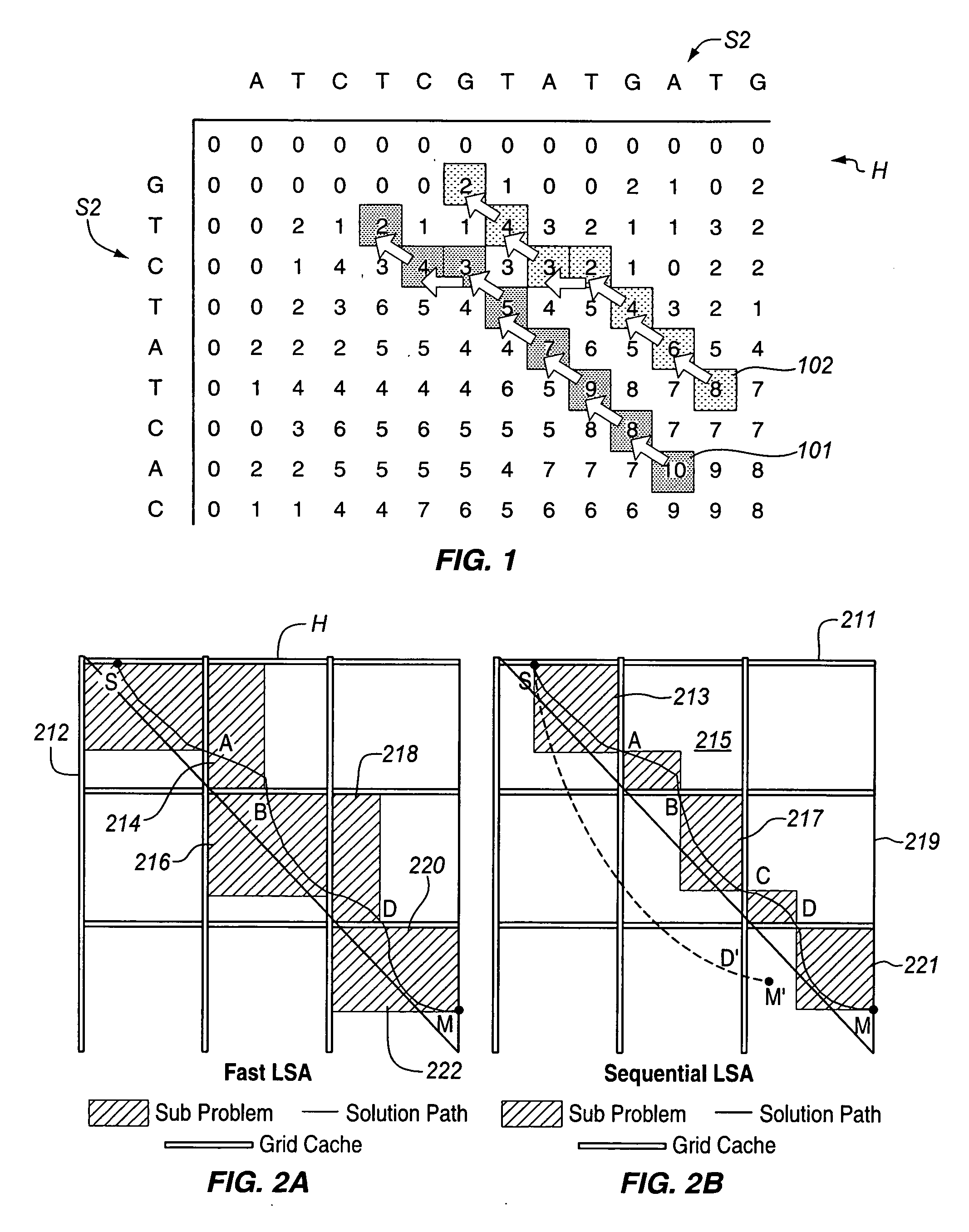
Fast alignment of large-scale sequences using linear space techniques
InactiveUS20070076936A1Character and pattern recognitionBiological testingMinimum cost pathSpace techniques
Large scale sequences and other types of patterns may be matched or aligned quickly using a linear space technique. In one embodiment, the invention includes, calculating a similarity matrix of a first sequence against a second sequence, determining a lowest cost path through the matrix, where cost is a function of sequence alignment, dividing the similarity matrix into a plurality of blocks, determining local start points on the lowest cost path, the local start points each corresponding to a block through which the lowest cost path passes, dividing sequence alignment computation for the lowest cost path into a plurality of independent problems based on the local start points, solving each independent problem independently, and concatenating the solutions to generate an alignment path of the first sequence against the second sequence.
Owner:INTEL CORP
Generalization of Features In A Digital Map
ActiveUS20070024624A1Simple processDrawing from basic elementsRoad vehicles traffic controlGraphicsTheoretical computer science
Owner:UBER TECH INC
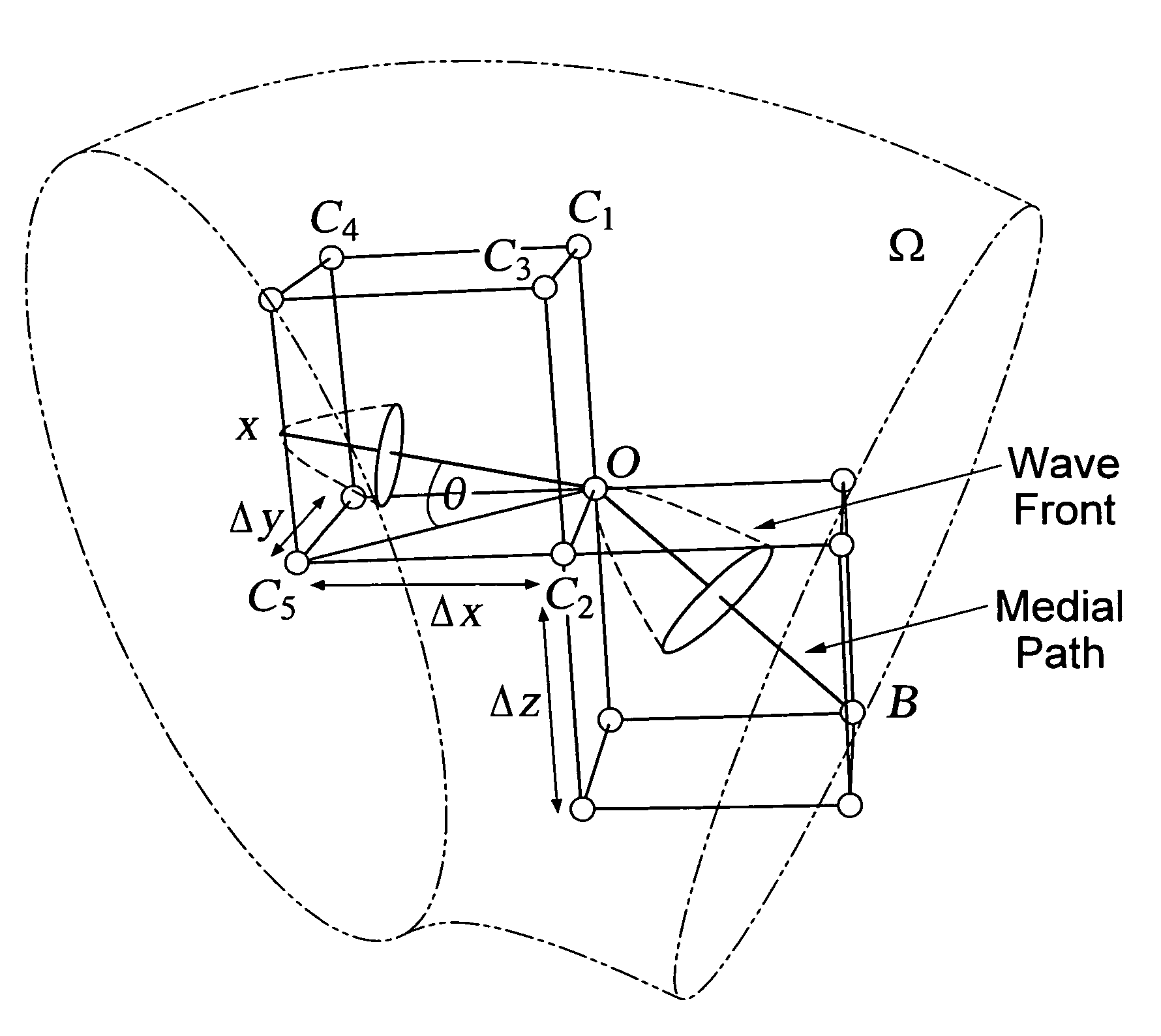
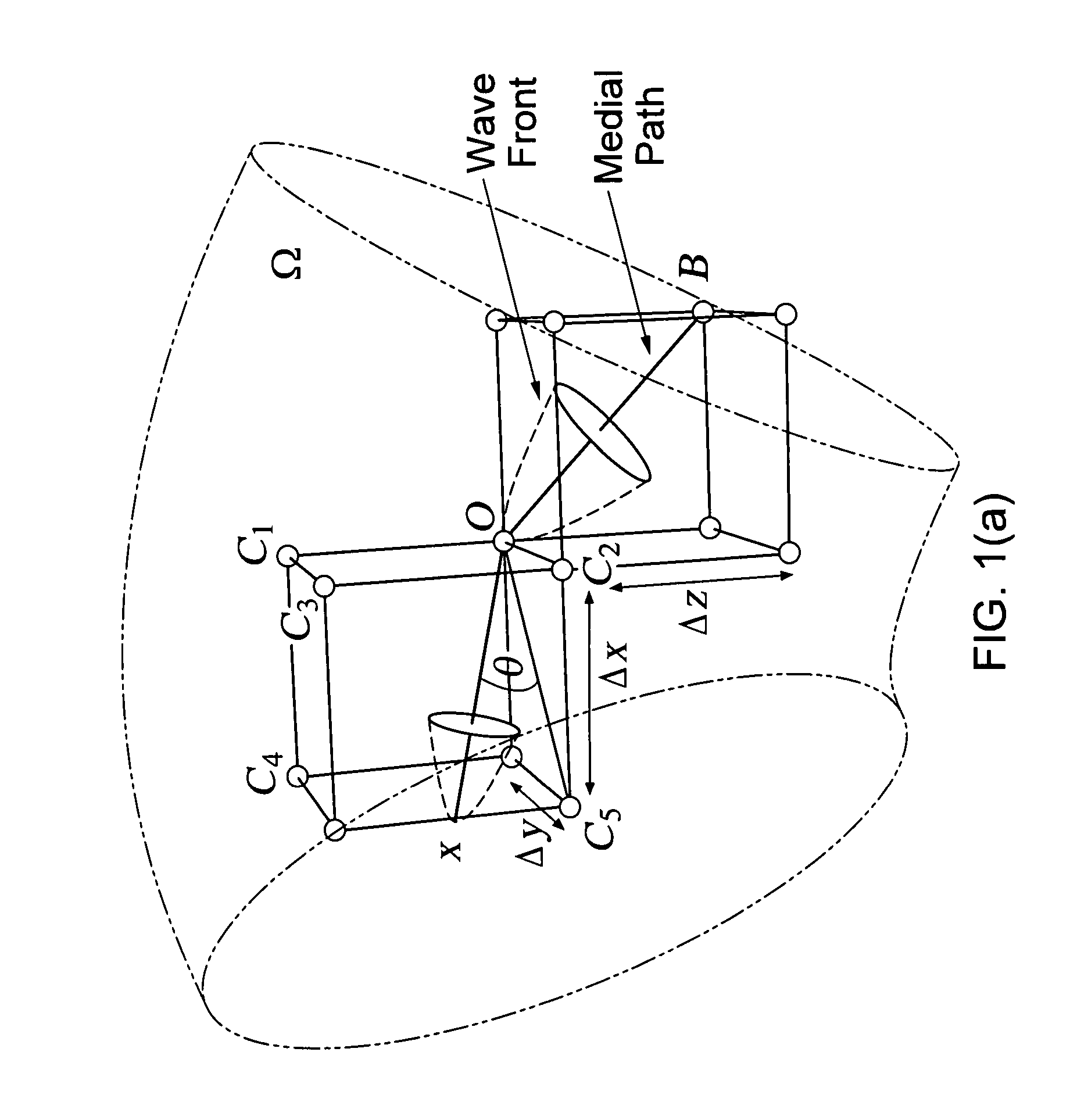
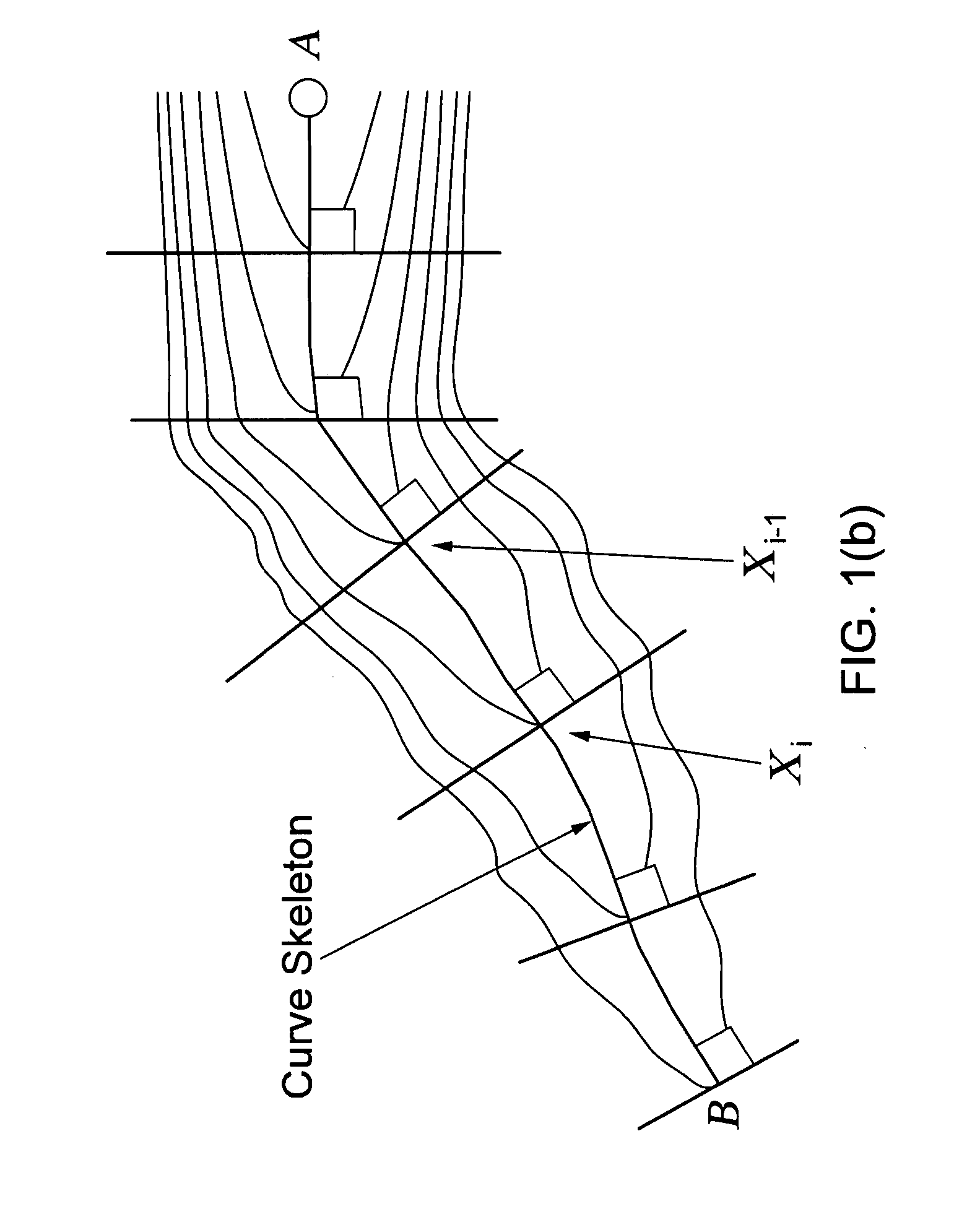
Method and software for shape representation with curve skeletons
Embodiments of the invention utilize a variational framework for computing curve skeletons (CS) of objects whose cross section is not necessary tubular. Embodiments utilize an energy function, which is proportional to some medialness function, such that the minimum cost path between any two medial voxels in the shape is a curve skeleton. Different medialness functions include the Euclidean distance field and a modified version of the magnitude of the gradient vector flow (GVF), which results in two different energy functions. The first energy function controls the identification of the topological nodes of the shape from which curve skeletons start, while the second one controls the extraction of the curve skeletons. Preferred embodiments are completely automated since all parameters are analytically estimated. Embodiments are highly less sensitive to boundary noise, are able to extract the entire curve skeletons, as well as only part of it given the starting and the end voxels, and do not require voxels to be isotropic. In addition, computed curve skeletons are highly centered and form a connected graph. Preferred embodiments have been validated the framework both quantitatively and qualitatively against several 3D shapes of different complexity.
Owner:UNIV OF LOUISVILLE RES FOUND INC
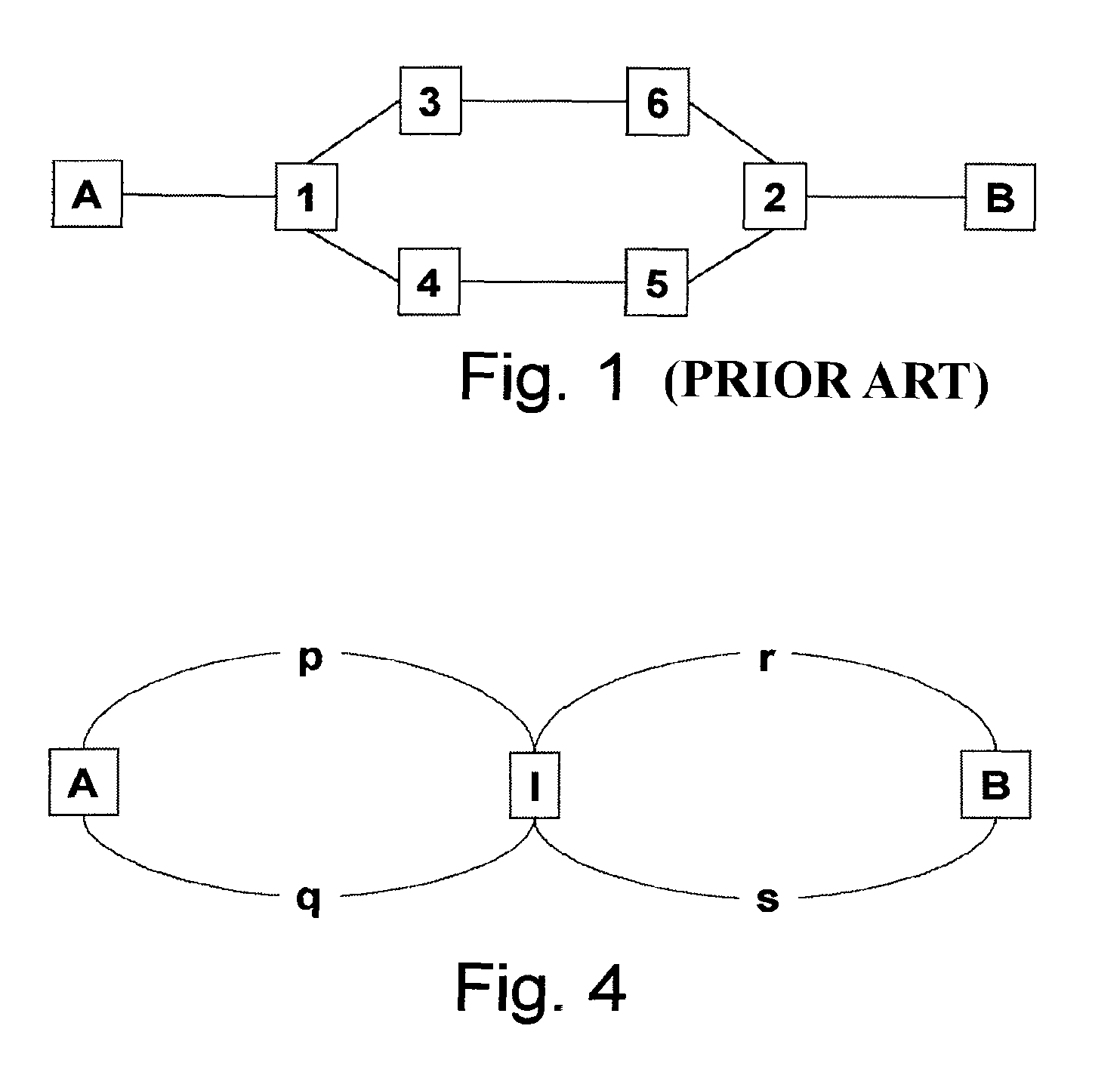
Tie-breaking in shortest path determination
InactiveUS7911944B2Simple calculationLower requirementError preventionFrequency-division multiplex detailsNODALTraffic flow
Owner:RPX CLEARINGHOUSE
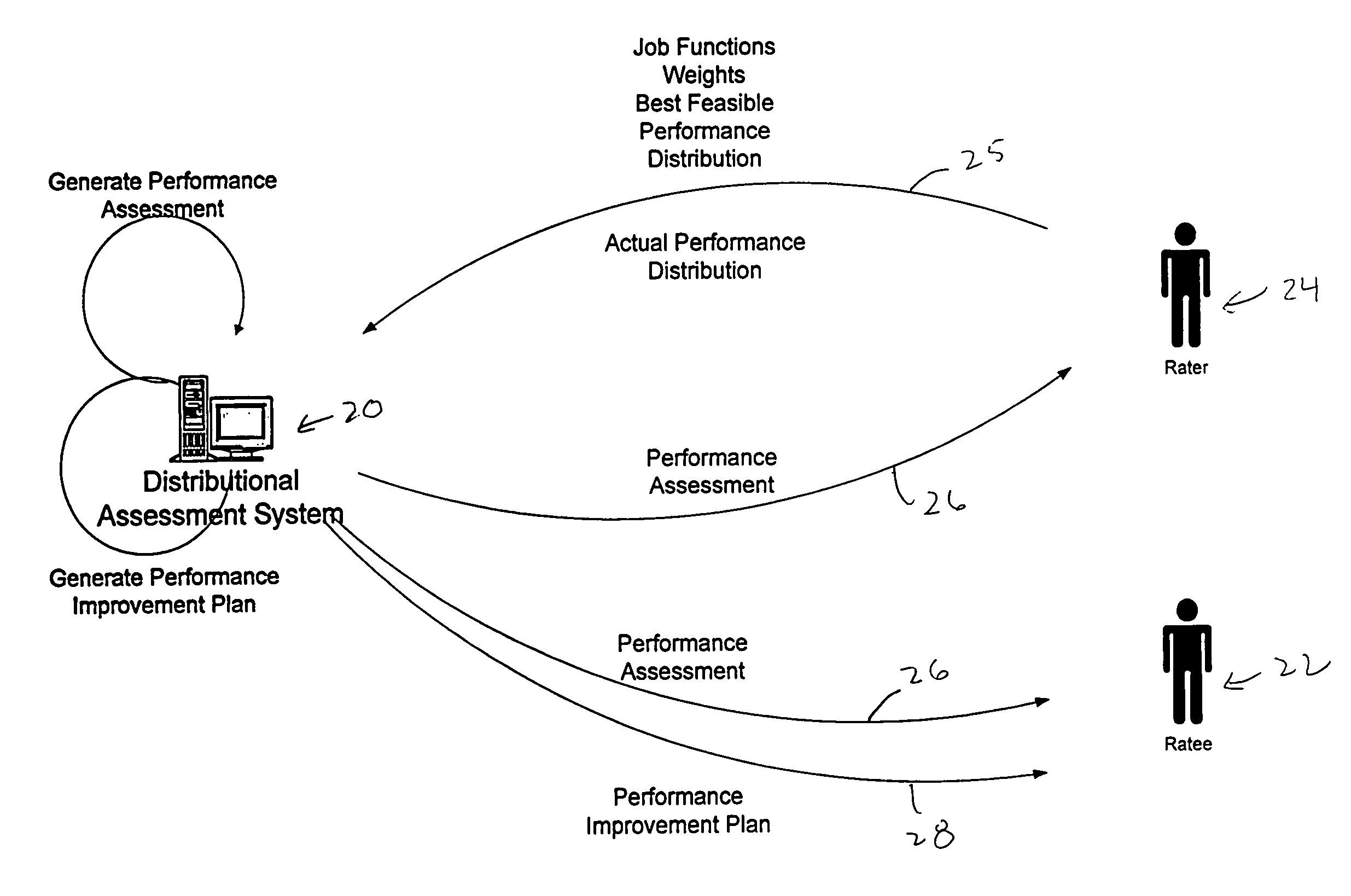
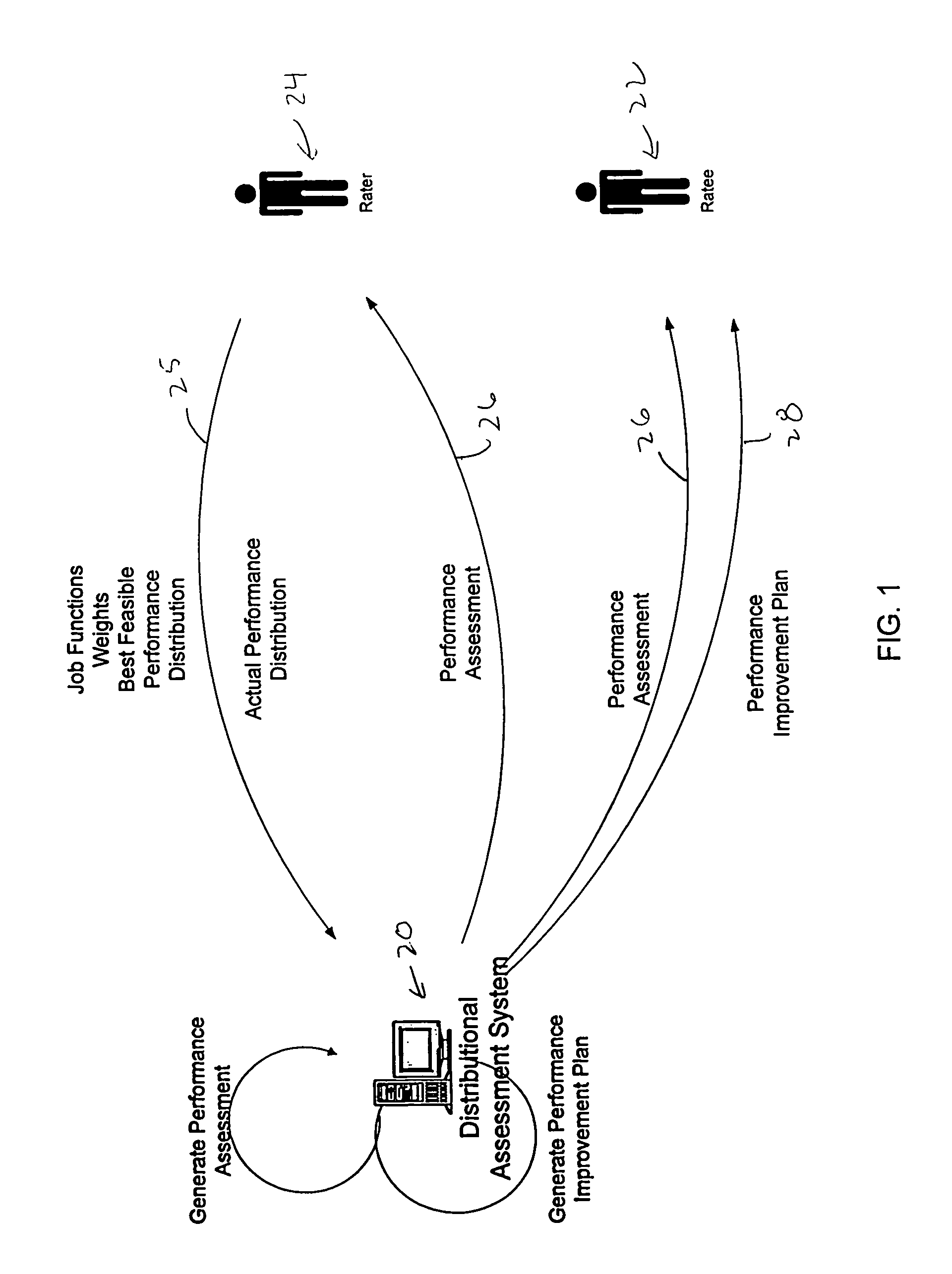
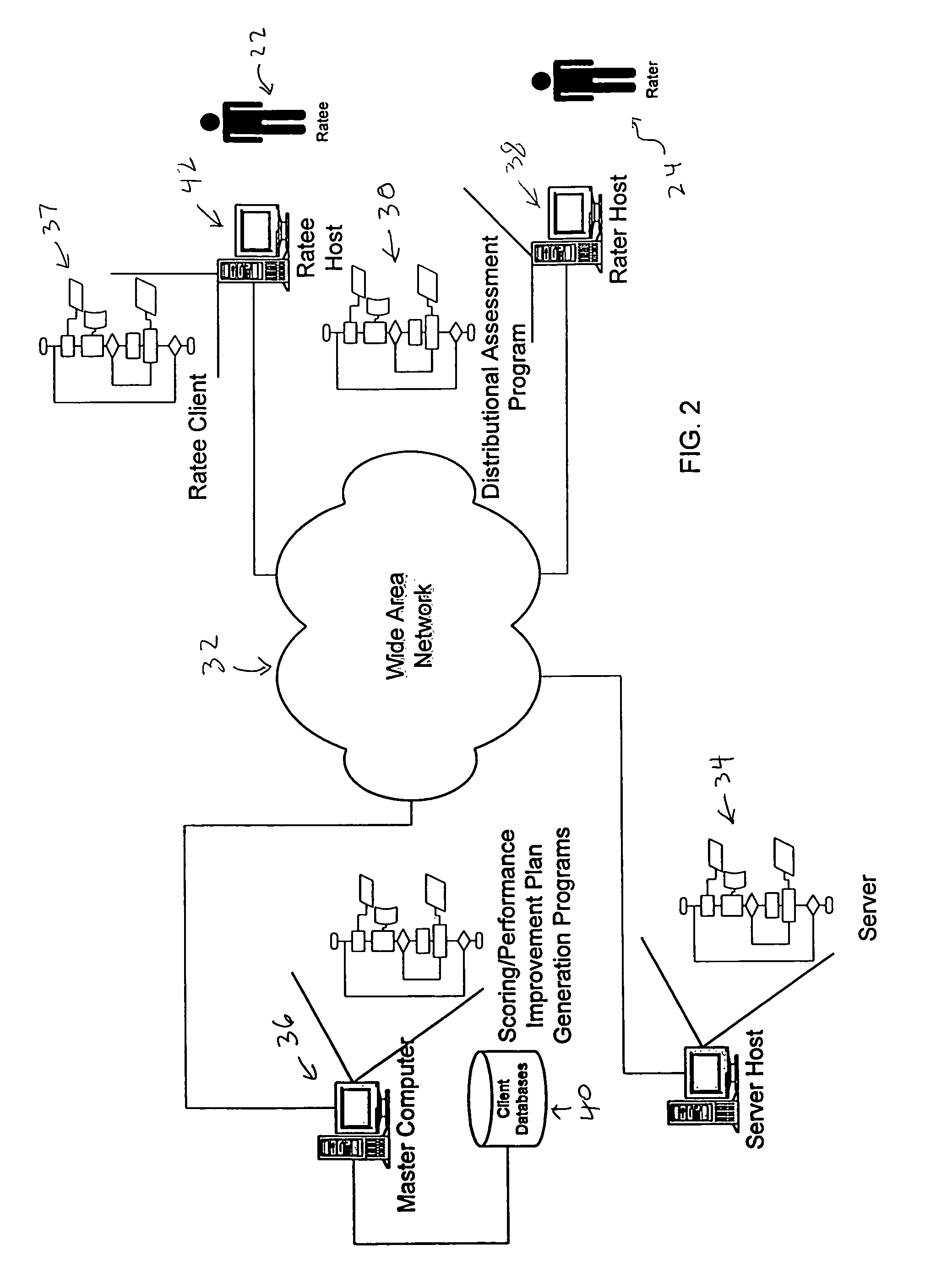
Distributional assessment system
InactiveUS7778865B1High level of performanceSpecial service for subscribersResourcesOrganisational performanceMinimum cost path
A distributional assessment system for assessing the job performance of individuals within an organization. A rater, uses the distributional assessment system to rate the performance of a ratee, such as an employee. The distributional assessment system guides the rater through a job function description process to generate a set of assigned weights and a best feasible performance rating. The weights and best feasible performance rating are used along with an actual performance rating to generate an overall distributional assessment of the ratee. The ratee may use the weights and distributional assessment to determine the lowest cost path to improving personal job performance. In addition, an organization can use aggregate distributional assessments to determine the overall performance rating of an organization and determine the lowest cost path to improving the organization's performance. Individual distributional assessments and new job function weights may be used to identify the most likely candidates for a job promotion.
Owner:KANE JEFFREY S
Method for determining similarities between data sequences using cross-correlation matrices and deformation functions
InactiveUS7328111B2Analogue computers for chemical processesCharacter and pattern recognitionCross correlation matrixCorrelation ratio
A method compares a first data sequence with a second data sequence. A cross-correlation matrix of distances between all possible pairs of values of the first and second data sequences is constructed. A minimum cost path between diagonally opposing corners of the cross-correlation matrix is determined. The minimum cost path is projected onto a transfer function that maps between the first data sequence and the second data sequence. Then, the minimum cost path is projected onto a deformation function that corresponds to a similarity between the first data sequence and the second data sequence.
Owner:MITSUBISHI ELECTRIC RES LAB INC
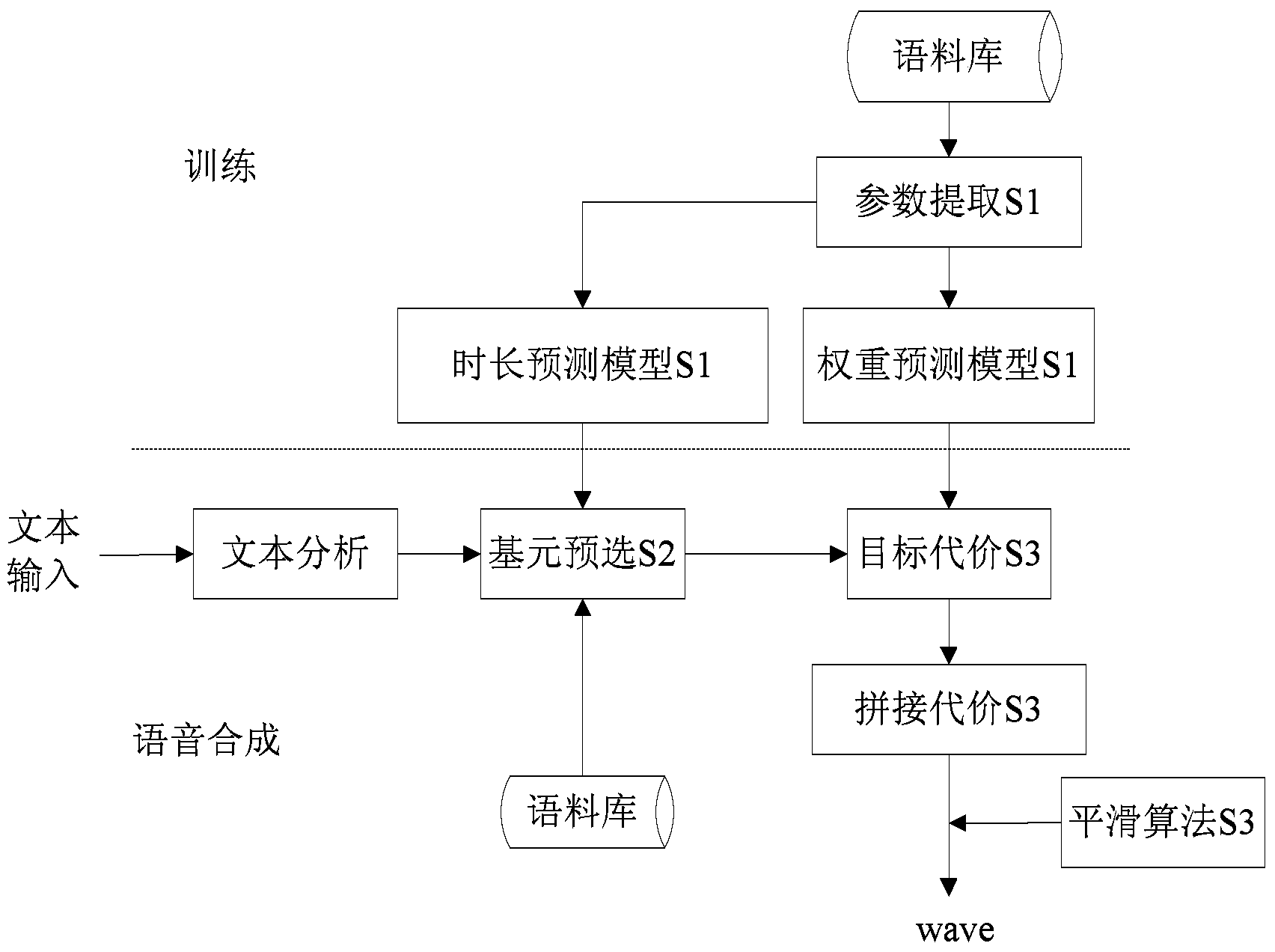
Text message based waveform concatenation speech synthesis method
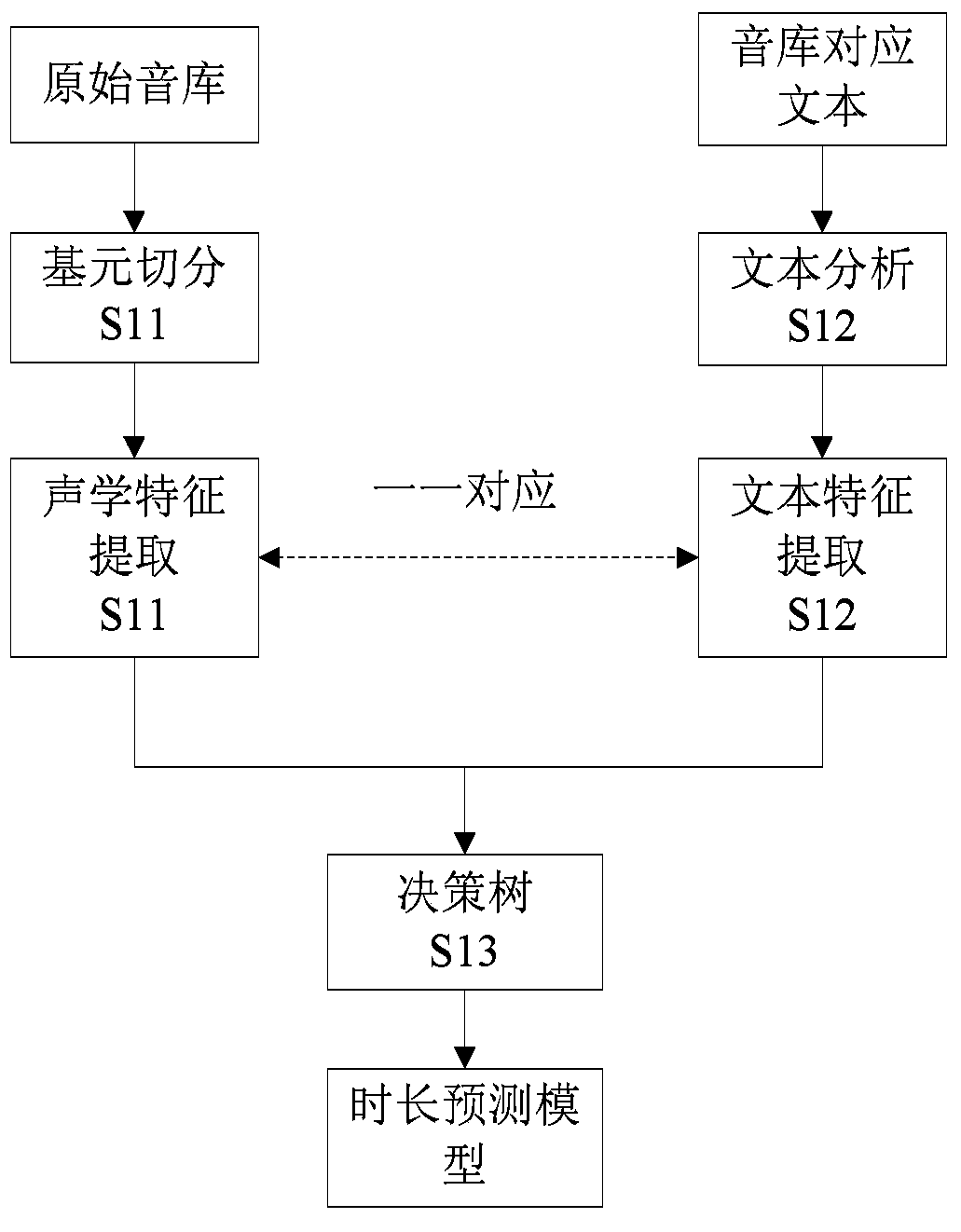
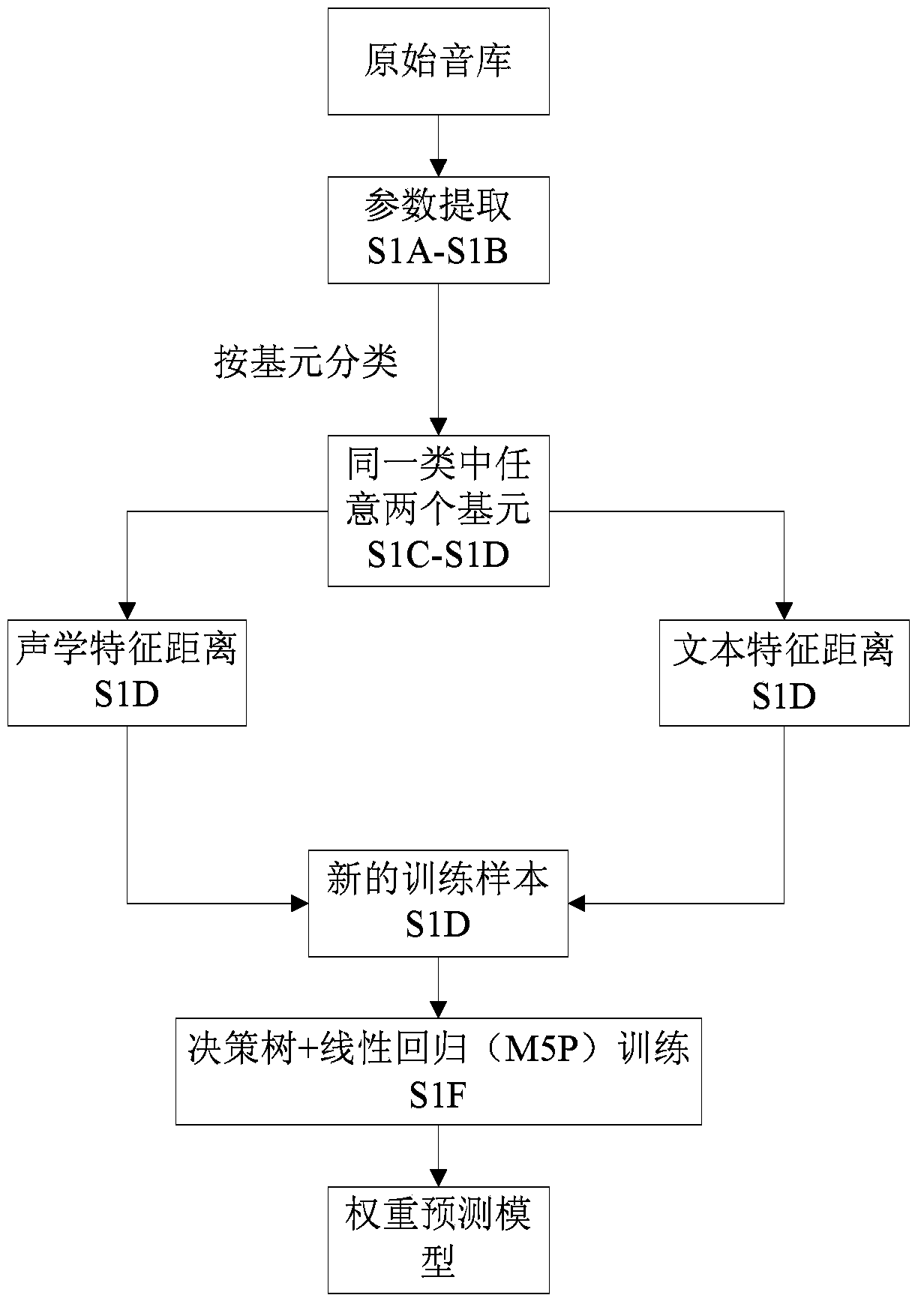
ActiveCN104112444AImprove efficiencyImprove naturalnessSpeech synthesisMinimum cost pathSpeech synthesis
The invention relates to a text message based waveform concatenation speech synthesis method. The text message based waveform concatenation speech synthesis method includes steps of S1, extracting acoustic parameters and text parameters of all elements in an original voice frequency through segment cutting, and training a duration prediction model and a weight prediction model according to extracted parameters; S2, using a layered pre-selection method to primarily pre-select the elements in a corpus to obtain candidate elements by means of a target element of text analysis and a duration predicted by the duration prediction model; S3, calculating the target element, the candidate elements, and weight information predicted by the weight prediction model to obtain a target cost; calculating Integrating degrees of two adjacent elements to obtain a concatenation cost; using a viterbi searching method to search the target cost and the concatenation cost to obtain a minimum cost path so as to further obtain an optimum element and obtain synthesis speeches through smooth concatenation.
Owner:INST OF AUTOMATION CHINESE ACAD OF SCI
Method for Temporally Editing Videos
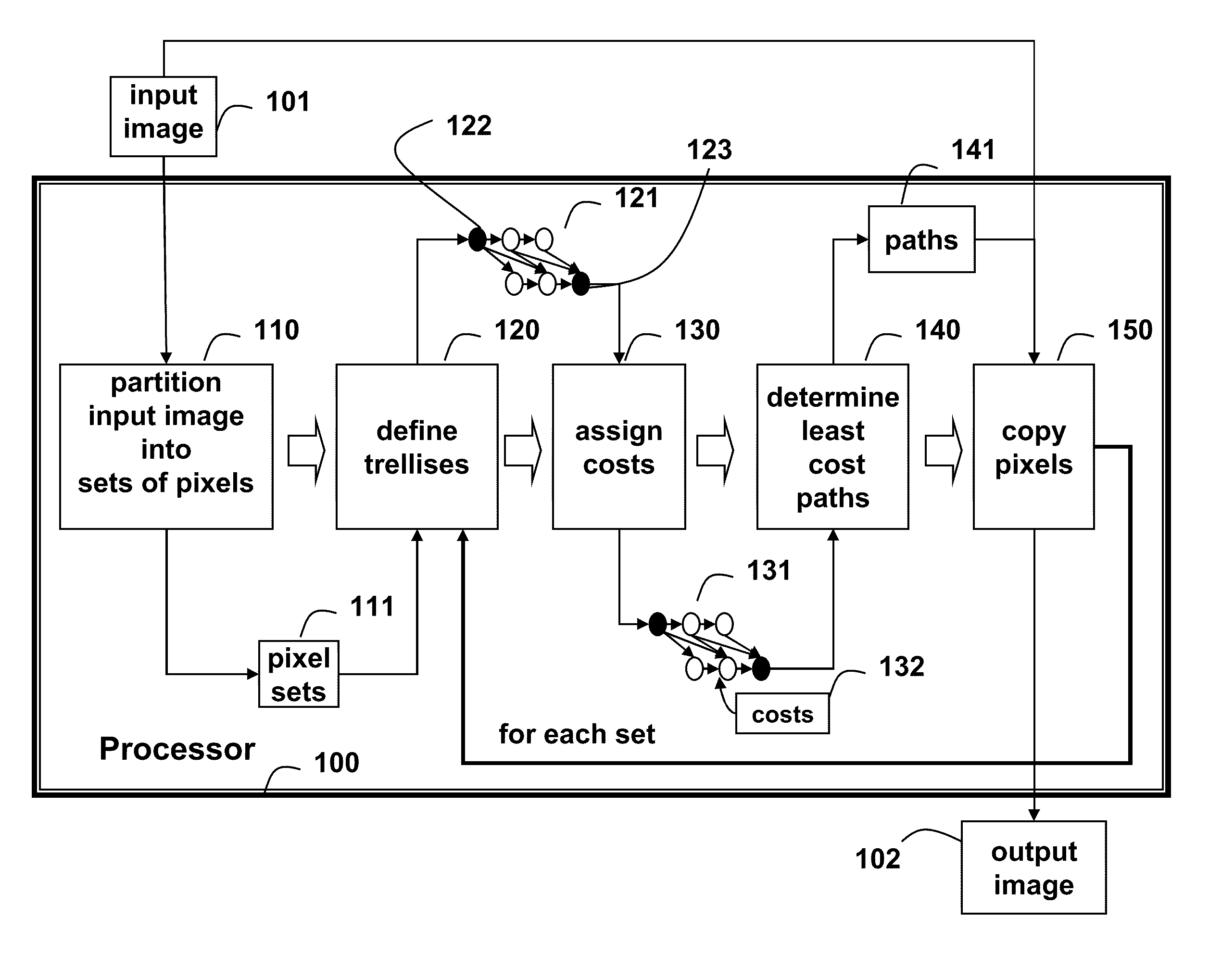
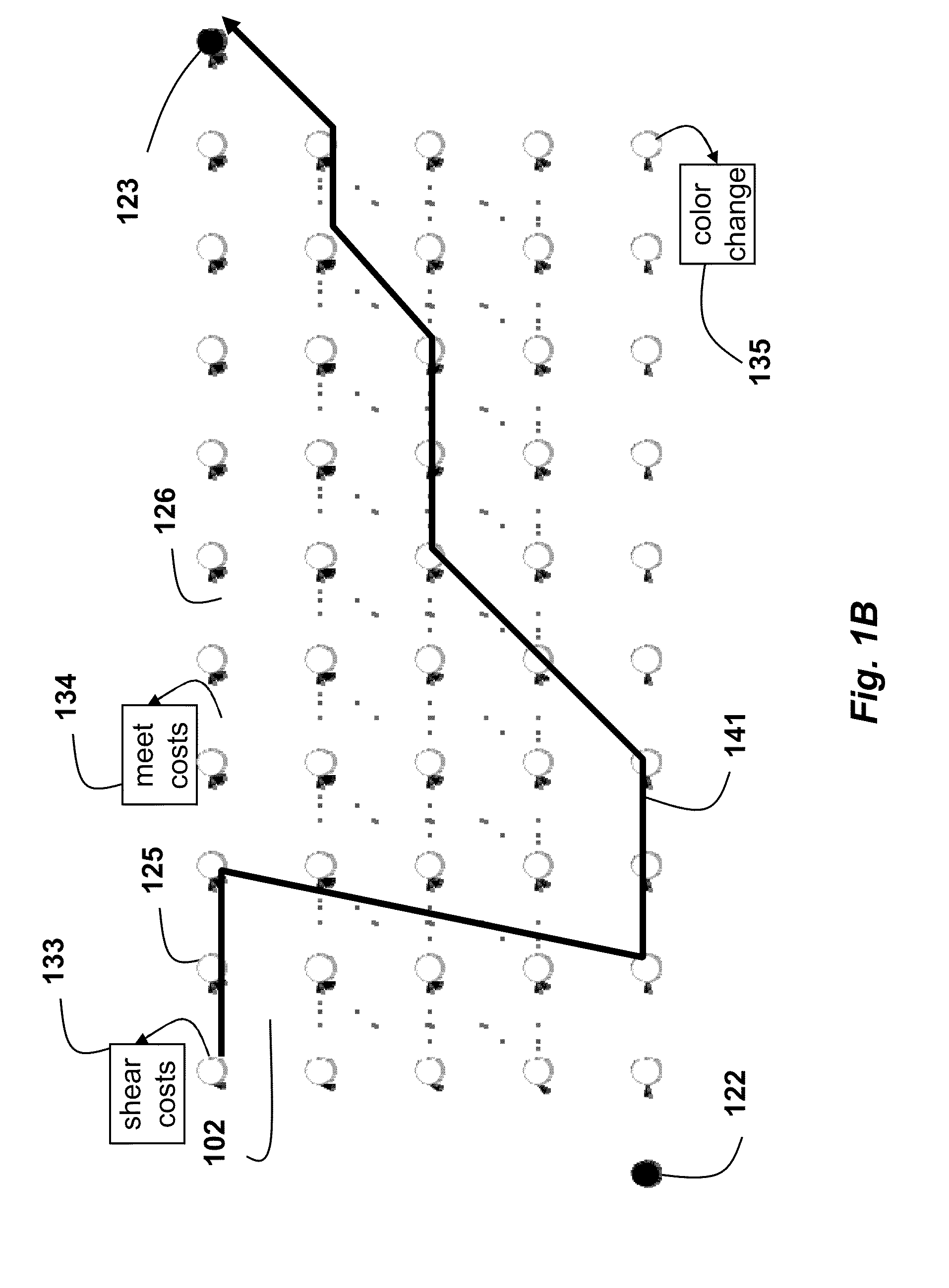
ActiveUS20100183243A1Minimal artifactMinimal distortionGeometric image transformationElectronic editing digitised analogue information signalsPosition dependentComputer vision
A method edits an input video to produce an output video. Pixels of the input video are partitioned into sets of pixels, wherein the pixels in the sets are adjacent, and for each set of pixels performing the following steps. A trellis having nodes connected by directed links is constructed. Each node corresponds to one of the pixels in the set of pixels, and each node is associated with an action and location of the pixel in the output image. Costs are assigned to the nodes and the links, wherein the costs are on apparent motion in the input video. A least cost path is determined through the trellis. Then, for each node on the path, apply the action associated the node to the corresponding pixel in the input video to edit the corresponding pixel at the location in the output video associated with the node.
Owner:MITSUBISHI ELECTRIC RES LAB INC
Load balancing in a network comprising communication paths having different bandwidths
Owner:AVAGO TECH INT SALES PTE LTD
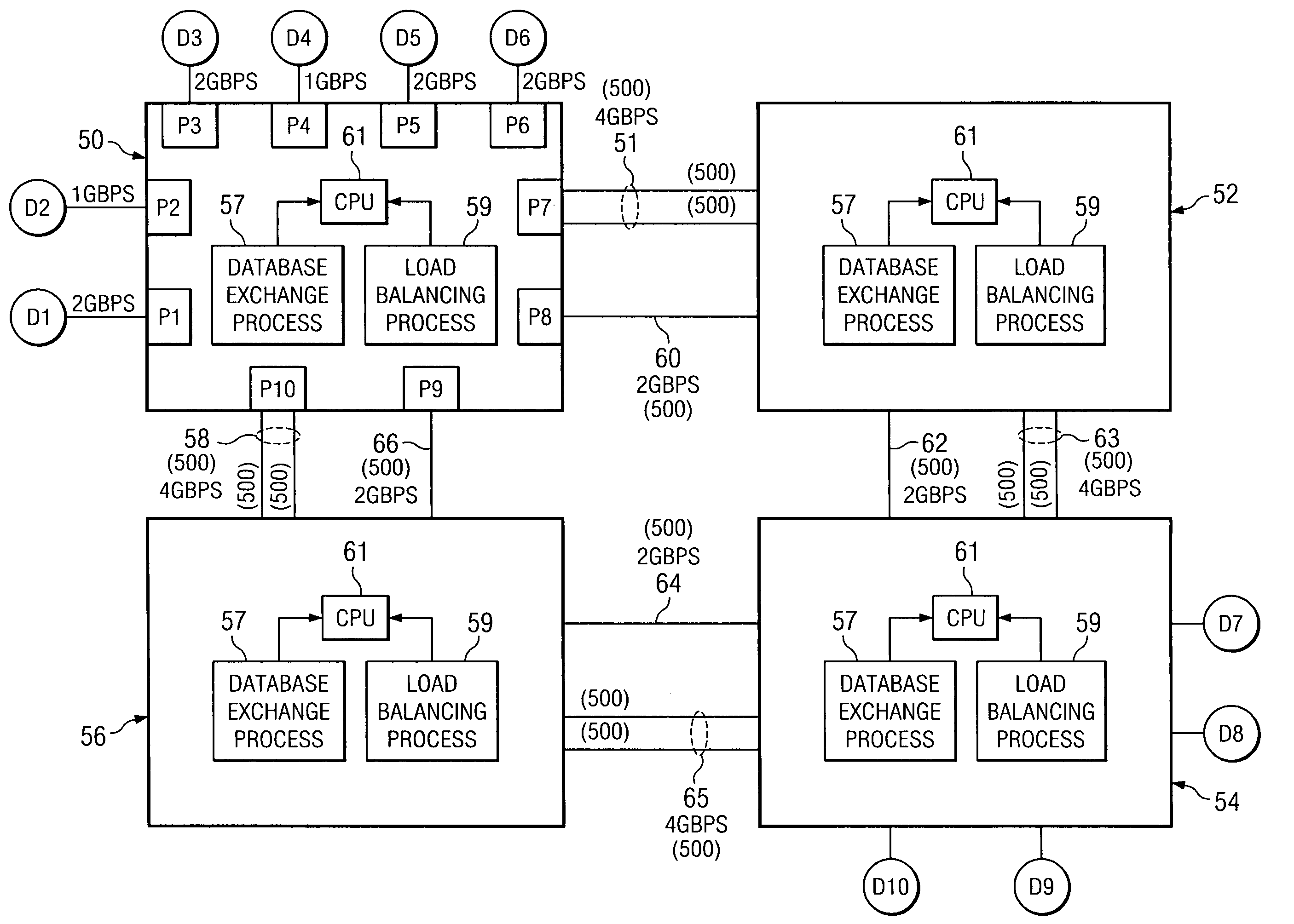
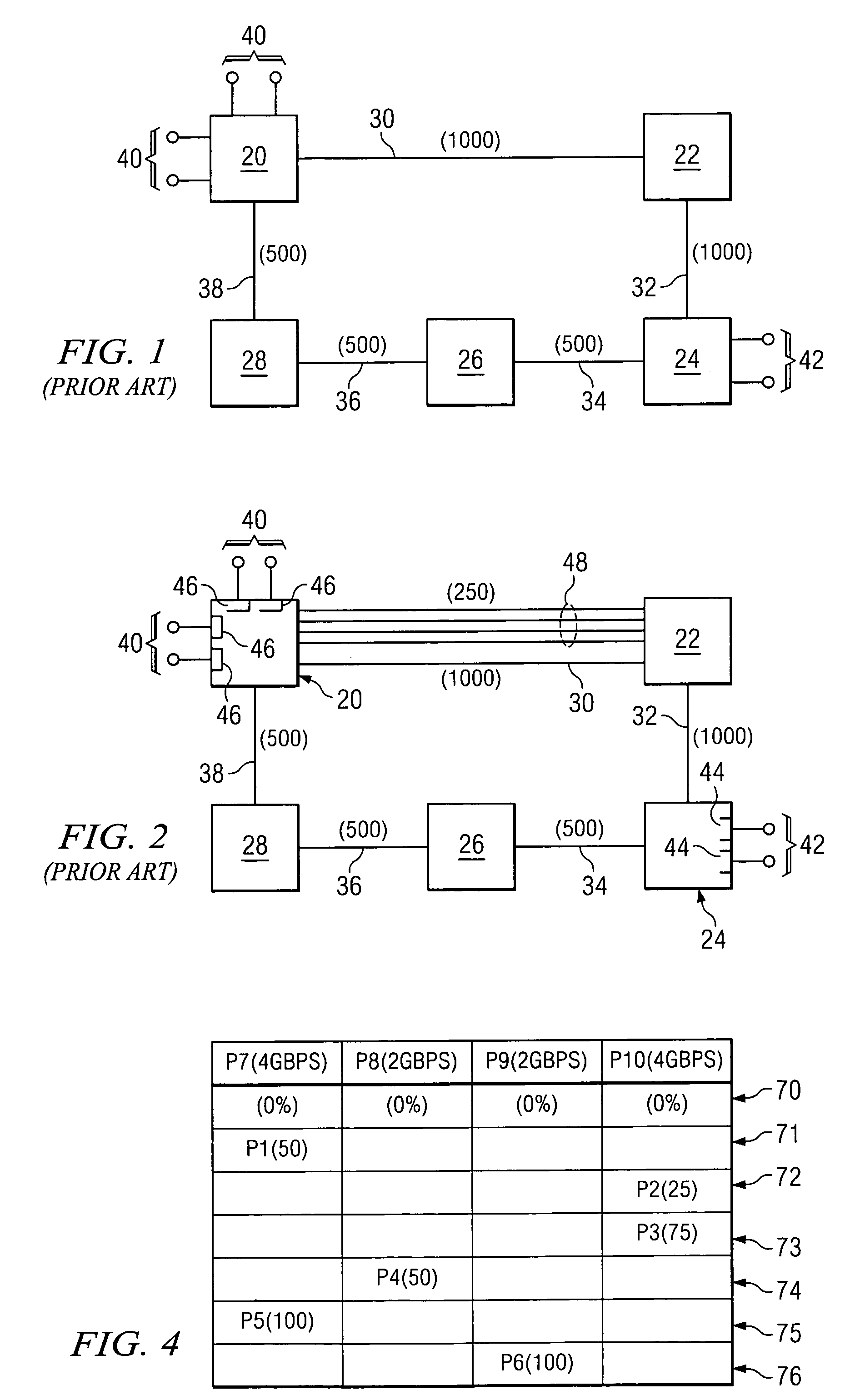
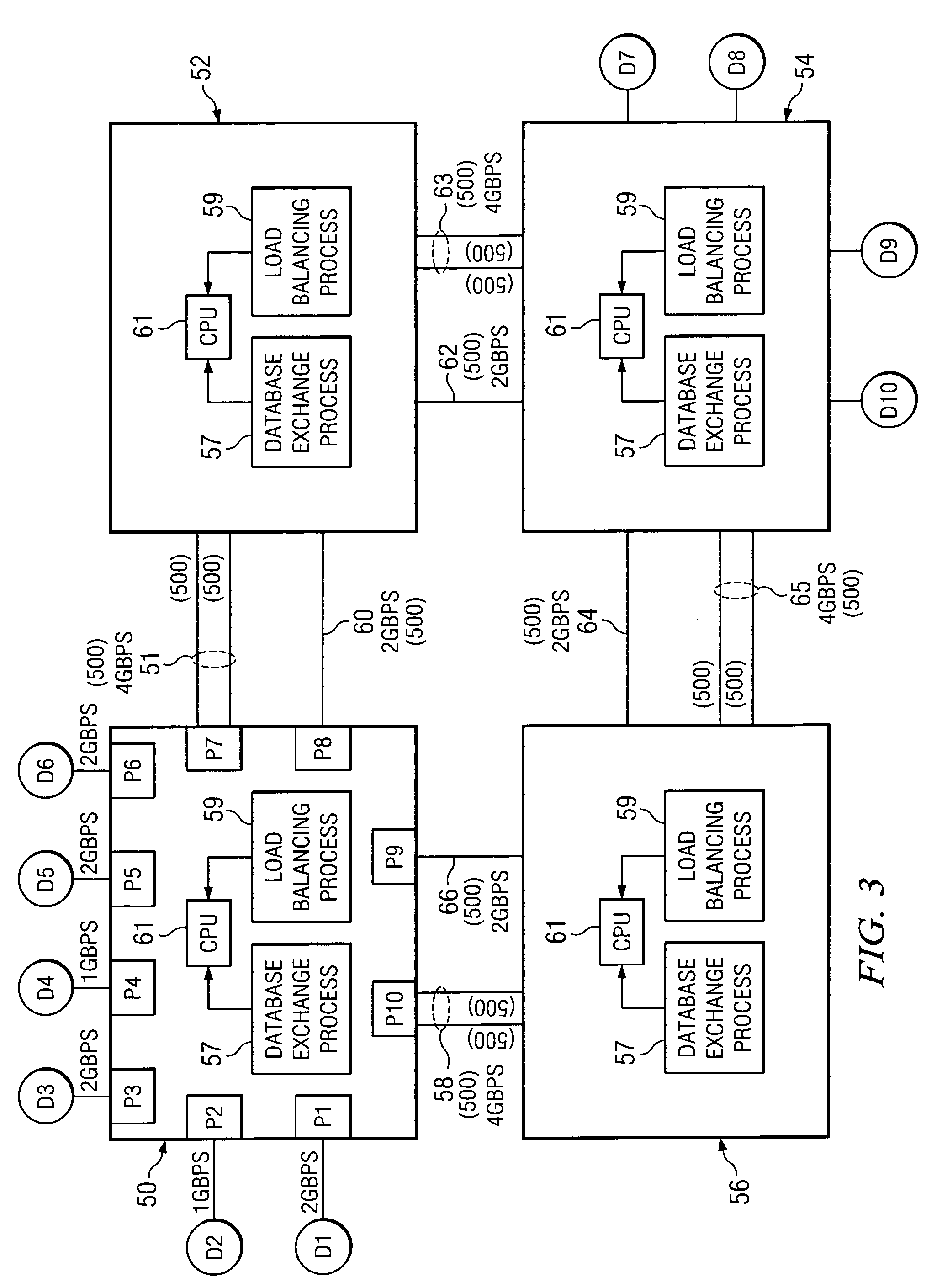
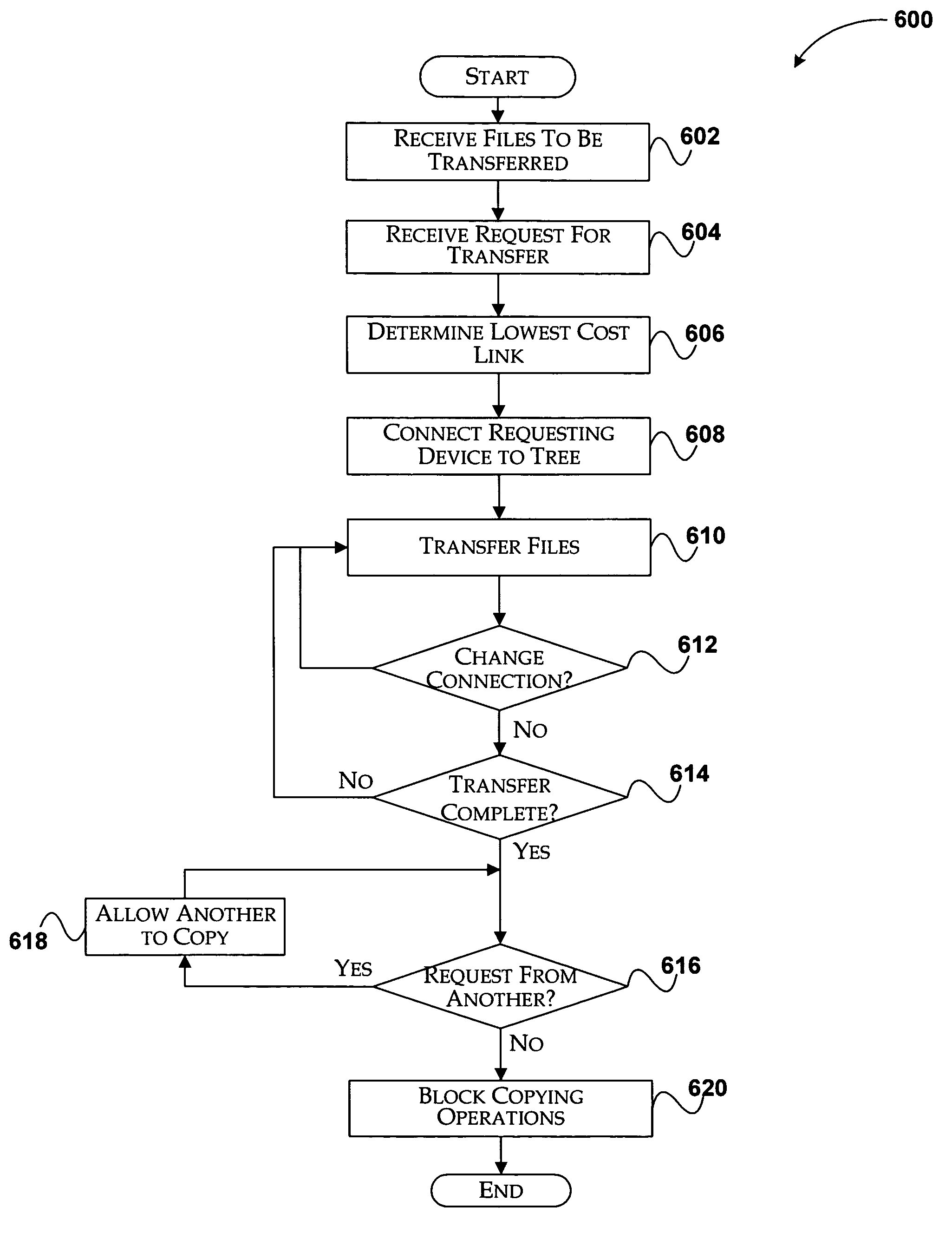
System and method for optimized distributed file transfer
InactiveUS7454408B2Low costOptimized distribution of filesData processing applicationsDigital data processing detailsClient-sideBinary tree
A system and method for optimized distribution of files from a file server to a high number of client machines. The client machines are interconnected as nodes in a binary tree structure with each level of nodes receiving the files from a higher level and transferring to a lower level. The file server is the root node of the tree. A database is arranged to store the tree structure information, register new client machines requesting file transfer, and determine lowest cost paths for new links within the tree structure. The lowest cost paths are determined based on cost parameters assigned to network switches between nodes of the tree. Each client machine acting as a child node is arranged to receive the files from a parent node as the files are stored in the parent node, and disconnect from the parent node upon receiving all of the files.
Owner:MICROSOFT TECH LICENSING LLC
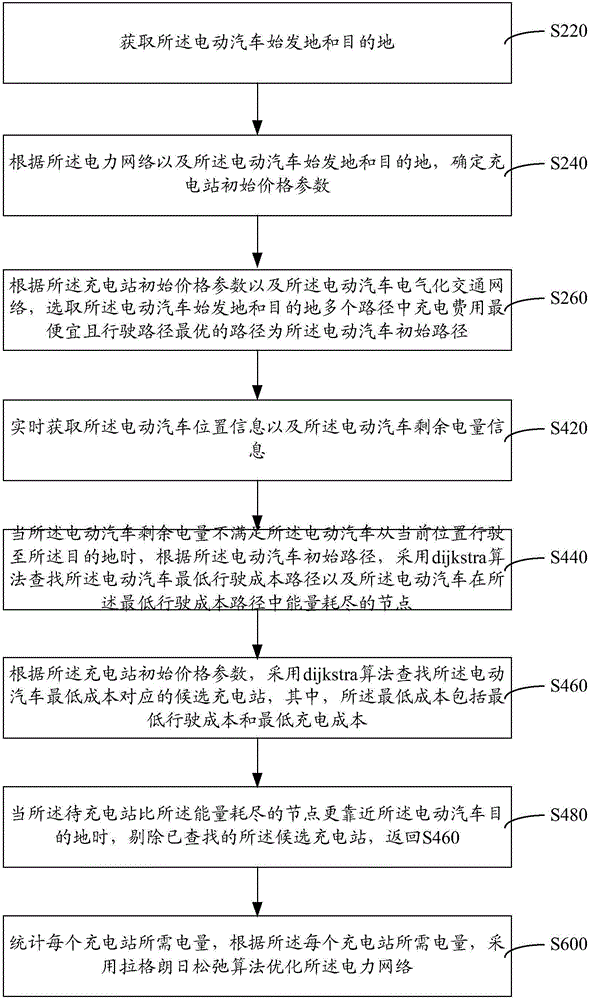
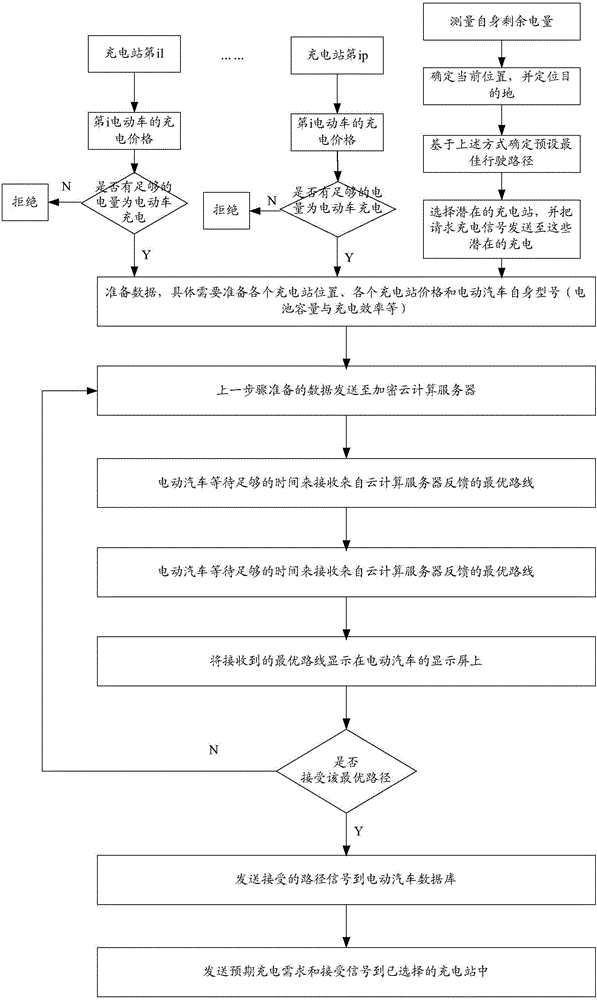
Cooperative optimization method and system for electrified traffic network and electric system
ActiveCN106042963ALow cost pathFacilitate Co-OptimizationCharging stationsOperating modesElectric power systemTraffic network
Owner:SYSU CMU SHUNDE INT JOINT RES INST +1
Features
- R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
Why Patsnap Eureka
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com