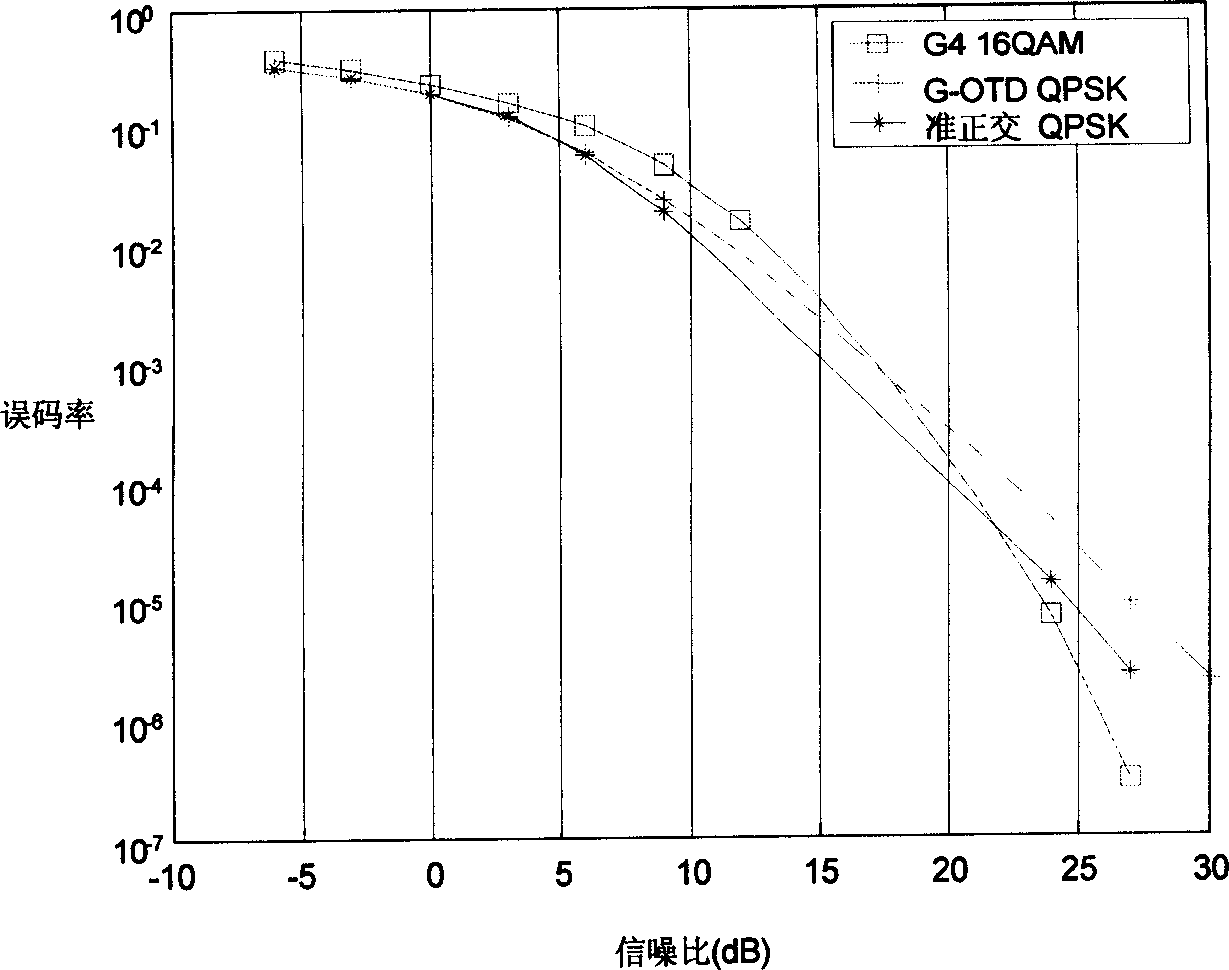
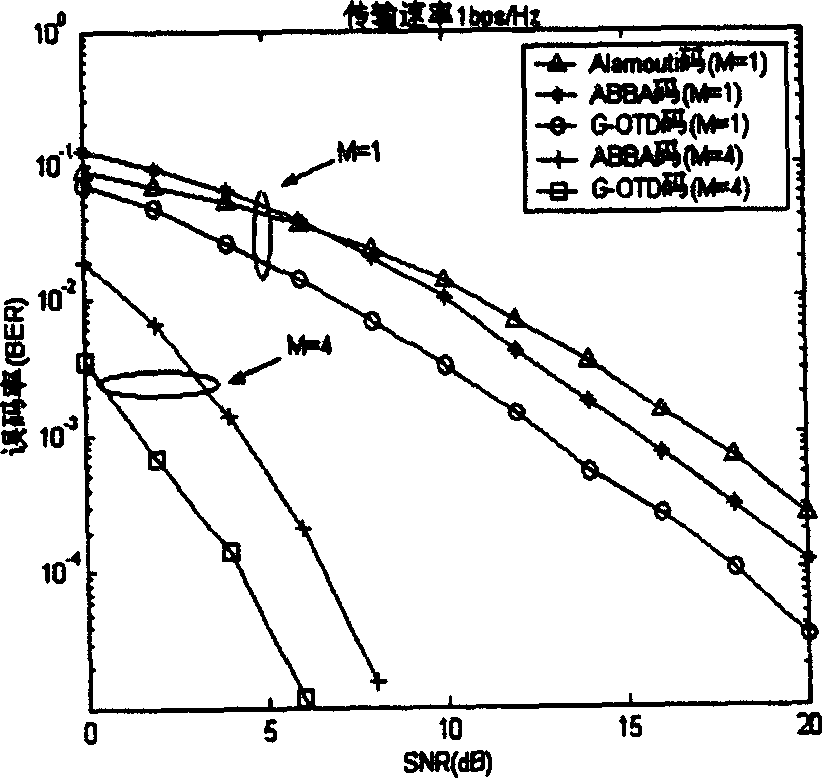
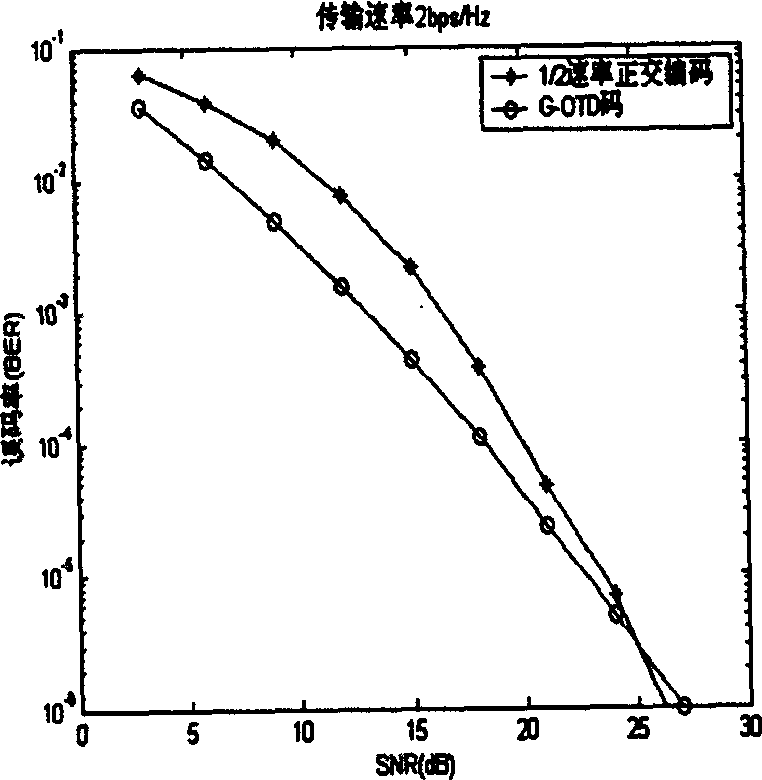
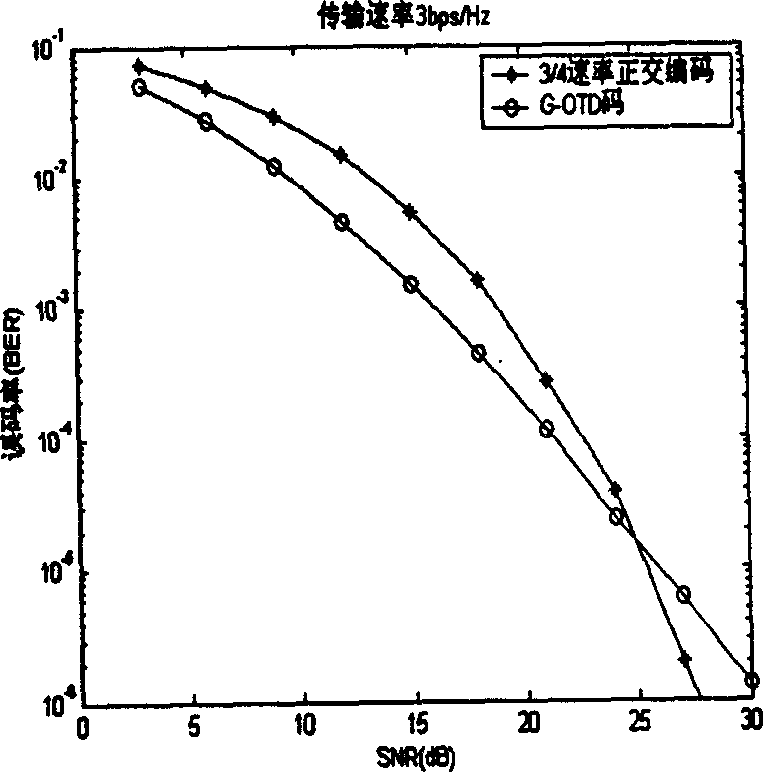
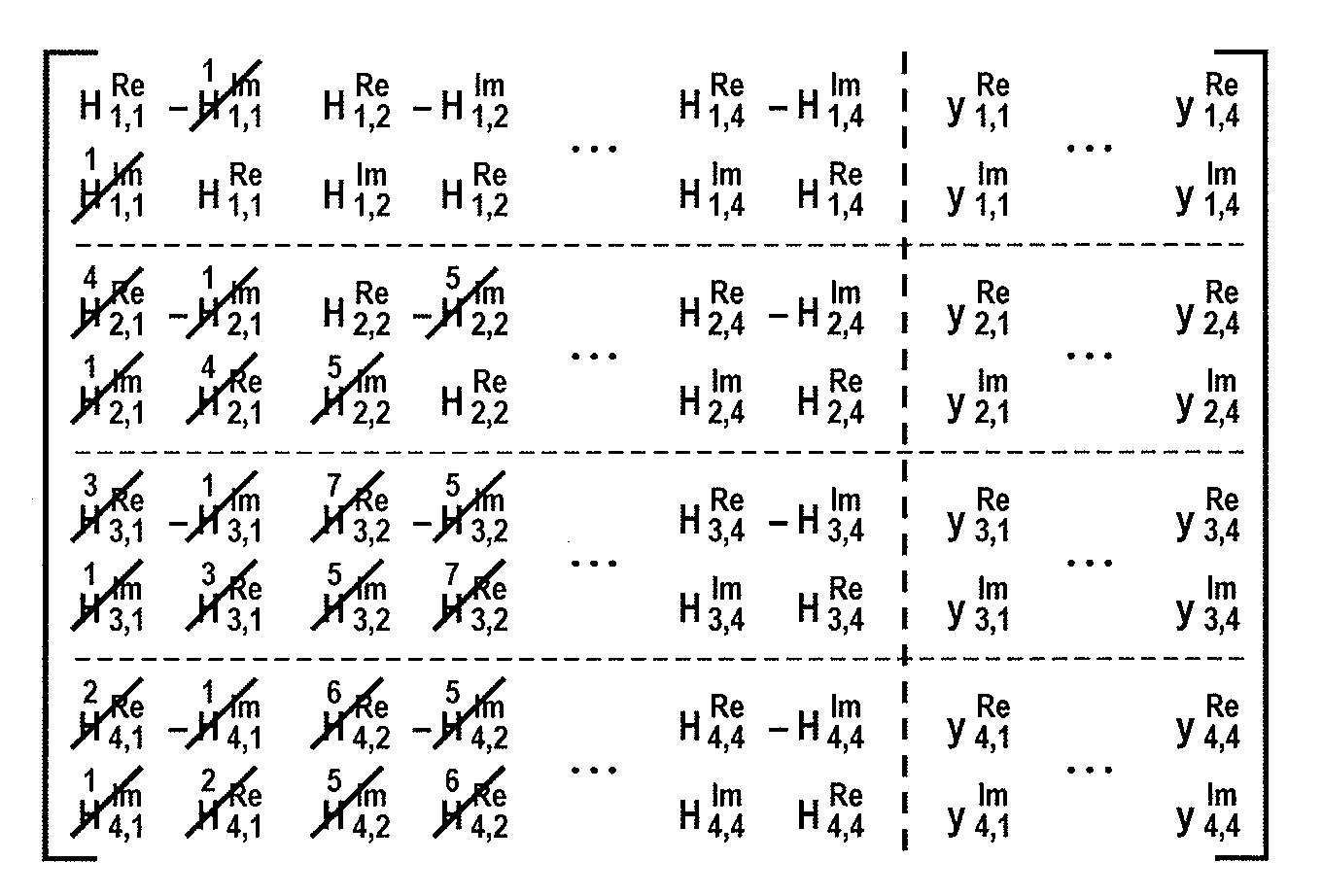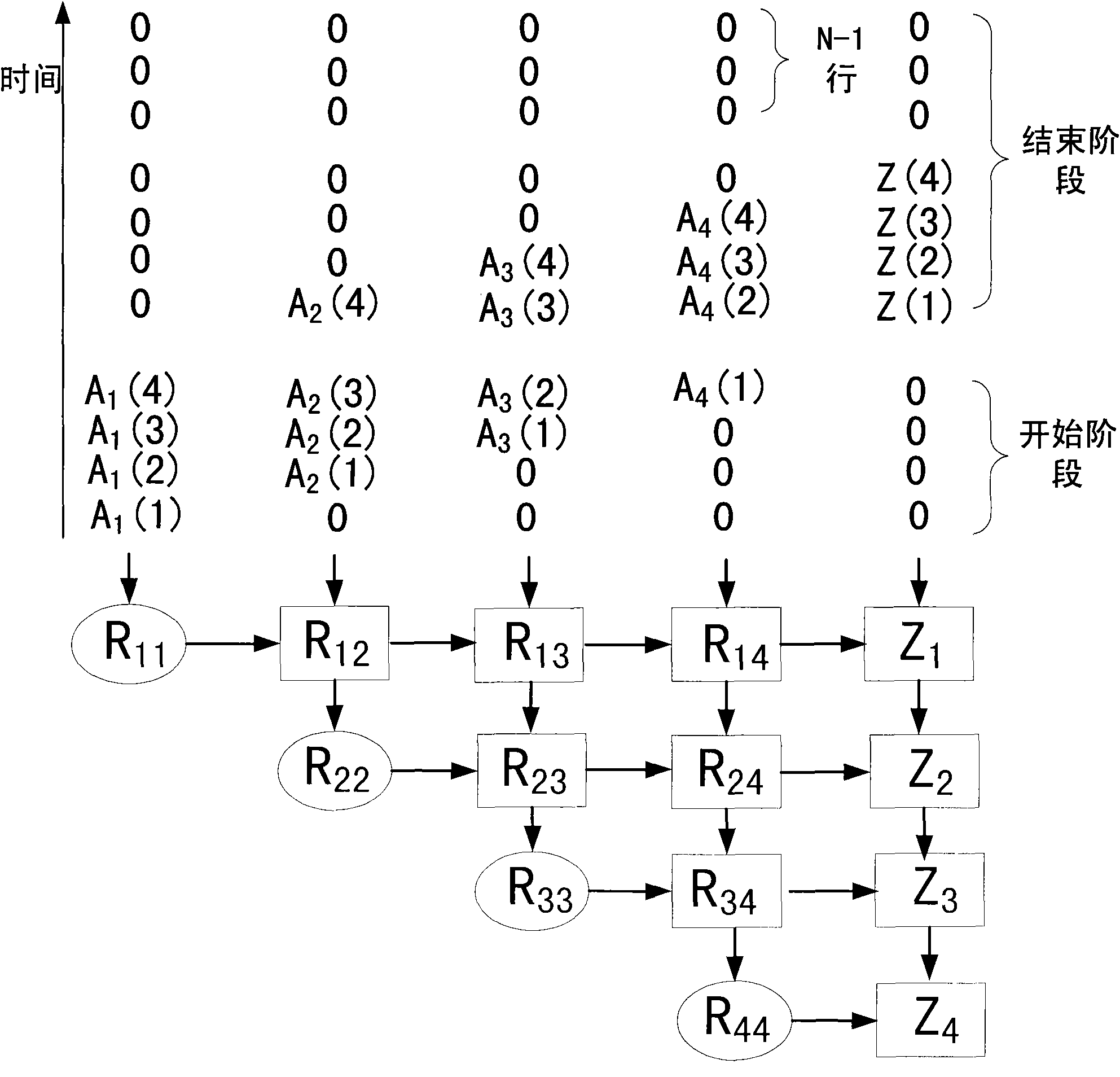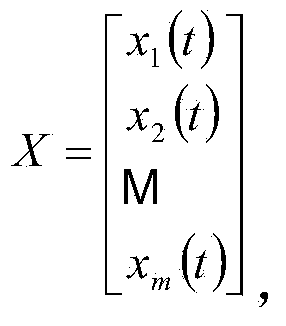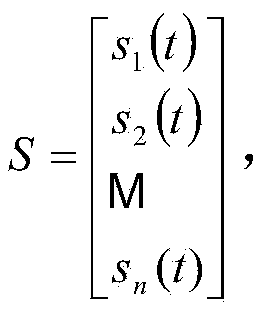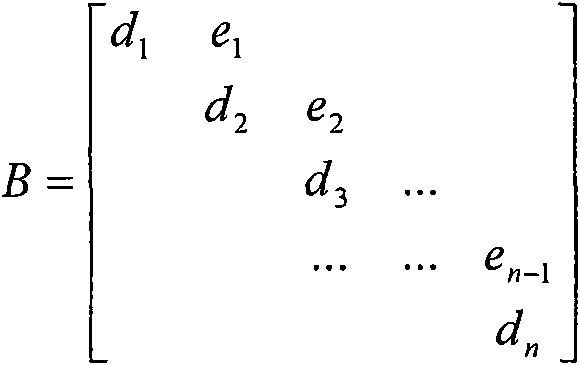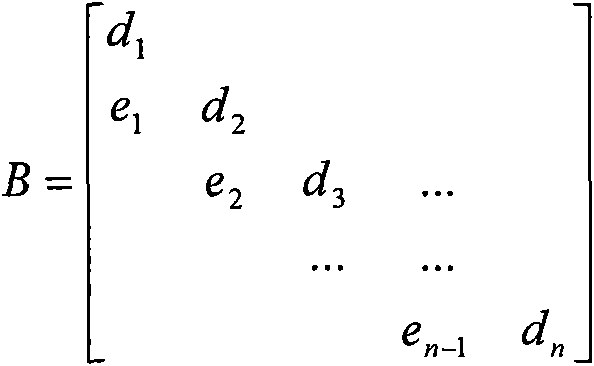Patents
Literature
57 results about "Givens rotation" patented technology
Efficacy Topic
Property
Owner
Technical Advancement
Application Domain
Technology Topic
Technology Field Word
Patent Country/Region
Patent Type
Patent Status
Application Year
Inventor
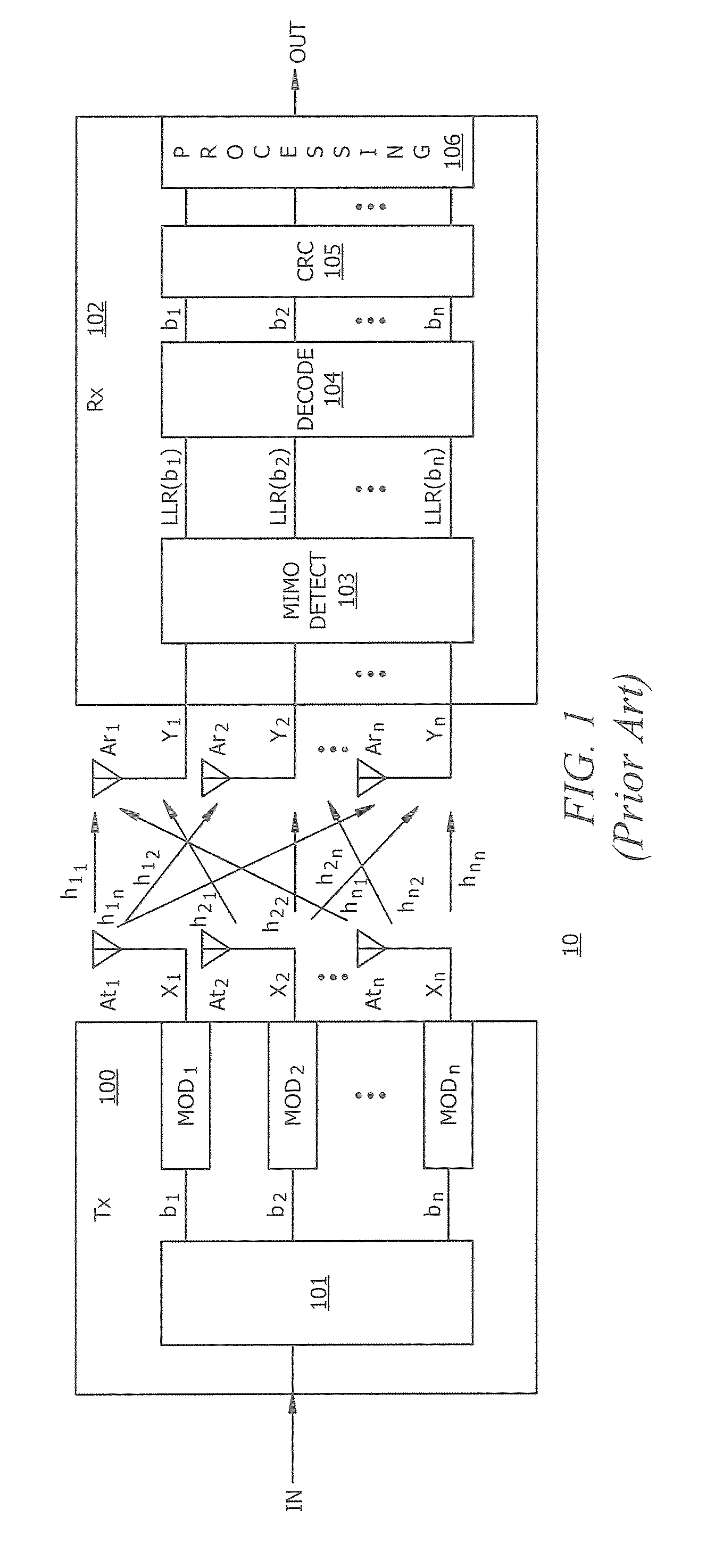
In numerical linear algebra, a Givens rotation is a rotation in the plane spanned by two coordinates axes. Givens rotations are named after Wallace Givens, who introduced them to numerical analysts in the 1950s while he was working at Argonne National Laboratory.
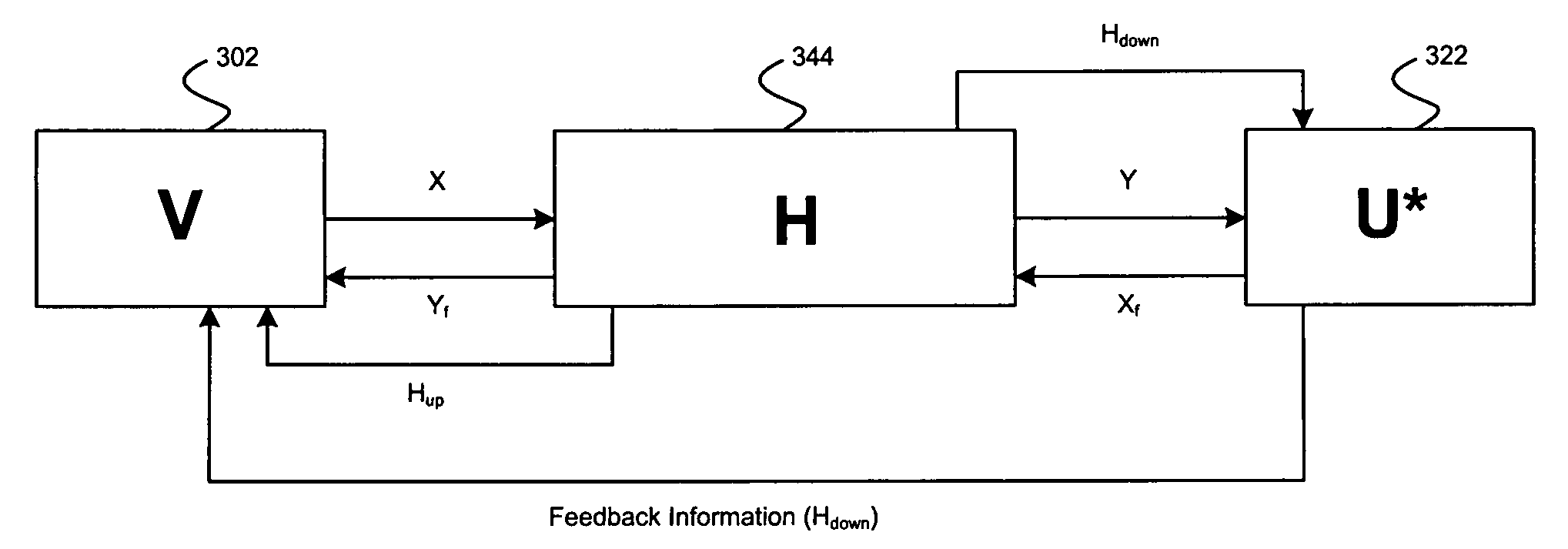
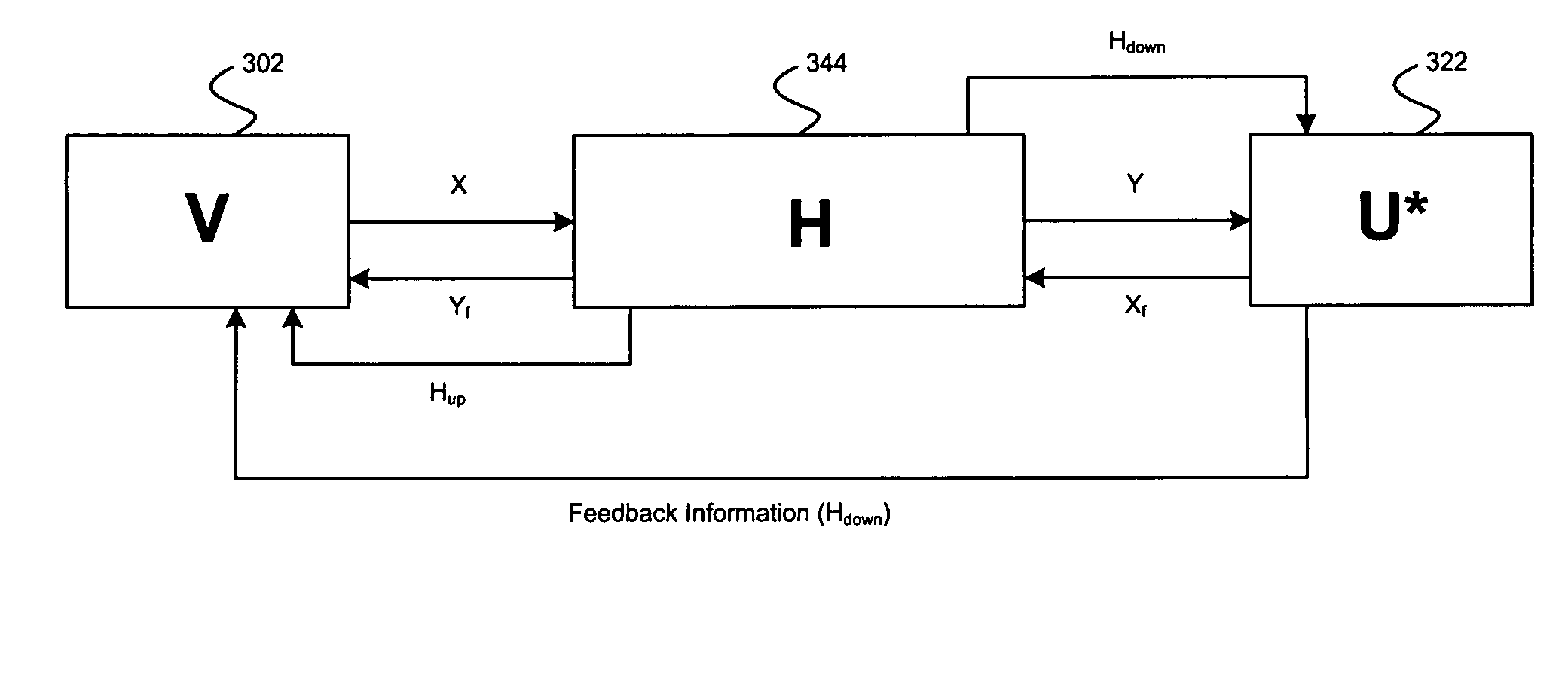
Method and system for utilizing givens rotation to reduce feedback information overhead
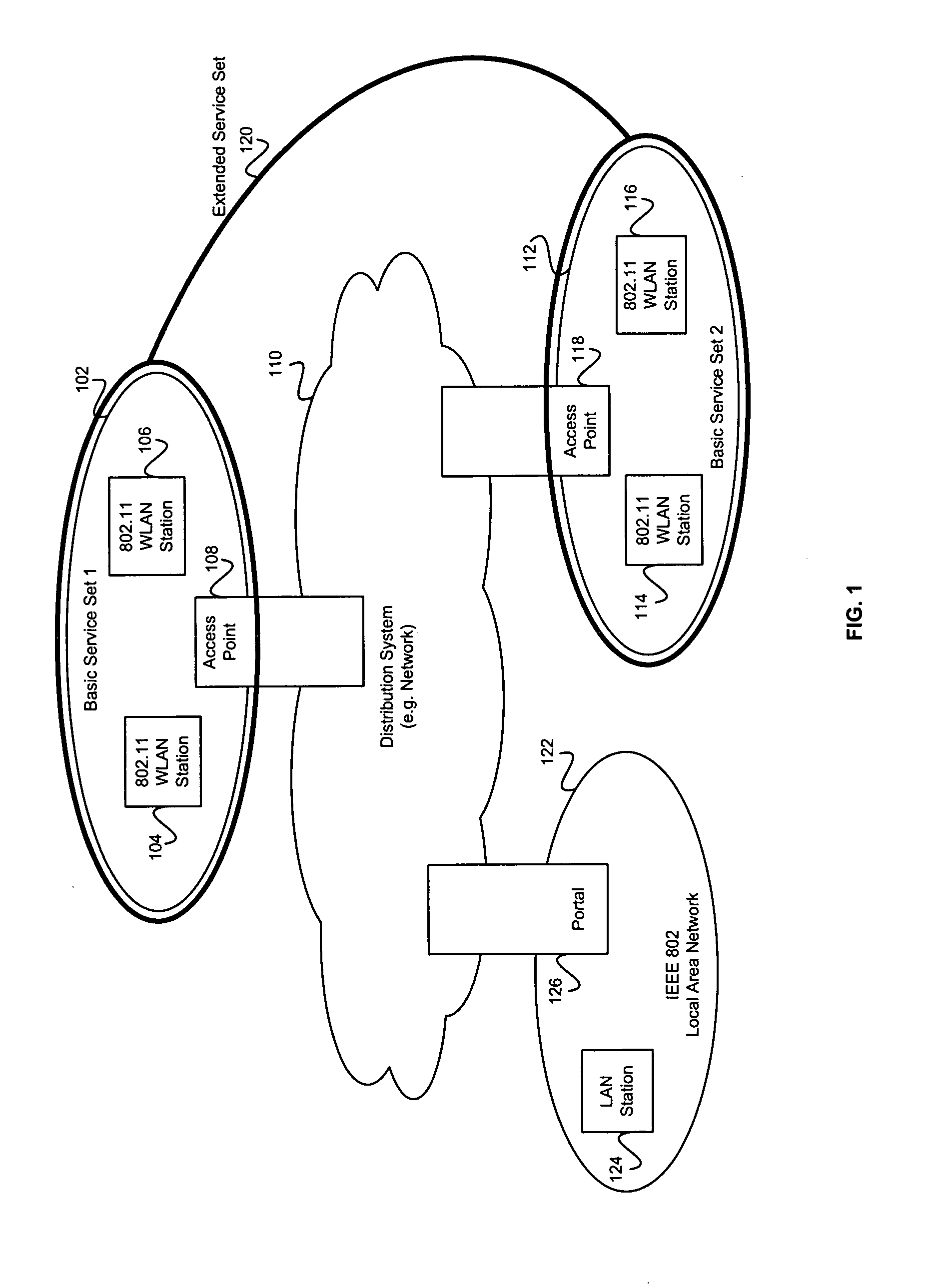
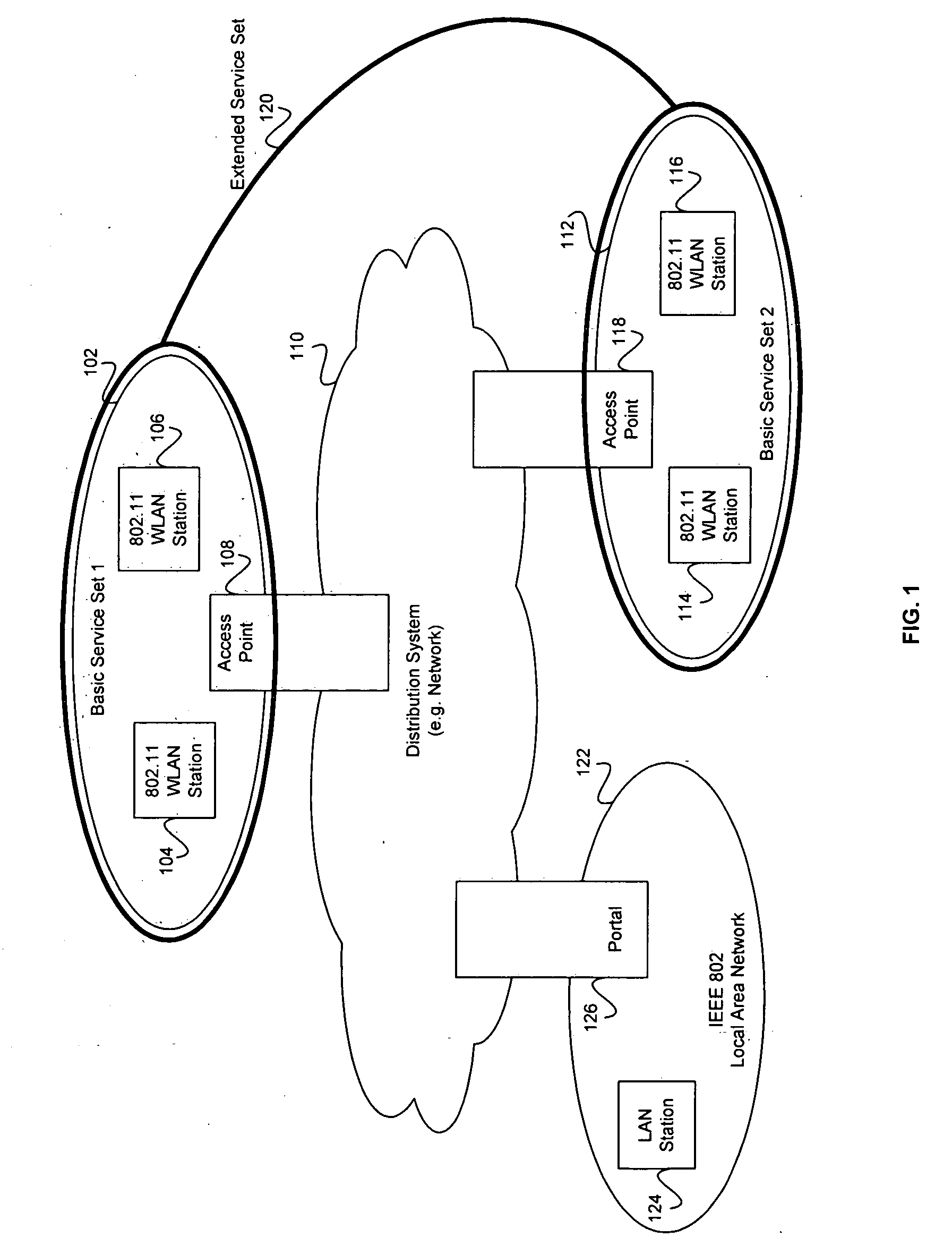
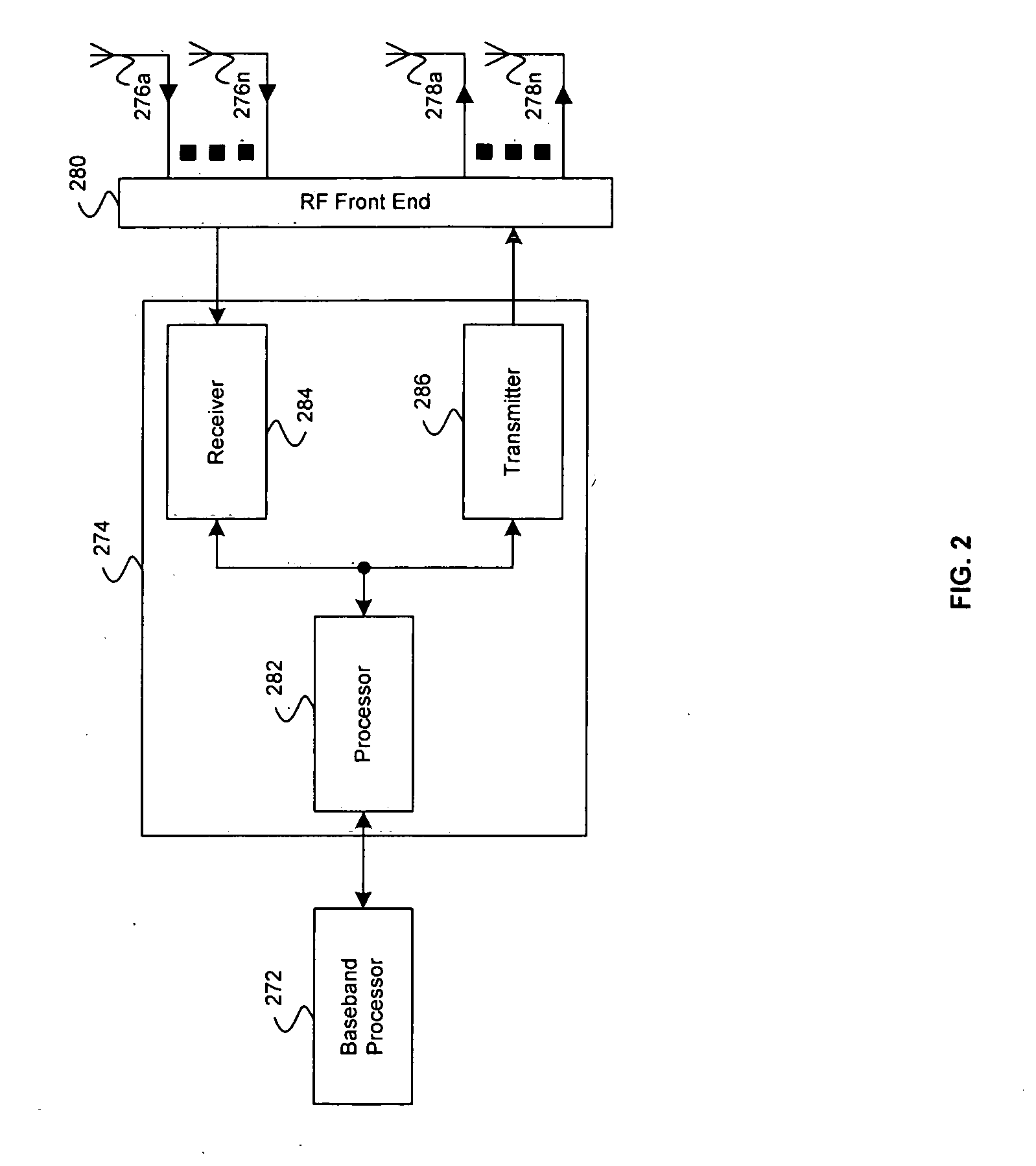
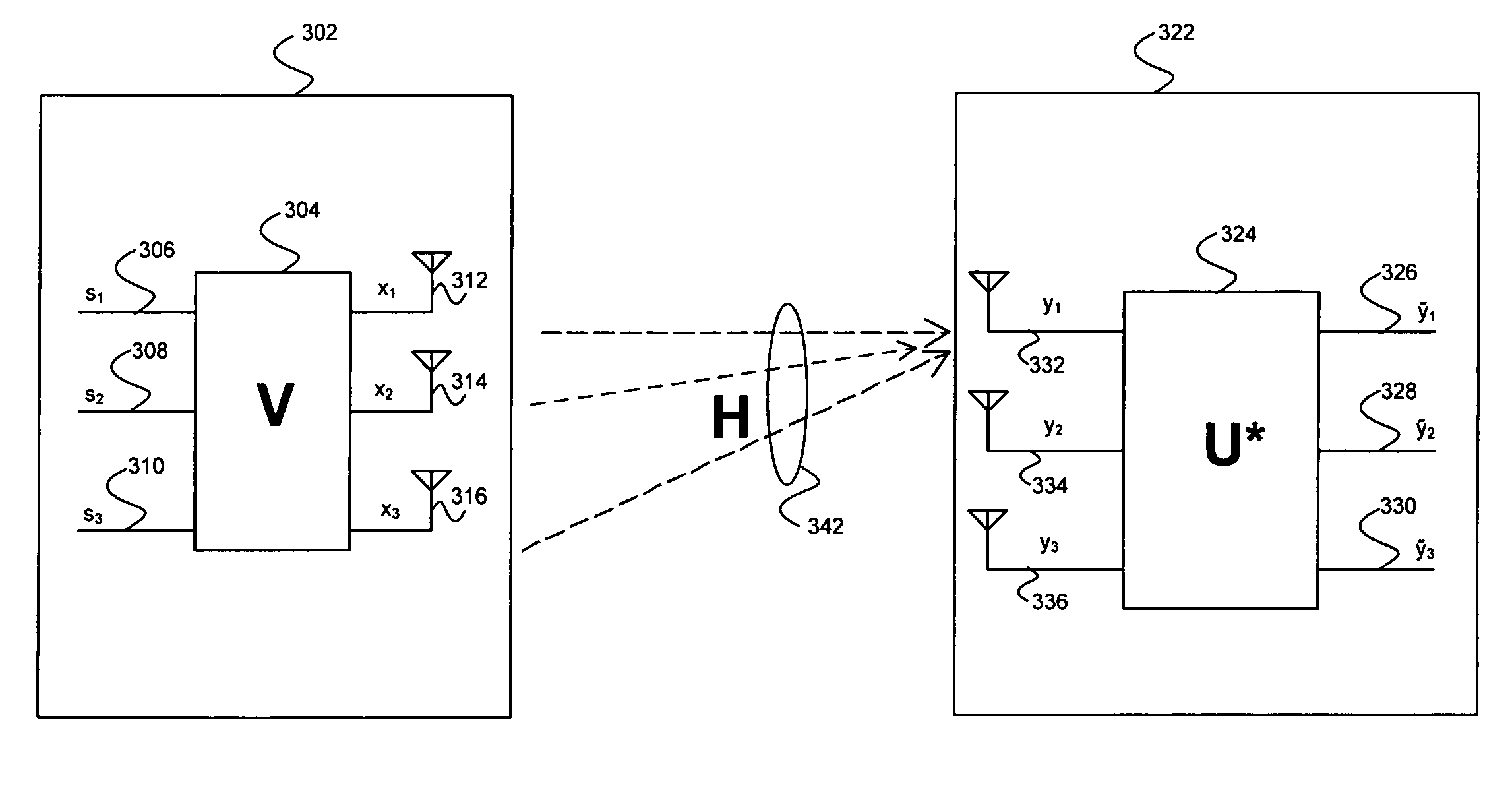
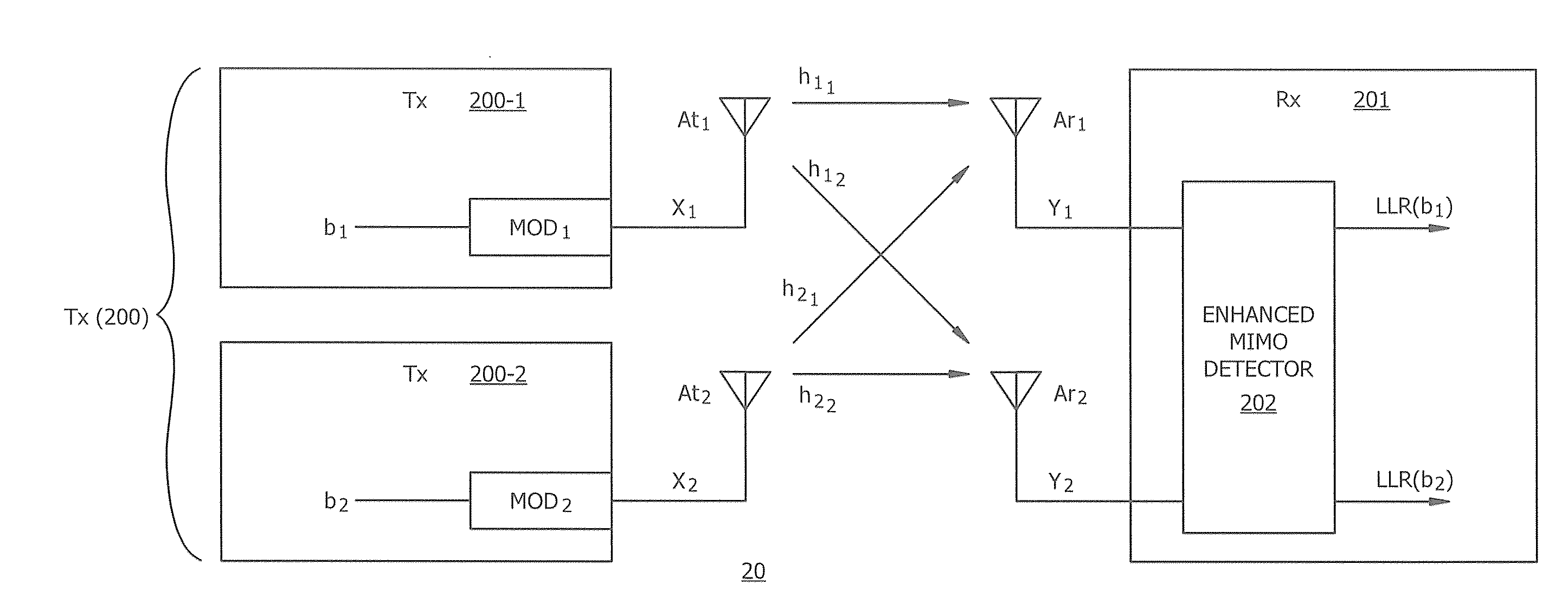
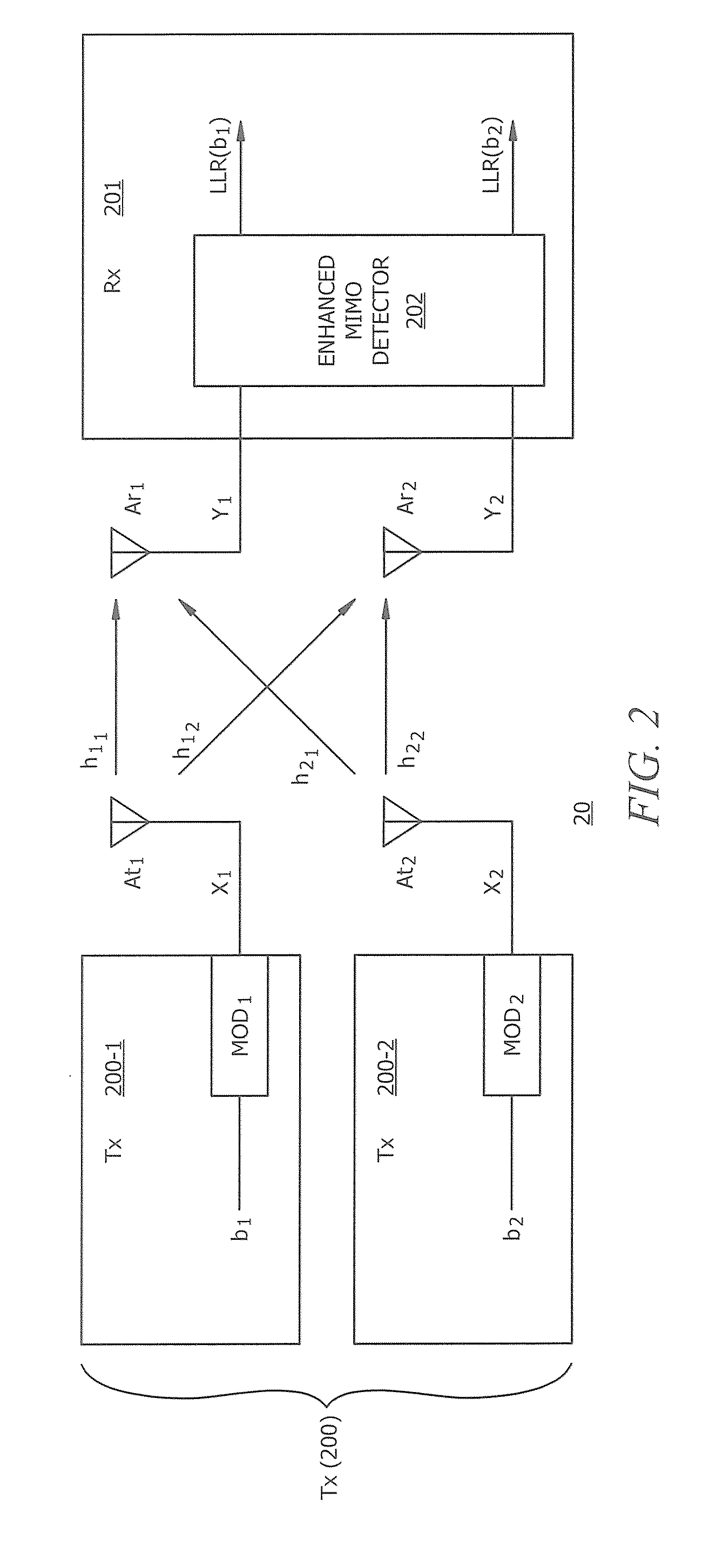
ActiveUS20070213013A1Spatial transmit diversityNetwork traffic/resource managementCommunications systemMultiple input
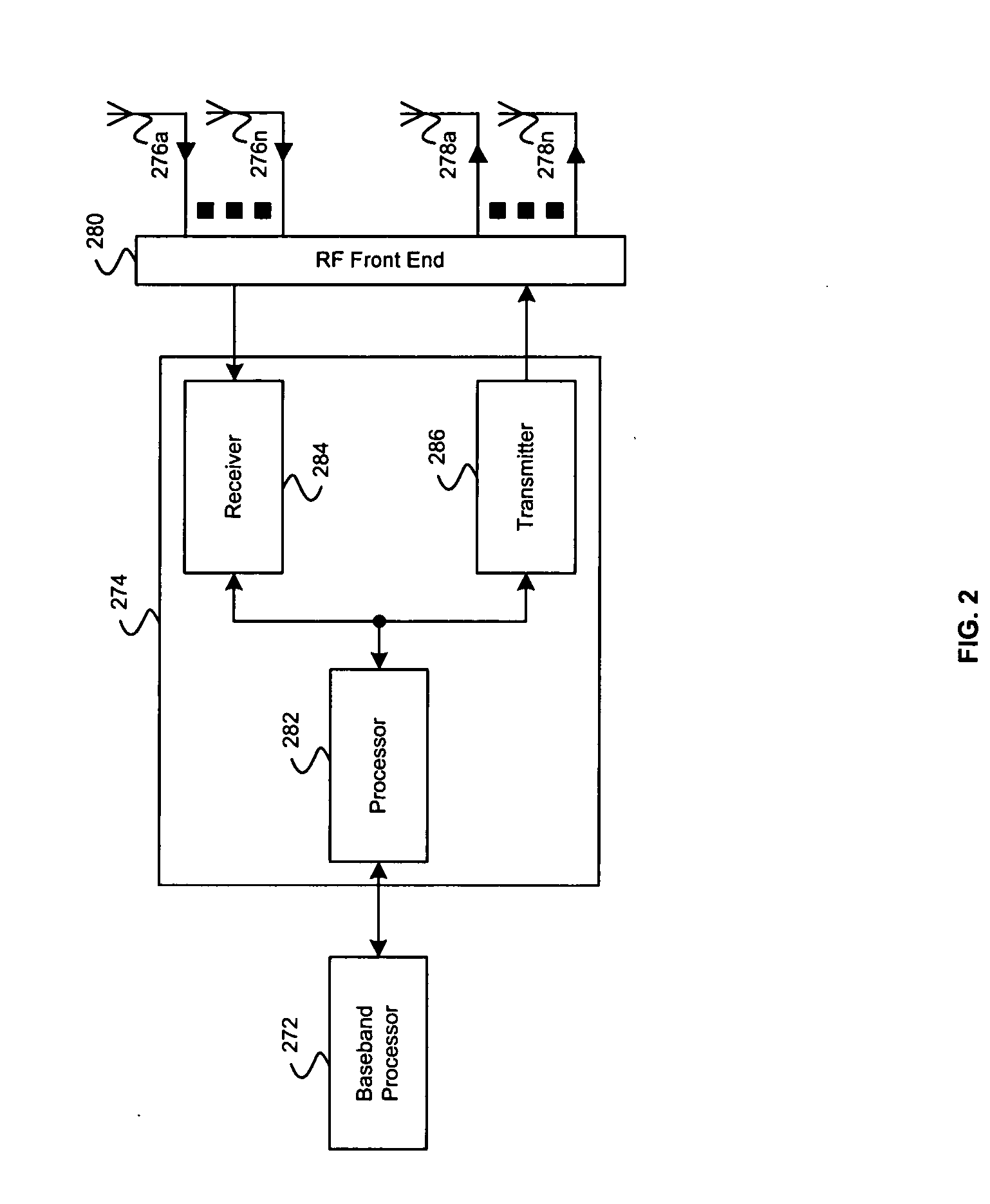
Aspects of a method and system for utilizing Givens rotation to reduce feedback information overhead are presented. Aspects of the system may include a receiver that may enable computation of a beamforming matrix for signals received from a transmitter in a multiple input multiple output (MIMO) communication system. The receiver may enable computation of Givens rotation angles and / or phase rotation angles based on the computed beamforming matrix. The receiver may also enable feedback of information containing the Givens rotation angles and / or phase rotation angles to the transmitter.
Owner:AVAGO TECH INT SALES PTE LTD
Method and system for quantization for a general beamforming matrix in feedback information
ActiveUS20070160011A1Radio/inductive link selection arrangementsRadio transmissionFormation matrixSignal-to-noise ratio (imaging)
Aspects of a method and system for utilizing Givens rotation expressions for quantization for a general beamforming matrix in feedback information. In one aspect of the invention, feedback information is computed at the receiving MIMO wireless device based on a geometric mean decomposition (GMD) method. The feedback information may include a matrix that describes a wireless medium. The matrix may represent a multiplicative product of at least one rotation matrix and at least one diagonal phase rotation matrix. Each of the rotation matrices may include at least one matrix element whose value is based on Givens rotation angle. The transmitting MIMO wireless device may subsequently transmit a plurality of signals via the wireless medium based on the received matrix information. The signal strength and / or signal to noise ratio (SNR) measurement (as measured in decibels, for example) associated with each of the transmitted plurality of signals may be about equal.
Owner:AVAGO TECH INT SALES PTE LTD
Method and system for utilizing givens rotation expressions for asymmetric beamforming matrices in explicit feedback information
Aspects of a method and system for utilizing Givens rotation expressions for asymmetric beamforming matrices in explicit feedback information are presented. In one aspect of the invention, Givens matrices may be utilized to reduce a quantity of information communicated in explicit feedback information via an uplink RF channel. The explicit feedback information may include specifications for a feedback beamforming matrix that may be utilized when transmitting signals via a corresponding downlink RF channel. The feedback beamforming matrix may represent a rotated version of an un-rotated matrix. The Givens matrices may be utilized to apply one or more Givens rotations to un-rotated matrix. The feedback beamforming matrix may be computed based on a matrix product of a plurality of Givens matrices. The feedback beamforming matrix may be encoded utilizing fewer bits than may be required to encode the un-rotated matrix.
Owner:AVAGO TECH INT SALES PTE LTD
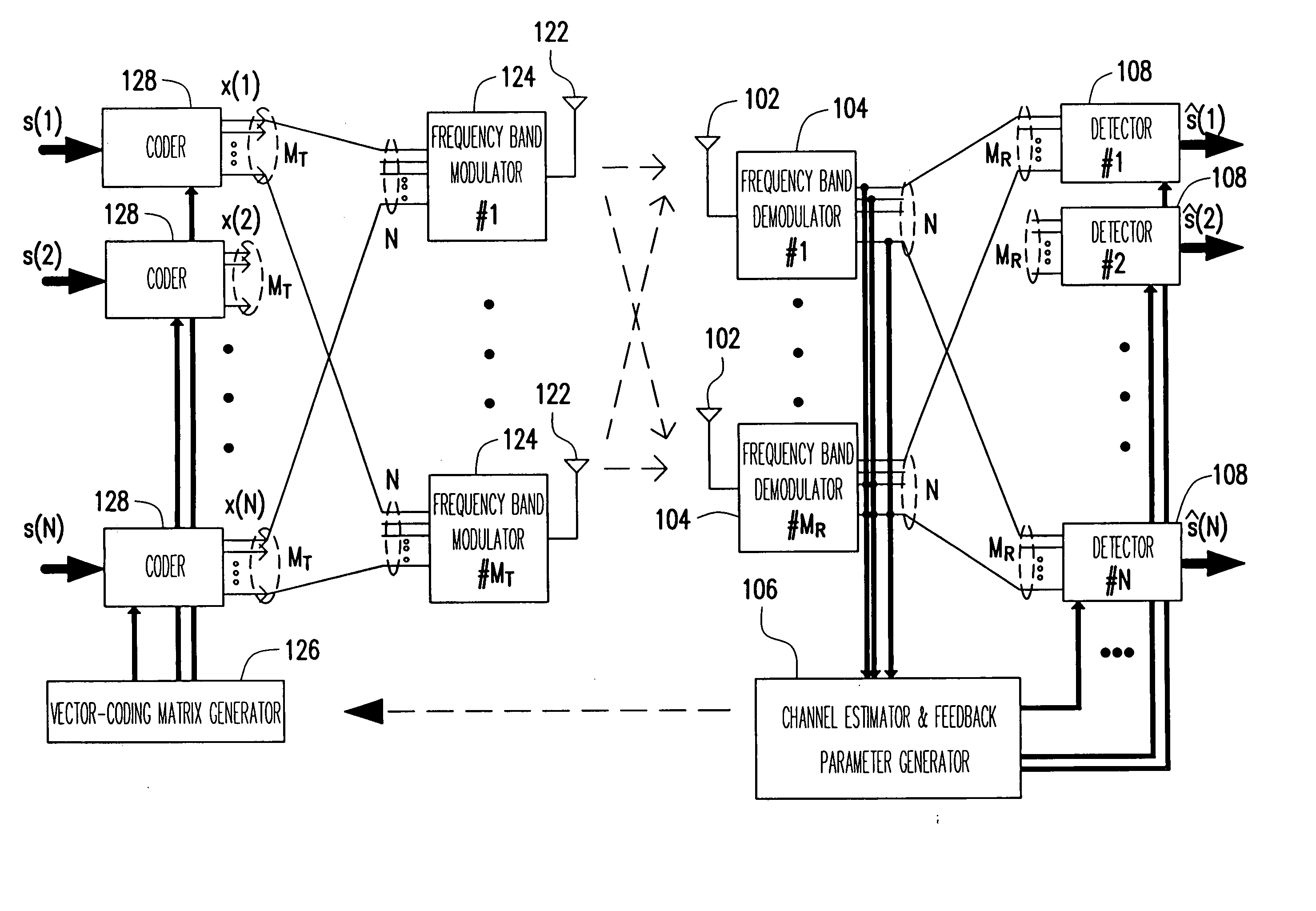
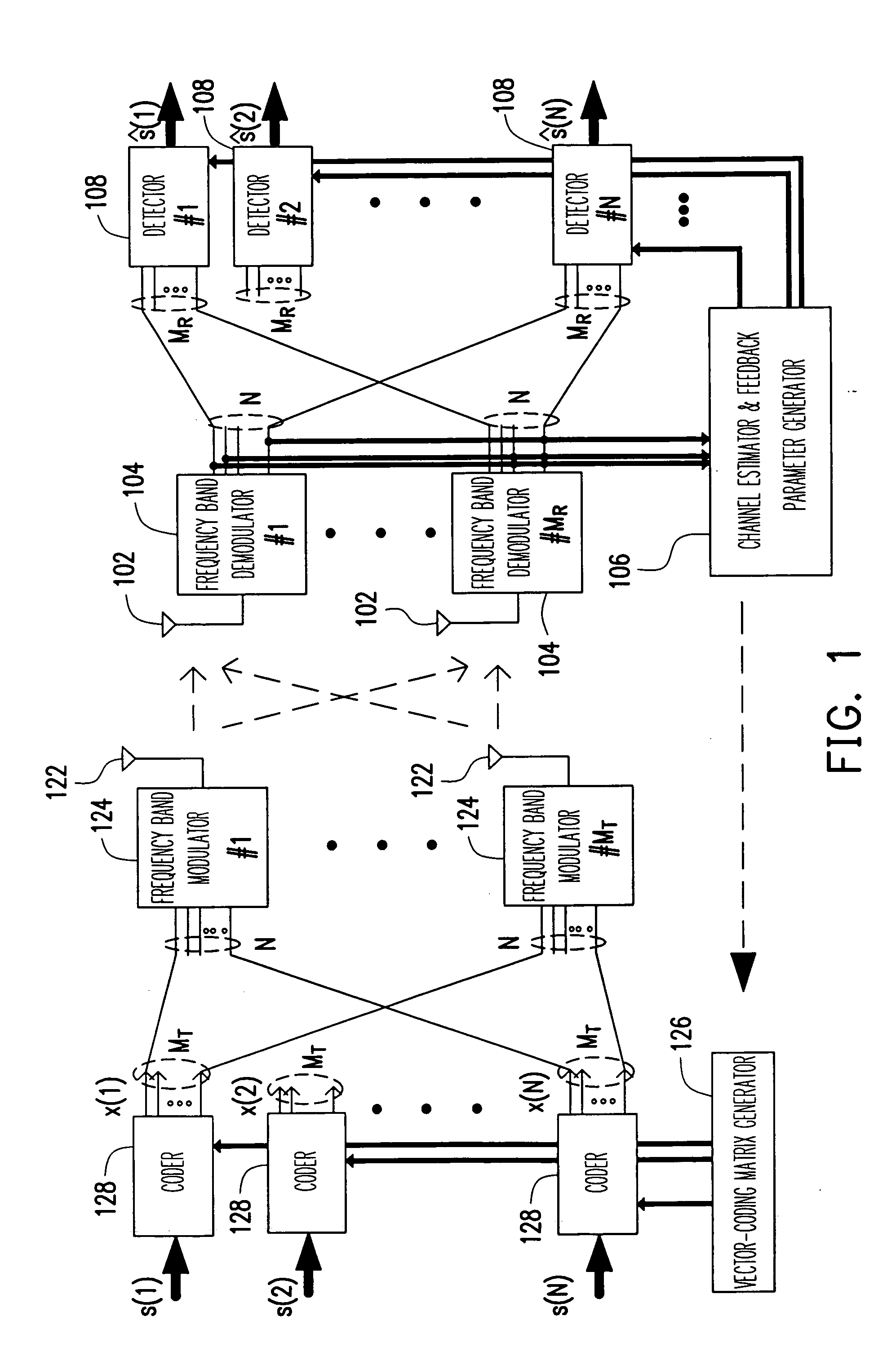
MIMO-OFDM system and pre-coding and feedback method therein
InactiveUS20070115799A1Better respondReduce complexityModulated-carrier systemsRadio transmissionChannel state informationRound complexity
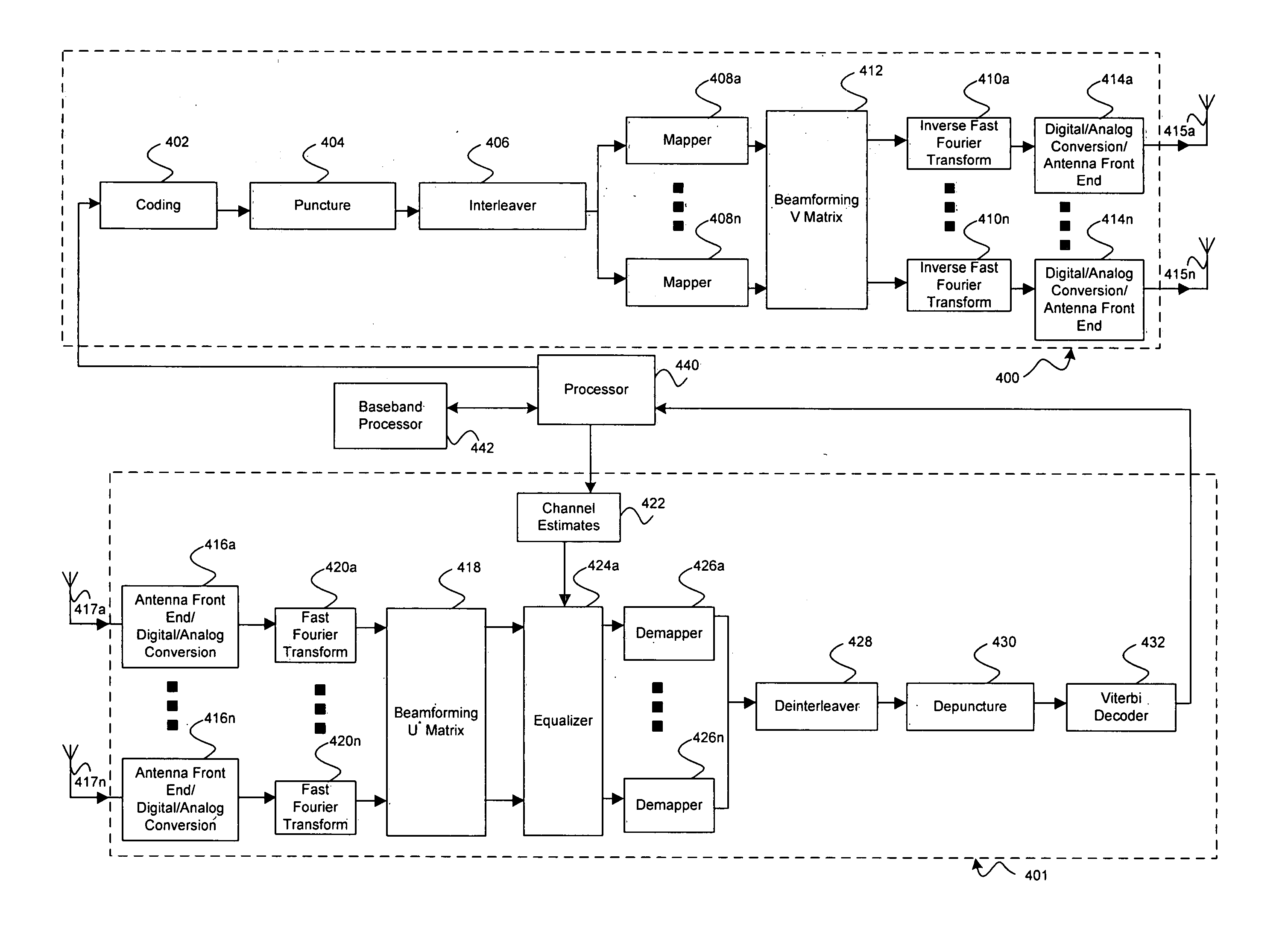
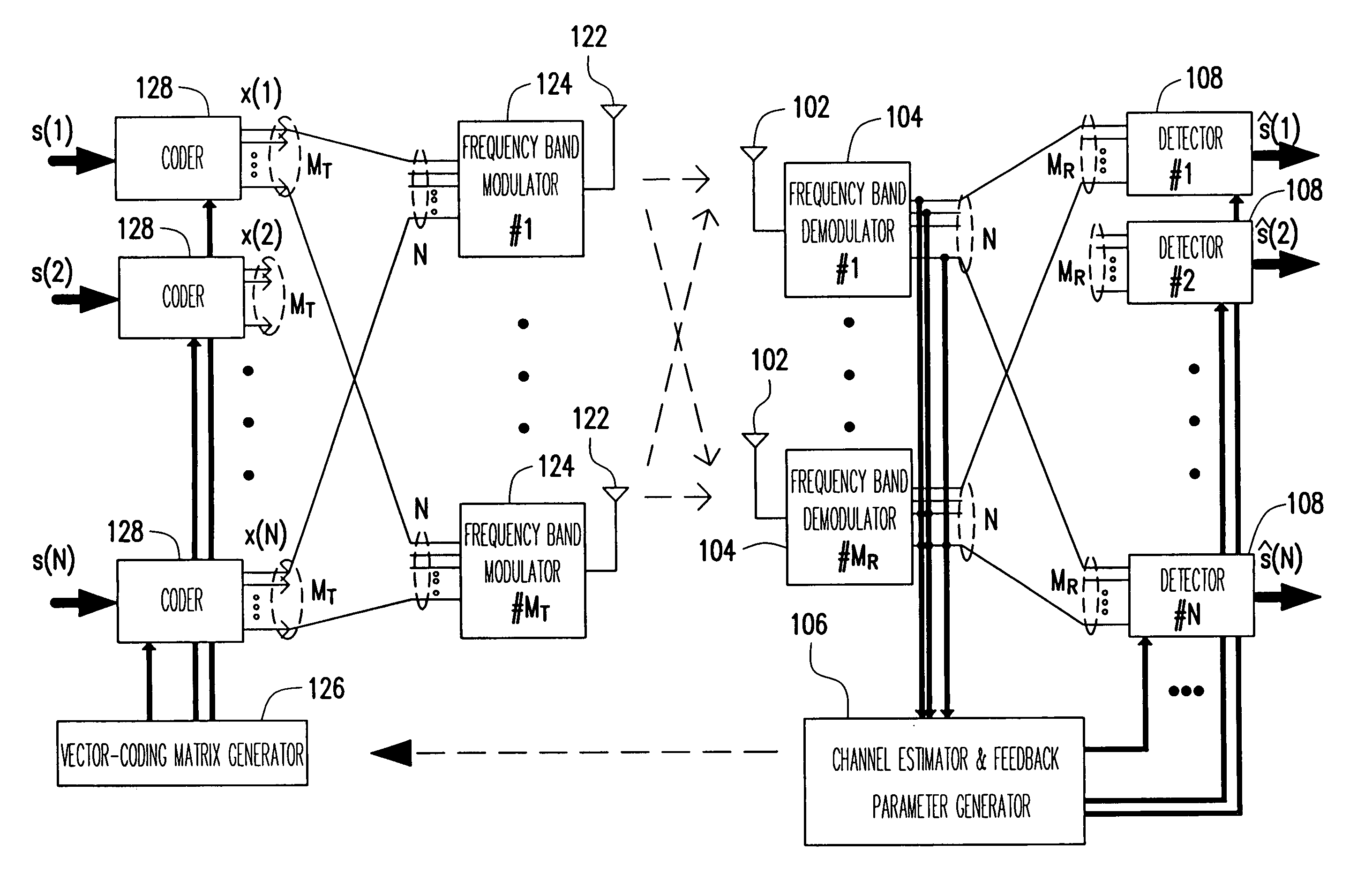
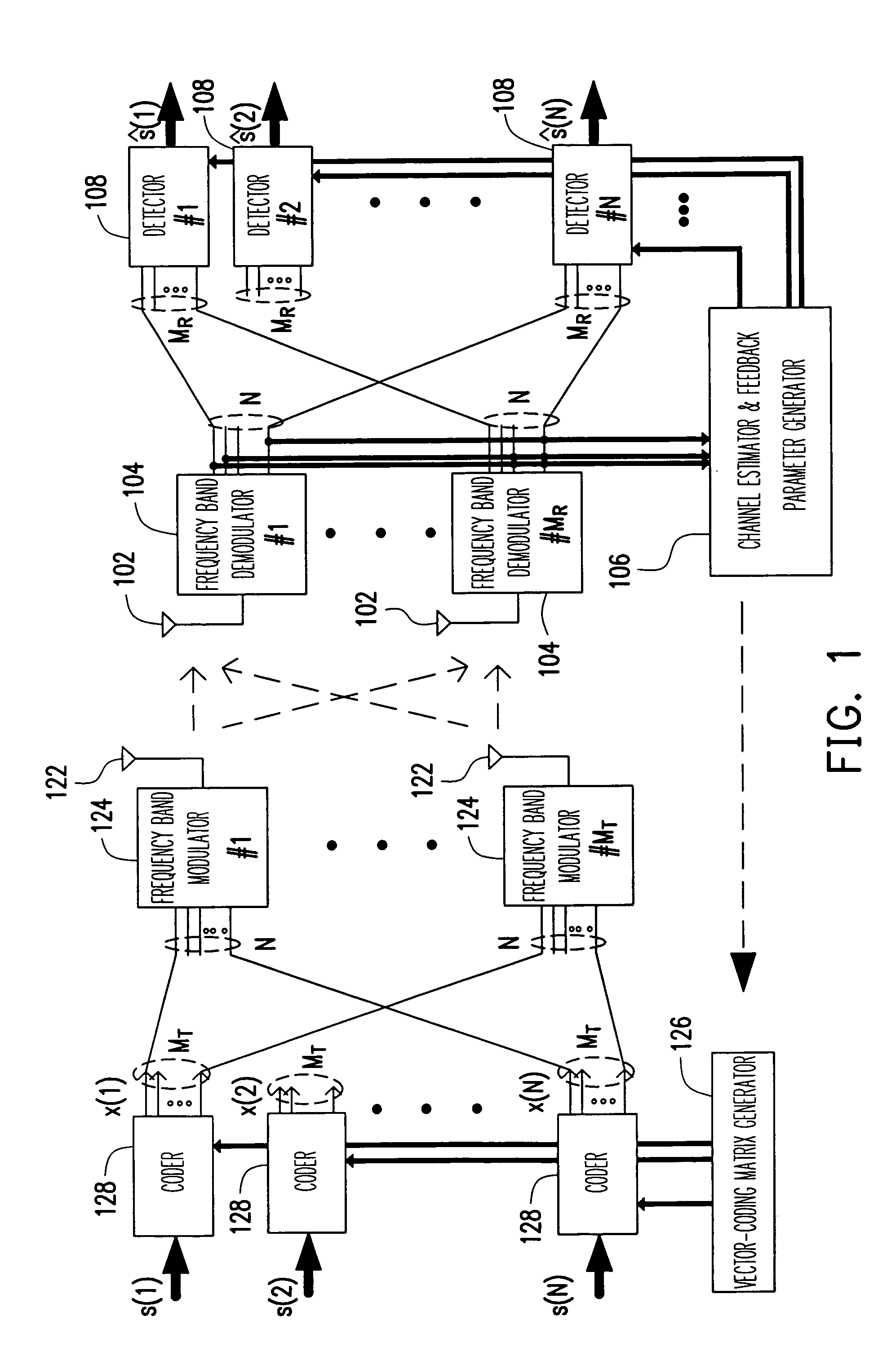
The present invention provides an antenna-array-based multiple-input multiple-output orthogonal-frequency-division-multiplexing (MIMO-OFDM) system and a pre-coding and feedback method used in the same. The present invention uses QR decompositions of the MIMO channel matrixes to parameterize the channel state information (CSI) of every OFDM frequency band. In addition, the present invention feeds back the information related to θ and φ in the Givens rotation matrixes of the partial frequency bands and then uses an interpolation method to generate θ and φ in the Givens rotation matrixes of all the frequency bands, which further is able to represent the CSI of all the frequency bands. In this way, the present invention has advantages of low complexity and low feedback rate requirement.
Owner:MEDIATEK INC
Method and system for transmitter beamforming for reduced complexity multiple input multiple output (MIMO) transceivers
ActiveUS20080043873A1Reduce complexityModulated-carrier systemsDiversity/multi-antenna systemsSingular value decompositionTransceiver
Aspects of a method and system for transmitter beamforming for reduced complexity multiple input multiple output (MIMO) transceivers are presented. Aspects of the system may include a MIMO transmitter that computes a channel estimate matrix and decomposes the computed channel estimate matrix based on singular value decomposition (SVD). Singular values in a singular value matrix may be rearranged and grouped to generate a plurality of submatrices. In one aspect, each of the submatrices may be decomposed based on GMD at a MIMO transmitter, while a MIMO receiver may utilize a vertical layered space time (VLST) method. In another aspect, the MIMO transmitter may utilize Givens rotation matrices corresponding to each of the submatrices, while the MIMO receiver may utilize maximum likelihood (ML) detection.
Owner:BELL NORTHERN RES LLC
Signal processing block for a receiver in wireless communication
ActiveUS20110264721A1Digital computer detailsIndependent non-interacting antenna combinationsResource utilizationParallel computing
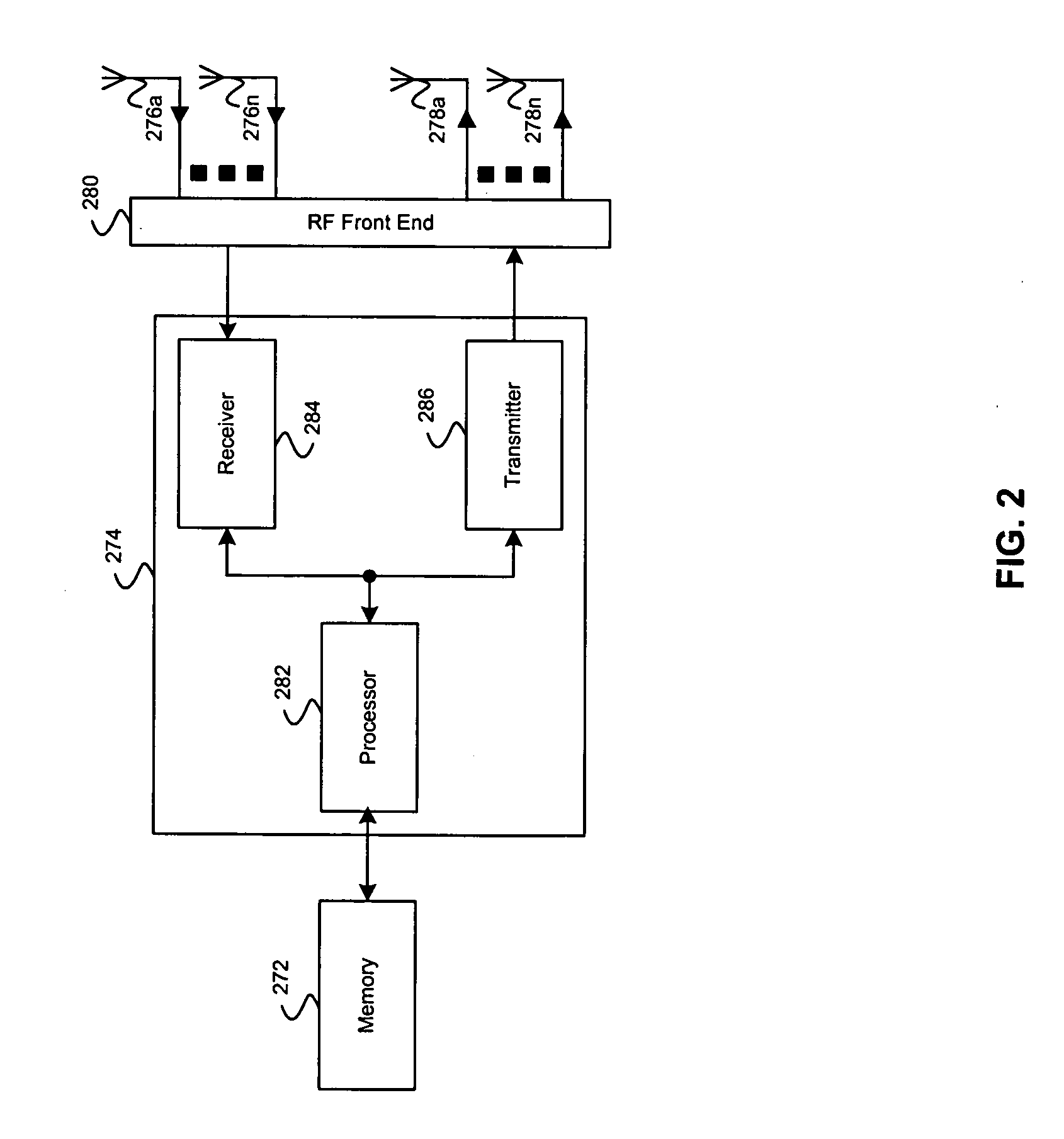
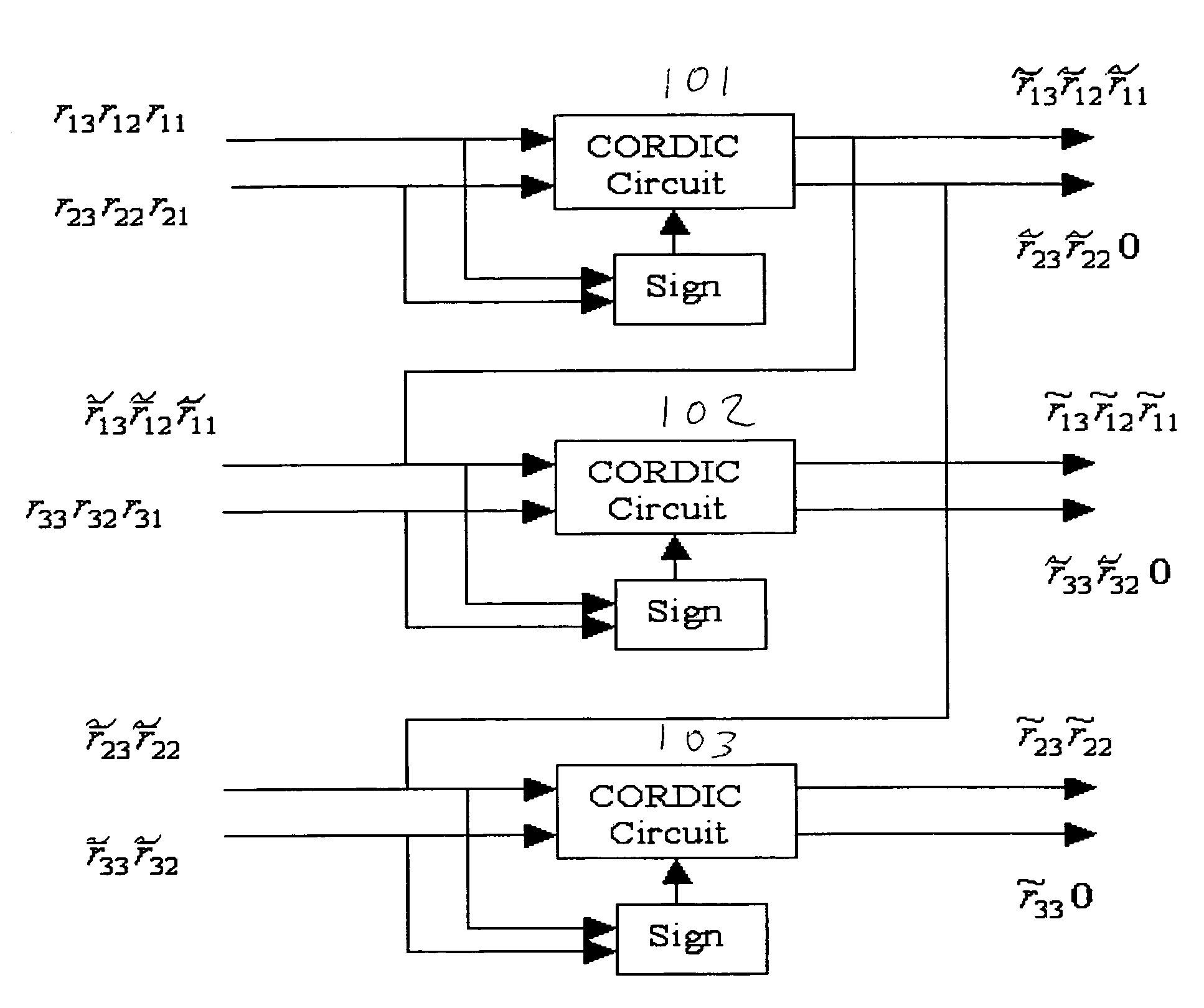
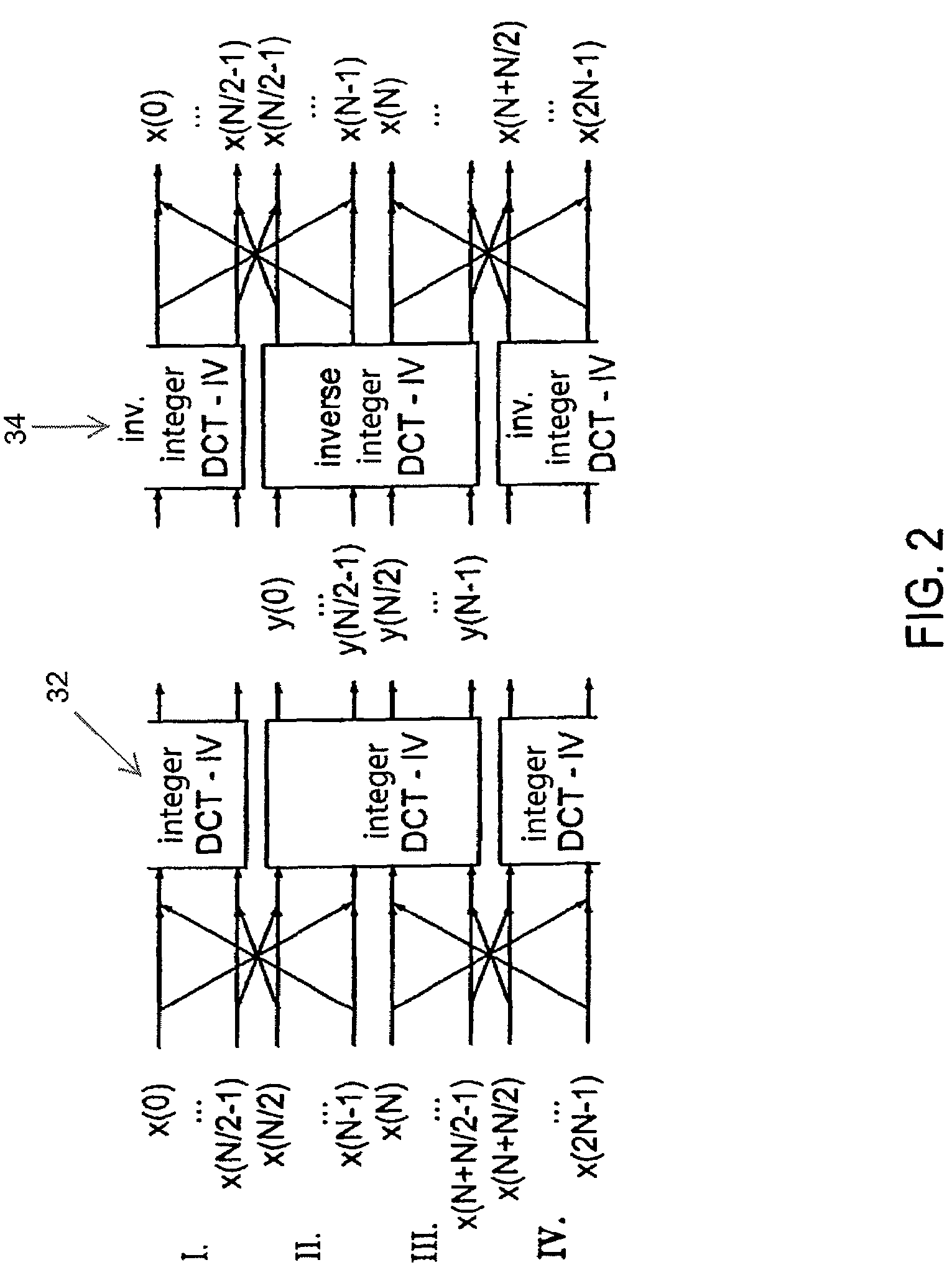
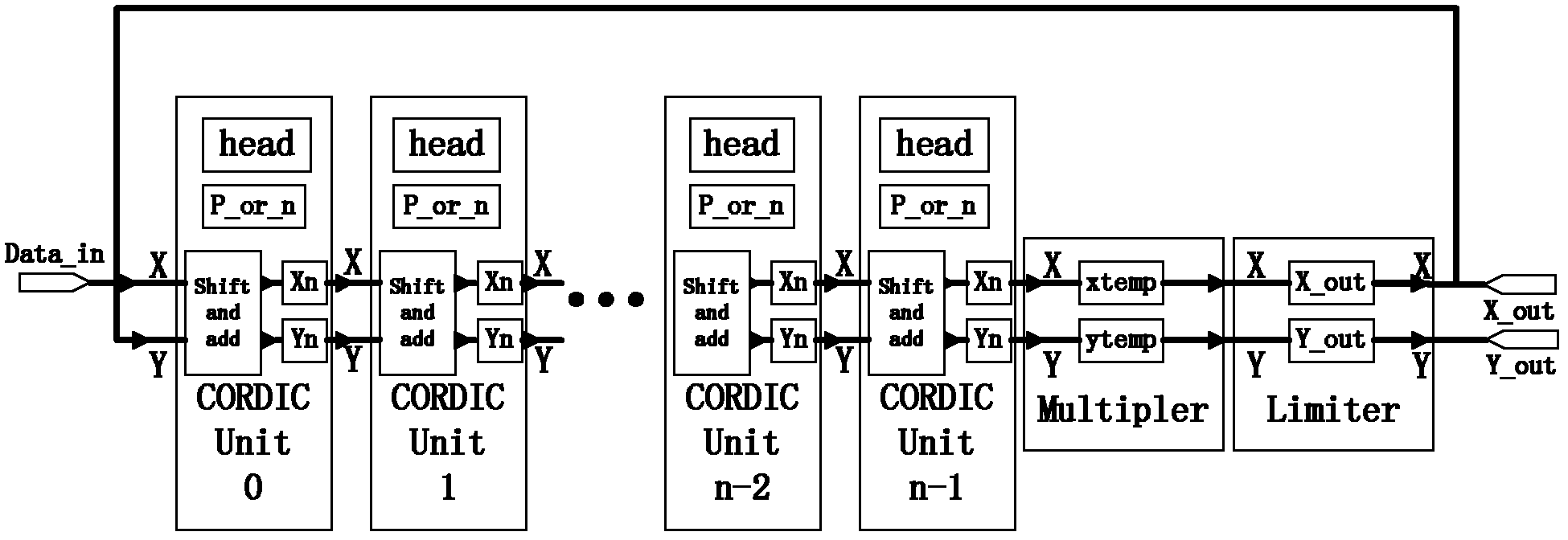
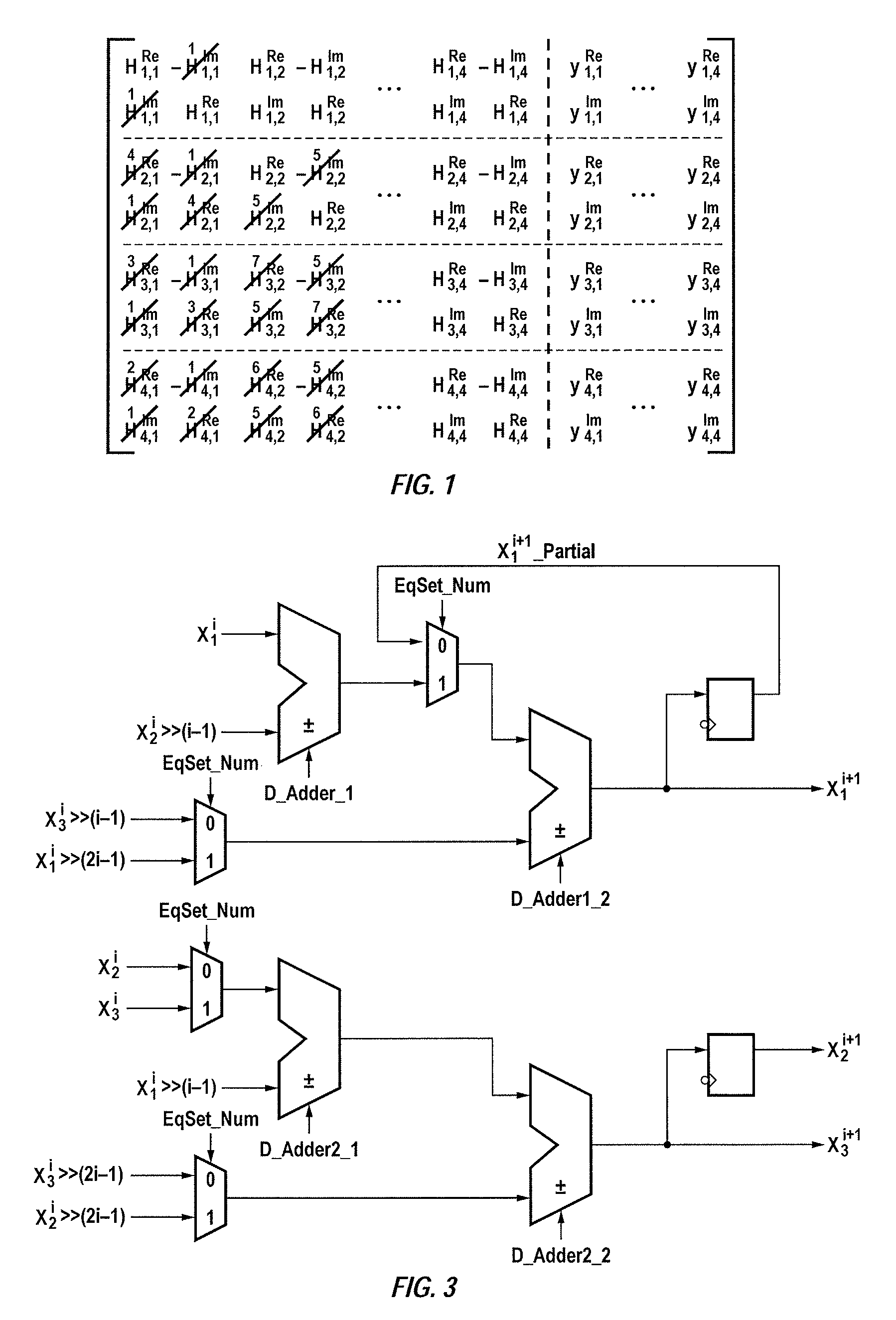
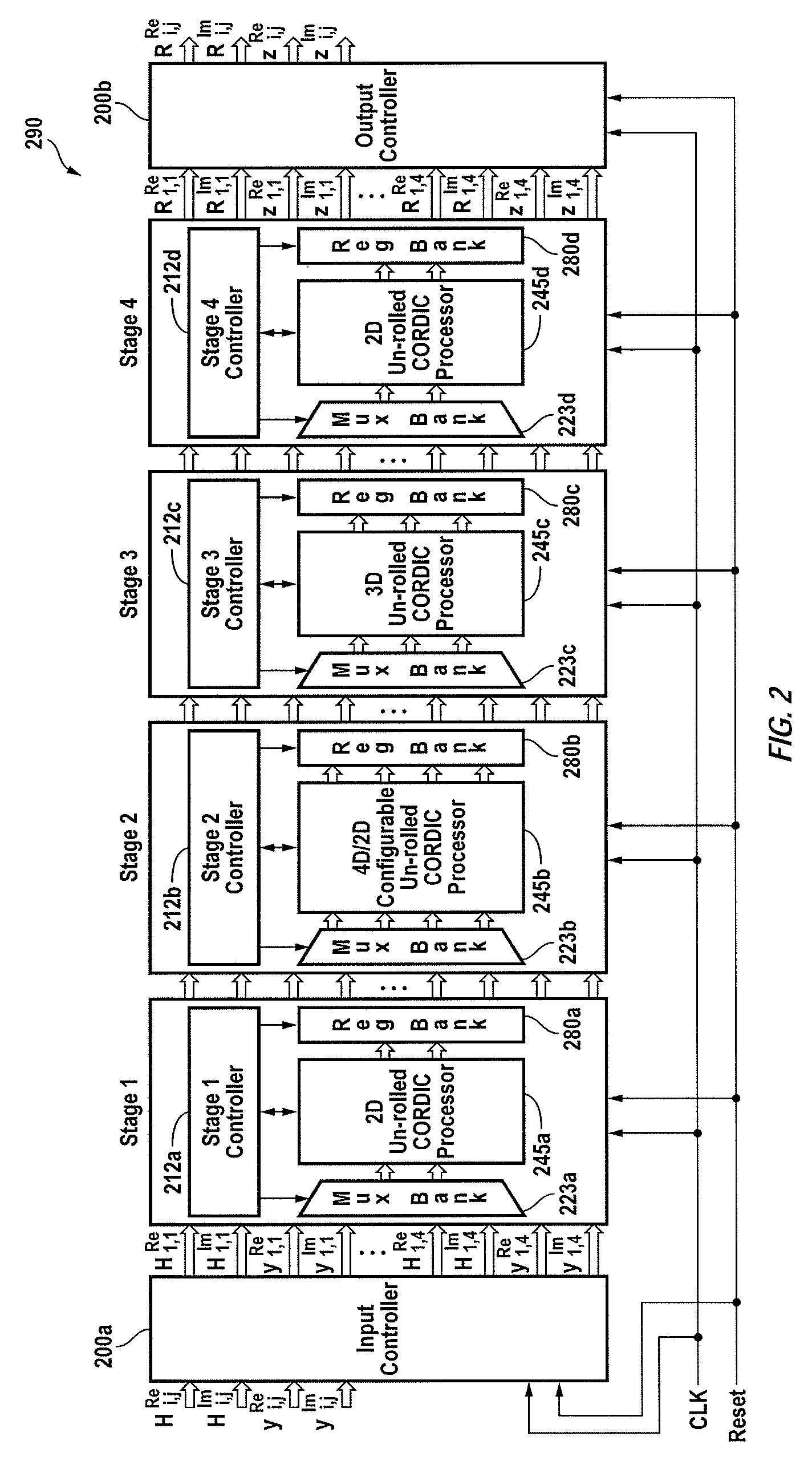
A QRD processor for computing input signals in a receiver for wireless communication relies upon a combination of multi-dimensional Givens Rotations, Householder Reflections and conventional two-dimensional (2D) Givens Rotations, for computing the QRD of matrices. The proposed technique integrates the benefits of multi-dimensional annihilation capability of Householder reflections plus the low-complexity nature of the conventional 2D Givens rotations. Such integration increases throughput and reduces the hardware complexity, by first decreasing the number of rotation operations required and then by enabling their parallel execution. A pipelined architecture is presented (290) that uses un-rolled pipelined CORDIC processors (245a to 245d) iteratively to improve throughput and resource utilization, while reducing the gate count.
Owner:MAXLINEAR INC
Method for wifi beamforming, feedback, and sounding (WIBEAM)
ActiveCN104737465ASimple structureImprove feedback efficiencySpatial transmit diversityForward error control useTime domainDecomposition
Methods for WiFi beamforming, feedback, and sounding (WiBEAM) are described. Codebook based beamforming feedback signaling and sounding mechanisms for use in wireless communications are disclosed. The methods described herein improve the feedback efficiency by using Givens rotation based decompositions and quantizing the resulting angles of the Givens rotation based decompositions using a range from a subset of [0, 2π]. Feedback may also be divided into multiple components to improve feedback efficiency / accuracy. Time domain beamforming reports for taking advantage of channel reciprocity while still taking into account practical radio frequency (RF) channel impairments are also described. Beamforming feedback that prioritizes the feedback bits in accordance with the significance of the bits is also disclosed. A preamble structure to enable the use of smoothing methods for improved channel estimation, codebook designs that may be used for codebook based beamforming feedback, and multi-resolution explicit feedback are disclosed as well.
Owner:INTERDIGITAL PATENT HLDG INC
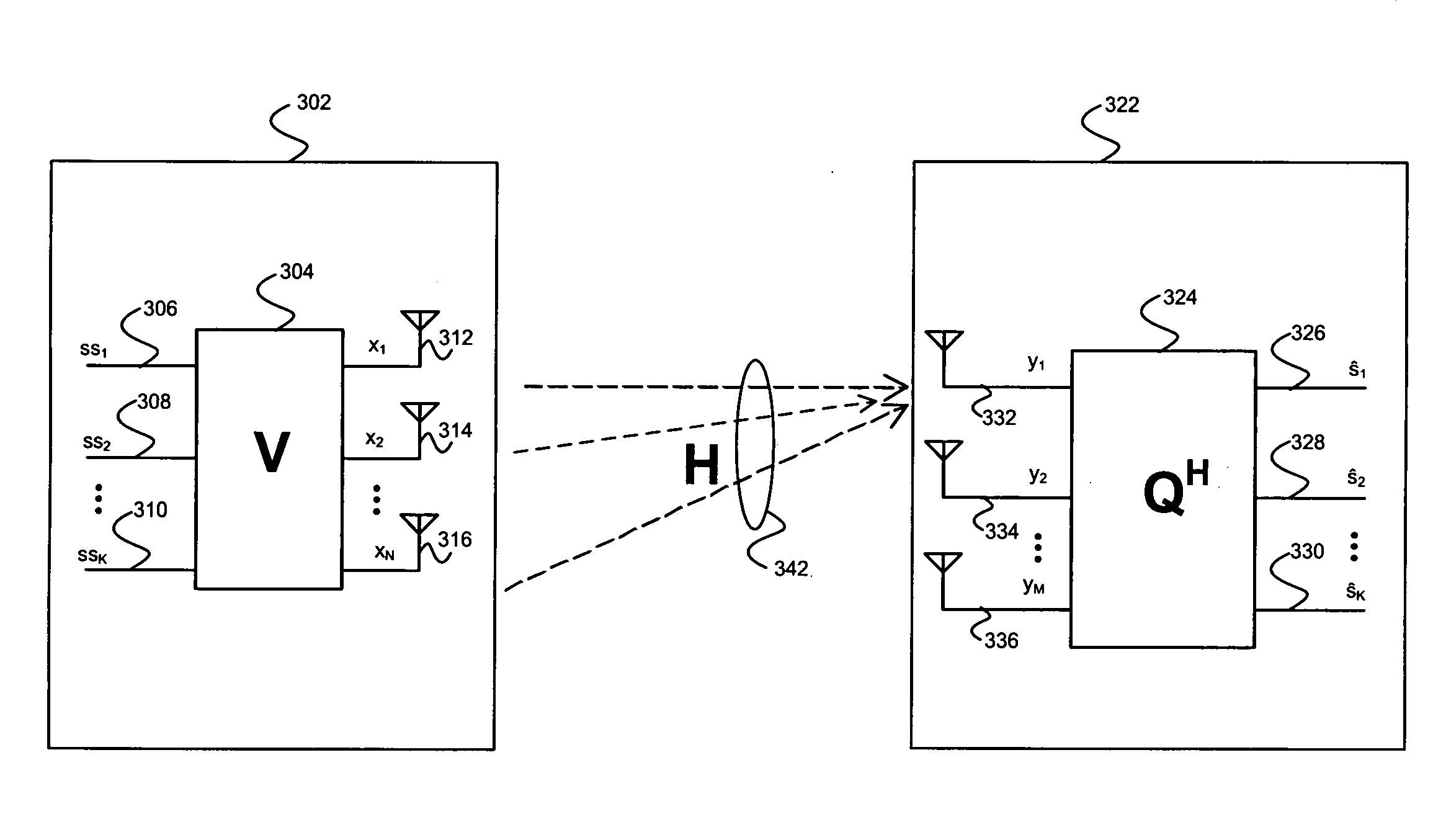
Efficient feedback of channel information in a closed loop beamforming wireless communication system
ActiveUS20060239374A1Diversity/multi-antenna systemsSecret communicationChannel state informationCommunications system
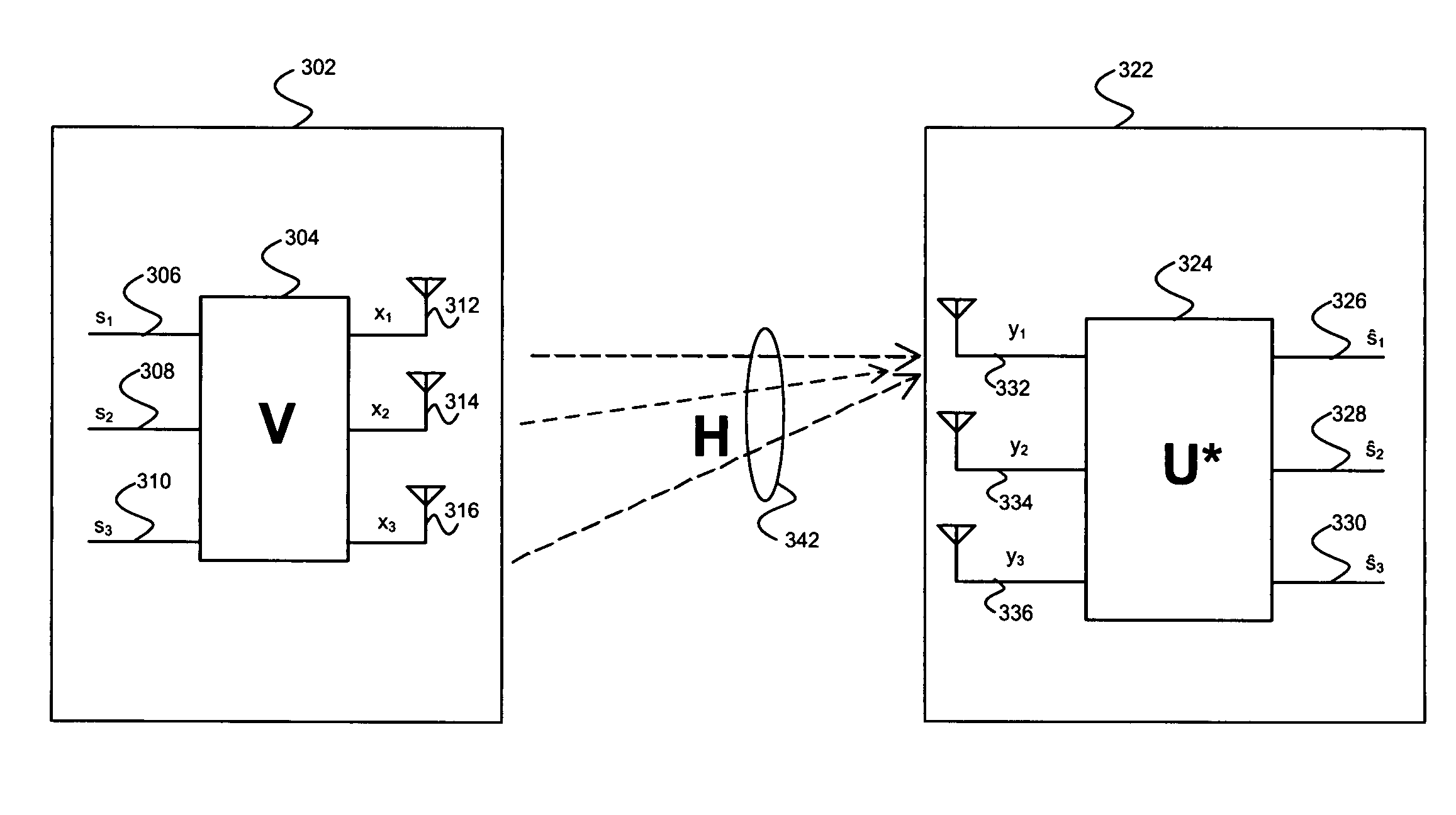
A method for feeding back transmitter beamforming information from a receiving wireless communication device to a transmitting wireless communication device includes a receiving wireless communication device receiving a preamble sequence from the transmitting wireless device. The receiving wireless device estimates a channel response based upon the preamble sequence and then determines an estimated transmitter beamforming unitary matrix based upon the channel response and a receiver beamforming unitary matrix. The receiving wireless device then decomposes the estimated transmitter beamforming unitary matrix to produce the transmitter beamforming information and then wirelessly sends the transmitter beamforming information to the transmitting wireless device. The receiving wireless device may transform the estimated transmitter beamforming unitary matrix using a QR decomposition operation such as a Givens Rotation operation to produce the transformer beamforming information.
Owner:BELL NORTHERN RES LLC
Method and system for utilizing tone grouping with givens rotations to reduce overhead associated with explicit feedback information
InactiveUS7873016B2Modulated-carrier systemsData switching by path configurationEngineeringRotation matrix
Owner:AVAGO TECH WIRELESS IP SINGAPORE PTE
Channel information feedback method and system
InactiveCN102811111AReduce the numberReduce Feedback OverheadRadio transmissionSignalling characterisationAlgorithmDecomposition
The invention discloses a channel information feedback method and a system. The channel information feedback method comprises the following steps: a pre-coding matrix required to be fed back can be decomposed into the product of a plurality of Givens rotating matrixes, wherein each rotating matrix is only related to a rotating angle; and the corresponding rotating angle of the rotating matrix after being decomposed is fed back. The method and the system provided by the invention are a channel compression quantized feedback solution based on the Givens transformation, wherein the pre-coding matrix required to be fed back can be transformed into a limited angle value through continuous Givens rotation, and a base station can rebuild a channel matrix by using the fed-back quantitative angles so as to calculate a pre-coding vector, so that the feedback cost can be effectively reduced. Compared with the traditional scalar quantization, the channel information feedback method can effectively reduce the number of the quantitative elements, thereby decreasing the feedback quantity. With respect to the vector quantization, the only requirement is to carry out the operation of decomposition and quantization, so that the system complexity can be effectively lowered under the condition of ensuring the system performance.
Owner:ZTE CORP
Method for calibrating PTZ camera by using only two scene images
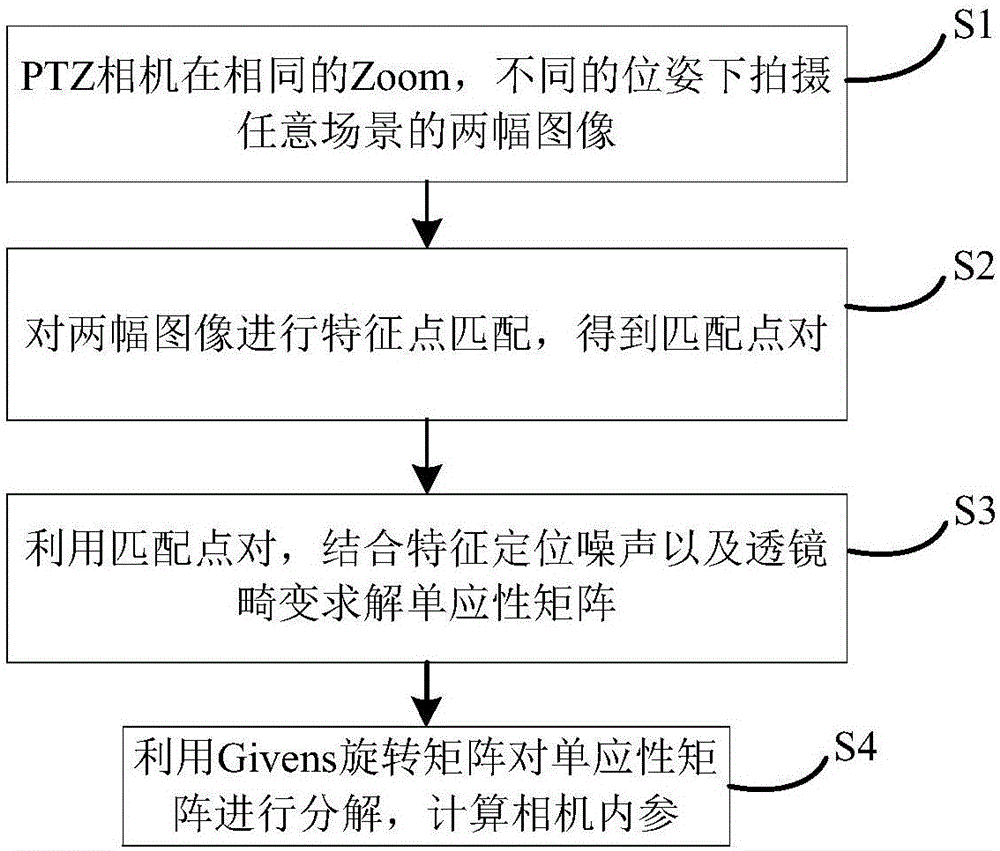
InactiveCN106530358ASimplify the internal calibration processHigh precisionImage analysisCamera lensPrincipal point
The present invention discloses a method for calibrating a PTZ camera by using only two scene images. Firstly, two images with overlapped areas of any scene in a same focal length and different Pan-Tilt angles relative to the PTZ camera are photographed, the two images are subjected to feature point matching, a matching feature point pair between the two images is obtained, the influences of the uncertainty of matching feature point positioning and camera lens distortion are considered, a homography matrix estimation method with the combination of feature point positioning noise and lens distortion is created, the homography matrix between the two images and the radial distortion coefficient of the PTZ camera under the focal length are obtained, finally a Givens rotation matrix is constructed to decompose the obtained homography matrix, and thus the four internal references (focal length, principal point coordinate, and aspect ratio) of the camera is resolved and obtained. According to the method, the online calibration of five parameters of the PTZ camera can be realized.
Owner:BEIHANG UNIV
Low-complexity quick parallel matrix inversion method
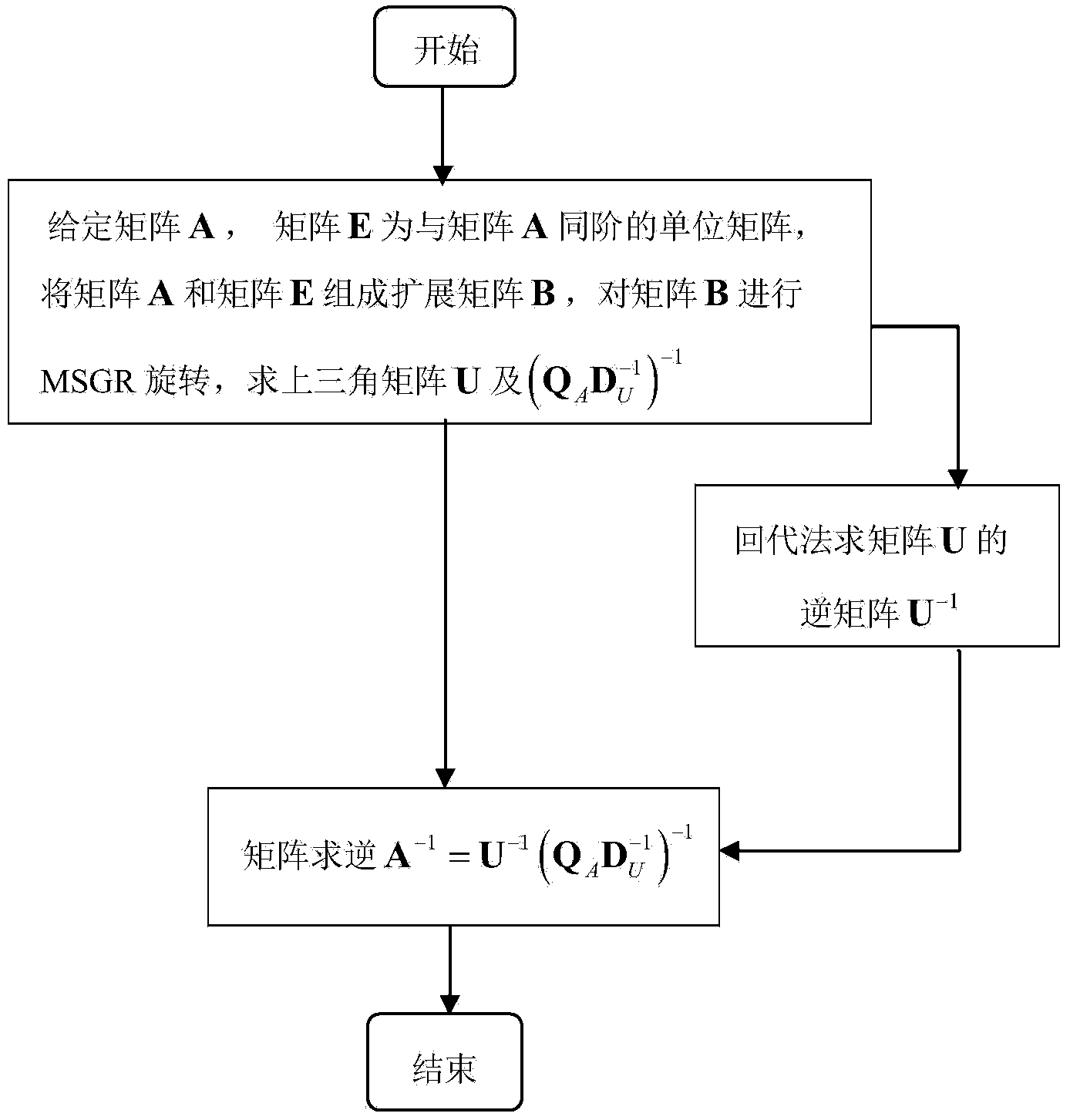
ActiveCN104298649AImprove efficiencyReduce complexityTransmitter/receiver shaping networksComplex mathematical operationsSubstitution methodSignal processing
The invention discloses a low-complexity quick parallel matrix inversion method. The method comprises the following steps that first, a matrix A is given, a matrix E is made to be a unit matrix with the same order as the matrix A, the matrix A and the matrix E form an expanding matrix B, modified Givens rotation (MSGR, Modified Square Givens Rotations) is carried out on the matrix B, an upper triangular matrix U and , wherein according to the define of the matrix U and , an SGR (Squared Givens Rotations) method is used for deforming the QR division of the matrix A according to the equation, and the relation between the QR division and original QR division meets the equations , , , and ; according to the MSRG method, the square root operation in the process of Givens rotation can be omitted while division operation is reduced, and algorithm complexity is obviously reduced; second, a back substitution method is used for working out the inverse matrix U-1 of the upper triangular matrix U; third, matrix inversion is carried out according to the equation . According to the low-complexity quick parallel matrix inversion method, a large amount of division operation and a large amount of square root operation are omitted, algorithm complexity is reduced, and the method can be used for matrix inversion of the fields of wireless communication, signal processing and numerical calculation.
Owner:南京易太可通信技术有限公司
Real-time implementation of field programmable gate arrays (FPGA) design in hyperspectral imaging
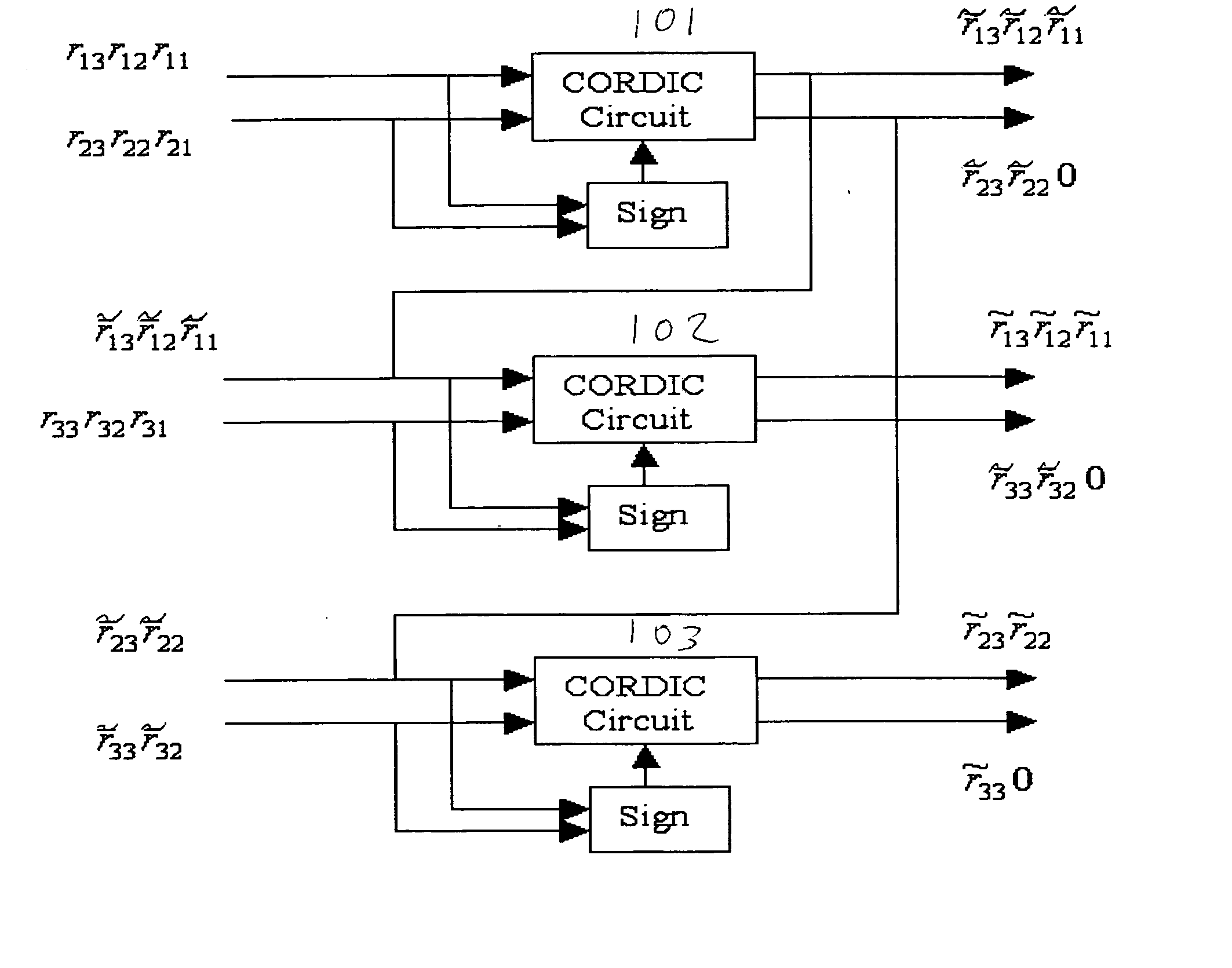
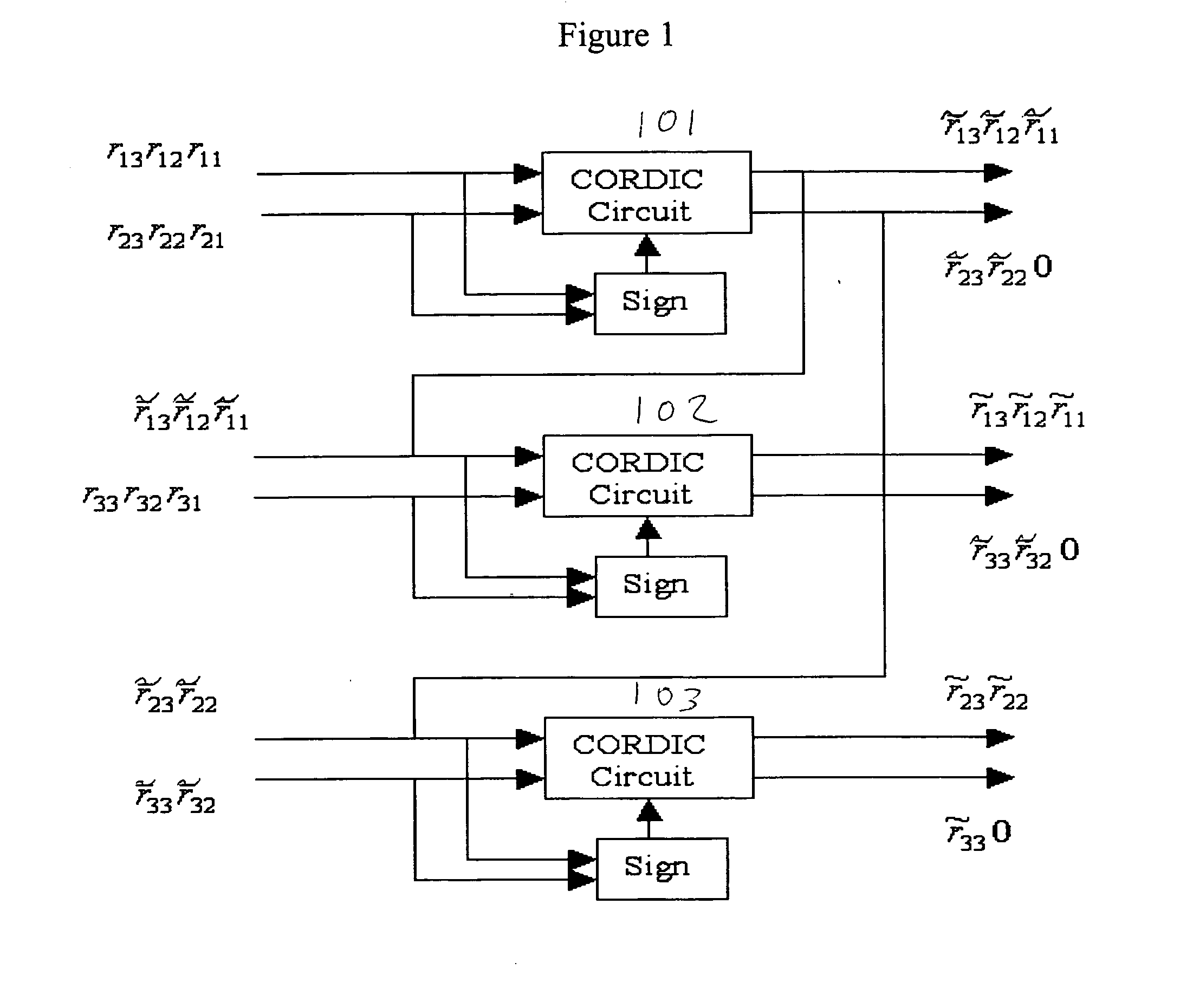
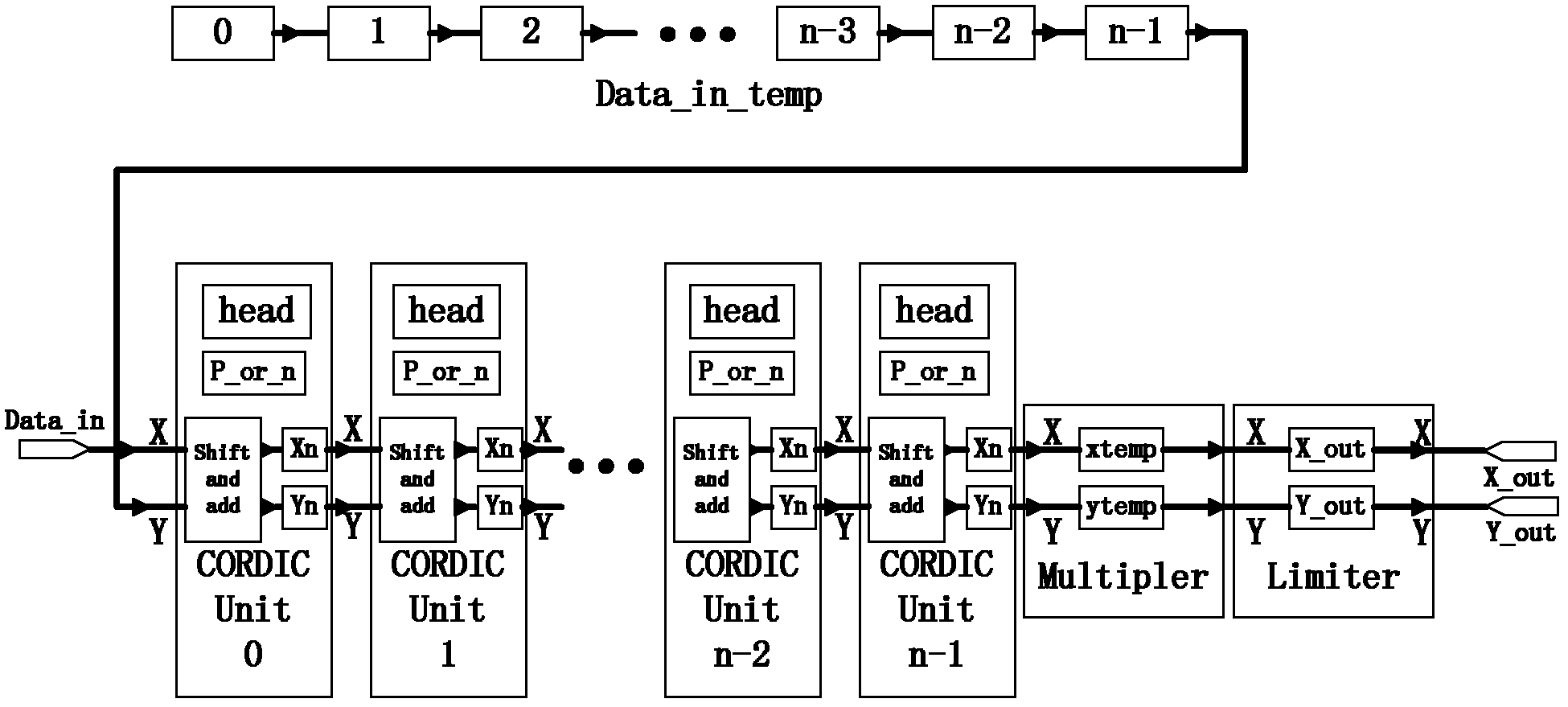
A Field Programmable Gate Arrays (FPGA) design uses a Coordinate Rotation DIgital Computer (CORDIC) algorithm that can convert a Givens rotation of a vector to a set of shift-add operations. The CORDIC algorithm can be easily implemented in hardware architecture, therefore in FPGA. Since the computation of the inverse of the data correlation matrix involves a series of Givens rotations, the utility of the CORDIC algorithm allows a causal Constrained Energy Minimization (CEM) to perform real-time processing in FPGA. An FPGA implementation of the causal CEM is described and its detailed architecture is also described.
Owner:UNIV OF MARYLAND BALTIMORE COUNTY
FPGA device for matrix QR decomposition
InactiveCN102111350AAdd depthReduce usageBaseband system detailsMatrix decompositionComputer science
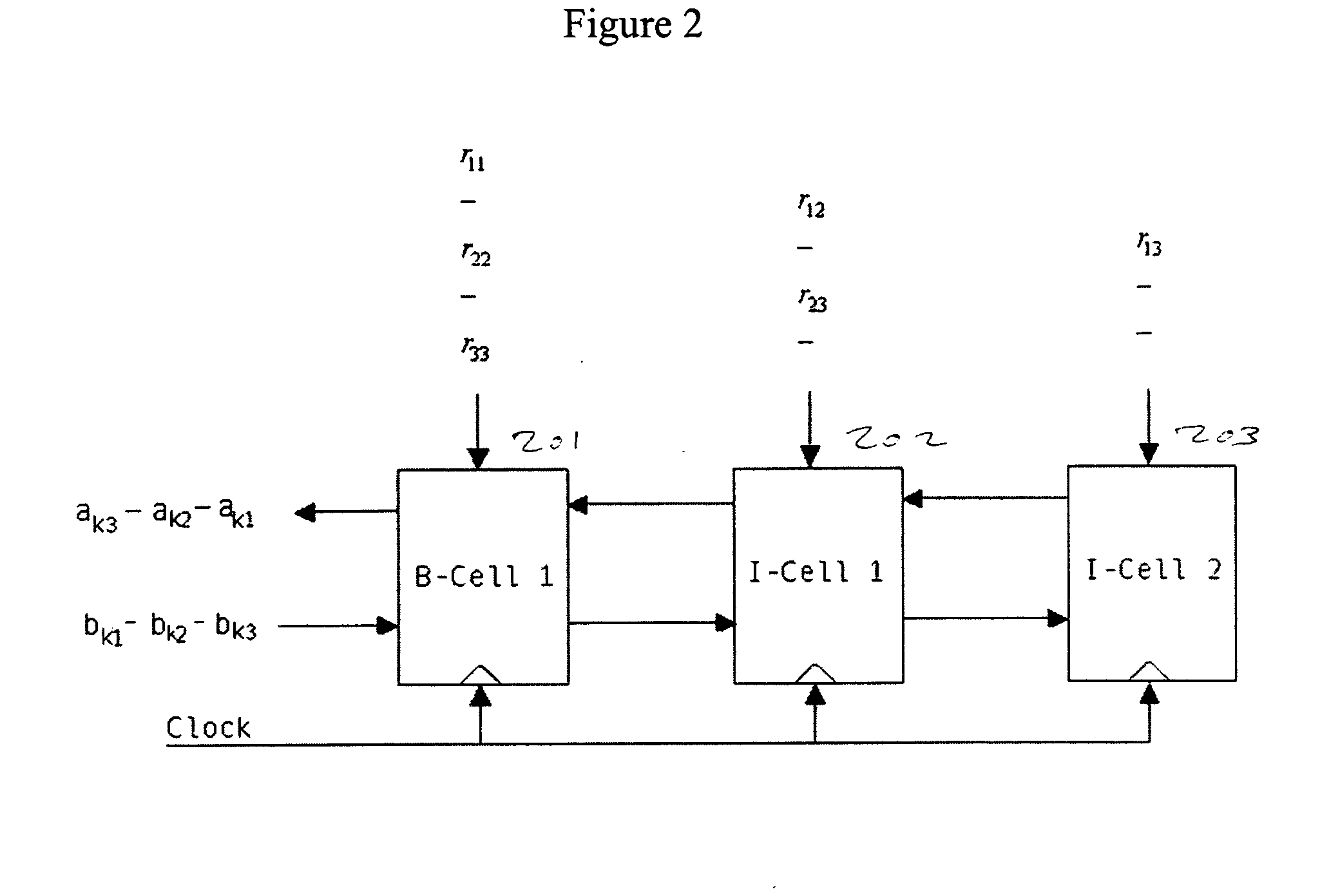
The invention discloses an FPGA (Field Programmable Gate Array) device for matrix QR decomposition, which greatly speeds up matrix QR decomposition. The technical scheme is that the FPGA device for matrix QR decomposition transmits data and corresponding control information to a processing unit by the aid of a dispatcher, is in charge of the processing sequence of systolic array and adopts the systolic array to achieve Givens rotation through the processing unit, and each element in the systolic array adopts the CORDIC (Coordinated Rotation Digital Computer) technology, so as to achieve coordinated rotation of both real and complex numbers.
Owner:NO 50 RES INST OF CHINA ELECTRONICS TECH GRP
MIMO-OFDM system and pre-coding and feedback method therein
InactiveUS7486655B2Avoid excessive computationHigh complexityModulated-carrier systemsPolarisation/directional diversityChannel state informationRound complexity
The present invention provides an antenna-array-based multiple-input multiple-output orthogonal-frequency-division-multiplexing (MIMO-OFDM) system and a pre-coding and feedback method used in the same. The present invention uses QR decompositions of the MIMO channel matrixes to parameterize the channel state information (CSI) of every OFDM frequency band. In addition, the present invention feeds back the information related to θ and φ in the Givens rotation matrixes of the partial frequency bands and then uses an interpolation method to generate θ and φ in the Givens rotation matrixes of all the frequency bands, which further is able to represent the CSI of all the frequency bands. In this way, the present invention has advantages of low complexity and low feedback rate requirement.
Owner:MEDIATEK INC
Multiple antenna spatial multiplexing optimal detection
ActiveUS20100329378A1Easy to useAmplitude-modulated carrier systemsDiversity/multi-antenna systemsComputer scienceSpatial multiplexing
MIMO detection is described that reduces the complexity of computations for finding the soft bit output. The detection process includes QR factorization splitting the distance calculations into two groups, subset lookup using a last cross constellation set (LCCS) lookup, and minimal distance lookup with soft bit output calculation. By grouping the distance calculations into a first group that has one antenna transmitting using a modulation scheme with a generally square constellation diagram and a second group for all of the other antenna constellation diagrams, the LCCS lookup process may be used which substantially reduces the number of calculations to be made in the detection process. Moreover, in the special case of 2×2 antenna, QR factorization is performed by applying a scaled Givens rotation to the channel matrix. The application of the scaled Givens rotation operator eliminates any square root operations that would be performed in a standard QR factorization.
Owner:HONG KONG APPLIED SCI & TECH RES INST
Linear minimum mean square error (LMMSE) detection method for multiple input multiple output-orthogonal frequency division multiplexing (MIMO-OFDM)
ActiveCN102111354AReduce processing timeBaseband system detailsError prevention/detection by diversity receptionNoise levelAlgorithm
The invention discloses a linear minimum mean square error (LMMSE) detection method for multiple input multiple output-orthogonal frequency division multiplexing (MIMO-OFDM). The method comprises the following steps of: presetting a detection systolic array by adopting an estimated noise level value obtained from a channel estimation module, performing Givens rotation on a multi-antenna channel matrix, simultaneously performing unitary transformation on data received by a plurality of antenna, and finally solving linear equations by using a back substitution method to obtain an estimated value of a space division multiplexing signal. The processing method is implemented according to a sub-carrier sequence. Compared with the conventional methods, the LMMSE detection method for the MIMO-OFDM has the advantages that: a calculated amount is far less than that of the conventional systolic array Givens rotation-based quick response (QR) decomposition performed on the multi-antenna channel augmented matrix, and the processing time is relatively shorter.
Owner:SOUTHEAST UNIV
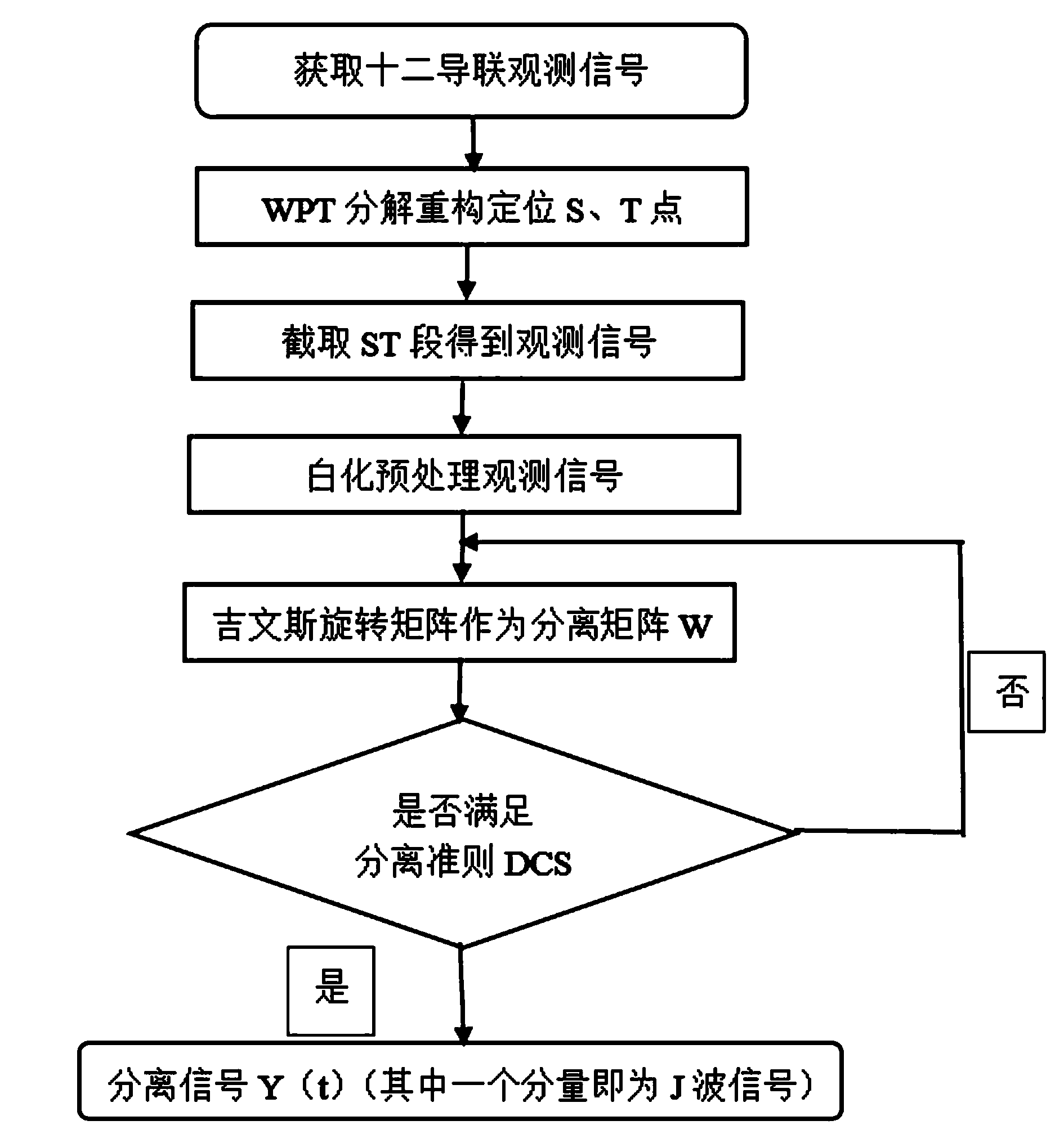
Blind source separation method for extracting J wave signals in electrocardiogram
ActiveCN104367315AFast convergenceAvoid interferenceDiagnostic recording/measuringSensorsJ waveTime domain
The invention relate to a J wave extraction method, in particular to a blind source separation for extracting J wave signals in an electrocardiogram on the basis of a cyclostationarity standard. According to the method, a Givens rotation matrix serves as a separation matrix. The J wave signals are a new index of upper chamber repolarization of the electrocardiogram (ECG), and it is indicated in clinical data that shapes of the J wave signals in the ECG are different, randomness is high and the J wave signals are lost in the normal ECG and can not be observed sometimes. In order to accurately extract the J wave signals, according to the method, wavelet packet transform (WPT) is adopted in advance to analyze, reconstruct and position an ST section where J waves are located, and accordingly the calculation amount of blind source separation (BSS) is reduced; according to the characteristics of the ECG and the J wave signals, the ECG stable in circulation and the non-cycle J wave signals are effectively separated by means of the BSS method based on higher-order cyclic cumulant, and guarantees are provided for research of the J wave signals in a time domain in the next step and separation of the good state and the high-risk state.
Owner:TAIYUAN UNIV OF TECH
Real-time implementation of field programmable gate arrays (FPGA) design in hyperspectral imaging
A Field Programmable Gate Arrays (FPGA) design uses a Coordinate Rotation DIgital Computer (CORDIC) algorithm that can convert a Givens rotation of a vector to a set of shift-add operations. The CORDIC algorithm can be easily implemented in hardware architecture, therefore in FPGA. Since the computation of the inverse of the data correlation matrix involves a series of Givens rotations, the utility of the CORDIC algorithm allows a causal Constrained Energy Minimization (CEM) to perform real-time processing in FPGA. An FPGA implementation of the causal CEM is described and its detailed architecture is also described.
Owner:UNIV OF MARYLAND BALTIMORE COUNTY
Method and device for singular value and feature value composition of matrix on processing system
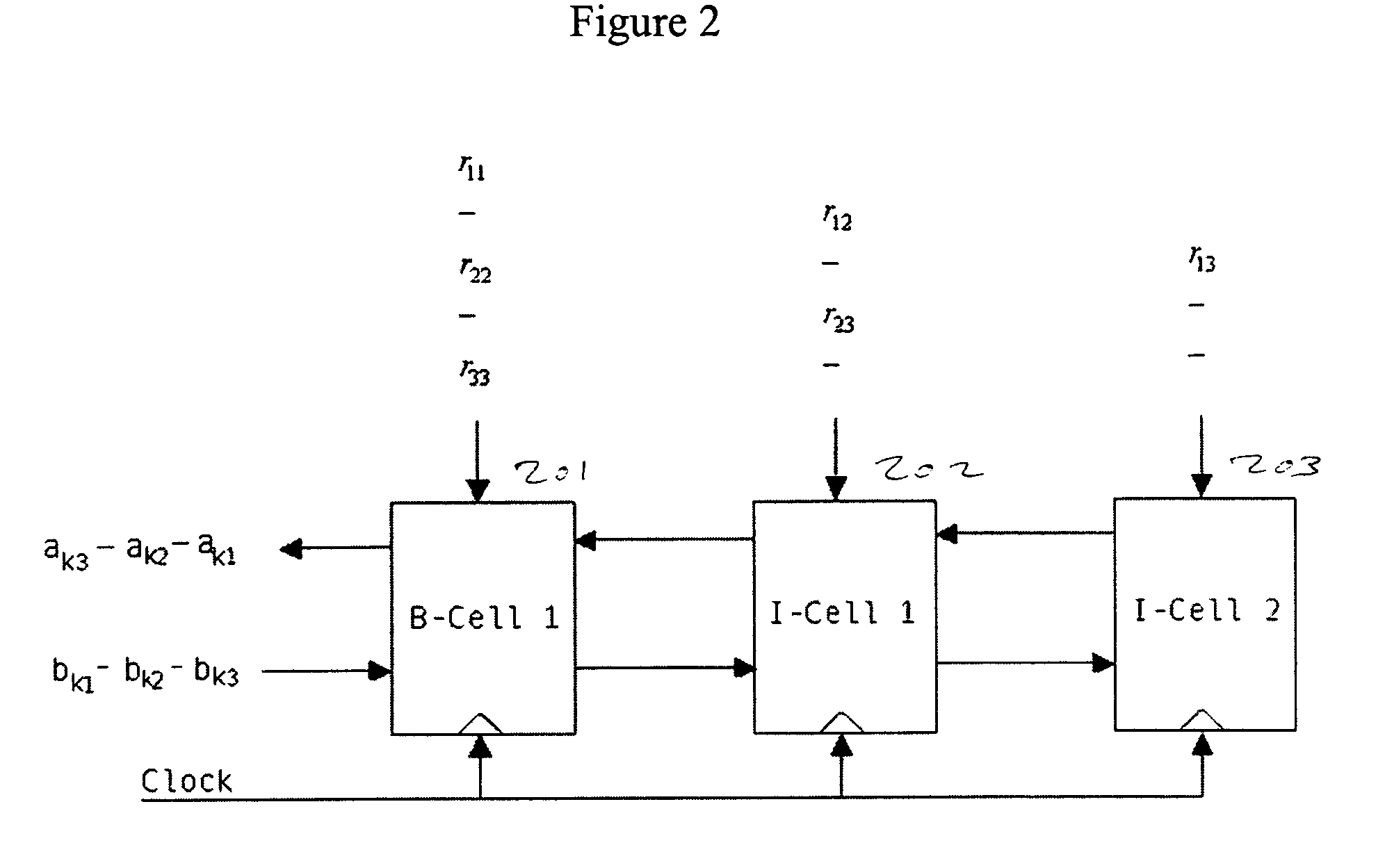
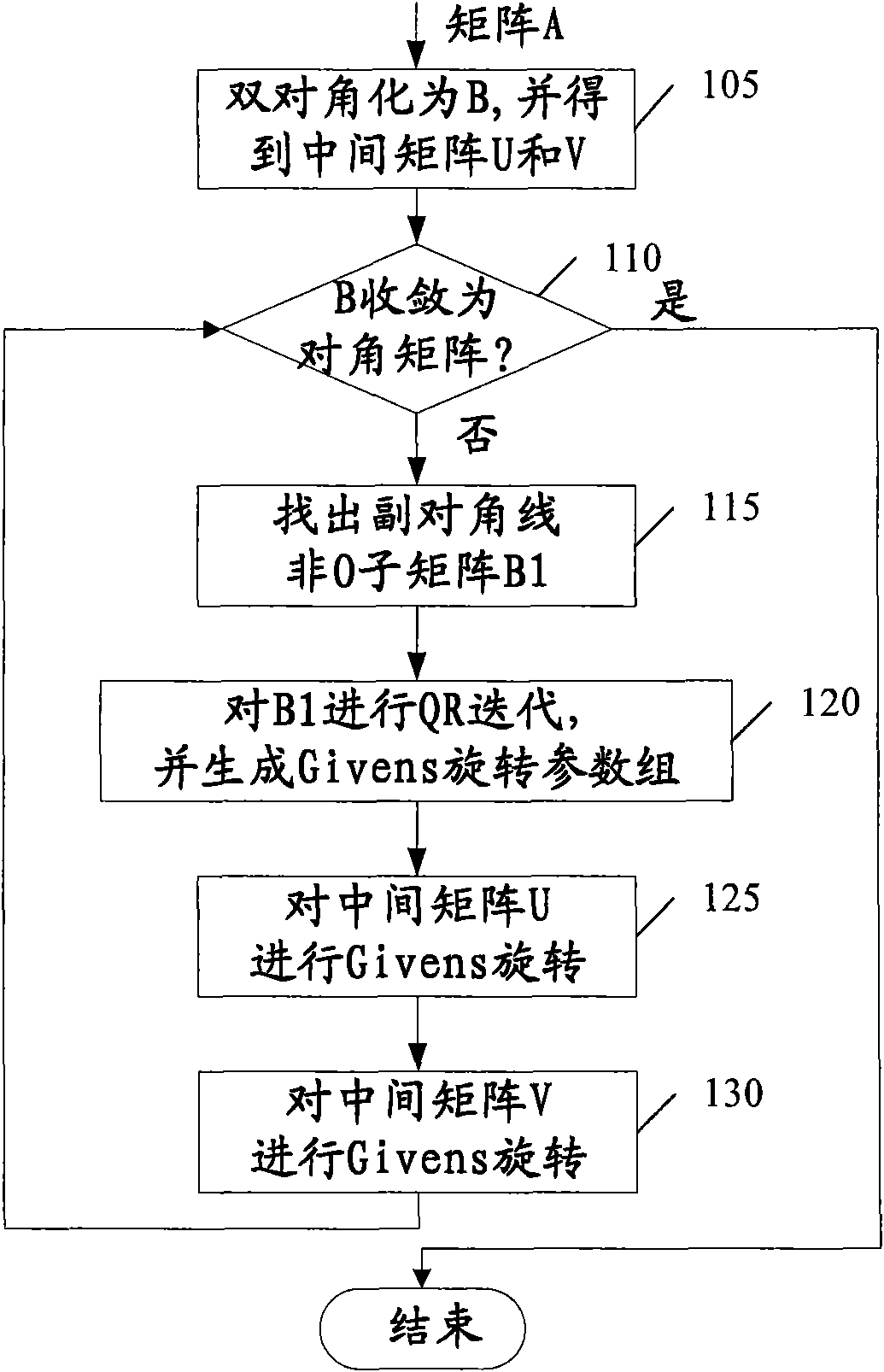
The invention provides a method and a device for the singular value and feature value composition of a matrix on a processing system. The method for singular value composition includes: the matrix is converted into a bidiagonal matrix, and a sandwich matrix which needs to be converted into a singular vector matrix is obtained at the same time; submatrixes of which the elements are not zero are found out and converted in an iterative way on the vice diagonals in the bidiagonal matrix so that the bidiagonal matrix can be converged into a diagonal matrix and the sandwich matrix can be converted into the singular vector matrix; in each iterative step: Givens rotation parameter groups generated in the QR iterative processes of the submatrixes and the positions of the left boundary and the right boundary of the corresponding submatrixes which need to use the Givens rotation parameter groups in the sandwich matrix are accumulated in a memory; and when the number of the accumulated Givens rotation parameter groups reaches the preset threshold value, the Givens rotation parameter groups are utilized to carry out the Givens rotation of the sandwich matrix, wherein the threshold value is an integer which is higher than or equal to 2.
Owner:IBM CORP
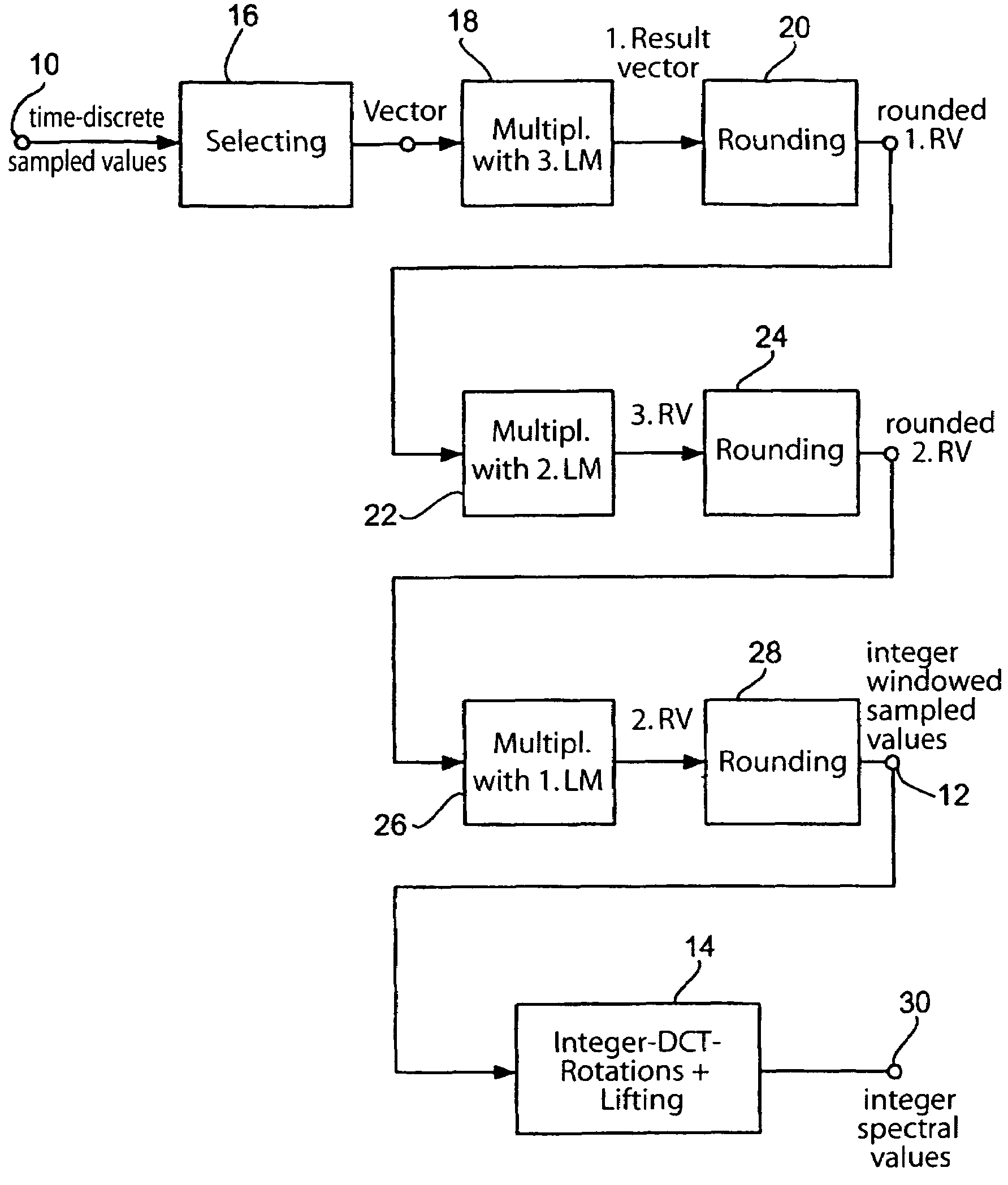
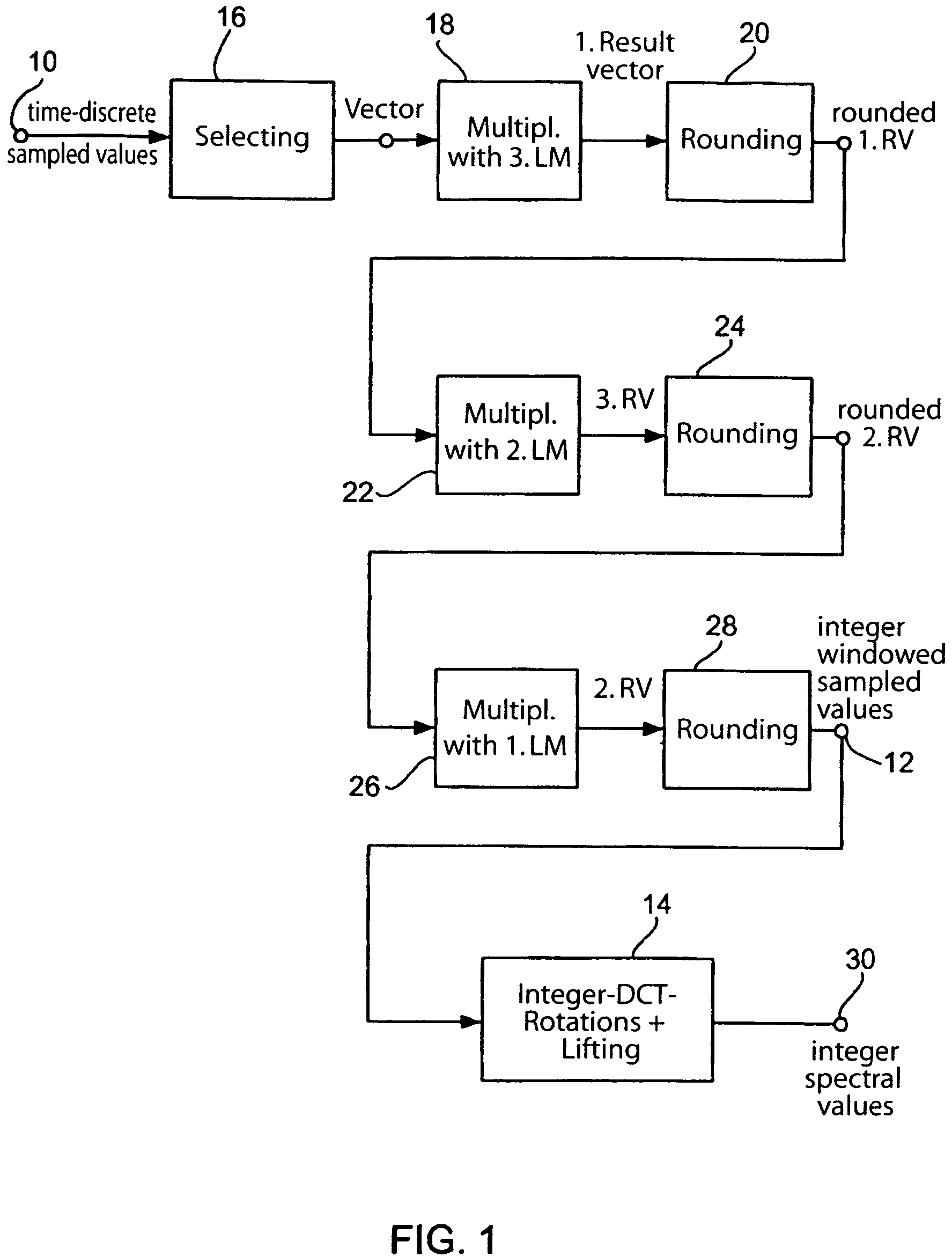
Method and apparatus for processing time-discrete audio sampled values
InactiveUS7512539B2Maintain good propertiesImprove frequency selectivitySpeech analysisCode conversionTime domainFrequency spectrum
An integer transform, which provides integer output values, carries out the TDAC function of a MDCT in the time domain before the forward transform. In overlapping windows, this results in a Givens rotation which may be represented by lifting matrices, wherein time-discrete sampled values of an audio signal may at first be summed up on a pair-wise basis to build a vector so as to be sequentially provided with a lifting matrix. After each multiplication of a vector by a lifting matrix, a rounding step is carried out such that, on the output-side, only integers will result. By transforming the windowed integer sampled value with an integer transform, a spectral representation with integer spectral values may be obtained. The inverse mapping with an inverse rotation matrix and corresponding inverse lifting matrices results in an exact reconstruction.
Owner:FRAUNHOFER GESELLSCHAFT ZUR FOERDERUNG DER ANGEWANDTEN FORSCHUNG EV
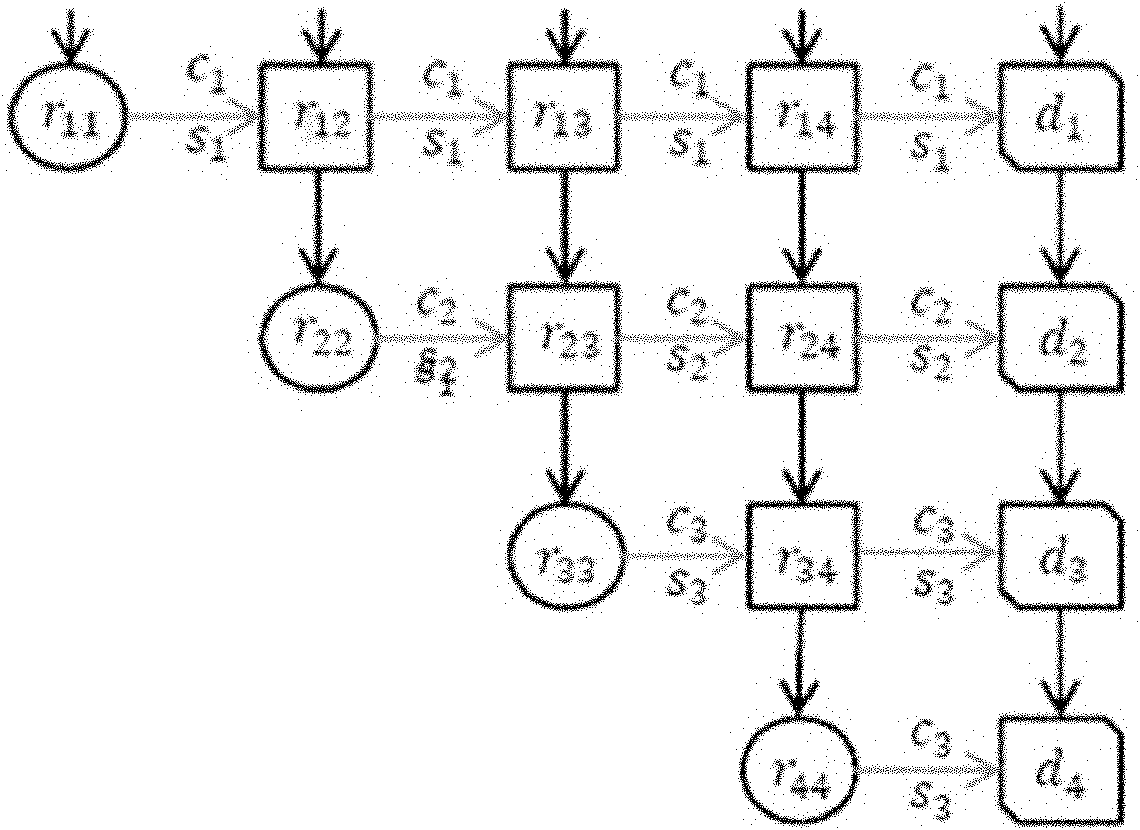
Extensible QR decomposition method based on pipeline working mode
The invention provides an extensible QR decomposition method based on a pipeline working mode. A layered and cascaded structure is adopted, wherein pipeline operation is realized among layers; two lines of matrix data of each layer are subject to Givens rotation; the Givens rotation is conducted by using a coordinate rotation digital computer (CORDIC) algorithm and realized by using operations of addition and displacement; the layer number is determined by the line number or the row number of matrices; a whole QR decomposition module consists of a controller and a data processing module; a line rotation module is arranged on each layer of the data processing module; output ports of upper layers of line rotation modules are connected with input ports of lower layers of line rotation modules; the matrix data to be composed are input from an input port of the first layer of line rotation module, and sequentially flow through all the line rotation modules; and all the line rotation modules work in parallel. The scalable QR decomposition method has the advantages that hardware resources are saved; and as the iterative process of the CORDIC algorithm is split at the inner part of each layer of the data processing module, a pipeline structure is formed, the rotation operation of multiple vector groups is processed in a time sharing manner, the throughput rate is increased, and the extension is flexible.
Owner:TSINGHUA UNIV
Method and system for quantization for a general beamforming matrix in feedback information
Aspects of a method and system for utilizing Givens rotation expressions for quantization for a general beamforming matrix in feedback information. In one aspect of the invention, feedback information is computed at the receiving MIMO wireless device based on a geometric mean decomposition (GMD) method. The feedback information may include a matrix that describes a wireless medium. The matrix may represent a multiplicative product of at least one rotation matrix and at least one diagonal phase rotation matrix. Each of the rotation matrices may include at least one matrix element whose value is based on Givens rotation angle. The transmitting MIMO wireless device may subsequently transmit a plurality of signals via the wireless medium based on the received matrix information. The signal strength and / or signal to noise ratio (SNR) measurement (as measured in decibels, for example) associated with each of the transmitted plurality of signals may be about equal.
Owner:AVAGO TECH INT SALES PTE LTD
Method and system for utilizing givens rotation to reduce feedback information overhead
ActiveUS8180314B2Spatial transmit diversityNetwork traffic/resource managementCommunications systemMultiple input
Owner:AVAGO TECH INT SALES PTE LTD
Method and system for signal transmission in multi-I/O OFDM system
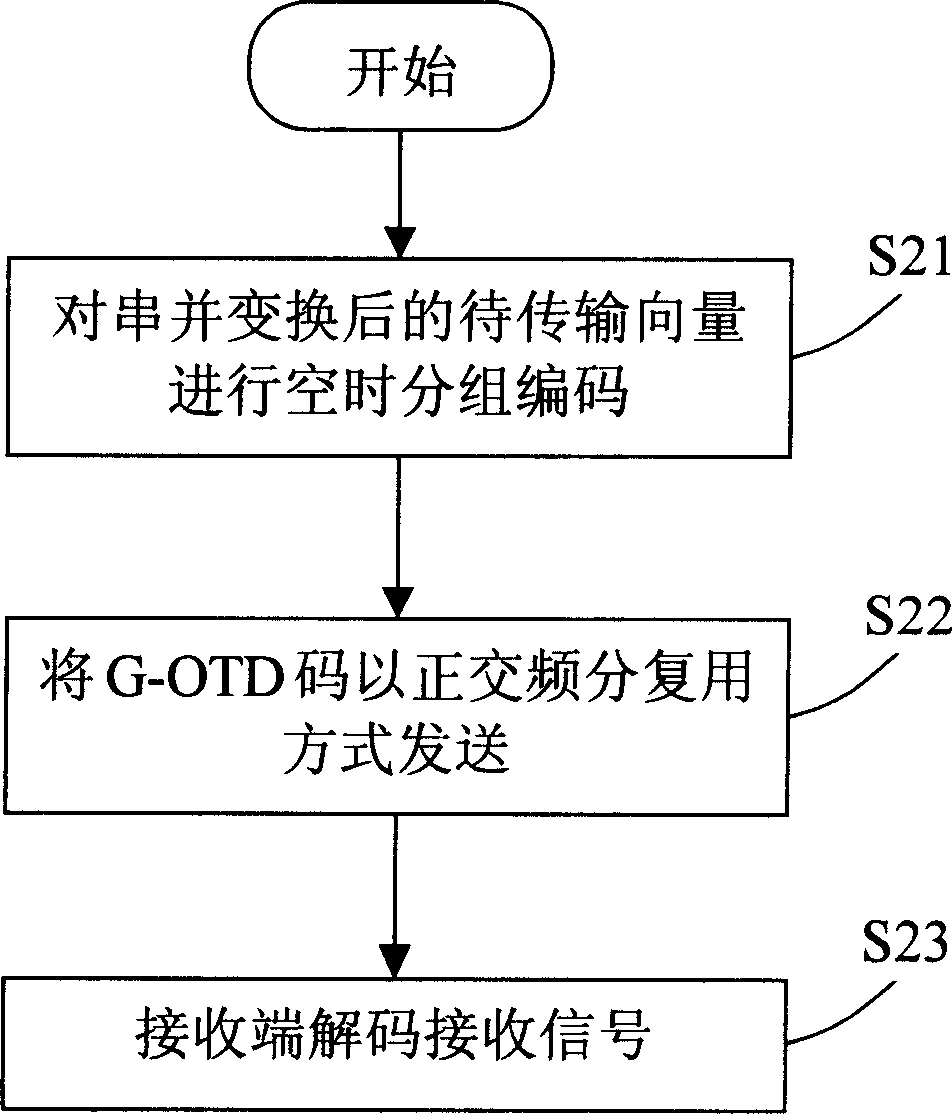
InactiveCN1905548AEliminate self-interference termsReduce decoding complexityMulti-frequency code systemsOrthogonal multiplexSelf interferenceBlock code
The invention relates to a signal transmission method in multi-in multi-out orthogonal frequency division multiplexing (OFDM) system, comprising the steps of: (a) at transmitting end, converting series / parallel converted data to be sent, into Givens rotation-based orthogonal transmitted diversity code; (b) transmitting continuous data vector in the diversity code through two or above transmitting aerials in OFDM mode. And the invention also provides a corresponding system. Relative to quasi-orthogonal space-time block code, the invention eliminates self-interference items from related matrix and reduces decoding complexity; relative to the system adopting full diversity gain orthogonal frequency space-time block code, the invention obtains full rate transmission.
Owner:HUAWEI TECH CO LTD
A method for eliminating non-orthogonal space-time block coding self-interference item based on matrix rotation
InactiveCN1545366AEliminate self-interference termsIncrease transfer rateSpatial transmit diversityCode division multiplexSelf interferenceSpace time transmit diversity
The invention is a matrix rotation based method for eliminating self-interference of a nonorthogonal space-time packet code, in view of the problem that there are self-interference items in the channel correlation matrix of nonorthogonal (or quasi-orthogonal) space-time packet code, adopting Givens rotation twice. Thus, one hand, it can effectively eliminate the self-interference items and rotates channel matrix into orthogonal matrix. During space-time transmit diversity, the maximum advantage caused by the channel matrix being an orthogonal matrix is that it can make linear decoding at receiving end, largely reducing decoding complexity. And at the same time it make the packet code corresponding to the channel matrix have an orthogonal structure, accordingly able to obtain maximum transmitting speed, partial diversity gain and receiving-end linear decoding.
Owner:XI AN JIAOTONG UNIV
Signal processing block for a receiver in wireless communication
ActiveUS9318813B2Digital computer detailsIndependent non-interacting antenna combinationsResource utilizationParallel computing
A QRD processor for computing input signals in a receiver for wireless communication relies upon a combination of multi-dimensional Givens Rotations, Householder Reflections and conventional two-dimensional (2D) Givens Rotations, for computing the QRD of matrices. The proposed technique integrates the benefits of multi-dimensional annihilation capability of Householder reflections plus the low-complexity nature of the conventional 2D Givens rotations. Such integration increases throughput and reduces the hardware complexity, by first decreasing the number of rotation operations required and then by enabling their parallel execution. A pipelined architecture is presented (290) that uses un-rolled pipelined CORDIC processors (245a to 245d) iteratively to improve throughput and resource utilization, while reducing the gate count.
Owner:MAXLINEAR INC
Method and System for Utilizing Tone Grouping With Givens Rotations to Reduce Overhead Associated With Explicit Feedback Information
InactiveUS20110116579A1Amplitude-modulated carrier systemsRadio transmissionEngineeringRotation matrix
Aspects of a method and system for utilizing tone grouping with Givens rotations to reduce overhead associated with explicit feedback information are presented. In one aspect of the invention, Givens matrices may be utilized to reduce a quantity of information communicated in explicit feedback information via an uplink RF channel. The explicit feedback information may include specifications for a feedback beamforming matrix that may be utilized when transmitting signals via a corresponding downlink RF channel. The feedback beamforming matrix may represent a rotated version of an un-rotated matrix. The Givens matrices may be utilized to apply one or more Givens rotations to un-rotated matrix. The rotated matrix may reduce the quantity of information communicated in the explicit feedback information. The quantity of information communicated in the explicit feedback information may be further reduced by utilizing tone grouping.
Owner:AVAGO TECH WIRELESS IP SINGAPORE PTE
Base vector matrix compression device based on high-speed systolic array and Givens transformation
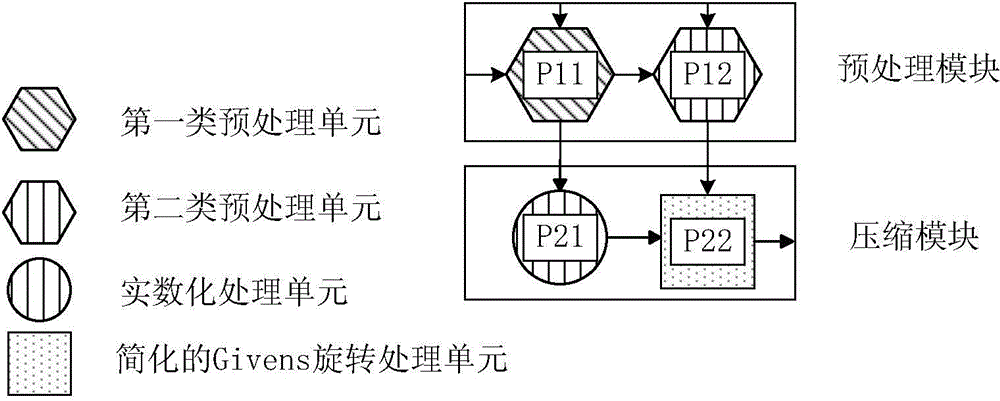
ActiveCN104462021AAchieve compressionSimplify Timing DesignComplex mathematical operationsAlgorithmHardware implementations
The invention discloses a base vector matrix compression device based on a high-speed systolic array and Givens transformation. The base vector matrix compression device is applied to a base vector matrix V with the dimensionality of M*N (M>=N) and comprises a preprocessing module and a compression module, wherein the preprocessing module is composed of a first-kind preprocessing unit and second-kind preprocessing units; the compression module is composed of real number processing units, Givens rotation processing units and simplified Givens rotation processing units. The base vector matrix compression device can guarantee the regularity of hardware implementation and parallel flow processing of data, is high in universality and can achieve compression of any base vector matrix with the dimensionality of M*N.
Owner:南京易太可通信技术有限公司
Physical layer multicast and multi-stream data transmitting method based on Givens rotation
ActiveCN103368701AAddress the issue of fairnessExpand the number of data streams to be transmittedError prevention/detection by diversity receptionMulti inputData stream
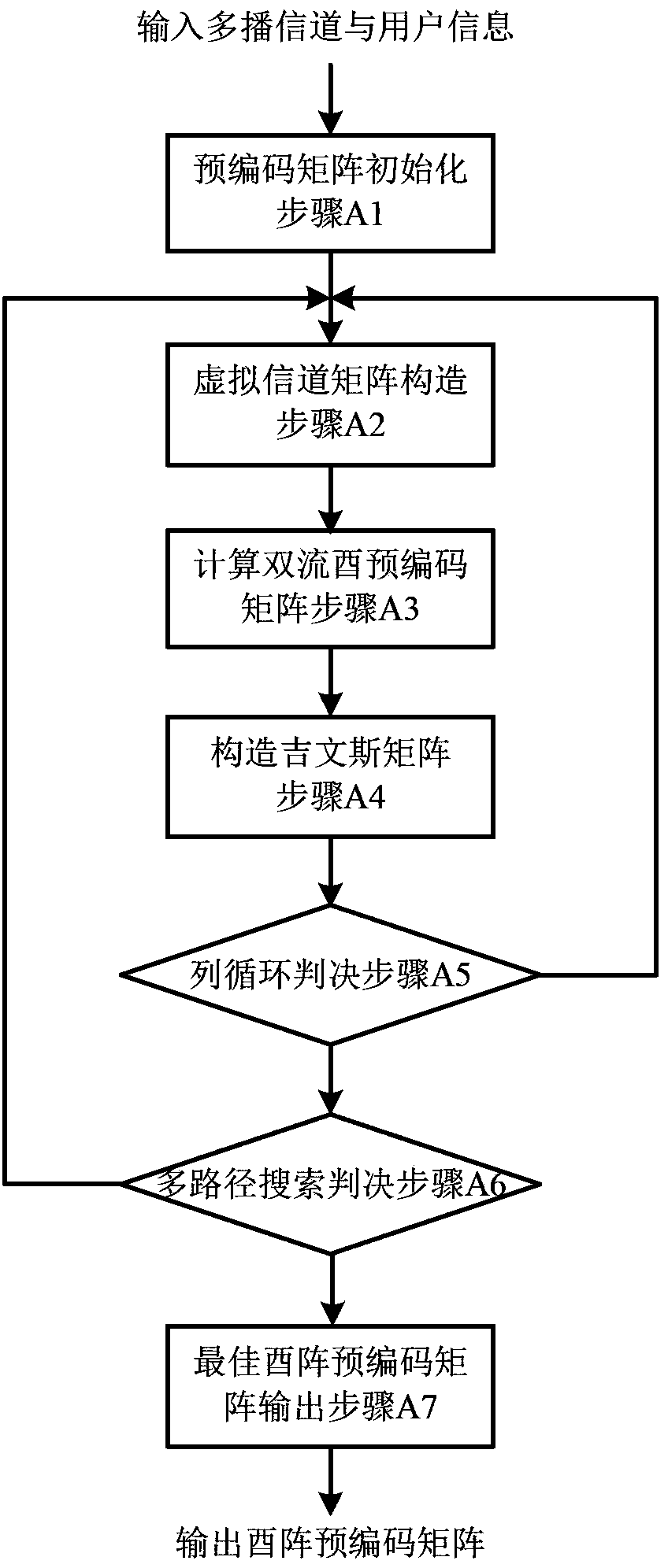
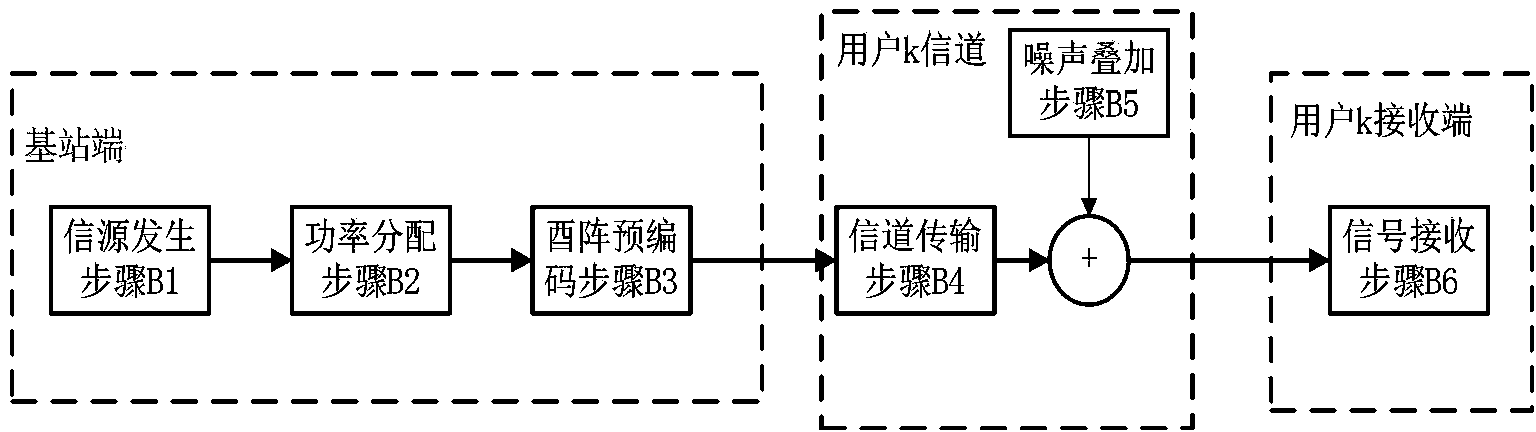
The invention discloses a physical layer multicast and multi-stream data transmitting method based on Givens rotation. The method is characterized in that on the basis of the basis thought that a unitary matrix can be obtained by constructing a plurality of Givens matrixes, a multi-input and multi-output physical layer multicast and double-current transmission matrix constructing method is utilized to construct a unitary matrix pre-coding matrix suitable for multi-stream transmission in an iteration method, and therefore multi-input and multi-output physical layer multicast and multi-path data stream transmission with a largest data stream capable of reaching the number of transmitting antennas is achieved. Compared with an existing pre-coding technology supporting multi-stream and multicast, the method can remarkably improve multicast link transmission quality, effectively improves signal-to-noise ratio fairness of adjacent data streams, and is applicable to a novel generation of broadband wireless and mobile communication systems such as 802.11 n, TD-HSPA+, TD-LTE and TD-LTE-Advanced.
Owner:UNIV OF SCI & TECH OF CHINA
Features
- R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
Why Patsnap Eureka
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com