Patents
Literature
Patsnap Copilot is an intelligent assistant for R&D personnel, combined with Patent DNA, to facilitate innovative research.
240 results about "Separation matrix" patented technology
Efficacy Topic
Property
Owner
Technical Advancement
Application Domain
Technology Topic
Technology Field Word
Patent Country/Region
Patent Type
Patent Status
Application Year
Inventor
Matrix Separation is predominantly engaged in General Industrial Machinery. Matrix Separation operates in Chattanooga Tennessee.
Methods, systems and apparatus for separation and isolation of one or more sample components of a sample biological material
ActiveUS7419784B2Bioreactor/fermenter combinationsBiological substance pretreatmentsElectrophoresisBiological materials
Devices, systems and methods for use in separating sample materials into different sample components and then isolating one or more of the sample components for further processing or analysis are disclosed. Devices employ configurations that optionally allow a sample material to be electrophoretically separated into sample components in a separation matrix within a separation conduit. The sample components may then be detected in a detection zone in the separation conduit, and then selected components shunted to a component collection conduit within the device downstream of the detection zone for further processing or analysis based on information received at the detection zone. Methods of using these devices, and systems that incorporate these devices are also envisioned.
Owner:CAPLIPER LIFE SCI INC
High throughput separations based analysis systems
InactiveUS7169277B2Increase flow resistanceSufficient flow resistanceSludge treatmentFixed microstructural devicesElectrophoresisBulk samples
Devices, systems and methods for use in separating sample materials into different fractions that employ bulk fluid flow for loading of samples followed by electrophoretic separation of the sample material. Devices employ configurations that optionally allow bulk sample loading with some or no displacement of a separation matrix within a separation conduit. Methods of using these devices, and systems that incorporate these devices are also envisioned.
Owner:CAPLIPER LIFE SCI INC
Purification of immunoglobulins
ActiveUS20060134805A1Faster and economic purificationIncrease capacitySolid sorbent liquid separationImmunoassaysCross-linkChemical physics
The present invention relates to a separation matrix comprised of porous particles to which antibody-binding protein ligands have been immobilised, wherein the ligand density is in the range of 5.0-10 mg/ml; the gel phase distribution coefficient of the particles expressed as Kav for a dextran of size 110 kDa is above 0.65 and the median particle diameter is between 65-84 μm. The carbohydrate material is preferably highly cross-linked agarose.
Owner:CYTIVA BIOPROCESS R&D AB
Methods, systems and apparatus for separation and isolation of one or more sample components of a sample biological material
ActiveUS20030215855A1AccuracyAccurate toleranceBioreactor/fermenter combinationsBiological substance pretreatmentsElectrophoresisBiological materials
Devices, systems and methods for use in separating sample materials into different sample components and then isolating one or more of the sample components for further processing or analysis are disclosed. Devices employ configurations that optionally allow a sample material to be electrophoretically separated into sample components in a separation matrix within a separation conduit. The sample components may then be detected in a detection zone in the separation conduit, and then selected components shunted to a component collection conduit within the device downstream of the detection zone for further processing or analysis based on information received at the detection zone. Methods of using these devices, and systems that incorporate these devices are also envisioned.
Owner:CAPLIPER LIFE SCI INC
Micro-electrophoresis chip for moving and separating nucleic acids and other charged molecules
A microelectrophoresis chip comprises a substrate in which there are formed one or more channels, one channel for each sample to be evaluated. The channels extend for the length of the chip, a distance of generally around 1 cm, and are about 1 to 10 mum wide and 1 to 10 mum in depth. The channels are filled with a homogeneous separation matrix which acts as an obstacle to the electrophoretic migration of the charged molecules. Microelectrodes disposed in the channels are used to induce an electric filed within the homogeneous separation medium. When a voltage is applied across two or more of the microelectrodes, the charged molecules are induced to move and separate according to the electric field density, the type of solvent film, and the charge, shape and size of the charged molecule. The chip may further comprise detectors, such as light polarization detectors, fluorescence emission detectors, biosensors, electrochemical sensors or other microcomponents which may include sites for enzymatic or chemical manipulation of the moved or separated charged molecules.
Owner:SIEMENS HEALTHCARE DIAGNOSTICS INC +1
Block copolymer membranes and associated methods for making the same
A separation matrix comprises a porous surface layer; and a bulk porous support, wherein both the porous surface layer and the bulk porous support comprising a block copolymer. The block copolymer comprises A-B or A-B-A repeating units, wherein A and B at each occurrence are two different blocks of oligomer, or polymer. A structural unit of block A is derived from one or more atom transfer radical polymerization (ATRP)-active monomer or oligomer and a structural unit of block B is derived from a thermoplastic ATRP-active macro initiator. A poly dispersity index of the block copolymer is at least about 2.
Owner:CYTIVA SWEDEN AB
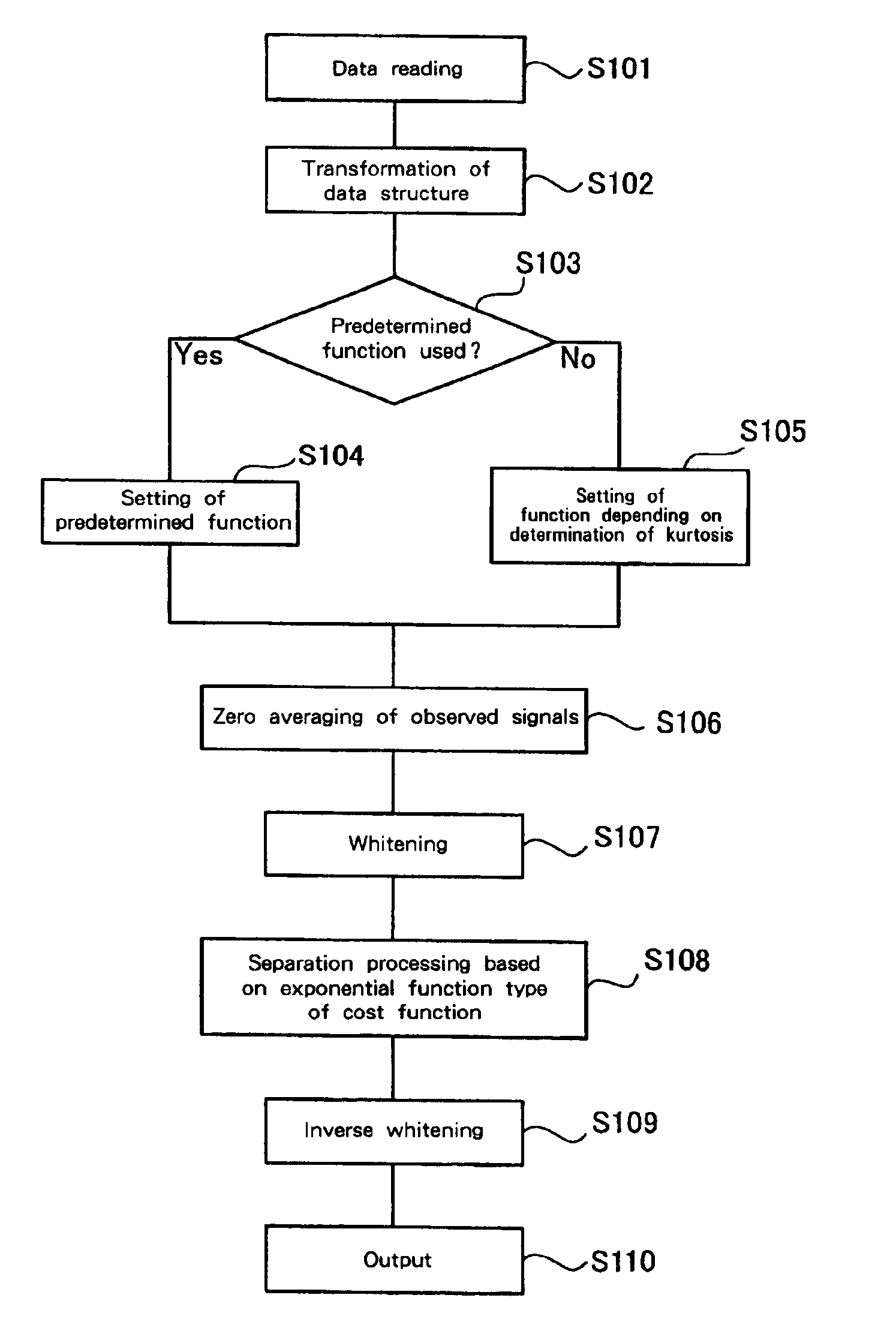
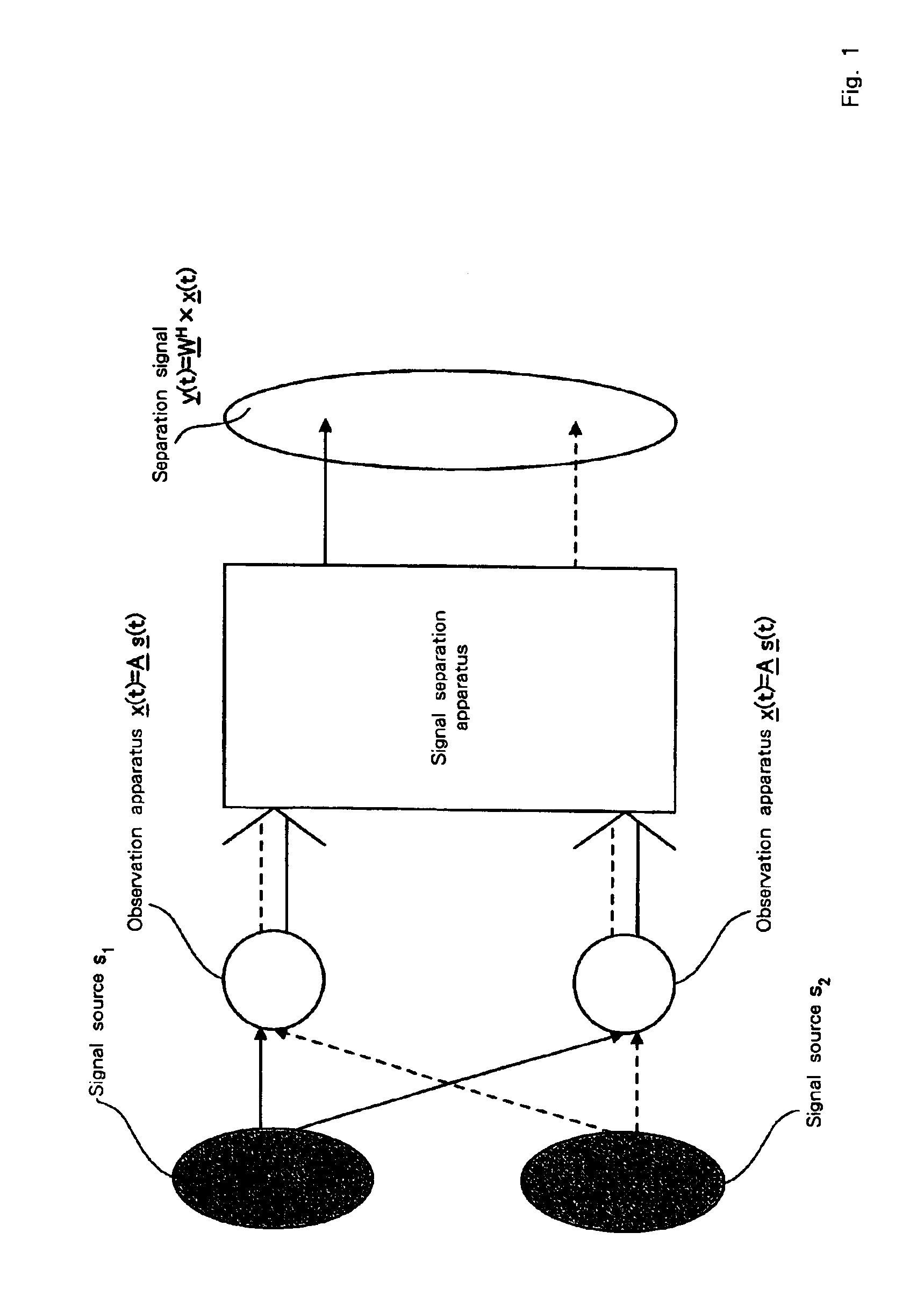
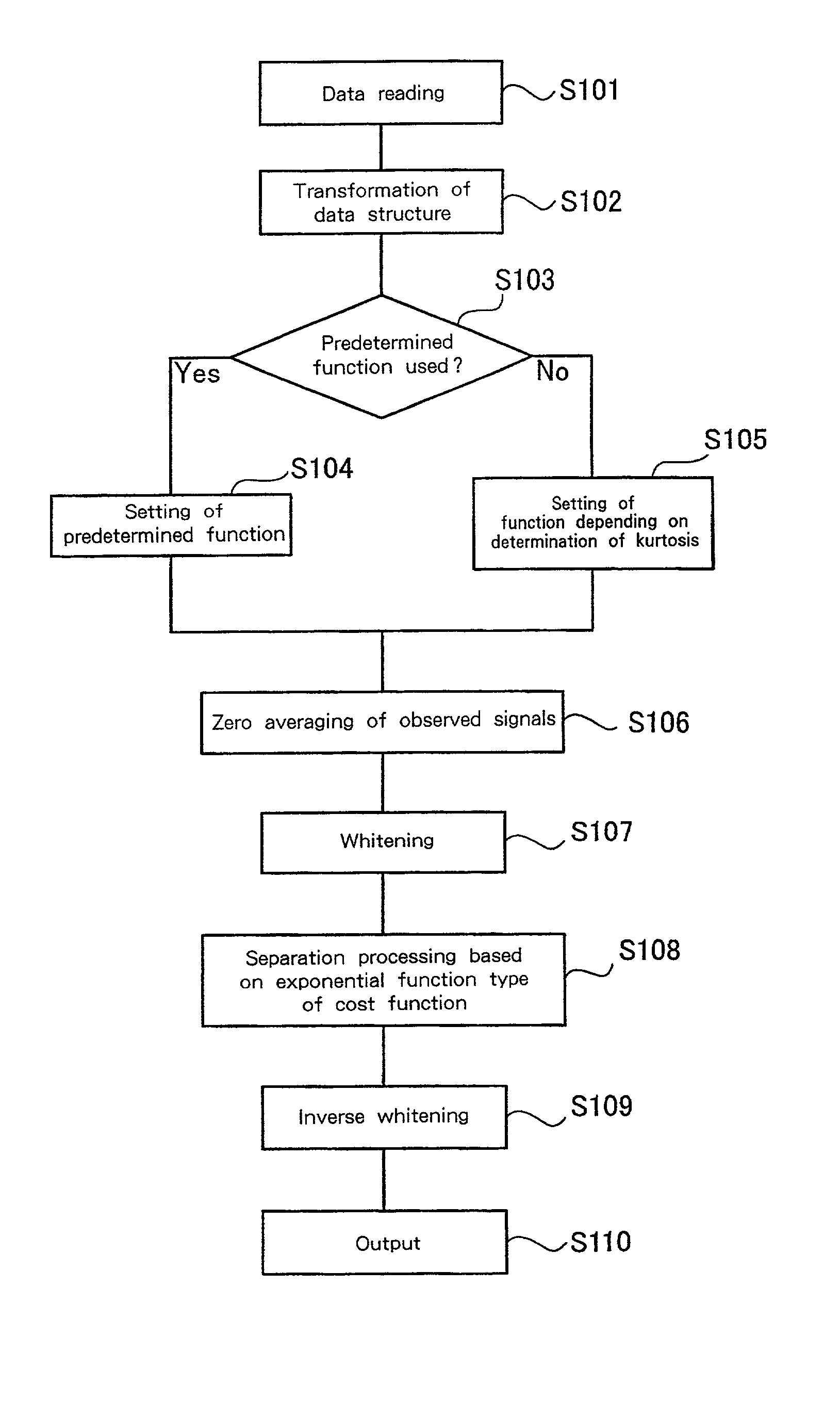
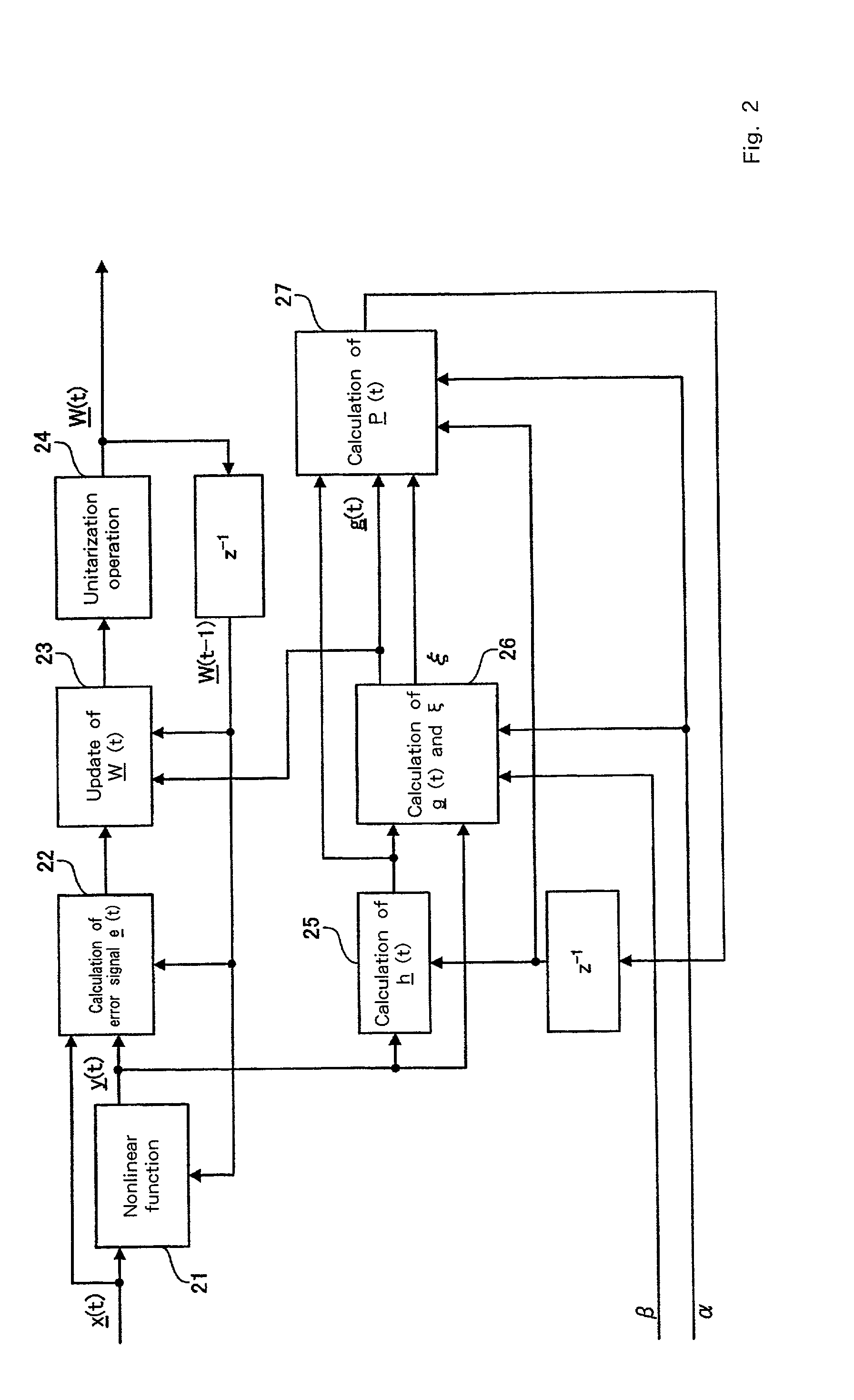
Signal separation method, signal processing apparatus, image processing apparatus, medical image processing apparatus and storage medium for restoring multidimensional signals from observed data in which multiple signals are mixed
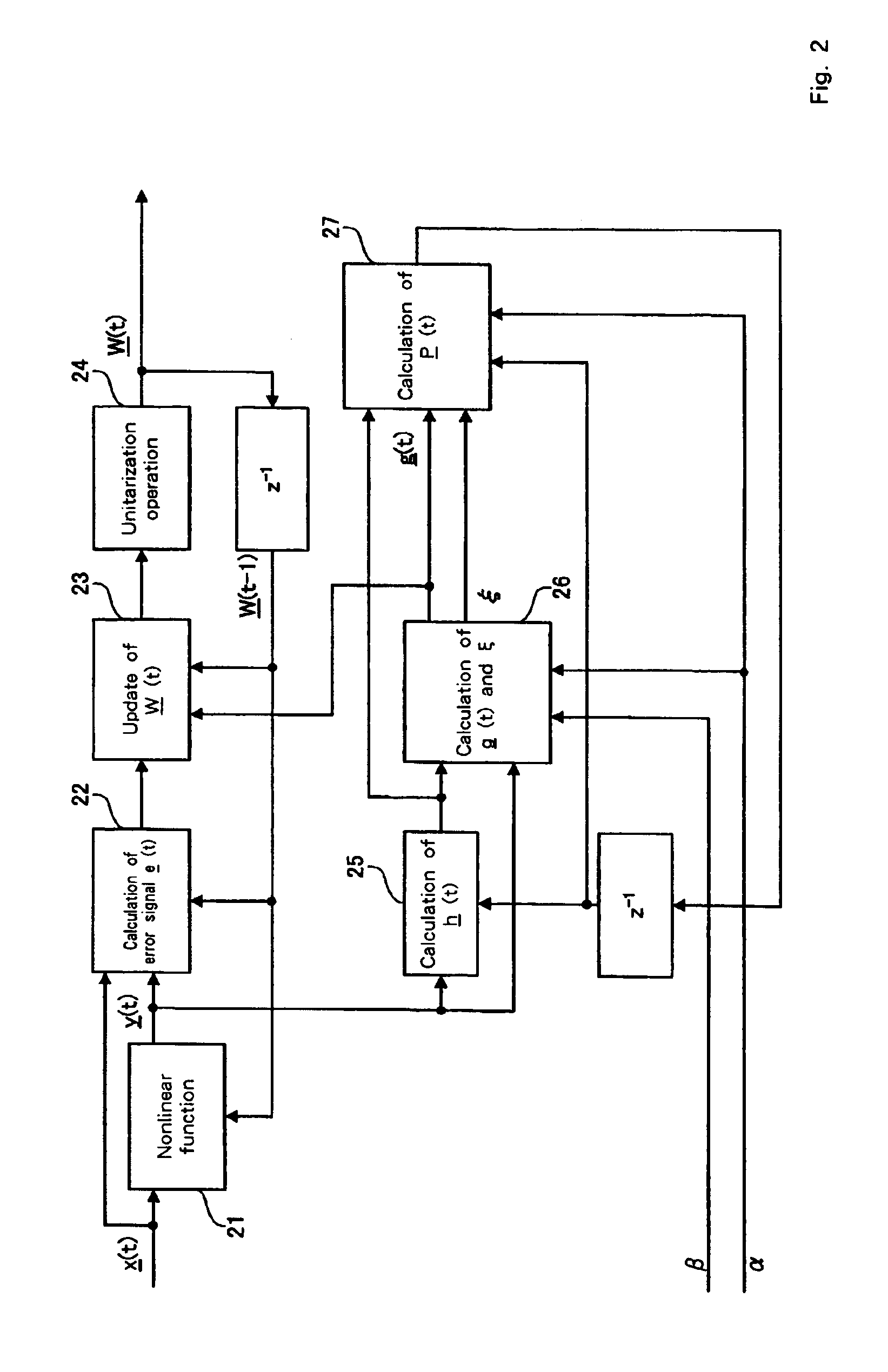
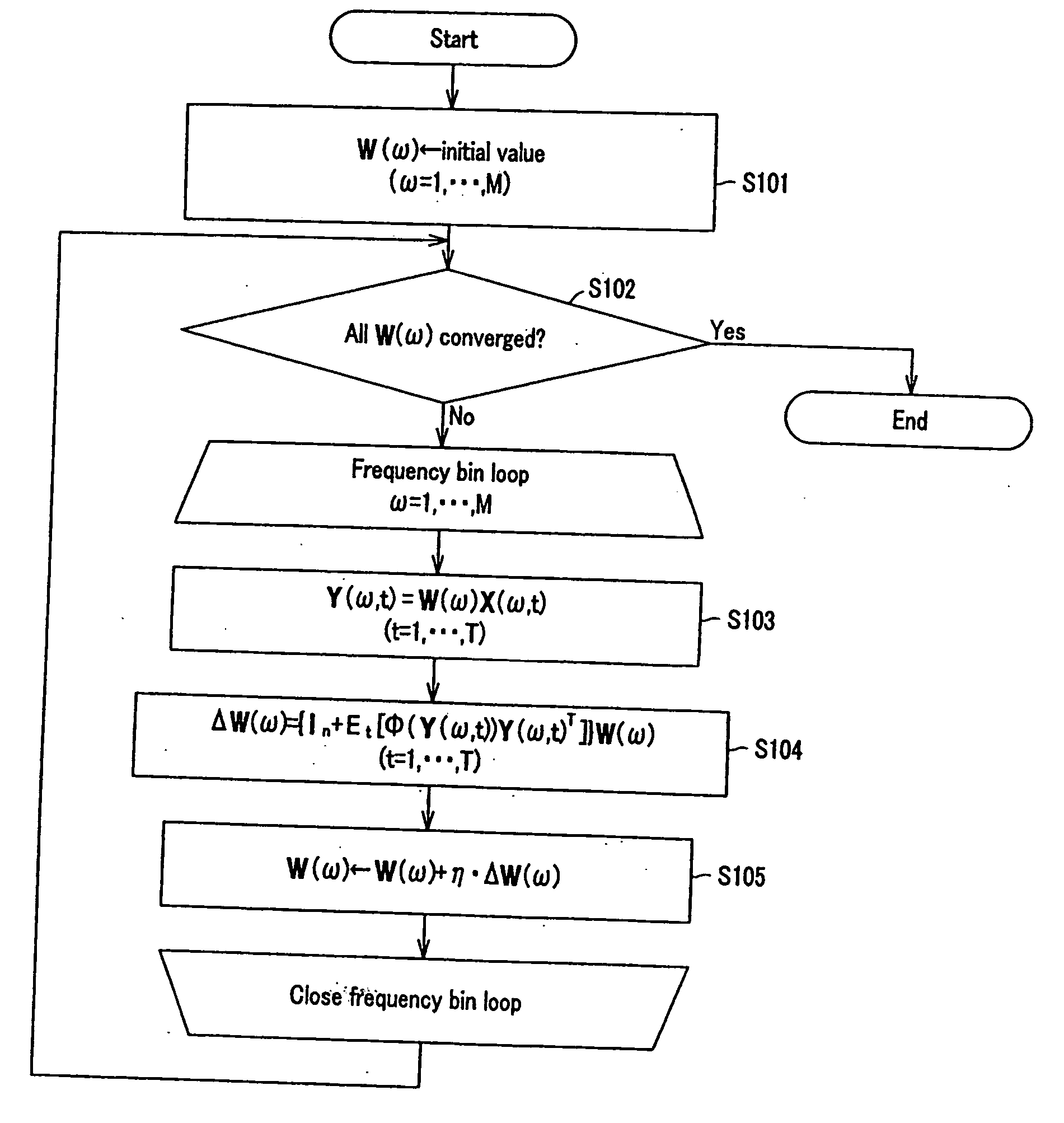
Signals are separated by introducing a function having a monotonously increasing characteristic like an exponential type function as a cost function, and applying an adaptive algorithm that minimizes that cost function in terms of a signal separation matrix. That is, there is provided a signal processing apparatus that separates and outputs an original signal from the observed signal x(t), in which multiple multidimensional signals are mixed, wherein the nonlinear function 21 is operated on an input observed signal x(t) and an estimated separation matrix W(t−1) estimated at a previous cycle. Then, an error signal e(t) is calculated 22 based on y(t) formed by this nonlinear function 21, the estimated separation matrix W(t−1) estimated at the previous cycle, and the observed signal x(t) at that time. Then, based on the calculated error signal e(t), the update of the separation matrix W(t) at that time is performed 23 such that consideration weight is increased when estimation errors are large using the cost function having a monotonously increasing characteristic.
Owner:UNILOC 2017 LLC
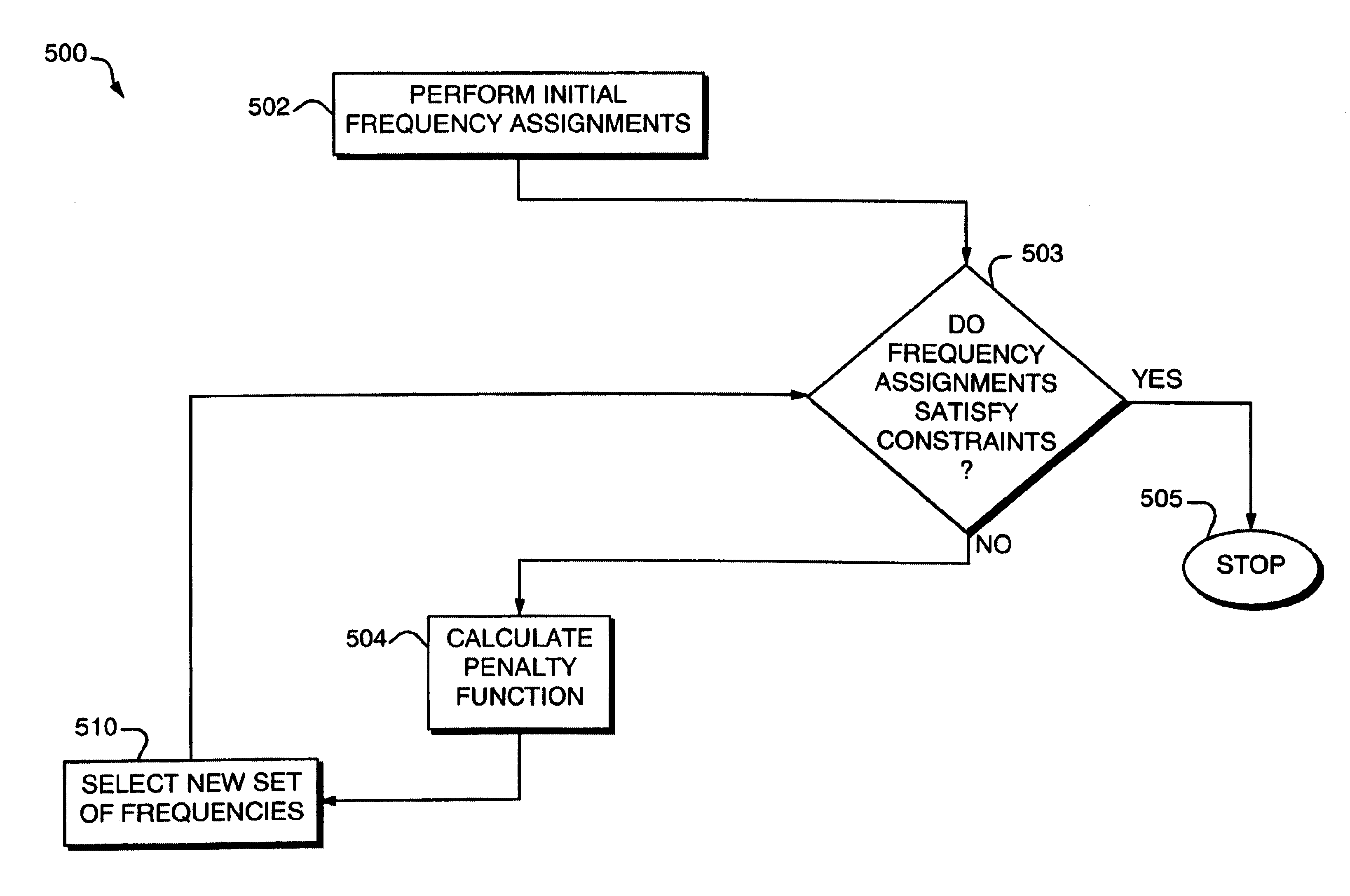
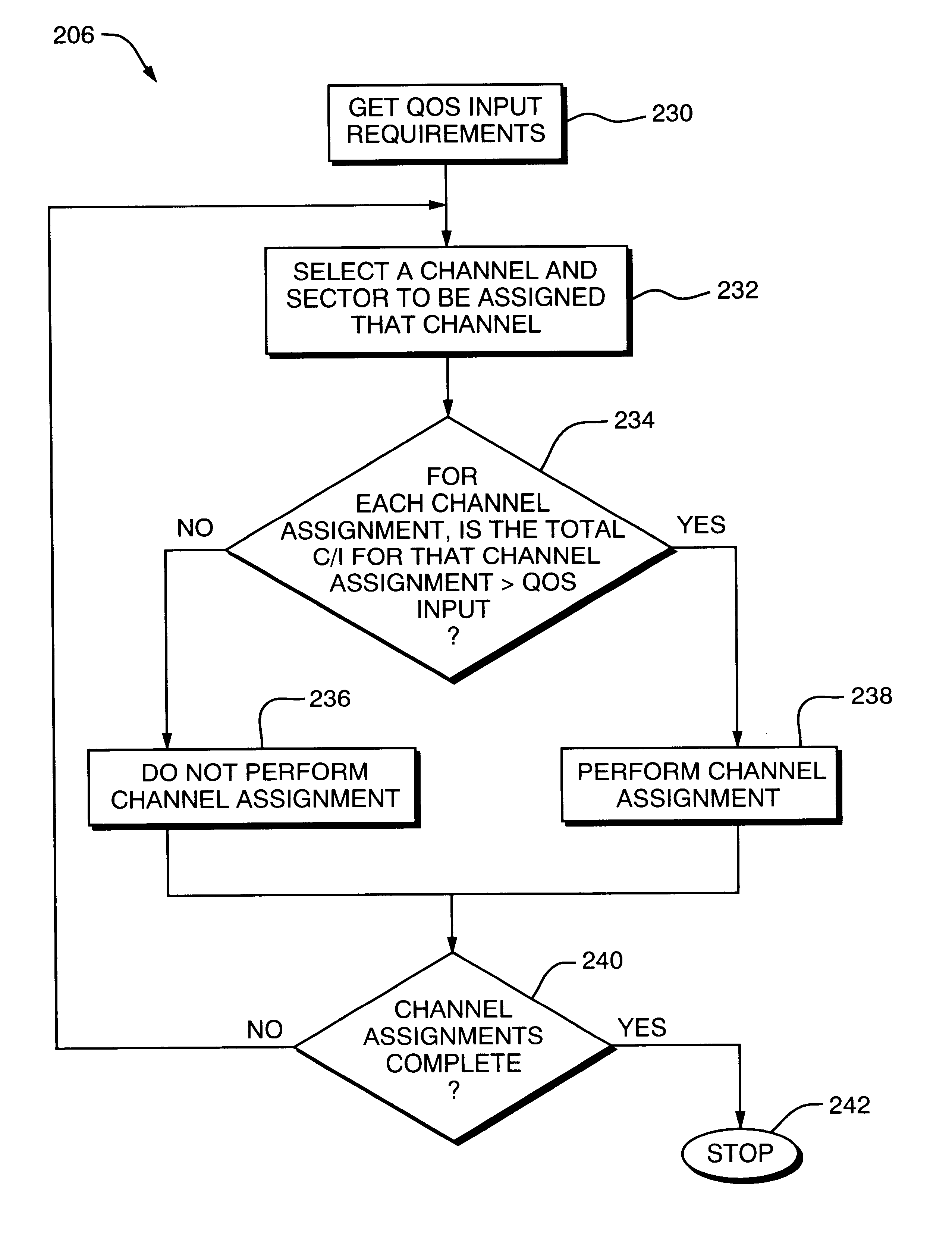
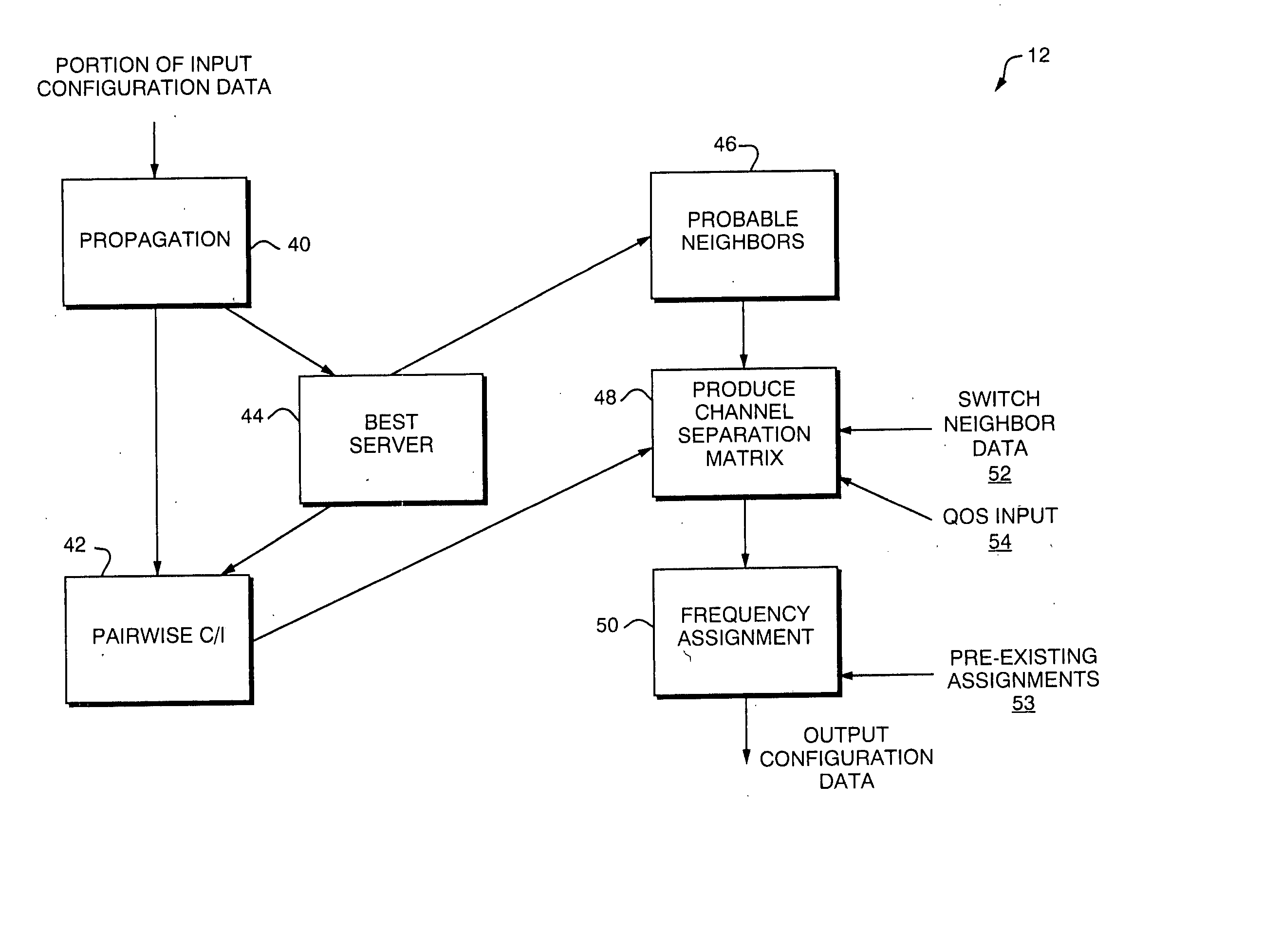
Methods and techniques in channel assignment in a cellular network
InactiveUS6871073B1Network traffic/resource managementRadio/inductive link selection arrangementsQuality of serviceReal-time computing
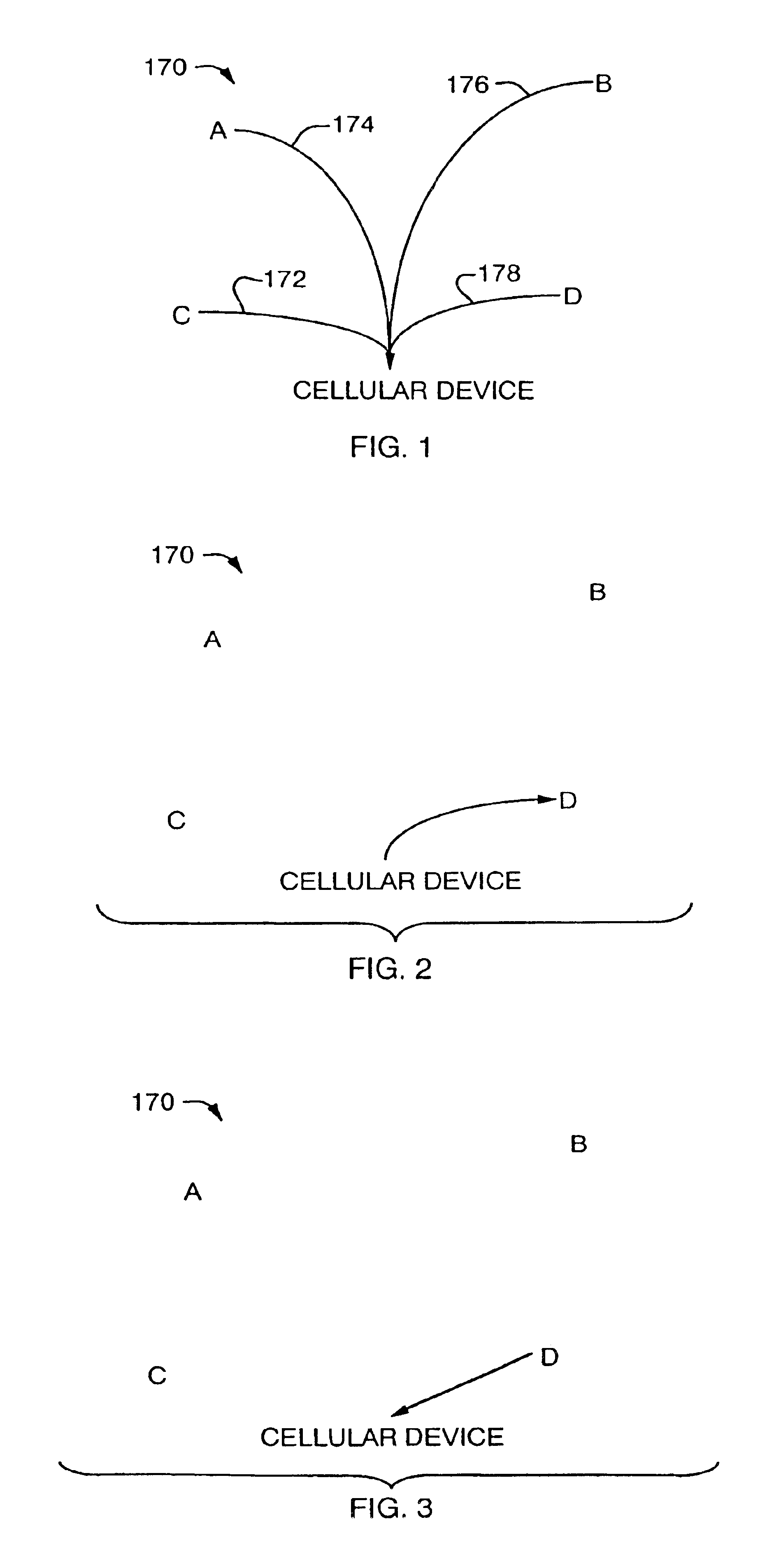
A cellular network configuration tool is described that performs frequency assignments for use in a cellular network. The channels are assigned in accordance with input configuration data such as a channel separation matrix, geographic data, and requested channel assignments for each sector included in the cellular network being configured. The configuration is performed in accordance with predetermined constraints and criteria and quality of service input. The tool uses frequency assignment techniques to perform the channel assignments in accordance with varying constraints and criteria.
Owner:VERIZON LAB
Affinity chromatography matrix
ActiveUS20130274451A1Increased elution pHGuaranteed cost-effective operationSolid sorbent liquid separationPeptide preparation methodsElutionA domain
The present invention relates to a method of separating one or more immunoglobulin containing proteins from a liquid. The method includes first contacting the liquid with a separation matrix comprising ligands immobilised to a support; allowing the immunoglobulin containing proteins to adsorb to the matrix by interaction with the ligands; followed by an optional step of washing the matrix containing the immunoglobulin containing proteins adsorbed thereon; and recovering said immunoglobulin containing proteins by contacting the matrix with an eluent which releases the proteins. The method improves upon previous separation methods in that each of the ligands comprises one or more of a protein A domain (E, D, A, B, C), or protein Z, or a functional variant thereof, with at least one of the monomers having a substitution of the Asparagine at the position corresponding to N28 of B domain of Protein A or Protein Z, and wherein the ligand provides an increase in elution pH compared to non-substituted ligand.
Owner:CYTIVA BIOPROCESS R&D AB
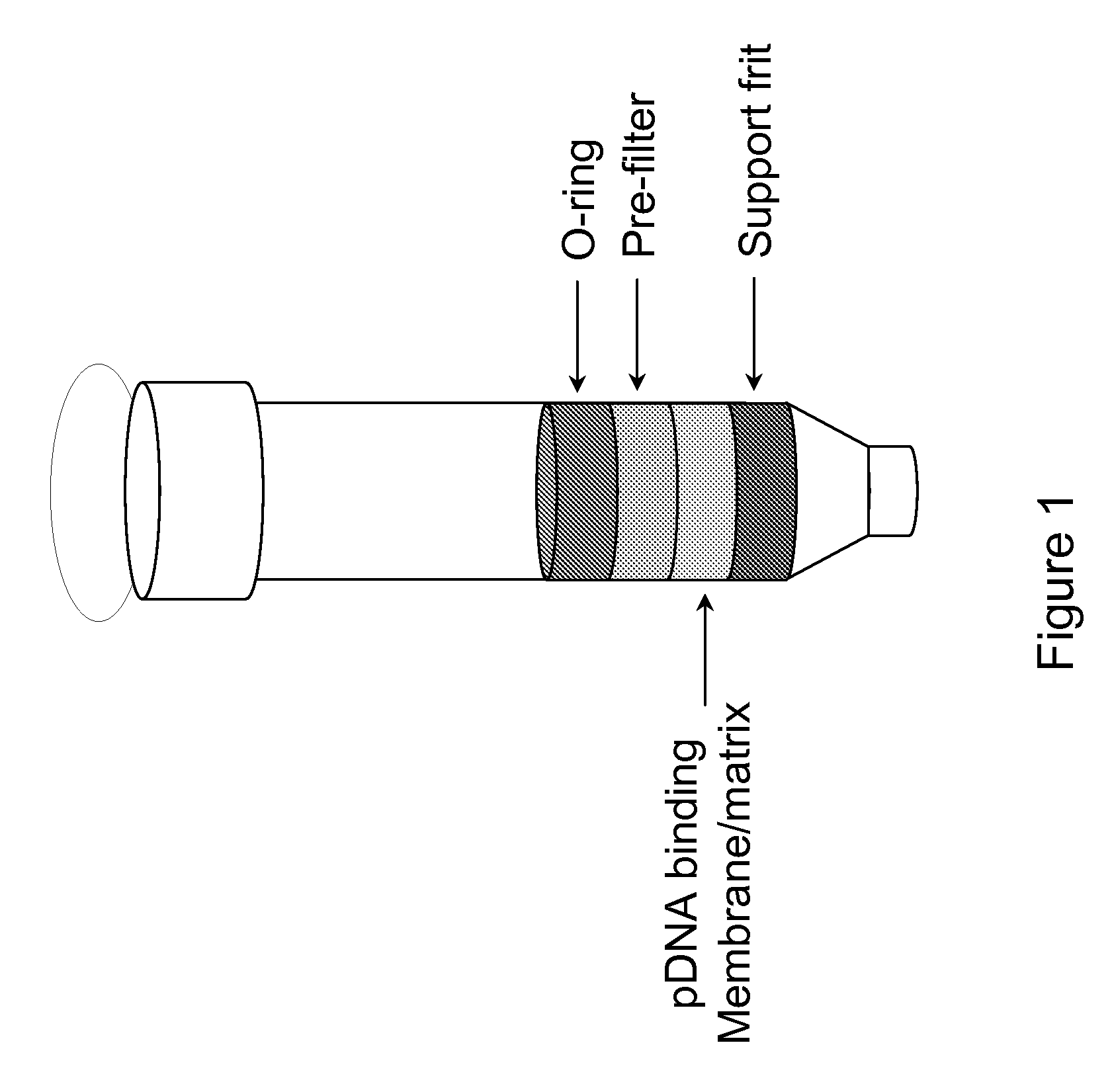
Modified spin column for simple and rapid plasmid DNA extraction
InactiveUS20080300397A1Rapid isolationImprove system performanceSamplingSugar derivativesCellular DebrisSpins
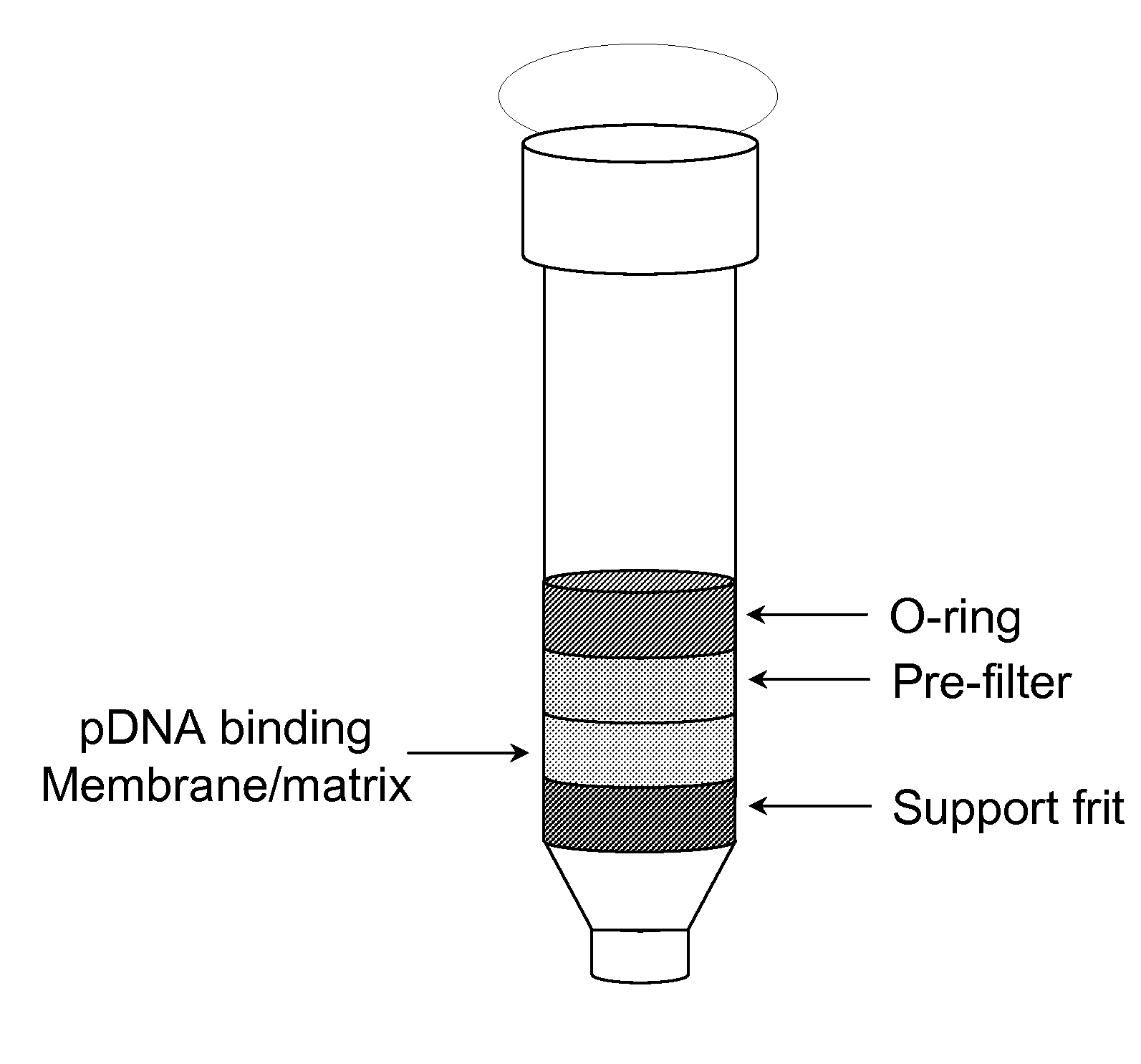
The invention relates to a modified spin column for the isolation and purification of plasmid DNA. A pre-filtration disc is included in a traditional spin column. During plasmid DNA isolation, the lysate can be loaded directly to the modified spin column, eliminates the need to first remove the flocculants containing cellular debris. This results in a much shortened process. Variation of the invention includes a depth filter in between the pre-filtration disc and the main separation matrix. Also provided are kits for isolation of plasmid DNA including the modified spin columns.
Owner:GE HEALTHCARE LTD
Signal separation method, signal processing apparatus, image processing apparatus, medical image processing apparatus and storage medium for restoring multidimensional signals from observed data in which multiple signals are mixed
InactiveUS20020085741A1Stable extractionMinimize cost functionImage enhancementTelevision system detailsMultidimensional signal processingMultidimensional scaling
Signals are separated by introducing a function having a monotonously increasing characteristic like an exponential type function as a cost function, and applying an adaptive algorithm that minimizes that cost function in terms of a signal separation matrix. That is, there is provided a signal processing apparatus that separates and outputs an original signal from the observed signal x(t), in which multiple multidimensional signals are mixed, wherein the nonlinear function 21 is operated on an input observed signal x(t) and an estimated separation matrix W(t-1) estimated at a previous cycle. Then, an error signal e(t) is calculated 22 based on y(t) formed by this nonlinear function 21, the estimated separation matrix W(t-1) estimated at the previous cycle, and the observed signal x(t) at that time. Then, based on the calculated error signal e(t), the update of the separation matrix W(t) at that time is performed 23 such that consideration weight is increased when estimation errors are large using the cost function having a monotonously increasing characteristic.
Owner:UNILOC 2017 LLC
Method and techniques for penalty-based channel assignments in a cellular network
InactiveUS7212822B1Network traffic/resource managementRadio/inductive link selection arrangementsQuality of serviceFigure of merit
A cellular network configuration tool is described that performs frequency assignments for use in a cellular network. The channels are assigned in accordance with input configuration data such as a channel separation matrix, geographic data, and requested channel assignments for each sector included in the cellular network being configured. The configuration is performed in accordance with predetermined constraints and criteria and quality of service input. The tool uses frequency assignment techniques to perform the channel assignments in accordance with varying constraints and criteria. A penalty function is used to determine a figure of merit for a particular set of frequency assignments.
Owner:VERIZON LAB
Methods and techniques in channel assignment in a cellular network
InactiveUS6728544B1Network traffic/resource managementRadio/inductive link selection arrangementsQuality of serviceComputer science
A cellular network configuration tool is described that performs frequency assignments for use in a cellular network. The channels are assigned in accordance with input configuration data such as a channel separation matrix, geographic data, and requested channel assignments for each sector included in the cellular network being configured. The configuration is performed in accordance with predetermined constraints and criteria and quality of service input. The tool uses frequency assignment techniques to perform the channel assignments in accordance with varying constraints and criteria.
Owner:VERIZON LAB
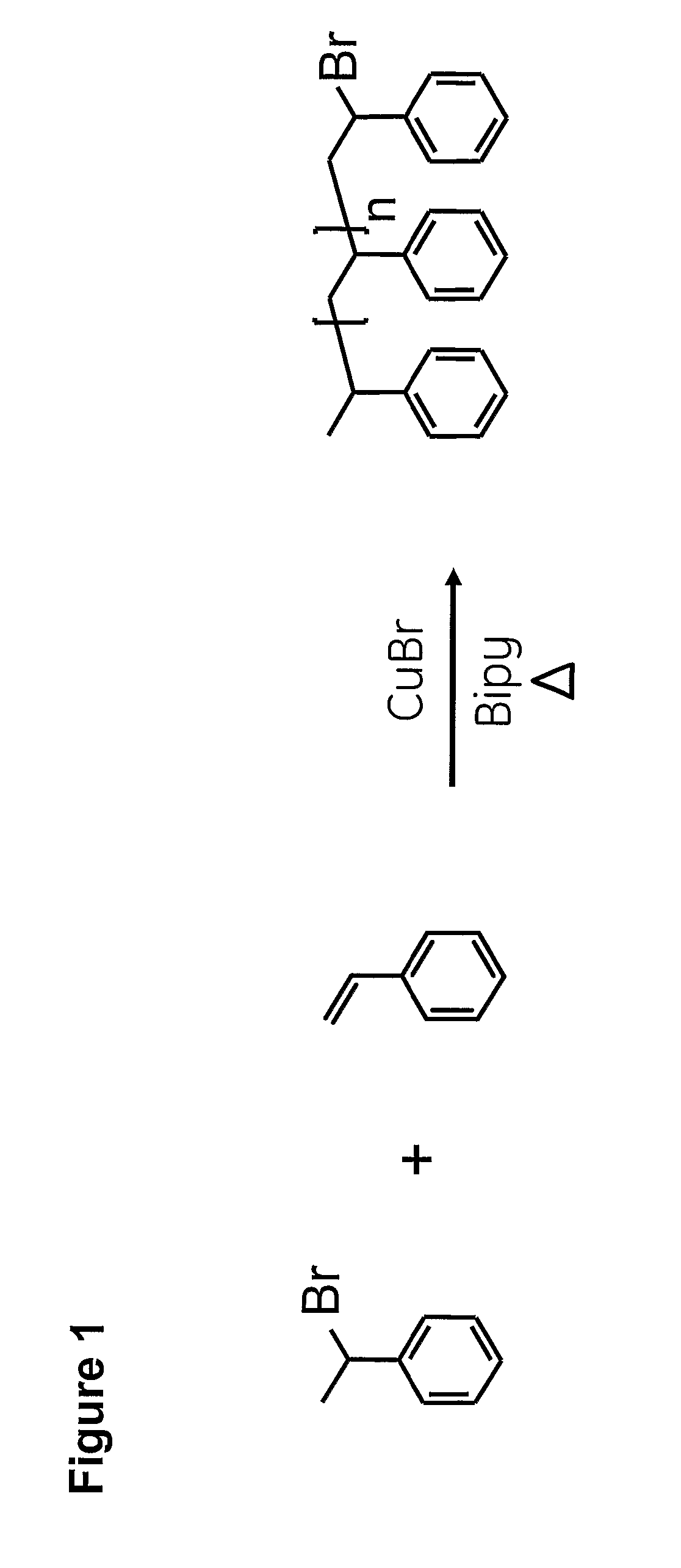
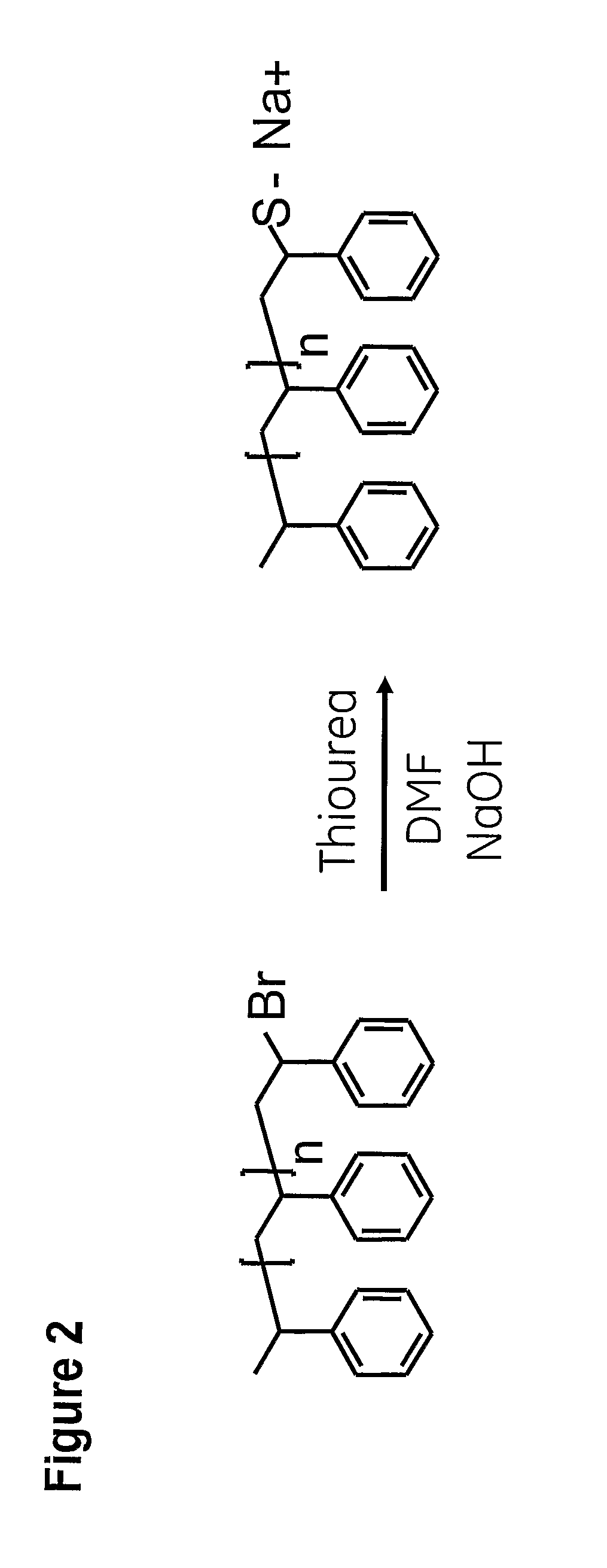
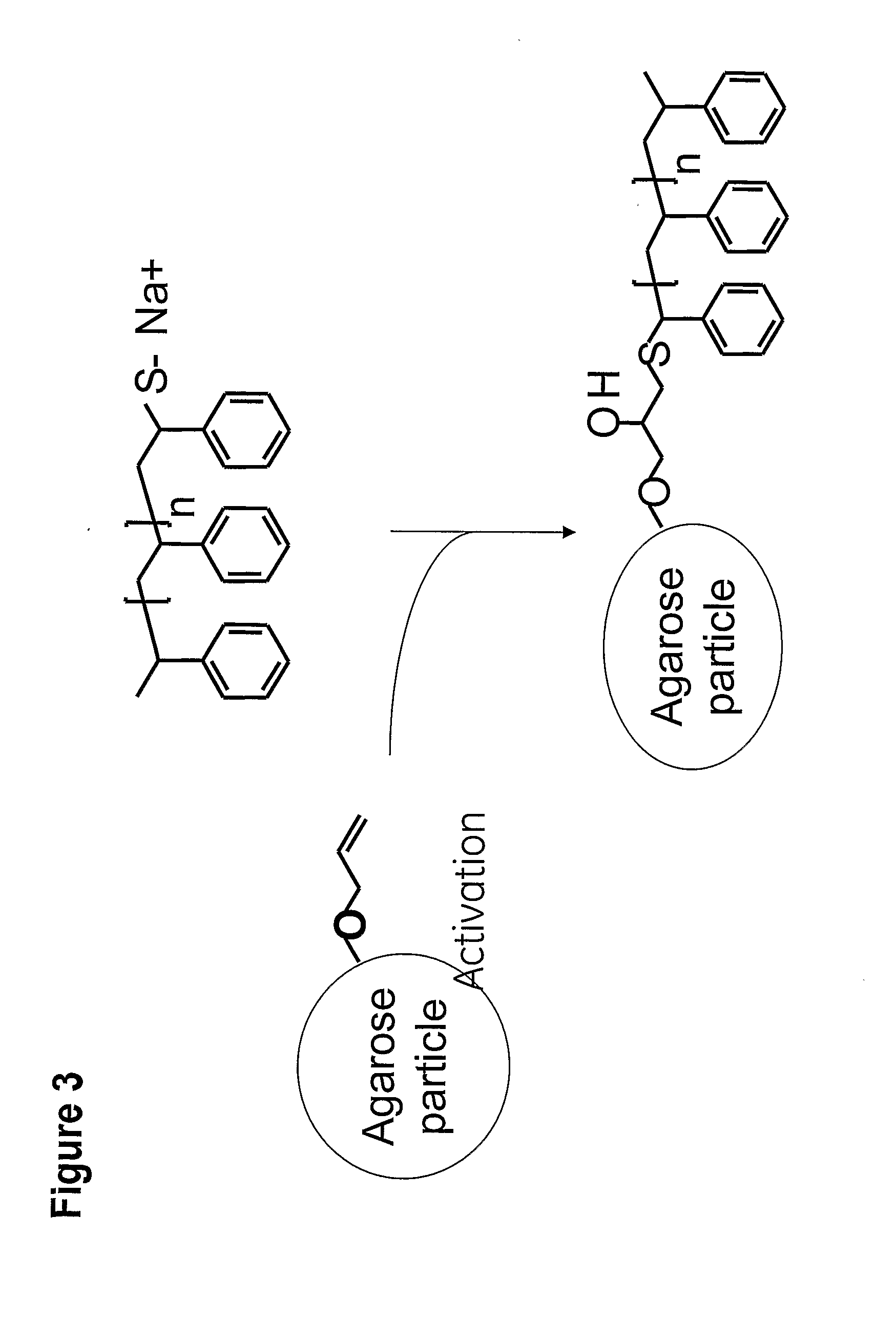
Method of preparing a separation matrix
InactiveUS20070193954A1Ion-exchange process apparatusOther chemical processesCouplingUnsaturated monomer
The present invention is a method of preparing a separation matrix, which method comprises providing unsaturated monomers comprising one or more chromatography functionalities; contacting said monomer(s) with initiator and catalyst; performing controlled radical polymerisation of said monomers; and coupling of the resulting polymers to a base matrix. The controlled polymerisation technique may e.g. be ATRP, RAFT or NMP. The method allows preparation of well characterised ligands useful e.g. for HIC or any other kind of chromatography.
Owner:GE HEALTHCARE BIO SCI CORP
Methods and techniques for penalty-based channel assignments in a cellular network
InactiveUS20060009226A1Network traffic/resource managementRadio/inductive link selection arrangementsQuality of serviceFigure of merit
A cellular network configuration tool is described that performs frequency assignments for use in a cellular network. The channels are assigned in accordance with input configuration data such as a channel separation matrix, geographic data, and requested channel assignments for each sector included in the cellular network being configured. The configuration is performed in accordance with predetermined constraints and criteria and quality of service input. The tool uses frequency assignment techniques to perform the channel assignments in accordance with varying constraints and criteria. A penalty function is used to determine a figure of merit for a particular set of frequency assignments.
Owner:VERIZON LAB
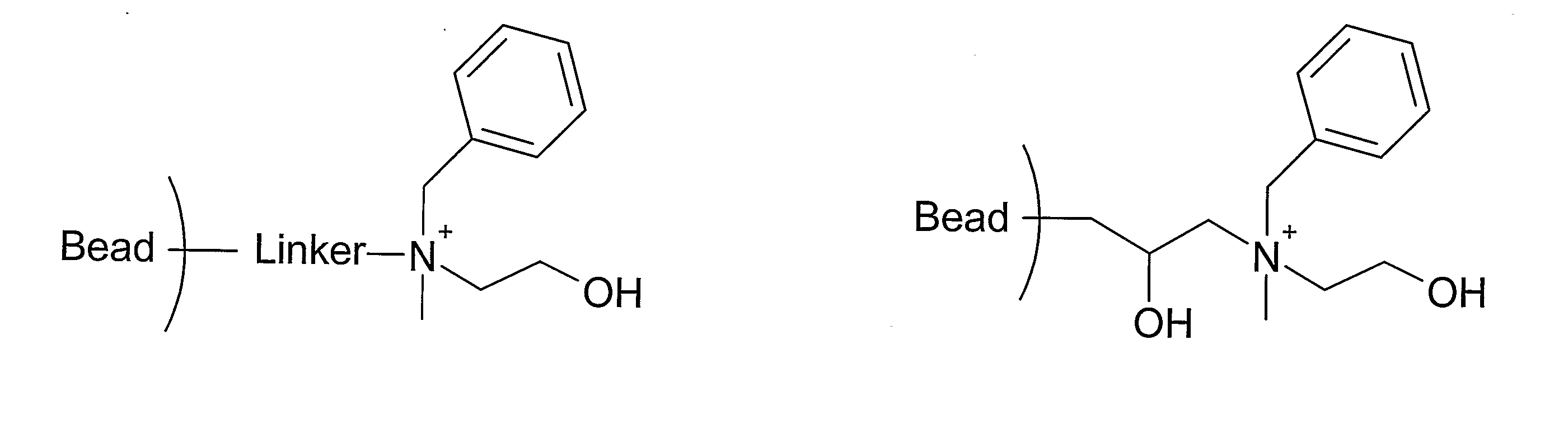
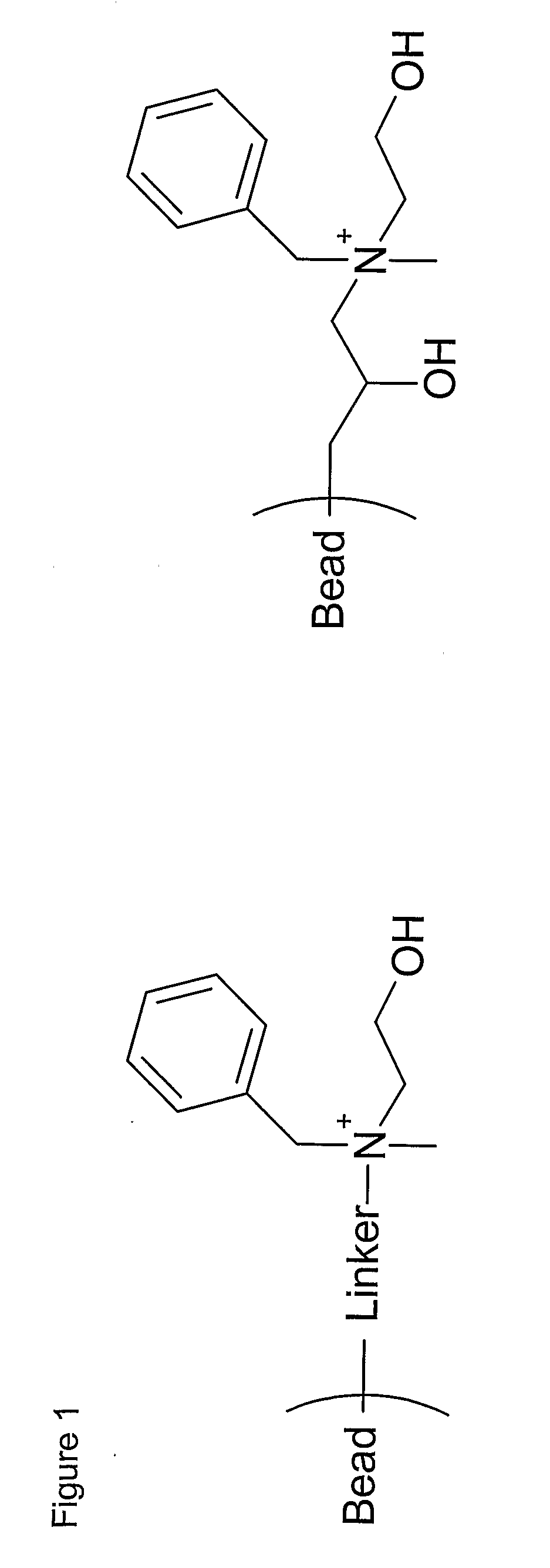
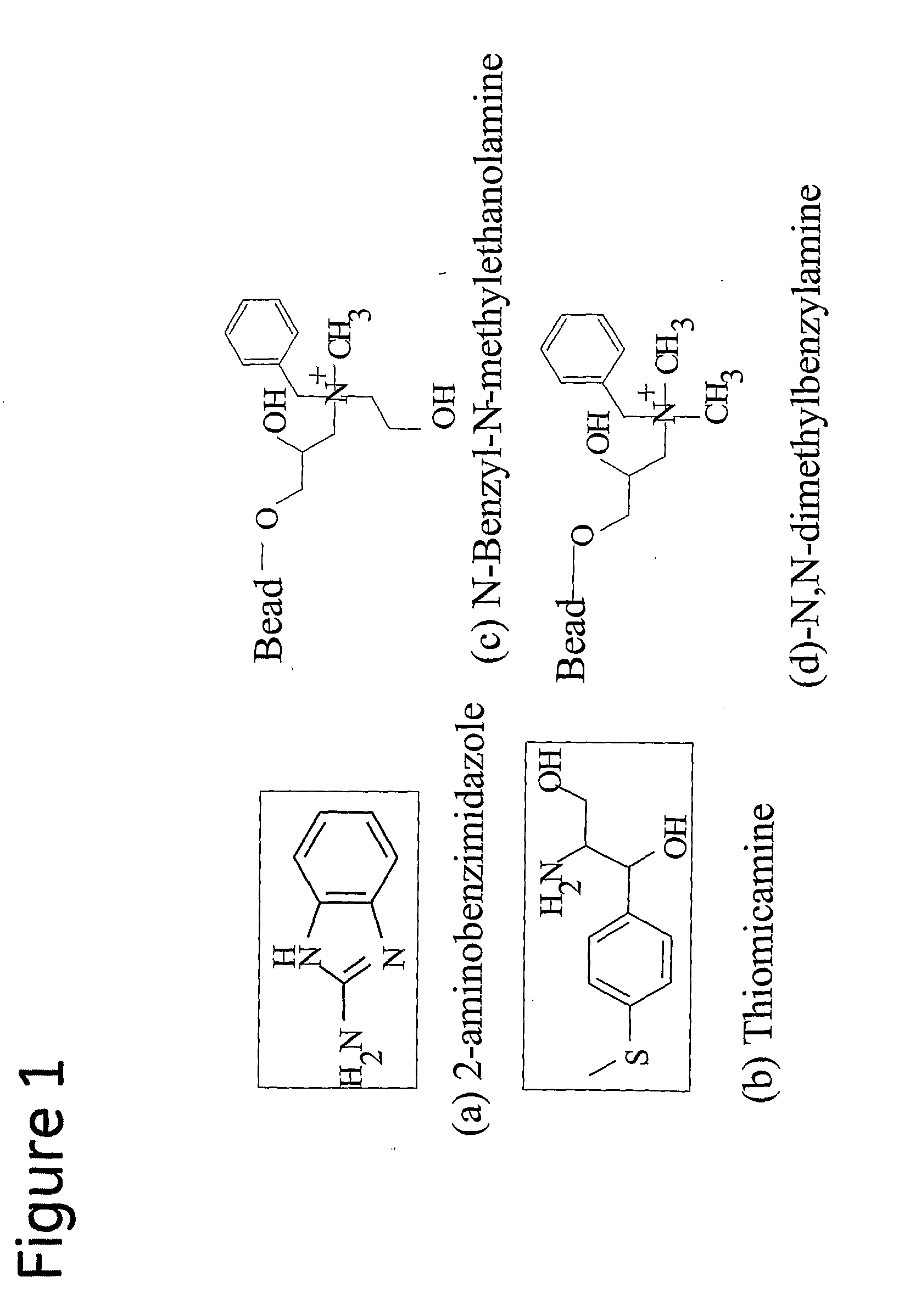
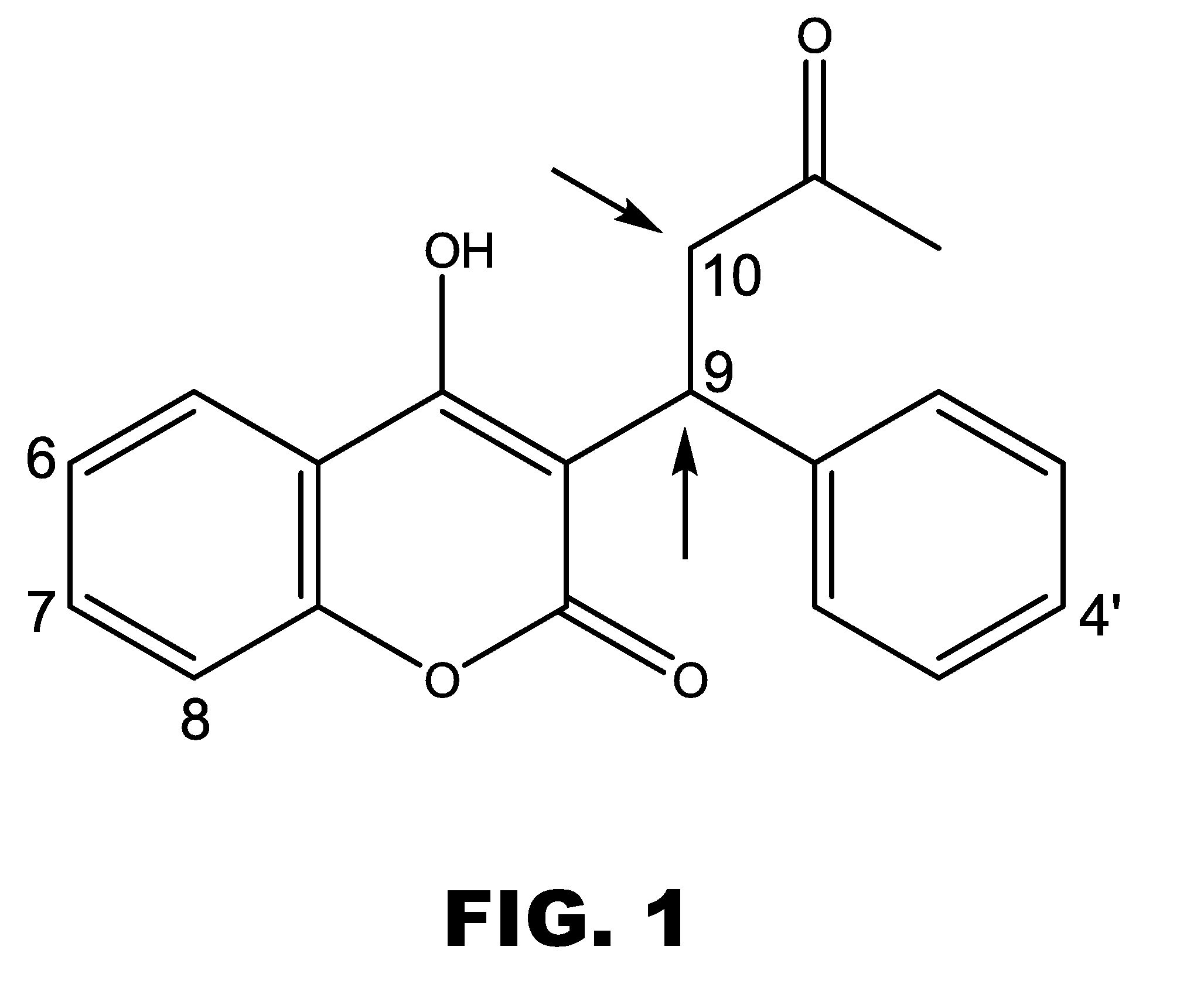
Chromatography Ligand
ActiveUS20070244307A1Bioreactor/fermenter combinationsBiological substance pretreatmentsSimple Organic CompoundsOrganic compound
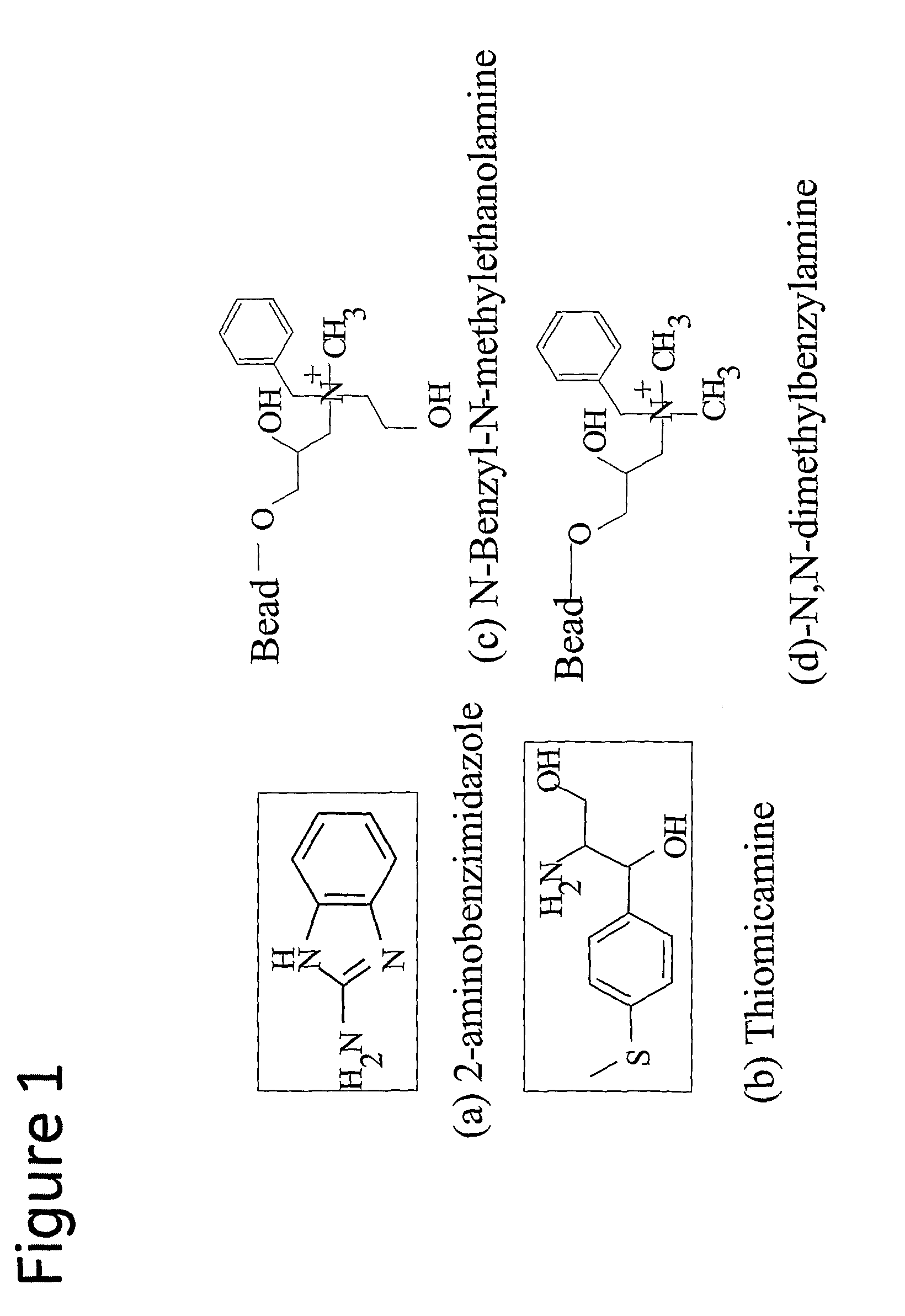
The present invention relates to a chromatography ligand defined by the following formula (I) R1—R2—N(R3)—R4—R5 wherein R1 is a substituted or non-substituted phenyl group; R2 is a hydrocarbon chain comprising 0-4 carbon atoms; R3 is a hydrocarbon chain comprising 1-3 carbon atoms; R4 is a hydrocarbon chain comprising 1-5 carbon atoms; and R5 is OH or H. The invention also comprises a separation matrix, comprising the described ligands coupled to a porous support, such as particles or a membrane. The ligand and matrix according to the invention is useful for purification of biomolecules or organic compounds, such as proteins, polypeptides, DNA etc. An advantageous use according to the invention is the purification of antibodies.
Owner:CYTIVA BIOPROCESS R&D AB
Position information estimation device, method thereof, and program
InactiveUS20050203981A1Avoid influenceReduce the amount of calculationMulti-channel direction-finding systems using radio wavesDigital computer detailsIndependent component analysisComputer science
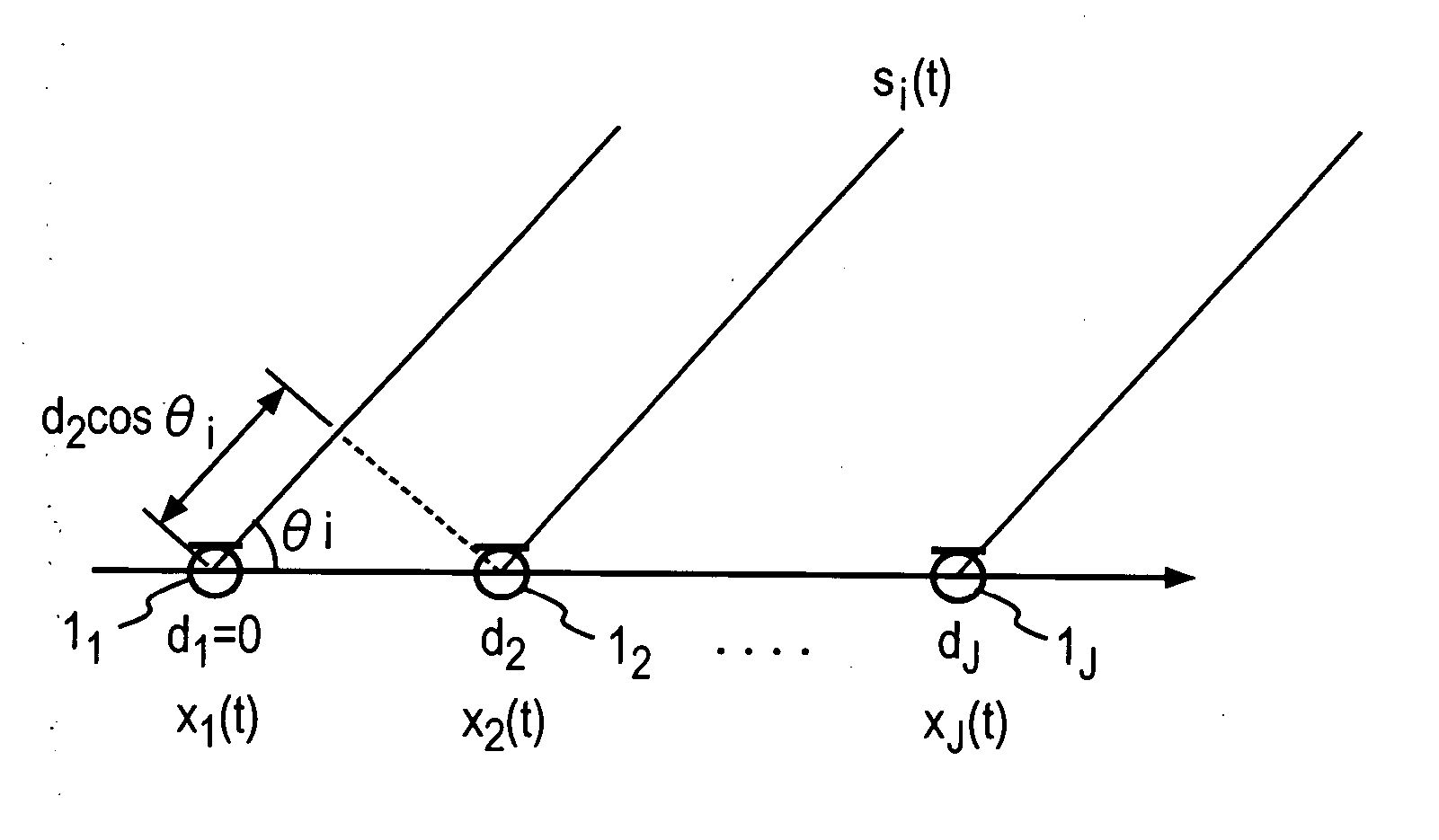
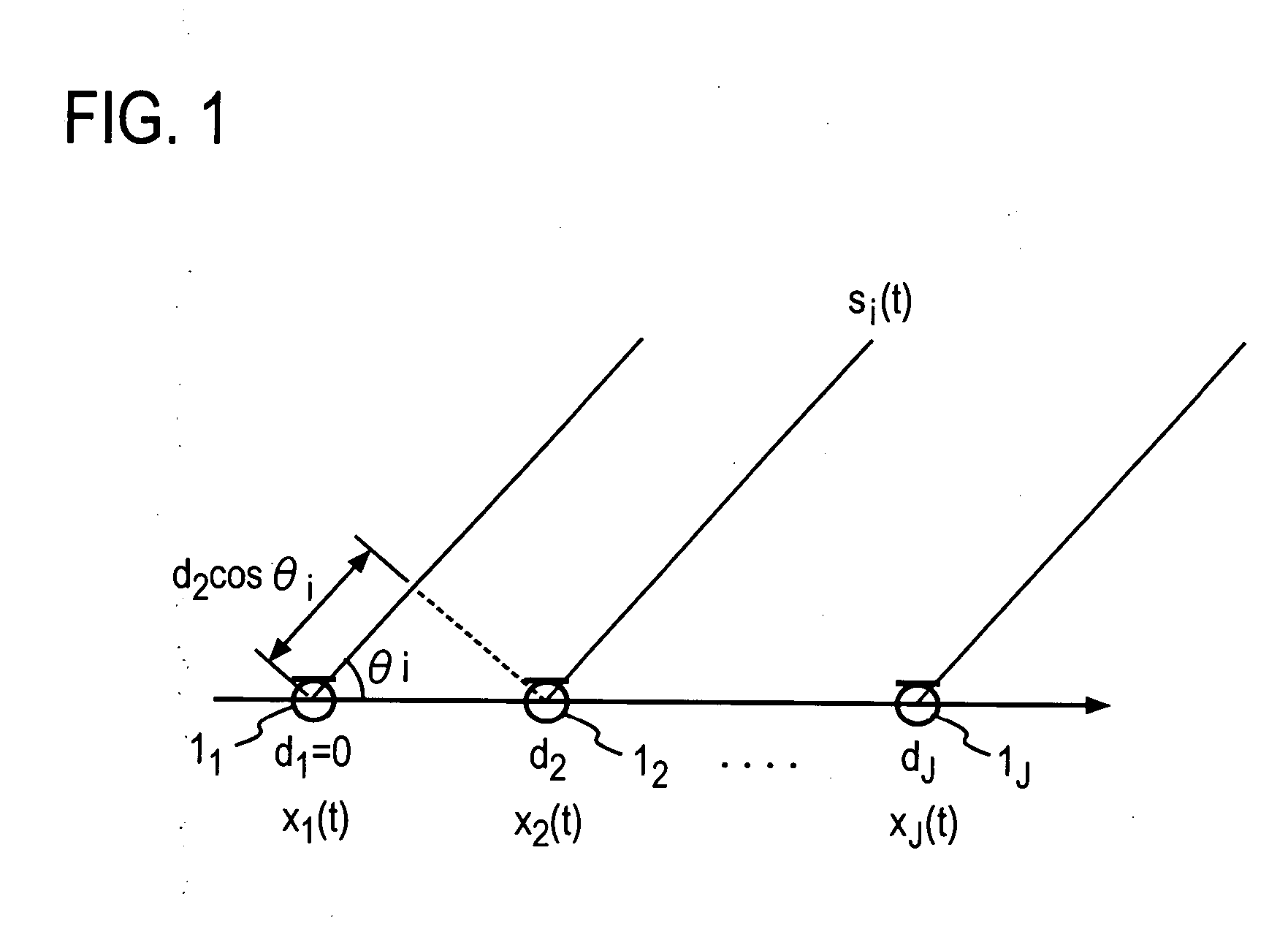
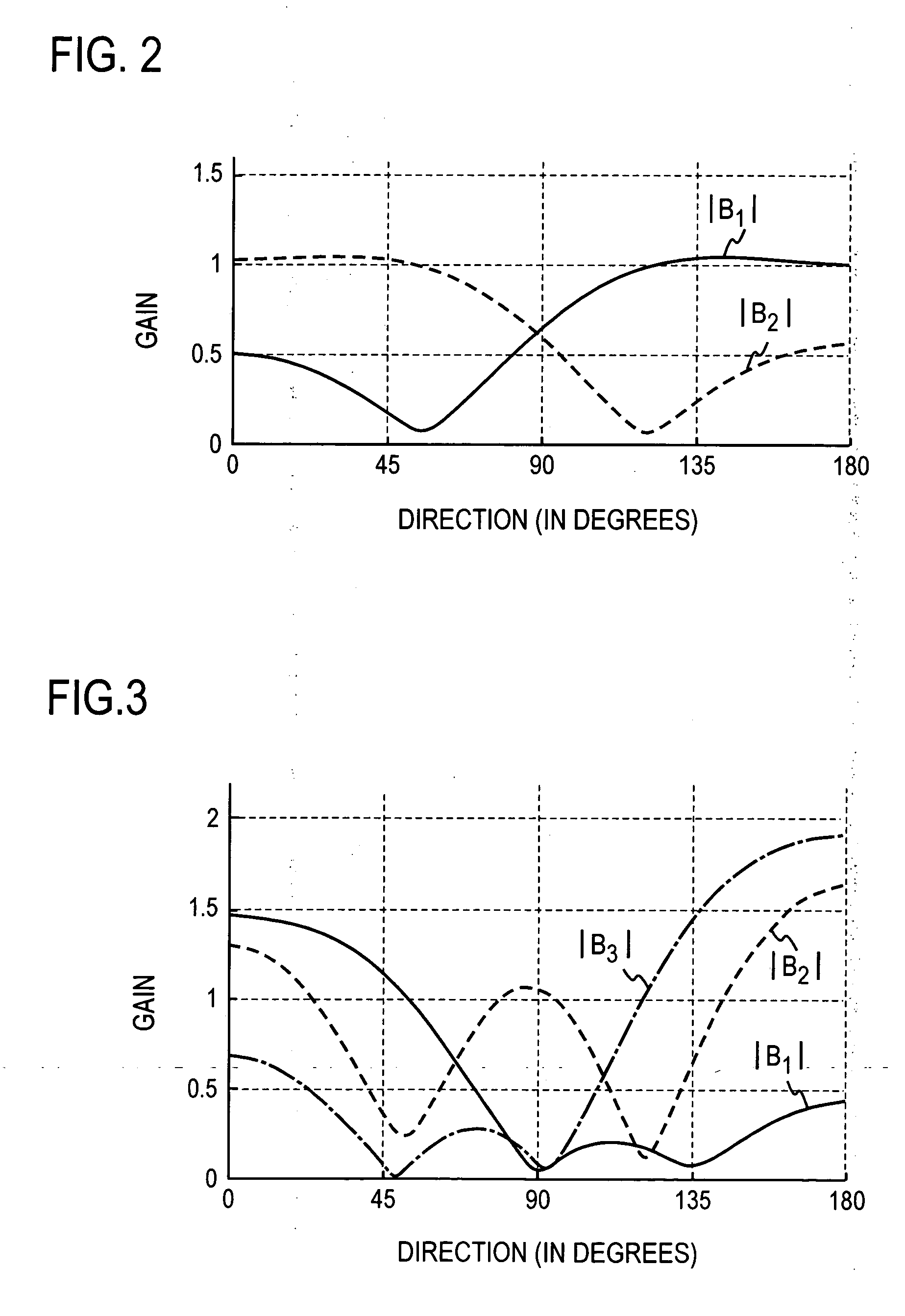
Observed signals x1(t) to xj(t) from a plurality of sensors disposed in two dimensions are subject to a short-time Fourier transform, from which signals X1(ω1) to X1(ωN), . . . XJ(ω1) to XJ(ωN) are derived. Using the independent component analysis process, separation matrices W(ω1) to W(ωN) are produced. Their inverse matrices H(ω1) to H(ωN) are calculated, and for each ωn (n=1, . . . , N), using a pair of elements from each column of H(ωn), Hji(ωn) and Hj′i(ωn), an angle {circumflex over (θ)}i,jj′(ωn)=cos−1(arg(|Hji(ωn)/Hj′i(ωn))/(ωnc−1∥dj−dj′∥)) is calculated where arg(α) represents an argument of α, c the propagation velocity of a signal, and ∥dj−dj′∥ represents a spacing between sensors i and j′. Columns are permuted so that {circumflex over (θ)}i,jj′(ωn) obtained from each column of H(ω1) to H(ωN) assume an ascending order. For columns which cannot be permuted, the equation ∥qi−dj′∥/∥qi−dj∥=|Hji(ωn)/Hj′i(ωn)|=DRi,jj′(ωn) is solved for qi to calculate Ri,jj′(ωn)=∥DRi,jj′(ωn)·(dj−dj′)/(DR2i,jj′(ωn)−1)|. Columns of H(ωn) is permuted so that Ri,jj′(ωn) assume an ascending order. H(ωn) is used to solve the permutation problem of W(ω).
Owner:NIPPON TELEGRAPH & TELEPHONE CORP
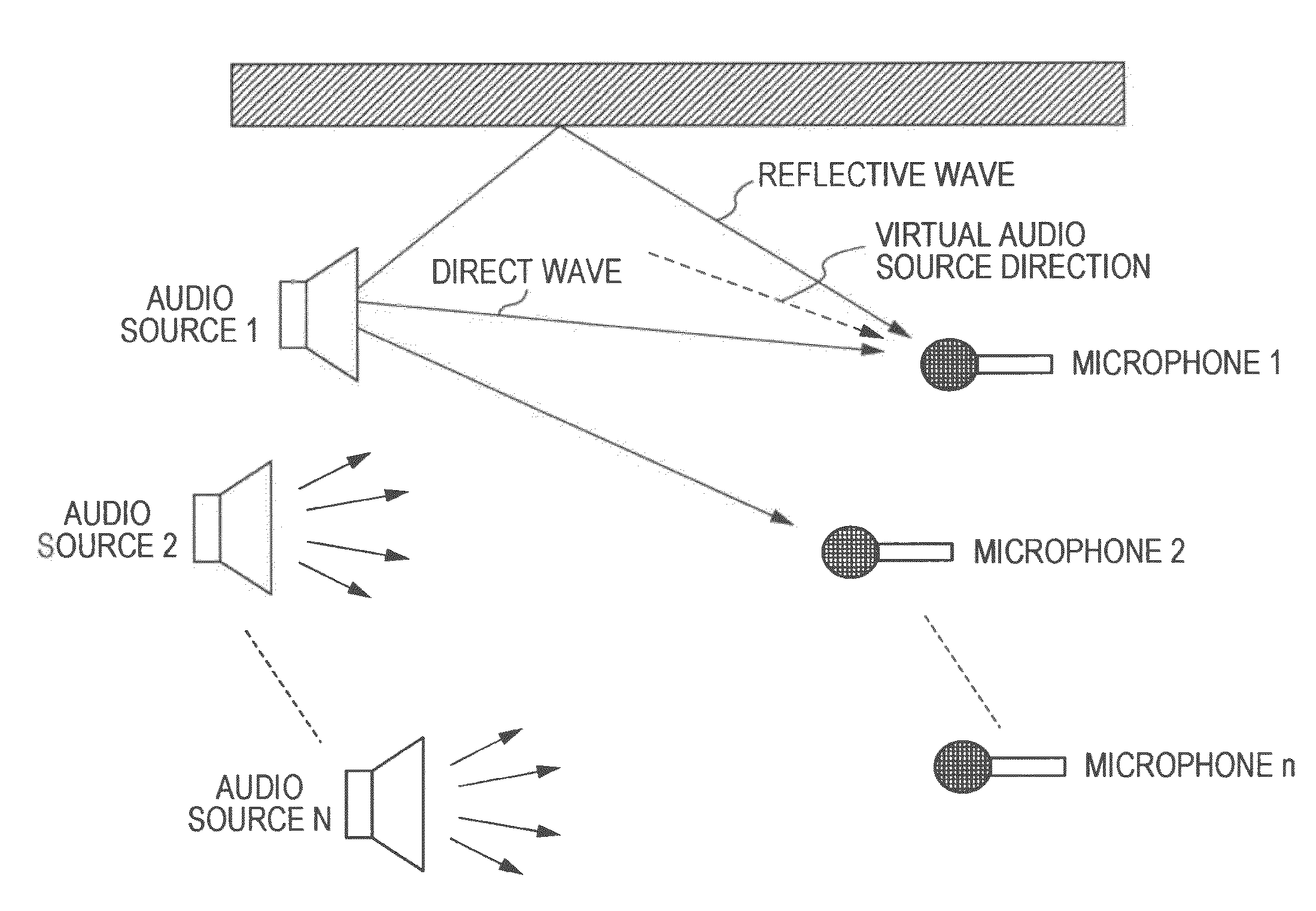
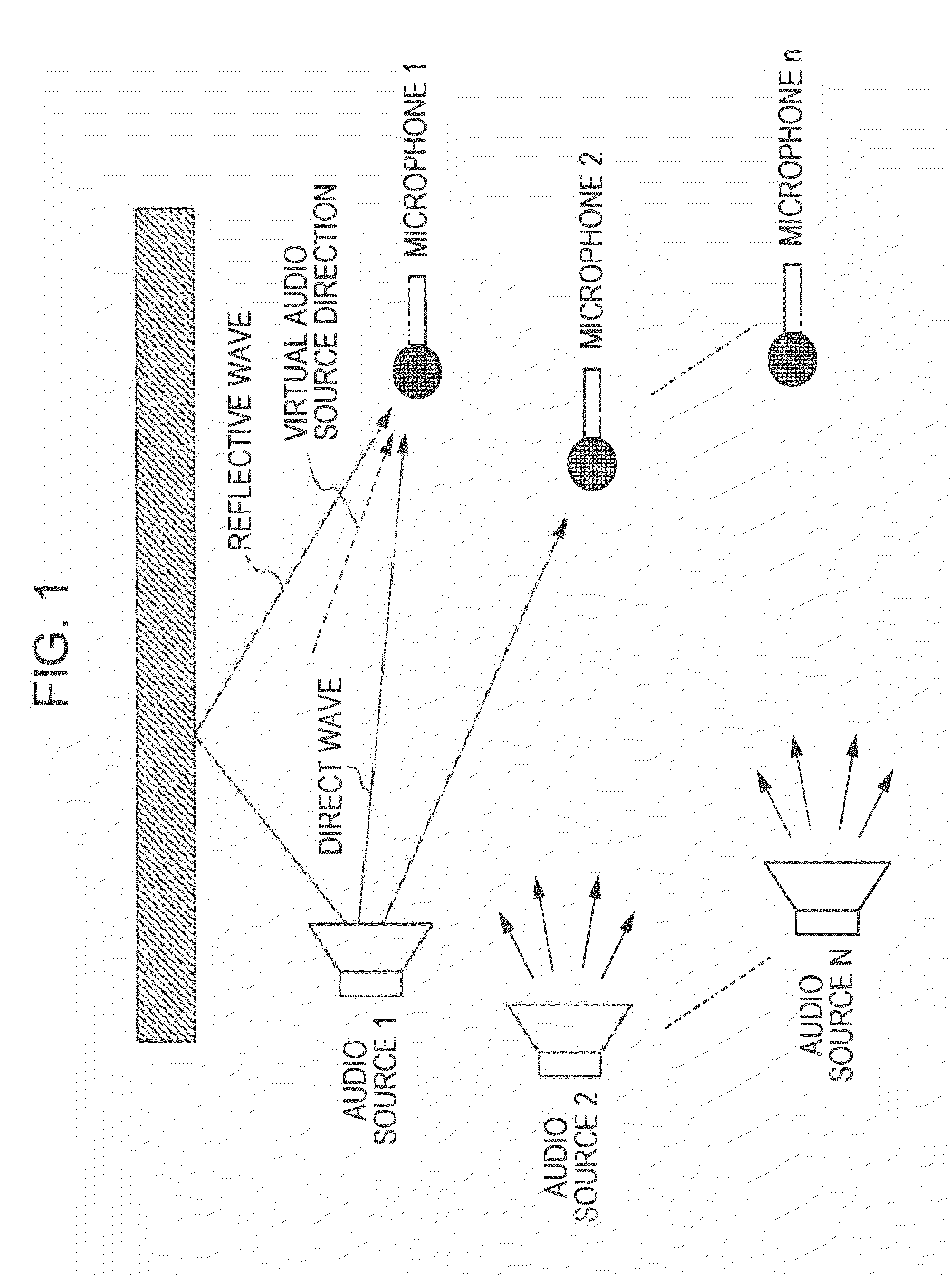
Apparatus and method for separating audio signals
InactiveUS20060206315A1Speech analysisMicrophones signal combinationTime domainIndependent component analysis
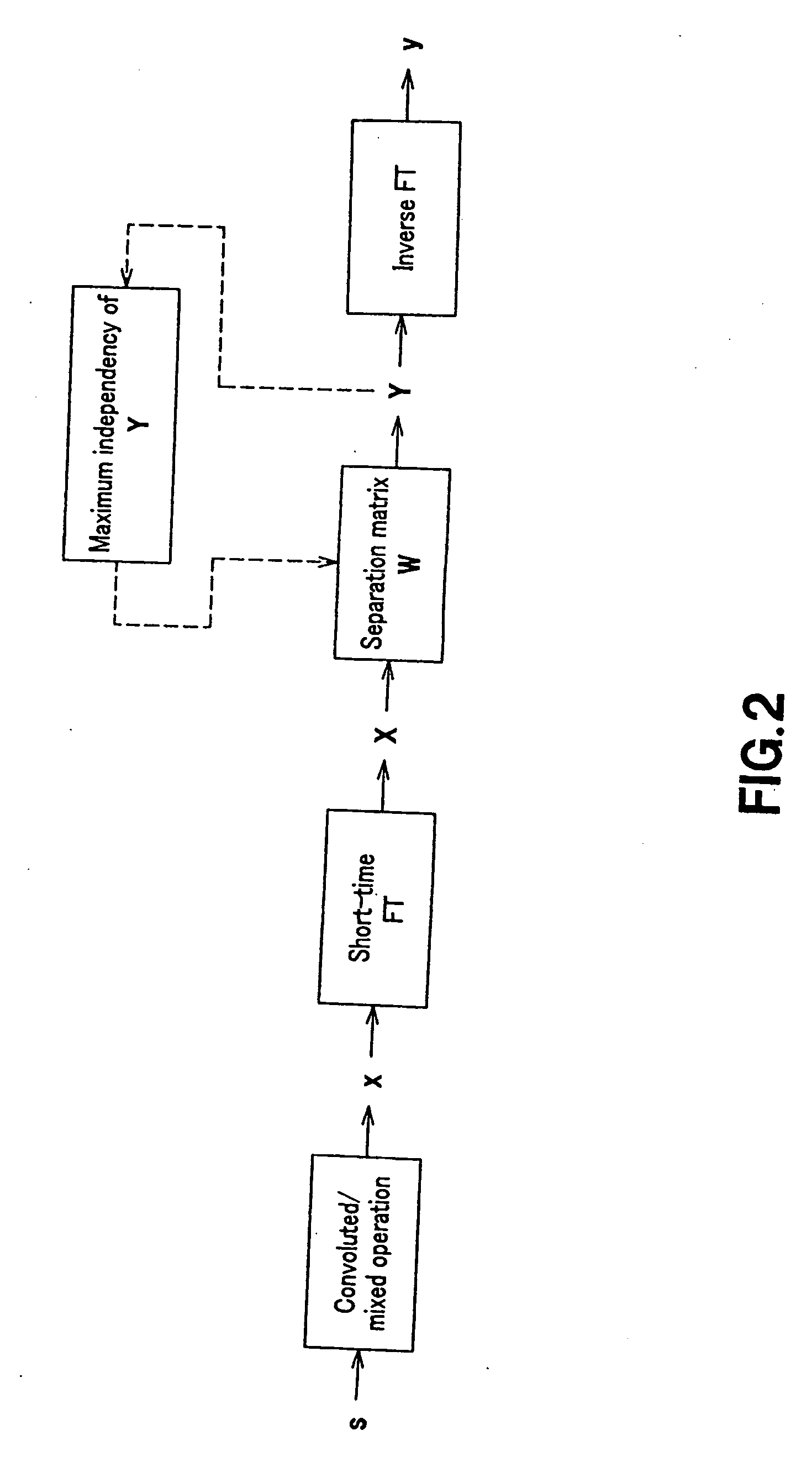
The present invention provides an apparatus for separating audio signals that can dissolve the problem of permutation when separating the plurality of mixed signals by independent component analysis. There is provided an audio signal separation apparatus for separating observation signals in a time domain of a mixture of a plurality of signals including audio signals into individual signals by means of independent component analysis to produce isolated signals, the apparatus including a first conversion section that converts the observation signals in the time domain into observation signals in a time-frequency domain, a separation section that produces isolated signals in a time-frequency domain from the observation signals in the time-frequency domain, and a second conversion section that converts the isolated signals in the time-frequency domain into isolated signals in a time domain, the separation section being adapted to produce isolated signals in a time-frequency domain from the observation signals in the time-frequency domain and a separation matrix substituted by initial values, compute the modified value of the separation matrix by using a score function using the isolated signals in the time-frequency domain and a multidimensional probability density function and the separation matrix, modify the separation matrix until the separation matrix substantially converges by using the modified value and produce isolated signals in the time-frequency domain by using the substantially converging separation matrix.
Owner:SONY CORP
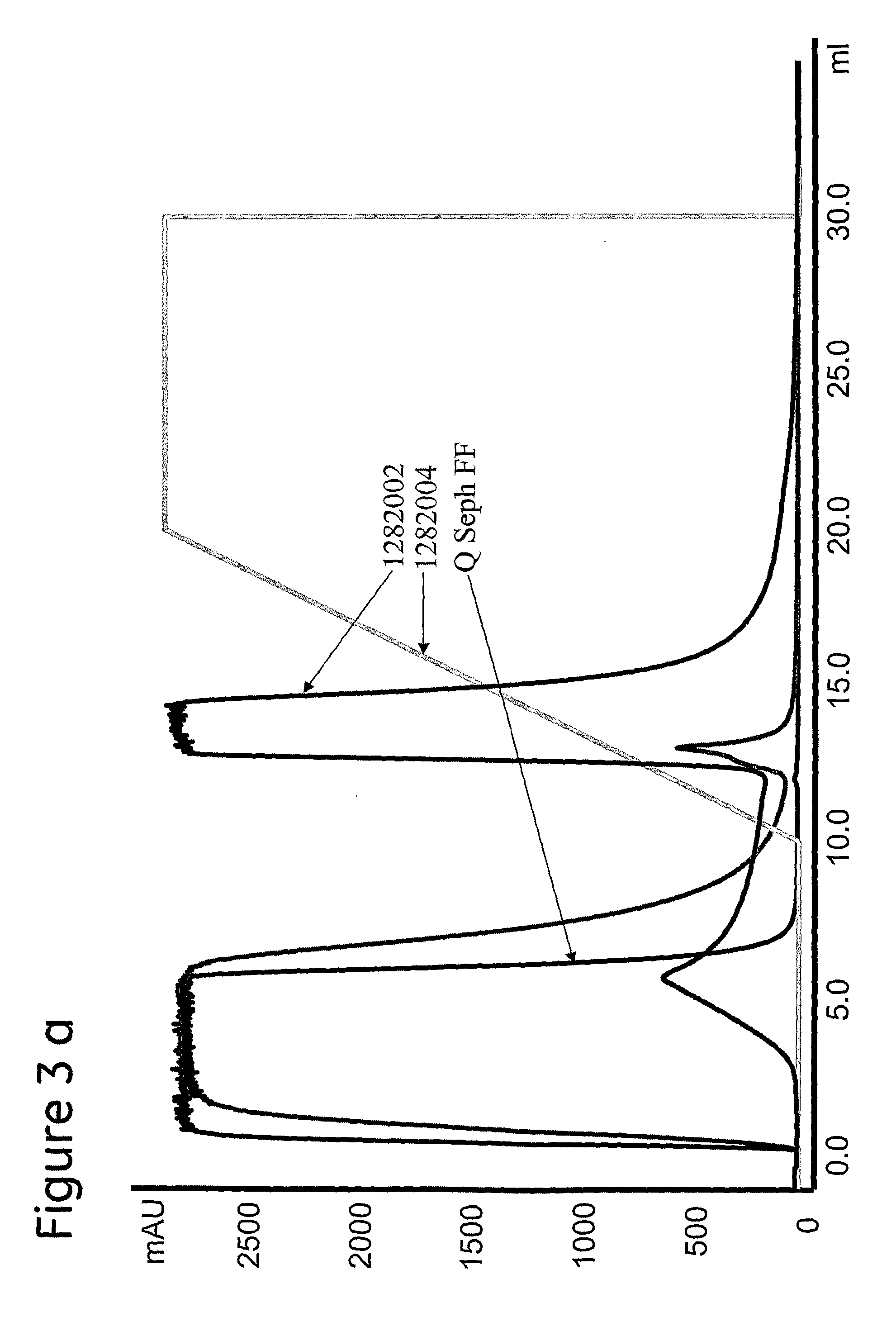
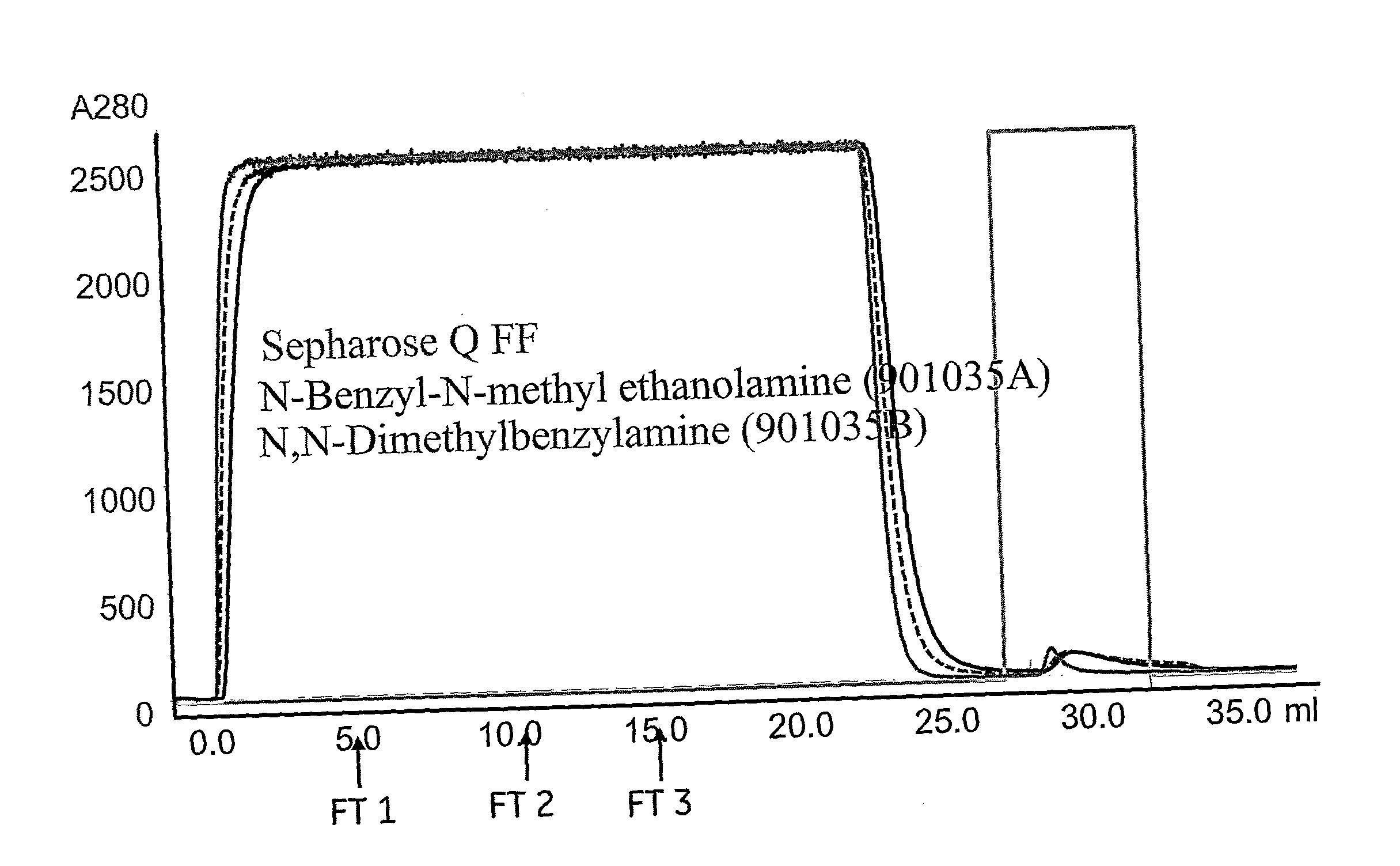
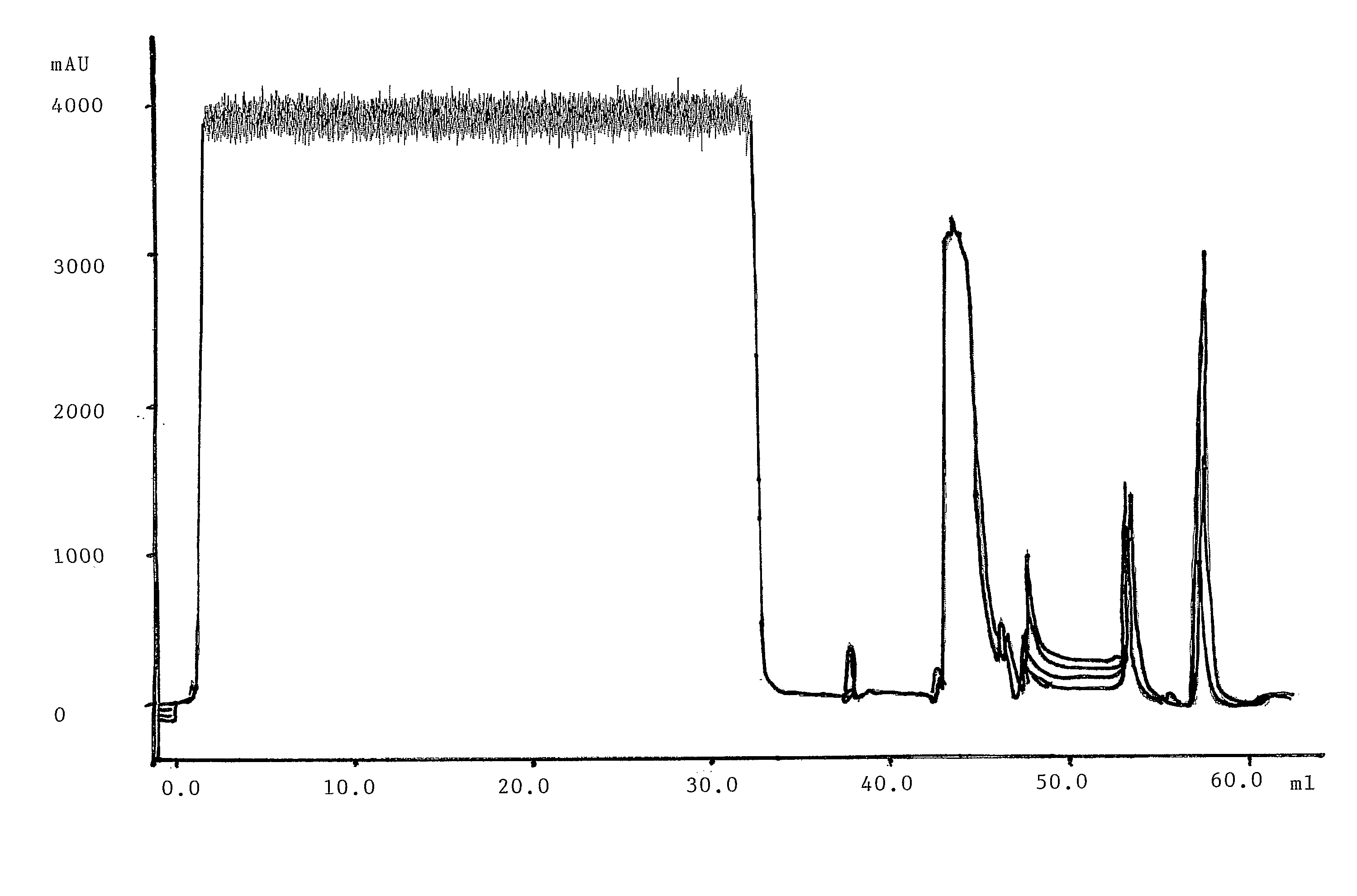
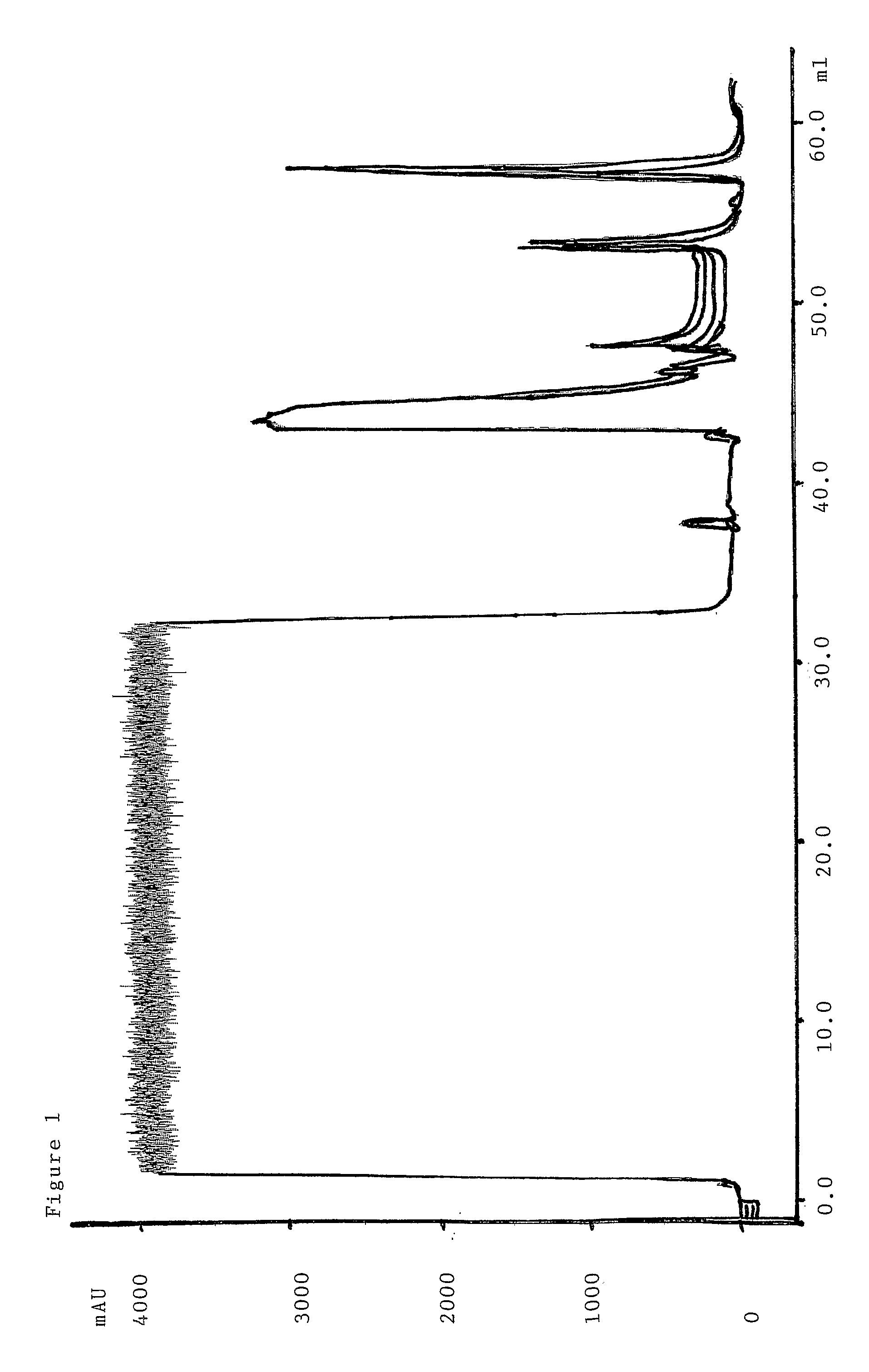
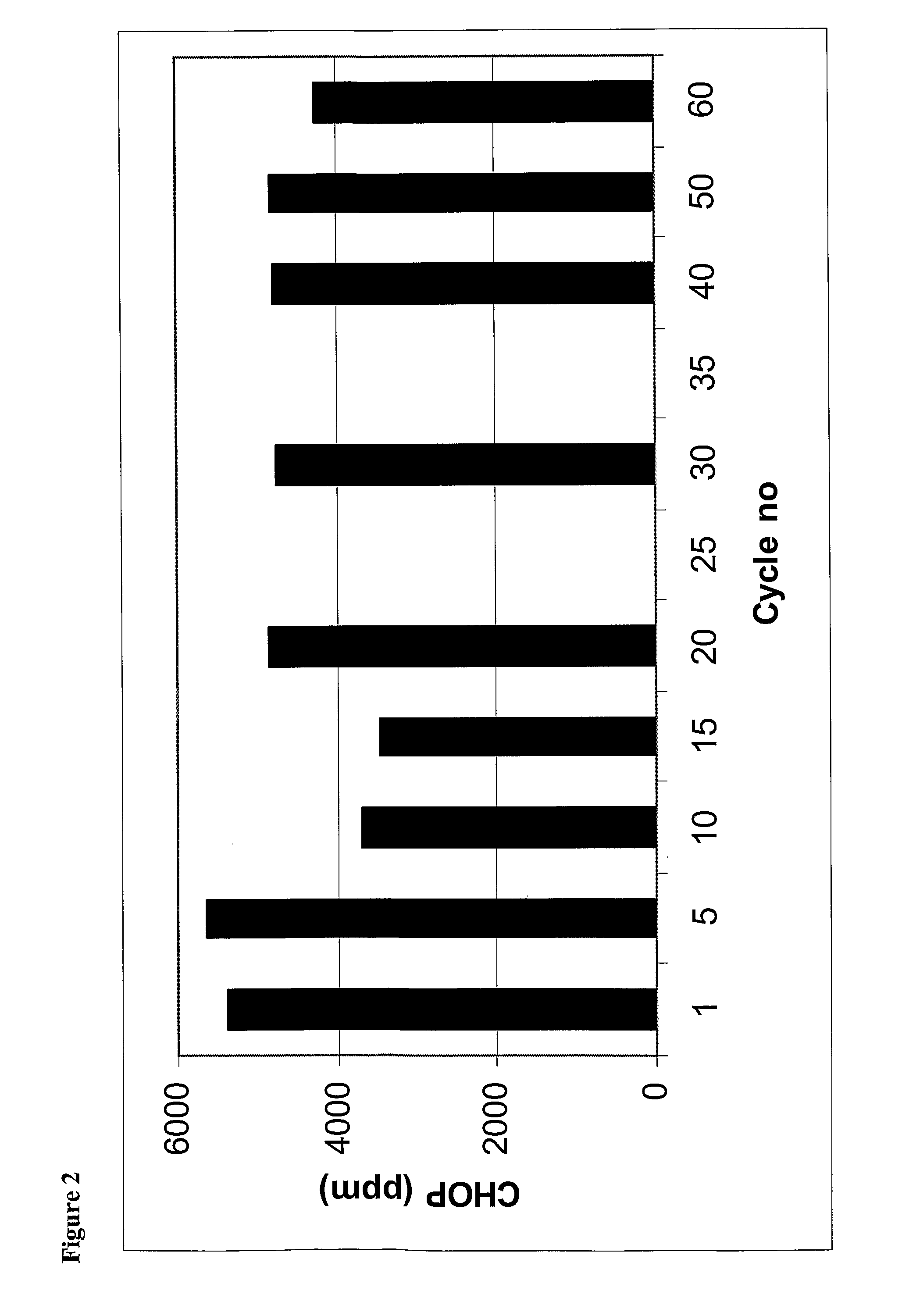
Separation matrix
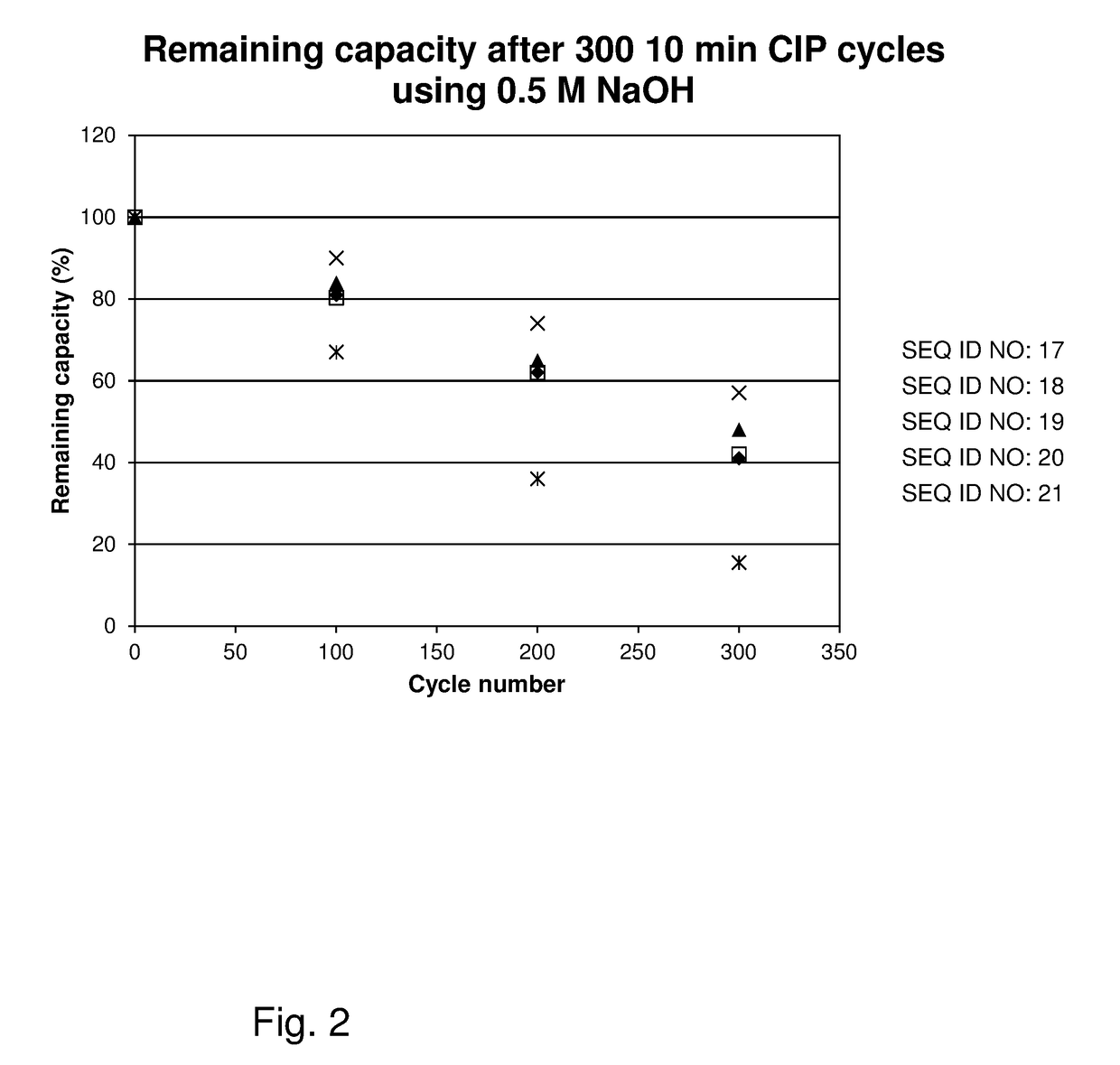
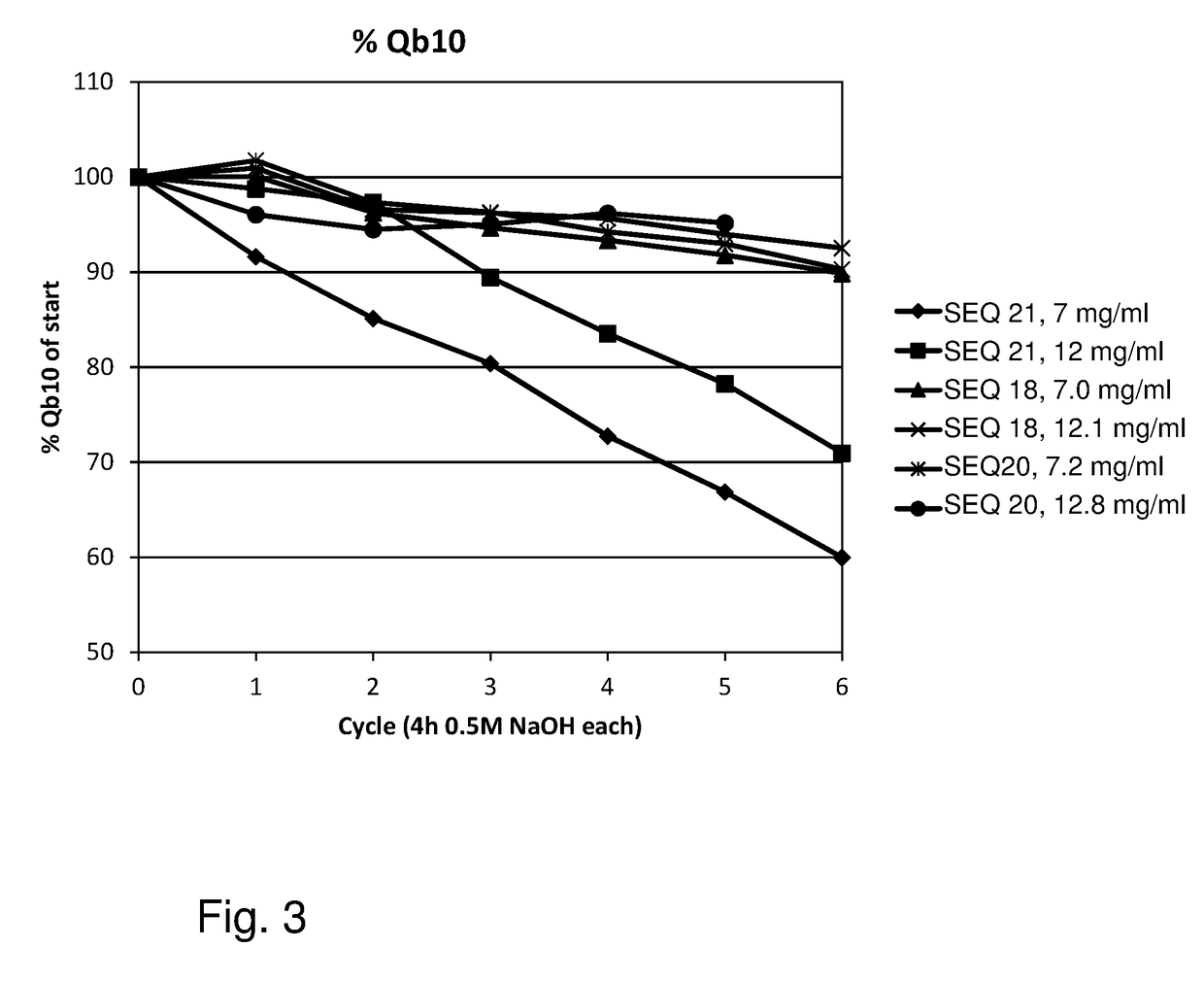
ActiveUS20170327534A1Improved alkaline stabilityImprove stabilityOther chemical processesImmunoglobulins against bacteriaCross-linkMicrometer
The invention relates to a separation matrix comprising at least 11 mg/ml Fc-binding ligands covalently coupled to a porous support, wherein:
- a) the ligands comprise multimers of alkali-stabilized Protein A domains, and
- b) the porous support comprises cross-linked polymer particles having a volume-weighted median diameter (d50,v) of 56-70 micrometers and a dry solids weight of 55-80 mg/ml.
Owner:CYTIVA BIOPROCESS R&D AB
Method of Antibody Purification
ActiveUS20070259453A1Few stepsLess timeOrganic anion exchangersChromatographic anion exchangersCompound (substance)Chromatography column
The present invention relates to a method of separating antibodies from other compound(s) in a liquid sample, wherein a mobile phase comprising said sample is contacted with a multi-modal separation matrix to adsorb undesired compounds while the antibodies remain free in the liquid, wherein the multi-modal separation matrix comprises first groups, which are capable of interacting with negatively charged sites of the target compounds, and second groups, which are capable of at least one interaction other than charge-charge interaction with said target compounds. The invention also relates to a chromatography column packed with the above-described multi-modal separation matrix and a filter having such multi-modal groups adsorbed to its surface
Owner:CYTIVA BIOPROCESS R&D AB
Signal processing device, signal processing method and program
InactiveUS20110261977A1Reduce computing costImprove accuracySignal processingSpeech analysisData setIndependent component analysis
A signal processing device includes a signal transform unit which generates observation signals in the time frequency domain, and an audio source separation unit which generates an audio source separation result, and the audio source separation unit includes a first-stage separation section which calculates separation matrices for separating mixtures included in the first frequency bin data set by a learning process in which Independent Component Analysis is applied to the first frequency bin data set, and acquires a first separation result for the first frequency bin data set, a second-stage separation section which acquires a second separation result for a second frequency bin data set by using a score function in which an envelope is used as a fixed one, and executing a learning process for calculating separation matrices for separating mixtures, and a synthesis section which generates the final separation results by integrating the first and the second separation results.
Owner:SONY CORP
Method for separating vibration signal blind sources under strong noise environment
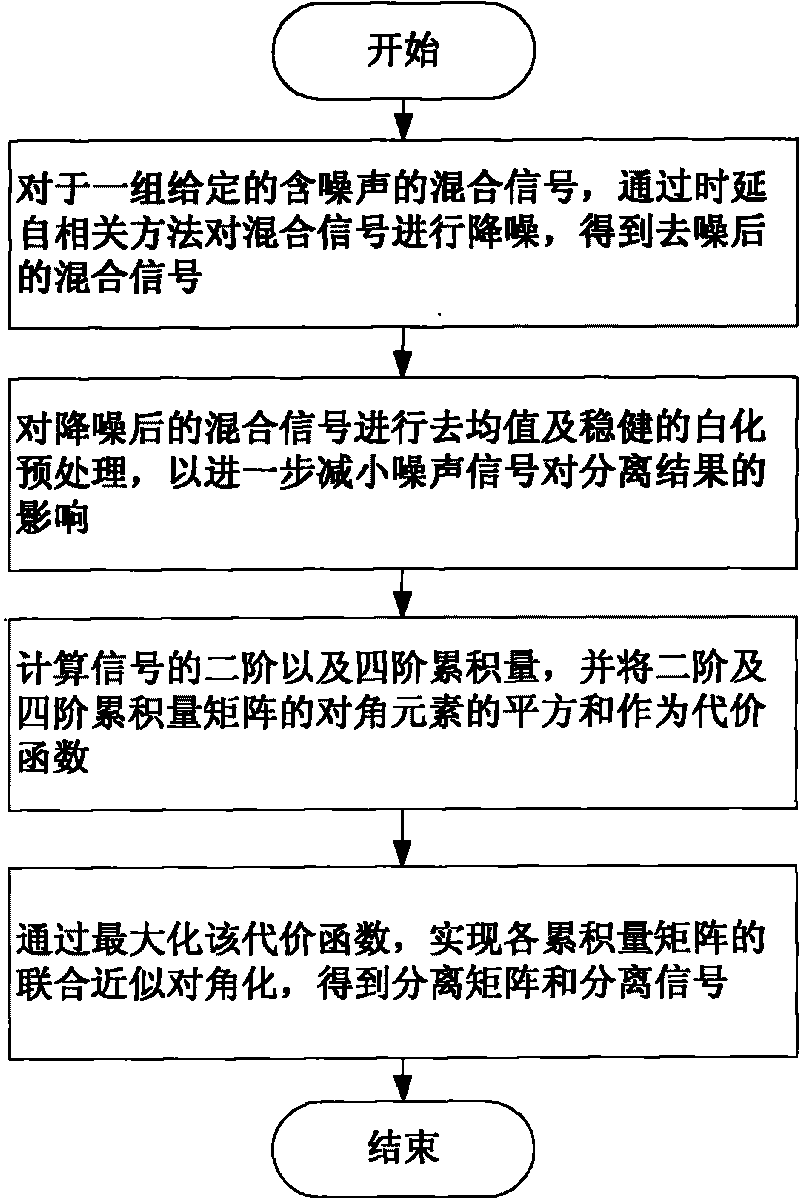
ActiveCN101729157AReduce the impactAchieve separationTransmitter/receiver shaping networksTransmission noise suppressionSignal onTime delays
The invention discloses an algorithm for separating vibration signal blind sources under a strong noise environment. The method comprises the following steps: 1, de-noising a group of given mixed signals containing noise through a time delay autocorrelation method to acquire de-noised mixed signals; 2, performing mean value removal and steady whitening pretreatment on the mixed signals acquired in the first step to further reduce the influence of the noise signals on the separation result; and 3, calculating second-order and fourth-order cumulated amount of the initial separate signals, using the sum of diagonal elements of second-order and fourth-order cumulated amount matrixes as a cost function, and maximizing the cost function to similarly diagonalize the joints of the cumulated amount matrixes so as to realize the separation of the signals of the independent sources and acquire orthogonal separation matrixes. The method combines the conventional de-noising method and the blind separation algorithm to realize the separation of the mixed signals under the strong noise environment, and has the advantages of good separation effect, high convergence rate and de-noising effect free from the limitation of the set threshold value compared with the conventional algorithm.
Owner:NANJING UNIV OF AERONAUTICS & ASTRONAUTICS
Sound source separation apparatus and sound source separation method
ActiveUS20120045066A1Degree of reductionReduce componentsSpeech analysisStereophonic arrangmentsSound source separationComputer science
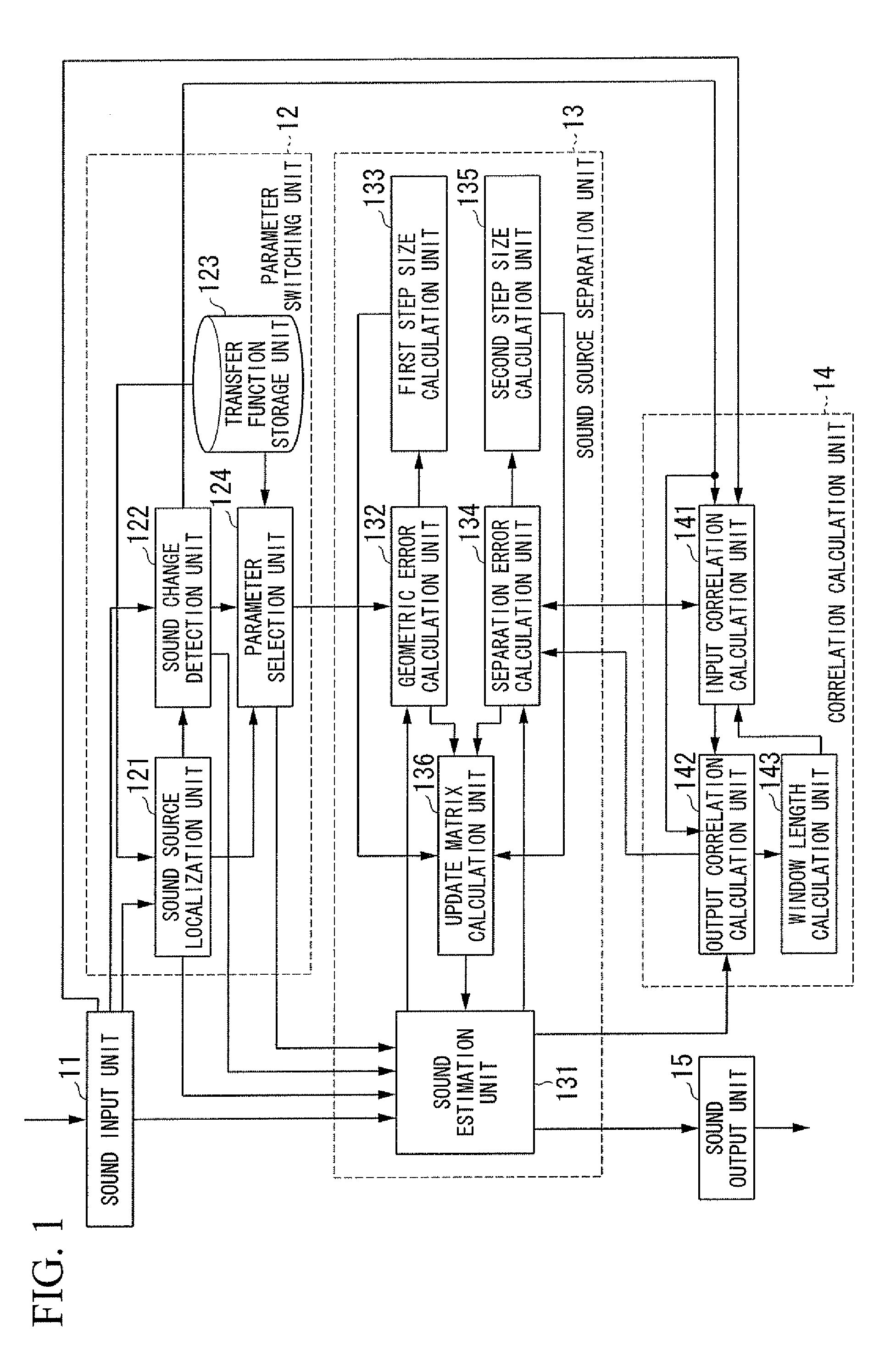
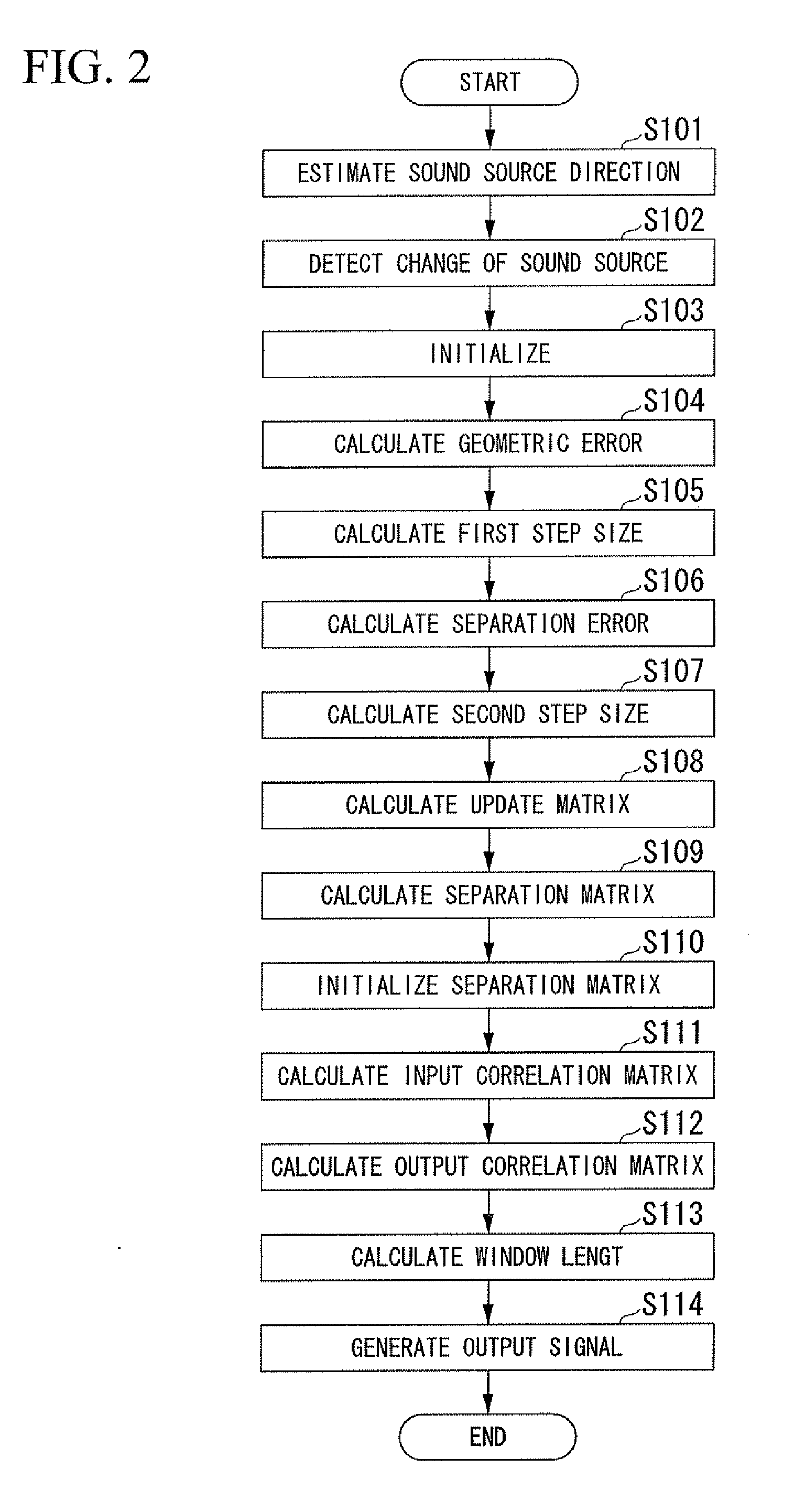
A sound source separation apparatus includes a transfer function storage unit that stores a transfer function from a sound source, a sound change detection unit that generates change state information indicating a change of the sound source on the basis of an input signal input from a sound input unit, a parameter selection unit that calculates an initial separation matrix on the basis of the change state information generated by the sound change detection unit, and a sound source separation unit that separates the sound source from the input signal input from the sound input unit using the initial separation matrix calculated by the parameter selection unit.
Owner:HONDA MOTOR CO LTD
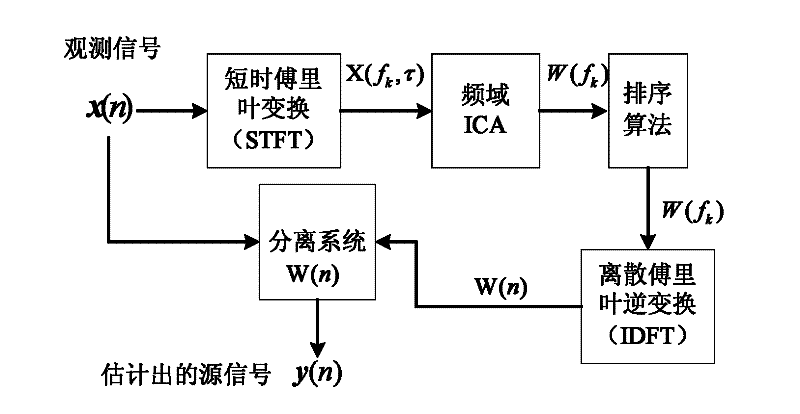
Frequency-domain blind separation sequencing algorithm of convolutive speech signals
InactiveCN102231280AImprove robustnessImprove accuracySpeech recognitionComplex mathematical operationsTime domainSorting algorithm
The invention provides a frequency-domain blind separation sequencing algorithm of convolutive speech signals, and is characterized by comprising the following steps: converting time domains of convolutive overlapping speech signals into frequency domains of the convolutive overlapping speech signals, and using a frequency-domain ICA (independent component analysis) algorithm to carry out blind separation on each frequency band; and carrying out sequencing by using the sequencing algorithm: (1) selecting standard frequency bands to carry out alignment; (2) sequencing remaining frequency bandsin accordance with the sequenced standard frequency bands; and (3) marking frequency bands which generate sequencing errors possibly, and using DOA (direction of arrival) evaluation based on separation matrixes to carry out complementary alignment. In the algorithm, the thoughts on standard frequency band alignment are combined with the advantages of a sequencing algorithm based on frequency bandcoherence and a sequencing algorithm based on the DOA, thus the algorithm provided by the invention has the advantage of good robustness and accuracy and is still applied in real environments.
Owner:SHANDONG UNIV
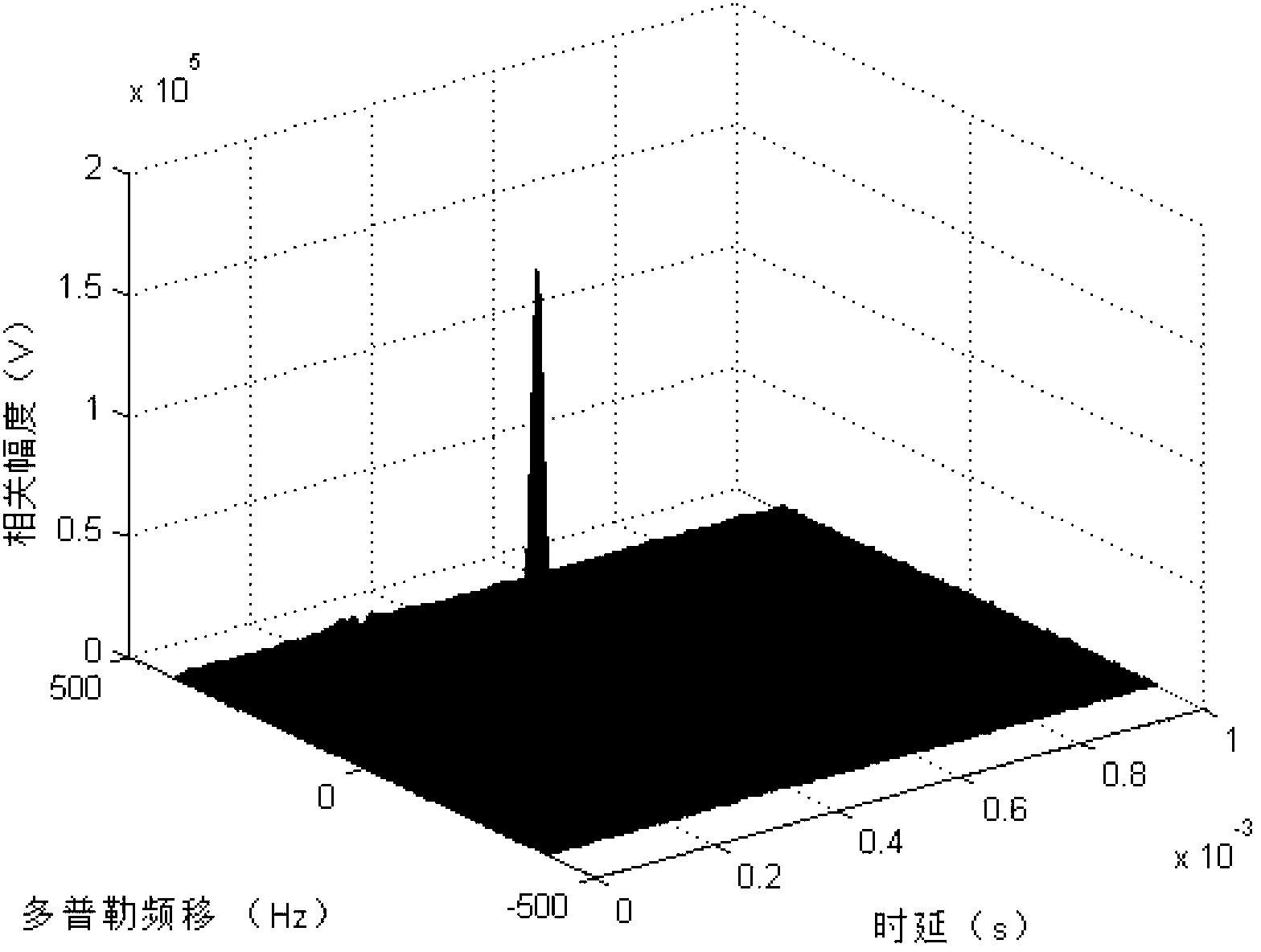
Method for estimating weak signal separation on basis of positioning for external radiation sources
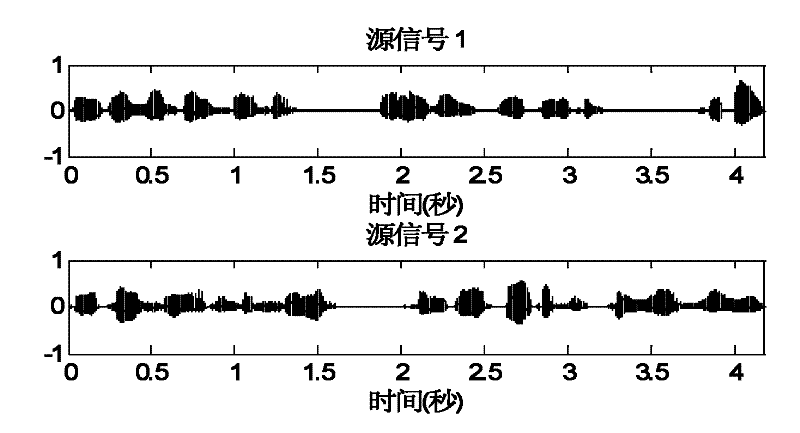
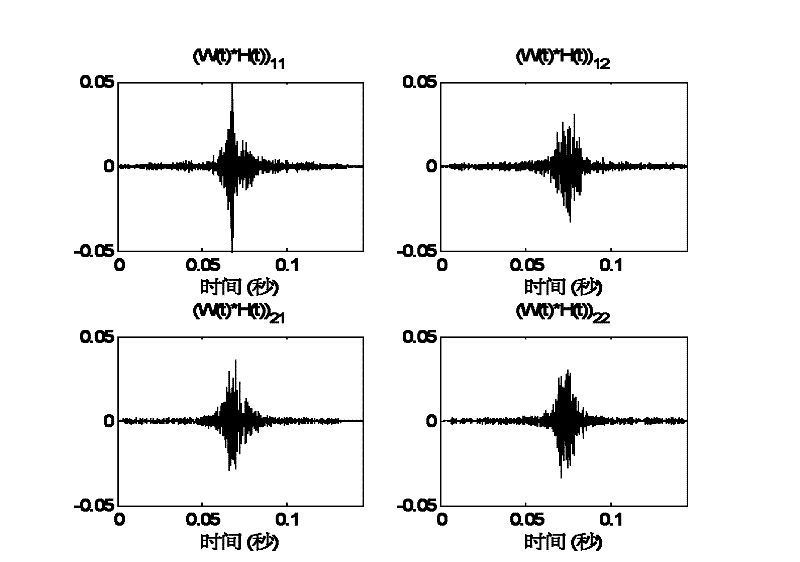
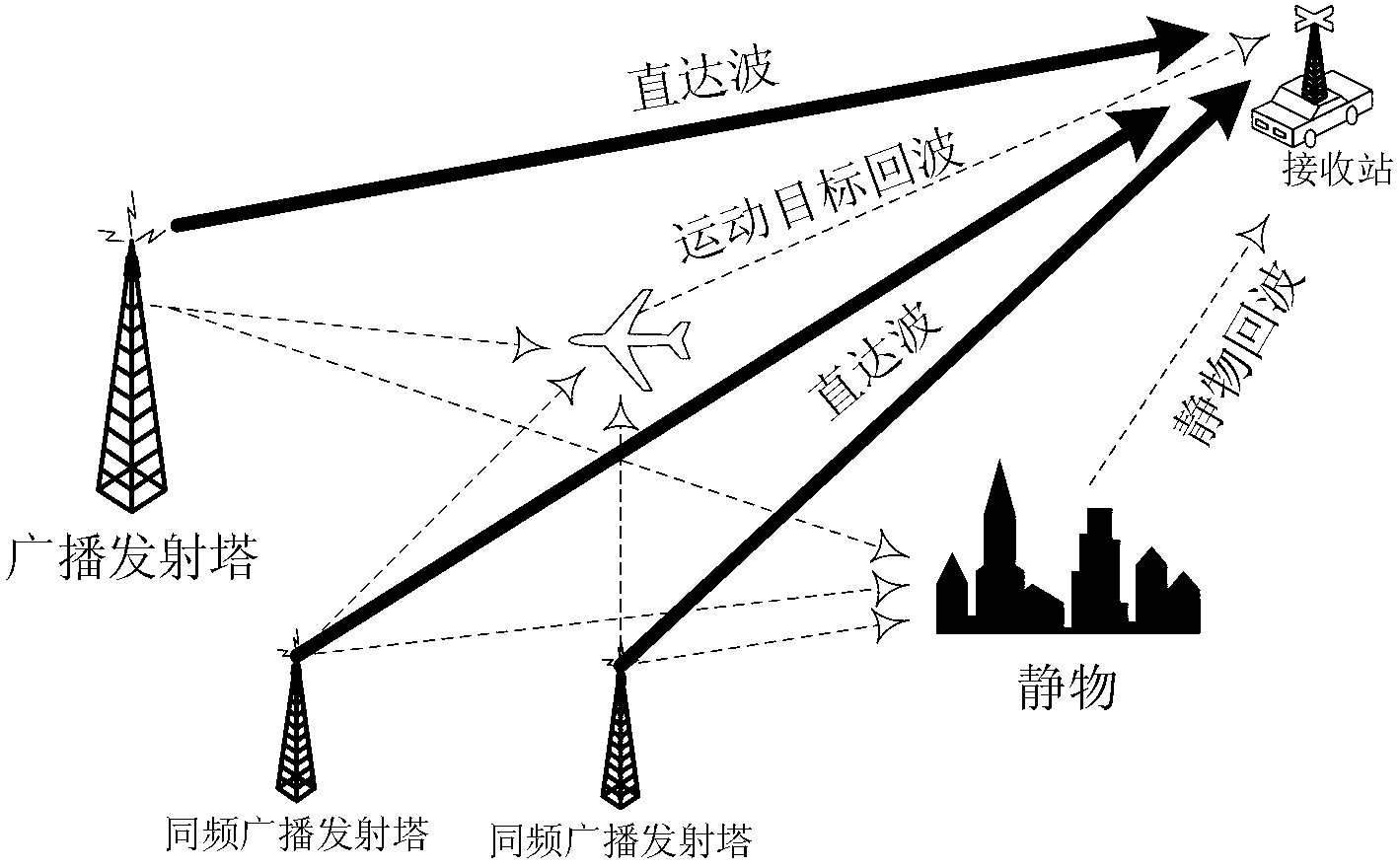
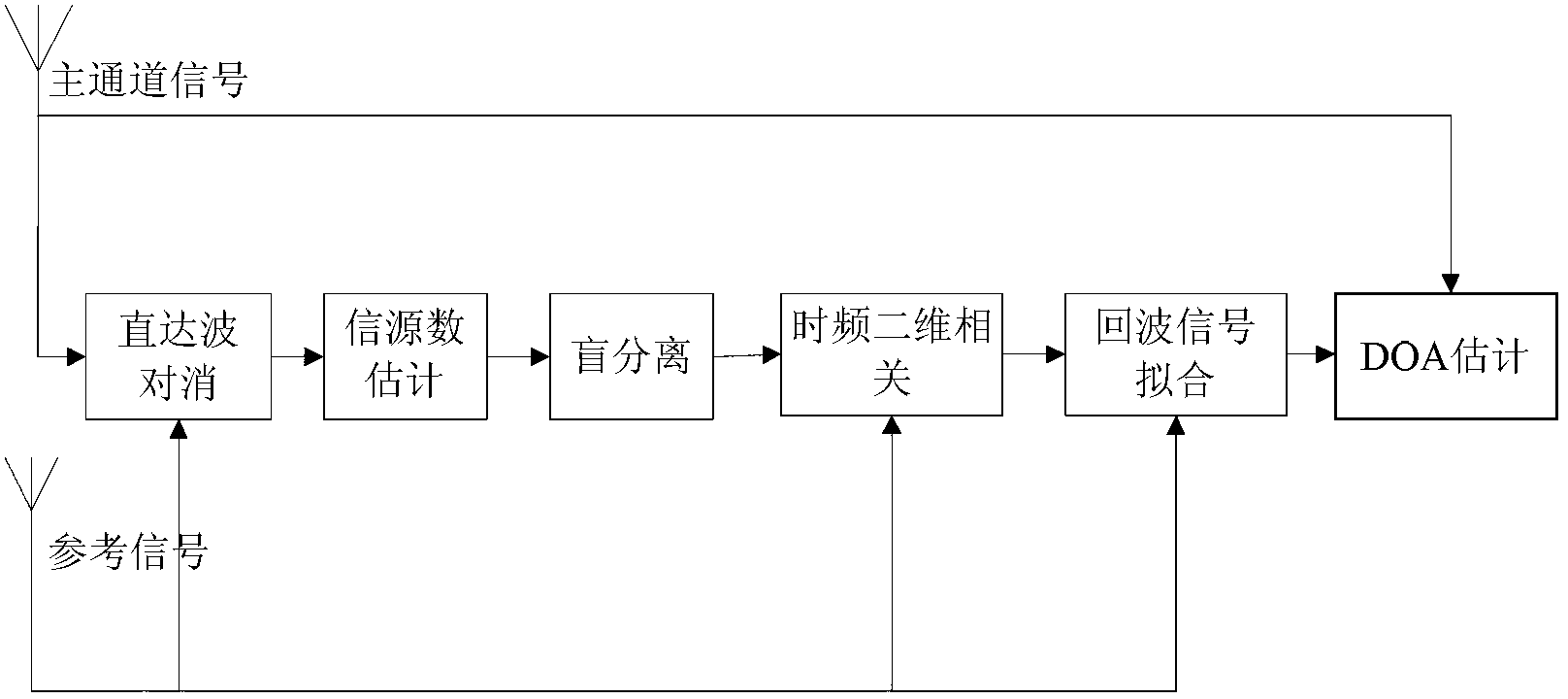
InactiveCN103235294AHelp delayDoppler shiftWave based measurement systemsMain channelSample sequence
The invention provides a method for estimating weak signal separation on the basis of positioning for external radiation sources. The method includes steps of performing direct-wave and multi-path cancellation for a sample sequence x (t) of a main channel by means of NLMS (normalized least mean square) to obtain output signals y<NLMS>(t); estimating the number of source signals of the output signals y<NLMS>(t) by an AIC (Akaike information criterion) or an MDL (minimum description length) criterion, preliminarily whitening the output signals y<NLMS>(t) to obtain whitened signals z(t), and updating a separation matrix W by an ICA (independent component analysis) algorithm to obtain M channels of estimated signals y(t); respectively performing time-frequency two-dimensional correlation for the M channels of estimated signals y<1>(t), ..., y<M>(t) and reference signals s<ref>(t); and searching a peak point in absolute correlation values phi(tau, f) corresponding to the M channels of estimated signals, and determining time delay and Doppler frequency shift which correspond to the peak point as time delay and Doppler frequency shift of a target when a signal-to-noise ratio of a certain channel of signals is larger than or equal to a threshold value.
Owner:UNIV OF ELECTRONICS SCI & TECH OF CHINA
Multiple stationary phase matrix and uses thereof
InactiveUS20120226054A1Electrolysis componentsIon-exchanger regenerationDiagnostic Radiology ModalityStationary phase
The present invention generally provides a separation matrix comprising at least two stationary phases and a stationary phase comprising at least one chiral modality and at least one achiral modality. Also provided are methods of using the separation matrix or the stationary phase to separate enantiomers of one or more chiral molecules.
Owner:BIOVENTURES LLC
Regeneration Of A Chromatography Matrix
InactiveUS20080230478A1Back pressureLower regenerationIon-exchange process apparatusIon-exchanger regenerationElutionReducing agent
The present invention relates to a process of regenerating a separation matrix, such as a chromatography matrix, comprising adsorption of at least one target molecule by contacting a mobile phase comprising at target molecule(s) with a matrix; removal of unbound material by washing the matrix; elution of target molecule(s) by contacting the matrix with an eluent; reducing regeneration by contacting said matrix with a reducing agent; alkaline regeneration by contacting the matrix with an alkaline solution; and equilibration of the matrix.
Owner:GE HEALTHCARE BIO SCI CORP
Adaptive voice separating method based on sound source positioning
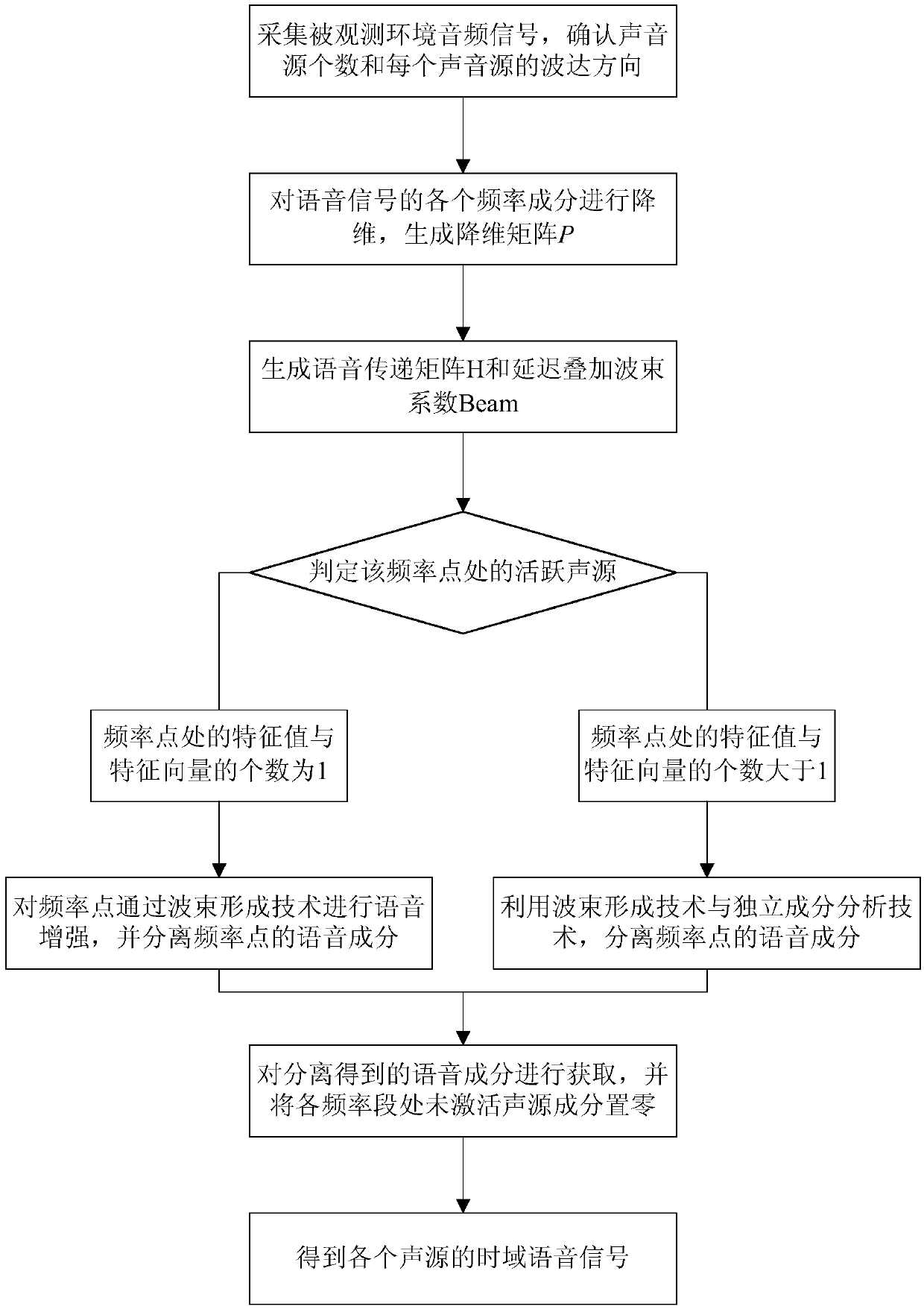
ActiveCN108986838AImprove signal-to-noise ratioImprove featuresSpeech analysisInformation processingSound sources
The invention provides an adaptive voice separating method based on sound source positioning, and relates to the technical field of information processing. The method includes steps: acquiring an audio signal of an observed environment, and confirming the number of sound sources and the direction of arrival of each sound source; generating a dimension reduction matrix P; generating a voice transfer matrix and a delay superposed wave beam coefficient; determining an active sound source of a frequency point and separating voice components; obtaining the obtained voice components and setting non-activated sound source components as zero; and obtaining time domain voice signals of the sound sources. According to the method, the number and the orientation of the sound sources in a current environment can be obtained through a sound source positioning technology, dimension reduction of each frequency band of the voice signal is performed with the cooperation of a PCA whitening technology toobtain an initial separation matrix, frequency components of each sound source channel are separated through the number of the activated sound sources at the frequency point by adaptive usage of the beam forming technology and the FDICA technology to restore the voice components, the obtained signal-to-noise ratio improvement characteristic is higher, better noise suppression performance is achieved, and the method is applicable to any sound source situations in the real voice environment.
Owner:NORTHEASTERN UNIV
Method of preparing a separation matrix
ActiveUS8309709B2Increase pressureReduce usageOrganic active ingredientsBiocideCross-linkAqueous solution
The present invention relates to a method of preparing an insoluble separation matrix, which method comprises salt-treatment of a polysaccharide gel followed by cross-linking of the polysaccharide polymers. In one embodiment, the method comprises providing an aqueous solution of a gelatable native polysaccharide; lowering the temperature of the polysaccharide solution to a value below its gelling point; salt-treatment by adding at least one salt to the resulting polysaccharide; and cross-linking the salt-treated polysaccharide. The polysaccharide may be prepared e.g. into particles, membranes or monoliths.Owner:CYTIVA BIOPROCESS R&D AB
Blind source separation method
InactiveCN105404783AEasy to fall into local optimal solutionSolve the premature convergence problemBiological modelsSpecial data processing applicationsLocal optimumTheoretical computer science
The present invention provides a blind source separation method, and belongs to the technical field of signal processing. The method comprises three steps of: blind source problem problem modeling, fitness evaluation, and separation matrix solving. According to the blind source separation method provided by the present invention, a parameter-adaptive particle swarm algorithm is adopted, and chaotic iteration and a cloud model are introduced into the particle swarm algorithm, so that a particle swarm alternate between chaos and stability and gets close to an optimal solution, thereby effectively solving problems that solving a separation matrix in a blind source separation problem is prone to fall into a local optimum solution and a premature convergence problem, greatly reducing a search time, and reducing time complexity of the blind source separation.
Owner:JILIN UNIV
Who we serve
- R&D Engineer
- R&D Manager
- IP Professional
Why Eureka
- Industry Leading Data Capabilities
- Powerful AI technology
- Patent DNA Extraction
Social media
Try Eureka
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic.
© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap