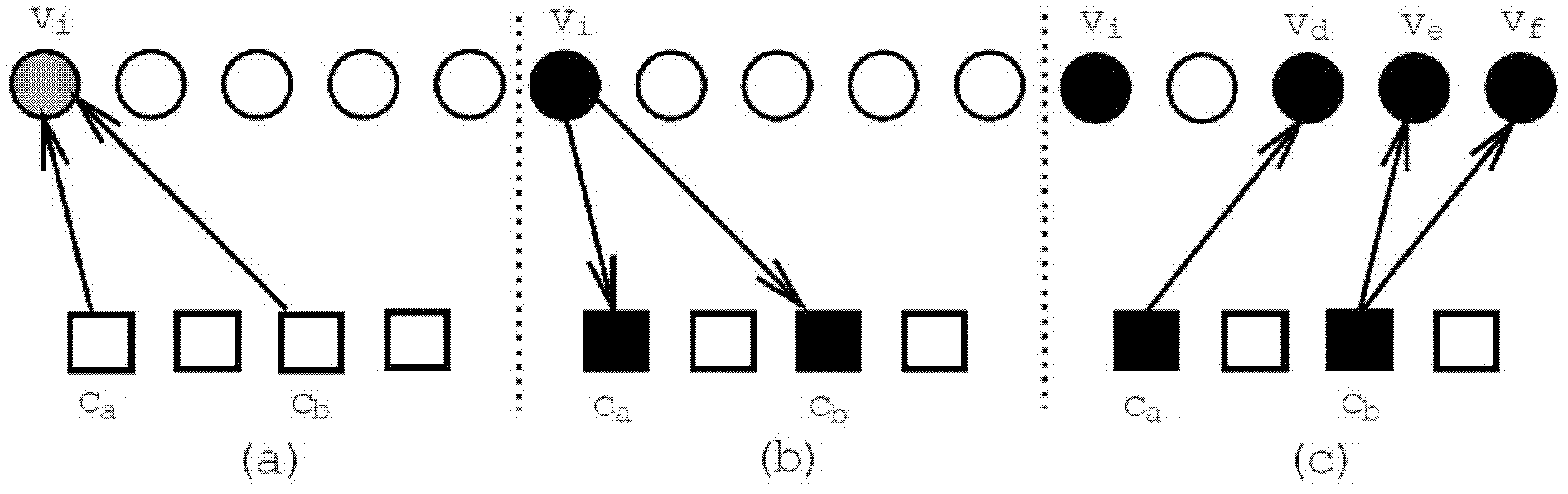
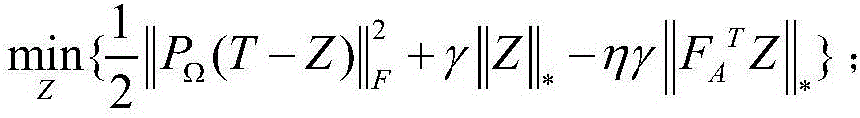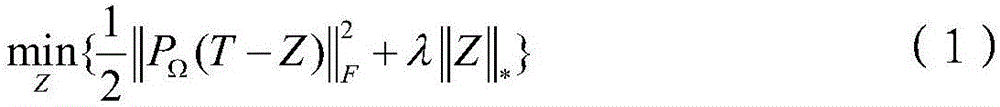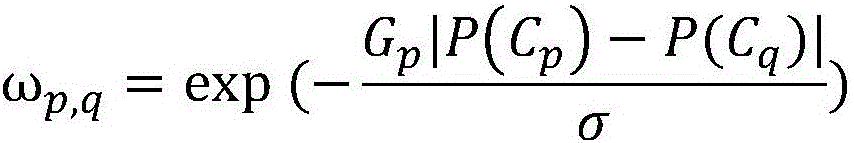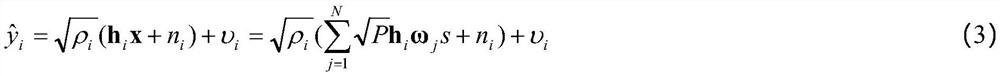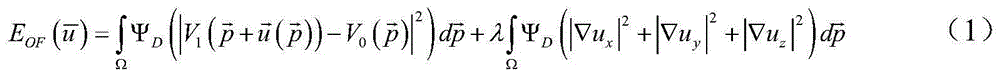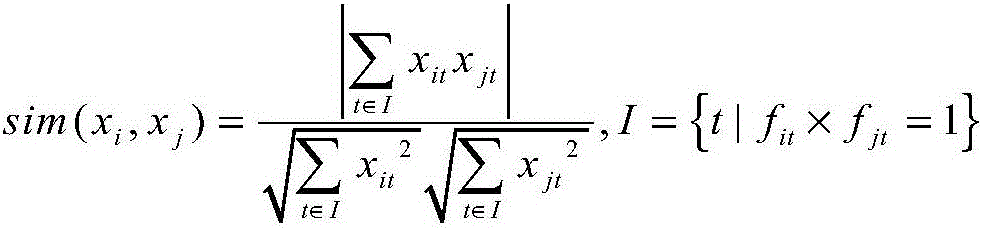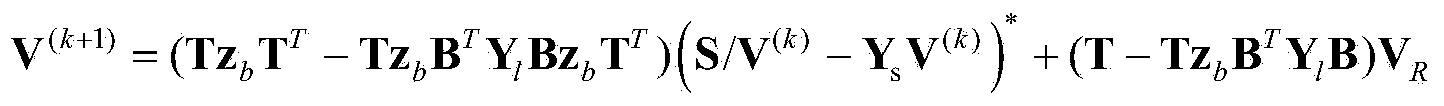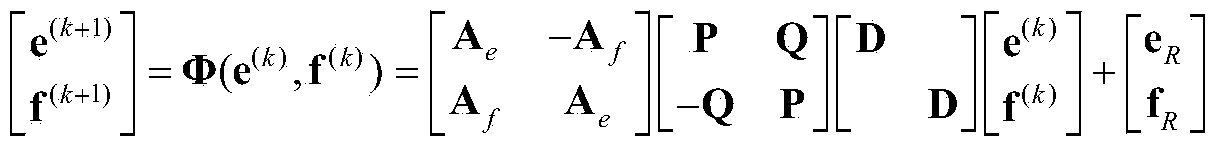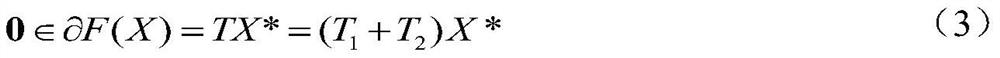Patents
Literature
56 results about "Fixed-point iteration" patented technology
Efficacy Topic
Property
Owner
Technical Advancement
Application Domain
Technology Topic
Technology Field Word
Patent Country/Region
Patent Type
Patent Status
Application Year
Inventor
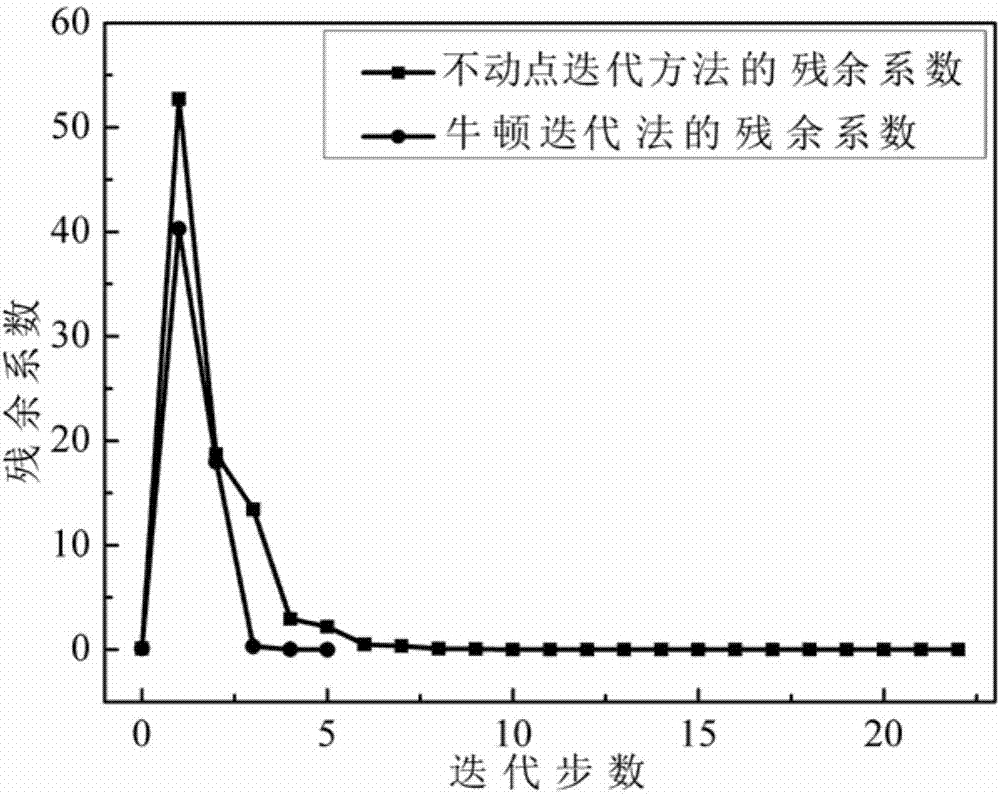
In numerical analysis, fixed-point iteration is a method of computing fixed points of iterated functions. More specifically, given a function f defined on the real numbers with real values and given a point x₀ in the domain of f, the fixed point iteration is xₙ₊₁=f(xₙ), n=0,1,2,… which gives rise to the sequence x₀,x₁,x₂,… which is hoped to converge to a point x. If f is continuous, then one can prove that the obtained x is a fixed point of f, i.e., f(x)=x.
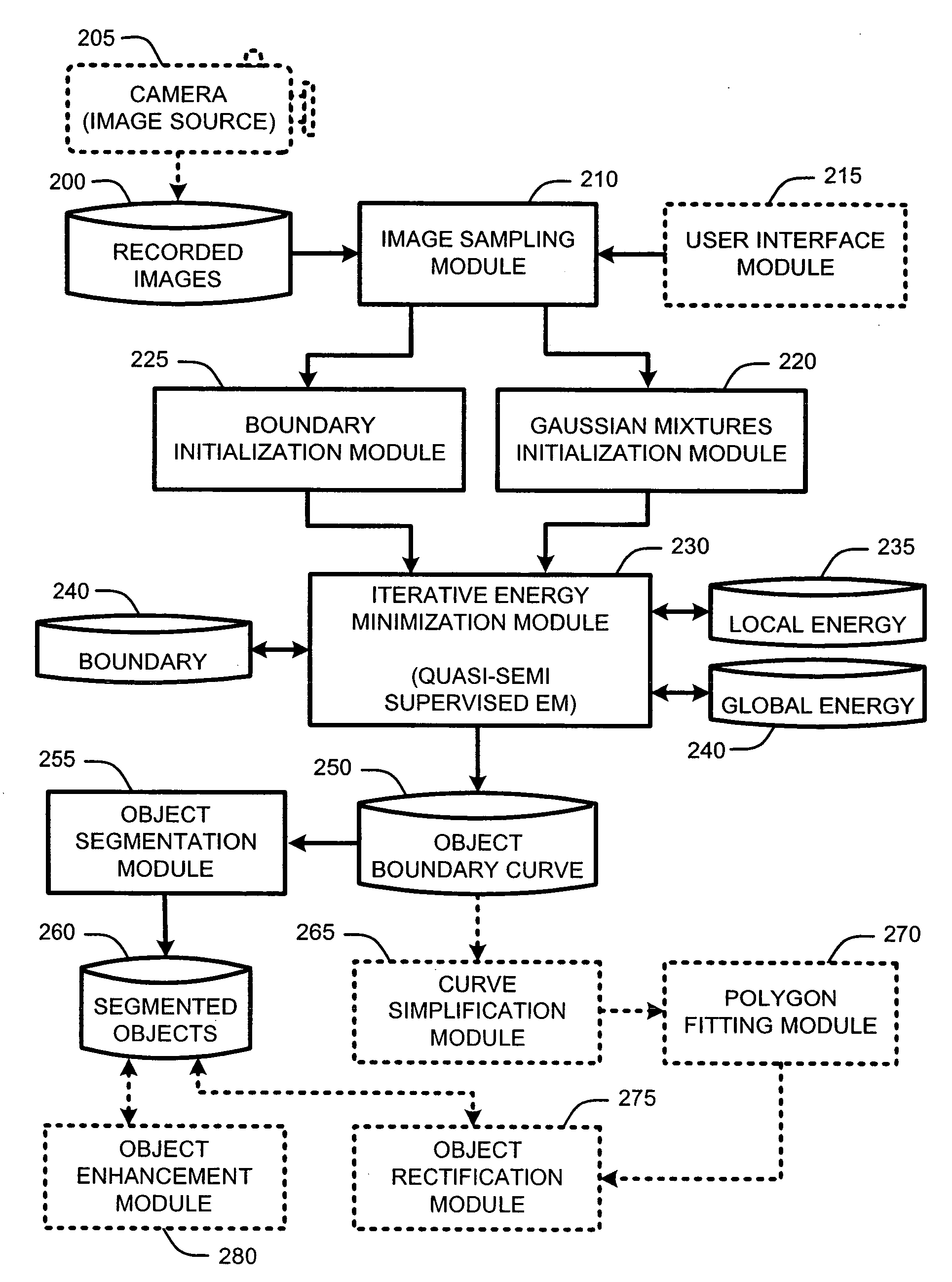
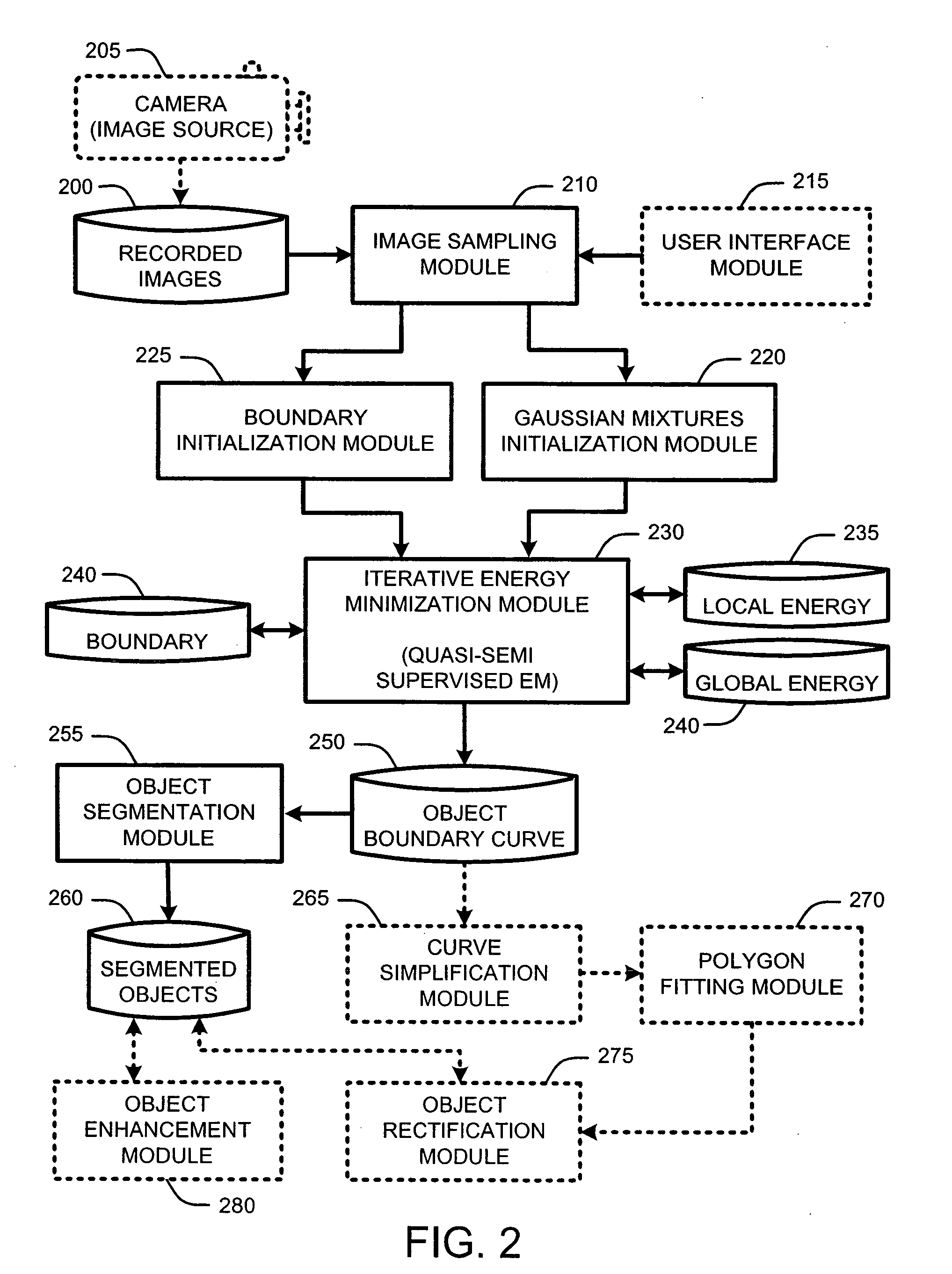
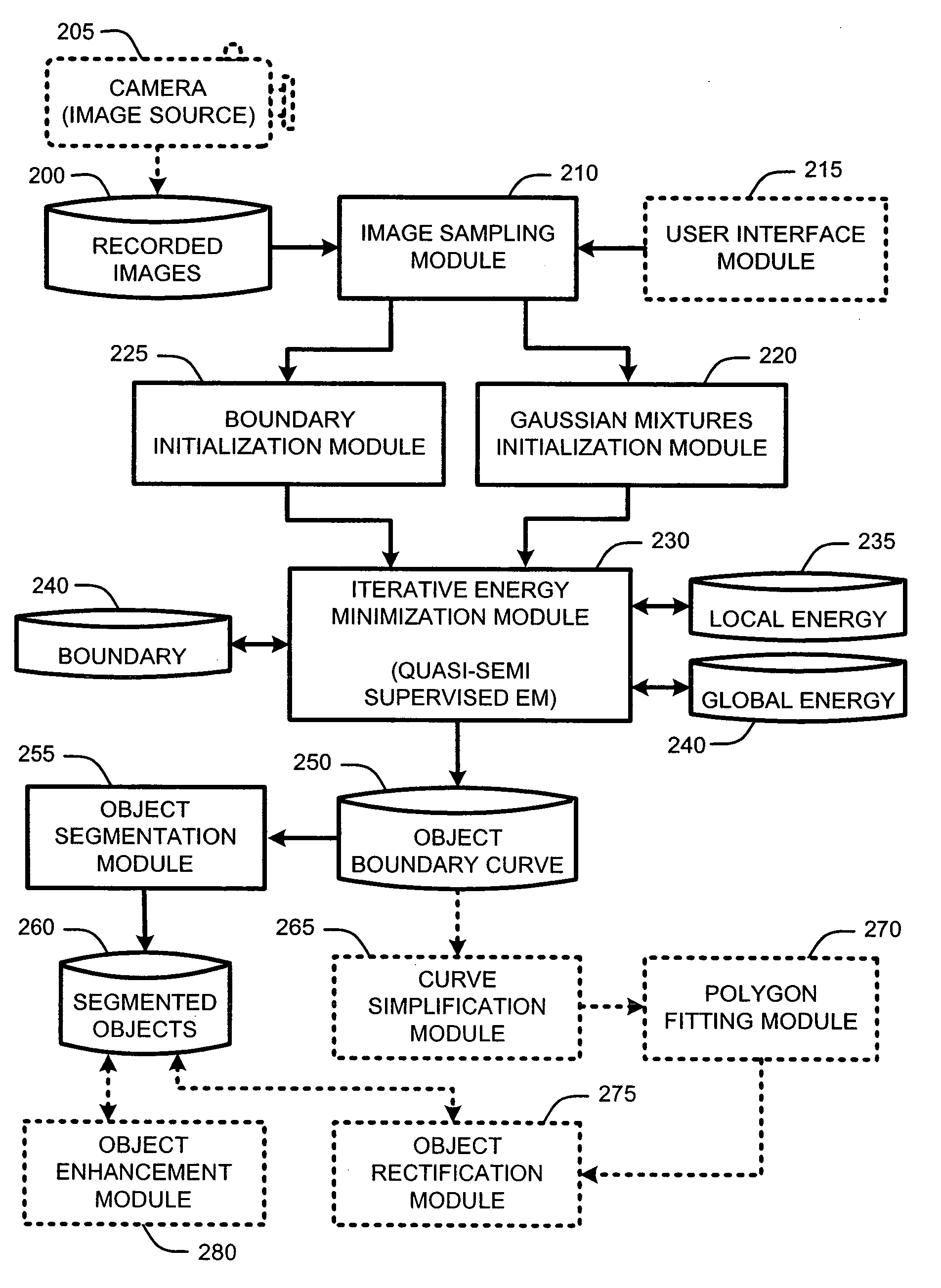
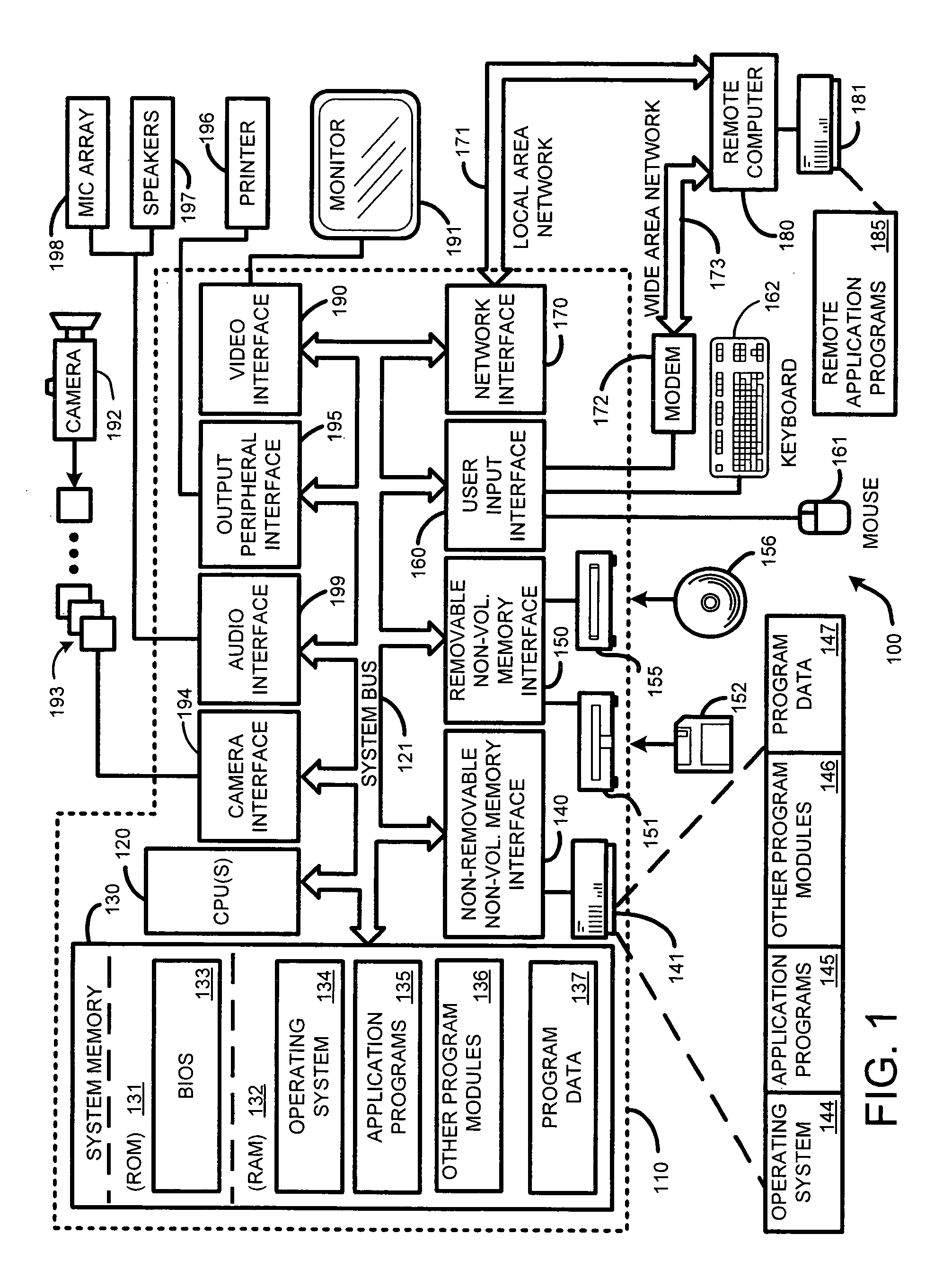
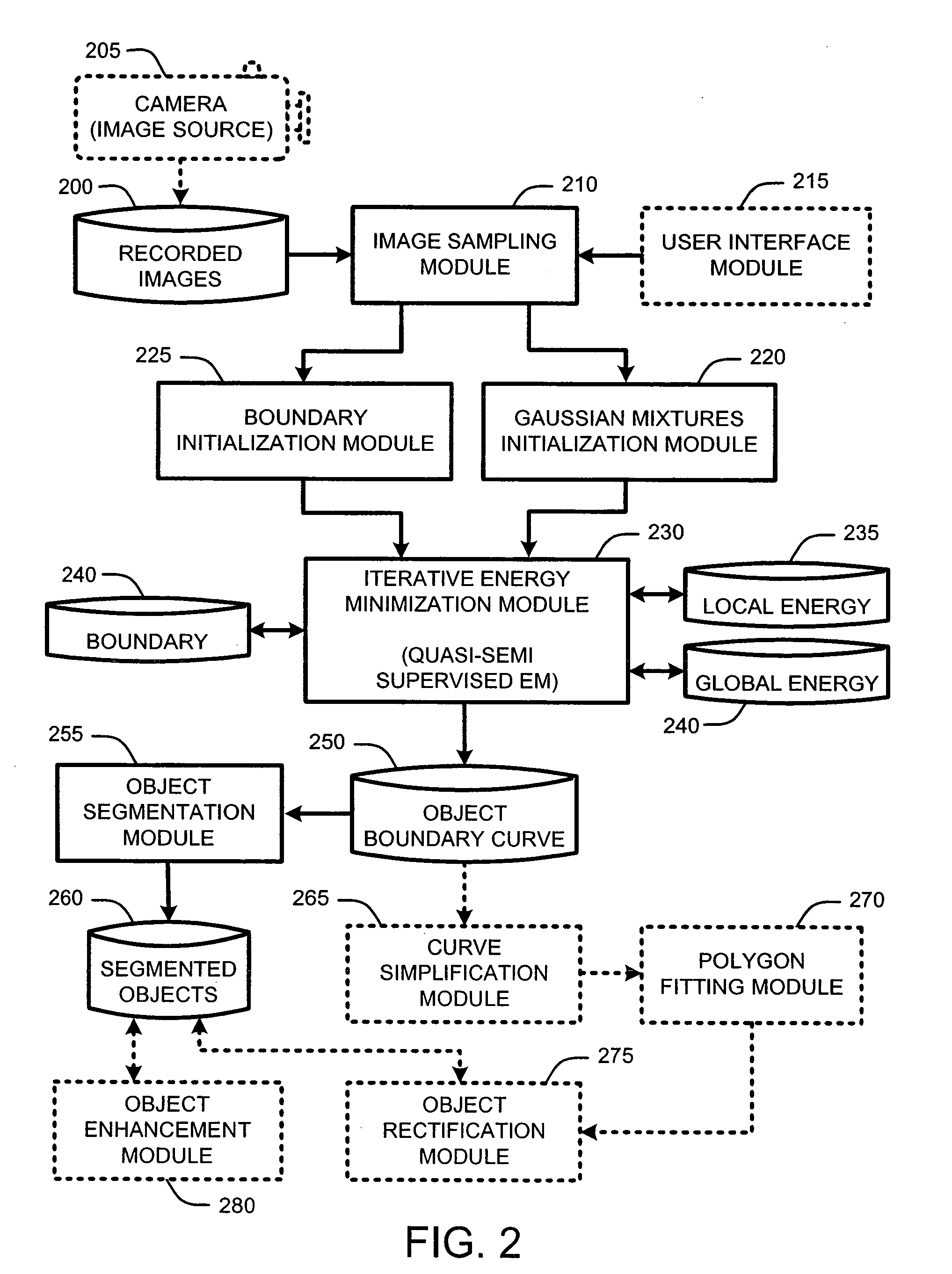
Segmentation of objects by minimizing global-local variational energy
InactiveUS20070122039A1Robust accurate estimationImage enhancementImage analysisImage segmentationBackground distribution
Owner:MICROSOFT TECH LICENSING LLC
Segmentation of objects by minimizing global-local variational energy
InactiveUS7706610B2Robust accurate estimationImage enhancementImage analysisImage segmentationBackground distribution
An “Image Segmenter” provides a variational energy formulation for segmentation of natural objects from images. In general, the Image Segmenter operates by adopting Gaussian mixture models (GMM) to capture the appearance variation of objects in one or more images. A global image data likelihood potential is then computed and combined with local region potentials to obtain a robust and accurate estimation of pixel foreground and background distributions. Iterative minimization of a “global-local energy function” is then accomplished by evolution of a foreground / background boundary curve by level set, and estimation of a foreground / background model by fixed-point iteration, termed “quasi-semi-supervised EM.” In various embodiments, this process is further improved by providing general object shape information for use in rectifying objects segmented from the image.
Owner:MICROSOFT TECH LICENSING LLC
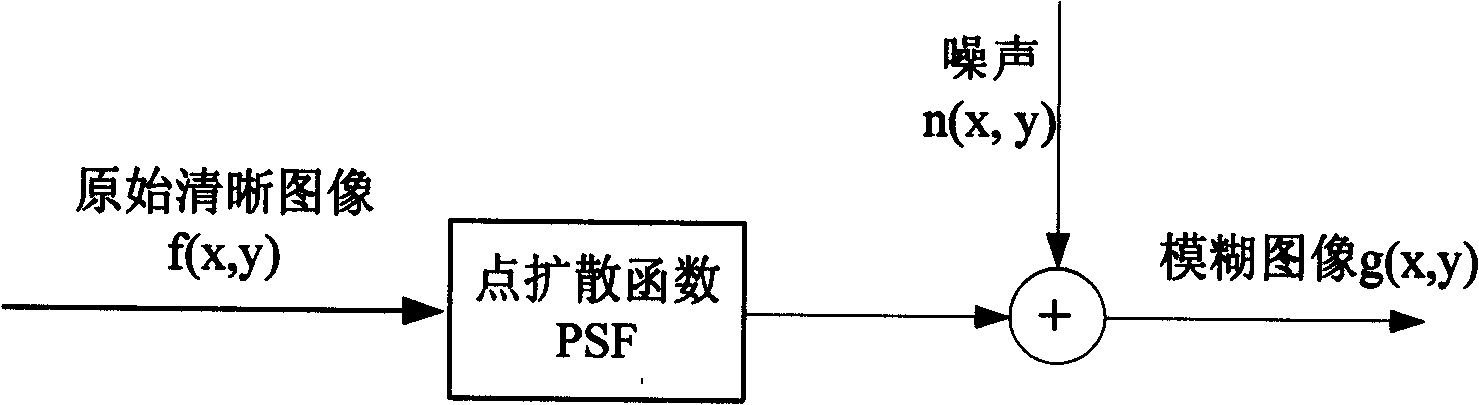
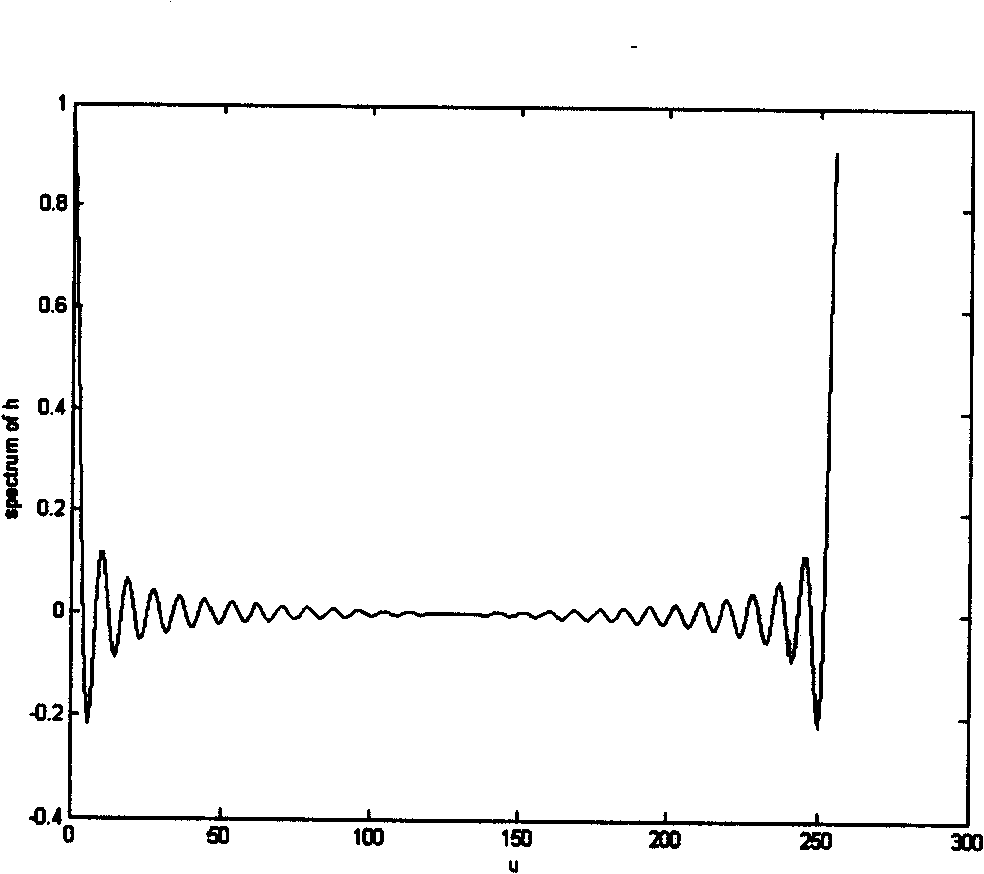
Blind restoration method for moving blurred image
InactiveCN101359398AImprove clarityOvercoming blurry smearing problemsImage enhancementComputer graphics (images)Inner loop
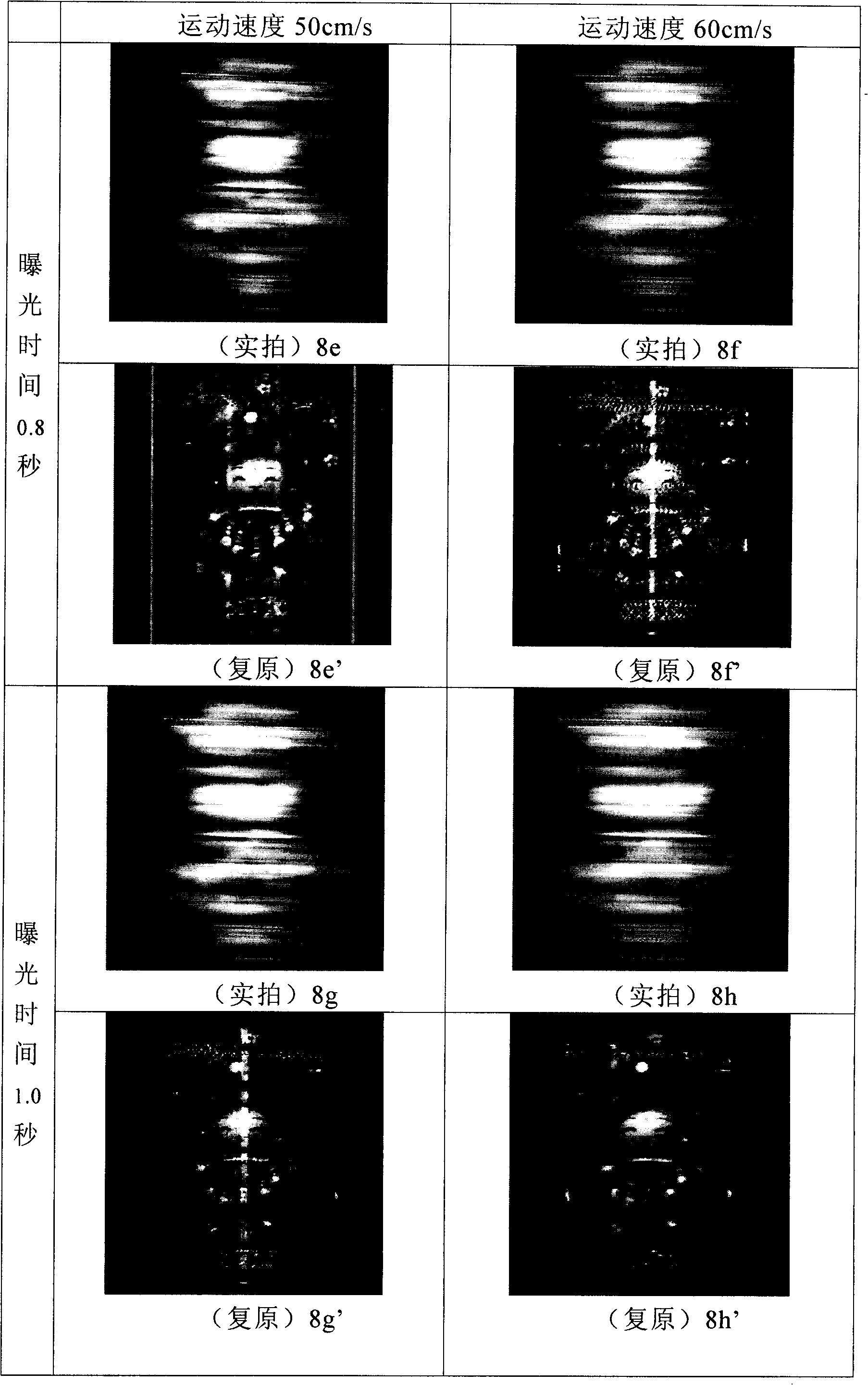
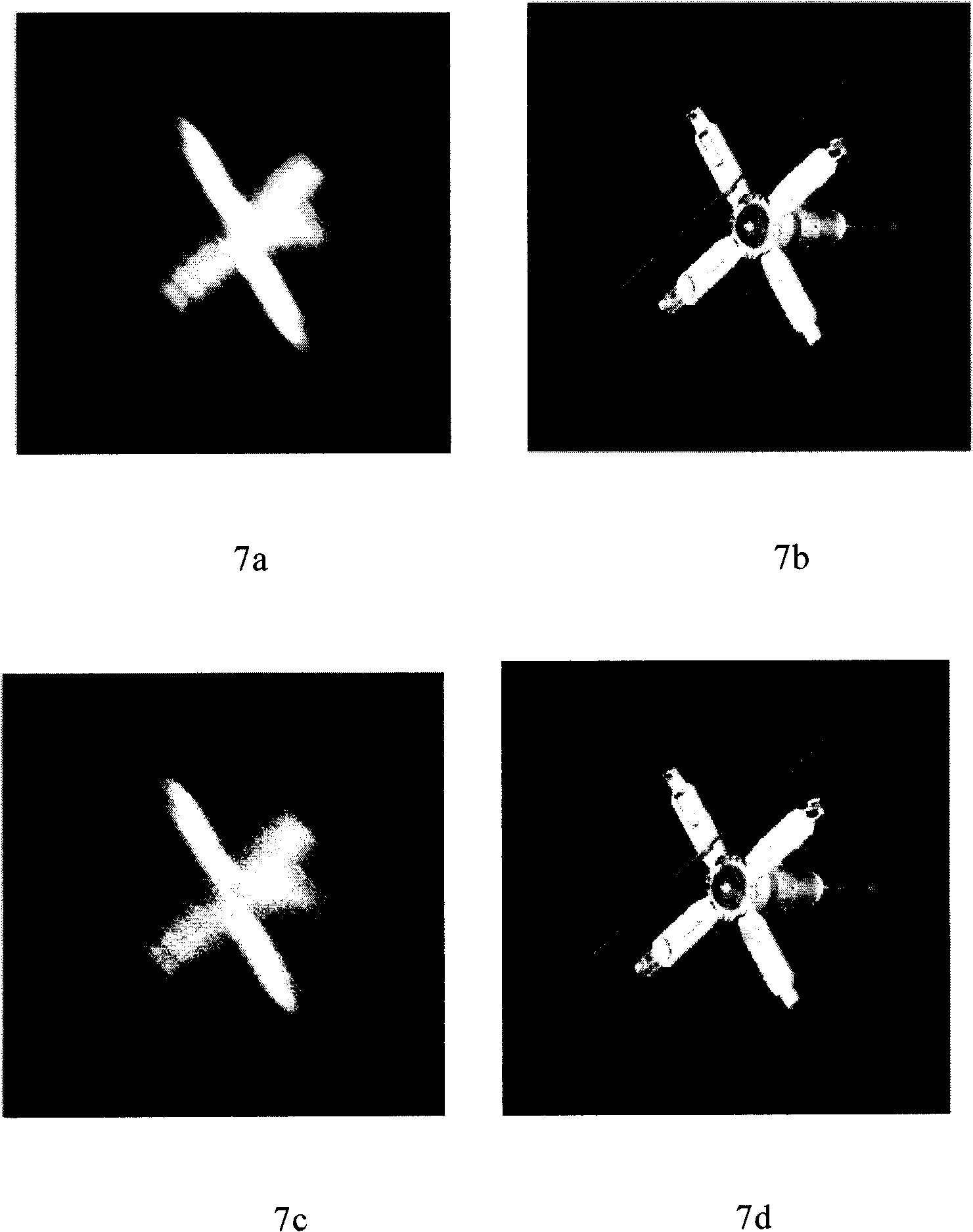
Disclosed is a blind restoration method for the motion blurred image; the steps are as follows: (1) the image is converted through the cepstrum method to figure out the blur extent and the blur direction of the blurred image; (2) the blur extent and the blur direction of the blurred image figured out in step (1), and the total variation (TV) method are adopted to process the restoration towards the blurred image. The method based on the total variation (TV) includes: the fixed-point iteration used as the outer-loop and the conjugate gradient method used as the inner-loop are adopted for loop iteration to obtain the restored image. The blind restoration method has the advantages of strong self-adaptation, strong anti-noise ability and good robustness; the blind restoration method has validity and practicality according to the processing effects of the simulation picture and the photographed picture.
Owner:BEIHANG UNIV
System and method for the automatic verification of privilege-asserting and subject-executed code
InactiveUS8006233B2Reverse engineeringPlatform integrity maintainanceTheoretical computer scienceFixed-point iteration
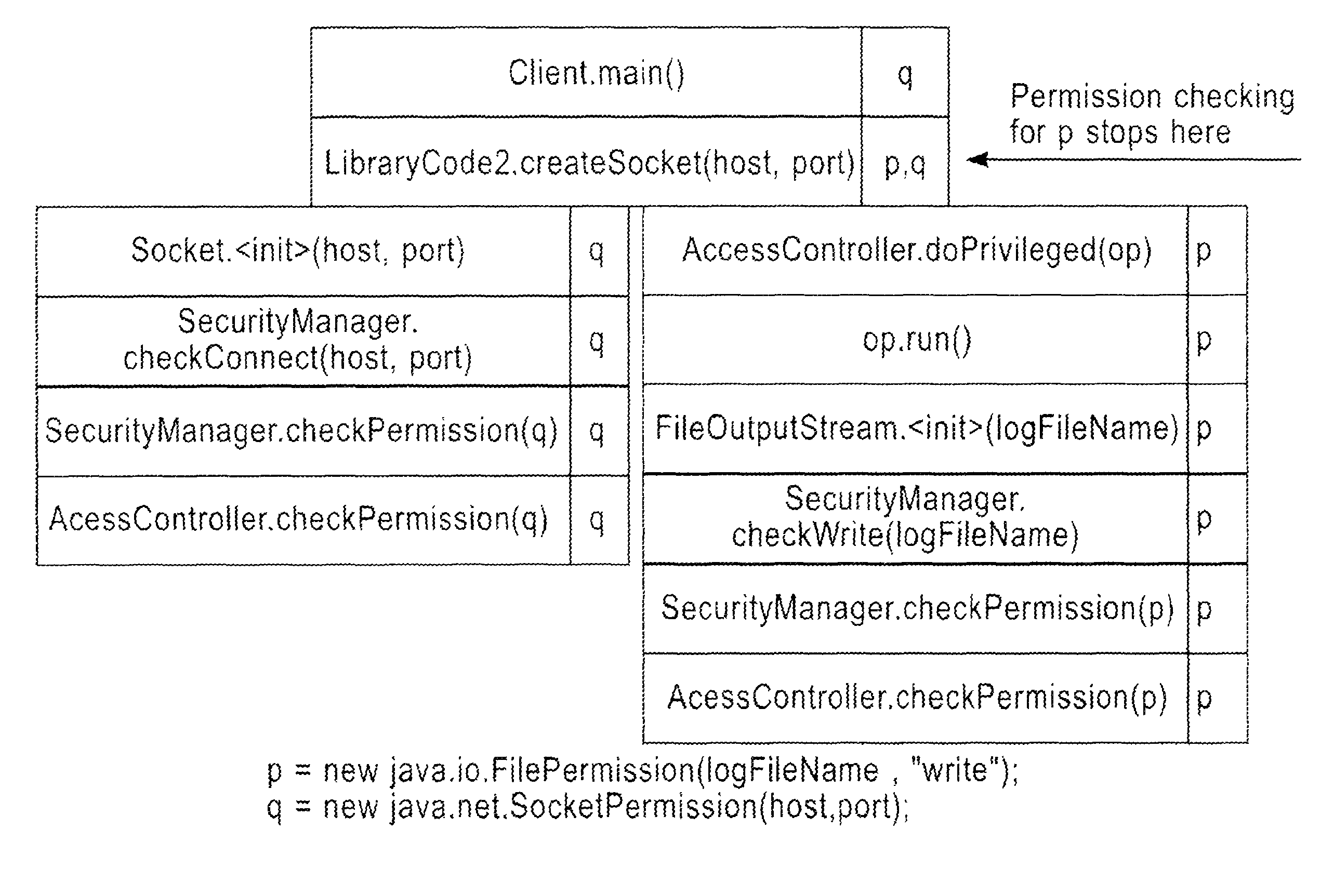
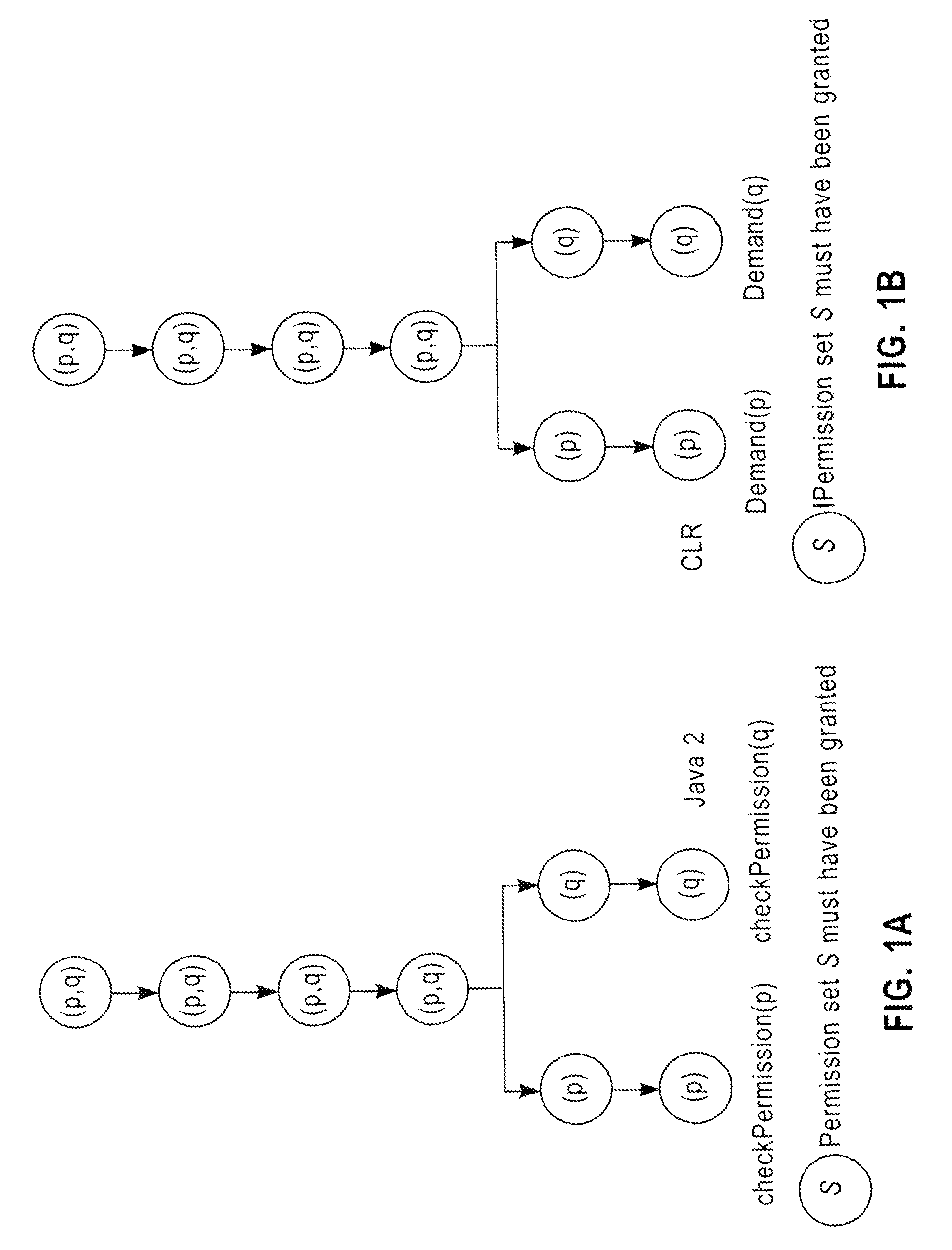
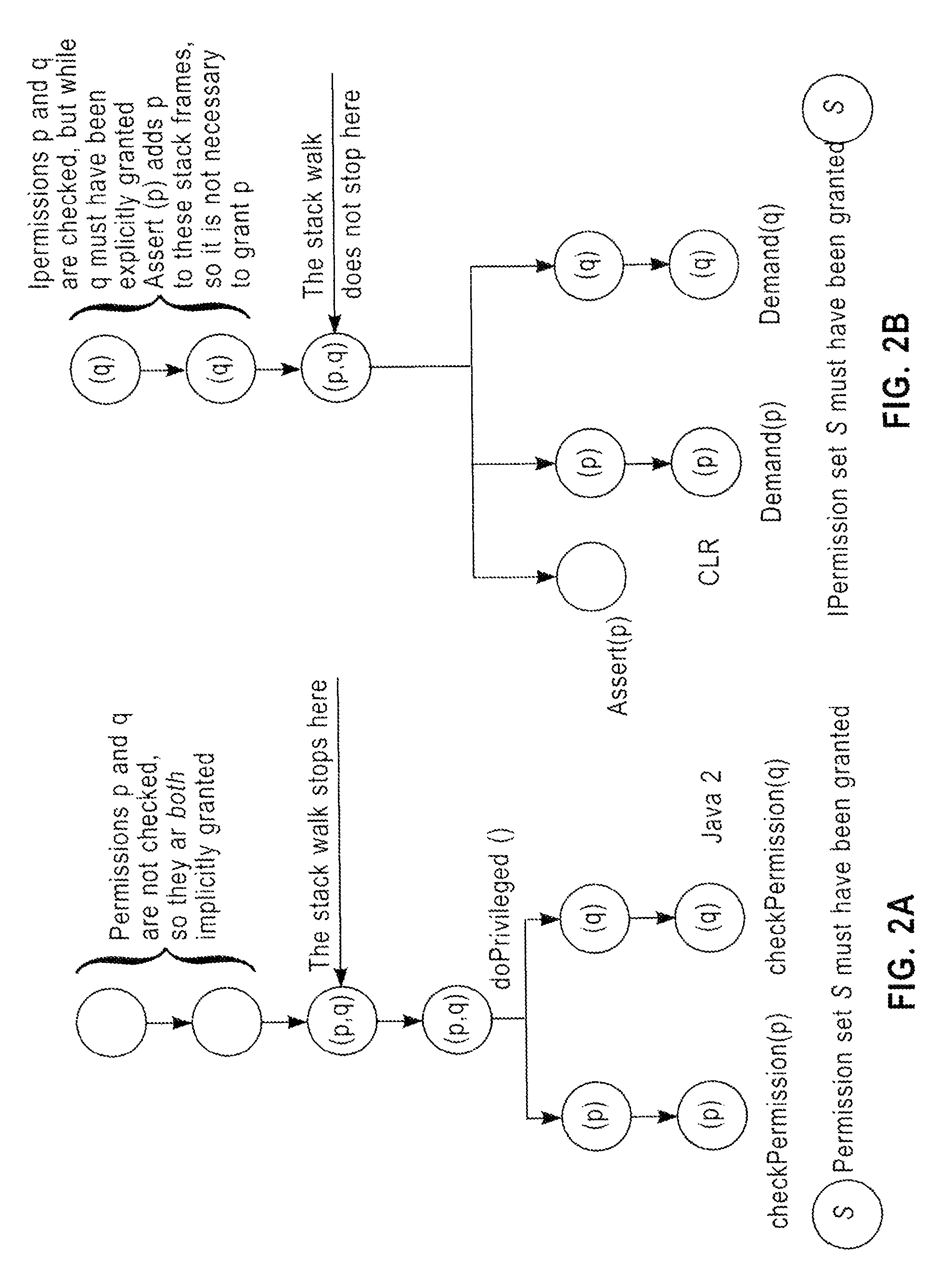
The present relates to a method for verifying privileged and subject-executed code within a program, the method further comprising the steps of constructing a static model of a program, identifying checkPermission nodes that are comprised within the invocation graph, and performing a fixed-point iteration, wherein each determined permission set is propagated backwards across the nodes of the static model until a privilege-asserting code node is reached. The method further comprises the steps of associating each node of the invocation graph with a set of Permission allocation sites, analyzing each identified privilege-asserting code node and subject-executing code node to determine the Permission allocation site set that is associated with each privilege-asserting code node and subject-executing code node, and determining the cardinality of a Permission allocation-site set that is associated with each privilege-asserting code node and subject-executing code node.
Owner:INT BUSINESS MASCH CORP
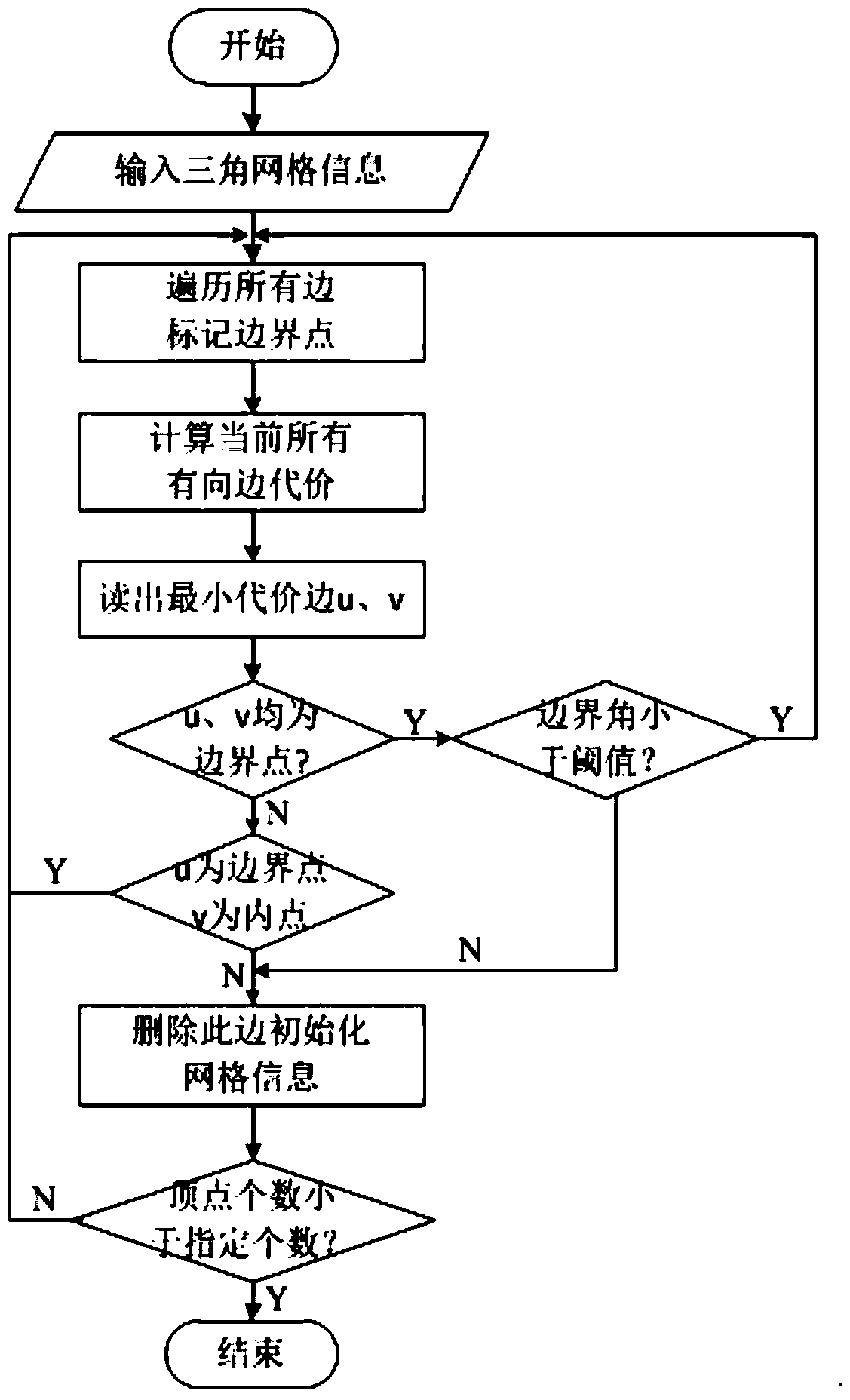
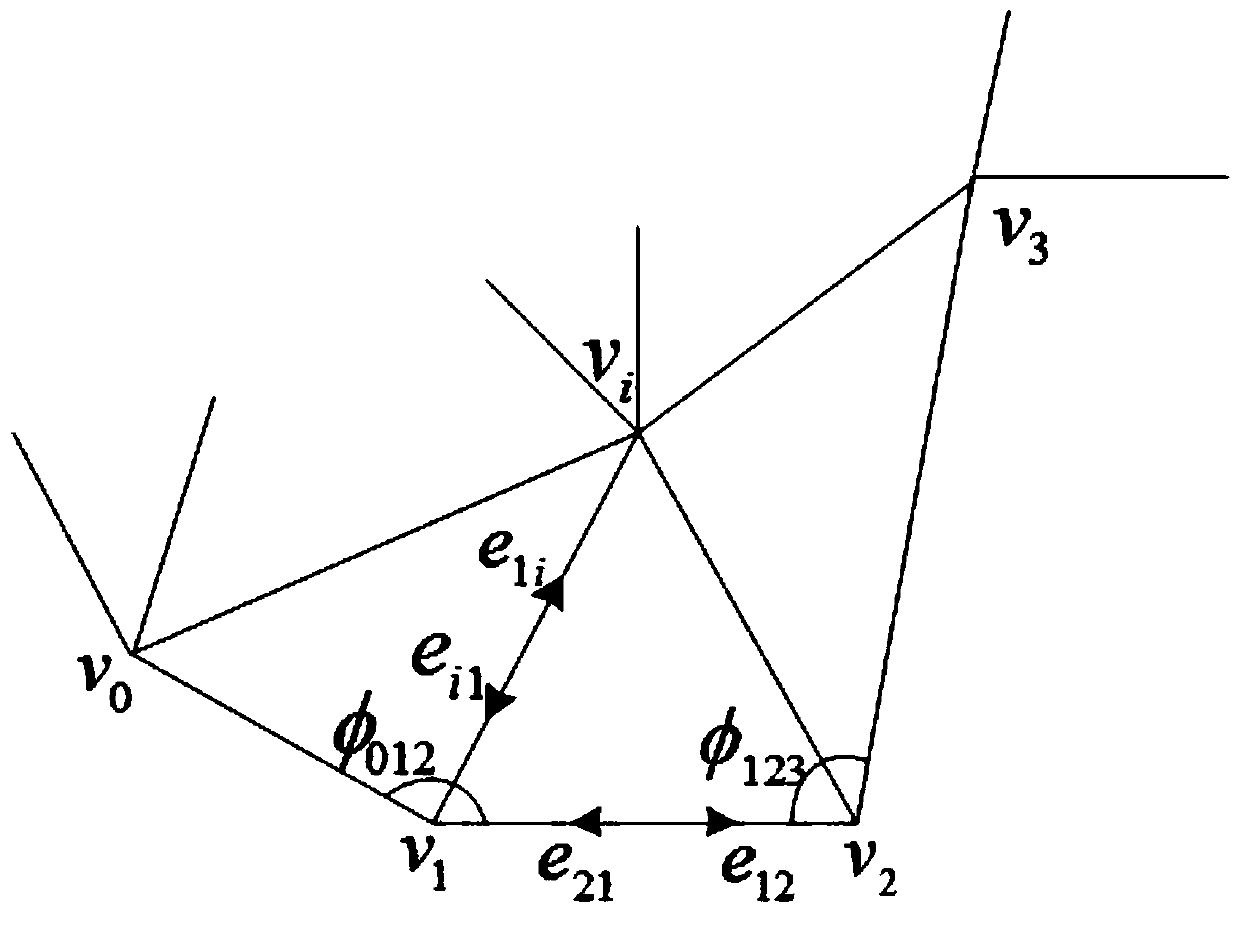
Texture mapping method based on triangular mesh simplification
InactiveCN104680573AReduce time complexityImprove timing performance3D-image rendering3D modellingPattern recognitionImaging processing
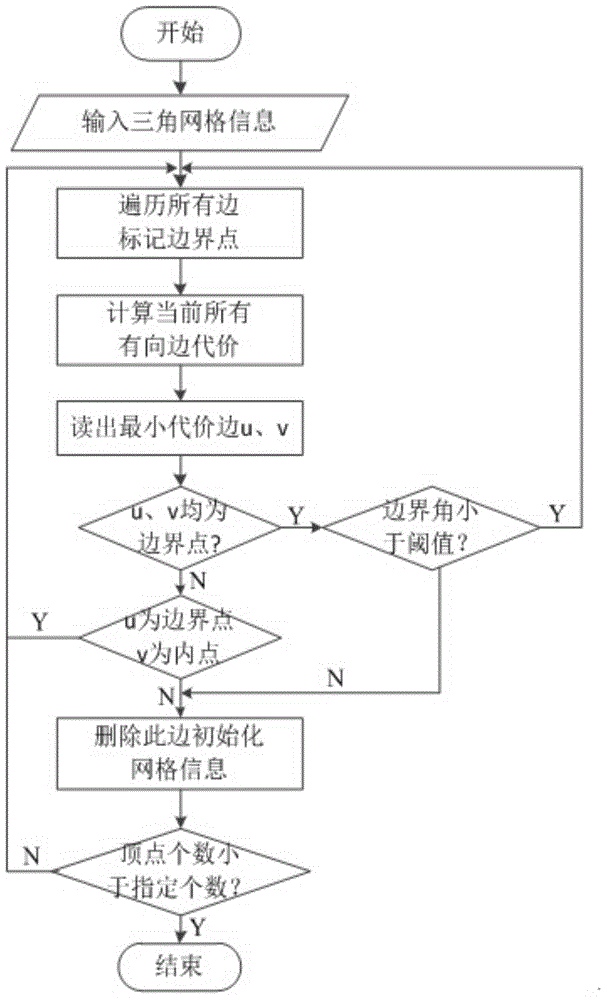
The invention belongs to the technical field of image processing and particularly relates to a texture mapping method based on triangular mesh simplification. The texture mapping method comprises the following steps: simplifying a triangular network model and establishing a spring-mass-point model; parameterizing the spring-mass-point model to a final position of a rectangular region; by utilizing a process of simplifying the triangular network model, calculating an initial position of a deleted point in the parameterized rectangular region to obtain positions of all vertexes of an initial model in the parameterized rectangular region; parameterizing the initial model to establish the spring-mass-point model; fixing the boundary vertex and triggering inner point iteration until the position of an inner point is balanced to obtain a spring-mass-point model revised parameterized coordinate; and carrying out normalization processing to obtain a texture coordinate of a grid vertex, and carrying out texture mapping. According to the method, the texture coordinate of each triangular network grid vertex does not need to be solved and texture mapping can be directly carried out; the time complexity of the method can be reduced to the great extent and the time performance is improved.
Owner:XIAN UNIV OF SCI & TECH
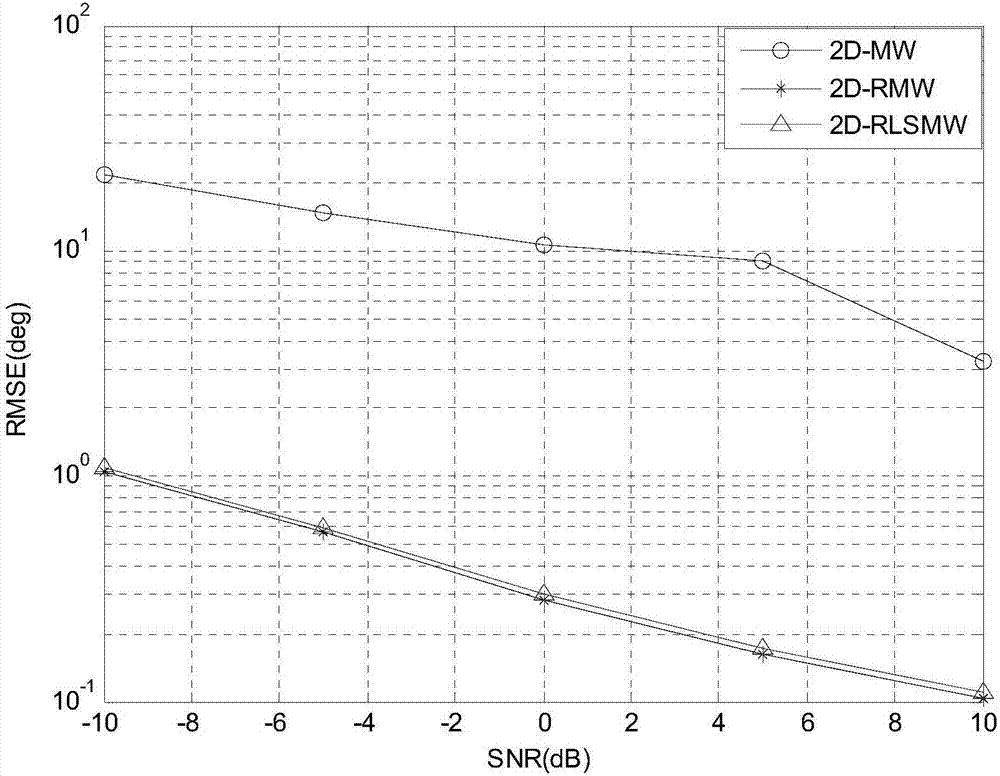
Robust large-array MIMO target transmitting and receiving angle joint estimation method
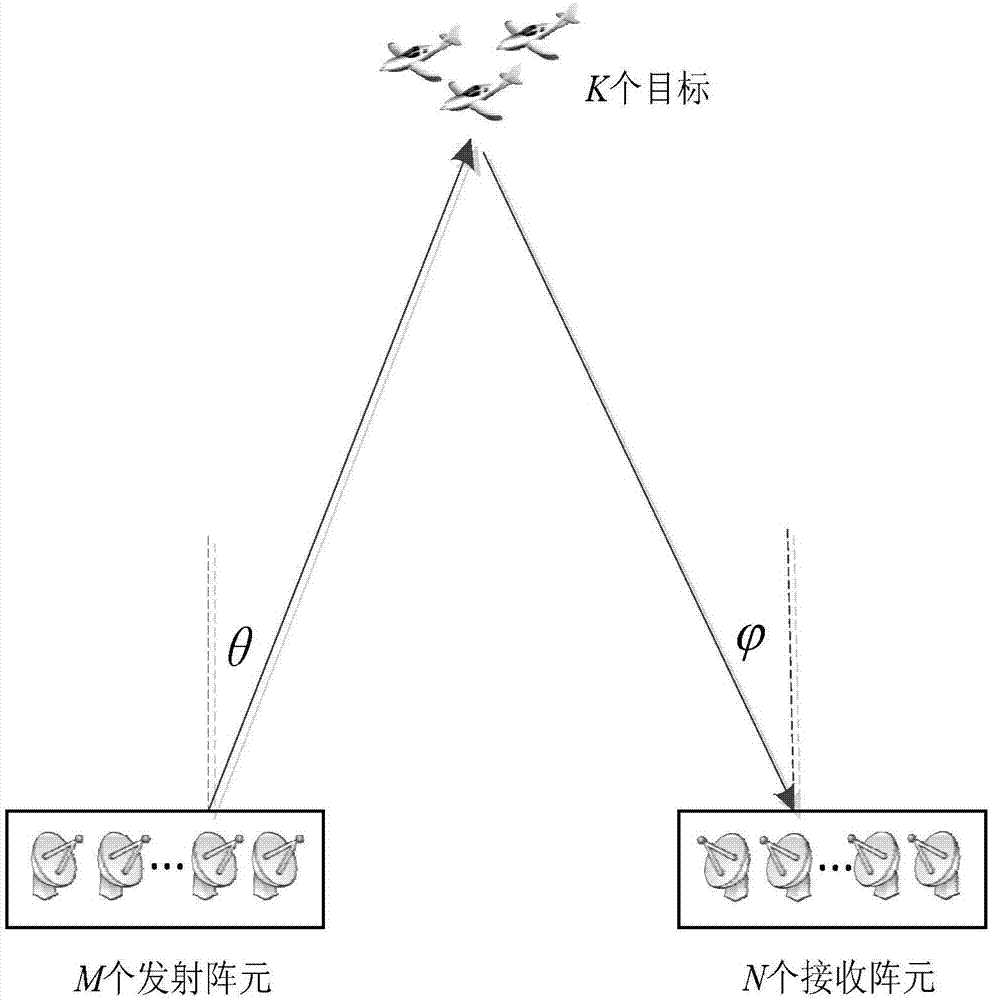
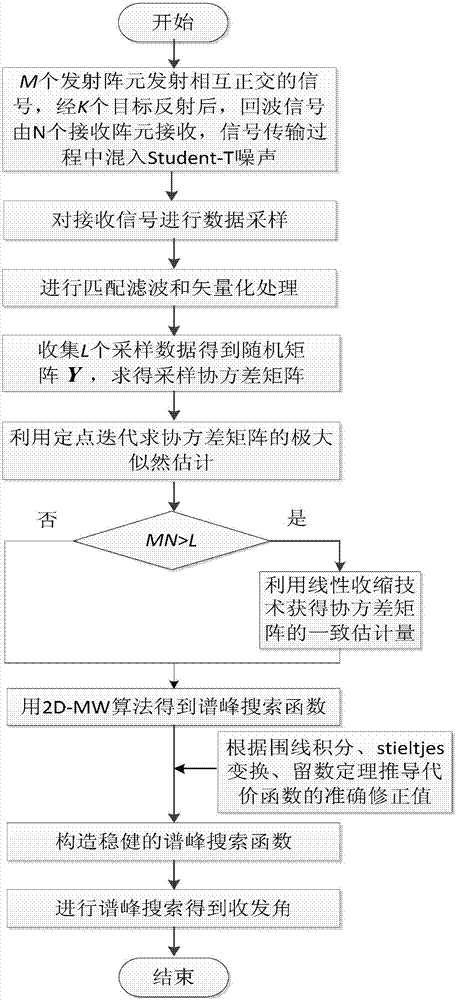
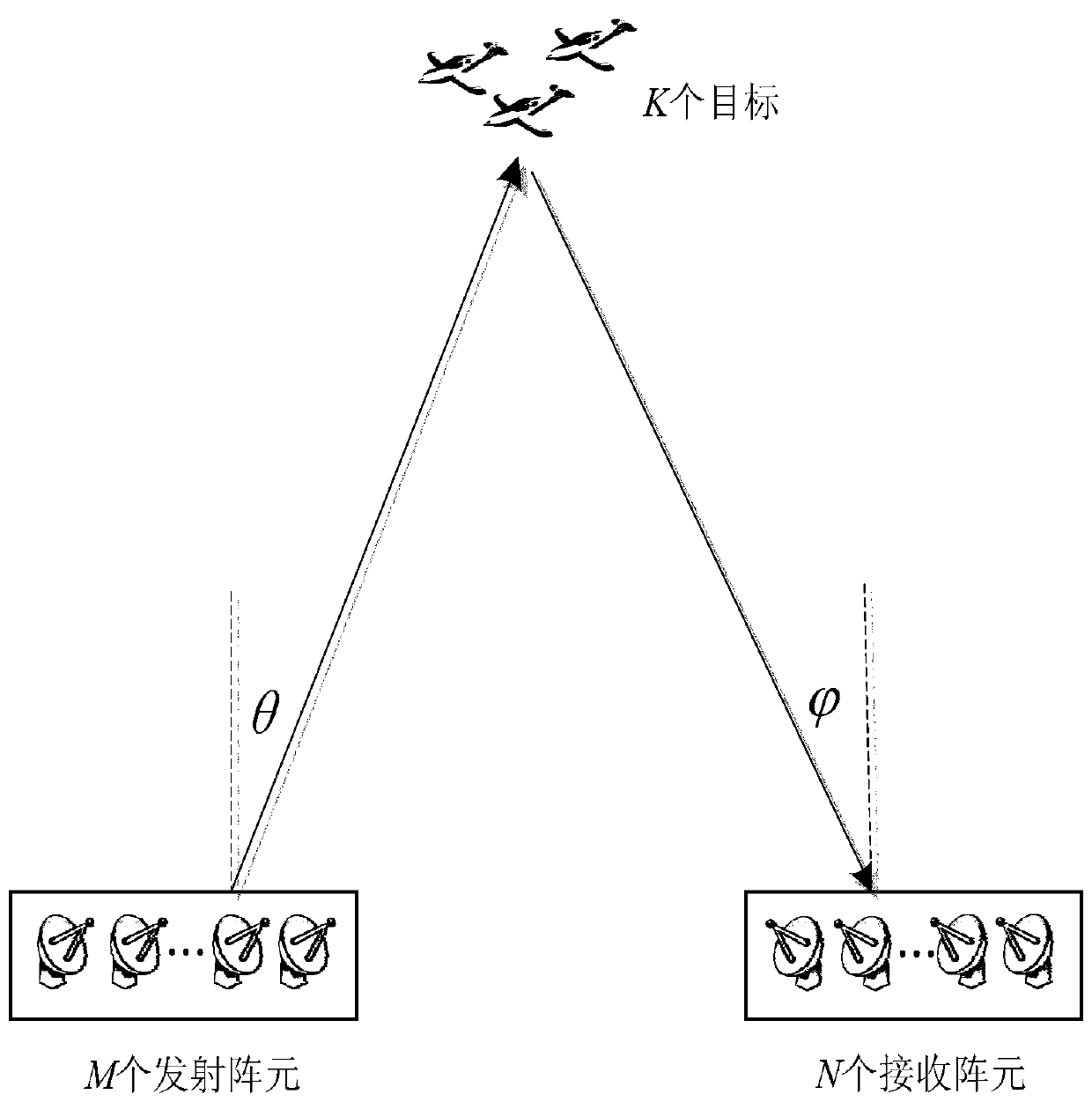
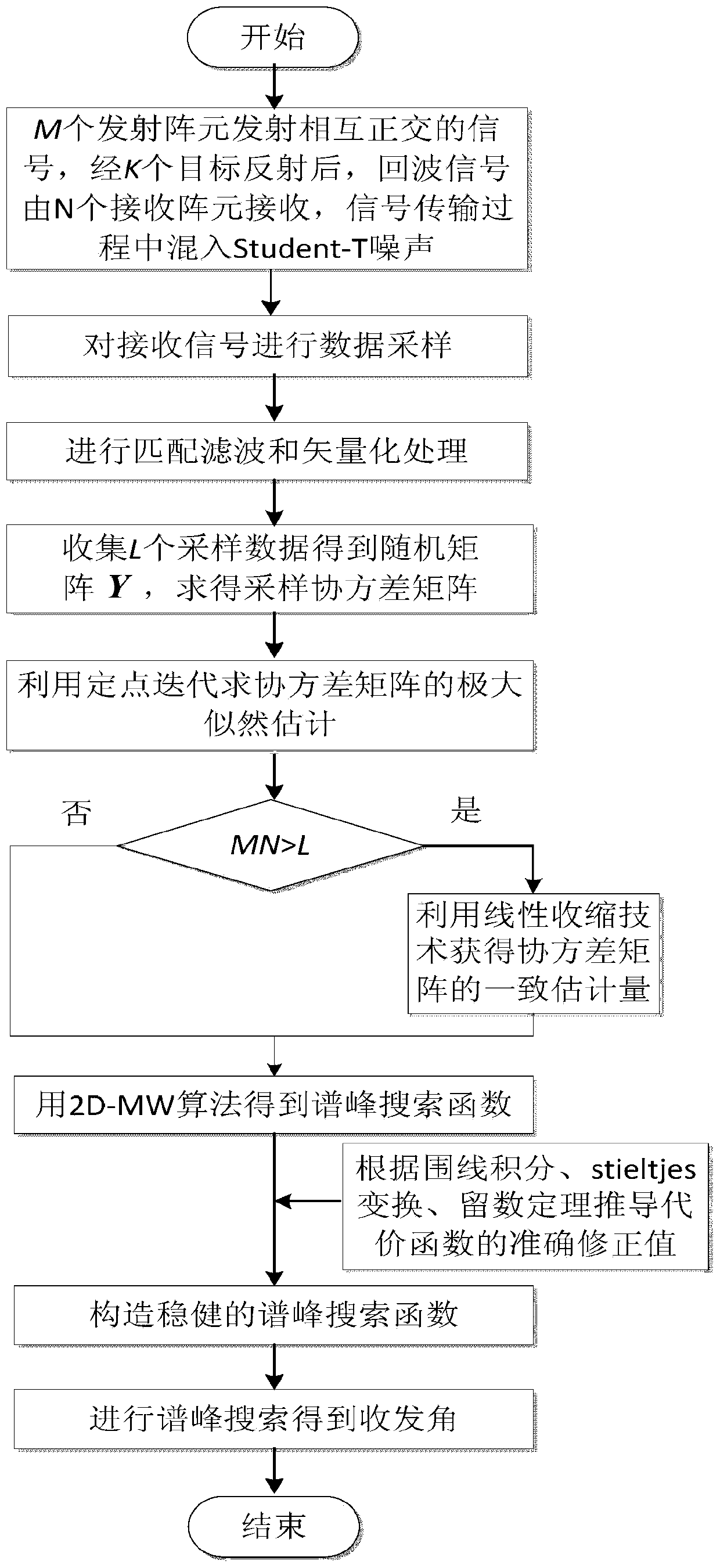
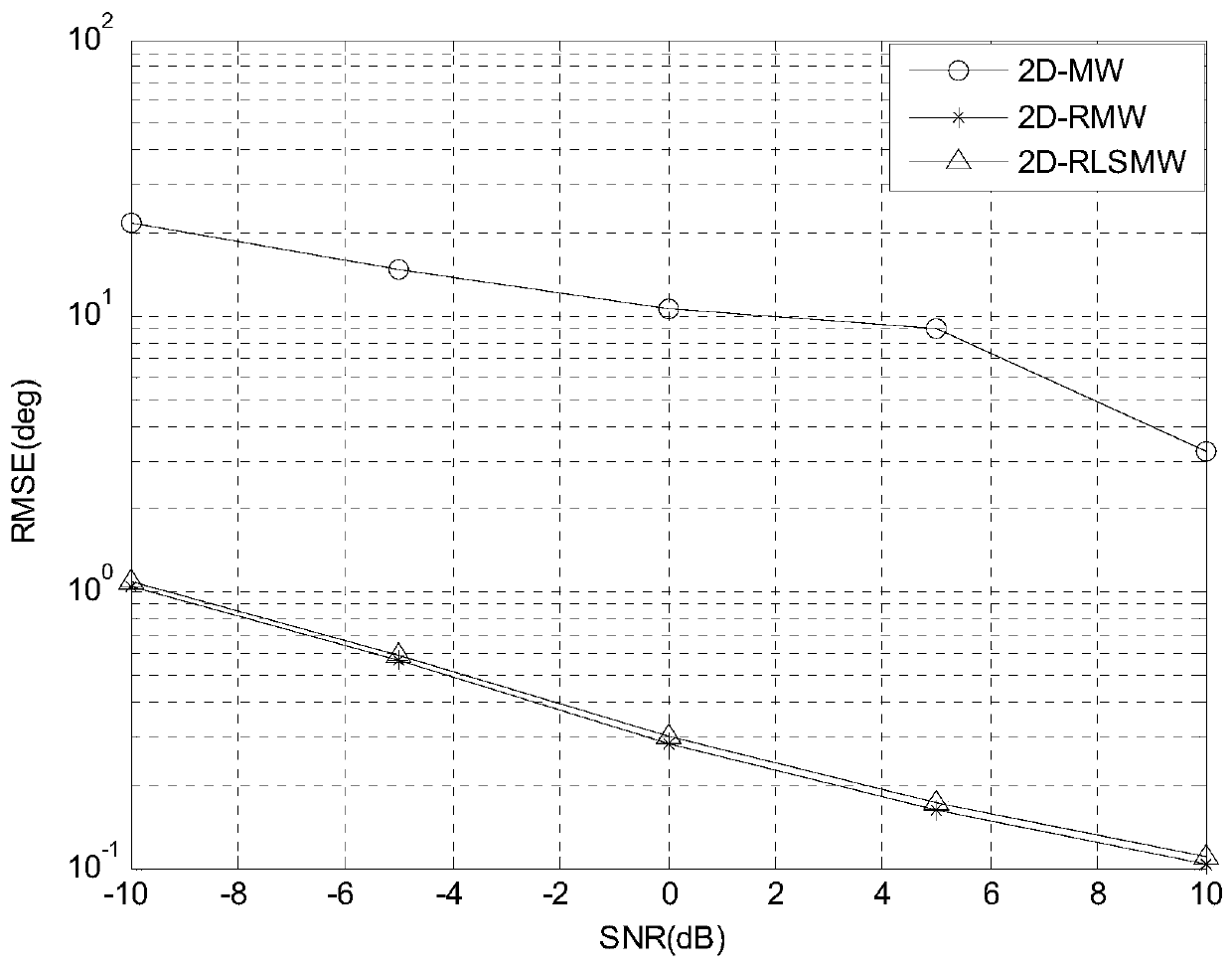
ActiveCN107167785ASolve the problem of inaccurate estimation of receiving and receiving anglesSolve the missing rank problemWave based measurement systemsEstimation methodsRadar
The invention provides a robust large-array MIMO target transmitting and receiving angle joint estimation method, and belongs to the field of multiple-input multiple-output radar target parameter estimation. The method provided by the invention is based on linear shrinkage and a random matrix theory. Implementation of the method comprises the steps of building a random matrix model of observed data by using echo signals, solving maximum likelihood estimation of a covariance matrix through fixed-point iteration under the non-Gaussian noise background, acquiring robust covariance matrix estimation by using a linear shrinkage technology when the number of transmitting and receiving array elements is greater than the number of snapshots, building a robust cost function by using contour integration, Stieltjes transform and a residue theorem, and performing spectrum peak search on the cost function so as to solve the target transmitting and receiving angle. The method provided by the invention has the advantages that the method has robust estimation performance under the non-Gaussian noise background, and the method is applicable to a large-array system with the number of transmitting and receiving array elements being greater than the number of snapshots at the same time.
Owner:JILIN UNIV
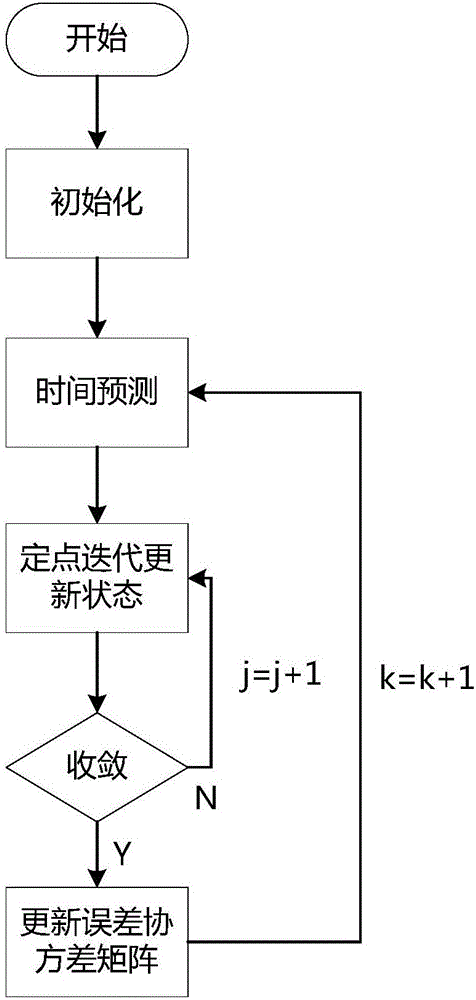
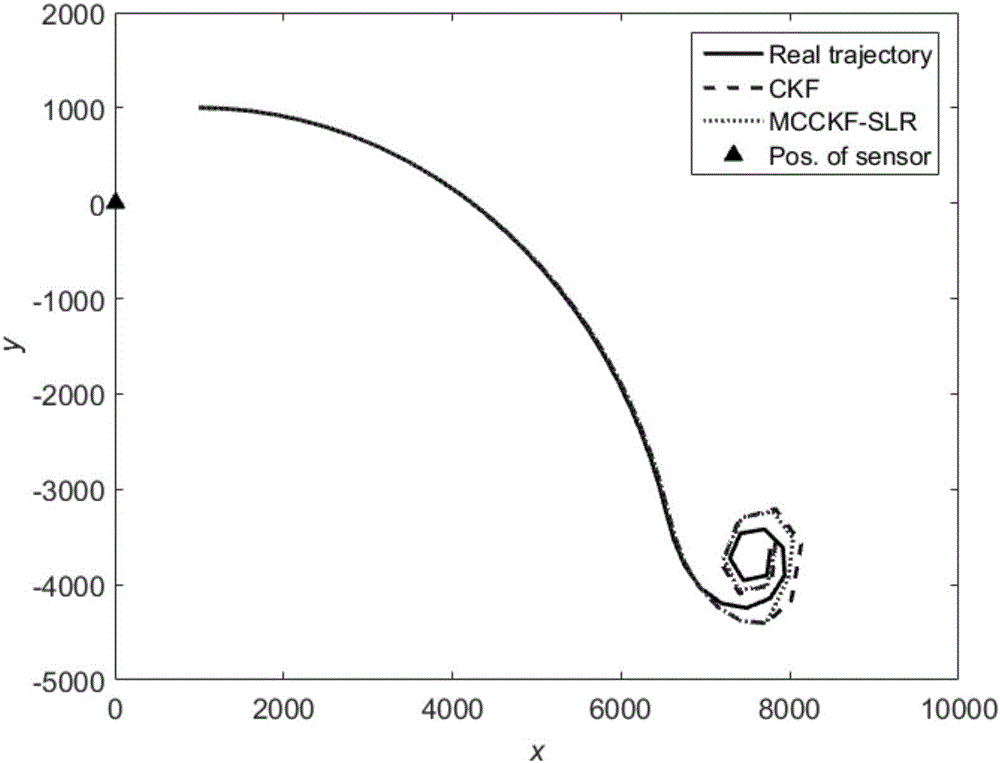
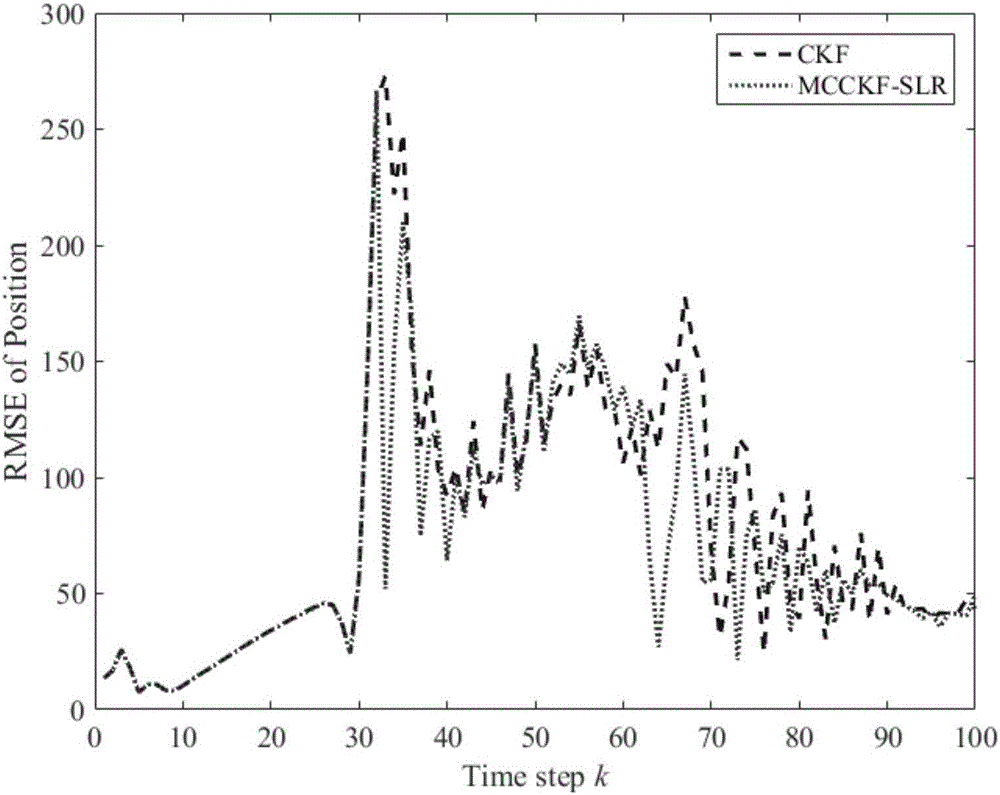
Maximum correntropy volume Kalman filtering method based on statistical linear regression
InactiveCN106487358AImprove LupineBoost and Noise ImmunityDigital technique networkKaiman filterLinear regression
The invention belongs to the technical field of signal processing, and providing a maximum correntropy volume Kalman filtering method based on statistical linear regression. After steps of filter initializing, time predicting, fixed-point iterating, error covariance matrix updating and the like are performed, the state of a nonlinear system can be estimated. Based on a maximum correntropy Kalman filtering device, a maximum correntropy cost function is integrated into the frame of a volume Kalman filtering device by utilizing a statistic linear regression method in the statistics, and then is applied to estimation to the state of the nonlinear system. Compared with the traditional volume Kalman filtering method in a nonlinear system state estimation process, the maximum correntropy volume Kalman filtering method based on statistical linear regression has remarkable improvement on the robustness and anti-noise capability; and the method can be widely applied to the nonlinear system, in particular when a noise item of the system is non-gaussian.
Owner:SOUTHWEST UNIVERSITY
Low-complexity dynamic asynchronous BP decoding method
InactiveCN102594367AFast convergenceImprove decoding performanceError correction/detection using multiple parity bitsRound complexityInformation transmission
The invention provides a low-complexity dynamic asynchronous information updating strategy aiming at the BP decoding algorithm of LDPC (Low Density Parity Check) codes. The low-complexity dynamic asynchronous information updating strategy comprises the steps of including a simple and direct positioning method based on the maximum fluctuation of the LLR (Log Likelihood Rate) of variable nodes and an information transmission form of utilizing the information calculation from two-step check nodes of check nodes to the variable nodes to the greatest degree, utilizing the principle that the convergence can be controlled by the control of the difference of the two adjacent calculation results in the error evaluation through the fixed-point iteration algorithm, selecting the LLR calculation of the variable nodes as an iterative function, and utilizing the check function of the check nodes to the greatest degree. According to the method, the variable nodes needing to be updated preferentially are positioned simply and directly, a trap set in the LDPC code words can be overcome rapidly, so that the iterations needed in decoding are reduced, the purpose that the algorithm can be converged rapidly can be achieved, and simultaneously, the decoding performance is promoted greatly.
Owner:SUN YAT SEN UNIV
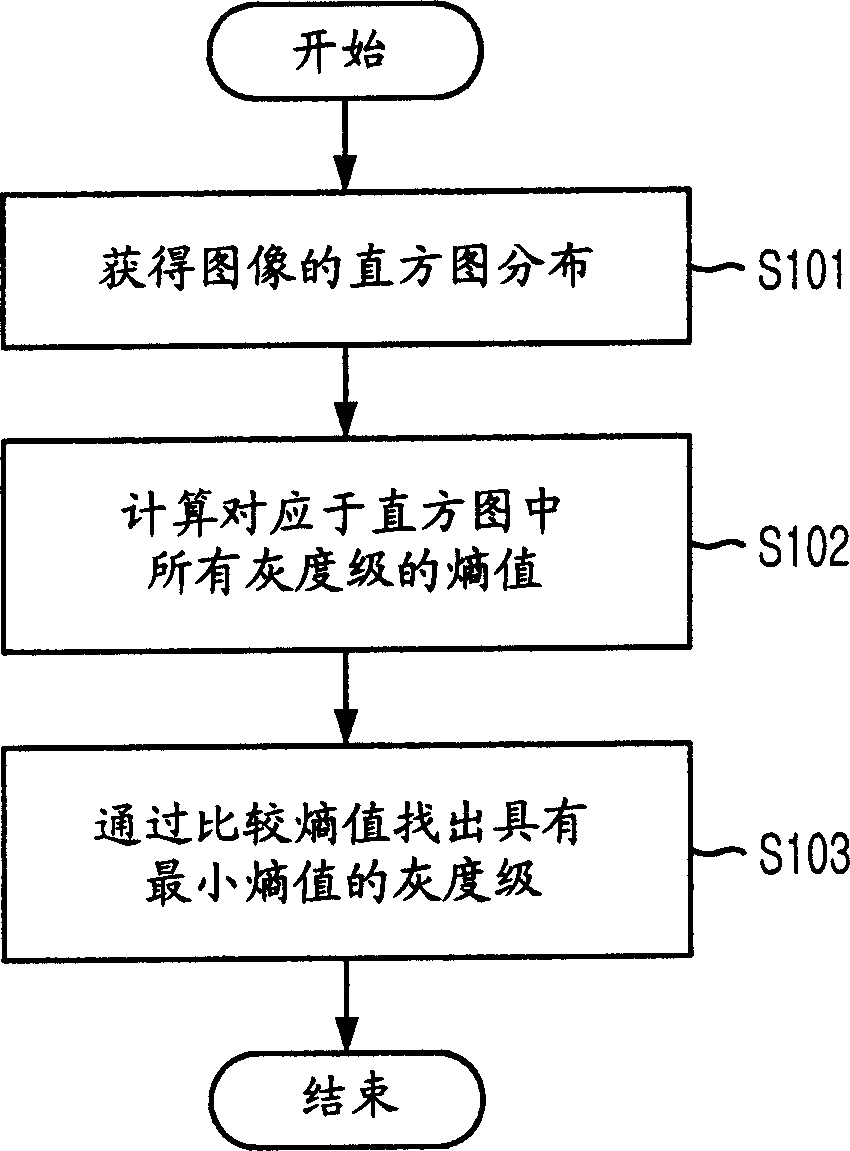
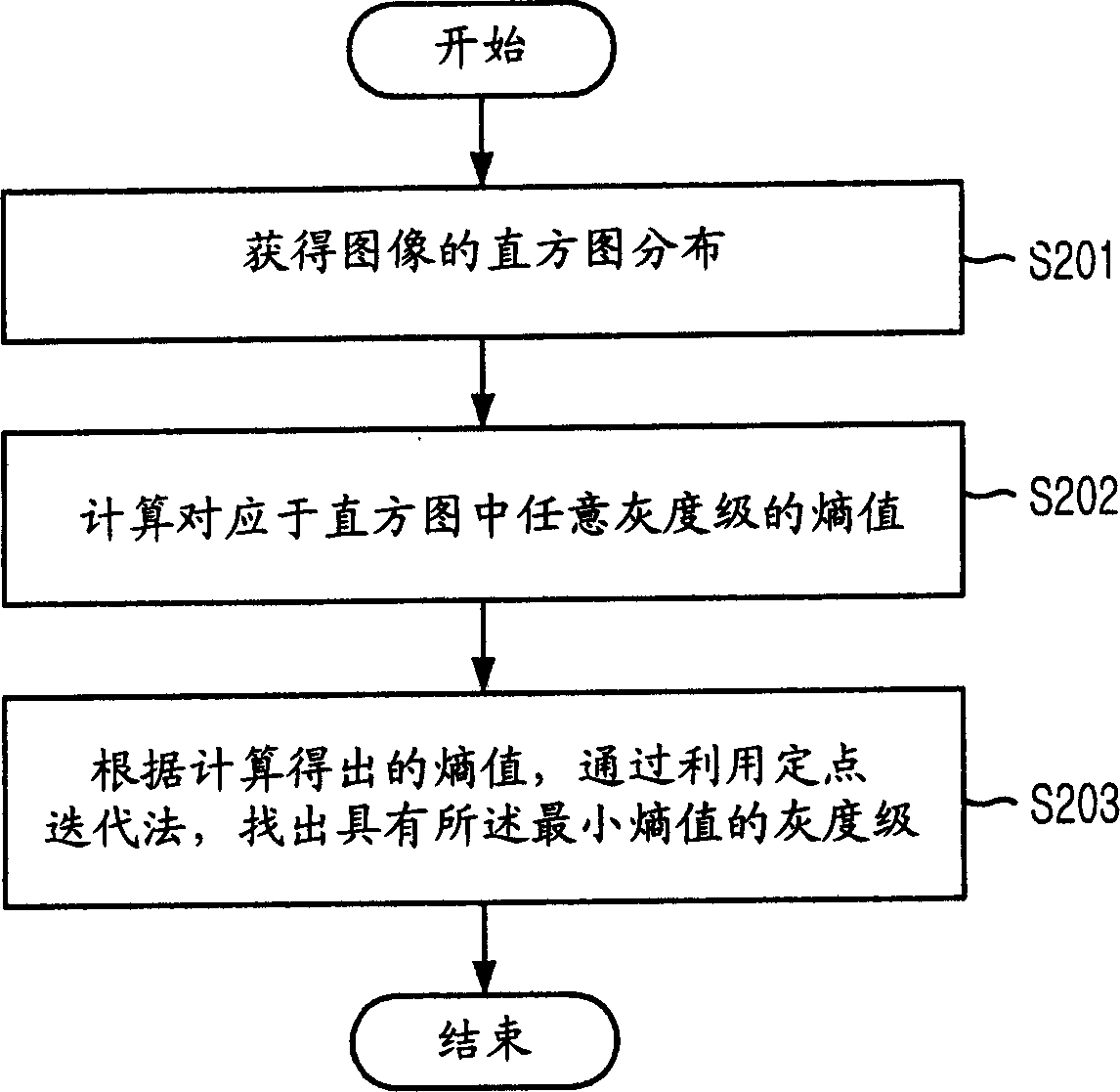
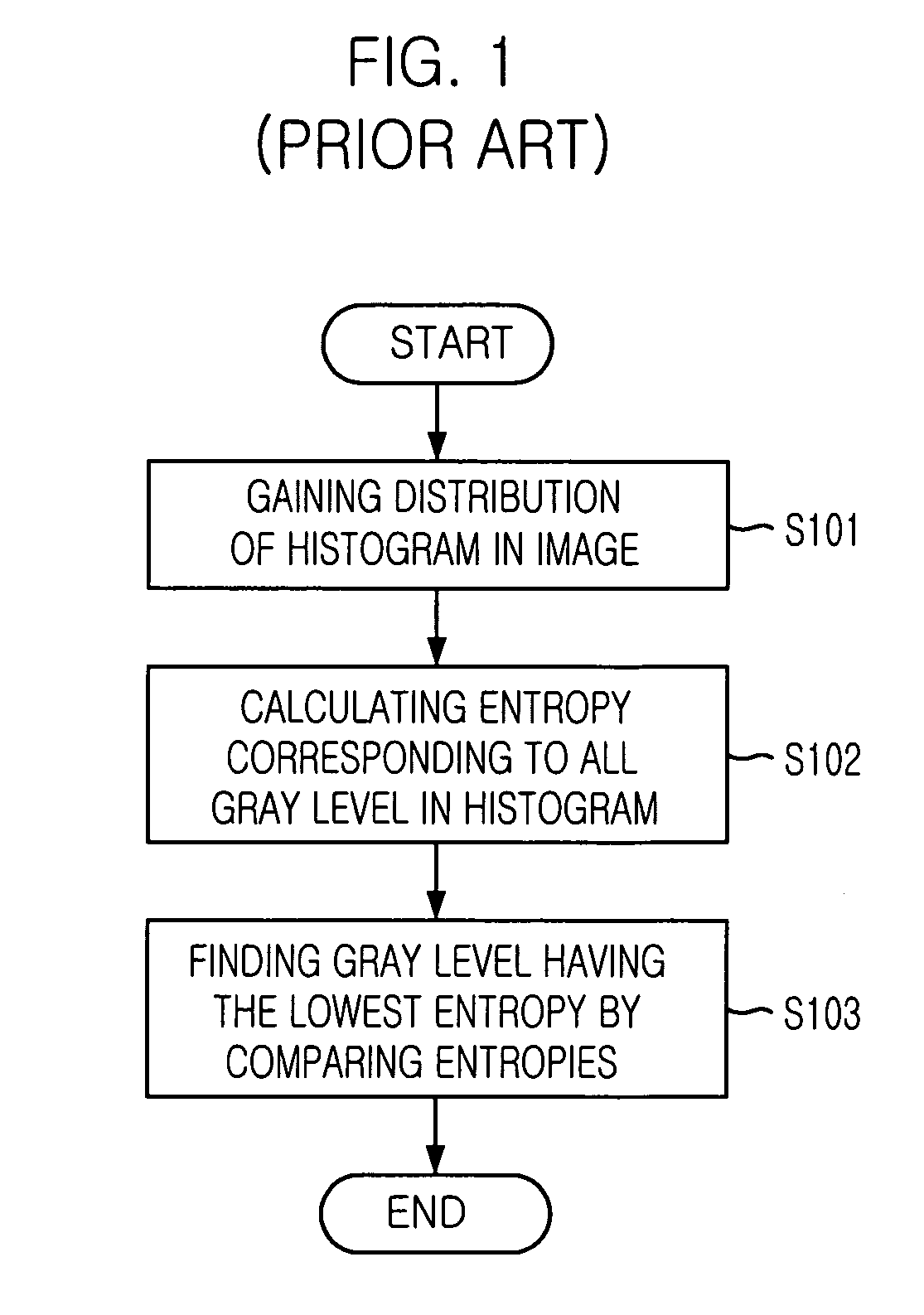
Method for looking up optinum threshold from image separation
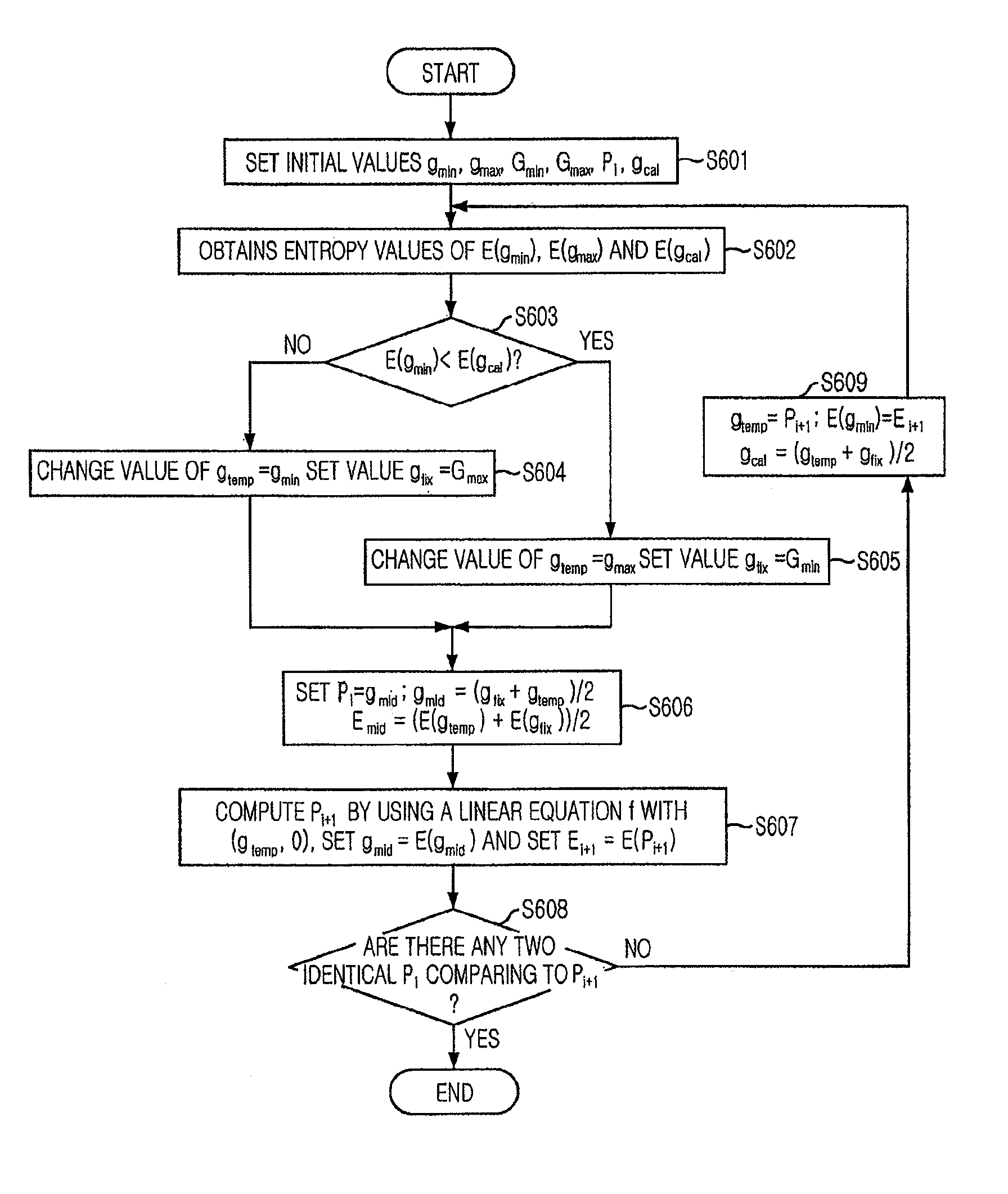
A method for finding the optimal threshold for image segmentation in image recognition is disclosed. The method includes the steps of: a) gaining histogram distribution of an image; b) computing entropy values corresponding to gray levels in the histogram; and c) gaining a minimum entropy value corresponding to the gray level as the threshold value by using a fixed point iteration FPI based on the computed entropy values. The invention is capable of finding out an optimal threshold in a short time by applying a fast analytical approach method based on an FPI(Fixed Point Iteration) method together with a division termination condition for an image having multi-threshold through analysis for an entropy feature of the image.
Owner:PANTECH CO LTD
D2D distributed power optimization method in cellular network
ActiveCN105813189AIncrease flexibilityFast convergencePower managementFrequency spectrumDistributed power
The invention discloses a D2D distributed power optimization method in a cellular network. The transmission power of a base station and a D2D user is solved in a distributed manner through fixed point iteration, so that the power distribution and communication rate of a D2D device and the base station on different channels are obtained. According to the invention, a non-convex problem is approximated as a divisible convex optimization problem by using a convex approximation method and an optimal solution of the convex problem is obtained through multi-layer iteration rapid convergence. The method provided by the invention is wide in application range, realizes frequency spectrum resource sharing, improves system performance flexibly, reduces computation amount and improves computation speed.
Owner:SOUTHEAST UNIV
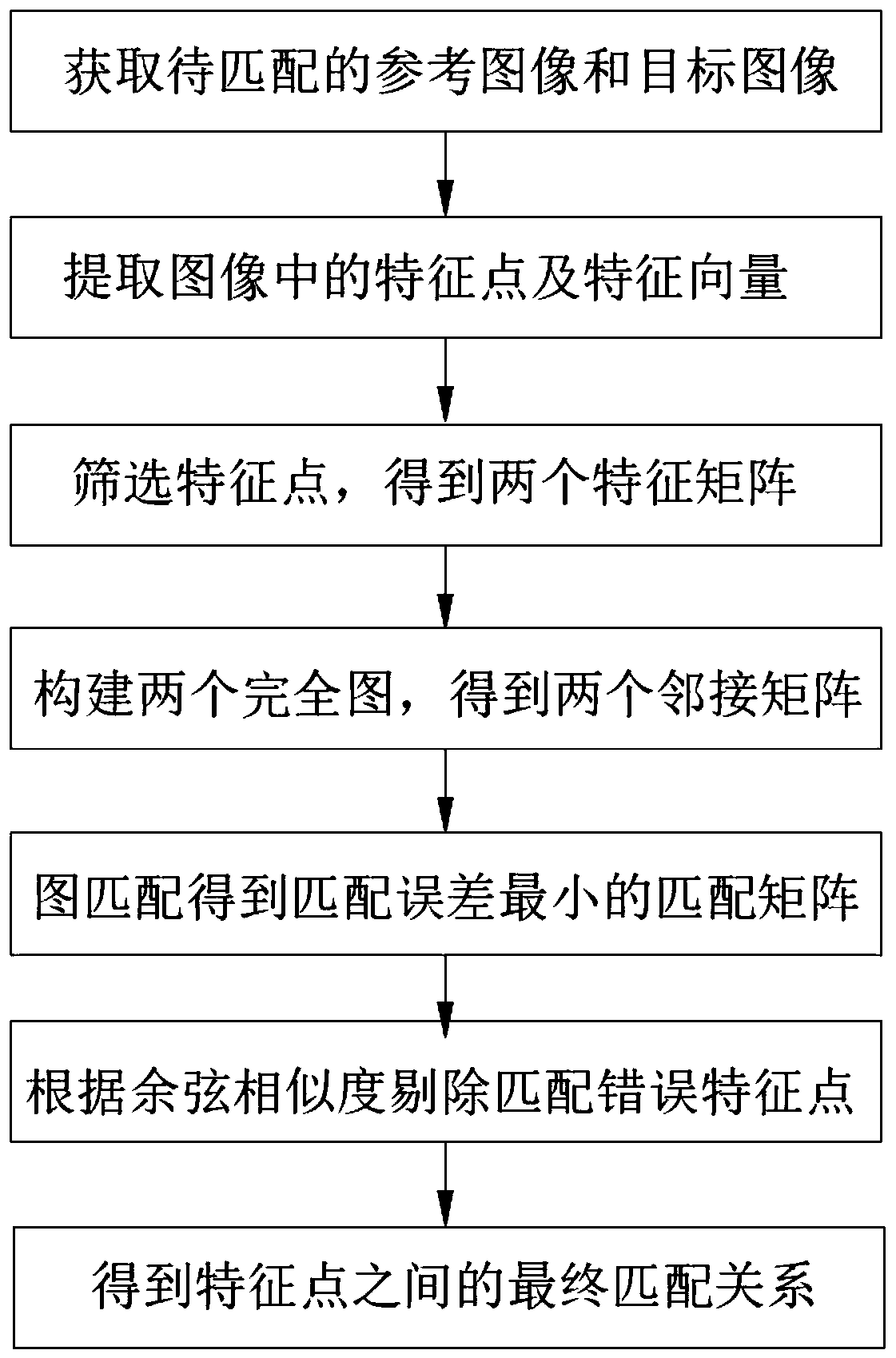
Image matching method and system based on image matching and storage medium
ActiveCN111242221AHigh speedImprove robustnessInternal combustion piston enginesCharacter and pattern recognitionAllocation algorithmImage matching
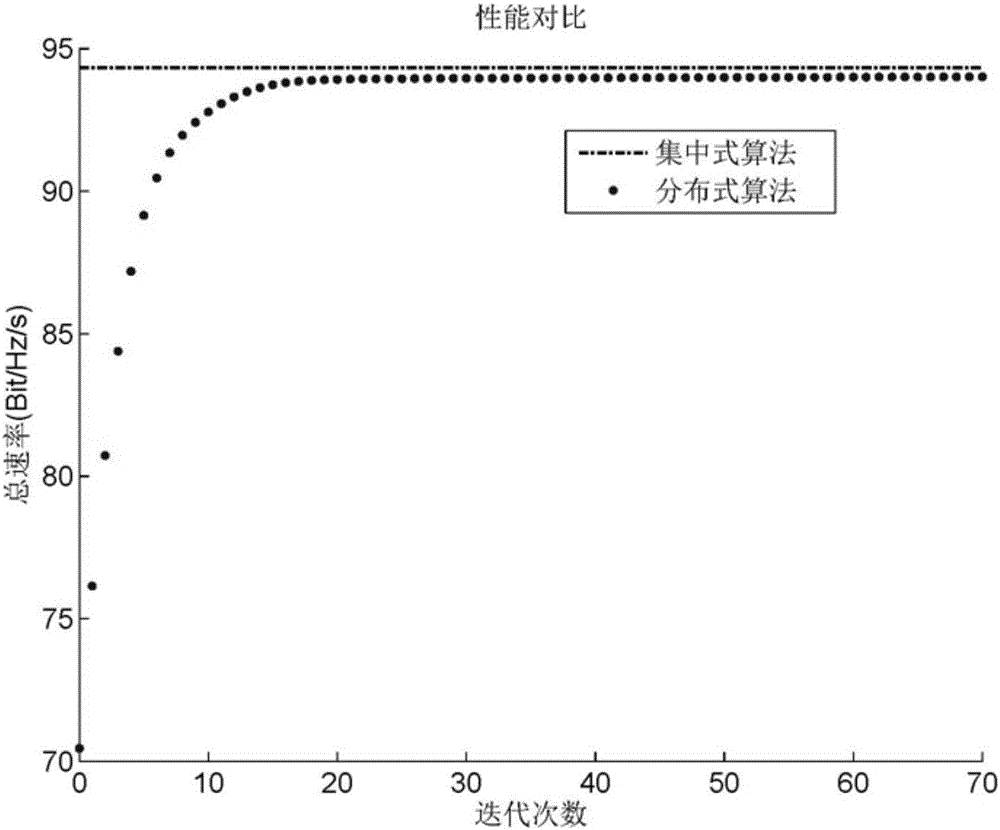
The invention discloses an image matching method and system based on image matching and a storage medium. According to the image matching method based on image matching, through feature point extraction and feature point screening, image construction is completed; an image matching method is adopted, matching is carried out by adding attributes of edges, even if local features are difficult to distinguish due to similarity or the local features of the same object in the two images change, feature matching can be accurately achieved through distance relation constraints between feature points,the robustness of the matching method is effectively enhanced, and matching precision is guaranteed. Meanwhile, compared with a classical image matching technology such as an integer projection fixedpoint method (IPFP) and a step-by-step allocation algorithm (GA), the method adopts an advanced fast continuous projection fixed point iteration method to solve the optimal solution, a new projectionmethod is provided, the calculated amount is simplified in the optimization process, the speed of the image matching method is greatly improved, and the accuracy is improved to a certain degree on thebasis of the high accuracy of the image matching technology.
Owner:XIAN JIAOTONG LIVERPOOL UNIV
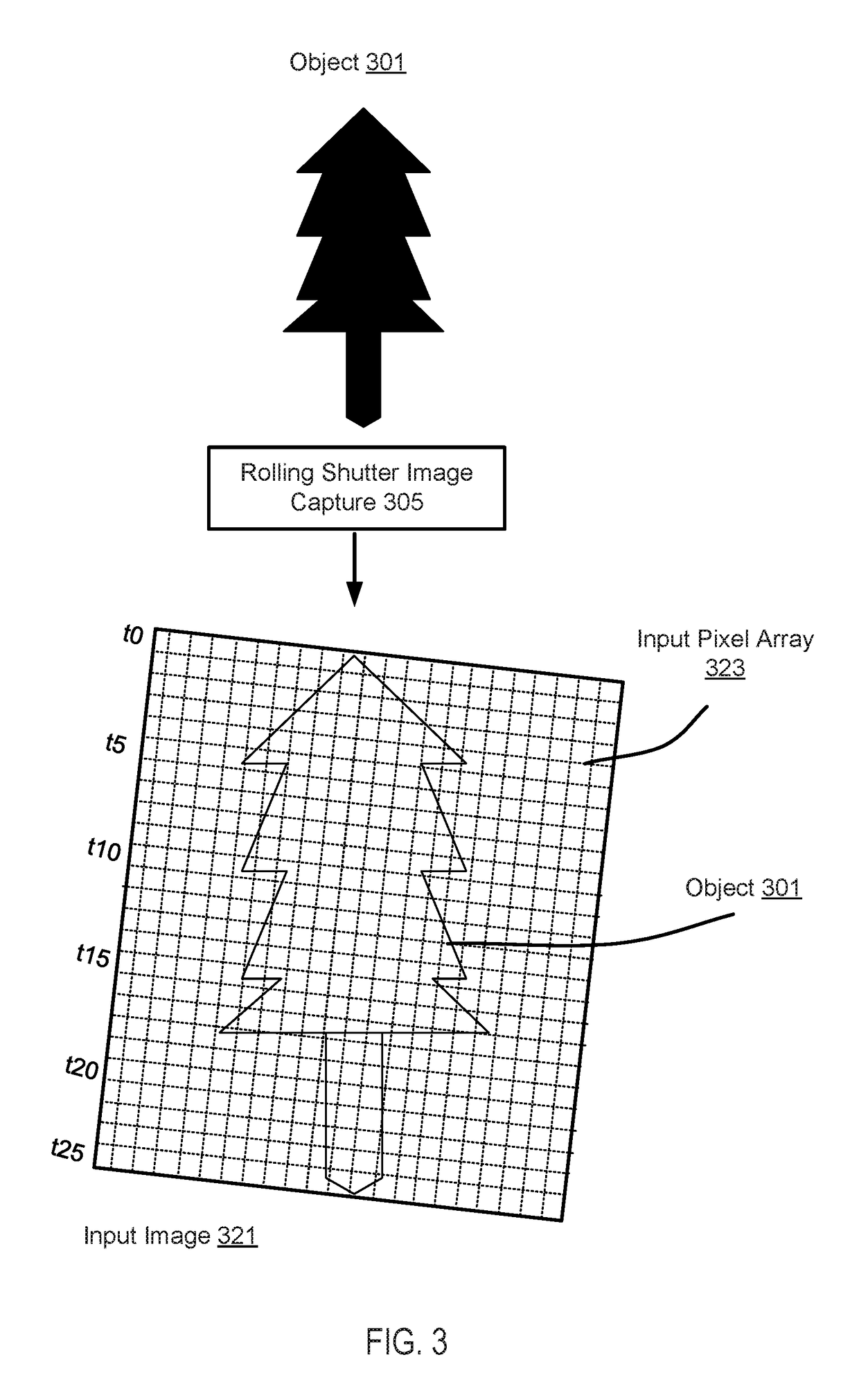
Systems and methods for rolling shutter compensation using iterative process
ActiveUS10194101B1Television system detailsGeometric image transformationRolling shutterImage capture
Image captured with an image capture device with a rolling shutter may be deformed due to changes in imaging sensor orientation during image capture. Image deformities may occur due to rolling shutter that exposes rows of pixels to light at slightly different times during image capture. Deformities such as wobble, for example, and / or other deformities may be corrected by constructing an output image. The output image may be constructed by determining corresponding pixels within the input image. The location of the input pixel may be determined by performing one or more fixed point iterations to identify one or more input pixels within the input image. A value of the output pixel within the output image may be determined based on a value of a corresponding pixel within the input image.
Owner:GOPRO
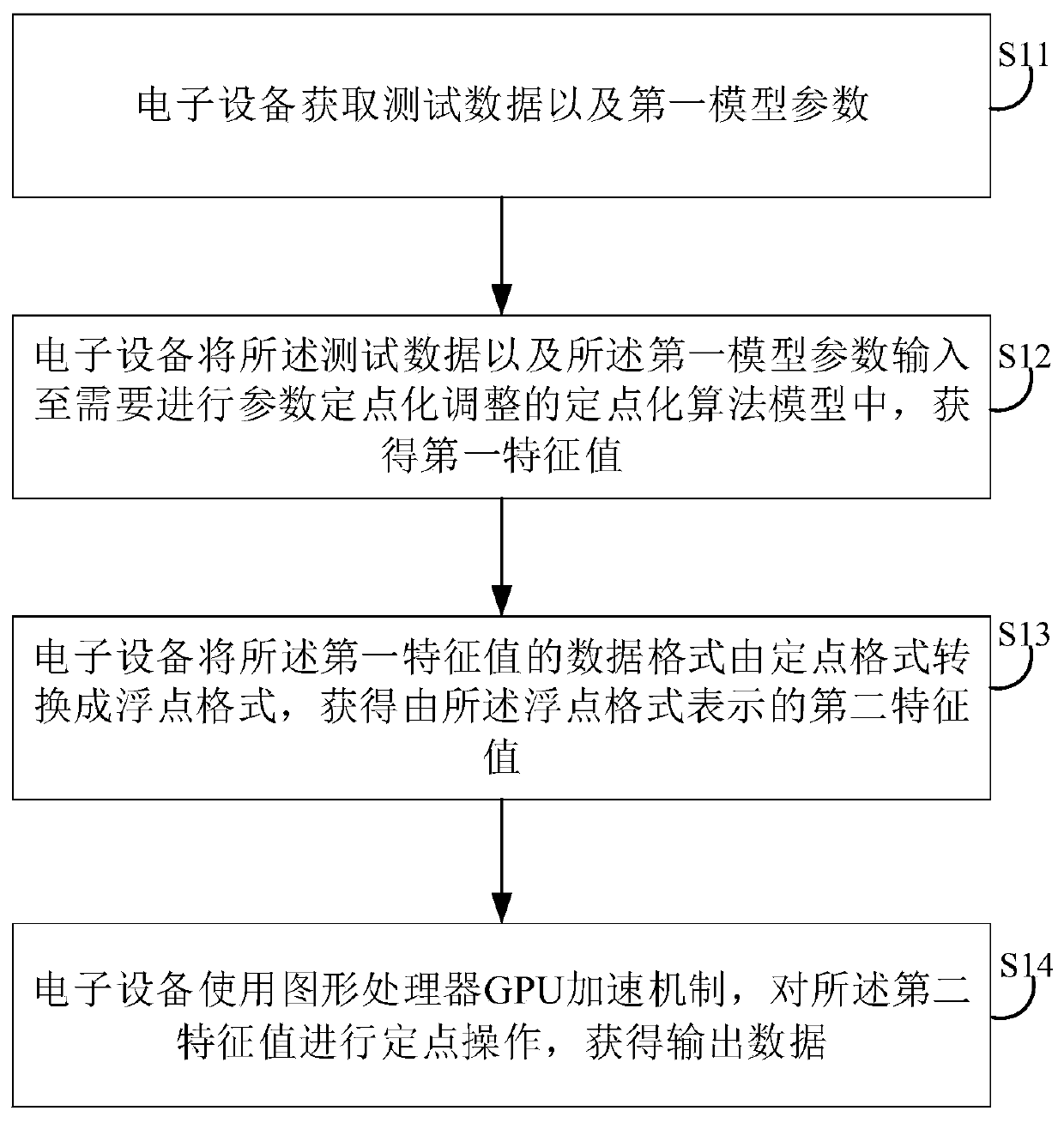
Data fixed-point acceleration method and device, electronic equipment and storage medium
ActiveCN109697083ASpeed up the iteration cycleMachine execution arrangementsAlgorithmFloating point
The invention discloses a fixed-point acceleration method for data. The method comprises the following steps: acquiring test data and first model parameters; inputting the test data and the first model parameters into a fixed-point algorithm model needing fixed-point parameter adjustment to obtain a first characteristic value; Converting the data format of the first characteristic value into a floating point format from a fixed point format, and obtaining a second characteristic value represented by the floating point format; and performing fixed-point operation on the second characteristic value by using a GPU acceleration mechanism to obtain output data. The invention further provides a fixed-point acceleration device, electronic equipment and a computer storage medium. According to theinvention, the calculation of the fixed-point algorithm model can be accelerated, and the fixed-point iteration period is accelerated.
Owner:SHENZHEN INTELLIFUSION TECHNOLOGIES CO LTD
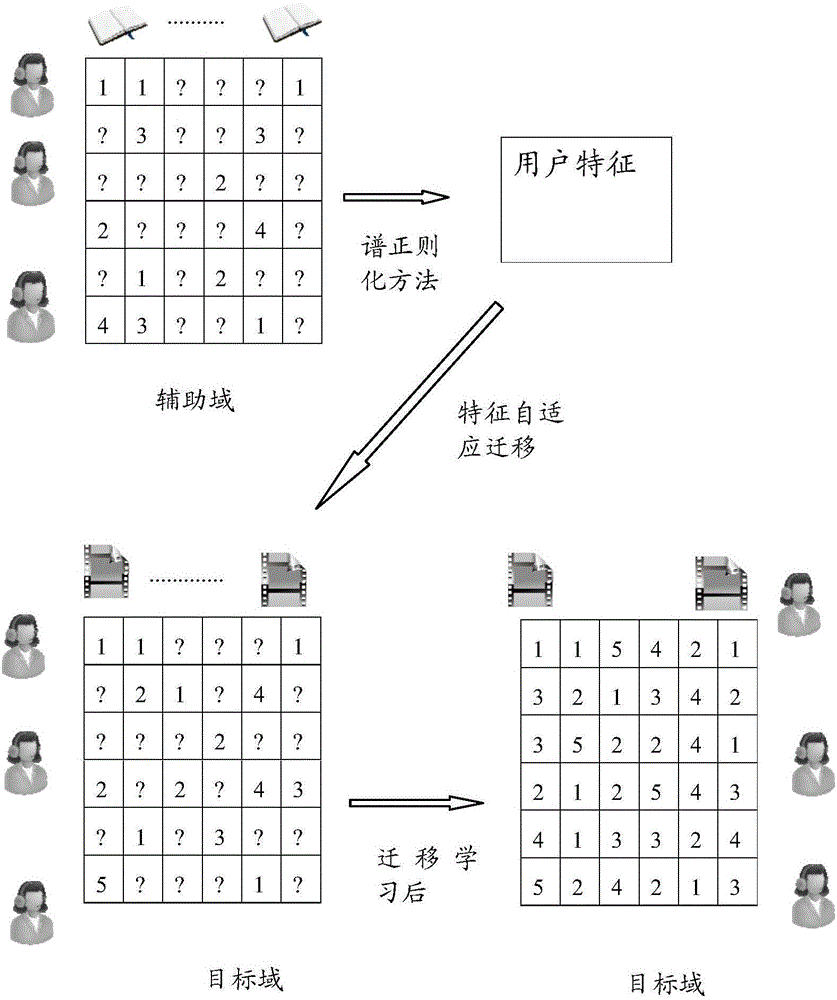
Collaborative filtering method based on domain correlation self-adaption
InactiveCN106227767AStrong correlationScore Prediction Adequate and EffectiveSpecial data processing applicationsAlgorithmThe Internet
A collaborative filtering method based on domain correlation self-adaption comprises the following steps that 1,the difference of an auxiliary domain and a target domain serves as a regularization term and is introduced into a traditional model to obtain a new model (shown in the description), wherein T is a rating matrix having a partially deleted item in the target domain, Z and T have the same rating item; the equation shown in the description represents an index set representing the target domain, wherein the equation is shown in the description; | | . | | F represents a Frobenius norm, wherein the equation is shown in the description; | | . | | * represents a nuclear norm,| | Z | | *represents the sum of all singular values of a matrix Z; gamma is a regularization parameter, eta < (0, 1) represents the similarity of the auxiliary domain and the target domain; 2,a regular optimization solution Z* = Z of the new model is calculated by using a fixed-point iteration algorithm. The collaborative filtering method can be applied to an Internet recommendation system, introduces the system to a prediction model of the target domain through self-adaptive estimation of their correlation, accordingly achieves knowledge migration effectively and improves the recommendation precision of the target domain.
Owner:HUAQIAO UNIVERSITY
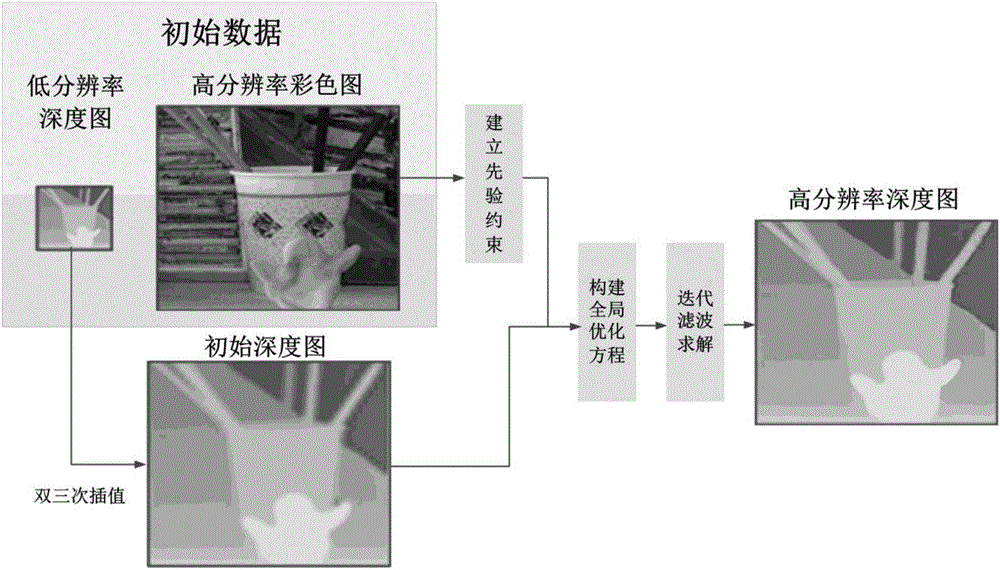
Depth computation reconstruction method combining global modeling with non-local filtration
InactiveCN106296706AHigh resolutionSimple procedureImage enhancementImage analysisFine structureColor image
The invention relates to a depth computation reconstruction method combining global modeling with non-local filtration, and belongs to the field of image processing. According to the method, by means of a high resolution color image, a depth computation construction model is established for an initial low-quality depth image in a global mode, and depth reconstruction is carried out by a non-local fixed point iteration filtering method. The method is simple in procedure and easy to implement and can obtain a depth image with a higher resolution; the global modeling method utilizes global information of the color image and has a good effect of recovering a depth edge and non-local fine structures in the depth image; and a fixed point iteration filtering algorithm is deduced out in a derivation mode, so that the problem of solving large-scale matrix inversion by adopting the least square, simplicity is kept in design and implementation, and the depth computation reconstruction method has low complexity in algorithm.
Owner:DALIAN UNIV OF TECH
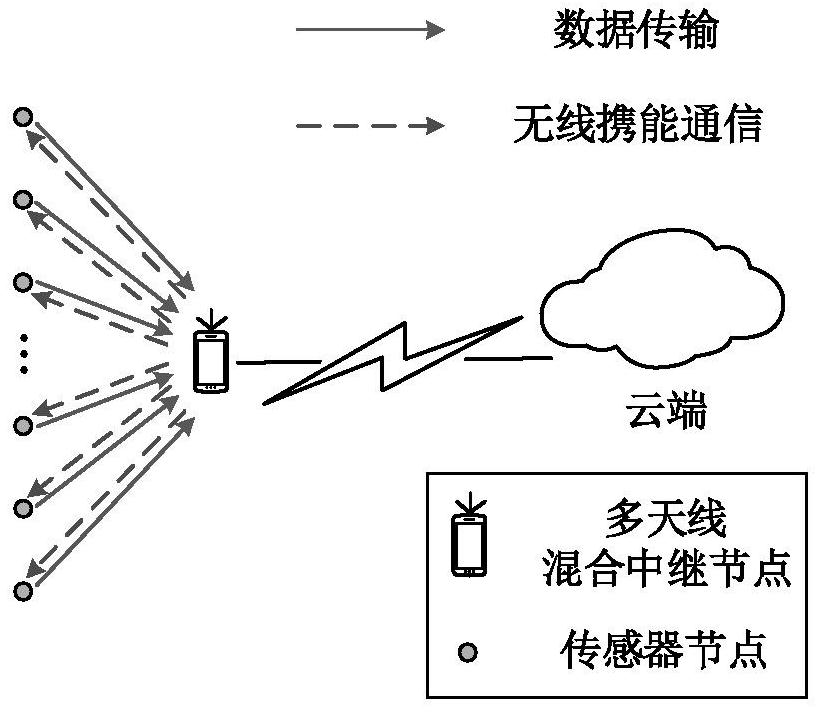
Wireless energy supply sensor network time distribution method based on fixed-point iteration
ActiveCN112040498AMinimize consumptionPower managementNetwork topologiesDistribution methodData transmission time
The invention discloses a wireless energy supply sensor network time distribution method based on fixed-point iteration, and aims to minimize the energy consumption of a network and prolong service time of an HAP under a condition that a throughput requirement of a sensor is met in ST-WPSNs. According to characteristics of a proposed optimization problem, a fixed-point iteration method is combined; and a low-complexity adaptive dynamic time distribution method is designed. Optimal energy transmission and sensor data transmission time distribution in a transmission period are obtained through calculation before each transmission period starts, and a purpose of minimizing network energy consumption is achieved under a constraint condition of meeting the throughput requirement of the sensor.Compared with an existing method for solving through a traditional convex optimization method, the method has advantages that operation complexity is obviously reduced, a special situation that a feasible set of an original optimization problem is empty is considered, higher robustness is achieved, and the method is more suitable for ST-WPSNs scenes.
Owner:HARBIN INST OF TECH SHENZHEN GRADUATE SCHOOL
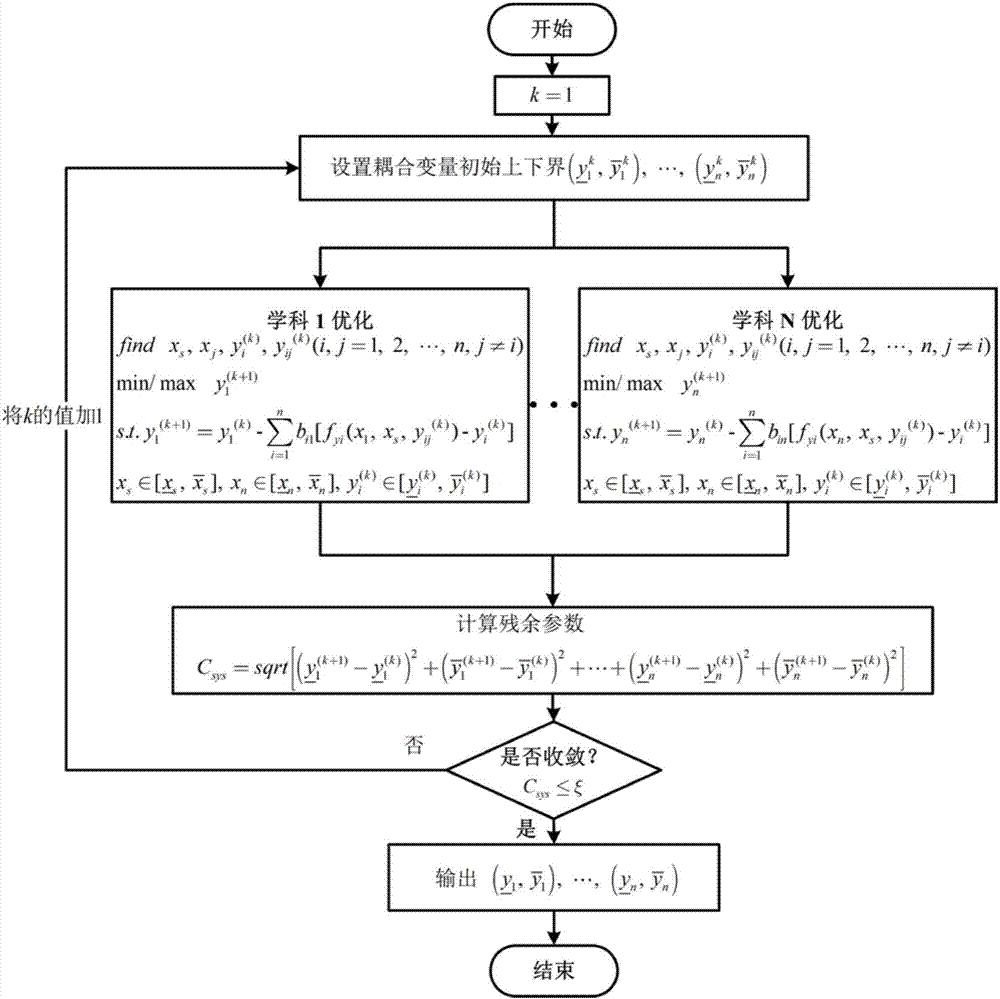
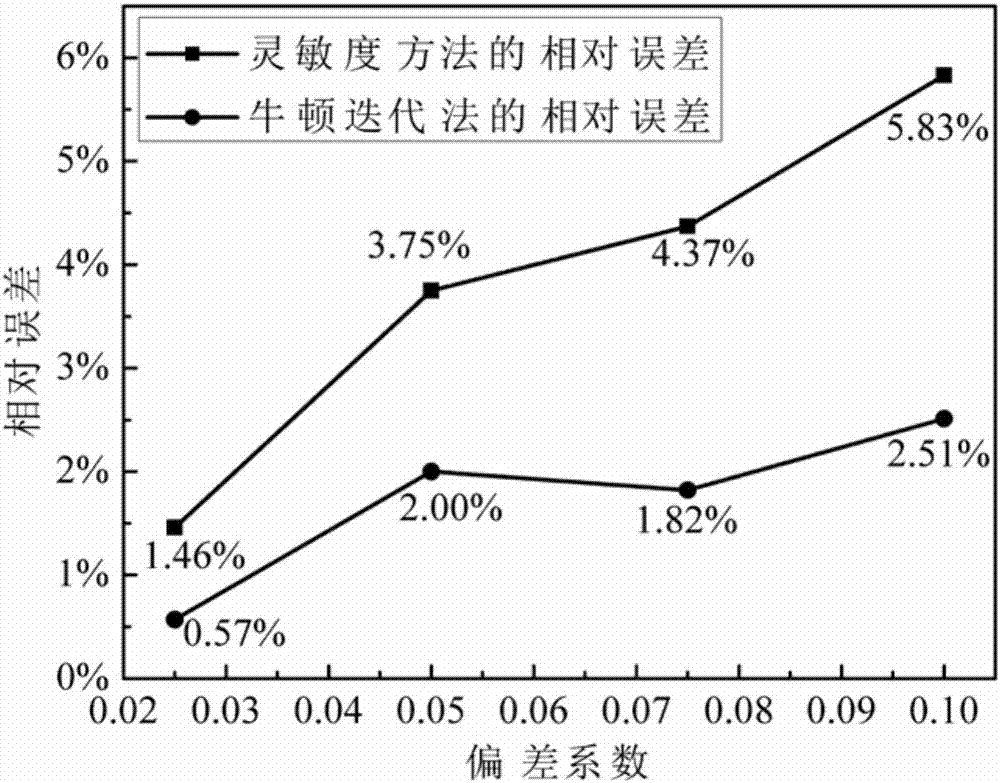
Multi-discipline uncertainty propagation analysis method based on Newton iteration
ActiveCN106874561AReduce dependenceReduce computing timeMulti-objective optimisationProbabilistic CADState variableCoupling
The invention discloses a multi-discipline uncertainty propagation analysis method based on Newton iteration and belongs to the field of multi-discipline uncertainty propagation analysis. The multi-discipline uncertainty propagation analysis method comprises the following steps: firstly, reasonably characterizing uncertainty parameters under conditions of poor information and less data by utilizing an interval as shown in the description; secondly, setting initial upper and lower bounds shown in the description of a suitable coupling variable, wherein the initial value of k is 1; thirdly, carrying out single-discipline optimization to obtain upper and lower bounds of y(k+1), wherein y(k+1) is a value of y obtained in the kth time of circulating; and finally, calculating residual parameters and judging whether residual parameters are converged or not; if so, outputting a responding interval of a coupling state variable; otherwise, carrying out the next time of circulating until the residual parameters are converged. A numerical example shows that the multi-discipline uncertainty propagation analysis method based on the Newton iteration can be used for obtaining an accurate coupling variable responding interval under certain conditions; and compared with a fixed point iteration method, the convergence speed is higher and a new method is provided for the multi-discipline uncertainty propagation analysis.
Owner:BEIHANG UNIV
Blind restoration method for moving blurred image
InactiveCN101359398BImprove clarityOvercoming blurry smearing problemsImage enhancementComputer graphics (images)Restoration method
Disclosed is a blind restoration method for the motion blurred image; the steps are as follows: (1) the image is converted through the cepstrum method to figure out the blur extent and the blur direction of the blurred image; (2) the blur extent and the blur direction of the blurred image figured out in step (1), and the total variation (TV) method are adopted to process the restoration towards the blurred image. The method based on the total variation (TV) includes: the fixed-point iteration used as the outer-loop and the conjugate gradient method used as the inner-loop are adopted for loopiteration to obtain the restored image. The blind restoration method has the advantages of strong self-adaptation, strong anti-noise ability and good robustness; the blind restoration method has validity and practicality according to the processing effects of the simulation picture and the photographed picture.
Owner:BEIHANG UNIV
Smoke model space editing method based on streamline deformation
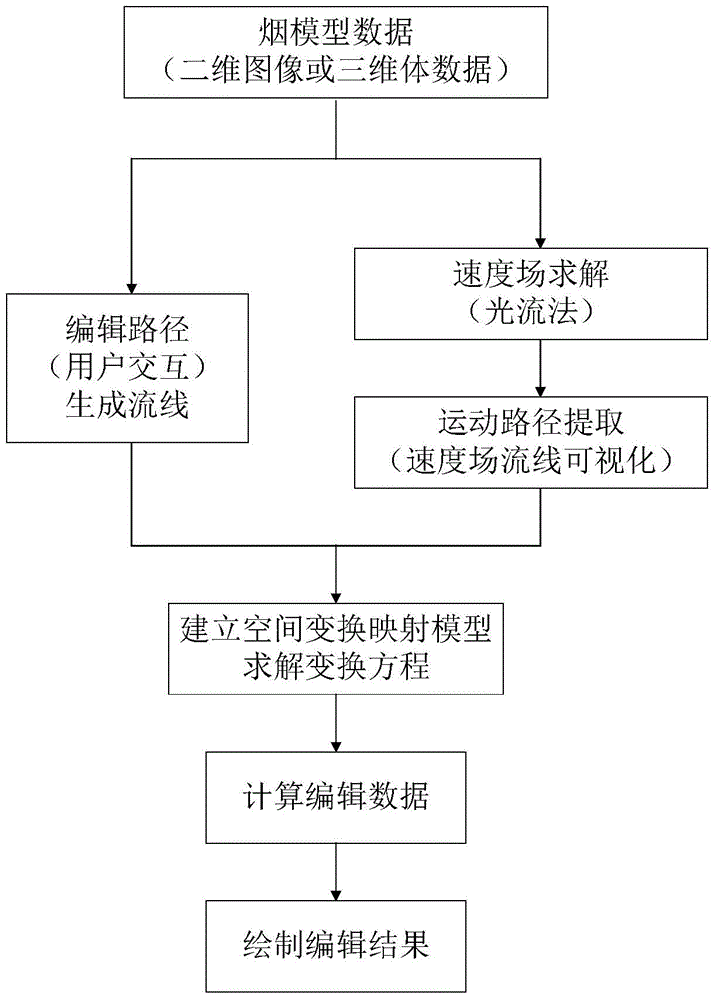
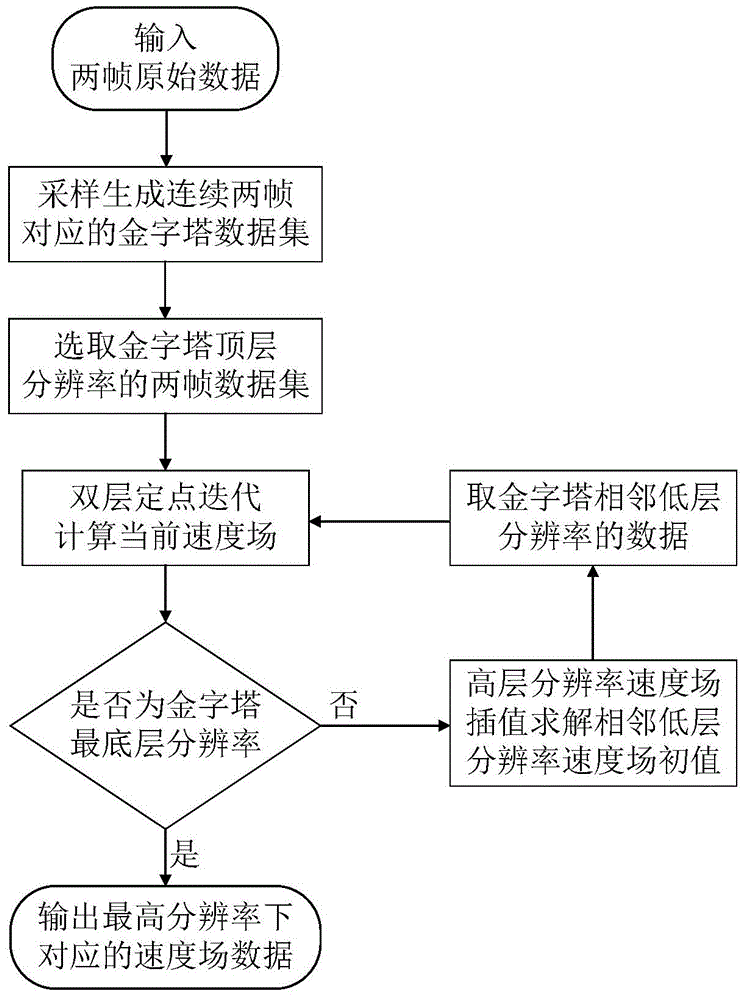
InactiveCN104361629AIncrease computing speedImprove calculation accuracy3D modellingData spaceComputer vision
The invention relates to a smoke model space editing method based on streamline deformation. The method is used for solving a space deformation model by the streamline deformation so as to edit smoke model data according to the model. The method comprises the following steps: (1) solving the velocity field of a smoke model data sequence based on a double-layer fixed-point iteration calculation method; (2) carrying out streamline visualization based on the velocity field obtained in the step (1), and extracting a main streamline representing the movement trend; (3) alternatively inputting edit paths by users to generate a streamline of edit data; (4) establishing and solving the space deformation model by taking the two groups of corresponding streamlines obtained in the steps (2) and (3) as constraint conditions; (5) solving the edit data of the smoke by combining the obtained space deformation model. After the method is used, the requirements for smoke model data space editing of the users can be met, and two-dimensional and three-dimensional smoke model data can be efficiently and vividly edited.
Owner:BEIHANG UNIV
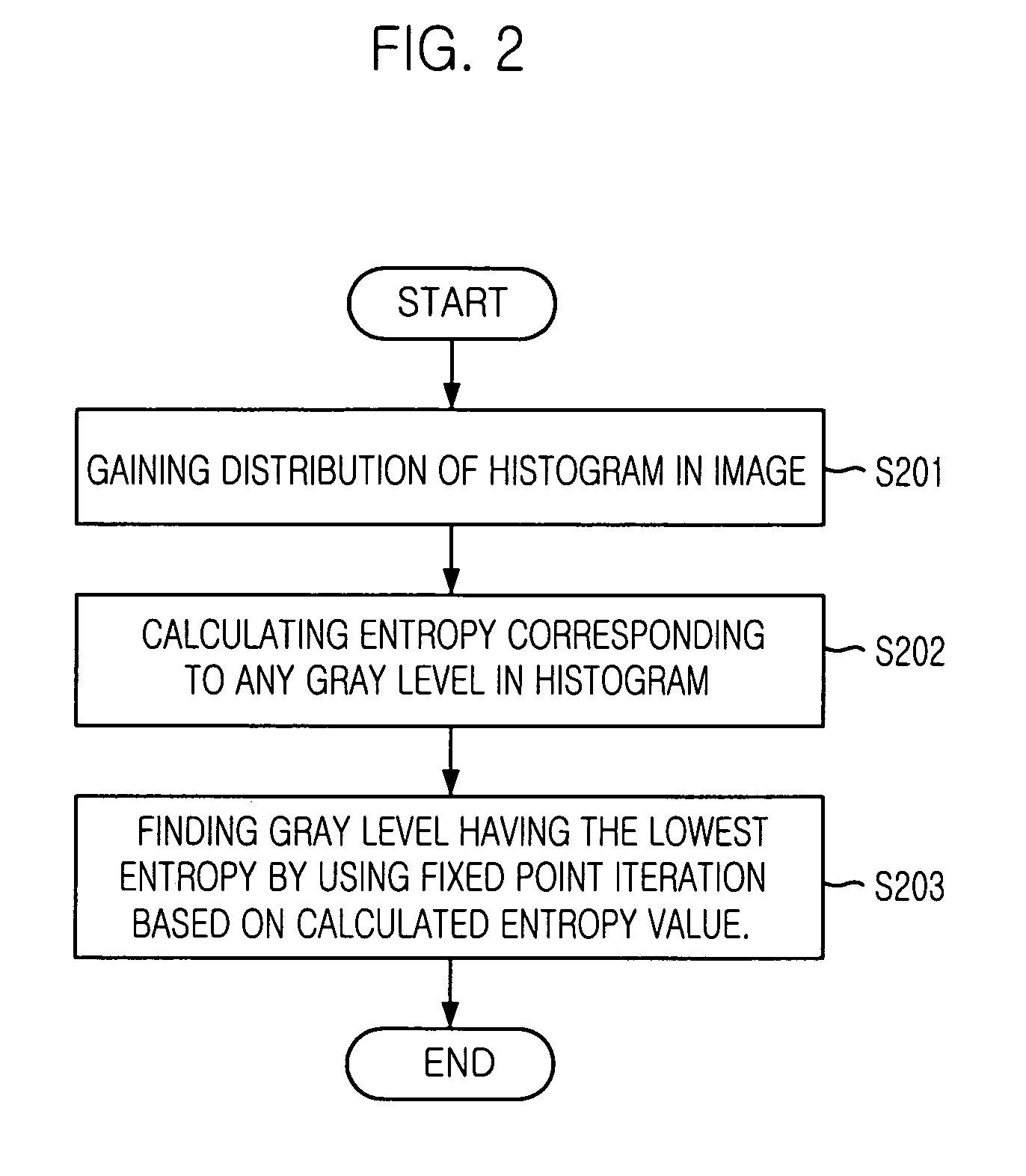
Method for finding optimal threshold for image segmentation
A method for finding the optimal threshold for image segmentation in image recognition is disclosed. The method includes the steps of: a) gaining histogram distribution of an image; b) computing entropy values corresponding to gray levels in the histogram; and c) gaining a minimum entropy value corresponding to the gray level as the threshold value by using a fixed point iteration FPI based on the computed entropy values.
Owner:PANTECH CO LTD
Seismic signal processing method based on improved FastICA algorithm
PendingCN107942376AReduce sensitivityFast convergenceSeismic signal processingAlgorithmNon-Gaussianity
The invention discloses a seismic signal processing method and corresponding processing system based on an improved FastICA algorithm. Through maximizing a negative entropy object function, a non-Gaussian maximum value required by observing signal linear projection is searched by using a fixed point iteration theory so as to fulfill an aim of separating signals; an iteration function is correctedby introducing correction factors improved by utilizing a gradient method, and the FastICA algorithm is optimized. According to the improved FastICA algorithm, the sensibility to an initial weight value is reduced, and the iteration times are reduced, so that the convergence speed of the algorithm is improved.
Owner:ZHENGZHOU YUNHAI INFORMATION TECH CO LTD
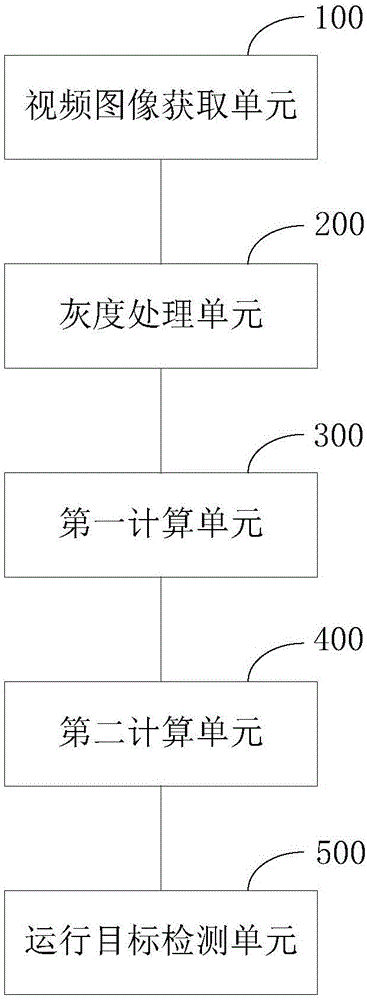
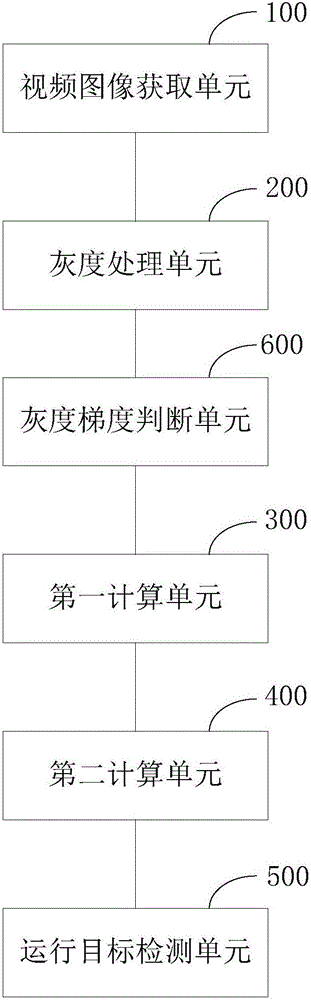
Moving object detection method and device
The invention provides a moving object detection method and device. The method comprises steps as follows: acquiring a video image; performing grey processing on the video image to acquire a grey image; calculating on the basis of the grey image, a preset CLG light stream model E and a preset condition to acquire a first formula; calculating light stream increments duk and dvk of the k layer of a pyramid with a fixed point iteration method according to the first formula and the grey linear invariant hypothesis; detecting a moving object according to the light stream increments duk and dvk of the k layer of the pyramid. According to the moving object detection method, the influence of illumination change on the detection result is considered, the algorithm for evaluation of the moving object is more accurate, and accordingly, the moving object can be detected stably and accurately when the illumination suddenly changes.
Owner:CHANGCHUN INST OF OPTICS FINE MECHANICS & PHYSICS CHINESE ACAD OF SCI
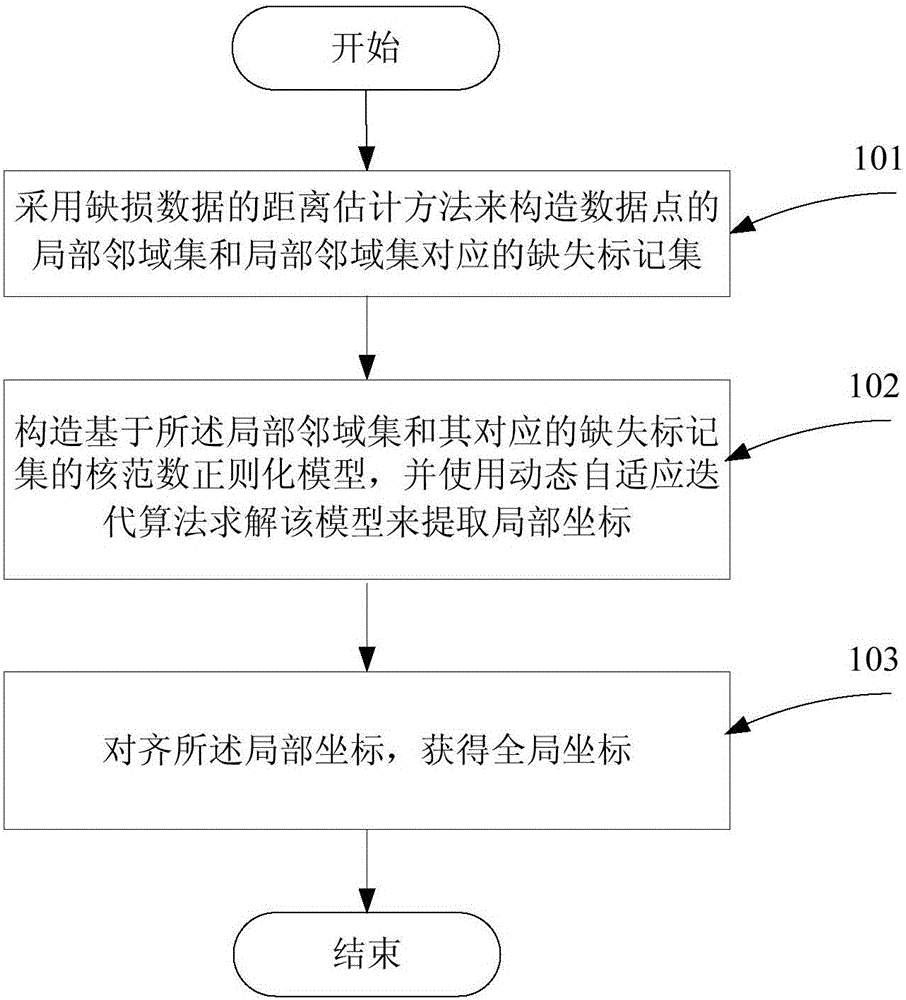
Nonlinear characteristic extraction and classification based on defect data
ActiveCN106203480APrecise constructionAccurate extractionCharacter and pattern recognitionNuclear norm regularizationEstimation methods
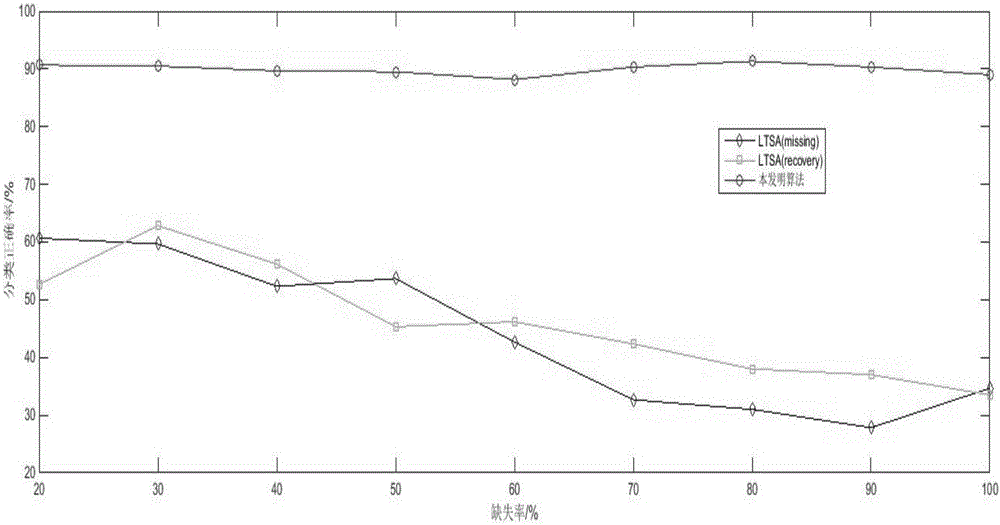
The present invention discloses a nonlinear characteristic extraction and classification based on defect data. The method comprises a step of using the distance estimation method of defect data to construct the local neighborhood set of a data point and a missing marker set corresponding to the local neighborhood set, a step of constructing a nuclear norm regularization model based on the local neighborhood set and the corresponding missing marker set, and using an adaptive fixed point iteration algorithm to solve the model to extract a local coordinate, and a step of aligning the local coordinate to obtain a global coordinate. According to the method, in facing the defect data, the local neighborhood set can be constructed, the local coordinate can be extracted, the global coordinate can be covered, and the nonlinear characteristic extraction and classification of the defect data are finally realized.
Owner:HUAQIAO UNIVERSITY
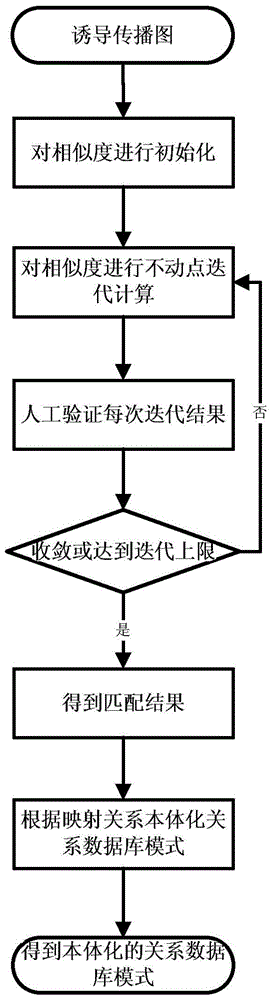
A Mapping Method Between Ontology and Relational Database Schema
ActiveCN104036048BMake it easier to getSpend less timeDatabase management systemsRelational databasesOntology schemaRelational database
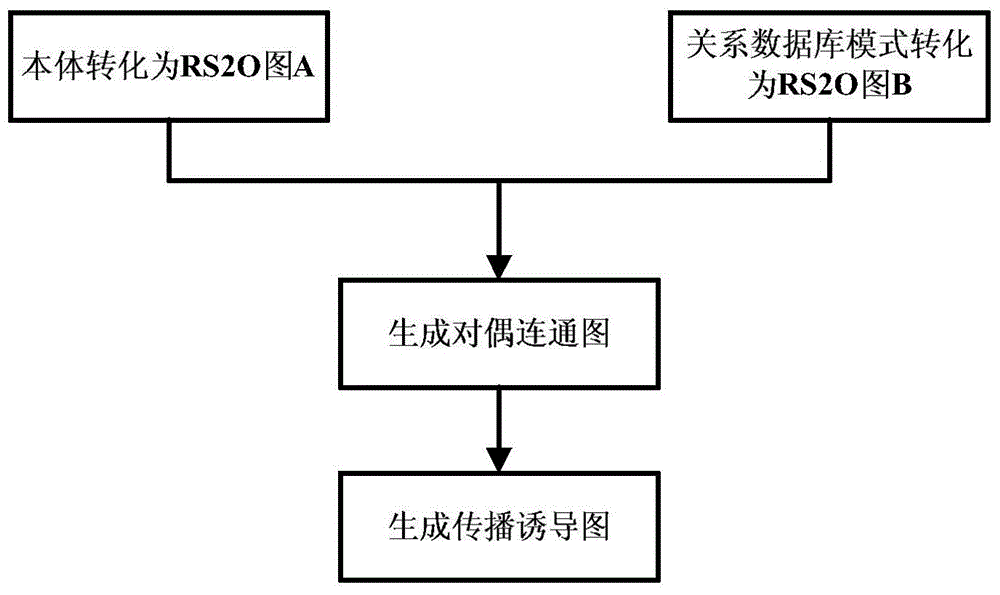
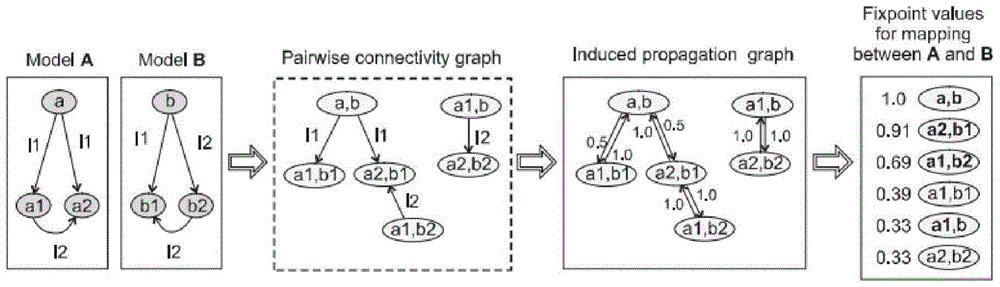
The invention discloses a mapping method between an ontology pattern and a relational database pattern, establishes an RS2O graph as an intermediate model between the ontology pattern and the relational pattern, converts both the ontology and the relational database pattern into an RS2O pattern; combines the RS2O pattern of the ontology and the relationship RS2O in the database mode establishes a dual connected graph, and constructs an induced propagation graph for the mapping pairs in the dual connected graph plus reverse edges; iteratively calculates the similarity of the mapping pairs and performs manual feedback, and matches the relationship according to the calculation results The mapping relationship between database schema elements and ontology elements. The candidate matching relationship is obtained through calculation, and after manual verification, the matching relationship is confirmed, which greatly reduces the labor cost. While reducing the difficulty and time spent on obtaining the mapping relationship, it also effectively guarantees the accuracy of the final mapping relationship. Yes for 100%. It is suitable for data exchange, sharing and integration among heterogeneous relational databases.
Owner:UNIV OF ELECTRONICS SCI & TECH OF CHINA
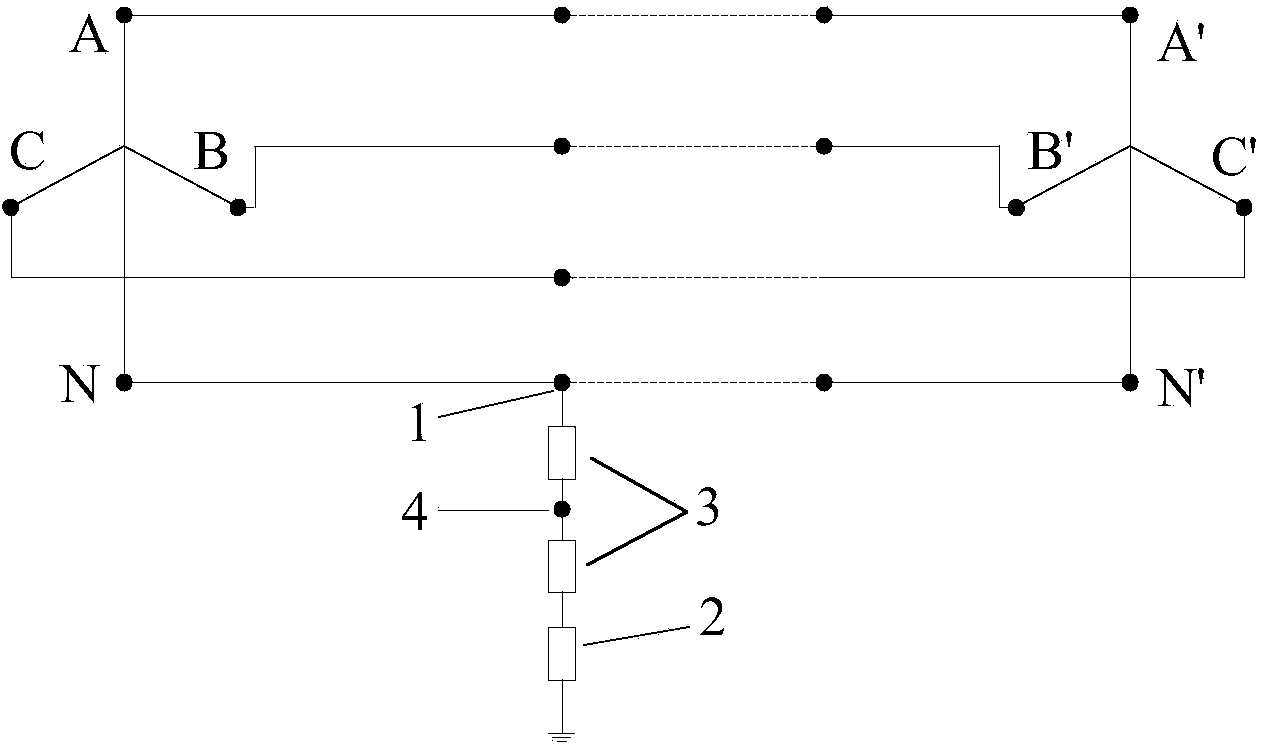
Impedance compensation method for enabling forward-back substitution load flow calculation of three-phase four-wire system power distribution network to be converged
InactiveCN104134012AHas engineering practical valueAchieve convergenceSpecial data processing applicationsNeutral lineGrounding resistance
The invention relates to an impedance compensation method for enabling forward-back substitution load flow calculation of a three-phase four-wire system power distribution network to be converged, and belongs to the technical field of power distribution network dispatching automation. The impedance compensation method solves the forward-back substitution load flow calculation convergence problem caused by too small neutral line grounding resistance, and the spectral radius of the jacobian matrix of fixed point iteration of the independent node voltage of the power distribution network in the power distribution network is utilized for judging the convergence of the load flow calculation. When the load flow calculation is not converged, a pair of opposite impedances is compensated between a neutral line grounding resistor and a grounding point through a spectrum in the power distribution network, after impedance compensation, a new node is added to the power distribution network, the newly-added node participates in the fixed point iteration of the independent node voltage of the power distribution network, the voltage of the newly-added node is obtained firstly, then the voltage of the newly-added node is utilized for solving the voltage of the neutral line node, therefore, the fixed point iteration is made to meet the condition of compressed mapping, and the convergence of the load flow calculation is achieved.
Owner:TSINGHUA UNIV +1
A Robust Joint Estimation Method of Transmitting and Receiving Angles for Large Array MIMO Radar Targets
ActiveCN107167785BSolve the missing rank problemSolve the problem of inaccurate estimation of receiving and receiving anglesWave based measurement systemsTransceiverArray element
The invention provides a robust large-array MIMO target transmitting and receiving angle joint estimation method, and belongs to the field of multiple-input multiple-output radar target parameter estimation. The method provided by the invention is based on linear shrinkage and a random matrix theory. Implementation of the method comprises the steps of building a random matrix model of observed data by using echo signals, solving maximum likelihood estimation of a covariance matrix through fixed-point iteration under the non-Gaussian noise background, acquiring robust covariance matrix estimation by using a linear shrinkage technology when the number of transmitting and receiving array elements is greater than the number of snapshots, building a robust cost function by using contour integration, Stieltjes transform and a residue theorem, and performing spectrum peak search on the cost function so as to solve the target transmitting and receiving angle. The method provided by the invention has the advantages that the method has robust estimation performance under the non-Gaussian noise background, and the method is applicable to a large-array system with the number of transmitting and receiving array elements being greater than the number of snapshots at the same time.
Owner:JILIN UNIV
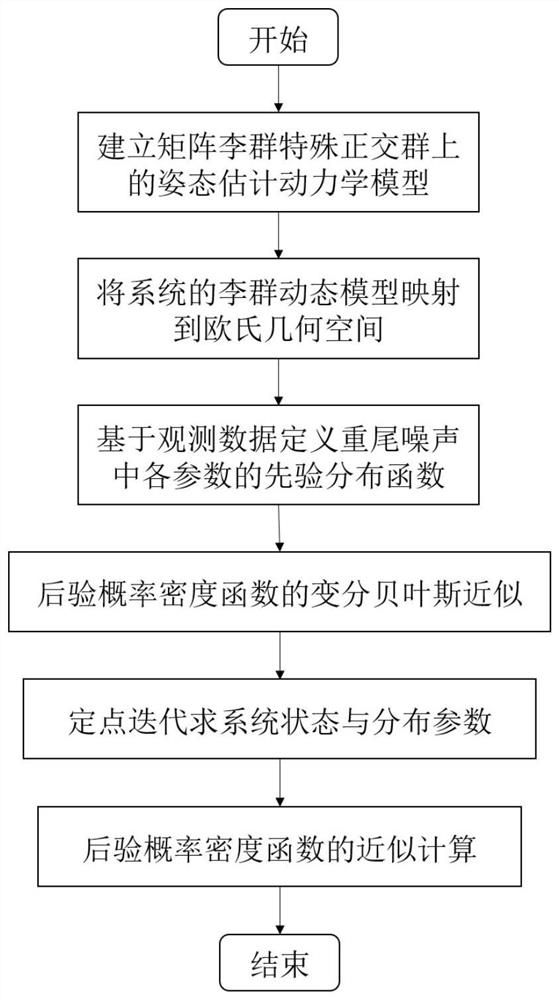
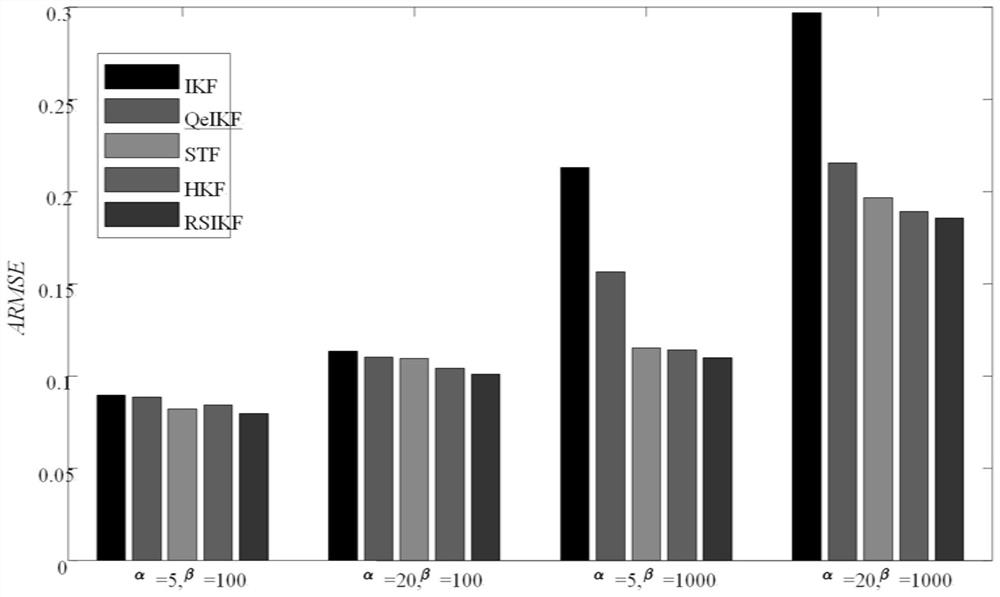
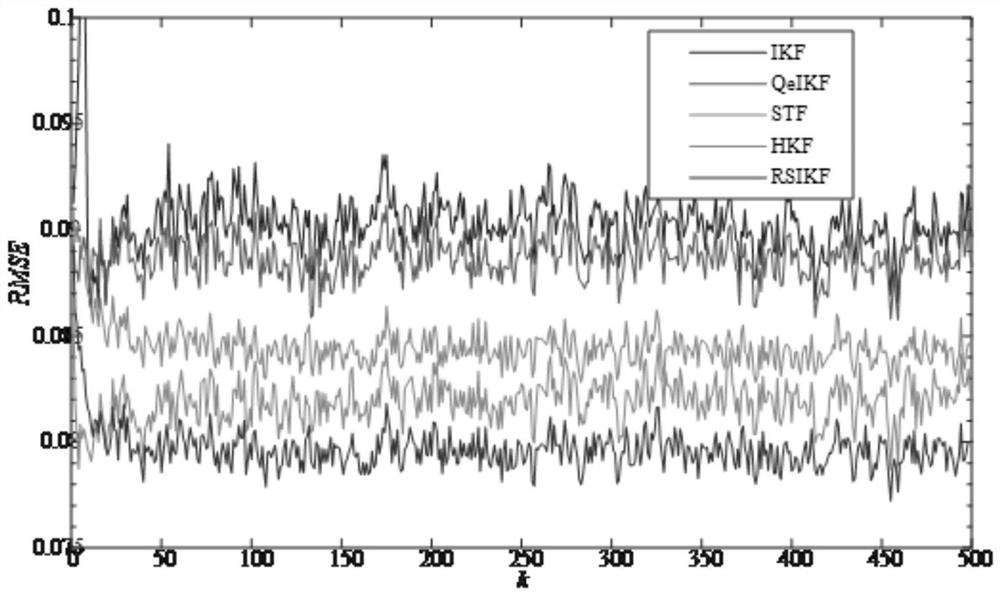
Lie group heavy-tail interference noise dynamic aircraft attitude estimation method based on variational iterative Kalman filtering
PendingCN113670315ASolving the Pose Estimation ProblemImprove robustnessNavigational calculation instrumentsComplex mathematical operationsNormal densityAlgorithm
The invention provides a Lie group heavy-tail interference noise dynamic aircraft attitude estimation method based on variational iterative Kalman filtering. The method comprises the following steps: 1 establishing an attitude dynamic model of a system on a Lie group special orthogonal group; 2 mapping the Lie group dynamic model of the system to an Euclidean geometric space; 3 defining a prior distribution function of each parameter in the heavy-tail noise based on the observation data; 4 carrying out variational Bayesian approximation on the probability density function of the heavy-tail noise; 5 solving distribution parameters of the system state and the probability density function through fixed-point iteration; and 6 substituting each parameter in the step 5 into the step 4 for calculation to obtain a posterior probability density function approximate value of the noise. According to the method, the Lie group attitude estimation problem of the system under the interference of the heavy-tail noise is well solved.
Owner:BEWIS TECH
A Texture Mapping Method Based on Triangular Mesh Simplification
InactiveCN104680573BReduce time complexityImprove timing performance3D-image rendering3D modellingComputational scienceImaging processing
The invention belongs to the technical field of image processing and particularly relates to a texture mapping method based on triangular mesh simplification. The texture mapping method comprises the following steps: simplifying a triangular network model and establishing a spring-mass-point model; parameterizing the spring-mass-point model to a final position of a rectangular region; by utilizing a process of simplifying the triangular network model, calculating an initial position of a deleted point in the parameterized rectangular region to obtain positions of all vertexes of an initial model in the parameterized rectangular region; parameterizing the initial model to establish the spring-mass-point model; fixing the boundary vertex and triggering inner point iteration until the position of an inner point is balanced to obtain a spring-mass-point model revised parameterized coordinate; and carrying out normalization processing to obtain a texture coordinate of a grid vertex, and carrying out texture mapping. According to the method, the texture coordinate of each triangular network grid vertex does not need to be solved and texture mapping can be directly carried out; the time complexity of the method can be reduced to the great extent and the time performance is improved.
Owner:XIAN UNIV OF SCI & TECH
An efficient and fast method for simulating hydraulic fracturing
ActiveCN108197358BEffective simulationTo achieve the purpose of dimension reduction processingDesign optimisation/simulationSpecial data processing applicationsSingular value decompositionEngineering
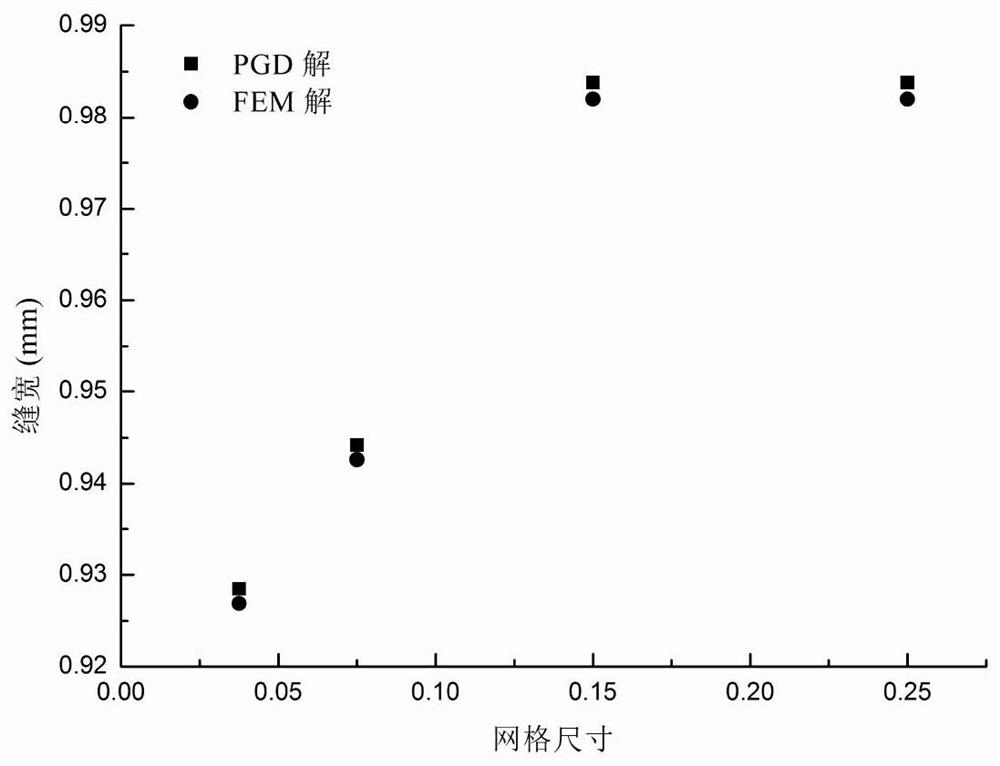
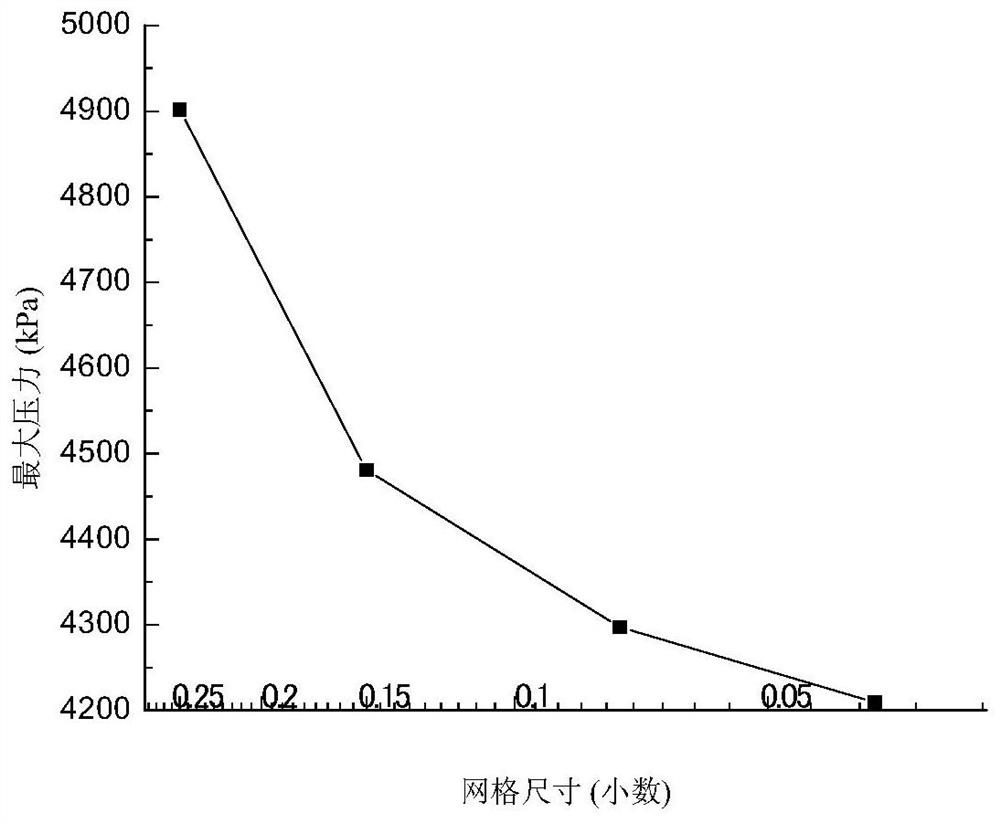
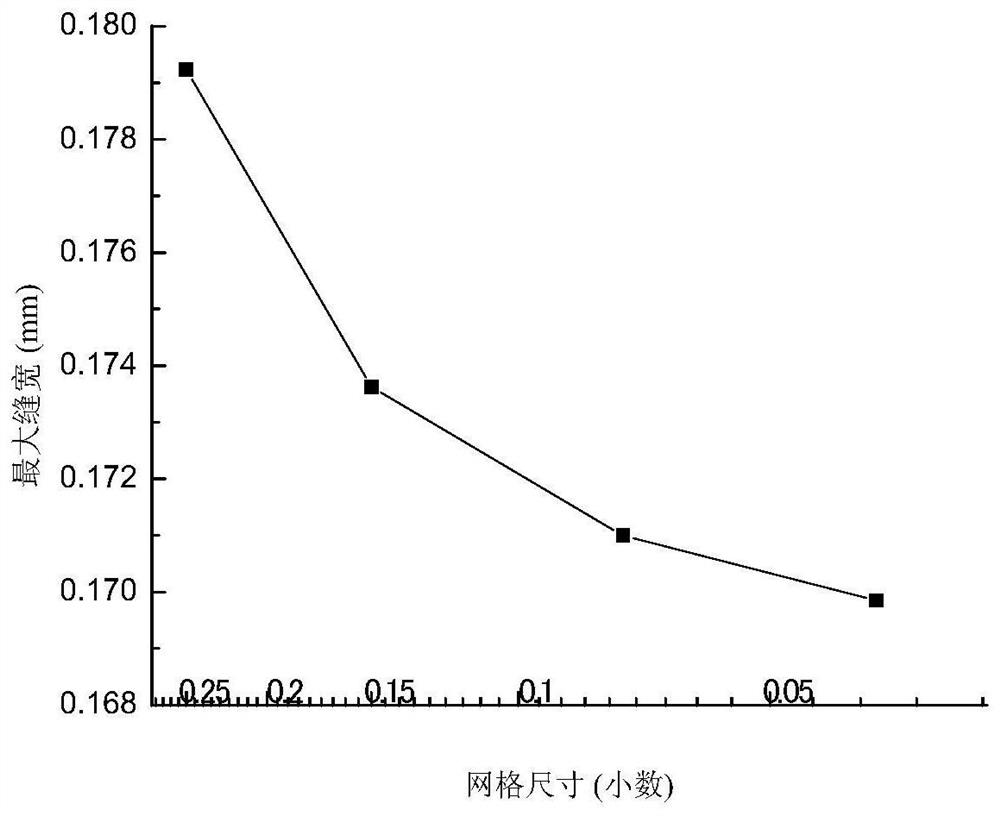
A method for quickly and efficiently simulating hydraulic fracturing, comprising the following steps: 1) according to the finite element variational principle, obtain the weak form of hydraulic fracturing equations; 2) according to the weak form of the equations, discretize the , and use finite difference approximation to the first derivative of the fluid equation with respect to time, and obtain the finite element discrete scheme; 3) Singular value decomposition is performed on the stiffness matrix of the fluid equation, and the time domain and the space domain are decomposed; 4) The PGD Substituting the solution into the discrete format, the discrete equations decomposed in the time domain and the space domain are obtained respectively; 5) Solve with the alternating direction iterative method to obtain the size of X and T; 6) Repeat steps 4) and 5) to obtain each item X m and T m ; 7) Each item X obtained in step 6 m and T m Multiply and sum to obtain the PGD solution of the pressure field; 8) Perform fixed-point iteration on the fluid equation; 9) Output the pressure field p, and then obtain the displacement field u according to the solid discrete equation; 10) Calculate the fracture geometry parameters.
Owner:BEIJING INSTITUTE OF PETROCHEMICAL TECHNOLOGY +1
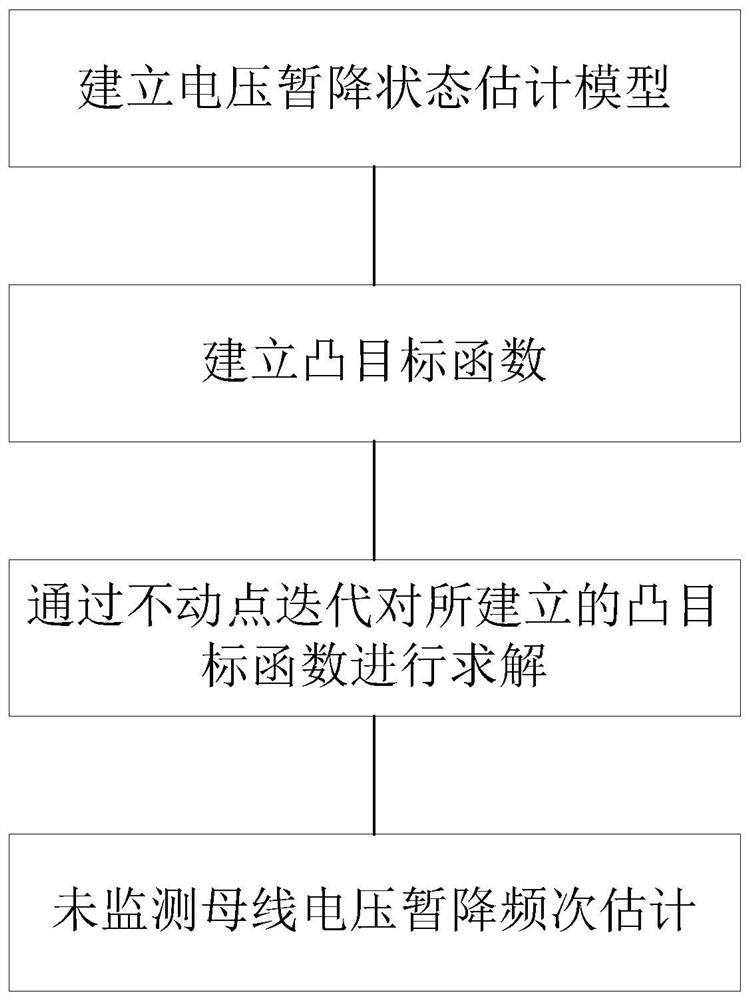
A method of voltage sag state estimation based on fixed point iteration
ActiveCN113363993BReduce monitoring costsFast convergenceAc network voltage adjustmentComplex mathematical operationsMonitoring siteMathematical model
Owner:ELECTRIC POWER RES INST STATE GRID JIBEI ELECTRIC POWER COMPANY +2
Features
- R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
Why Patsnap Eureka
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com