Patents
Literature
55results about How to "Fully analyzed" patented technology
Efficacy Topic
Property
Owner
Technical Advancement
Application Domain
Technology Topic
Technology Field Word
Patent Country/Region
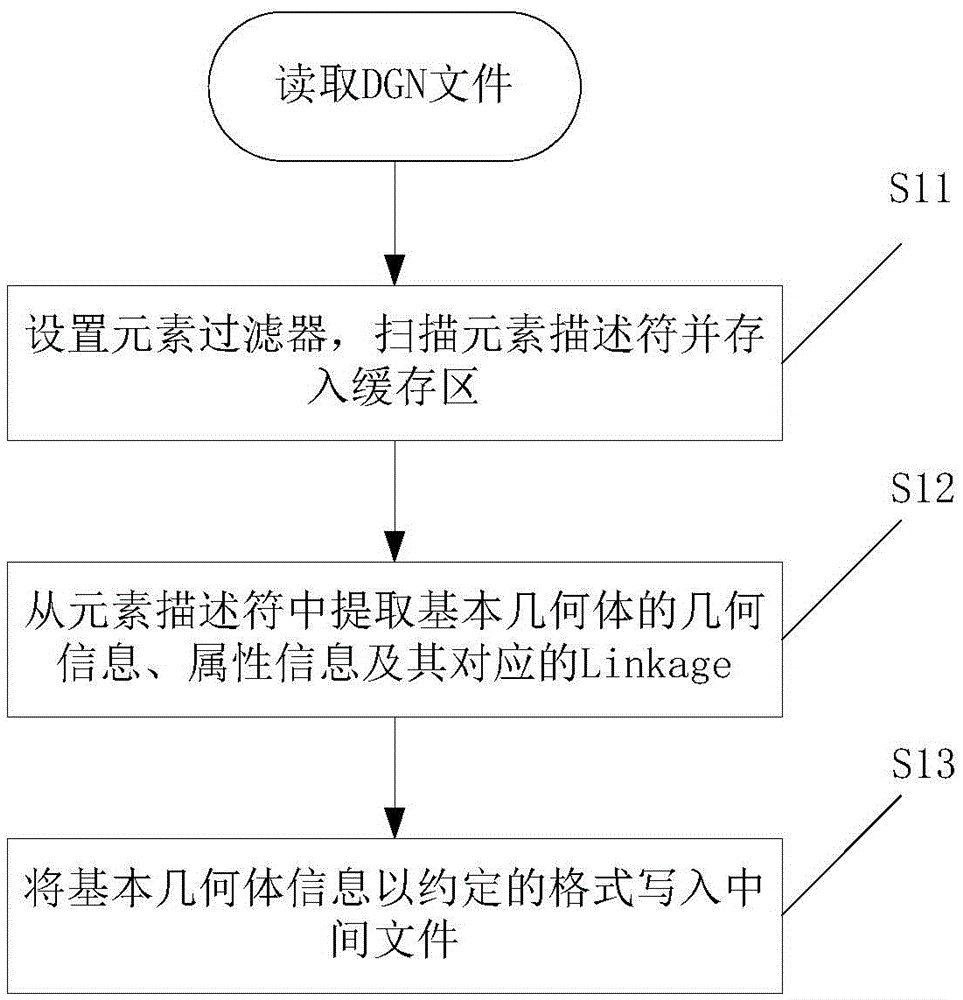
Patent Type
Patent Status
Application Year
Inventor
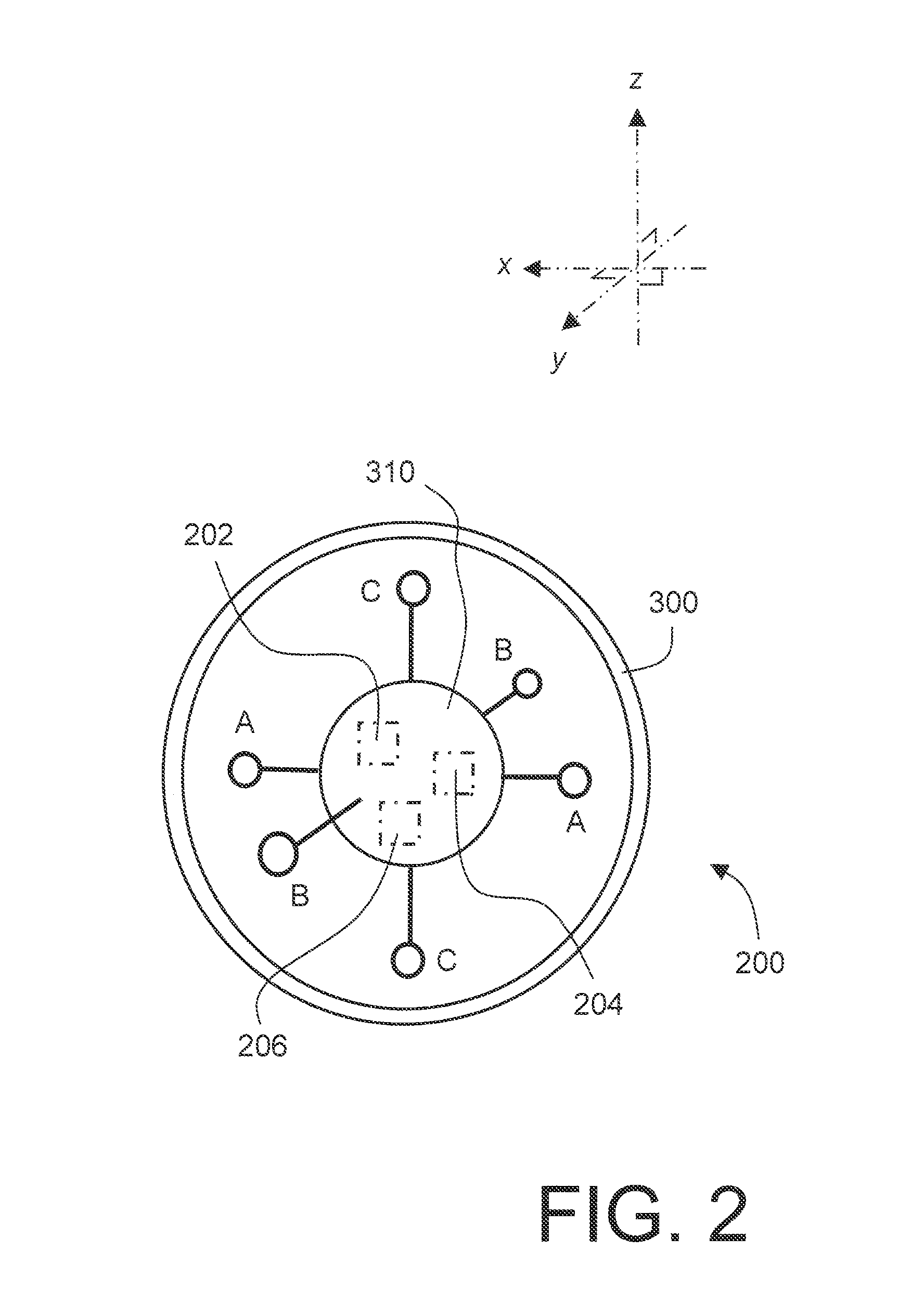
Sports apparatus and method
ActiveUS20140120960A1Fully analyzedPosition fixationServices signallingData processing systemSports equipment
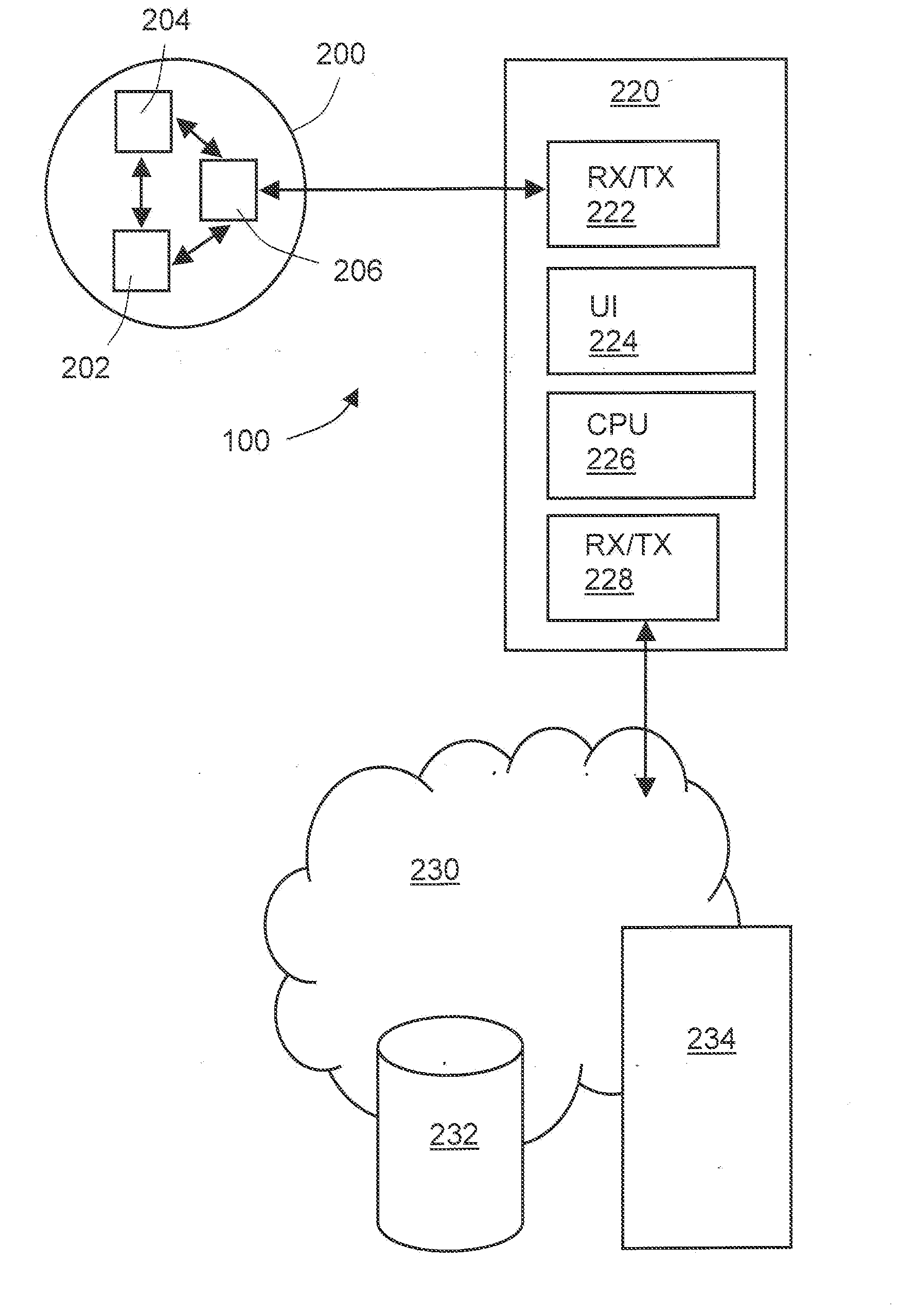
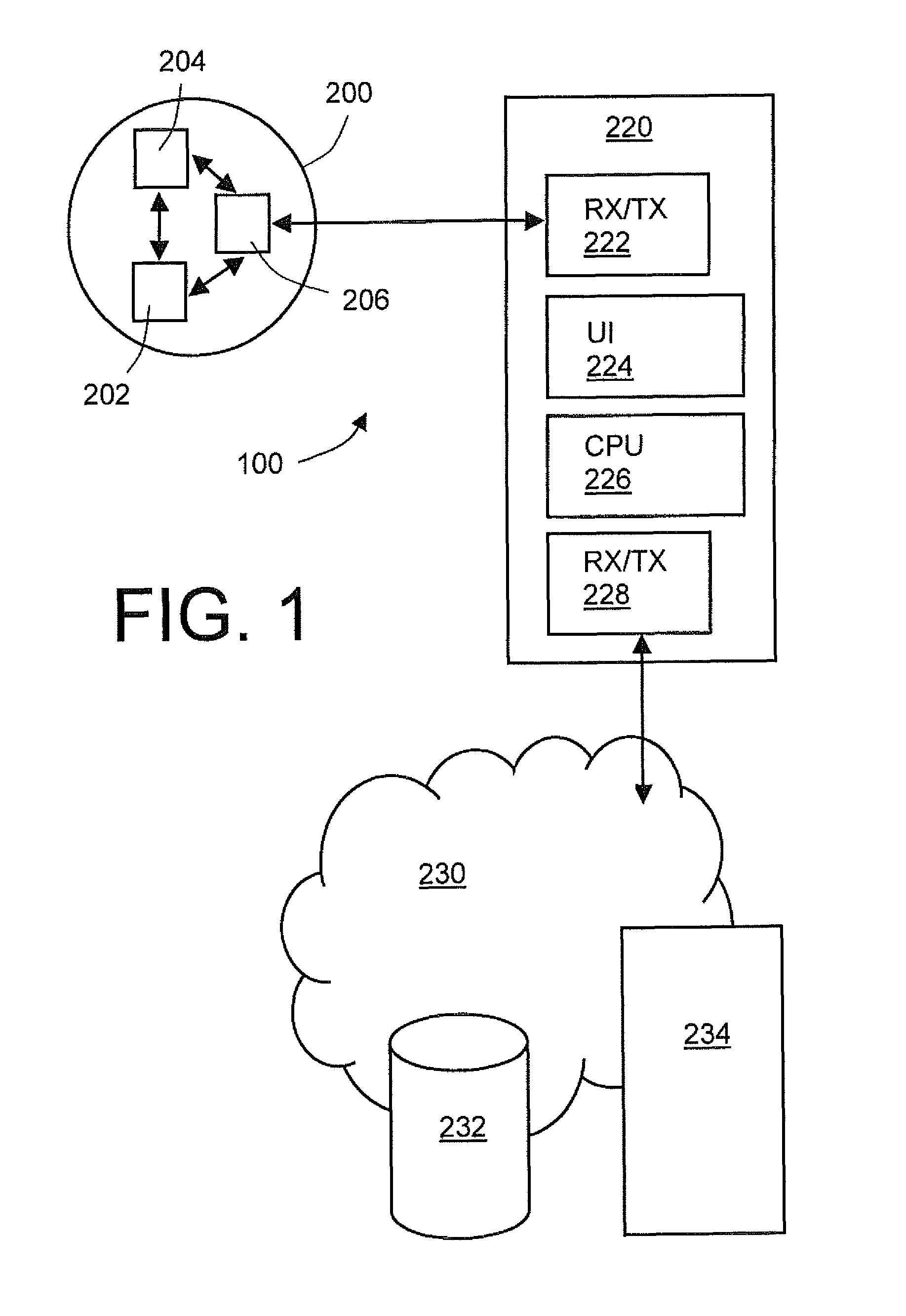
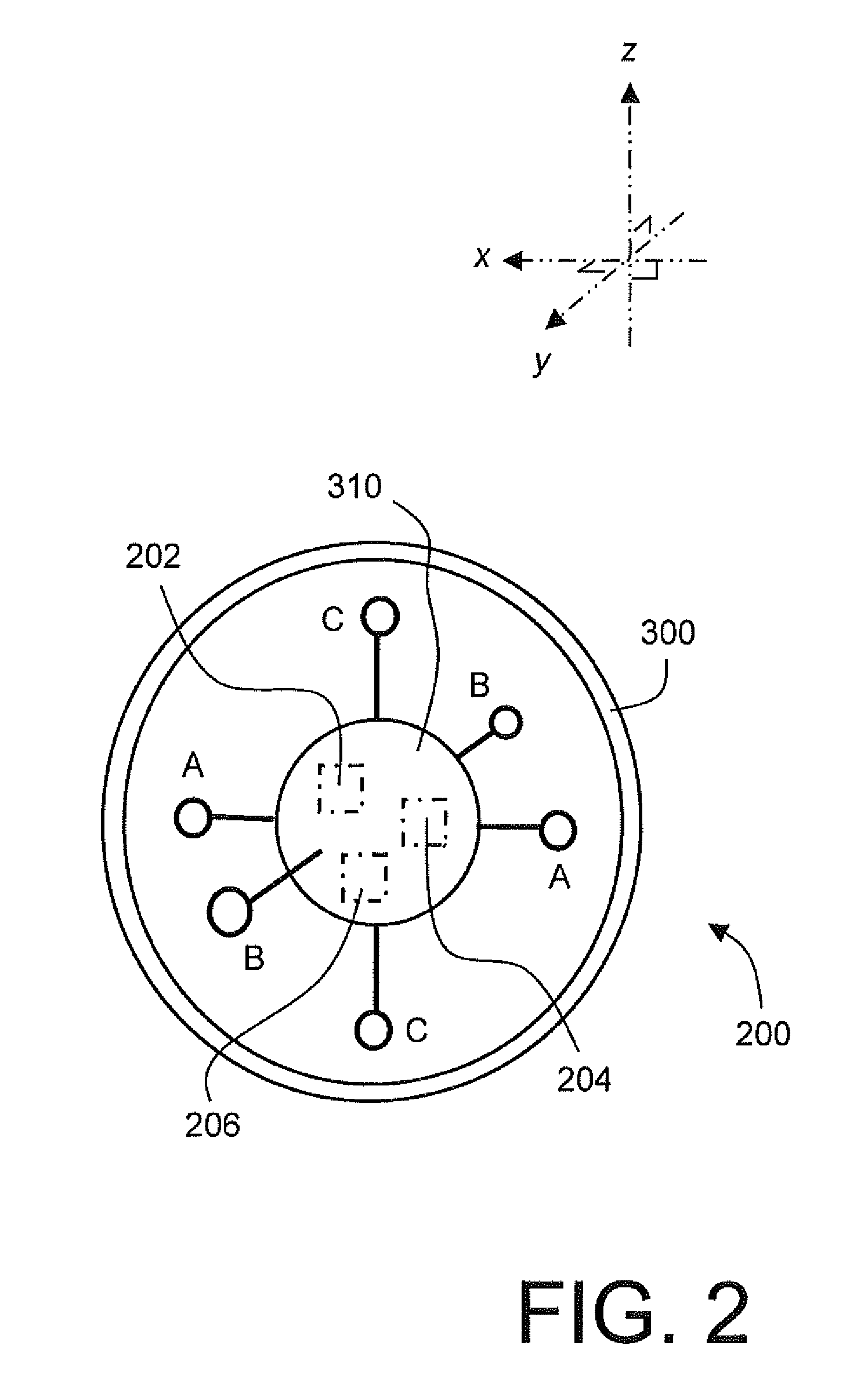
A sports apparatus is provided for monitoring movement of one or more projectiles associated with a sporting event. The apparatus includes a data processing system for processing sampled data signals generated in operation by one or more sensors (202, 204) included in the one or more projectiles. Moreover, the apparatus includes a mobile telephone coupled in wireless communication with the one or more projectiles for receiving the sampled data signals indicative of motion of the one or more projectiles. Furthermore, the mobile telephone is operable to execute one or more software products therein for analyzing the sampled data signals received at the mobile telephone for providing analysis results indicative of a nature of trajectory of the one or more projectiles.
Owner:SSTATZZ
Underwater acoustic signal target classification and recognition method based on deep learning
ActiveCN109800700AEffective Voiceprint FeaturesImprove robustnessBiological neural network modelsCharacter and pattern recognitionFeature extractionDecomposition
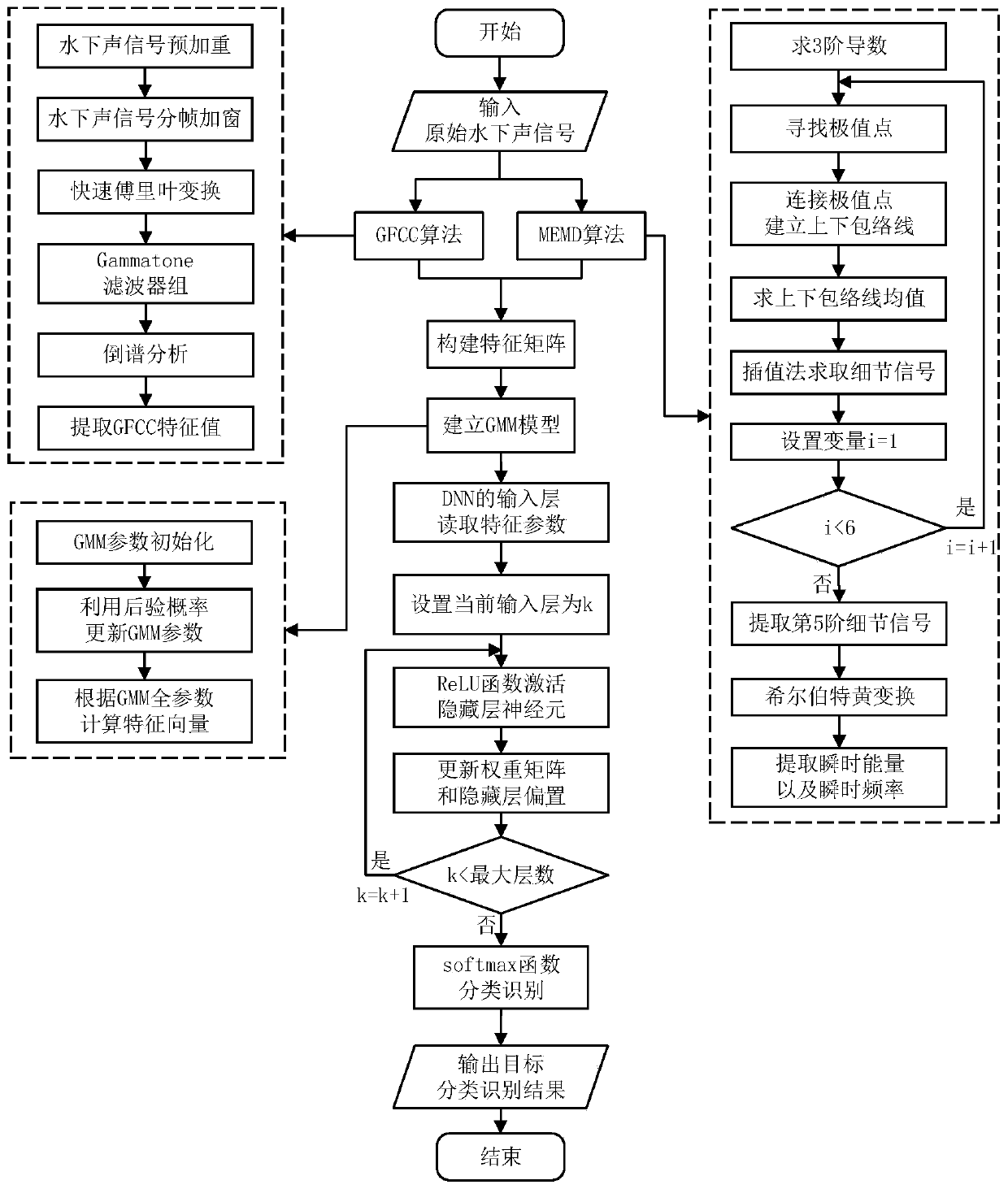
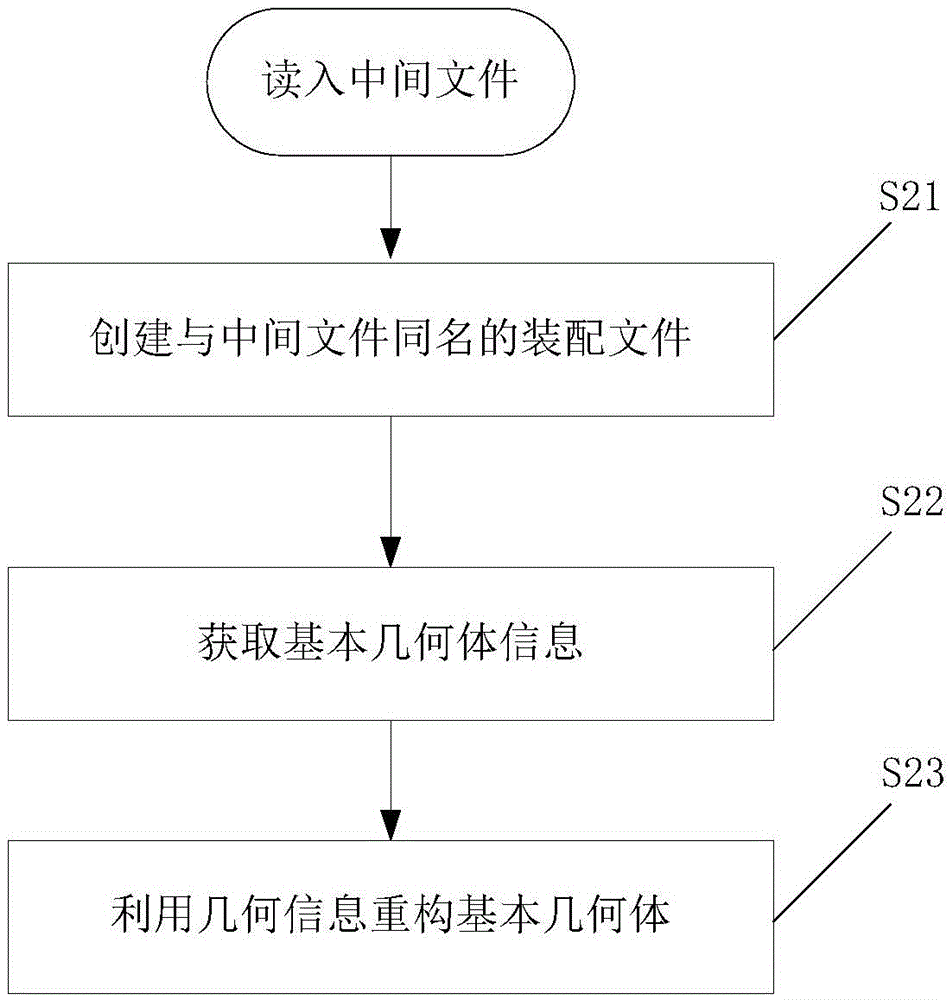
The invention belongs to the technical field of underwater acoustic signal processing, and particularly relates to an underwater acoustic signal target classification and recognition method based on deep learning. The method comprises the following steps: (1) carrying out feature extraction on an original underwater acoustic signal through a Gammatone filtering cepstrum coefficient (GFCC) algorithm; (2) extracting instantaneous energy and instantaneous frequency by utilizing an improved empirical mode decomposition (MEMD) algorithm, fusing the instantaneous energy and the instantaneous frequency with characteristic values extracted by a GFCC algorithm, and constructing a characteristic matrix; (3) establishing a Gaussian mixture model GMM, and keeping the individual characteristics of theunderwater acoustic signal target; And (4) finishing underwater target classification and recognition by using a deep neural network (DNN). According to the underwater acoustic signal target classification and recognition method, the problems that a traditional underwater acoustic signal target classification and recognition method is single in feature extraction and poor in noise resistance can be solved, the underwater acoustic signal target classification and recognition accuracy can be effectively improved, and certain adaptability is still achieved under the conditions of weak target acoustic signals, long distance and the like.
Owner:HARBIN ENG UNIV
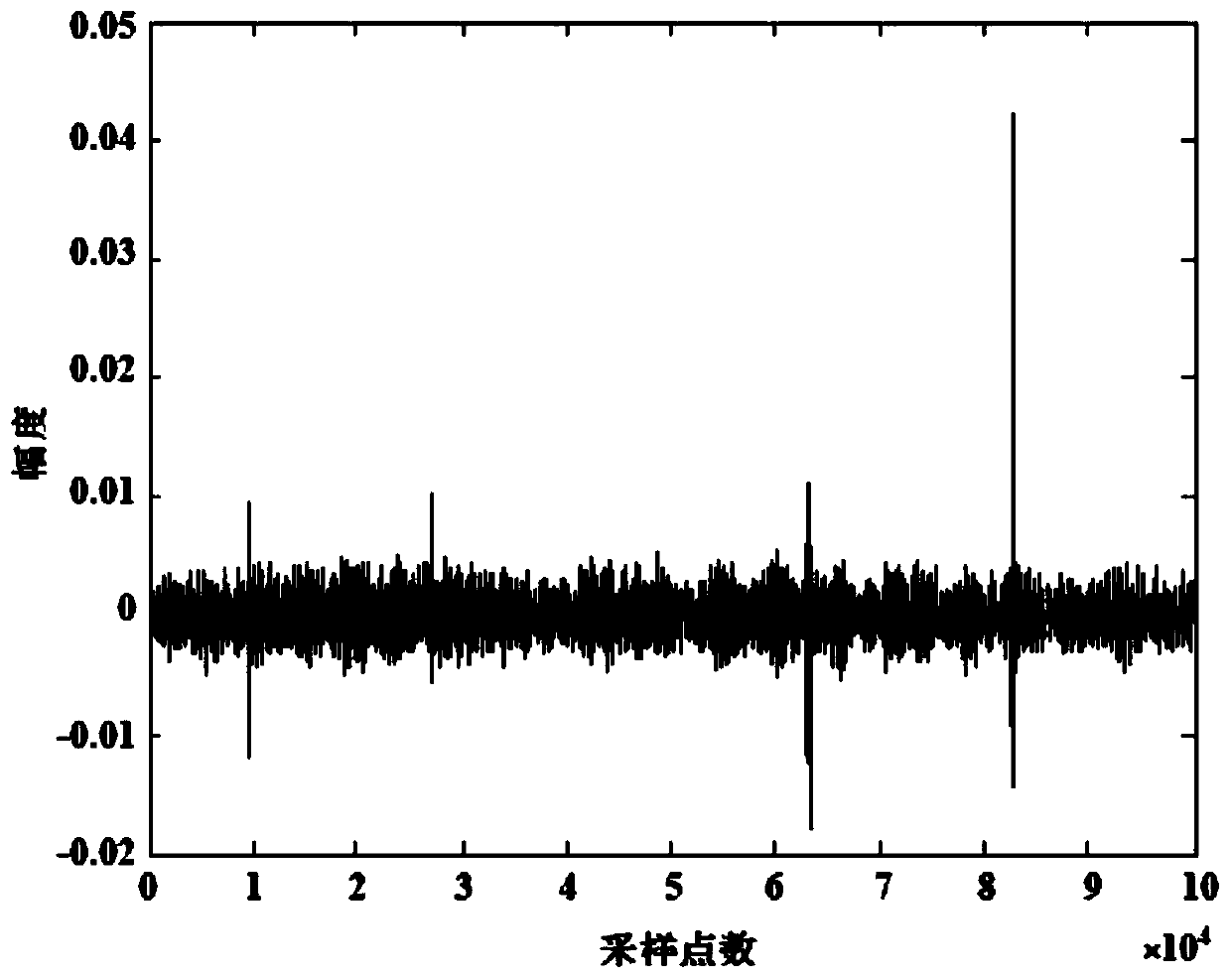
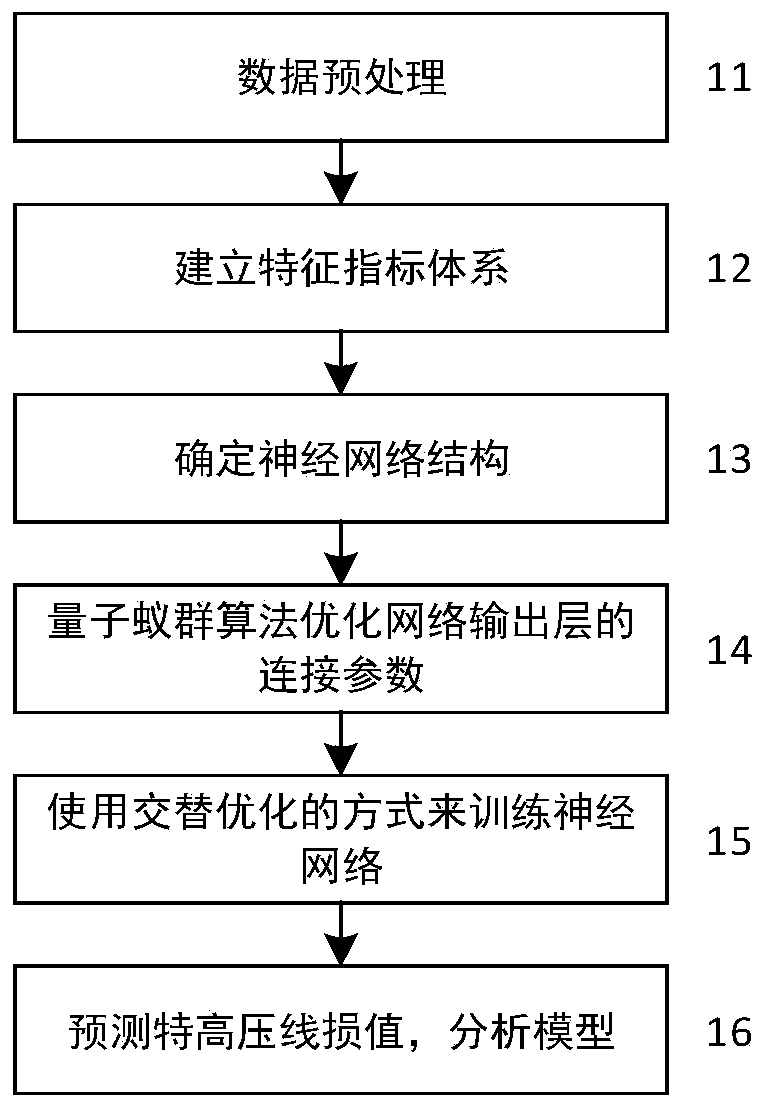
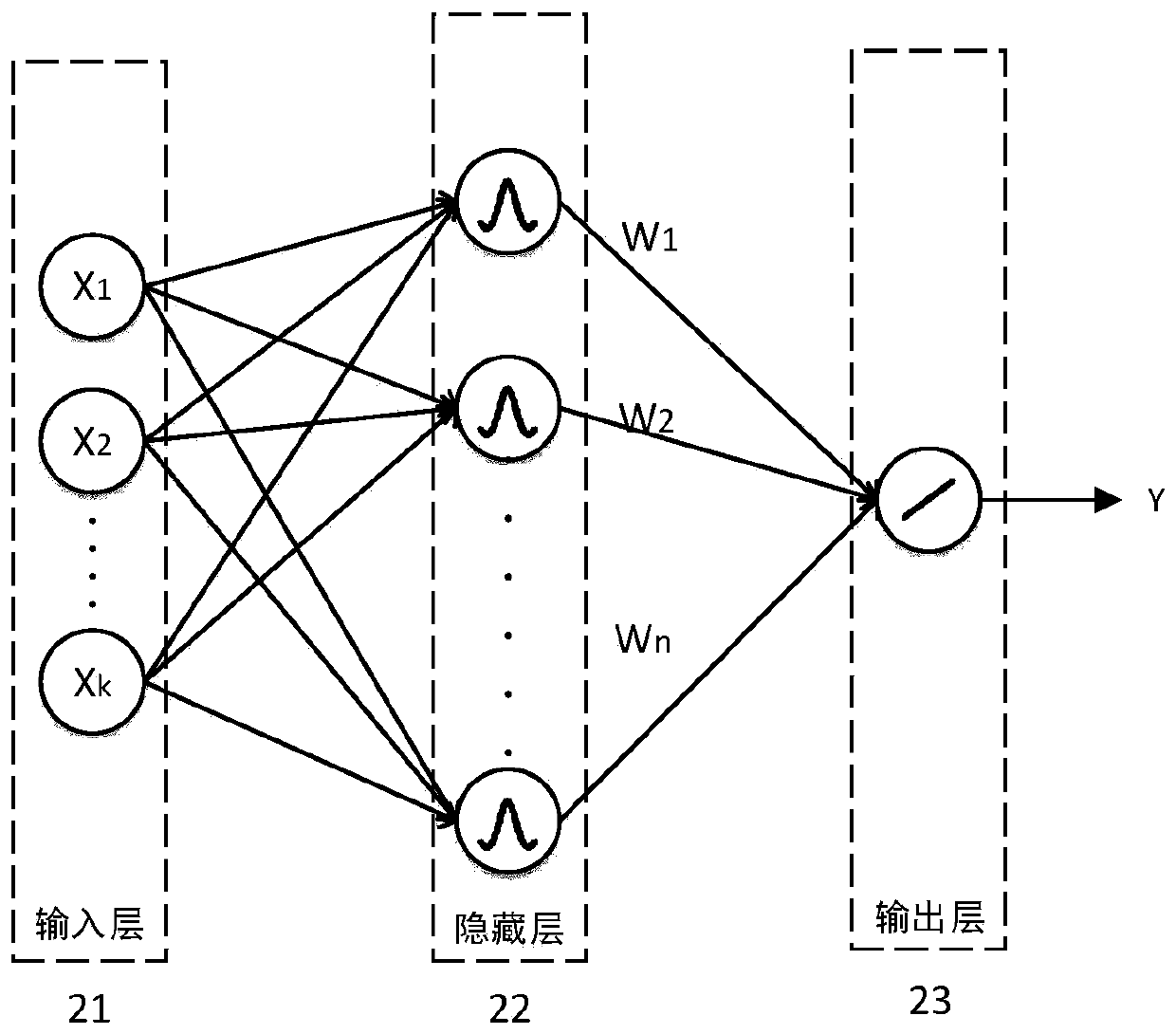
Extra-high voltage transmission line loss prediction method based on quantum ant colony optimization RBF network
InactiveCN110765700AFit closelyEasy to useCharacter and pattern recognitionDesign optimisation/simulationElectric power systemPredictive methods
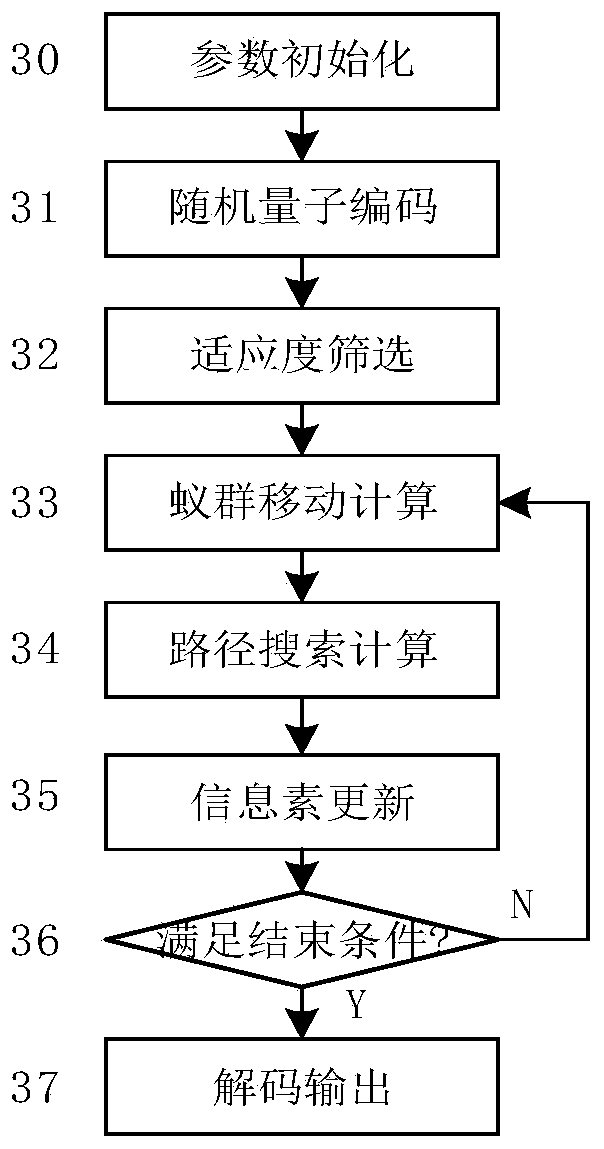
The invention discloses an extra-high voltage transmission line loss prediction method based on a quantum ant colony optimization RBF network, and belongs to the technical field of combination of an electric power system and deep learning. The method comprises the following steps: (1) preprocessing data; (2),establishing a characteristic index system; 3, determining a neural network structure; (4)optimizing connection parameters of a network output layer by a quantum ant colony algorithm; (5) training the neural network by using an alternate optimization mode; (6) predicting the extra-high voltage line loss value, and analyzing the prediction model. According to the invention, by use of a neural network calculation mode, various nonlinear relationships are easy to fit, calculation detailsdo not need to be manually controlled when the relationship between input parameters and line loss is found, and use is simple; the RBF neural network is used for guaranteeing that the training speedis high, the local approximation characteristic is achieved, and the calculation process is simple; the quantum ant colony algorithm is introduced into the optimization process of the neural network,and the problem that the optimization of the neural network is easy to fall into the local optimal solution is improved.
Owner:CENT CHINA BRANCH OF STATE GRID CORP OF CHINA
PDS three-dimensional model analysis and reconstruction method
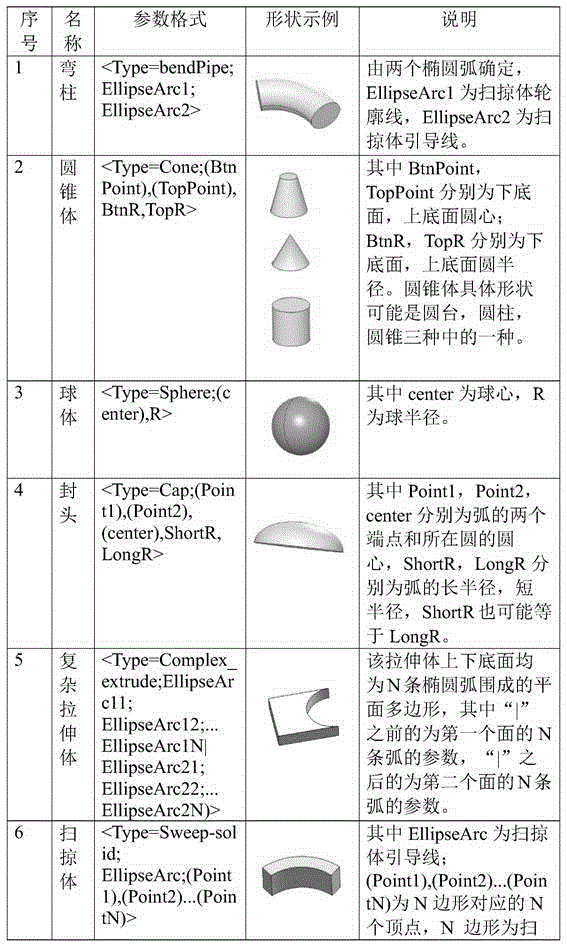
ActiveCN105488254AAccurate virtual simulation verificationAccurate displayDetails involving 3D image dataSpecial data processing applicationsInformation analysisAlgorithm
Owner:SHANGHAI NUCLEAR ENG RES & DESIGN INST CO LTD
SDN-based Internet of Things network data forwarding system
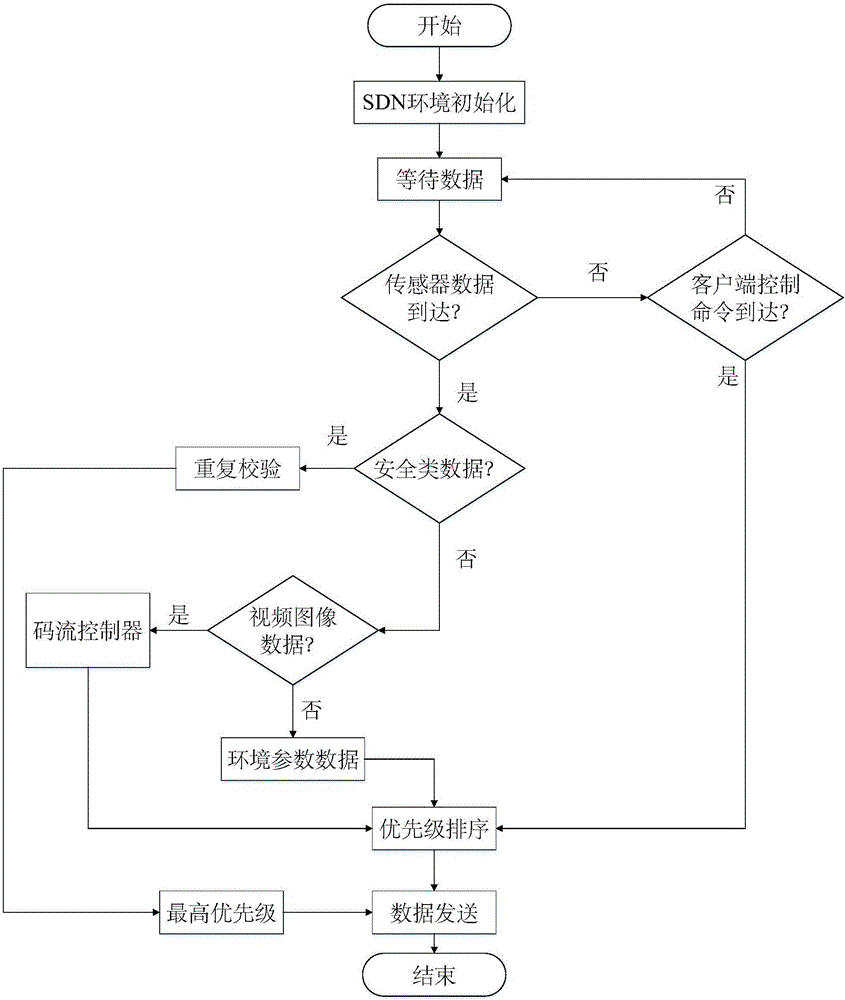
InactiveCN106302254AImprove data forwarding efficiencyImprove forwarding efficiencyData switching networksTraffic capacityControl layer
The invention discloses a SDN-based Internet of Things data forwarding system, and belongs to the control application field of the SDN network traffic. The system comprises an Internet of Things equipment layer, an OpenFlow switch layer, a SDN control layer, a REST API abstract layer, an Internet of Things client layer. After the Internet of Things data is collected, the system firstly classifies the data in the Internet of Things, and then performs secondary processing on pointedly according to the classification result, the data after the secondary processing is sent to a priority controller to judge the priority, and the data is forwarded according to the network environment. The SDN is combined with the forwarding of the Internet of Things data, the data forwarding is pointedly performed according to the features of the Internet of Things data while processing large-scale Internet of Things data; the utilization efficiency of the network is improved, the robustness of the network is guaranteed, and the system has actual application value.
Owner:SUZHOU RES INST SHANDONG UNIV
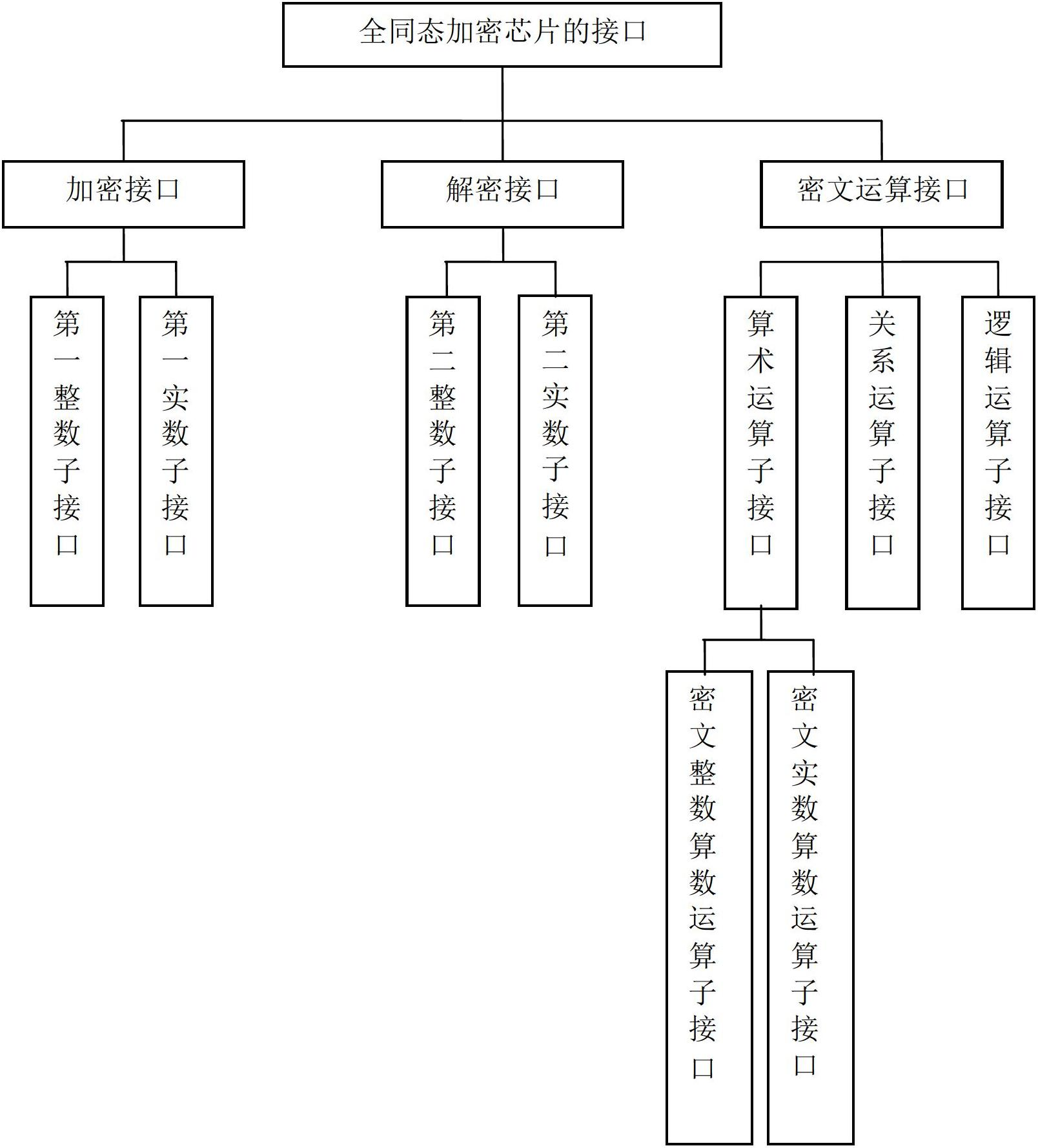
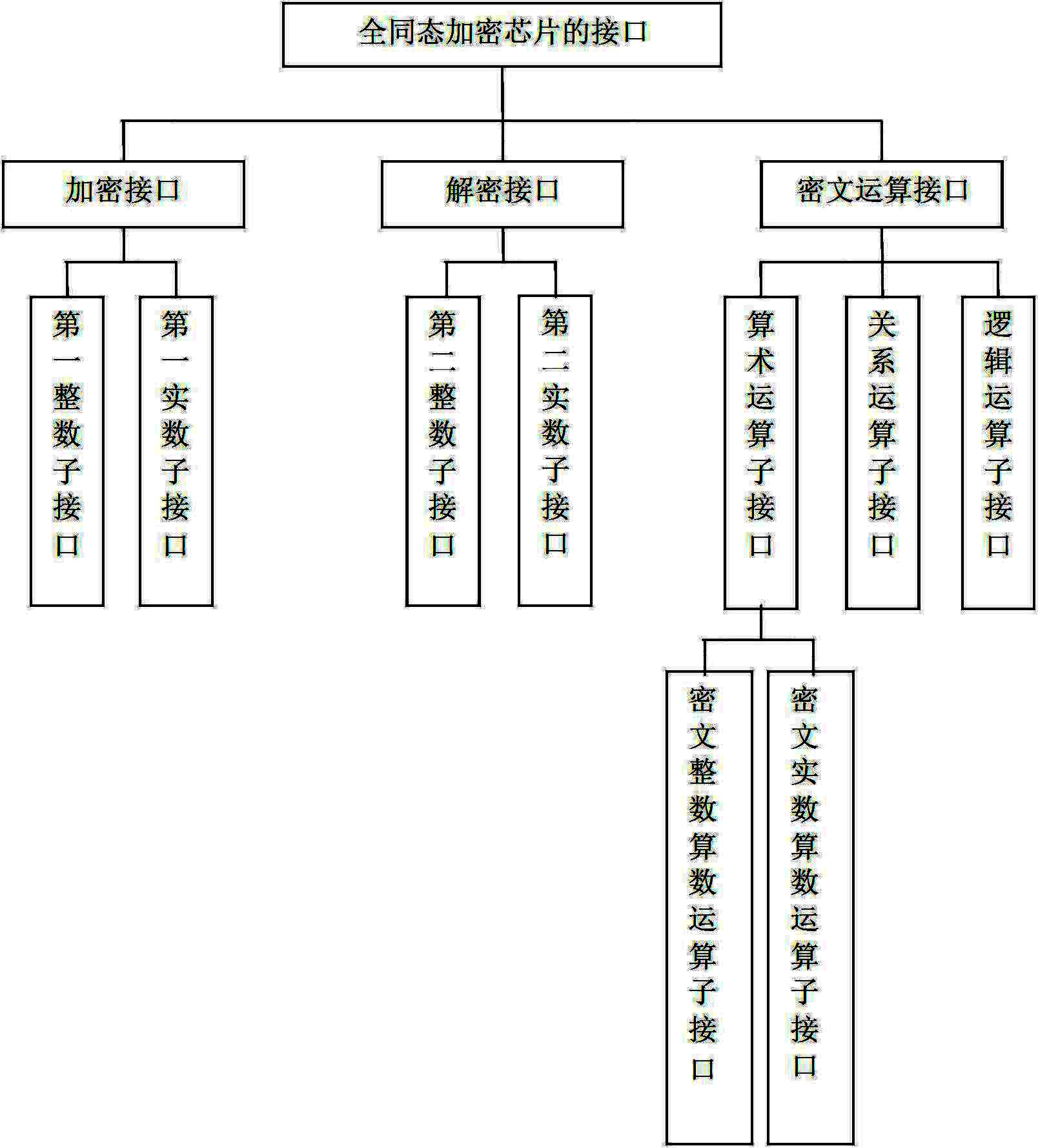
Interface unit for fully homomorphic encryption chip
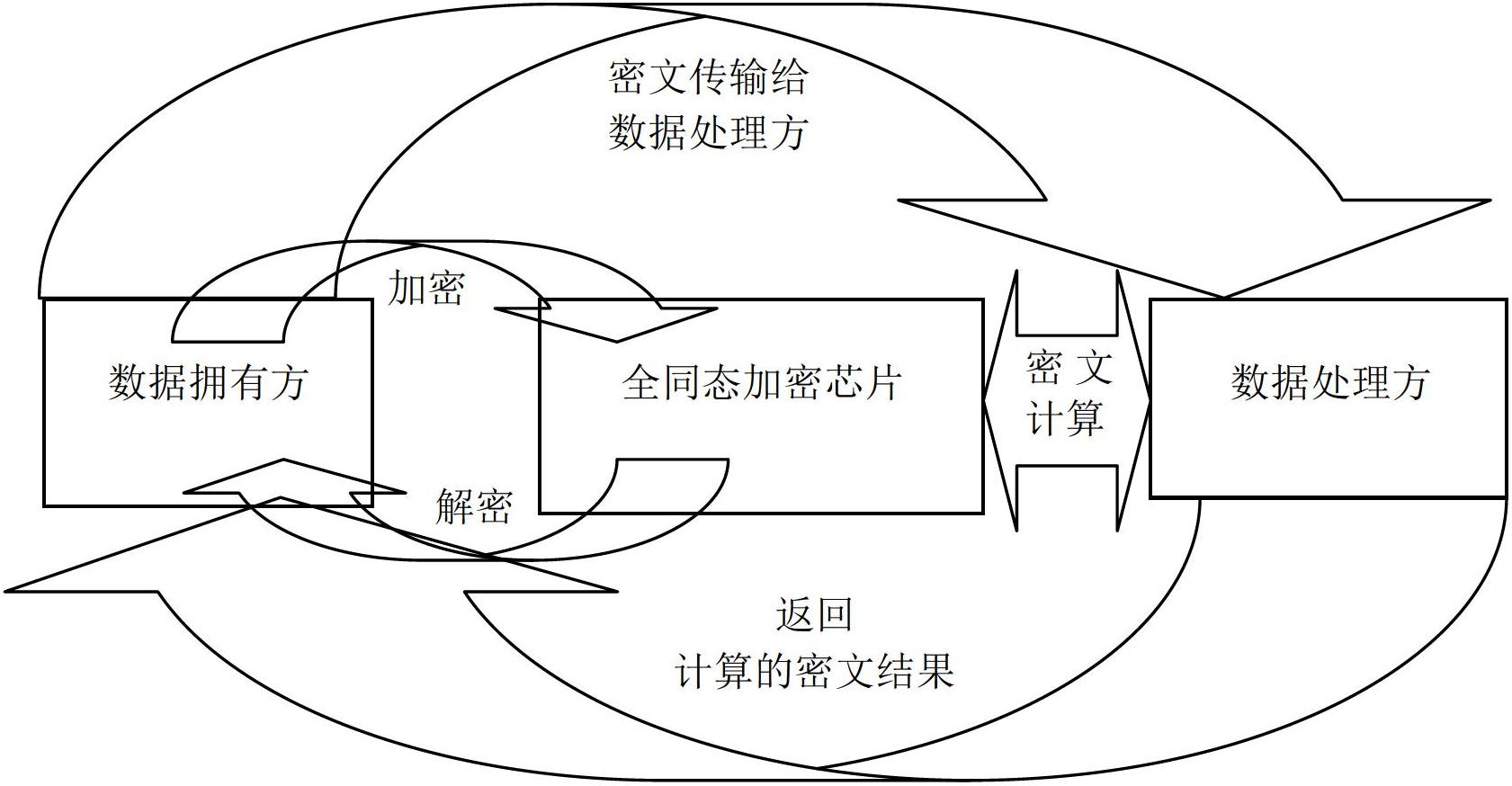
ActiveCN102694644ARealize encryption and decryptionImplement security protectionCoding/ciphering apparatusCommunication with homomorphic encryptionComputer hardwarePlaintext
The invention discloses an interface unit for a fully homomorphic encryption chip. The interface unit comprises an encryption interface, a decryption interface and a cipher text operation interface. The encryption interface is used for encrypting data of a data owner to generate cipher texts and transmitting the cipher texts to a data processor. The cipher text operation interface is used for receiving the cipher texts from the data processor to operate the cipher texts and transmitting the operated cipher texts to the data owner. The decryption interface is used for receiving the operated cipher texts from the data owner, decrypting the cipher texts to generate plain texts, and transmitting the plain texts to the data owner. The encryption interface comprises a first integer sub-interface and a first real sub-interface, wherein the first integer sub-interface is used for encrypting plain text integers and plain text unsigned integers, and the first real sub-interface is used for encrypting plain text real numbers, plain text floating numbers, plain text double-precision floating numbers and plain text format real numbers. The interface unit for the fully homomorphic encryption chip can complete arithmetic operation, relation comparison operation and logical operation under encryption and can guarantee information safety.
Owner:HUAZHONG UNIV OF SCI & TECH
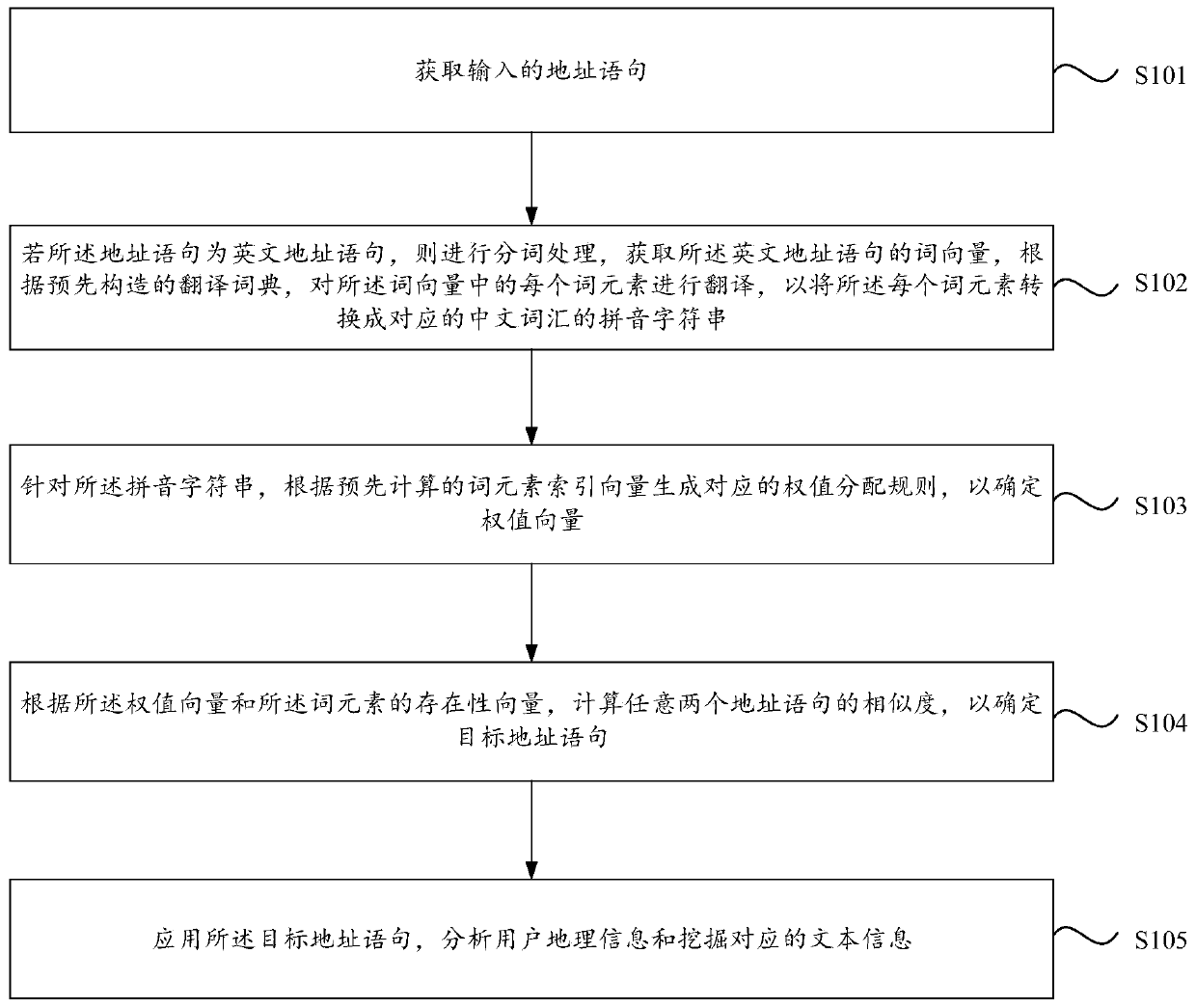
User geographic information analysis and text mining method and device
InactiveCN110209771AFully analyzedFully parsedText database indexingText database queryingInformation analysisText mining
The invention relates to a user geographic information analysis and text mining research method and device based on natural language processing. The method comprises the steps of obtaining an input address statement; if the address statement is an English address statement, performing word segmentation processing to obtain a word vector of the English address statement, and translating each word element in the word vector according to a pre-constructed translation dictionary to convert each word element into a pinyin character string of the corresponding Chinese vocabulary; for the pinyin character string, generating a corresponding weight distribution rule according to a pre-calculated word element index vector so as to determine a weight vector; calculating the similarity of any two address statements according to the weight vector and the existence vector of the word element so as to determine a target address statement; and analyzing the geographic information of the user and mining the corresponding text information by applying the target address statement. Therefore, the geographic information analysis of the user can be fully analyzed to fully reflect the community characteristics of the user.
Owner:哈尔滨哈银消费金融有限责任公司
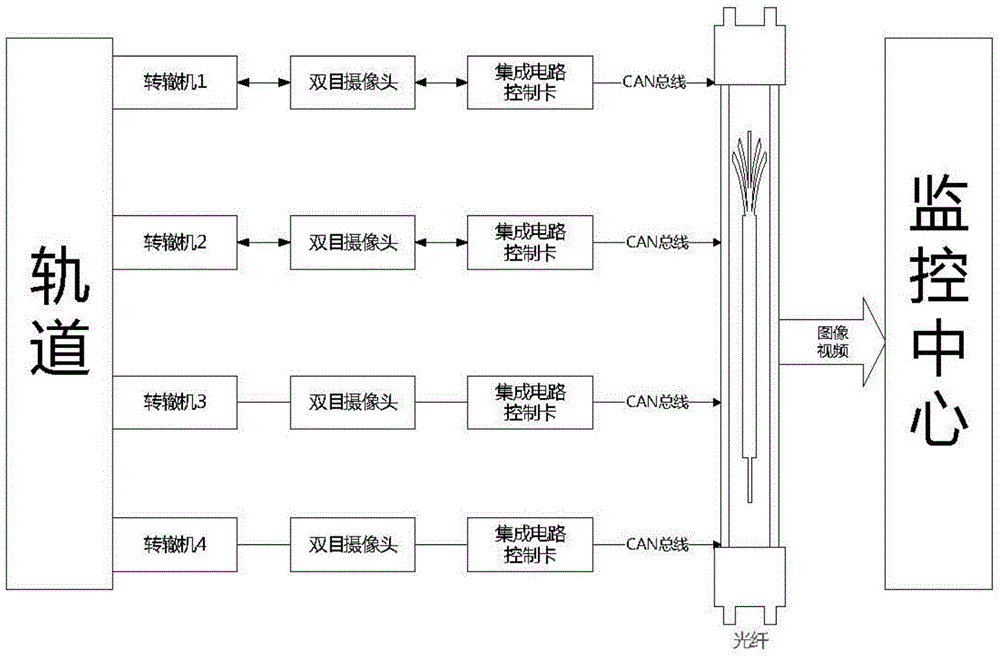
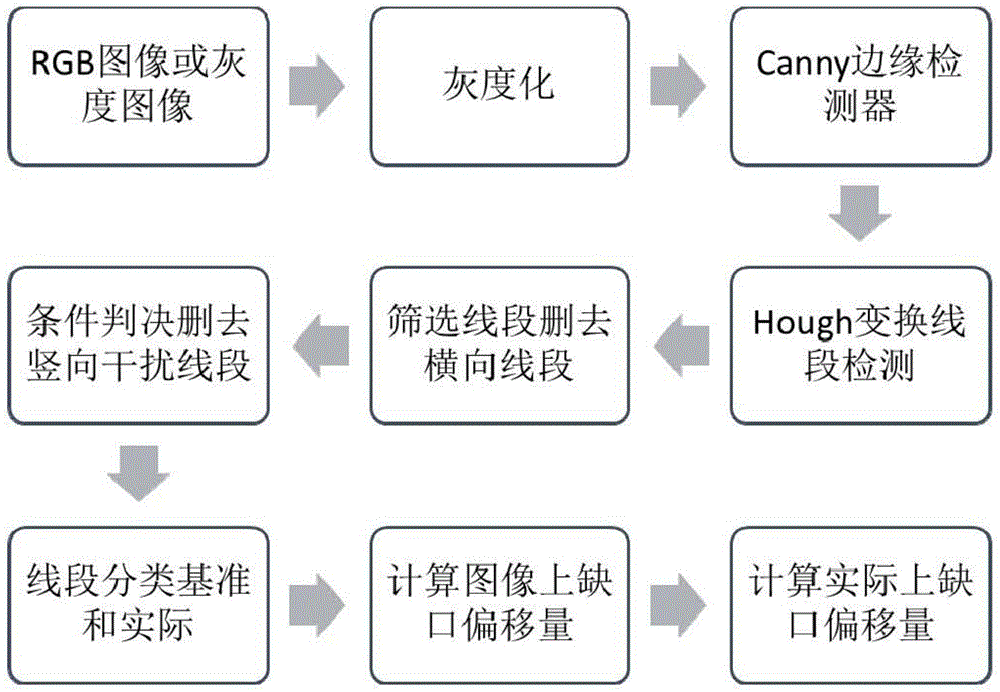
Switch machine notch monitoring system and method based on binocular visual processing identification
PendingCN105472355ASolve complexityFully analyzedClosed circuit television systemsUsing optical meansMonitoring systemVisual perception
The invention provides a switch machine notch monitoring system and method based on binocular visual processing identification, relating to the switch machine notch monitoring field. The detection system comprises an on-site binocular collection subsystem, a CAN bus fiber transmission subsystem and a monitoring subsystem. The binocular collection subsystem collects notch images, and transmits the images to the monitoring subsystem through the CAN bus fiber transmission subsystem; the monitoring subsystem performs visual processing, and employs a gauss filter to perform smooth filtering de-noising processing; a Canny edge detector extracts notch edge information, performs Hough transformation on edge images to detect line segments, and identifies line segment information in the images. Through a series of constraint conditions, effective line segments on the top left side of notch edges are screened, reference mark and real marking line segment coordinates are recorded, and notch offsets on the images are calculated according to image geometrical distances. According to proportions, real notch offsets are calculated. A left image and a right image are both processed according to the processing flow, thereby improving calculating accuracy.
Owner:JIANGSU GENTURE ELECTRONICS INFORMATION SERVICE CO LTD
Long-range rocket launching initial state error spreading estimation method
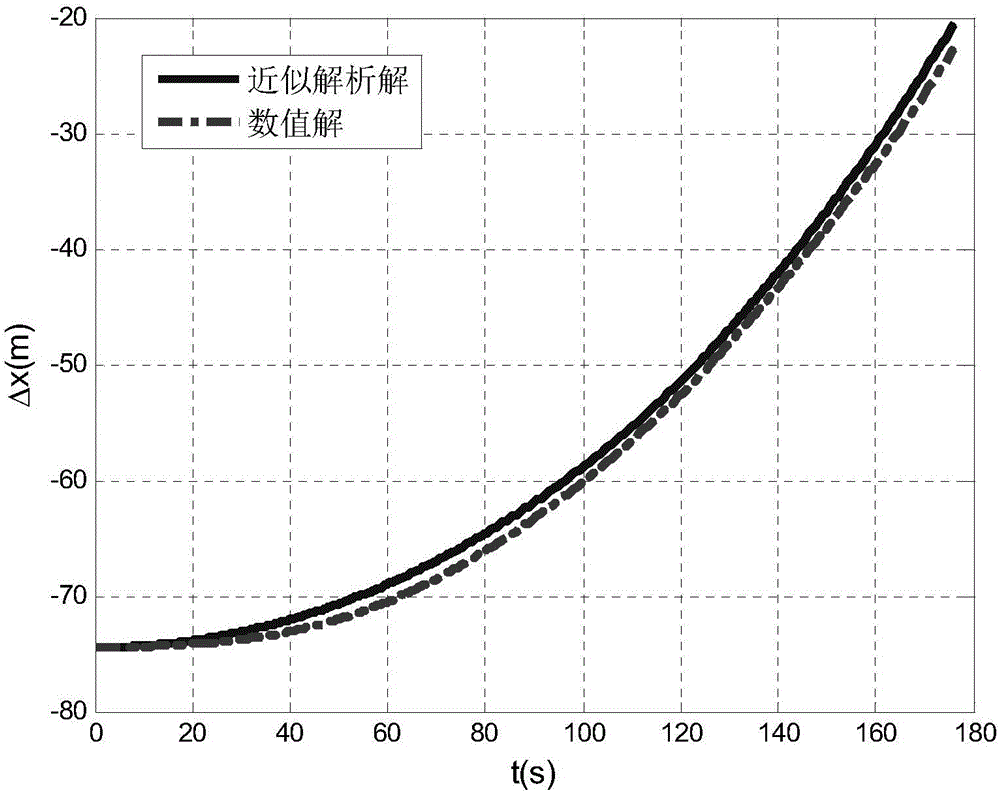
ActiveCN105069311AImprove computing efficiencyFully analyzedSpecial data processing applicationsPropagation of uncertaintyEstimation methods
The invention provides a long-range rocket launching initial state error spreading estimation method, and relates to the long-range rocket launching initial state error spreading estimation method. The method aims at solving the problems that the calculation efficiency of burnout point position deviation, speed deviation, landing point longitudinal deviation and transverse deviation is low due to the existing launching initial state error, so that the spreading mechanism of the launching initial state error in the trajectory design process cannot be sufficiently analyzed. The goal of the method is achieved through the following technical scheme that the method comprises the following steps of: 1, building a kinetics perturbation equation; 2, solving long-range rocket thrust acceleration deviation, pneumatic acceleration deviation, normal gravitational acceleration deviation, Coriolis acceleration deviation and centrifugal acceleration deviation; and 3, obtaining similar analytical solutions of the burnout point position deviation and the speed deviation due to the long-range rocket launching initial state error and similar analytical solutions of the landing point longitudinal deviation and transverse deviation according to the first step and the second step. The method is applied to the field of long-range rocket or carrier rocket flight dynamics.
Owner:HARBIN INST OF TECH
Intelligent contract fuzzy test method and device and storage medium
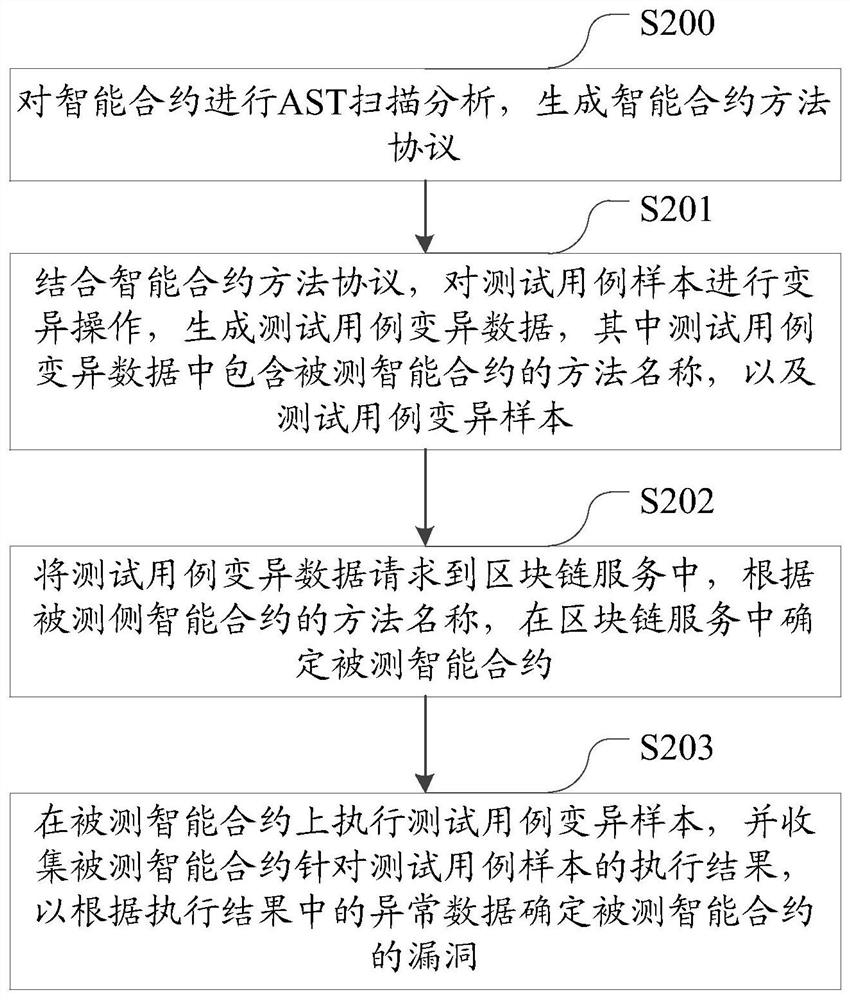
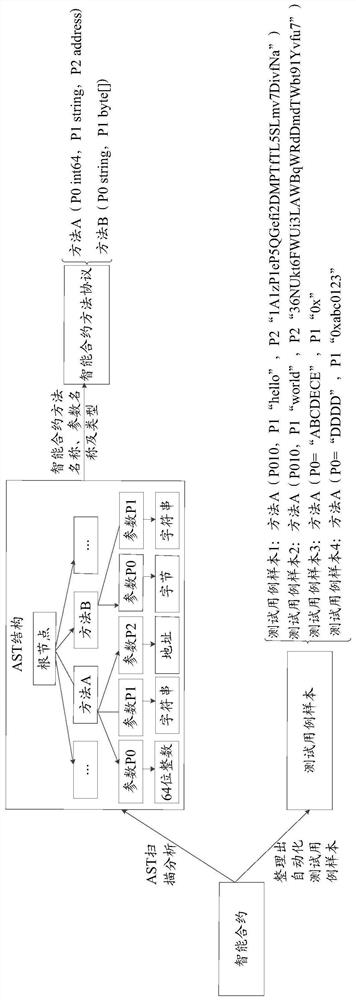
ActiveCN112131115AEnsure safetyAvoid lostSoftware testing/debuggingPlatform integrity maintainanceSmart contractComputer science
The invention provides an intelligent contract fuzzy test method and device, and a storage medium, relates to the technical field of block chains, and is used for improving the security of an intelligent contract in a block chain and avoiding unnecessary loss. AST scanning analysis is carried out on the intelligent contract to generate an intelligent contract method protocol; in combination with an intelligent contract method protocol, mutation operation is carried out on the test case sample to generate test case mutation data, and the test case mutation data comprises a method name of the tested intelligent contract and a test case mutation sample; the method also includes requesting the test case variation data to a blockchain service, and determining a tested smart contract in the blockchain service according to the method name of the tested smart contract; and executing the test case variation sample on the tested smart contract, and collecting an execution result of the tested smart contract for the test case sample so as to determine a vulnerability of the tested smart contract according to abnormal data in the execution result.
Owner:TENCENT TECH (SHENZHEN) CO LTD
Multi-round dialogue method and device based on dialogue state prediction and computer equipment
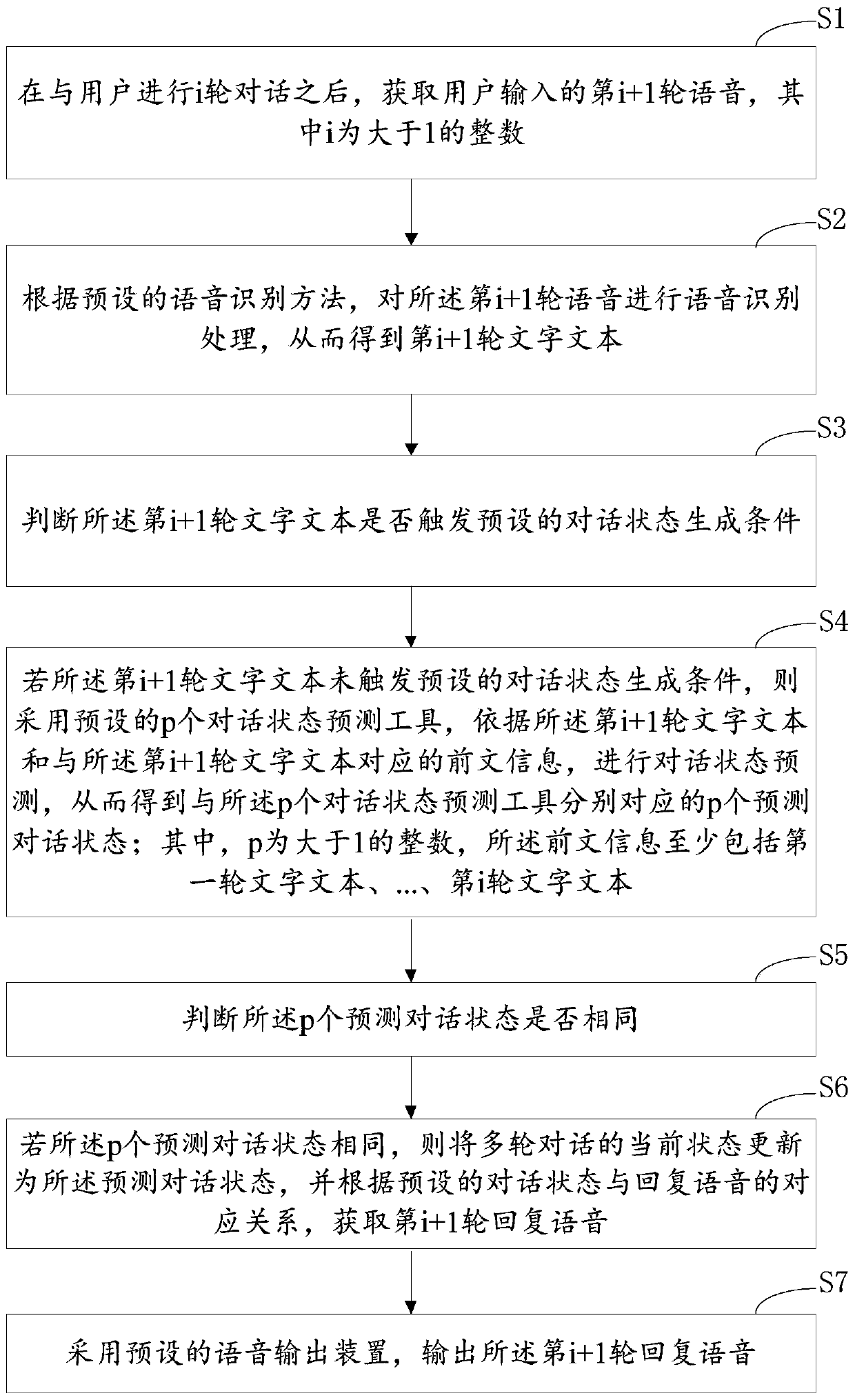
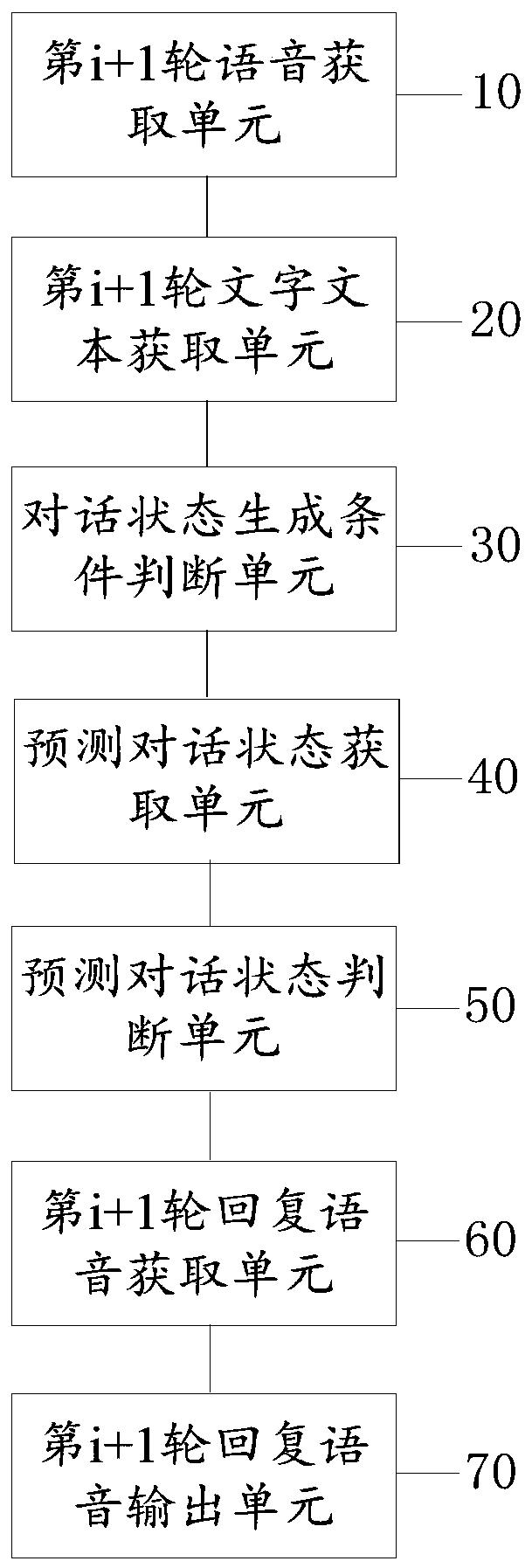
PendingCN111475616AImprove generalization abilityAccurate analysisNatural language data processingSpeech recognitionState predictionEngineering
The invention discloses a multi-round dialogue method and device based on dialogue state prediction, computer equipment and a storage medium, and the method comprises the steps: obtaining the (i + 1)th round of voice inputted by a user after the i round of dialogue with the user; performing speech recognition processing on the (i + 1) th round of speech to obtain an (i + 1) th round of text; judging whether the (i + 1) th round of text triggers a dialogue state generation condition or not; if the preset dialogue state generation condition is not triggered, performing dialogue state predictionby adopting p preset dialogue state prediction tools to obtain p predicted dialogue states; if the p predicted dialogue states are the same, updating the current state of the multiple rounds of dialogues to the predicted dialogue state, and obtaining the (i + 1) th round of reply voice according to the preset corresponding relationship between the dialogue state and the reply voice; and outputting the (i + 1) th round of reply voice by adopting a preset voice output device. Therefore, the generalization ability of the multi-round dialogue scheme is improved, and the fluency is ensured.
Owner:PING AN TECH (SHENZHEN) CO LTD
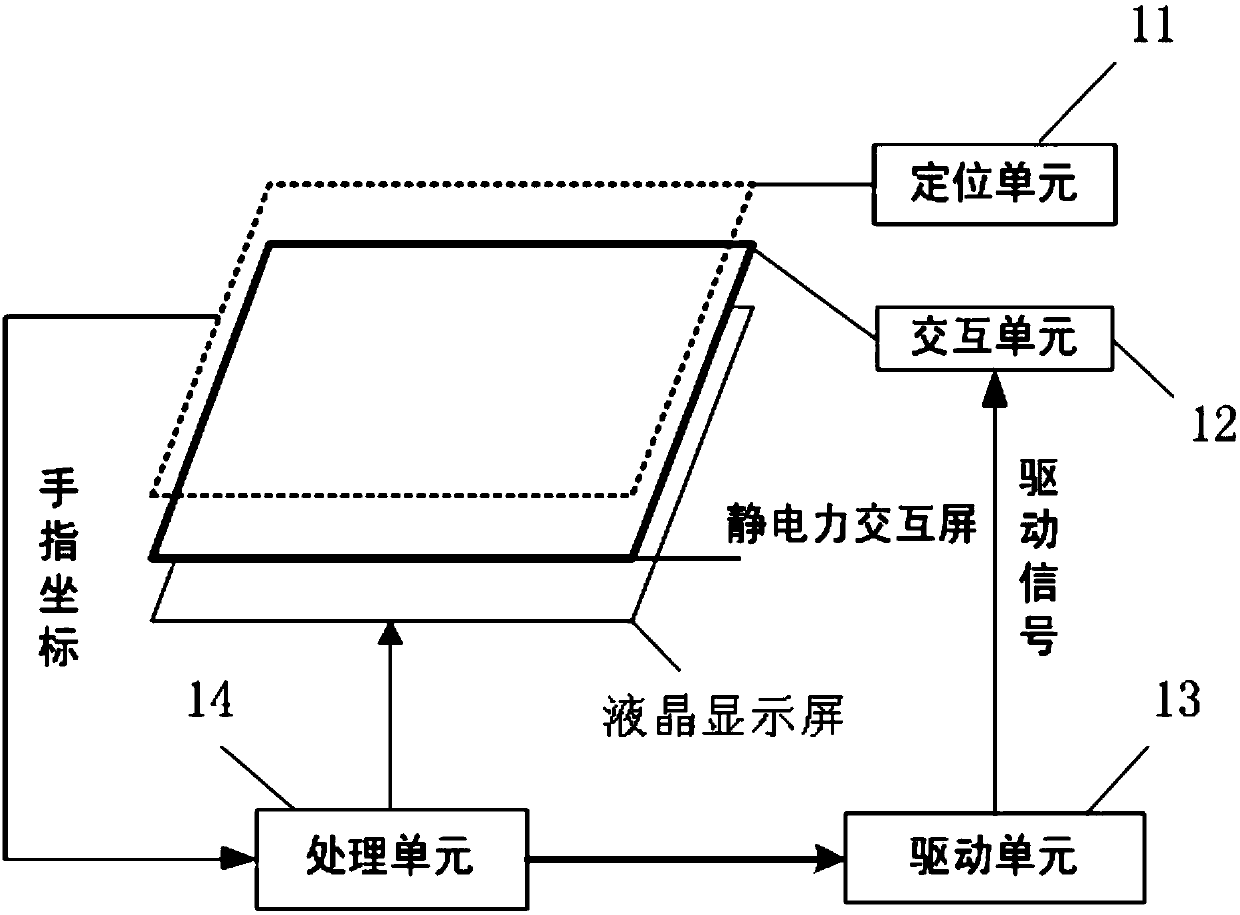
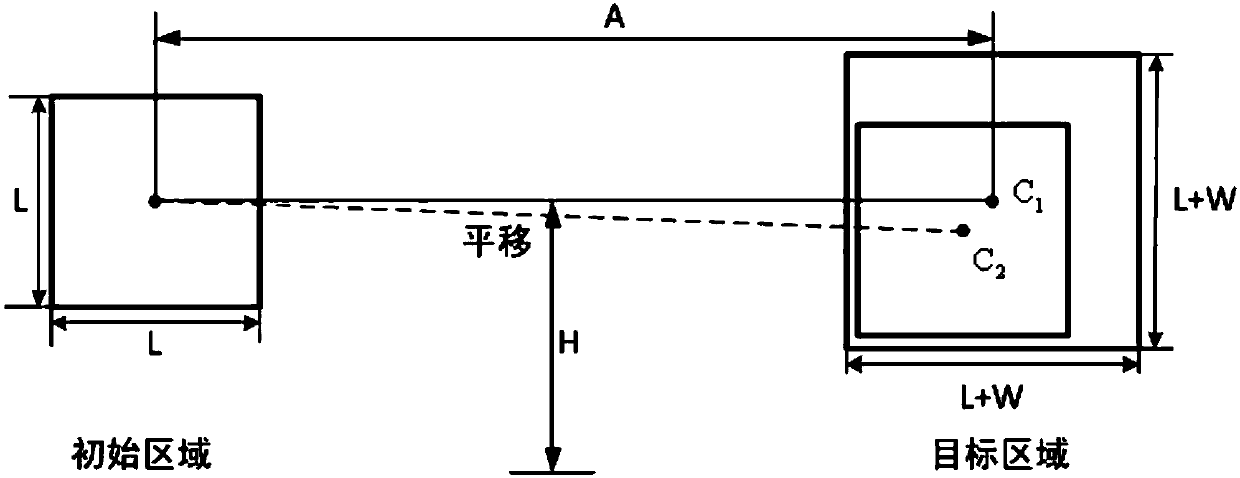
Optimal driving voltage selection method taking translation interaction efficiency as an index
ActiveCN109656361AFully analyzedRealize quantitative evaluationInput/output for user-computer interactionGraph readingKernel principal component analysisHuman–robot interaction
The invention relates to an optimal driving voltage selection method taking translation interaction efficiency as an index, and belongs to the field of human-computer interaction. An electrostatic force tactile feedback device is used; translation gesture interaction efficiency experimental data under two conditions of electrostatic force tactile feedback and electrostatic force tactile feedback are obtained, and a matrix is constructed; A kernel principal component analysis method is used for calculating a kernel matrix and obtaining corresponding kernel feature spaces, quantitative evaluation of the influence of electrostatic force tactile feedback on translation interaction efficiency is achieved by calculating the distance between the two kernel feature spaces, and the method is used for selecting the optimal driving voltage of the electrostatic force feedback device with the translation interaction efficiency as an index. The influence degree of electrostatic force tactile feedback on translation interaction efficiency can be quantitatively evaluated, the data theory is fully analyzed, and the obtained conclusion is high in universality; The method can also be expanded to quantitative evaluation of the influence of different electrostatic force touch driving modes on the gesture interaction performance, and is easy to popularize and apply.
Owner:JILIN UNIV
JSON character string processing method and device
ActiveCN110263104AAvoid loading cumbersome issuesAccurate storageDatabase management systemsRelational databasesAlgorithmJSON
The invention provides a JSON character string processing method and device. The method comprises the steps that of conducting deserialization processing is conducted on a JSON character string to extract a bottom layer element in the JSON character string, and the bottom layer element comprisinges a bottom layer key name and a corresponding first key value; for each underlying element in the underlying elements, generating an index of the underlying element based on the underlying key name of the underlying element; and generating structured data based on the generated index of each underlying element and the corresponding first key value. By utilizing the method disclosed by the invention, the JSON character string can be stored in a structured manner, so that subsequent loading and use are facilitated.
Owner:ADVANCED NEW TECH CO LTD
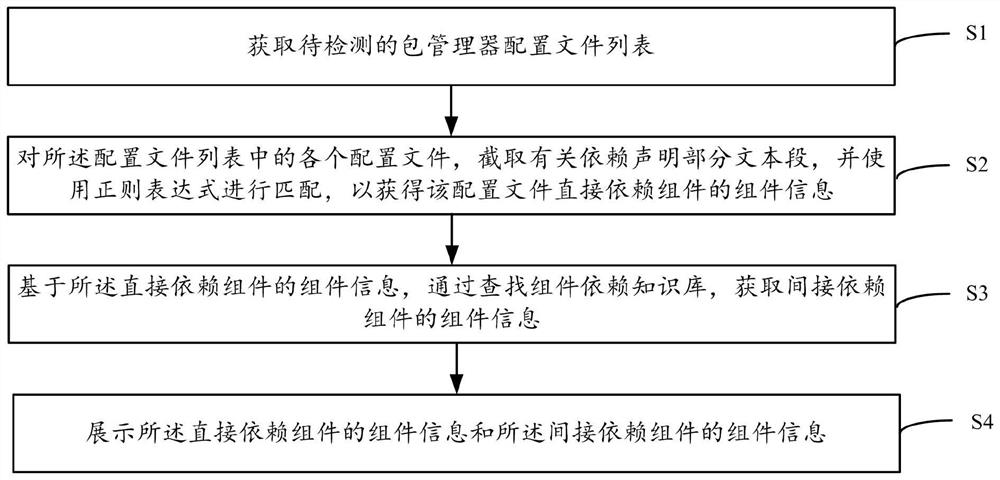
Dependent component information extraction method and device and computer readable storage medium
The invention discloses a dependent component information extraction method and device and a computer readable storage medium. The dependent component information extraction method comprises the steps of obtaining a to-be-detected package manager configuration file list; for each configuration file in the configuration file list, intercepting a part of text segments related to the dependency declaration, and performing matching by using a regular expression to obtain component information of a component directly dependent on the configuration file; based on the component information of the direct dependent component, obtaining the component information of the indirect dependent component by searching a component dependent knowledge base; and displaying the component information of the direct dependent component and the component information of the indirect dependent component. By the adoption of the invention, text analysis depending on the configuration file can be achieved, dependence constraints such as a local private warehouse environment and a network environment are eliminated, constraints of analysis commands of an existing package manager are eliminated, the dependence relation of components can be completely analyzed, and the hierarchical structure of a project module can be completely analyzed.
Owner:苏州棱镜七彩信息科技有限公司
Aircraft measurement system, short message communication method and storage medium
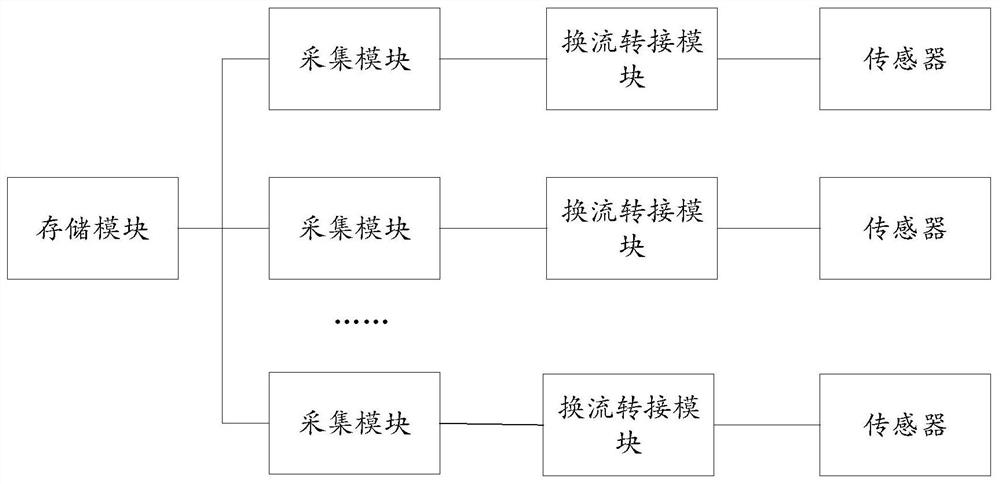
PendingCN113008300AFully analyzedImprove accuracyMeasurement devicesRadio transmissionFlight vehicleEmbedded system
The invention provides an aircraft measurement system, a storage medium and an electronic device, and the aircraft measurement system comprises a sensor which is used for monitoring the environment parameters of a target area, obtaining a sensor signal, and transmitting the sensor signal to a conversion switching module; the conversion switching module which is connected with the sensor and the acquisition module and is used for sending the sensor signal to an acquisition module; the acquisition module which is used for analyzing the acquired sensor signals to obtain acquired data and sending the acquired data to a storage module; and the storage module which is used for storing the received acquisition data so as to judge whether to send an instruction for starting a Beidou short message communication function to the aircraft measurement system or not according to the acquisition data. The problem that data analysis or processing is incorrect due to the fact that information obtained through measurement of all sensors cannot be analyzed in an aircraft measurement system in the prior art is solved.
Owner:BEIJING INFORMATION SCI & TECH UNIV
Sports apparatus and method
ActiveUS9079090B2Fully analyzedGymnastic exercisingPosition fixationData processing systemData signal
Owner:SSTATZZ
Tea processing technology
The invention relates to a tea processing technology. The tea processing technology comprises the steps that picked fresh green tea leaves are cleaned thoroughly and then are dried at the temperature of 80-100 DEG C for 5-10 minutes; the dried tea leaves are immersed in ethanol with the mass concentration 55-65% for 5-10 seconds and then are taken out, then the tea leaves are transferred into an ultrasonic processor to undergo ultrasonic processing under the conditions of 15-60 KHZ and 80-150 w for 10-15 minutes; ultrasonically processed tea leaves are transferred into a frying pan, tea oil and salt are added, the addition amount of the tea oil is 10-20% by weight of the tea leaves, the addition amount of the salt is 5-10% by weight of the tea leaves, the tea leaves are stir-fried at the temperature of 100 DEG C for 10-20 minutes, and then the tea leaves are taken out of the pan and cooled. The tea processing technology is simple, a production cycle is short, the whole process only needs 25-45 minutes, the produced tea leaves can be rapidly brewed with warm water or cold water, can be directly eaten or eaten after being soaked and well meets the travel and outgoing demands of people.
Owner:SHAOWU FUTENG CULTURAL TOURISM DEV CO LTD
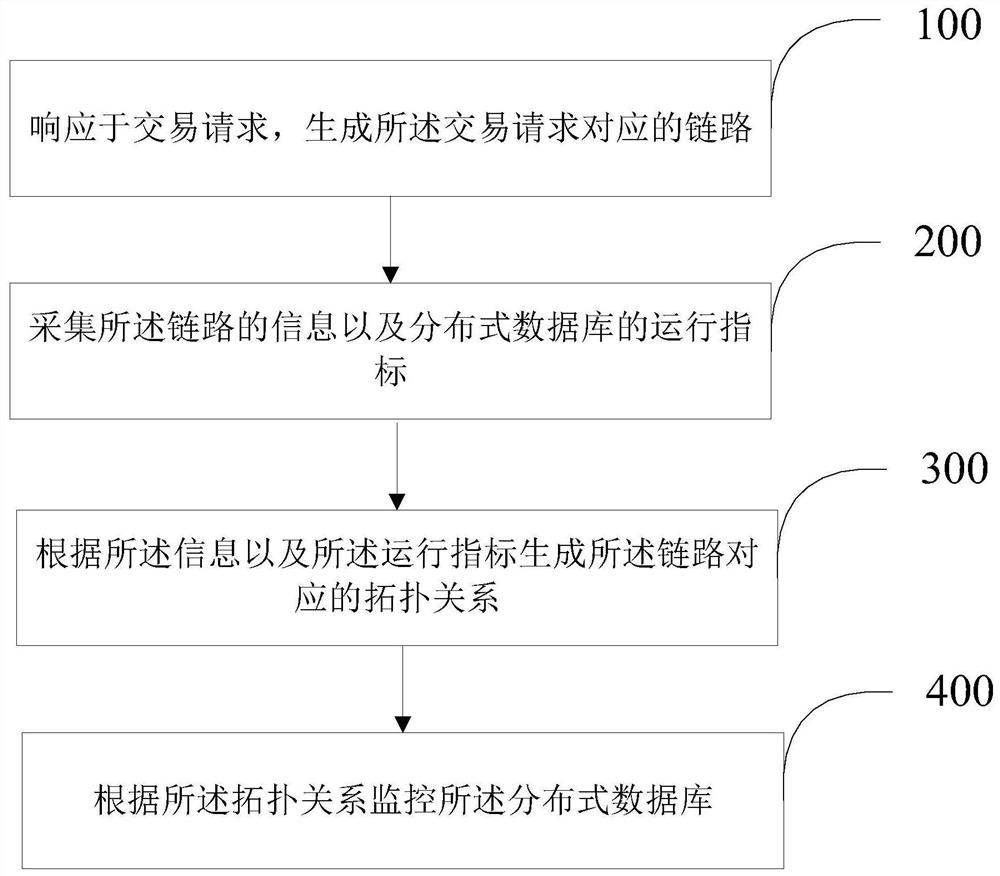
Distributed database monitoring method and device based on full-link monitoring
Owner:INDUSTRIAL AND COMMERCIAL BANK OF CHINA
Processing technology of picked fresh tea
InactiveCN106720530AEfficient SupplementRemoval of pesticide residuesPre-extraction tea treatmentPesticide degradationFermentation
The invention discloses a processing technology of picked fresh tea.The processing technology comprises the following steps that 1, the picked fresh tea is spread until a moisture content of the tea is 65-75%; 2, the tea obtained in the step 1 is placed in a pesticide degradation device to degrade residual pesticides, then the tea is dried after washed, the dried tea is immersed in ethanol and ultrasonically processed for 6-8minutes; 3, the tea obtained in the step 2 is dried and the dried tea is put into a fresh bamboo tube for aerobic fermentation; 4,the tea after fermentation processing is rolled by a rolling machine; 5,the rolled tea is put into a steam-hot fixation machine to be fixed for three times; 6, after fixation is completed, the tea is transferred to a deblocking machine to be scattered, and after deblocked, the tea is put into a dryer to be dried and taken out until the moisture content of the tea is 20-30%; 7,the tea is spread and dried for moisture regaining, formation is carried out at the temperature of 80-90 DEC C, and then the tea is dried until the moisture content is equal to or less than 6%.
Owner:潜山县彭河幸福茶场
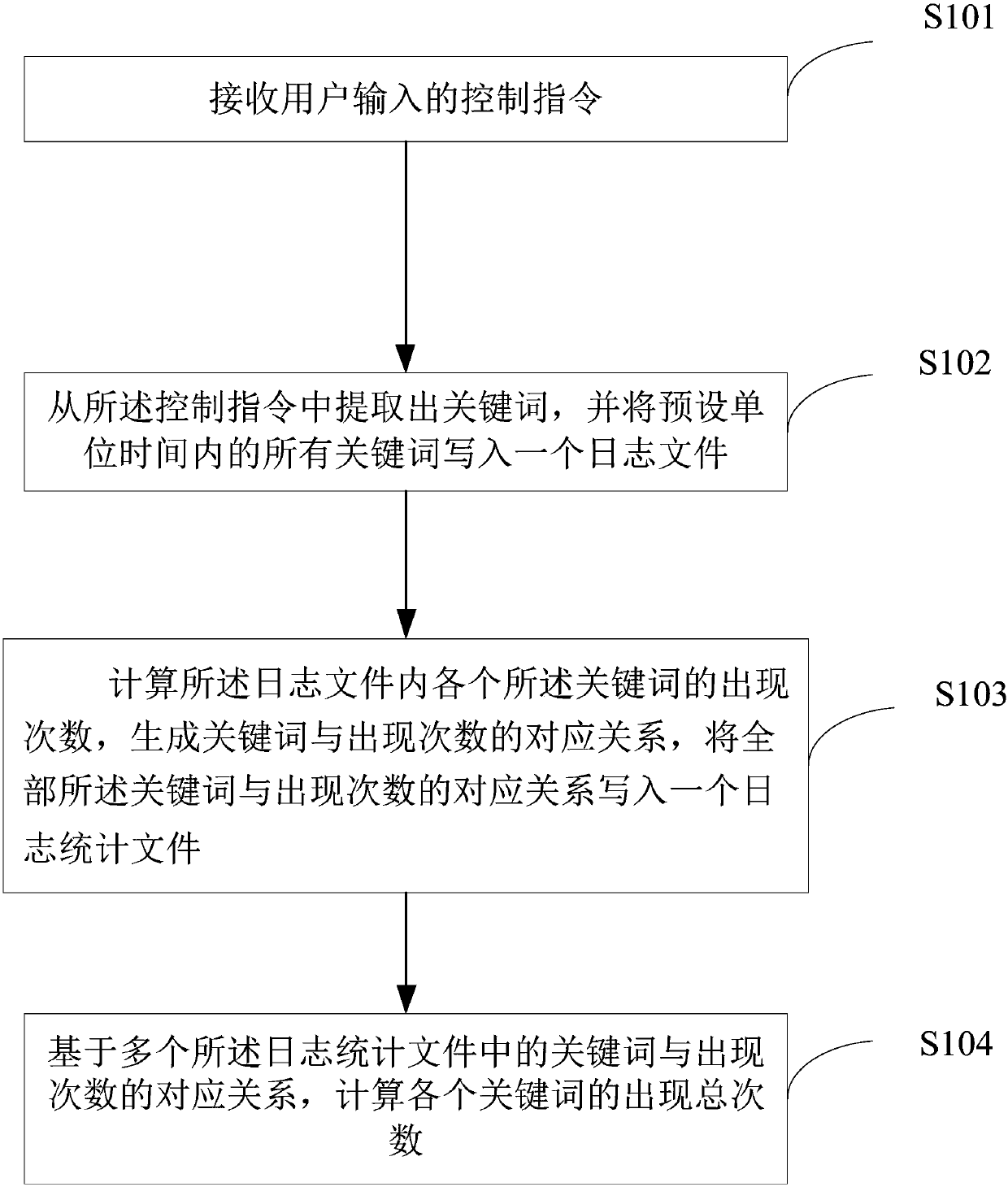
User data statistics method and device
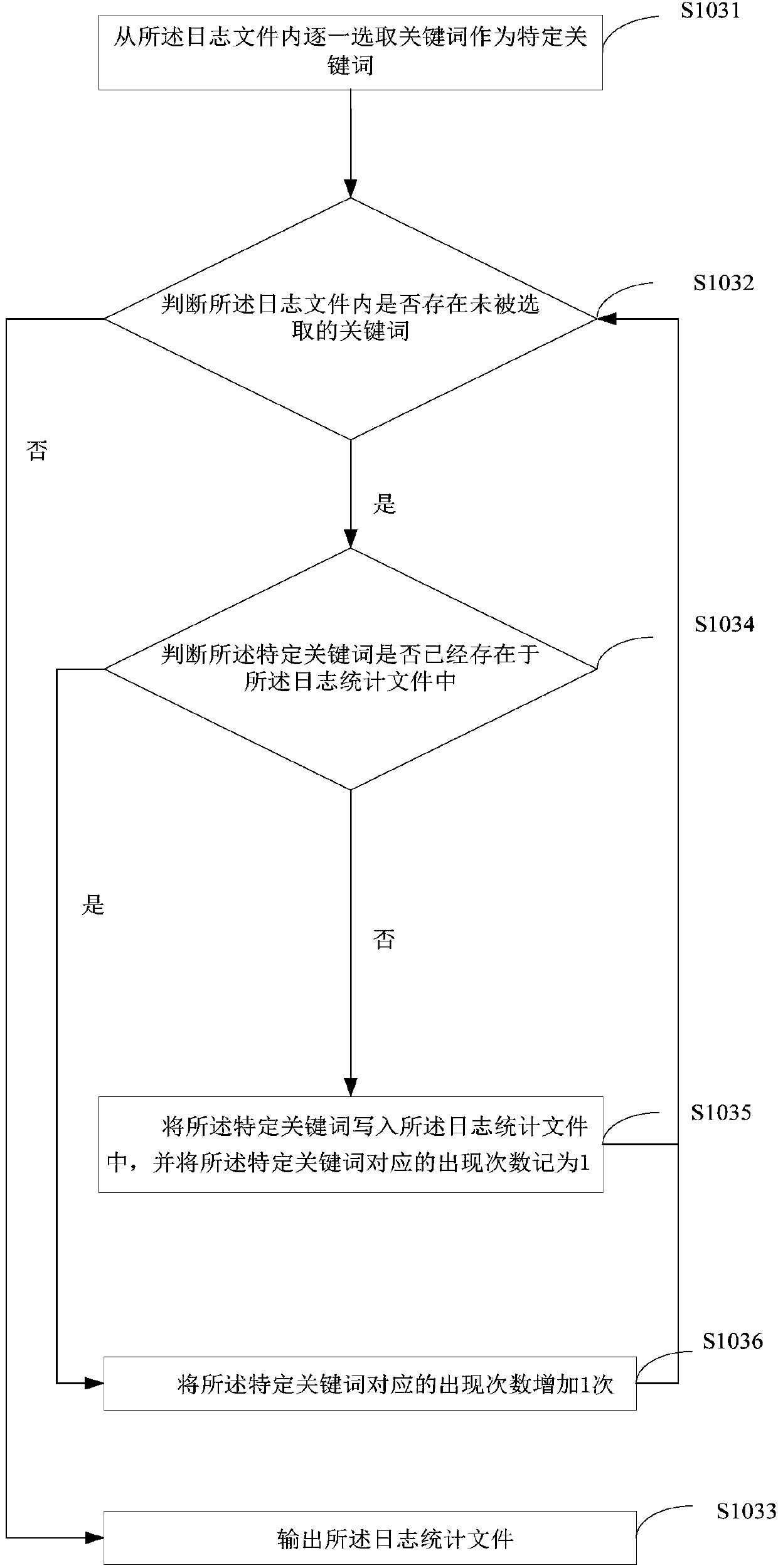
InactiveCN109976984AFully analyzedAdequate data supportHardware monitoringMarket data gatheringUser inputData analysis
The invention belongs to the technical field of data analysis, and particularly relates to a user data statistics method and device, and the method comprises the steps: receiving a control instructioninput by a user, extracting keywords from the control instruction, and writing all the keywords in a preset unit time into a log file; generating a log statistical file based on the occurrence frequency of each keyword in the log file; and calculating the total occurrence frequency of each keyword based on the corresponding relationship between the keywords in the log statistical files and the occurrence frequency so as to calculate the keywords in the control instruction, thereby fully analyzing the control instruction and providing sufficient data support for the subsequent analysis of theuser behavior.
Owner:TCL CORPORATION
Acquisition method, device and processing method of positioning error data
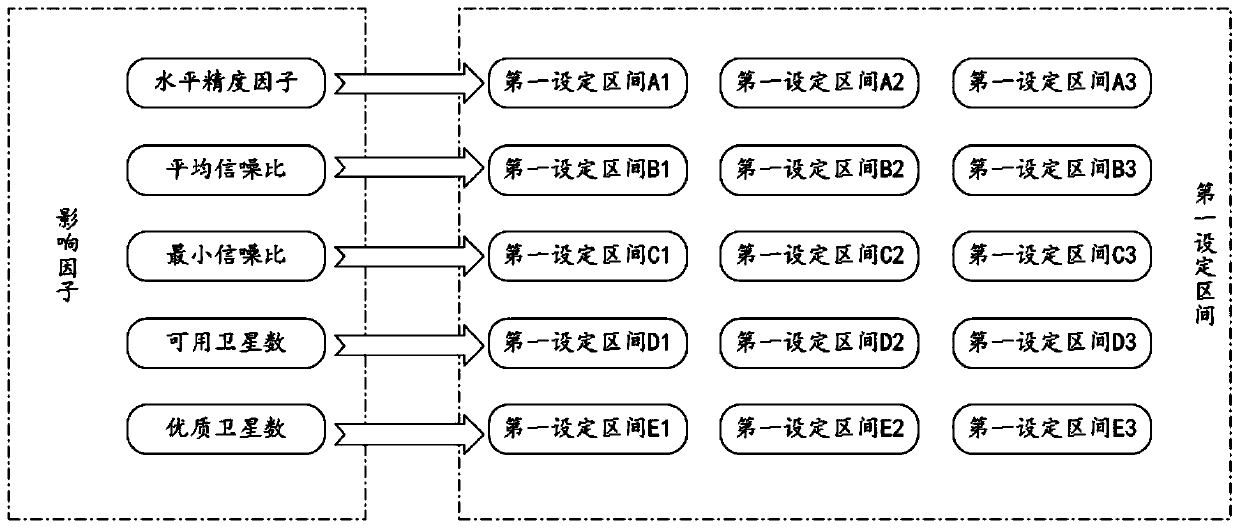
ActiveCN111123303AFully analyzedMultidimensional analysisSatellite radio beaconingData setData acquisition
The invention relates to the technical field of satellite positioning, and discloses a method for acquiring positioning error data. The method comprises the following steps of: acquiring first positioning data of a measured positioner in a plurality of epochs, acquiring second positioning data of a standard positioner in the same epochs, and correspondingly processing a second coordinate value inresponse to an instruction of determining a positioning state to obtain a standard coordinate value; according to the first coordinate value and the standard coordinate value, performing calculation to obtain a positioning error value of the measured positioner in the plurality of epochs; and associating the positioning error value of each epoch with influence factor data, and then performing storing to obtain a positioning error data set. The invention has the technical effects that: in the acquisition method, the automation degree of data collection and processing is higher, the requirementfor the site is relatively low, meanwhile, the obtained positioning data can reflect numerical value changes of influence factors of the measured positioner in different states, and help can be provided for analyzing positioning errors more sufficiently and more dimensionally.
Owner:广东星舆科技有限公司
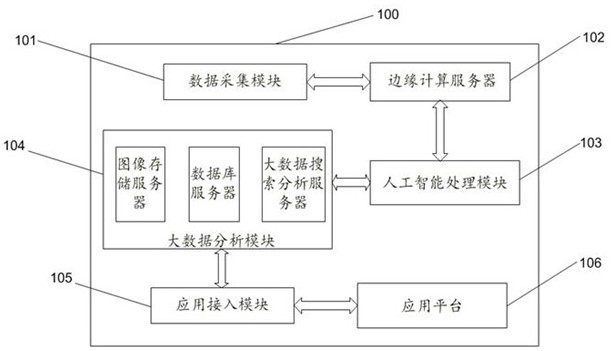
Big data analysis processing system and method
InactiveCN113239792ASatisfy real-timeMeet storageDatabase distribution/replicationClosed circuit television systemsEdge computingData acquisition
The embodiment of the invention belongs to the technical field of big data, and relates to a big data analysis processing system and method. The system comprises a data acquisition module, an edge computing server, an artificial intelligence processing module, a big data analysis module, and an application access module. The data acquisition module is used for acquiring video image data of each distributed acquisition point in real time, and performing balanced forwarding through a Kafka forwarding service; the edge computing server is used for pre-processing video image data and pushing the pre-processed video image data to the artificial intelligence processing module; the application access module is used for caching multiple paths of video image data and performing structured analysis processing on the video image data to obtain multi-dimensional structured image information, outputting the multi-dimensional structured image information to the big data analysis module, performing professional storage and big data analysis, and providing a quick search interface for the application access module through a distributed real-time search engine; and the application access module is used for providing an access interface for the application platform access system. The working efficiency of the big data application is improved.
Owner:深圳市安软科技股份有限公司 +1
Insulation paper water content evaluation method based on robust wavelength screening
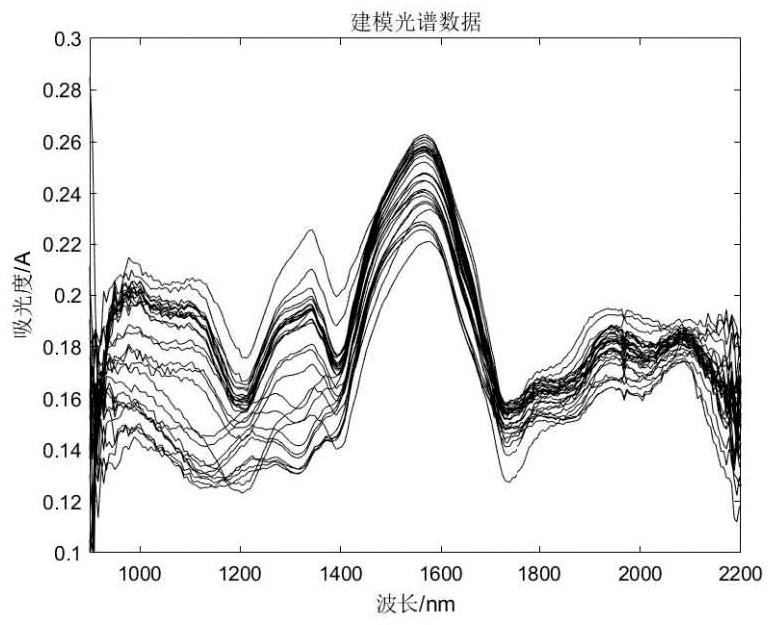
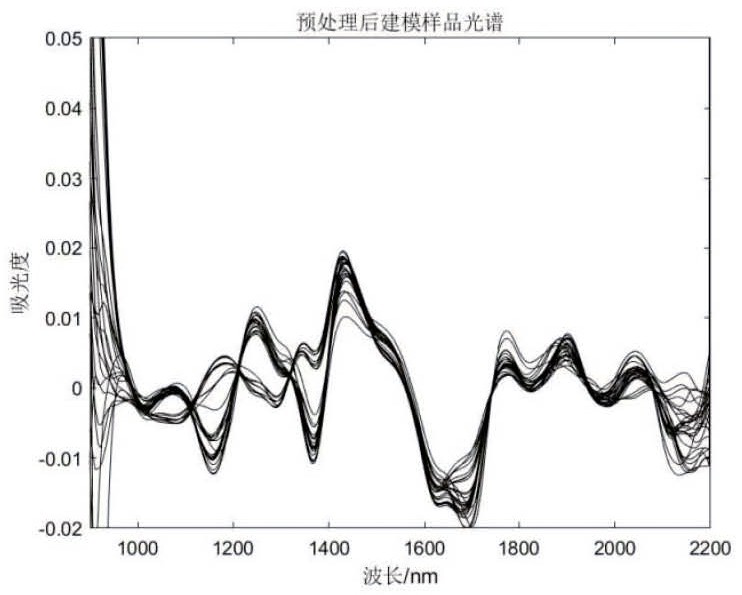
PendingCN114088660AWon't hurtCause damageMaterial analysis by optical meansFt ir spectraProcess engineering
The invention discloses an insulation paper water content evaluation method based on robust wavelength screening. The method comprises the following steps: 1, constructing an evaluation model; 2, acquiring a near infrared spectrum of the tested insulation paper; 3, substituting the obtained near infrared spectrum of the tested insulation paper into the evaluation model to obtain the water content of the tested insulation paper; according to the method, the correction model of the water content of the insulation paper is established by using the near infrared spectrum analysis technology, the water content of the insulation paper can be rapidly predicted on site, sampling is not needed, damage to insulation is avoided, and meanwhile the method has high precision, robustness and prediction capacity; according to the method, the characteristic information of the spectrum can be fully analyzed, high-quality wavelength point data can be extracted, the data dimension can be reduced, the problems of over-fitting or insufficient fitting and the like can be avoided to a certain extent, and a new technical thought is provided for the field.
Owner:ELECTRIC POWER RES INST OF STATE GRID ANHUI ELECTRIC POWER
Long-term evolution rapid analysis method for inclined geosynchronous orbit
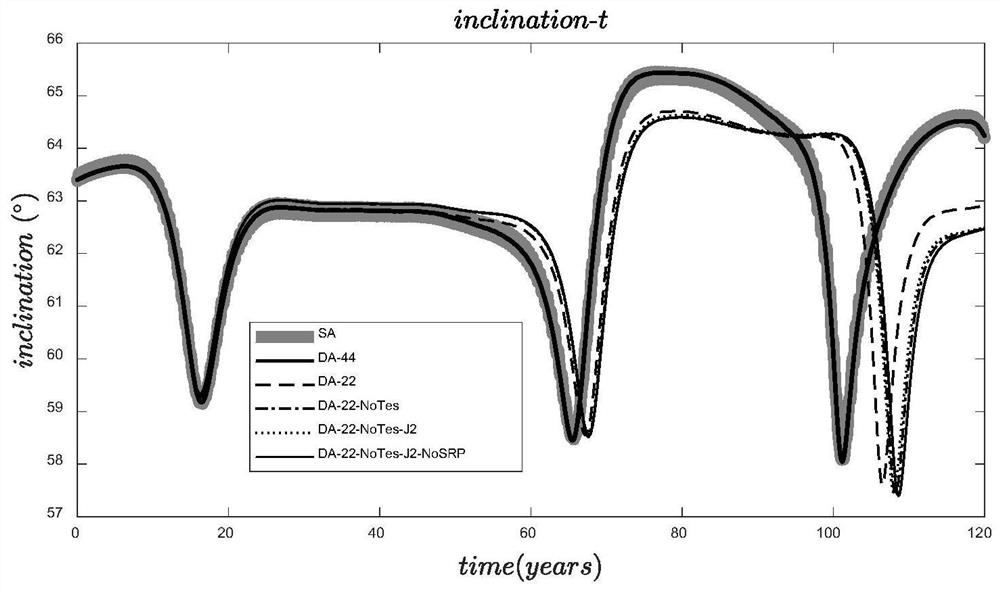
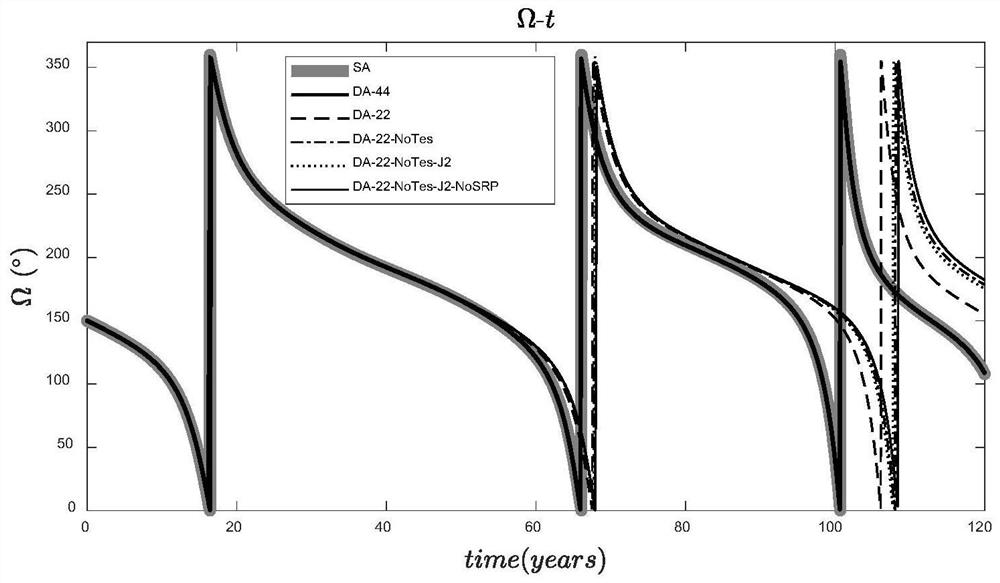
ActiveCN112036037ACalculation speedSimplified quadratic mean semi-analytical orbit repeaterDesign optimisation/simulationSpecial data processing applicationsOrbit perturbationOrbital elements
A long-term evolution rapid analysis method for an inclined geosynchronous orbit comprises the following steps: firstly, deducing a primary or secondary average perturbation force function of each perturbation item, including 1:1 resonance parts of earth non-spherical perturbation field harmonic items J22, J31, J32, J33, J41, J42, J43 and J44 with harmonic items, sun-moon gravitation perturbationLegendre expansion intercepting 4-order items and solar light pressure perturbation; secondly, establishing a secondary average semi-analytical orbit recursor of the IGSO orbit through a Lagrange typeorbit perturbation equation in combination with an average perturbation force function; comparing and analyzing IGSO orbit long-term evolution conditions under consideration of different perturbationsources and orders, so that the model is simplified, and the orbit recursion efficiency is further improved; and finally, by means of efficient orbit recursion, drawing a series of dynamic grid diagrams of complete orbit elements and initial epoch moment combinations, wherein the divisible orbit elements are (e, i, [Omega], [omega]), all binary combinations of the divisible orbit elements are e-i, [omega]-[Omega];e-[omega], i-[Omega], e-[Omega], i-[omega], all binary combinations of the initial epoch moment are InitialEpoch-e, InitialEpoch-i, InitialEpoch-[Omega], and InitialEpoch-[omega], and rapid and comprehensive analysis of IGSO orbit long-term evolution is completed according to the dynamic grid chart.
Owner:BEIJING INSTITUTE OF TECHNOLOGYGY
Method for predicting residual life of gear based on LSTM-AON
PendingCN111475986ATo achieve the purpose of excavationAccurate predictionDesign optimisation/simulationNeural architecturesHidden layerEngineering
The invention relates to a gear residual life prediction method based on LSTM-AON, and belongs to the field of big data and intelligent manufacturing. According to the invention, the method comprisesthe steps: designing a novel LSTM-AON neural network to predict the residual life of the gear; based on an LSTM network, improving a hidden layer of the LSTM-AON network, so the LSTM-AON network selects an interlayer position where an element with the maximum attention coefficient is located as a hierarchical position by calculating the attention coefficients of related elements and labels; guiding the division of the hierarchical structure by attention and is determined by an element most similar to the label; and embedding the tree-shaped hierarchical structure into the recurrent neural network through the attention degree of the information so as to mine the inter-layer sequence information ignored by the traditional network. Compared with a traditional LSTMs network, the LSTM-AON network adopted by the method is high in calculation speed, small in calculation amount and higher in precision.
Owner:CHONGQING UNIV
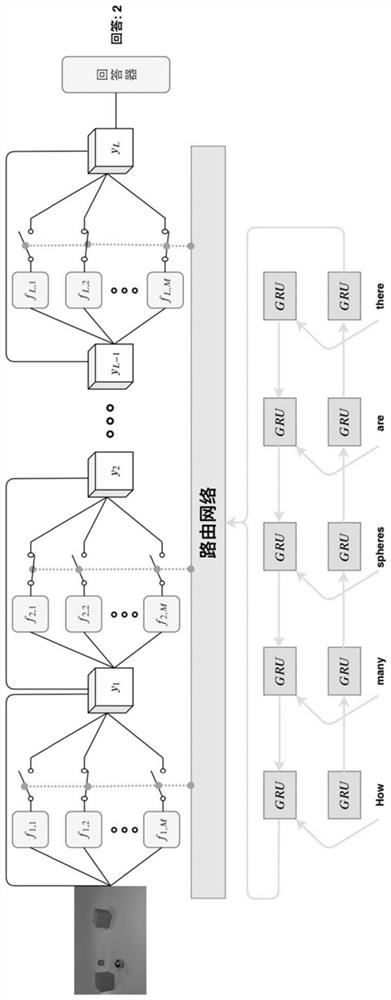
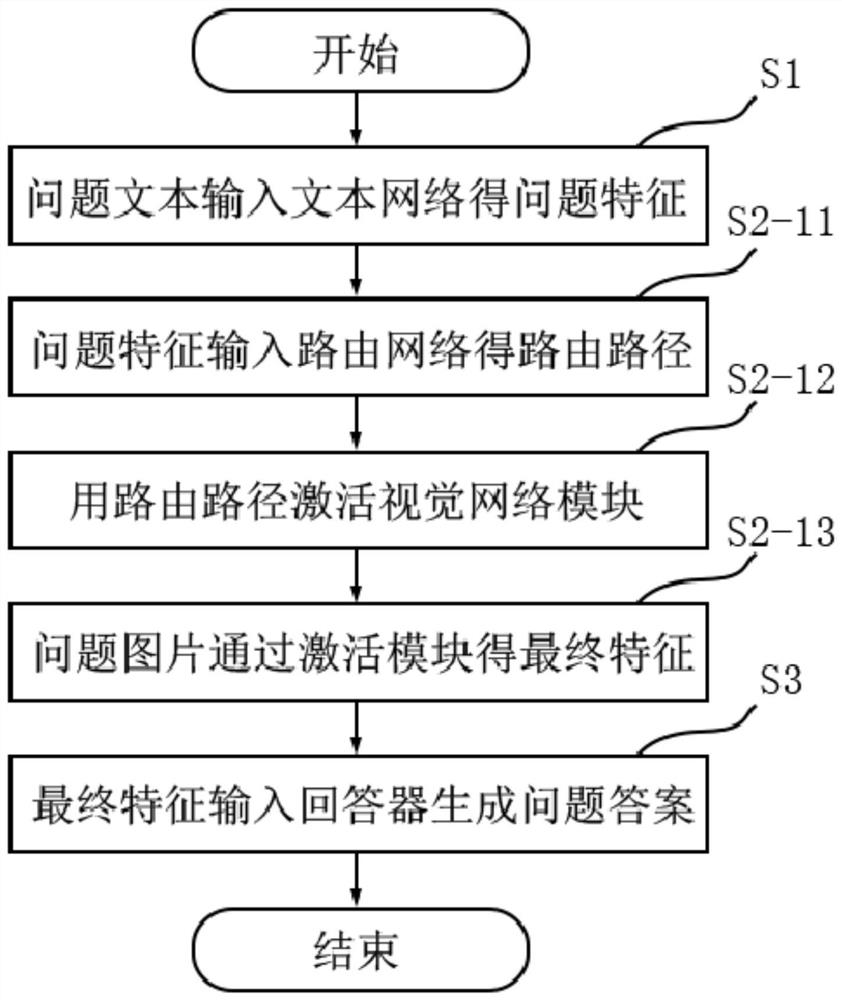
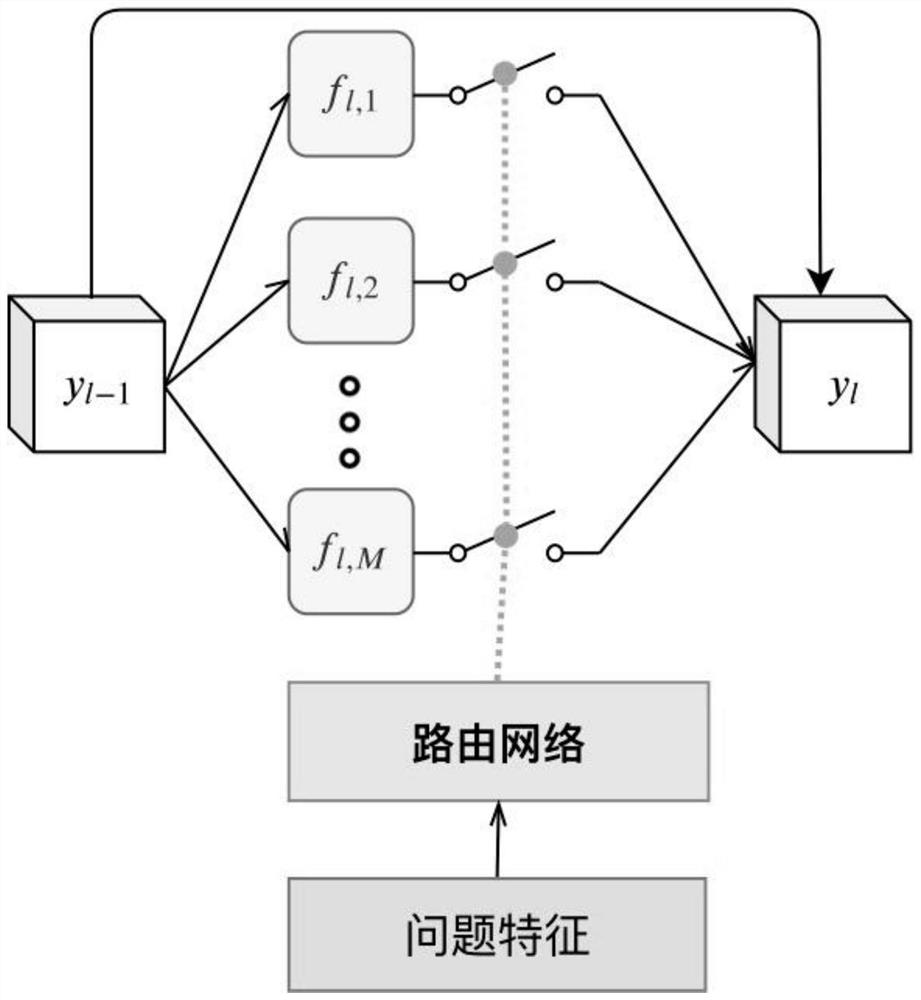
Visual question and answer method based on module routing network model
PendingCN114138946AFully analyzedCharacter and pattern recognitionNeural architecturesText modeTheoretical computer science
The invention provides a visual question answering method based on a module routing network, which is used for processing a natural language question text and an input question picture according to a module routing network model and generating a question answer, and is characterized in that the module routing network model is provided with a text network, a routing network and a visual network, comprising the following steps: step 1, inputting a natural language question text into a text network to extract question features; 2, activating a corresponding module in the visual network to become an activation module according to a routing path generated by the routing path at least based on the problem features, inputting the problem picture into the visual network, and extracting image features from the problem picture by the activation module to form corresponding final features; and step 3, inputting the final features into the responder to generate answers to the questions. According to the method, the text mode and the vision mode are fused in multiple levels, expert knowledge and supervision information are not needed when complex questions are answered, and the method can be widely applied to the situation that multiple modes need to be combined.
Owner:FUDAN UNIV
Method for automatically analyzing transaction logs of a distributed computing system
PendingUS20210342702A1High precisionFully analyzedDetecting faulty hardware using neural networksNatural language data processingTheoretical computer scienceTransaction log
An aspect of the invention relates to a method for automatically analysing a transaction log of a distributed computing system, comprising a plurality of lines, the method comprising the following steps:For each line:Cutting the line into words;Constructing a comparison vector by comparing the line with the other lines of the same size as the line;Constructing a pattern from the comparison vector;Creating an event per pattern;Constructing at least one prediction model by training an artificial neural network on a group of training events, the prediction model being configured to predict the next event in the transaction log;For at least one event:Using the prediction model to predict the event, from a group of prediction events;Generating from the prediction model, a causal graph of the event comprising a causal relation for each event of the group of prediction events responding to a relevance condition.
Owner:BULL SA
Making method of rose health vinegar
InactiveCN107904125AWith tonicWith bloodMicroorganism based processesVinegar preparationRed yeast riceFlavor
The invention relates to a making method of rose health vinegar, involving 200 parts of glutinous rice, 400 parts of fragrant rice, 300 parts of red yeast rice, 3 parts of Saccharomyces cerevisiae, 3parts of rose flower, 1530 parts of bran, 300 parts of chaff, 4500 parts of fresh water, and 0.4 part of acetic bacteria. The main materials used herein include glutinous rice, fragrant rice and red yeast rice; the vinegar made with the main materials as compared with the single main material used in the existing vinegar making processes is more unique in flavor; the vinegar made with the fragrantrice has better vinegar fragrance; the glutinous rice as the raw material enables the vinegar to be more gentle and functional in tonifying deficiency, tonifying blood, invigorating spleen and warming stomach, reducing seating and the like; in addition, the red yeast rice as the raw material for vinegar making enables the vinegar to be effective in invigorating spleen and helping digest, and activating blood to remove stasis.
Owner:安徽爱家食品有限公司
Method for detecting solid-phase reaction between inclusions and alloy matrix in thermal treatment process
InactiveCN104237280AAvoid inconvenienceFully analyzedMaterial analysis using wave/particle radiationPreparing sample for investigationNon-metallic inclusionsSolid reaction
The invention provides a method for detecting solid-phase reaction between inclusions and an alloy matrix in a thermal treatment process. On the one hand, the limitation that the solid-phase reaction between the inclusions and the alloy matrix can not be clearly observed due to too small size of the inclusions is broken through, on the other hand, the situation of an interface between the inclusions and the alloy matrix and the influence of the solid-phase reaction between the inclusions and the alloy matrix on components, natures and physical phases of the inclusions and the alloy matrix are disclosed. The method integrates a high-temperature confocal laser microscope pre-melting process, a quartz tube sealing process, a thermal treatment process and the like, detects the solid-phase reaction and a reaction mechanism between a Fe-Mn-Si steel matrix alloy and MnO-SiO2-FeO-MnS series inclusions in the thermal treatment process at the temperature of 1473K to verify that the technology can be used for effectively reflecting the solid-phase reaction and the reaction mechanism between the non-metallic inclusions and the steel matrix and has an important experimental and production guide effect and good application and popularization prospects.
Owner:UNIV OF SCI & TECH BEIJING
Features
- R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
Why Patsnap Eureka
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com