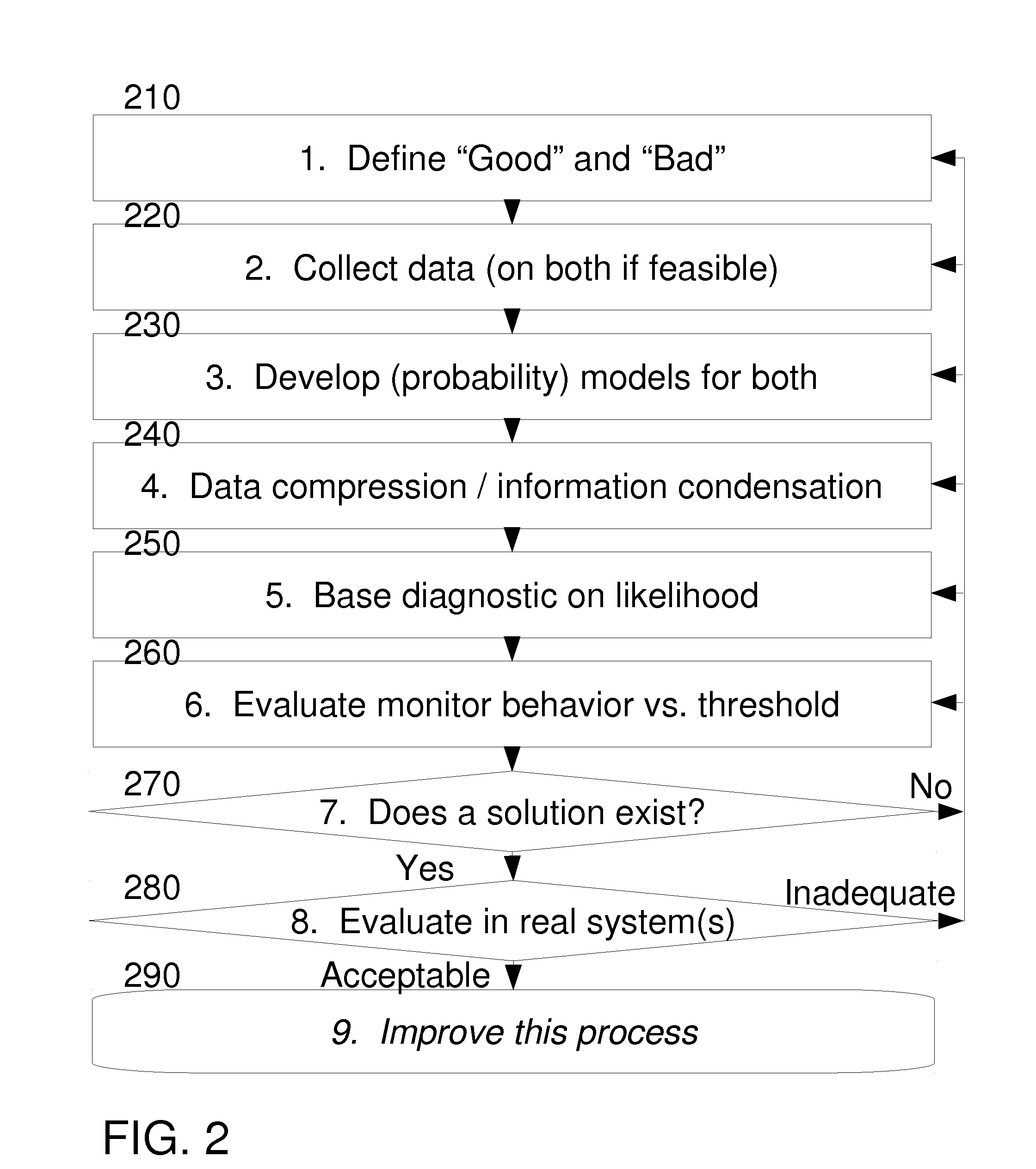
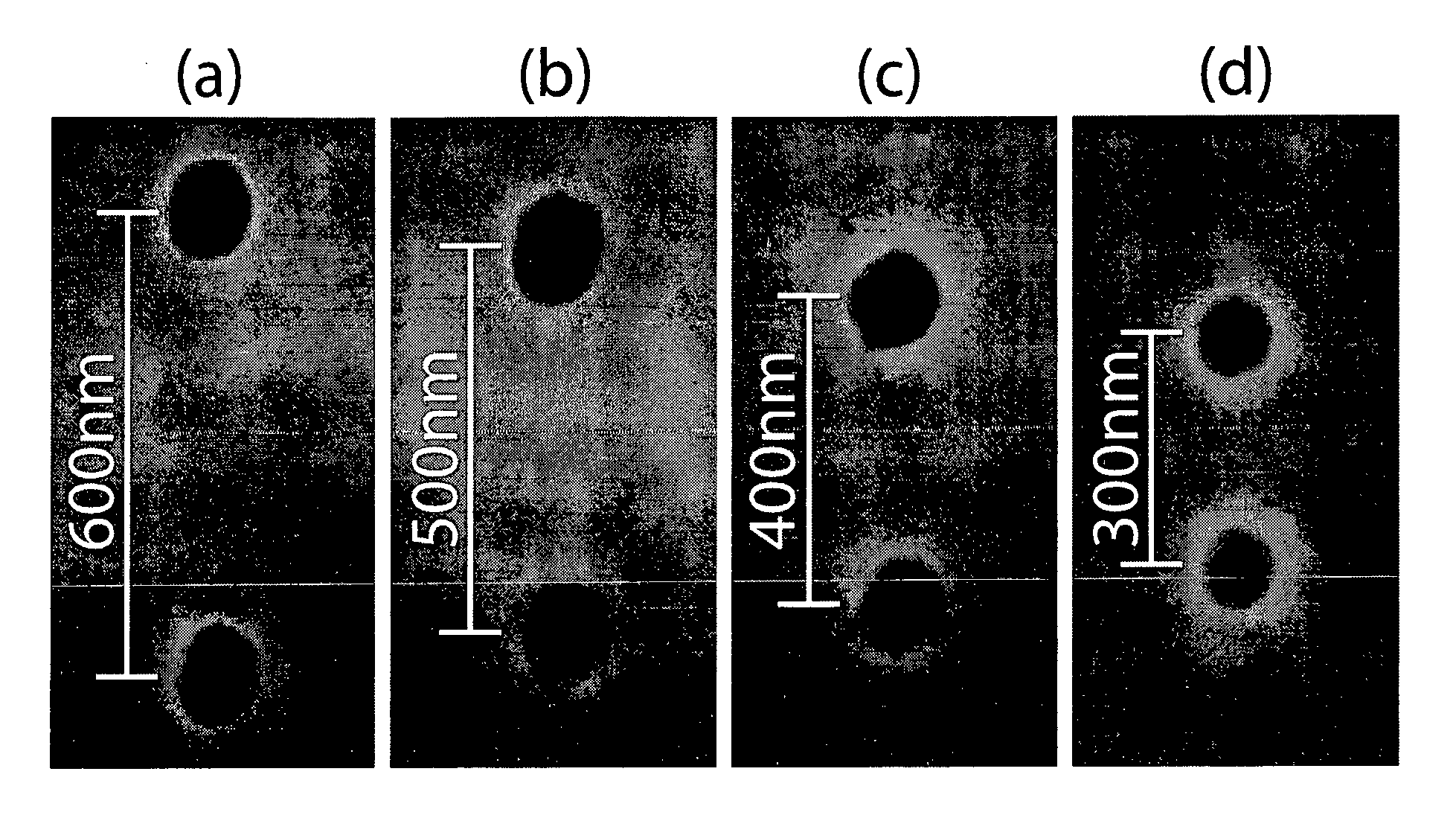
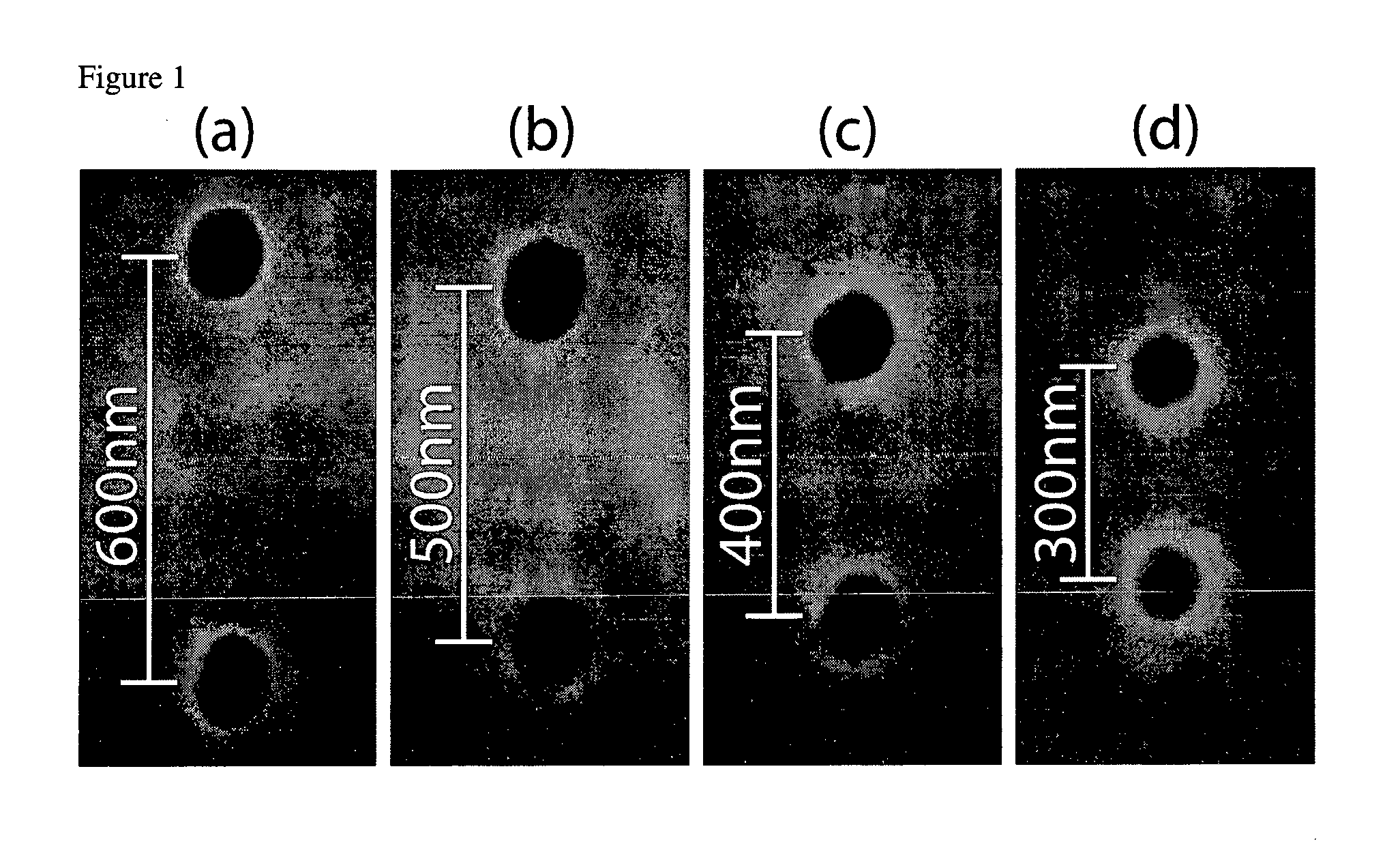
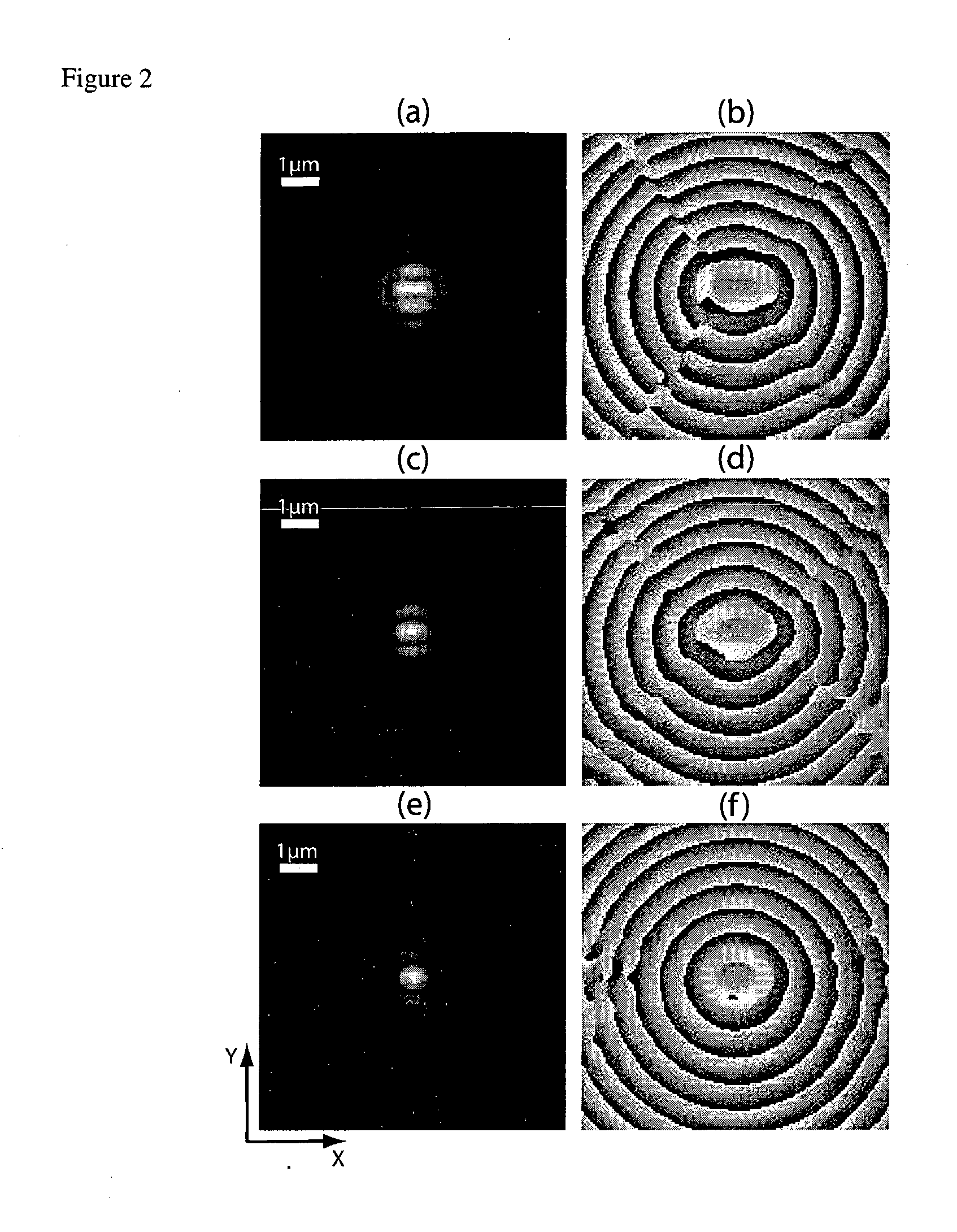
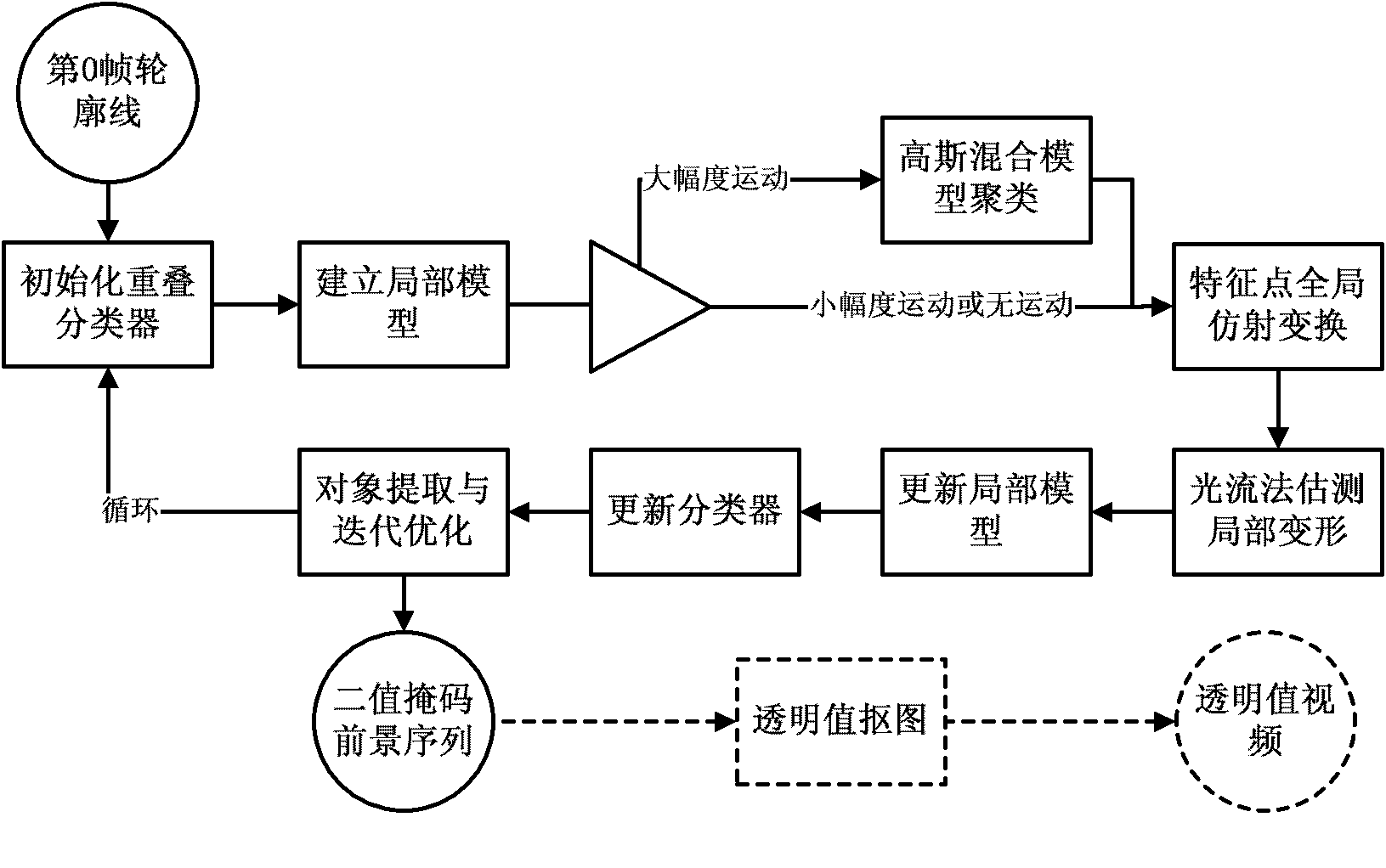
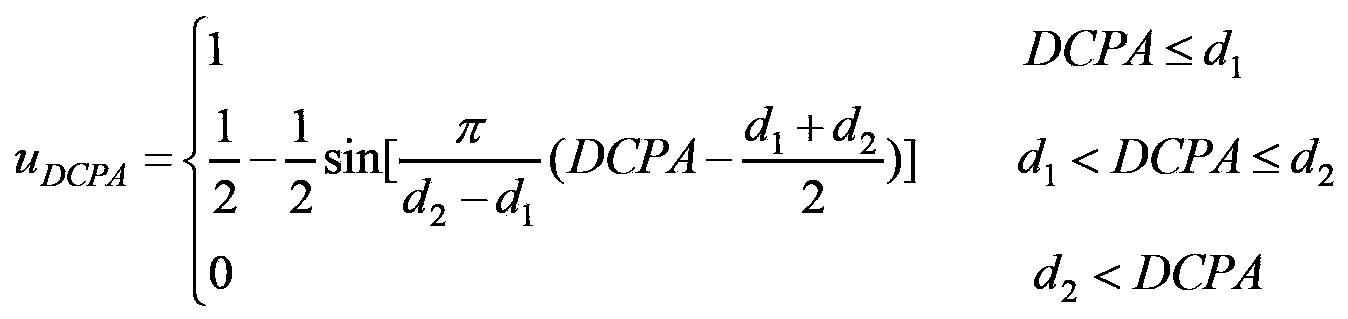Patents
Literature
277 results about "Technology in Star Trek" patented technology
Efficacy Topic
Property
Owner
Technical Advancement
Application Domain
Technology Topic
Technology Field Word
Patent Country/Region
Patent Type
Patent Status
Application Year
Inventor
The technology in Star Trek has borrowed freely from the scientific world to provide storylines. Episodes are replete with references to tachyon beams, baryon sweeps, quantum fluctuations and event horizons. Many of the technologies created for the Star Trek universe were done so out of simple financial necessity—the transporter was created because the limited budget of the original series in the 1960s did not allow expensive shots of spaceships landing on planets.
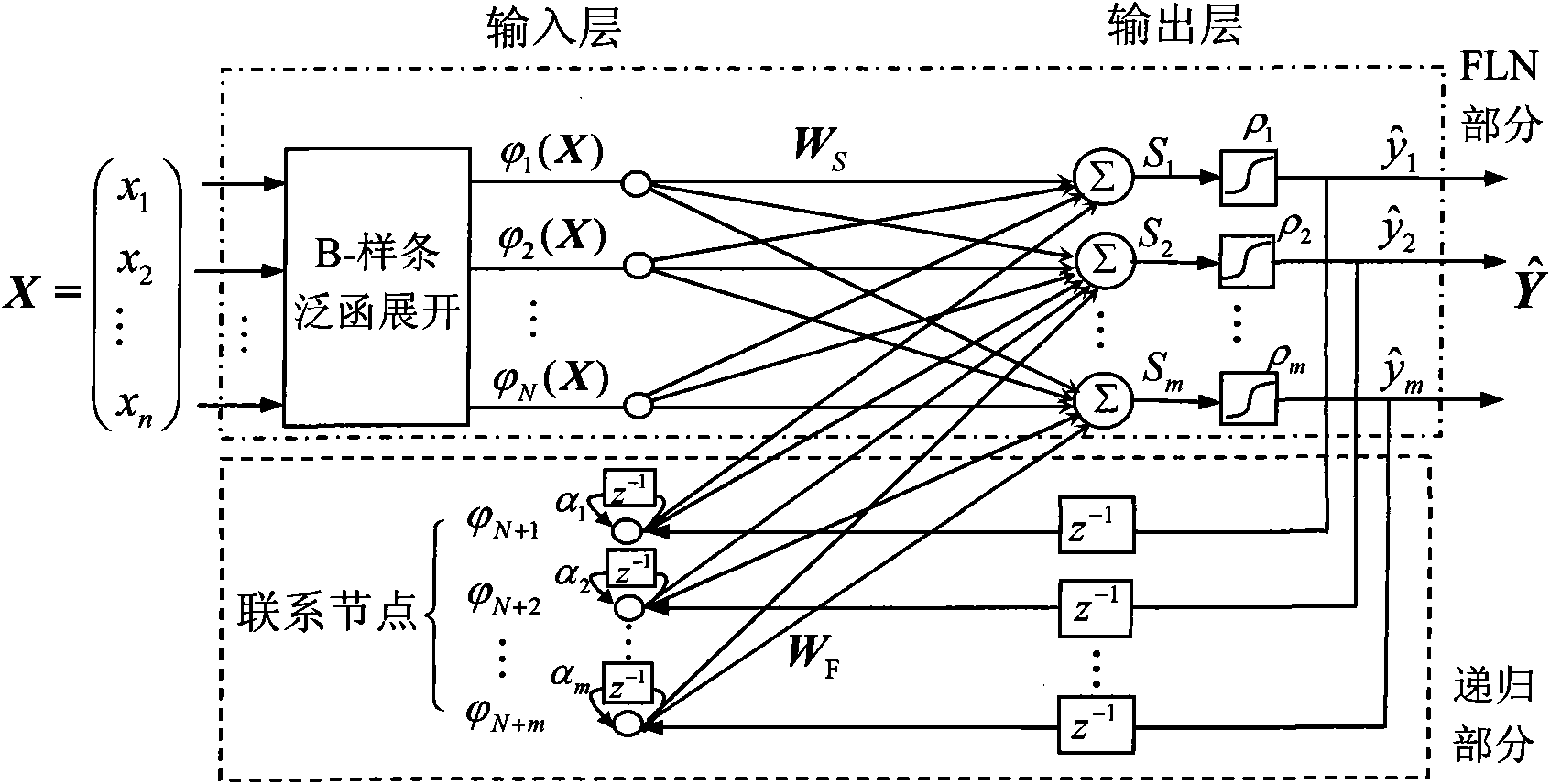
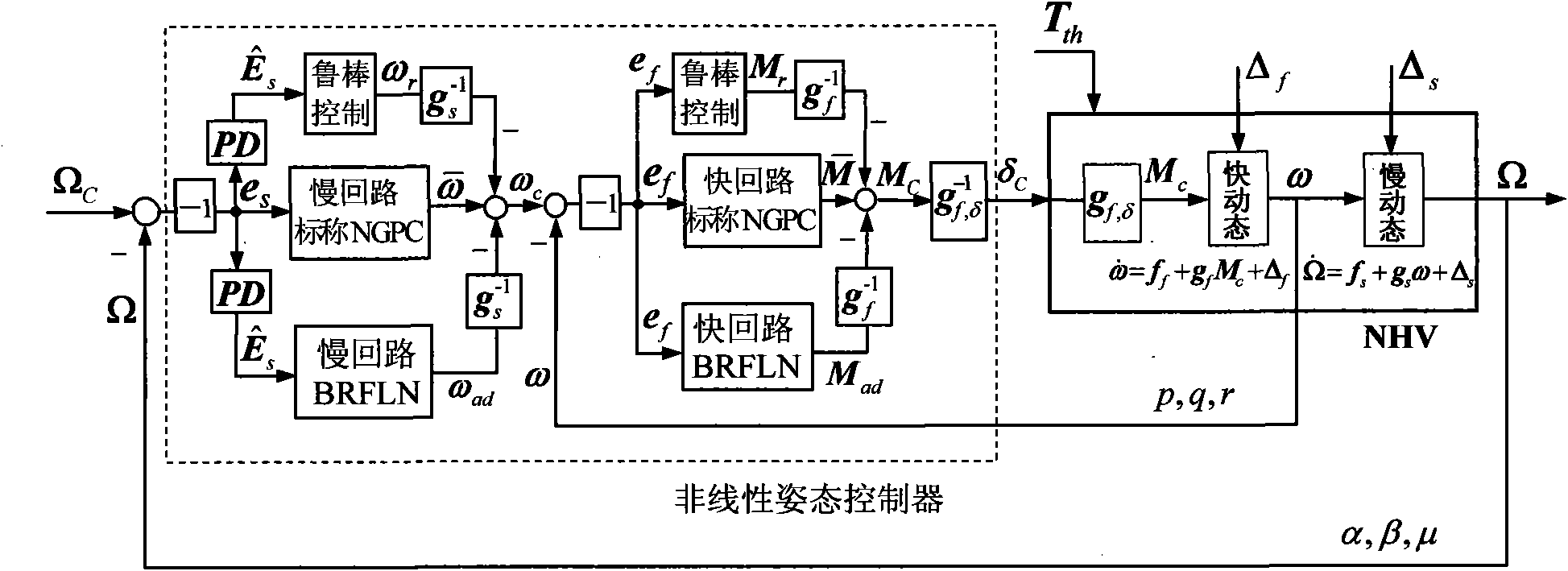
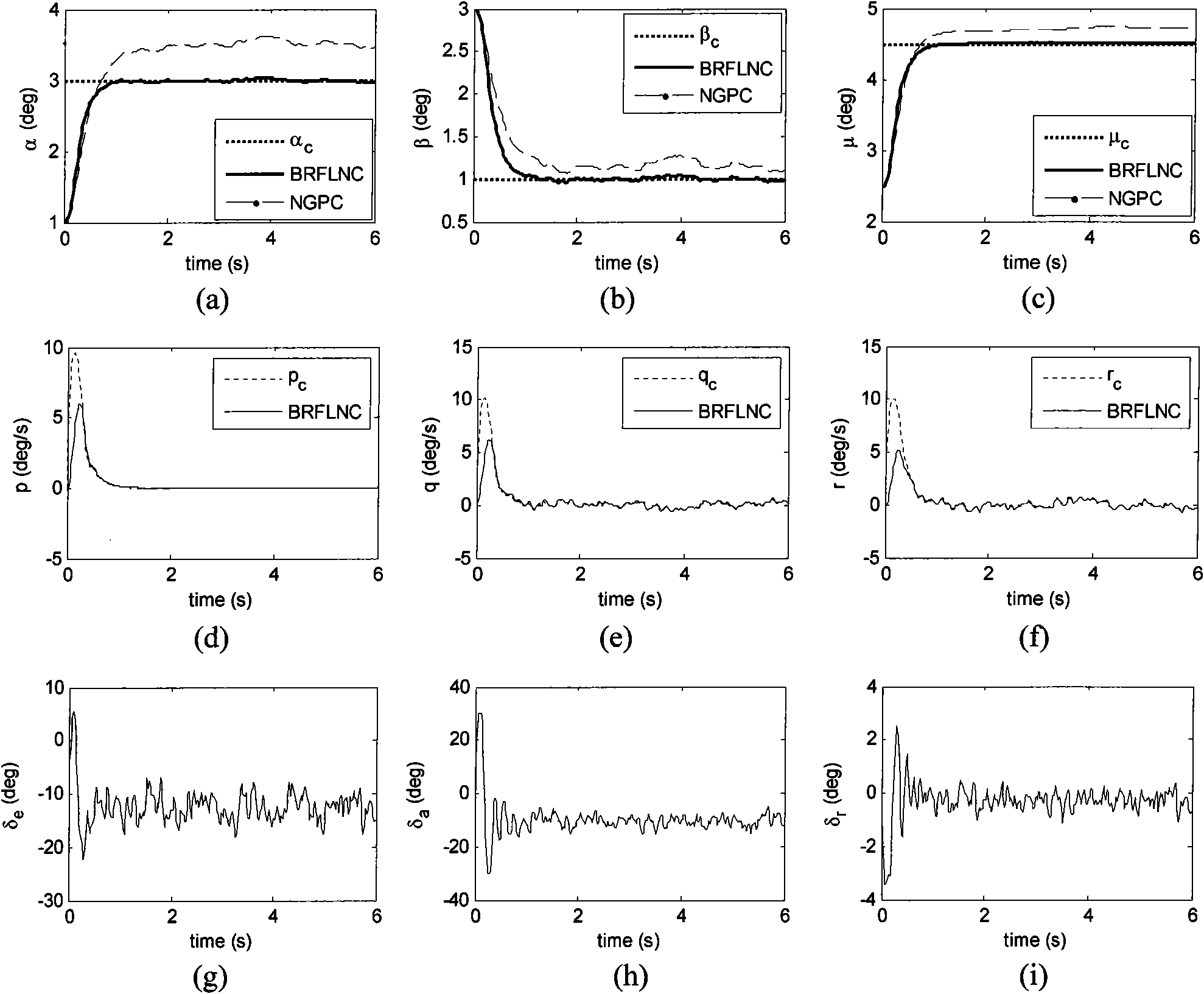
Nonlinear self-adaption control method of near-space hypersonic vehicle
InactiveCN101937233ATake advantage ofLighten the computational burdenAttitude controlAdaptive controlAviationNonlinear adaptive control
The invention discloses a nonlinear self-adaption control method of near-space hypersonic vehicle (NHV), which belongs to a flight control method in the technical field of aerospace. The control method mainly comprises three control law parts: a nominal nonlinear generalized predictive control law (NGPC), a B-spline recursive functional linkage network (BRFLN) self-adaption control law, and a robust control law of gain self-adaption adjustment. The invention integrates the simplicity of the NGPC method and the effectiveness of dynamic uncertainty of the BRFLN learning, targets the immeasurable dynamic uncertainty and fast interference of an attitude system in the flight of the NHV, brings favorable learning effect, and realizes the nonlinear accurate control to the attitude angle.
Owner:NANJING UNIV OF AERONAUTICS & ASTRONAUTICS
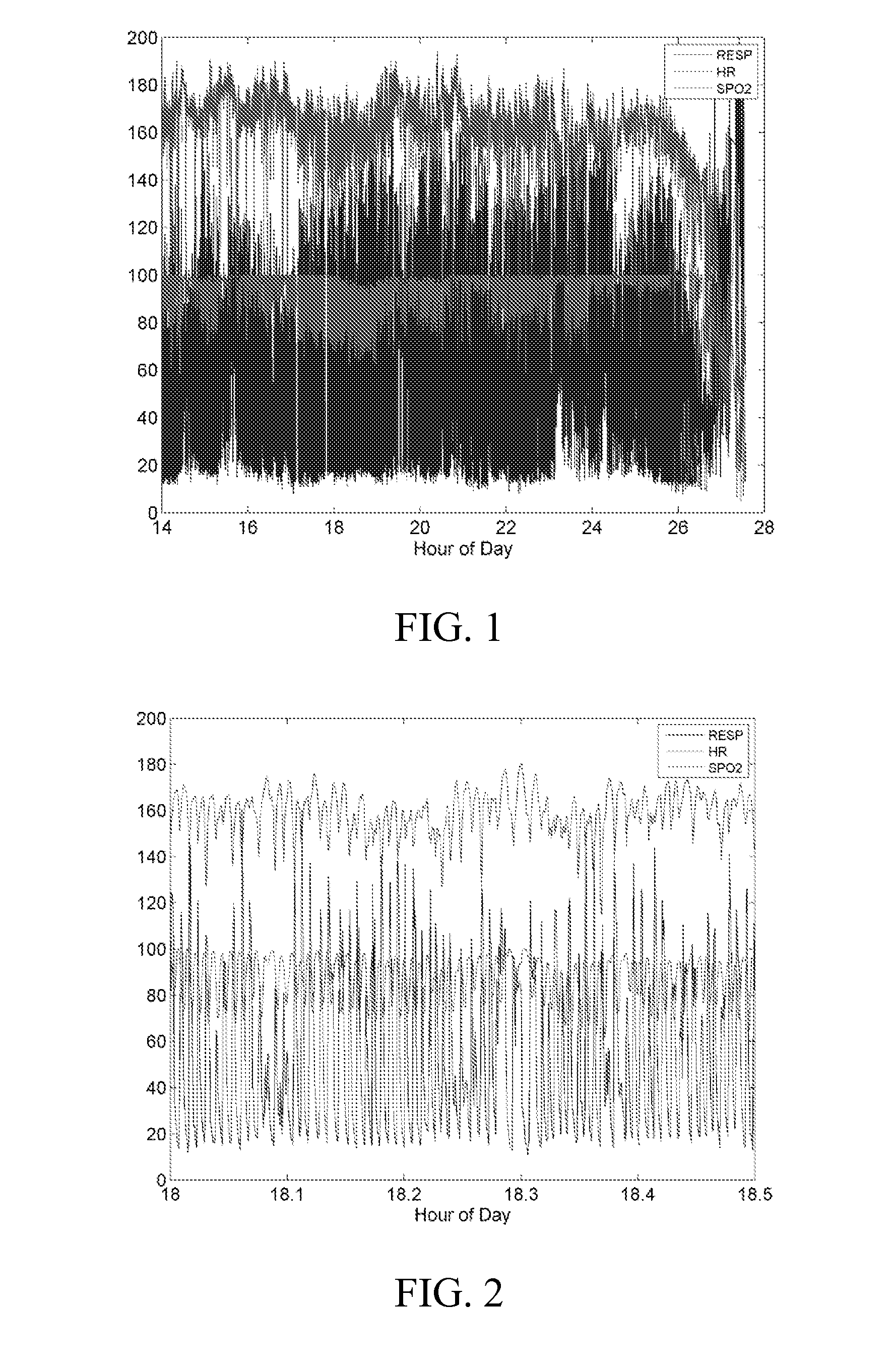
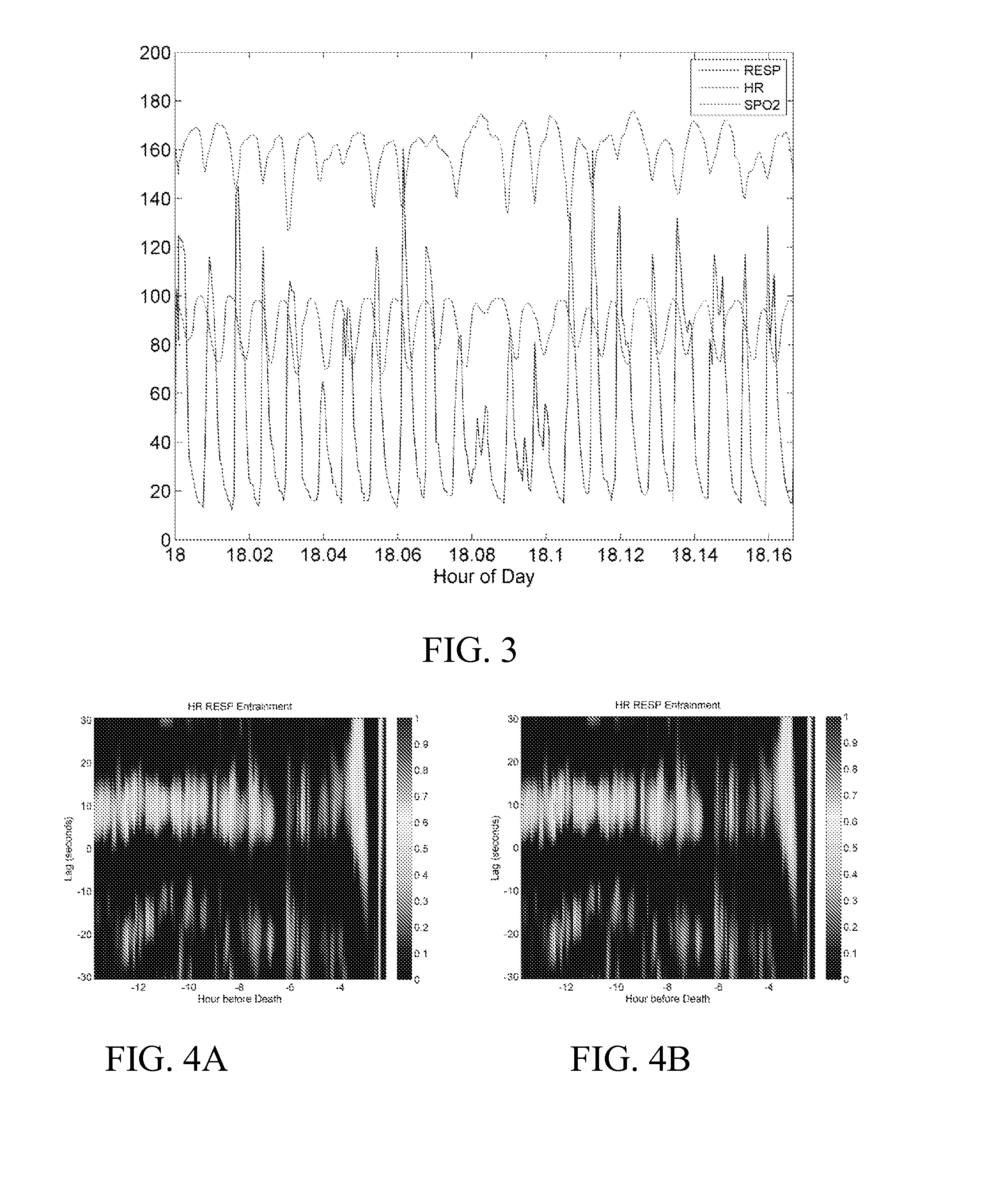
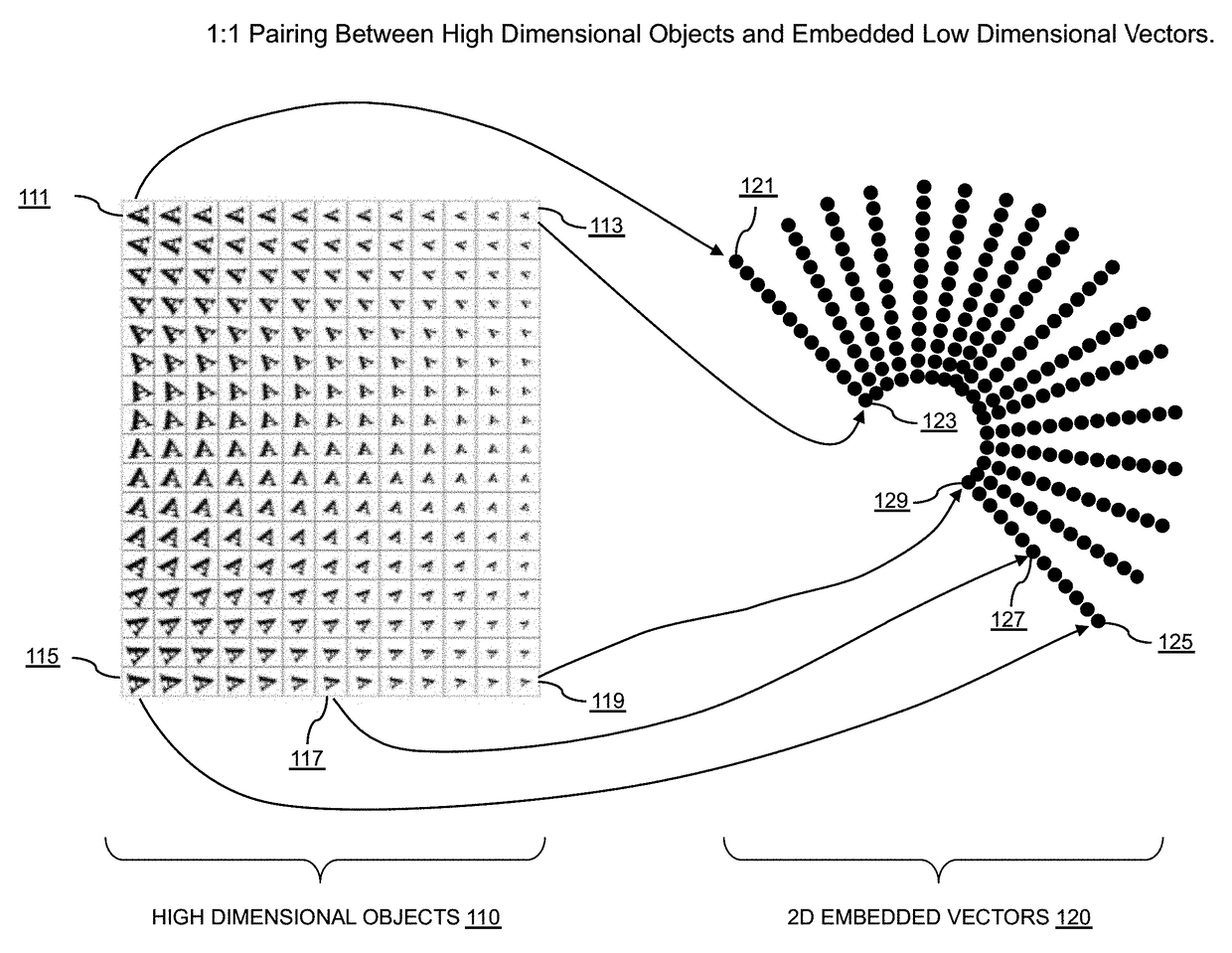
Multidimensional time series entrainment system, method and computer readable medium
PendingUS20160143594A1Useful in detectionData processing applicationsMedical automated diagnosisTime series representationAlgorithm
Illness signatures are mathematically characterized by entrainment relationships among multiple time series representations of physiological processes. Such characteristics include time and phase lags, window lengths for optimum detection, which time series are most entrained with each other, the degree of entrainment relative to the rest of the large database, and the concordance or discordance of the time-varying changes. These optimum disease-specific characteristics can be determined, for example, from large, clinically well-annotated databases of time series representations of physiological processes during health and illness. These characteristics of the entrainment relationships among multiple time series representations of physiological processes are used to make mathematical and statistical predictive models using multivariable techniques such as, but not limited to, logistic regression, nearest-neighbor techniques, neural and Bayesian networks, principal and other component analysis, and others. These models are quantitative expressions that transform measured characteristics to the probability of an illness, or p(illness).
Owner:UNIV OF VIRGINIA ALUMNI PATENTS FOUND
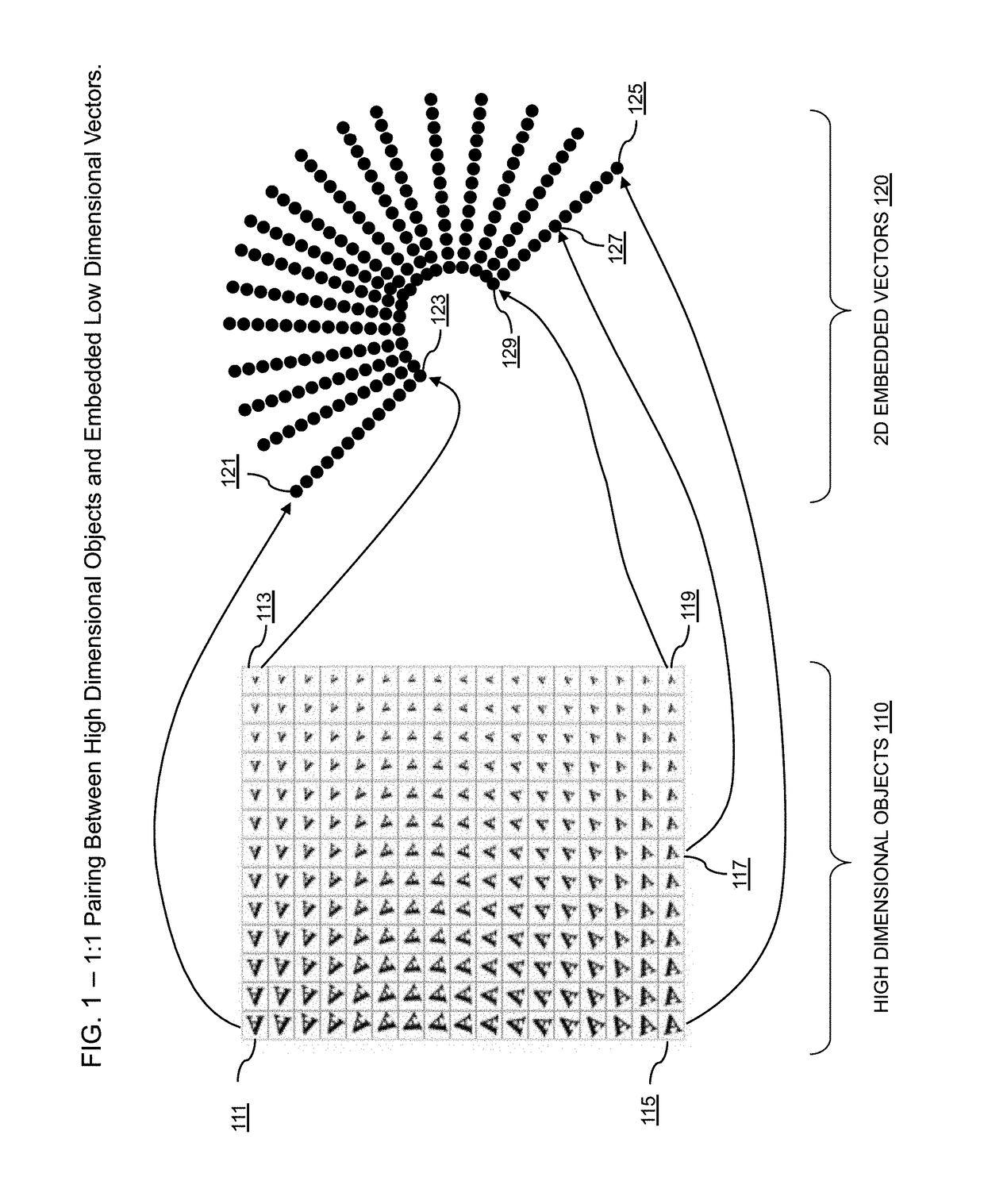
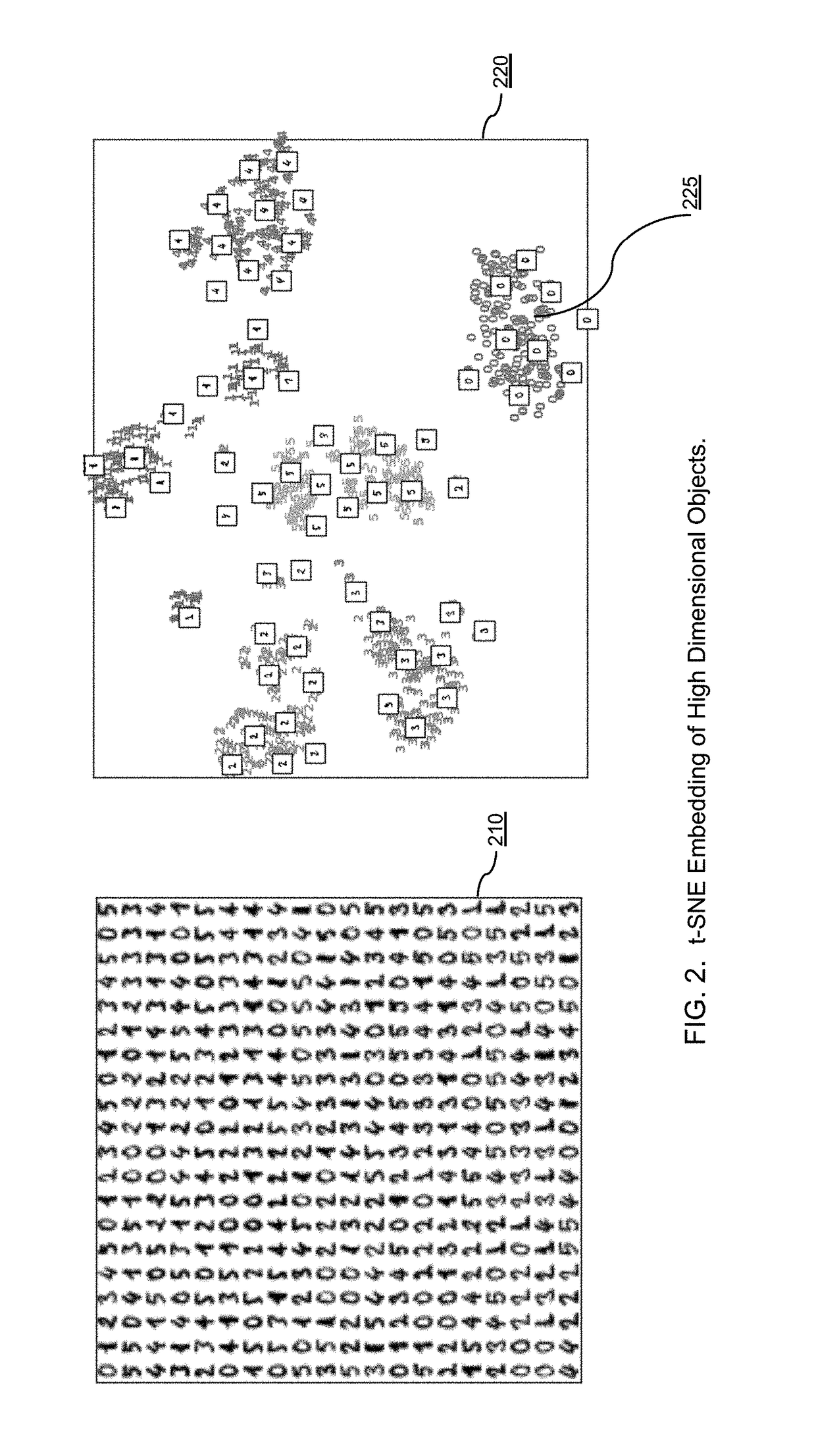
Systems and methods for fast and repeatable embedding of high-dimensional data objects using deep learning with power efficient GPU and FPGA-based processing platforms
ActiveUS9990687B1Reduce total powerShorten the timeCharacter and pattern recognitionImage watermarkingPower efficientAlgorithm
Embodiments of the present invention are directed to providing new systems and methods for using deep learning techniques to generate embeddings for high dimensional data objects that can both simulate prior art embedding algorithms and also provide superior performance compared to the prior art methods. Deep learning techniques used by embodiments of the present invention to embed high dimensional data objects may comprise the following steps: (1) generating an initial formal embedding of selected high-dimensional data objects using any of the traditional formal embedding techniques; (2a) designing a deep embedding architecture, which includes choosing the types and numbers of inputs and outputs, types and number of layers, types of units / nonlinearities, and types of pooling, for example, among other design choices, typically in a convolutional neural network; (2b) designing a training strategy; (2c) tuning the parameters of a deep embedding architecture to reproduce, as reliably as possible, the generated embedding for each training sample; (3) optionally deploying the trained deep embedding architecture to convert new high dimensional data objects into approximately the same embedded space as found in step (1); and optionally (4) feeding the computed embeddings of high dimensional objects to an application in a deployed embodiment.
Owner:GENERAL DYNAMICS MISSION SYST INC
Path planning method of passable area divided at unequal distance
InactiveCN103528585AOvercome memory spaceOvercome timeNavigational calculation instrumentsUndirected graphPlanning approach
The invention belongs to the technical field of path or flight path planning of robots as well as low-altitude flight aircrafts, specifically relates to a path planning method of a passable area divided at unequal distance, and is used for solving the problem that existing planning algorithm has large time complexity in time and space complexity. The path planning method comprises the following steps of: calculating convex extreme points of each barrier curve; dividing the passable area by using each convex extreme point as a horizontal line; abstracting each small area obtained by dividing into a peak of a graph; forming an undirected graph by all peaks; finding out a peak serial number corresponding to the small area at which a starting point and a final point are located; finding out all paths for the undirected graph by breadth-first or depth-first scanning; finding out an actual to-be-travelled path of a moving object according to the situation on an actual map. The path planning method disclosed by the invention has the beneficial effect of overcoming the problems of algorithms of A* and the like on memory space and operation time, and overcoming a convergence problem of an ant colony algorithm at the same time. Besides, time complexity and space complexity are improved greatly in comparison with other algorithms.
Owner:ZHONGBEI UNIV
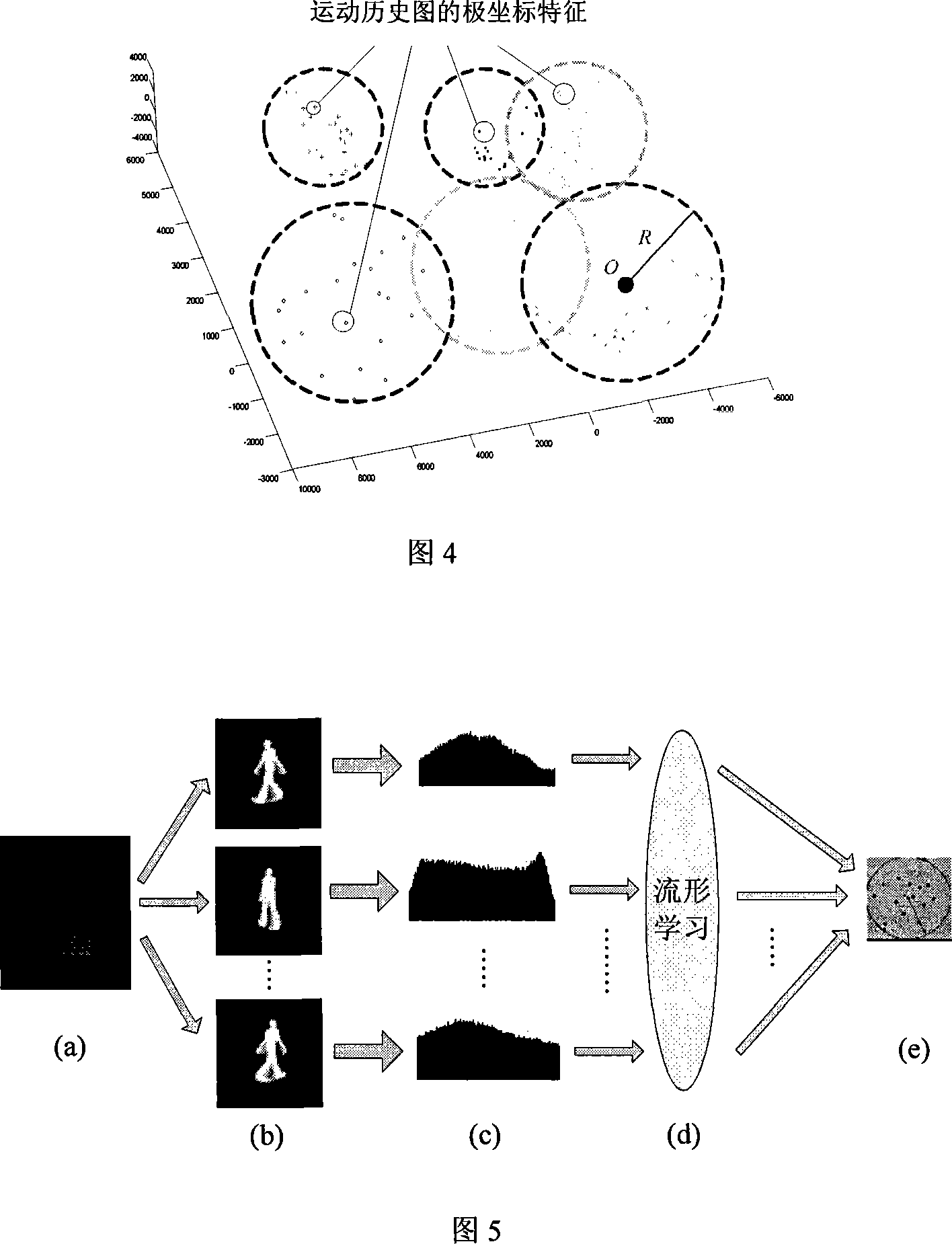
An identification method for movement by human bodies irrelevant with the viewpoint based on stencil matching
InactiveCN101216896ASimple structureGood for action recognitionCharacter and pattern recognitionClosed circuit television systemsVideo monitoringHuman body
The invention discloses a view-independent human action identification method based on template matching, which can identify a plurality of pre-defined typical actions in a video. When constructing a template, a motion history image under a plurality of projection viewpoints are calculated for each sample action and polar coordinate characteristics are extracted, the polar coordinate characteristics are mapped to a low-dimensional sub-space by adopting a manifold learning method, and super balls are constituted for the sample actions in the sub-space on the basis of the low-dimensional coordinate of the multi-viewpoint polar coordinate characteristics. An action template is composed of a plurality of super balls with known ball centers and radiuses. When an unidentified action is given, the motion history image and the corresponding polar coordinate characteristics of the action are firstly calculated, then the polar coordinate characteristics are projected into the template action sub-space to obtain the low-dimensional coordinate, the distances from the coordinate to all the ball surfaces of the super balls are calculated, and the nearest super ball is selected as the identification result. The technology provided by the invention realizes the view-independent action identification and has higher application value in the video monitoring field.
Owner:ZHEJIANG UNIV
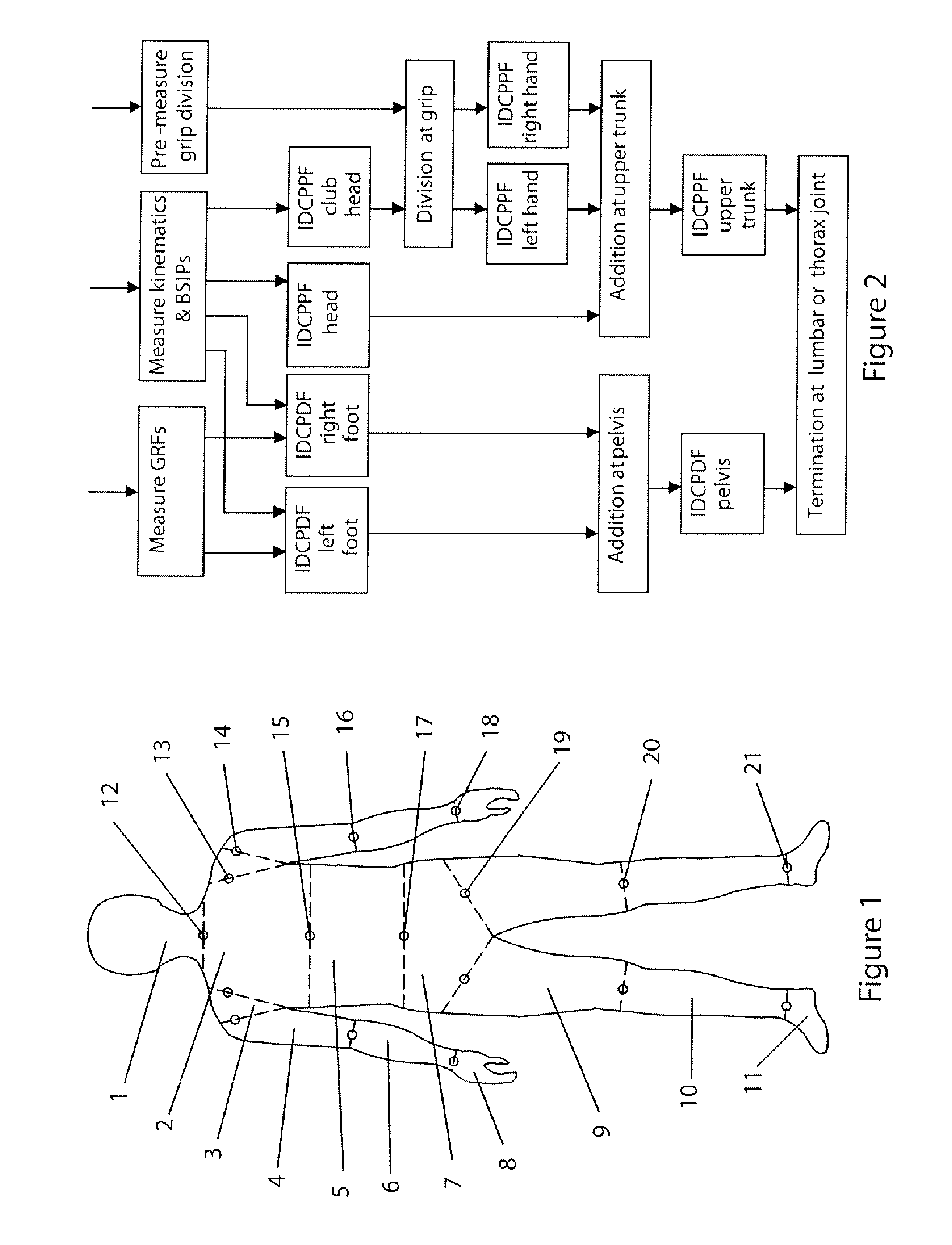
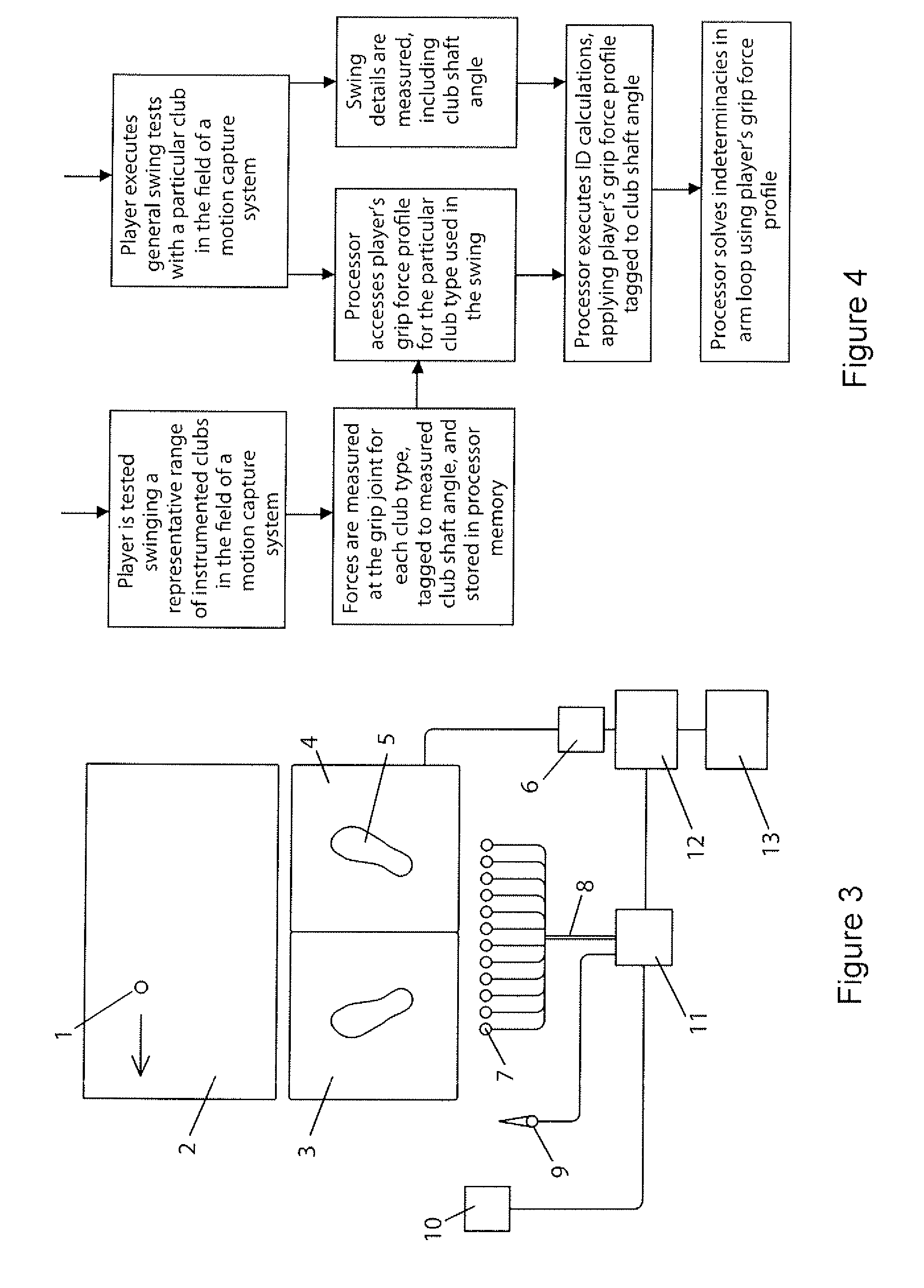
Apparatus and method for analysing a golf swing
ActiveUS20140342844A1Gymnastic exercisingCharacter and pattern recognitionInverse dynamicsHighly skilled
The system analyses a golf swing, determining individual joint powers generated in a player's body with high levels of accuracy, using inverse dynamics and detailed modelling of the player's body. A depth camera is used to measure body segment shapes and a magnetic motion capture system and 3D force plate system used to measure swing parameters. The system produces an expeditious analysis without the need for highly skilled technical personnel and is suitable for individual coaching and compilation of large golf swing databases.
Owner:MOONEY BRIAN FRANCIS
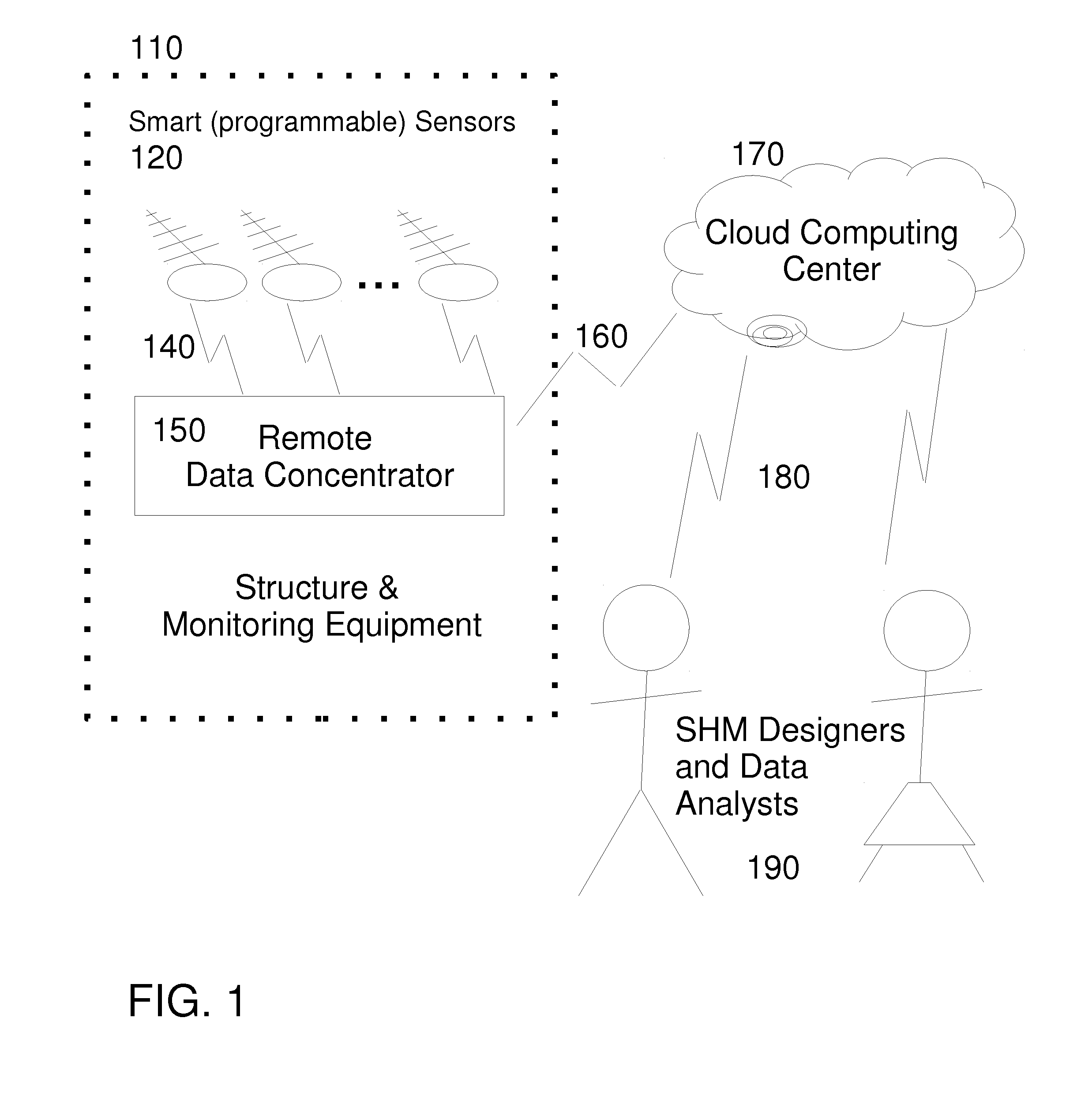
Software to facilitate design, data flow management, data analysis and decision support in structural health monitoring systems
InactiveUS20120123981A1Improve productivityEasy to controlDigital data information retrievalDigital data processing detailsData compressionStructural health monitoring
This patent application describes (a) software to help people design monitoring systems and (b) methods to facilitate enhanced data flow management (including from large numbers of simultaneous sources), diagnostic and statistical analyses based on novel concepts of data compression using statistical state space techniques. The design assistance is structured around known but not widely practiced procedures such as documented in Graves, Rens and Rutz (2011). For data flow management, the present invention may transmit and store an estimated state space model only when the last stored model is not adequate to predict recent observations. It may also transmit and store outliers and samples of regular observations. This unique data storage format requires new methods for data analysis to properly extract the information contained therein.
Owner:GRAVES SPENCER B +2
Complex index refraction tomography with sub lambda/6-resolution
The present invention discloses a method to improve the image resolution of a microscope. This improvement is based on the mathematical processing of the complex field computed from the measurements with a microscope of the wave emitted or scattered by the specimen. This wave is, in a preferred embodiment, electromagnetic or optical for an optical microscope, but can be also of different kind like acoustical or matter waves. The disclosed invention makes use of the quantitative phase microscopy techniques known in the sate of the art or to be invented. In a preferred embodiment, the complex field provided by Digital Holographic Microscopy (DHM), but any kind of microscopy derived from quantitative phase microscopy: modified DIC, Shack-Hartmann wavefront analyzer or any analyzer derived from a similar principle, such as multi-level lateral shearing interferometers or common-path interferometers, or devices that convert stacks of intensity images (transport if intensity techniques: TIT) into quantitative phase image can be used, provided that they deliver a comprehensive measure of the complex scattered wavefield. The hereby-disclosed method delivers superresolution microscopic images of the specimen, i.e. images with a resolution beyond the Rayleigh limit of the microscope. It is shown that the limit of resolution with coherent illumination can be improved by a factor of 6 at least. It is taught that the gain in resolution arises from the mathematical digital processing of the phase as well as of the amplitude of the complex field scattered by the observed specimen. In a first embodiment, the invention teaches how the experimental observation of systematically occurring phase singularities in phase imaging of sub-Rayleigh distanced objects can be exploited to relate the locus of the phase singularities to the sub-Rayleigh distance of point sources, not resolved in usual diffraction limited microscopy. In a second, preferred embodiment, the disclosed method teaches how the image resolution is improved by complex deconvolution. Accessing the object's scattered complex field—containing the information coded in the phase—and deconvolving it with the reconstructed complex transfer function (CTF) is at the basis of the disclosed method. In a third, preferred embodiment, it is taught how the concept of “Synthetic Coherent Transfer Function” (SCTF), based on Debye scalar or Vector model includes experimental parameters of MO and how the experimental Amplitude Point Spread Functions (APSF) are used for the SCTF determination. It is also taught how to derive APSF from the measurement of the complex field scattered by a nanohole in a metallic film. In a fourth embodiment, the invention teaches how the limit of resolution can be extended to a limit of λ / 6 or smaller based angular scanning. In a fifth embodiment, the invention teaches how the presented method can generalized to a tomographic approach that ultimately results in super-resolved 3D refractive index reconstruction.
Owner:ECOLE POLYTECHNIQUE FEDERALE DE LAUSANNE (EPFL)
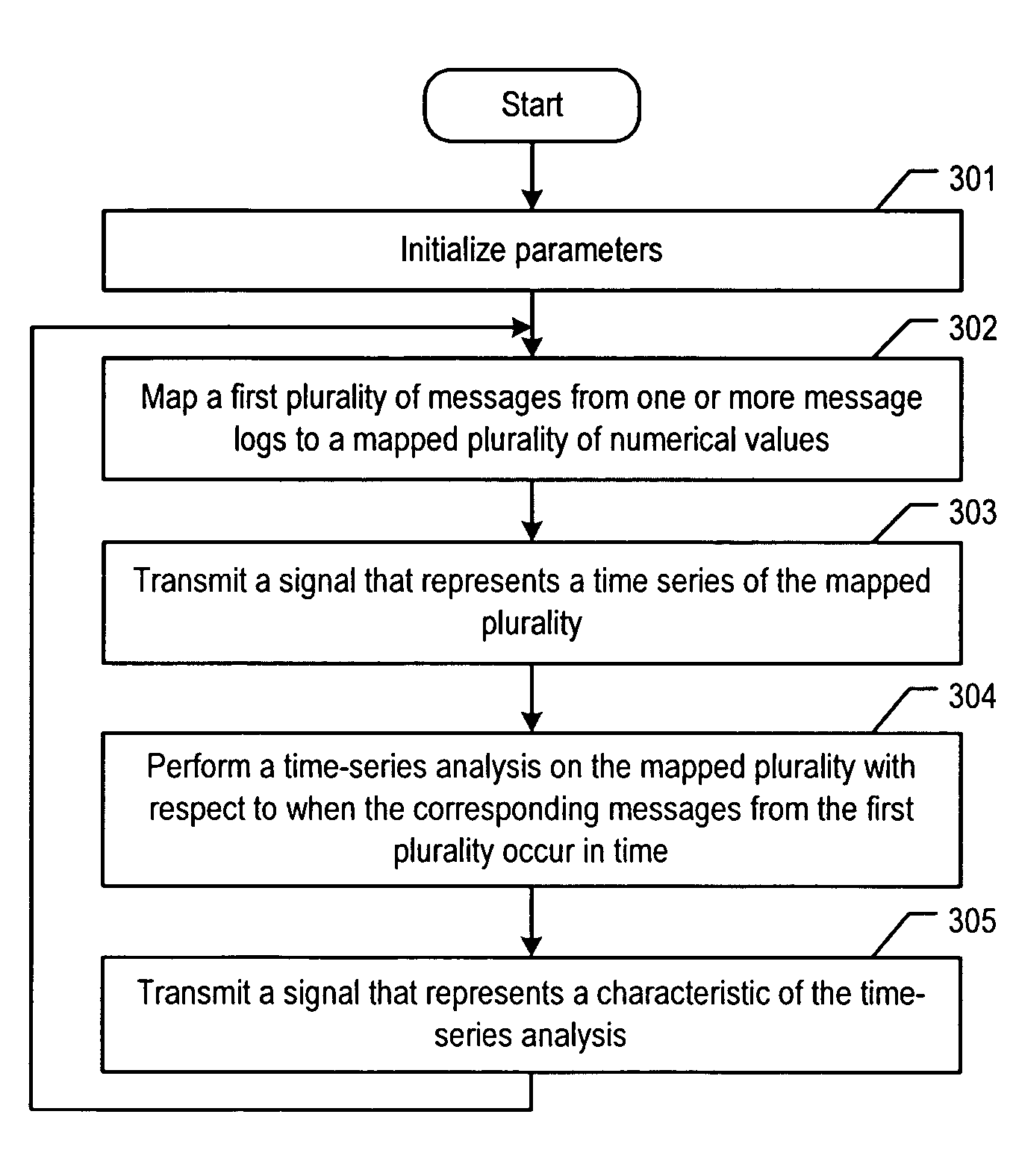
Message log analysis for system behavior evaluation
ActiveUS8073806B2Digital computer detailsFuzzy logic based systemsData processing systemAnalysis data
Owner:AVAYA INC
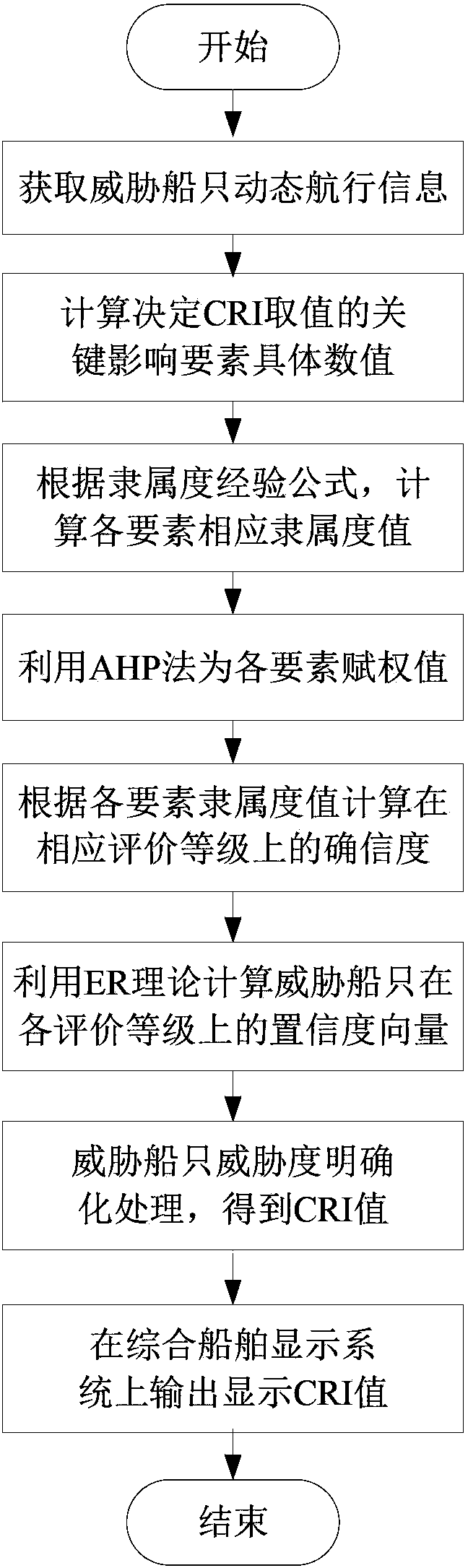
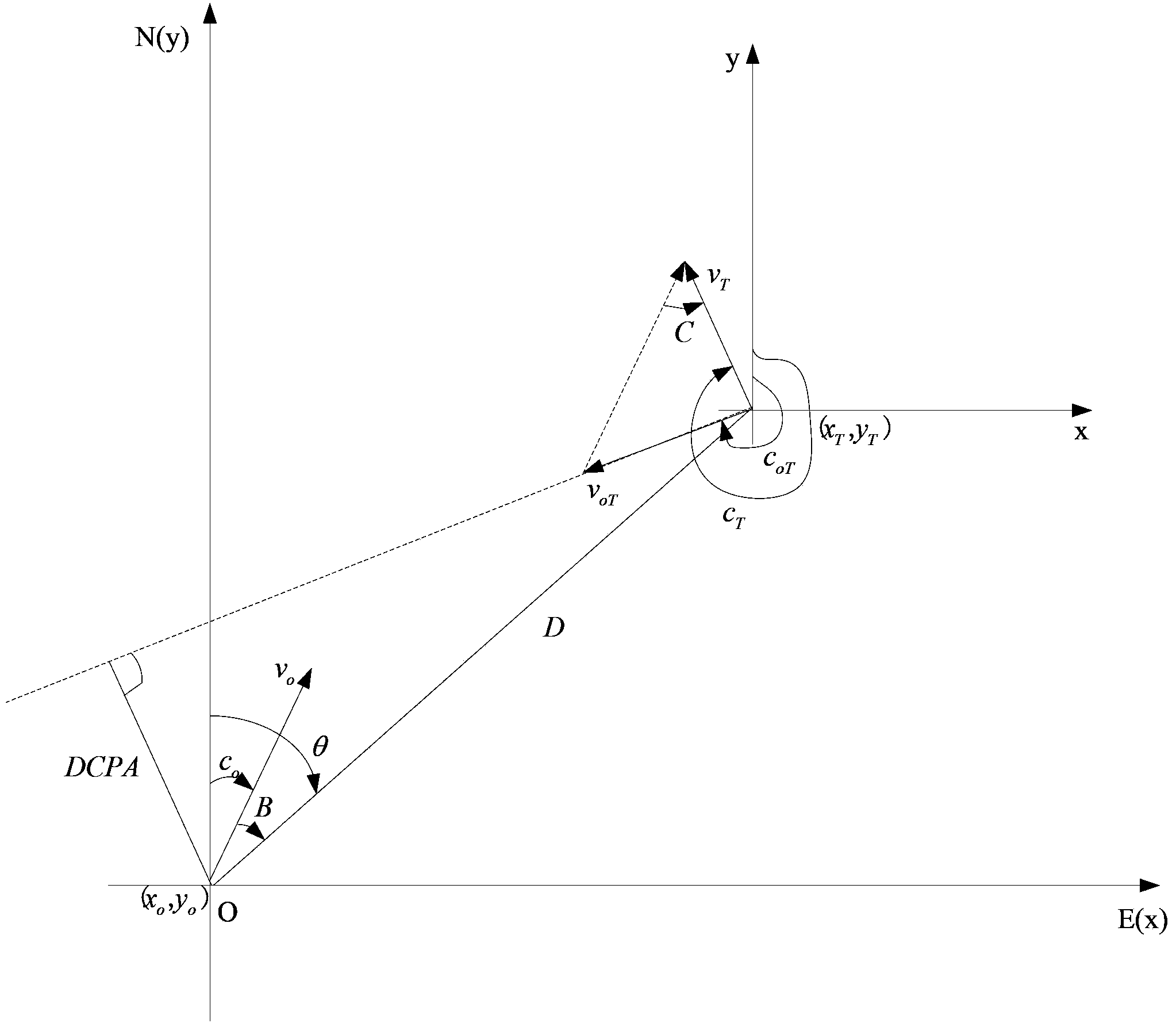
Method for detecting degree of risk of ship collision
ActiveCN104050329AGuaranteed reasonablenessEasy to integrateSpecial data processing applicationsClassification methodsDynamic data
The invention relates to the technical field of ship collision avoidance, in particular to a method for detecting the degree of risk of ship collision on the basis of an evidential reasoning theory, wherein the method is used for assisting ship drivers in making decisions and guaranteeing safe navigation of ships. The method for detecting the degree of risk of ship collision includes the steps that dynamic data of navigation of threatening ships are acquired through an automatic identification system (AIS) of a ship, values of influential factors are calculated, subjection degree values of all the factors are calculated, weights are allocated to five factors through a hierarchical classification method, and confidence coefficient values of all the factors on the corresponding evaluation levels are calculated; confidence coefficient vectors of the threatening ships on the evaluation levels are calculated; degrees of threat of the threatening ships are crystallized, and CRI values of the threatening ships are obtained; the obtained CRI values are output and displayed on a comprehensive ship display system. According to the method for detecting the degree of risk of ship collision, while the uncertainty of obtained data of the threatening ships and the uncertainty of expert experience are fully considered, the degrees of threat of the threatening ships to the current ship are reasonably evaluated through superiority of the evidential reasoning theory for representing and fusing uncertain information.
Owner:HARBIN ENG UNIV
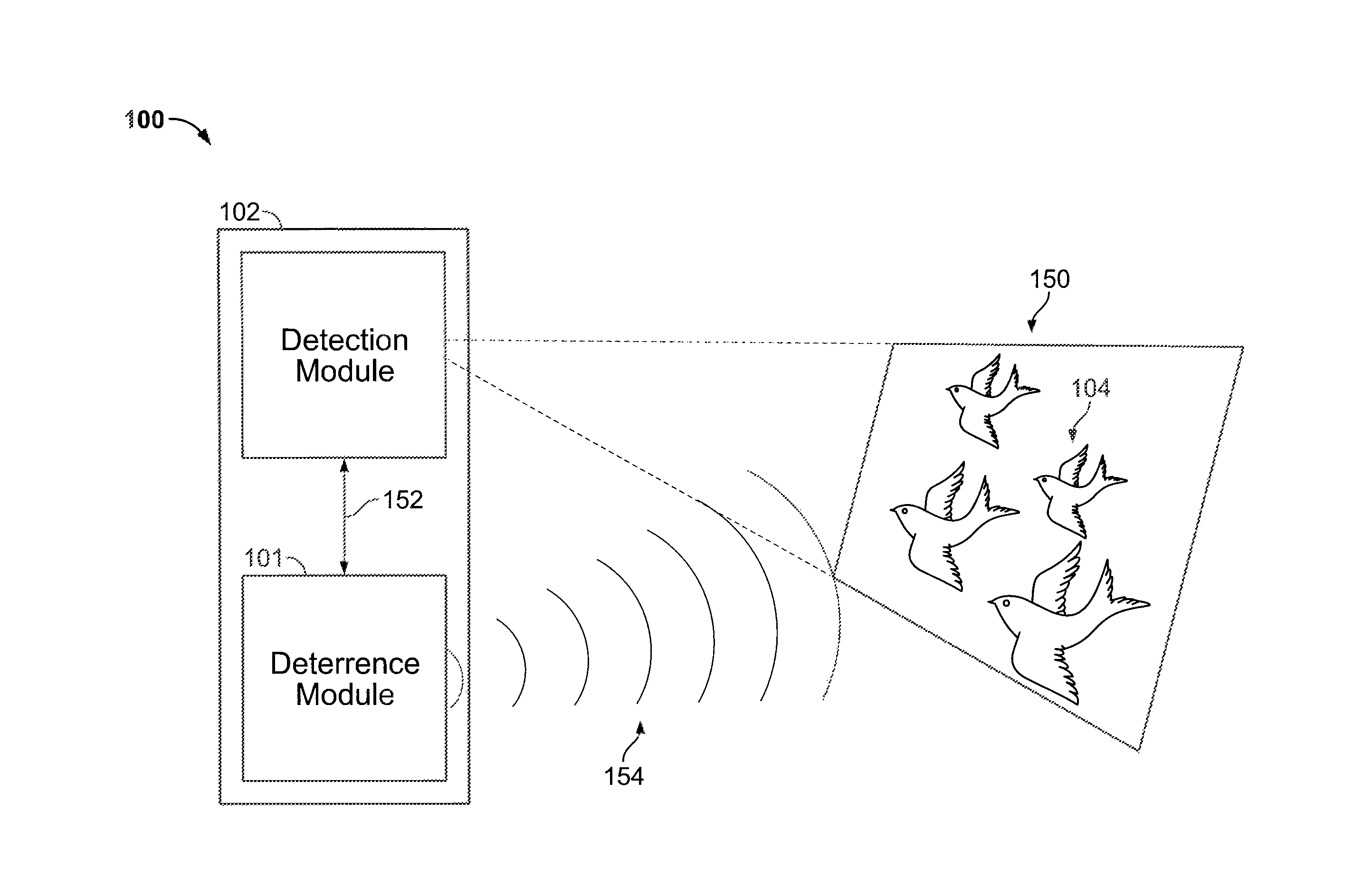
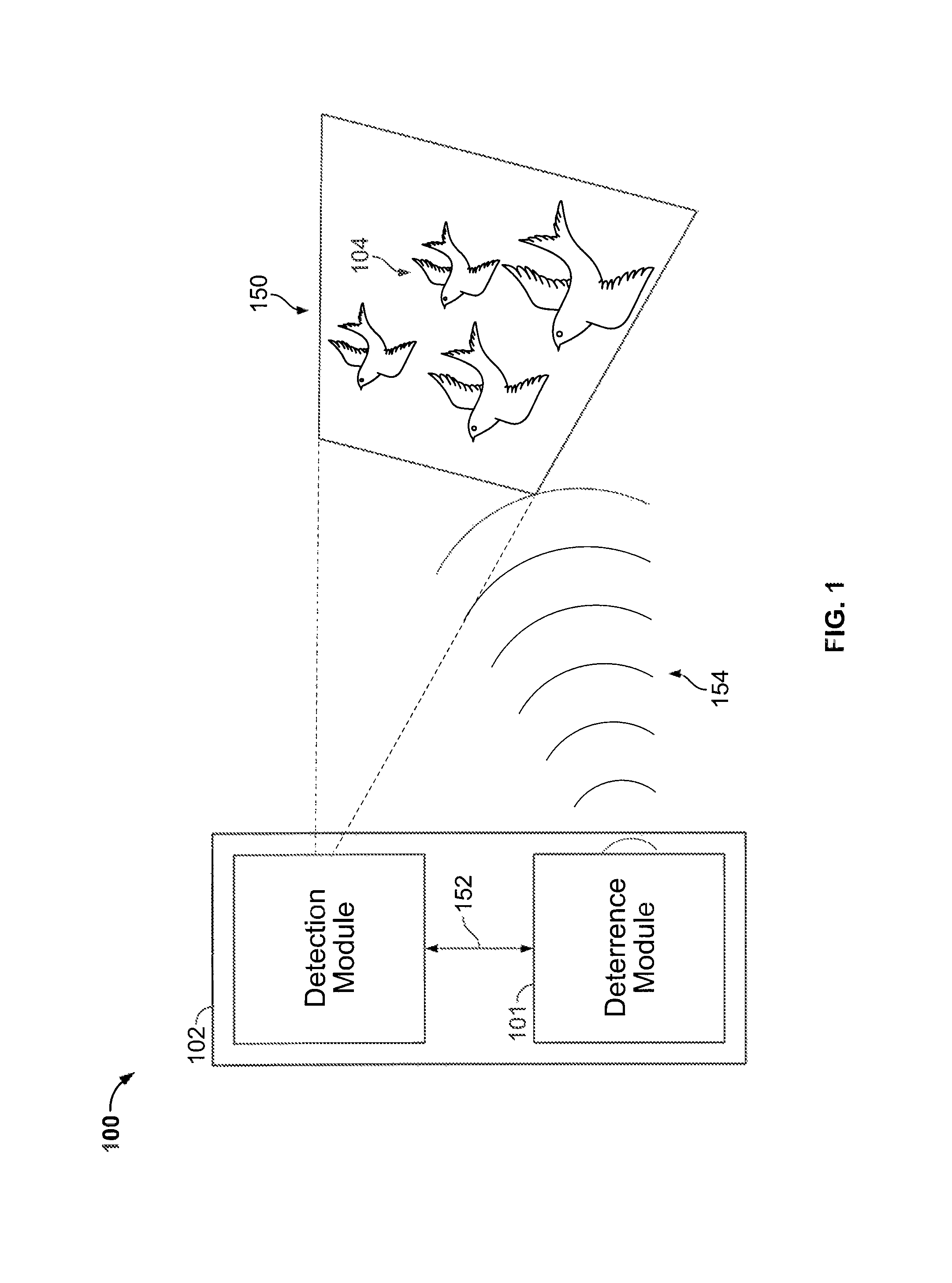
Animal collision avoidance system
Owner:VOLACOM
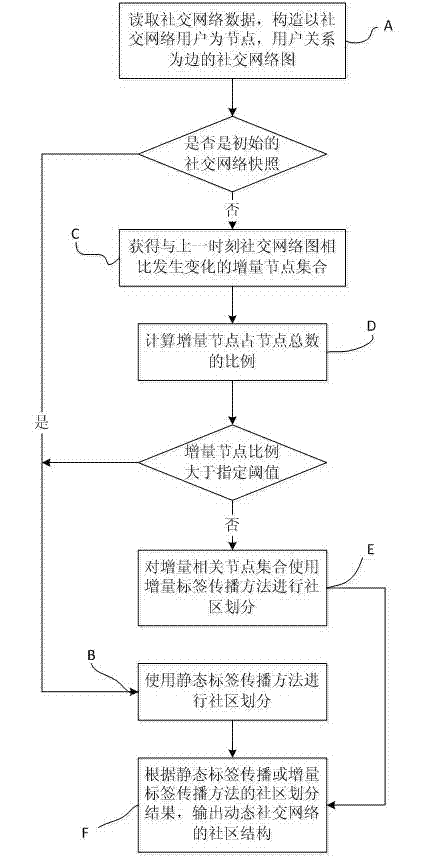
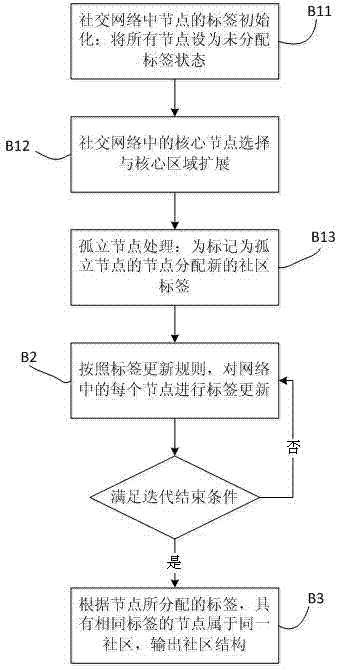
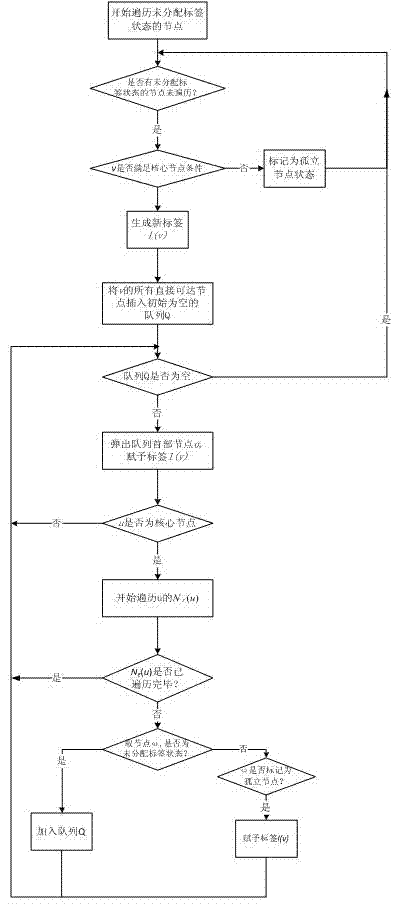
Dynamic community detection method in social network
InactiveCN103678671AImprove stabilityEasy to handleData processing applicationsWebsite content managementSocial graphStructure of Management Information
The invention relates to the technical field of social networks, in particular to a dynamic community detection method in the social network. The method comprises the steps that a snapshot of a certain time slice (moment) of the social network is obtained for the social network changing dynamically, and then a social network chart is constructed; community division is carried out on the social network chart of the initial moment, and the snapshot of a subsequent certain time slice (moment) of the social network is compared with the snapshot of a former moment to find an increment node set; the proportion occupied by increment nodes is calculated, if the proportion of the increment nodes exceeds a specified threshold value, community division is carried out on a complete snapshot network, and otherwise, community division is carried out on the increment node set, and then the community structure of the snapshot of a certain time slice (moment) of the social network is obtained. The method can effectively explore the community structure in the social network and can be applied to the fields of target group mining and precision marketing.
Owner:FUZHOU UNIV
System for extracting ralation between technical terms in large collection using a verb-based pattern
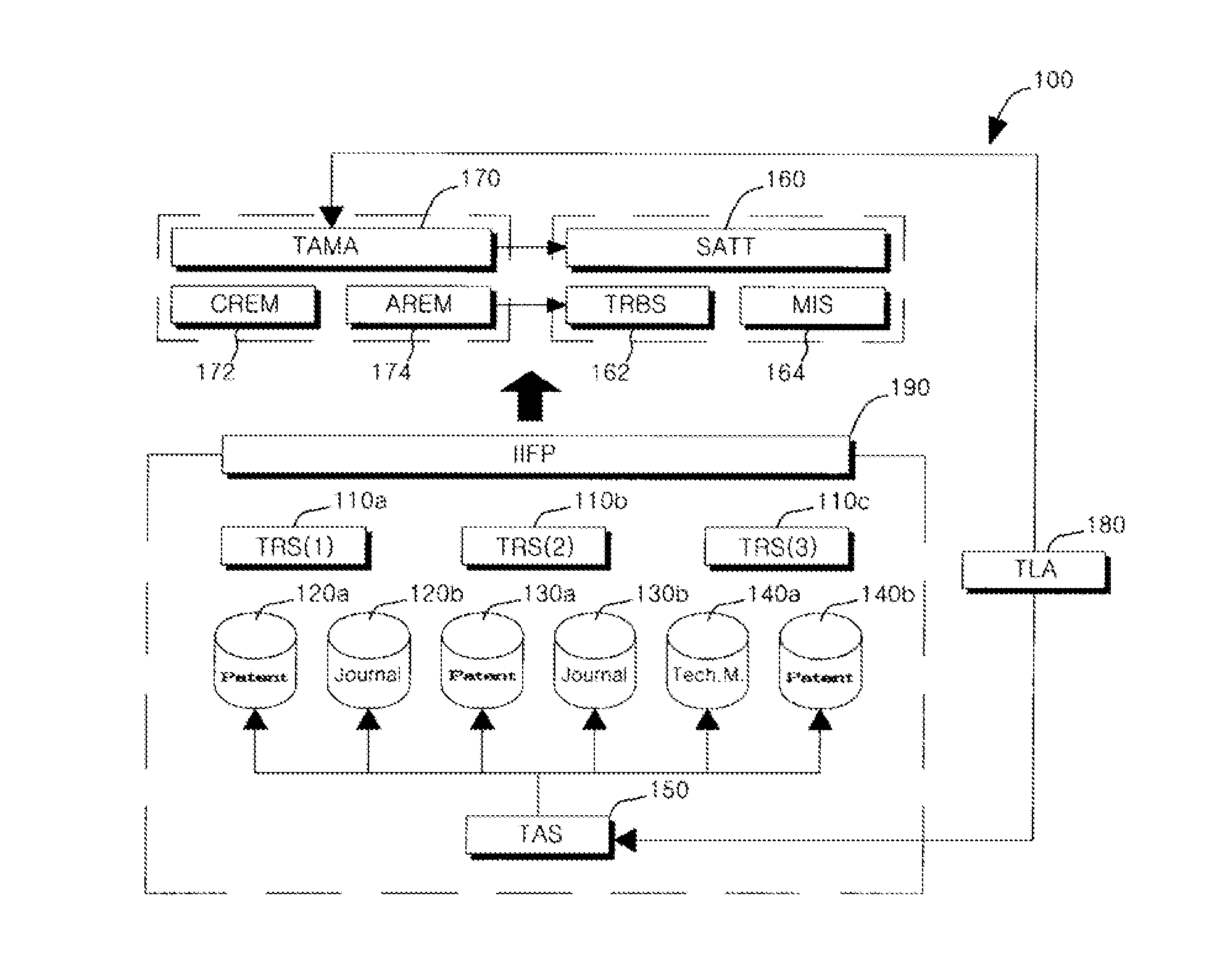
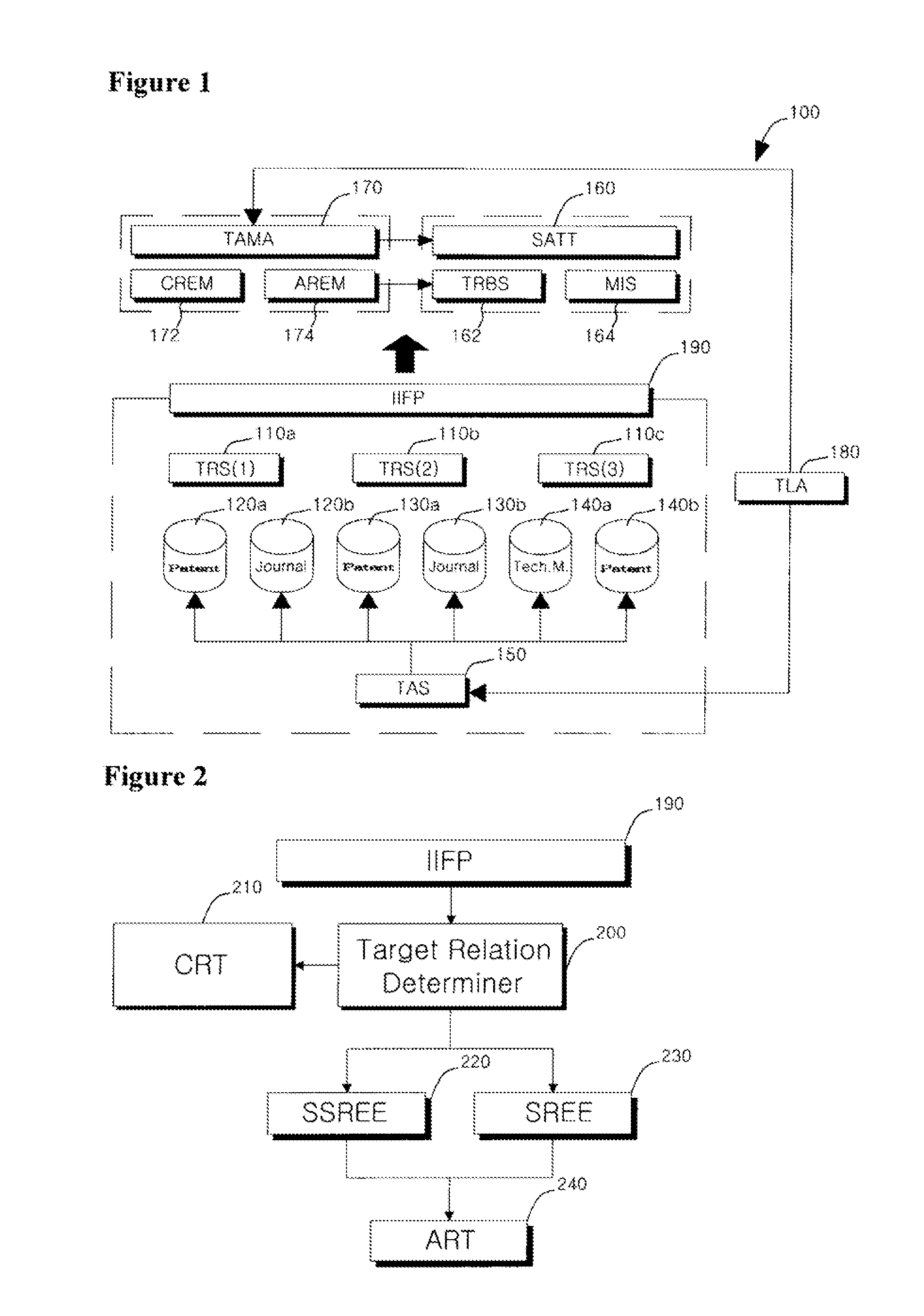
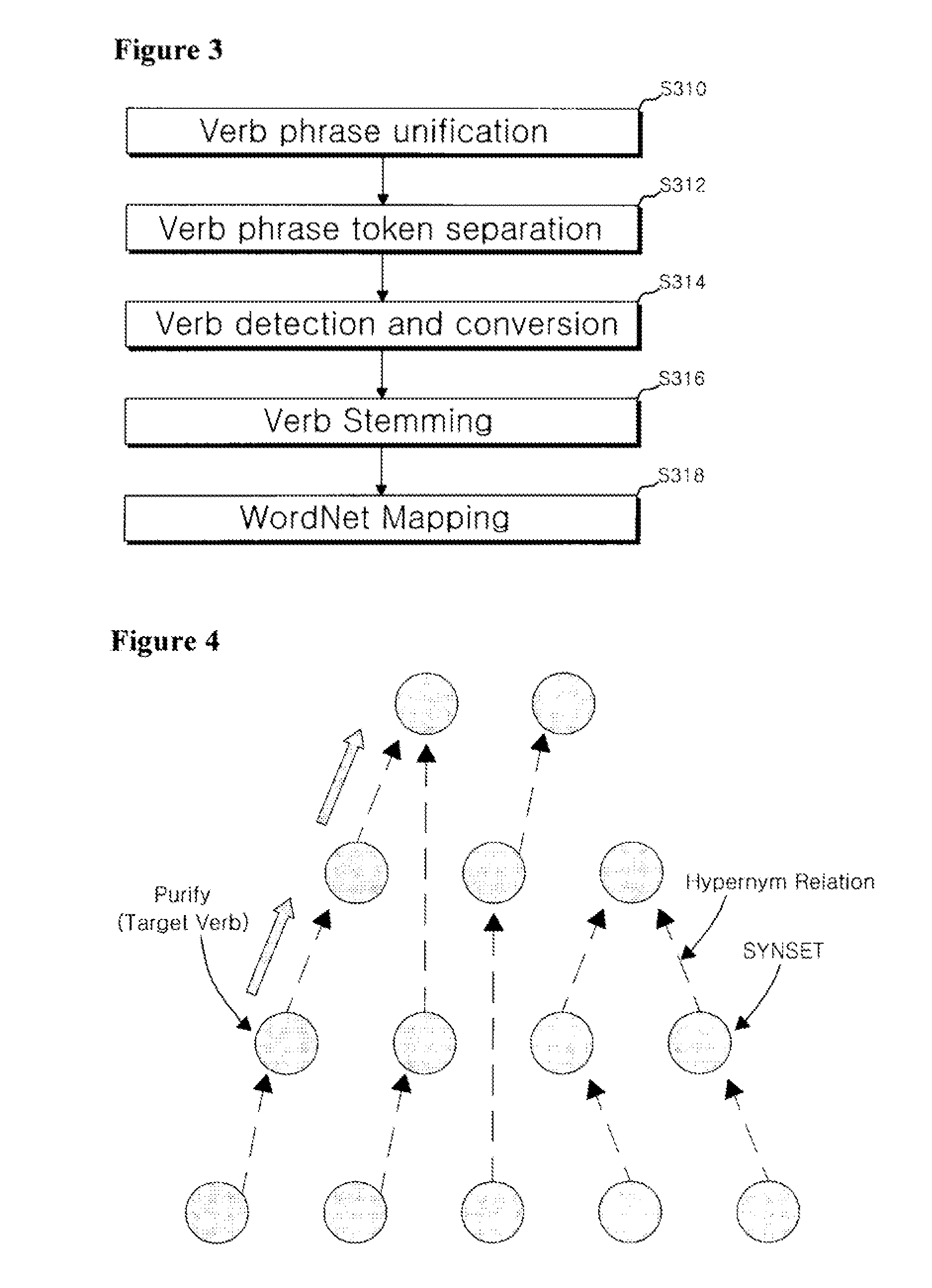
InactiveUS20110213804A1Digital data processing detailsSpecial data processing applicationsRelationship extractionBibliographic database
Disclosed herein is a system structure for extracting relations between technical terms within a large amount of literature information using verb-based patterns. The present invention provides a system that is capable of extracting relations based on verb-based patterns from abstract and bibliography databases in all fields of science and technology using a Tech Association Mining Appliance (TAMA) capable of detecting the technical terms of text and relations therebetween in academic literature databases in the fields of science and technology. The present invention has an advantage of providing a practical relation extraction system structure using a number of academic databases.
Owner:KOREA INST OF SCI & TECH INFORMATION
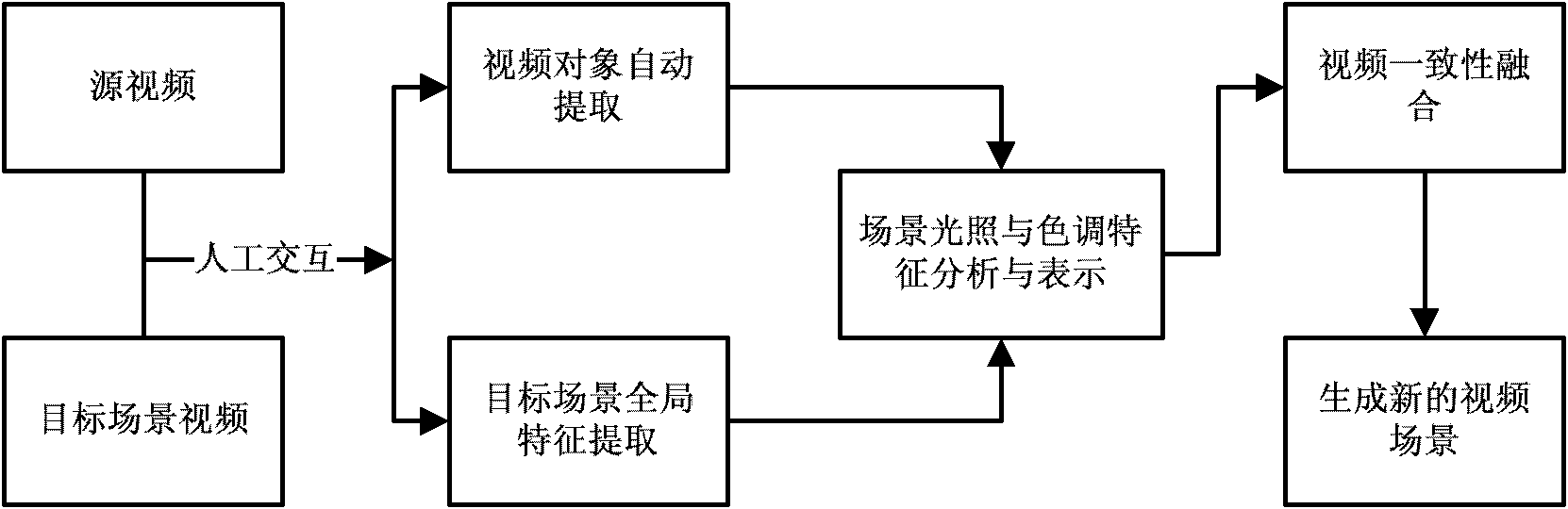
Video consistent fusion processing method
ActiveCN101945223AImprove efficiencyHighly harmonious natureTelevision system detailsColor television detailsReference imageEconomic benefits
The invention relates to a processing method for carrying out consistent fusion on video images from different sources. The method is mainly characterized by not only ensuring no seam and nature near the boundary in the video fusion process, but also comprehensively considering the global illumination and hue information of a target scene, wherein the information can be extracted from the target scene by the simple manual interactions and expressed by generating a corresponding reference image so as to diffuse into an object to be fused in an image fusion mode, thereby finally generating a new video with high reality. The invention can be used in the fields of post production of film and television programs, design of special effects of game scenes, manufacture of advertisements, news media, multimedia educational technologies and the like, provides powerful theoretical and technical support for fast development, and can reduce the manufacturing cost, thereby obtaining great economic benefit.
Owner:ZHEJIANG UNIV
Optimal test suite reduction as a network maximum flow
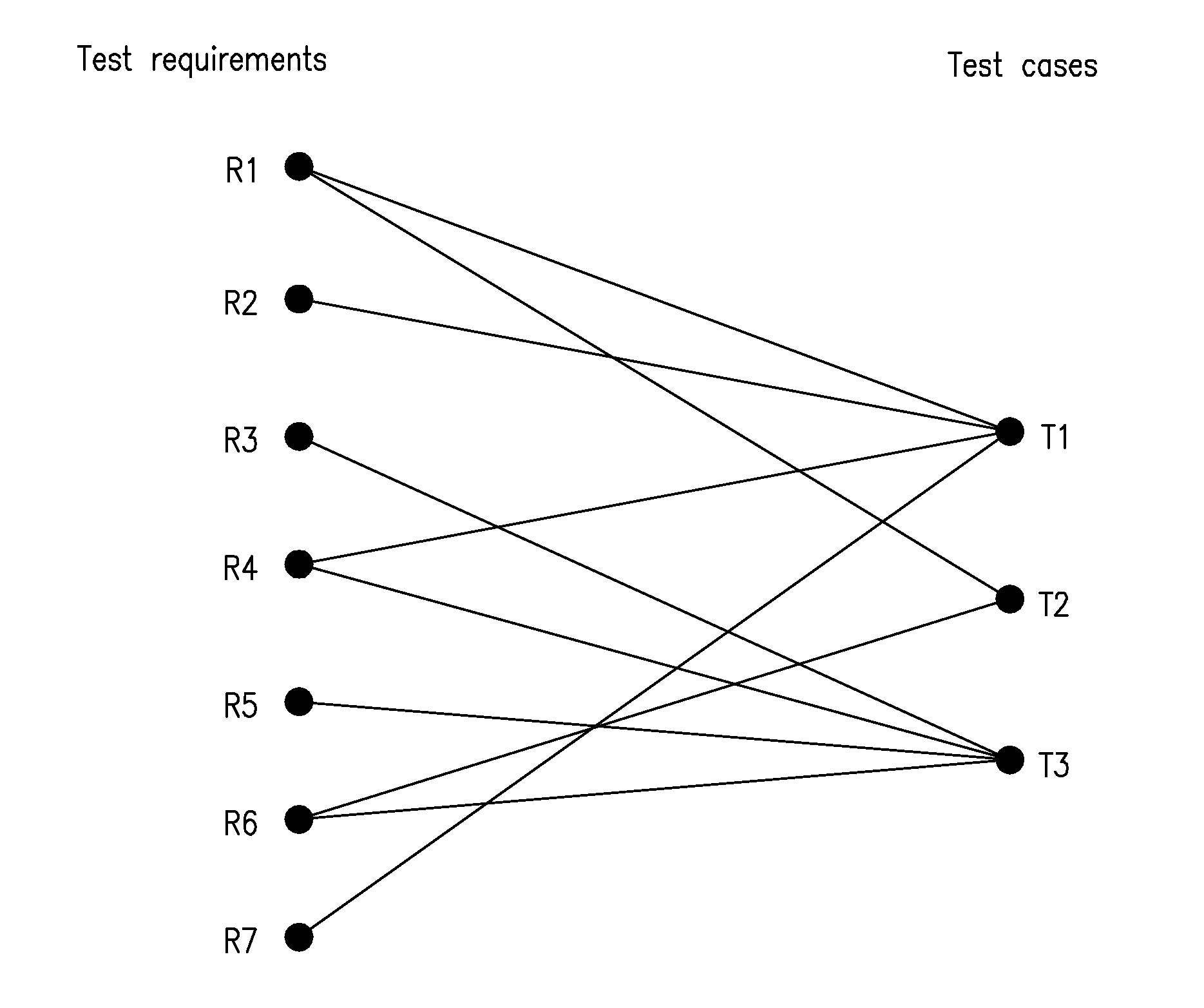
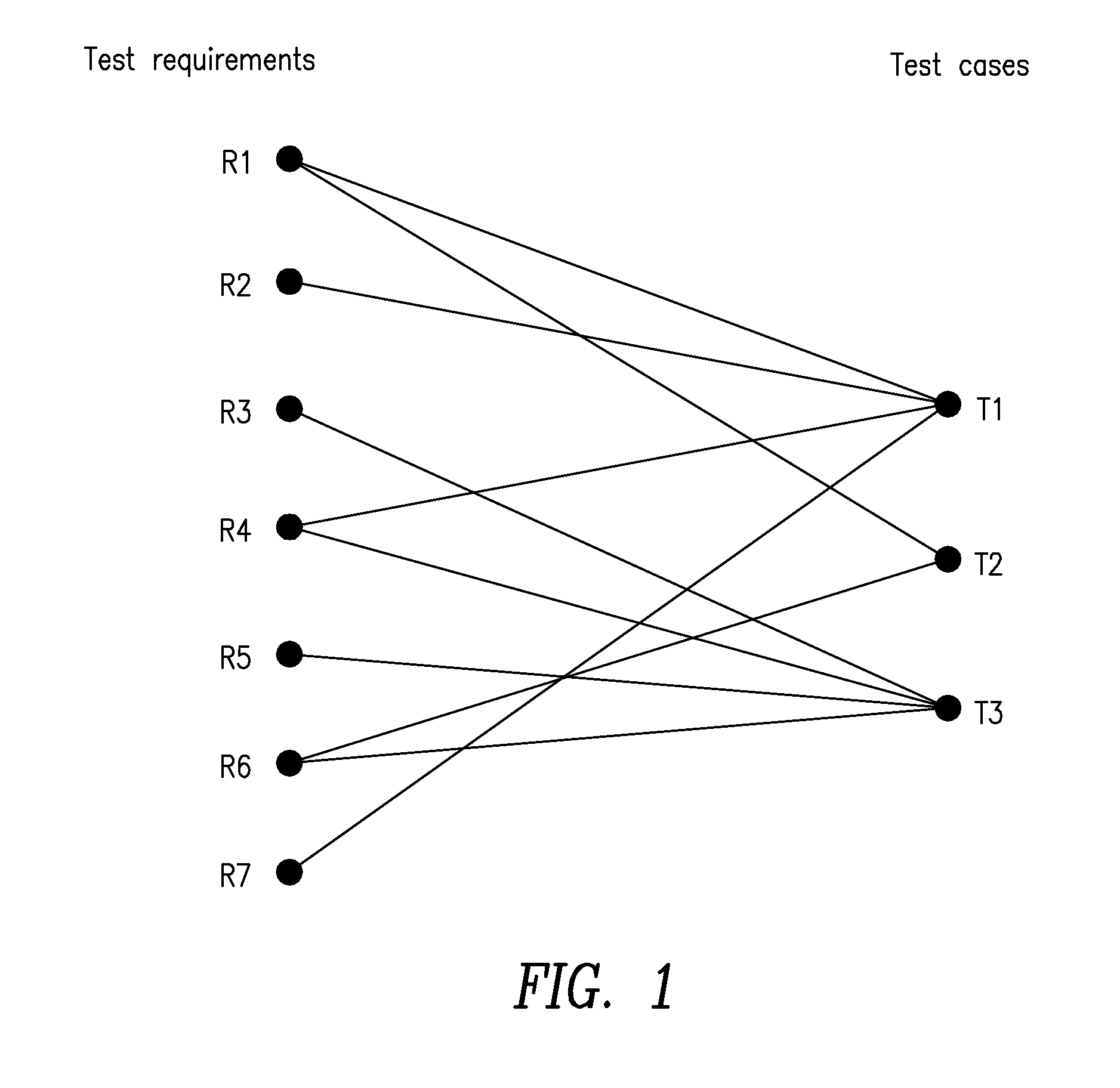
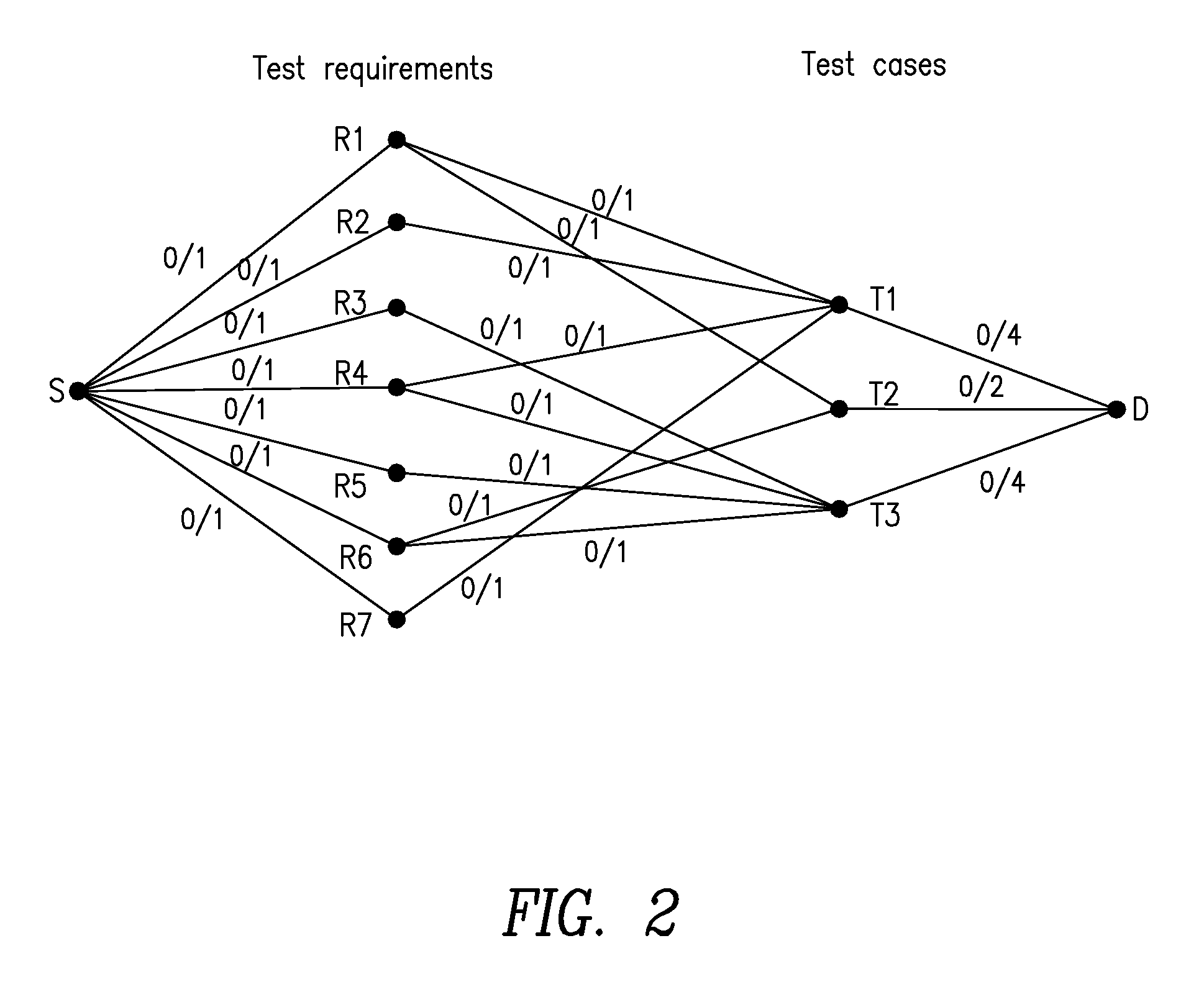
InactiveUS20160019135A1Small sizeMaintain qualitySoftware testing/debuggingSpecific program execution arrangementsReduction rateDirected graph
A novel approach to test-suite reduction based on network maximum flows. Given a test suite T and a set of test requirements R, the method identifies a minimal set of test cases which maintains the coverage of test requirements. The approach encodes the problem with a bipartite directed graph and computes a minimum cardinality subset of T that covers R as a search among maximum flows, using the classical Ford-Fulkerson algorithm in combination with efficient constraint programming techniques. Test results have shown that the method outperforms the Integer Linear Programming (ILP) approach by 15-3000 times, in terms of the time needed to find the solution. At the same time, the method obtains the same reduction rate as ILP, because both approaches compute optimal solutions. When compared to the simple greedy approach, the method takes on average 30% more time and produces from 5% to 15% smaller test suites.
Owner:SIMULA INNOVATIONS
Method for computing equivalent elastic parameters of fiber reinforced composite material
ActiveCN103871059AImprove calculation accuracyCommon processImage analysisMicro structurePore distribution
The invention provides a method for computing equivalent elastic parameters of a fiber reinforced composite material, and belongs to the technical field of calculation of statics performance parameters of composite materials. A composite material micro-structure model is established by using an XCT (X-ray computed tomography) technology and more approaches a true situation; important parameters affecting elasticity modulus, such as fiber bundle shape, fiber volume ratio, porosity and pore distribution, can be automatically obtained without a hypothesis. The method is more reasonable, higher in computation accuracy, and more universal in flow; various paradoxical hypotheses and complicated mathematical derivations are eliminated, and an engineer accepts and masters the method more easily.
Owner:NANJING UNIV OF AERONAUTICS & ASTRONAUTICS
System and method for face recognition robust to multiple degradations
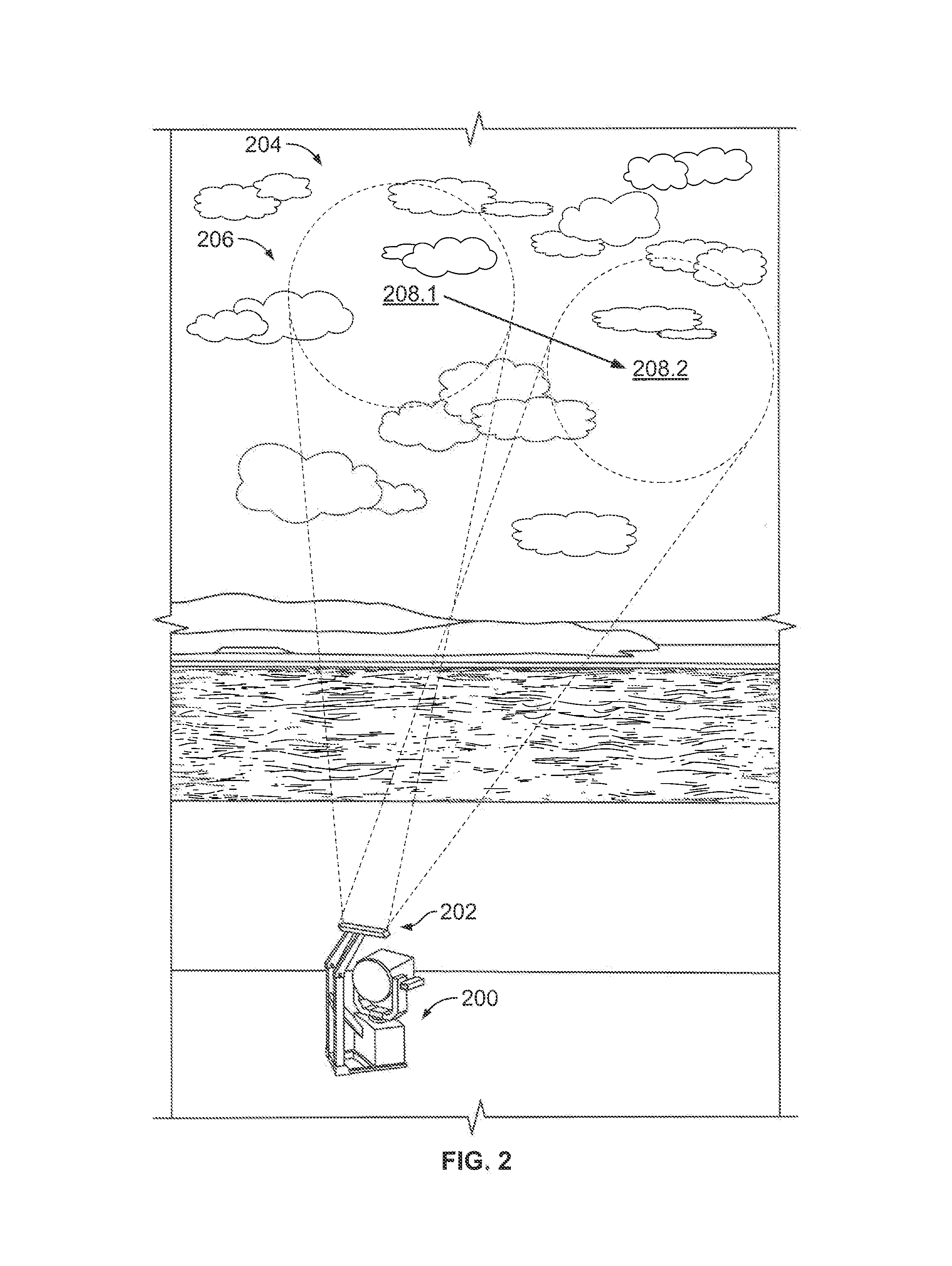
ActiveUS10002286B1Improve performanceImage enhancementImage analysisFiducial pointsTechnology in Star Trek
A novel, unified technique for analyzing, synthesizing, and recognizing faces captured by various modalities, and under a variety of often seen real-world circumstances, using thin-plate splines for densification of points of a face from an initial set of fiducial points.
Owner:CARNEGIE MELLON UNIV
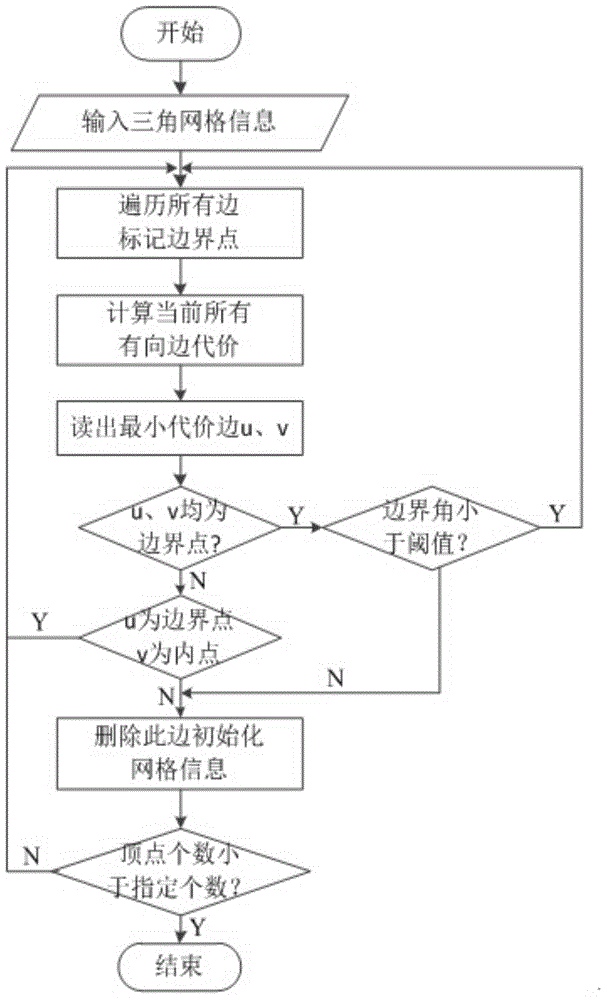
Texture mapping method based on triangular mesh simplification
InactiveCN104680573AReduce time complexityImprove timing performance3D-image rendering3D modellingPattern recognitionImaging processing
The invention belongs to the technical field of image processing and particularly relates to a texture mapping method based on triangular mesh simplification. The texture mapping method comprises the following steps: simplifying a triangular network model and establishing a spring-mass-point model; parameterizing the spring-mass-point model to a final position of a rectangular region; by utilizing a process of simplifying the triangular network model, calculating an initial position of a deleted point in the parameterized rectangular region to obtain positions of all vertexes of an initial model in the parameterized rectangular region; parameterizing the initial model to establish the spring-mass-point model; fixing the boundary vertex and triggering inner point iteration until the position of an inner point is balanced to obtain a spring-mass-point model revised parameterized coordinate; and carrying out normalization processing to obtain a texture coordinate of a grid vertex, and carrying out texture mapping. According to the method, the texture coordinate of each triangular network grid vertex does not need to be solved and texture mapping can be directly carried out; the time complexity of the method can be reduced to the great extent and the time performance is improved.
Owner:XIAN UNIV OF SCI & TECH
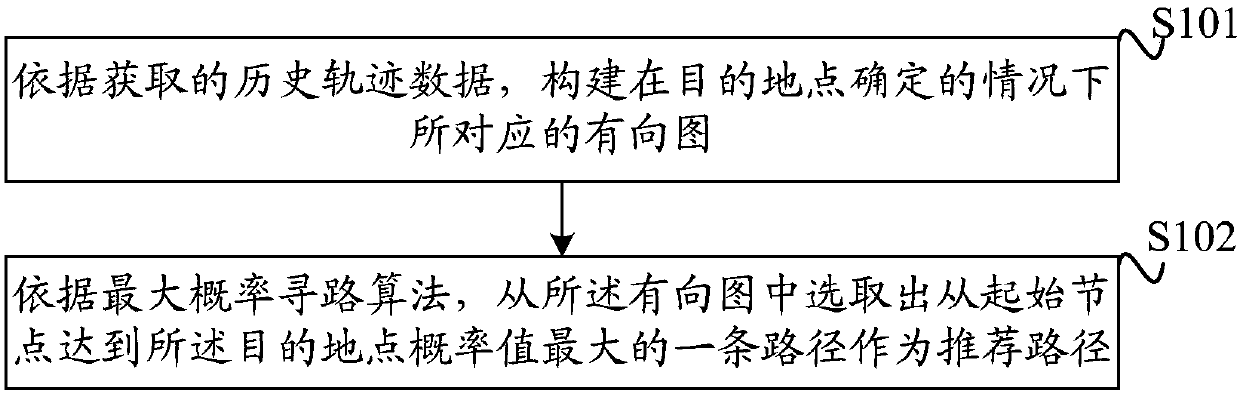
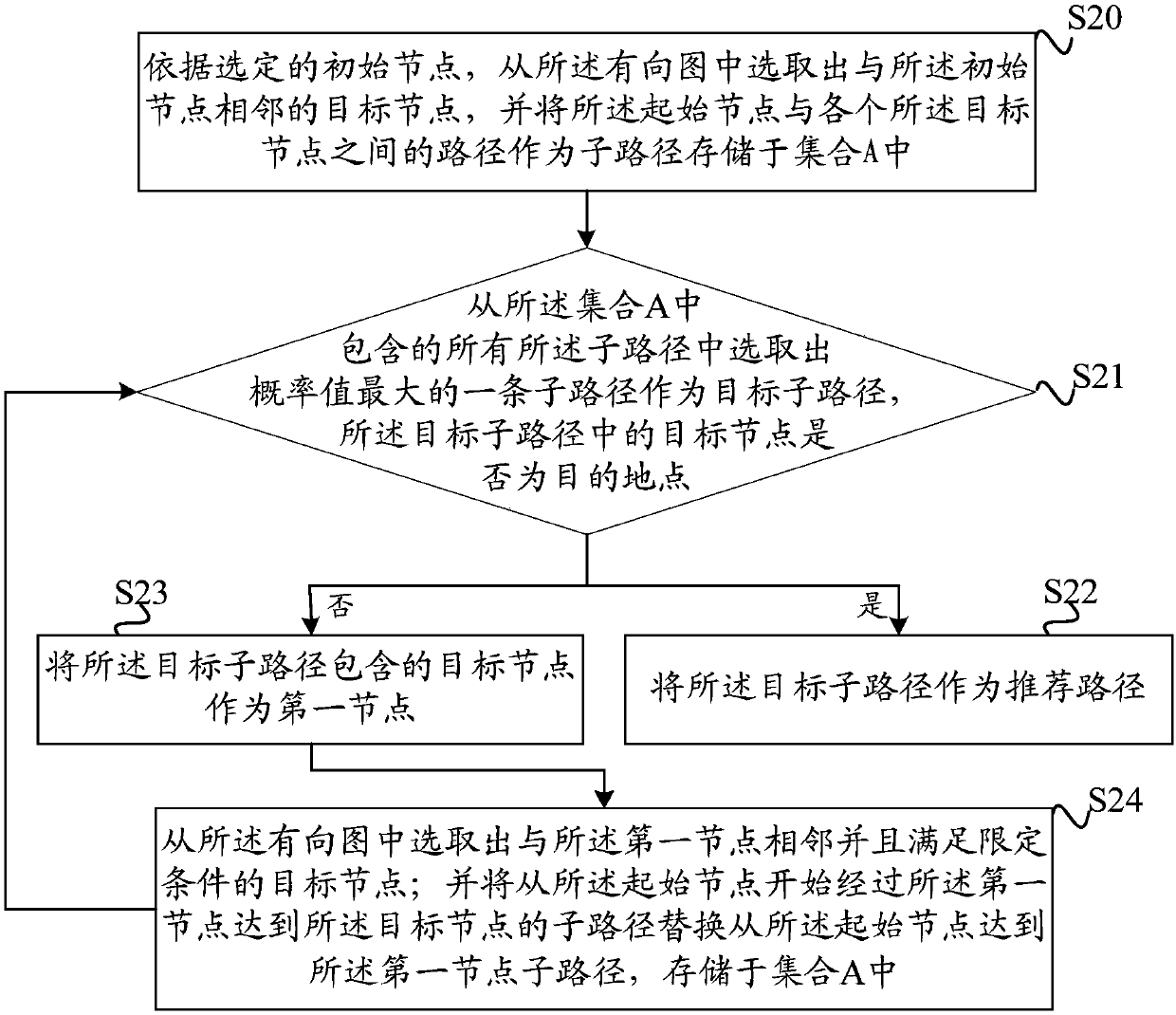
Path recommendation method and device
ActiveCN107643085AComplies with complex changesMeet travel requirementsInstruments for road network navigationDirected graphAlgorithm
An embodiment of the invention discloses a path recommendation method and device. The path recommendation method includes: according to acquired historical trajectory data, establishing a corresponding directed graph under the condition that a target site is determined, wherein segments corresponding to any two adjacent nodes contained in the directed graph have corresponding steering probabilityvalues; according to a maximum-probability pathfinding algorithm, selecting one path with the maximum probability value from a starting node to the target site as a recommended path. The problem aboutcomplex and changeful road conditions is solved by no longer being limited to using prior knowledge to build a large number of models; compared with a method that existing mainstream navigation adopts trajectory planning generated from calculation of algorithm models and strategies, the method has the advantages that patterns of user travel are mined by analyzing the historical trajectory data, complex changes of the road conditions in real environment are met, the most popular path, namely the recommended path can be mined according to the established directed graph, and travel requirementsof users can be well met.
Owner:SUZHOU UNIV
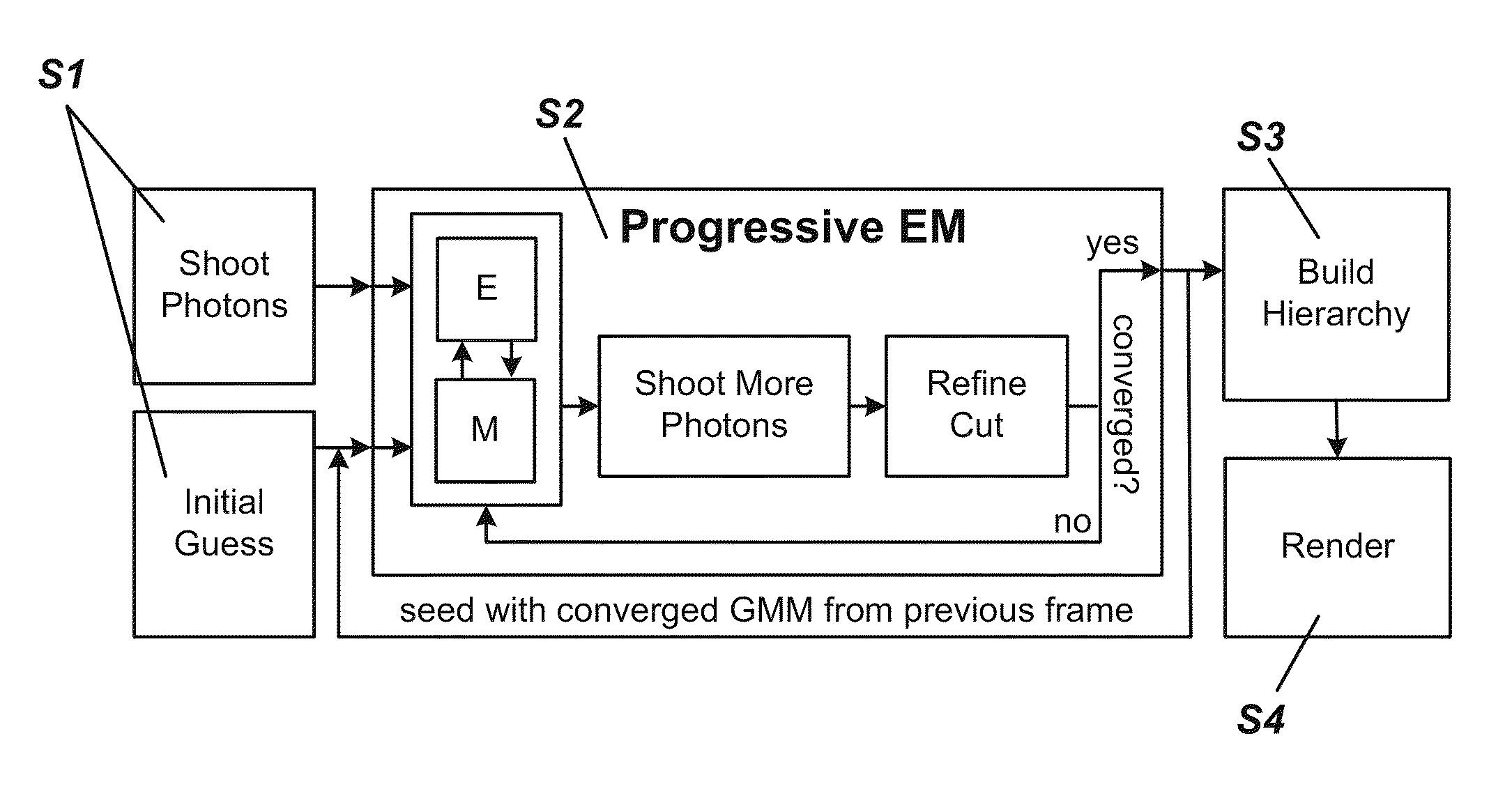
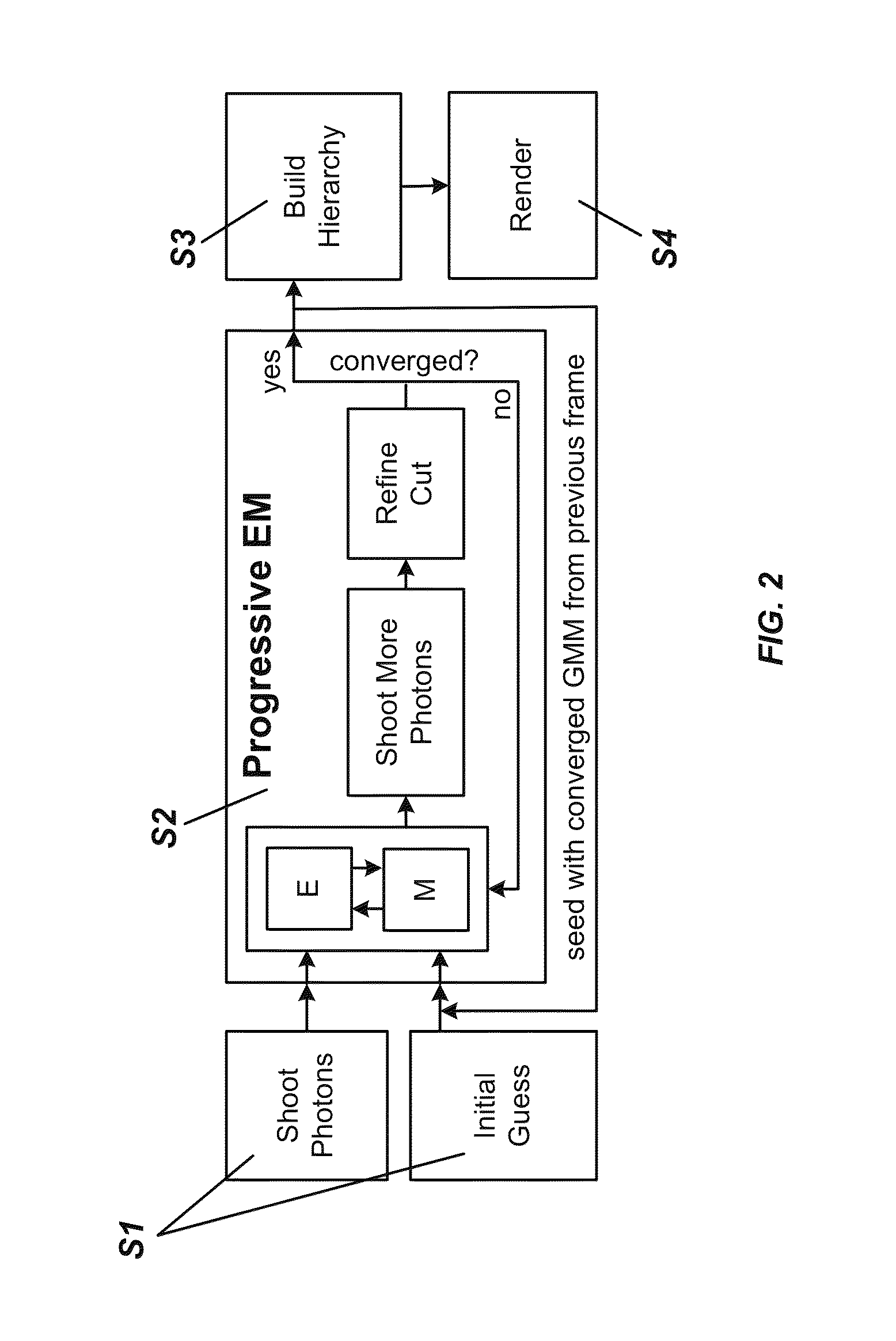
Progressive expectation-maximization for hierarchical volumetric photon mapping
ActiveUS9013484B1EfficientlyAccurate reconstruction3D-image rendering3D modellingExpectation–maximization algorithmRadiance
State-of-the-art density estimation methods for rendering participating media rely on a dense photon representation of the radiance distribution within a scene. A parametric density estimation technique is used to represent radiance using a hierarchical Gaussian mixture. Coefficients of this mixture are efficiently obtained for use in a progressive and accelerated form of the Expectation-Maximization algorithm. Noise-free renderings of high-frequency illumination are created using only a few thousand Gaussian terms, where millions of photons are traditionally required. Temporal coherence is trivially supported within this framework, and the compact footprint is also useful in the context of real-time visualization. A hierarchical ray tracing-based implementation is demonstrated, as well as a fast splatting approach that can interactively render animated volume caustics.
Owner:ETH ZURICH EIDGENOESSISCHE TECHN HOCHSCHULE ZURICH +1
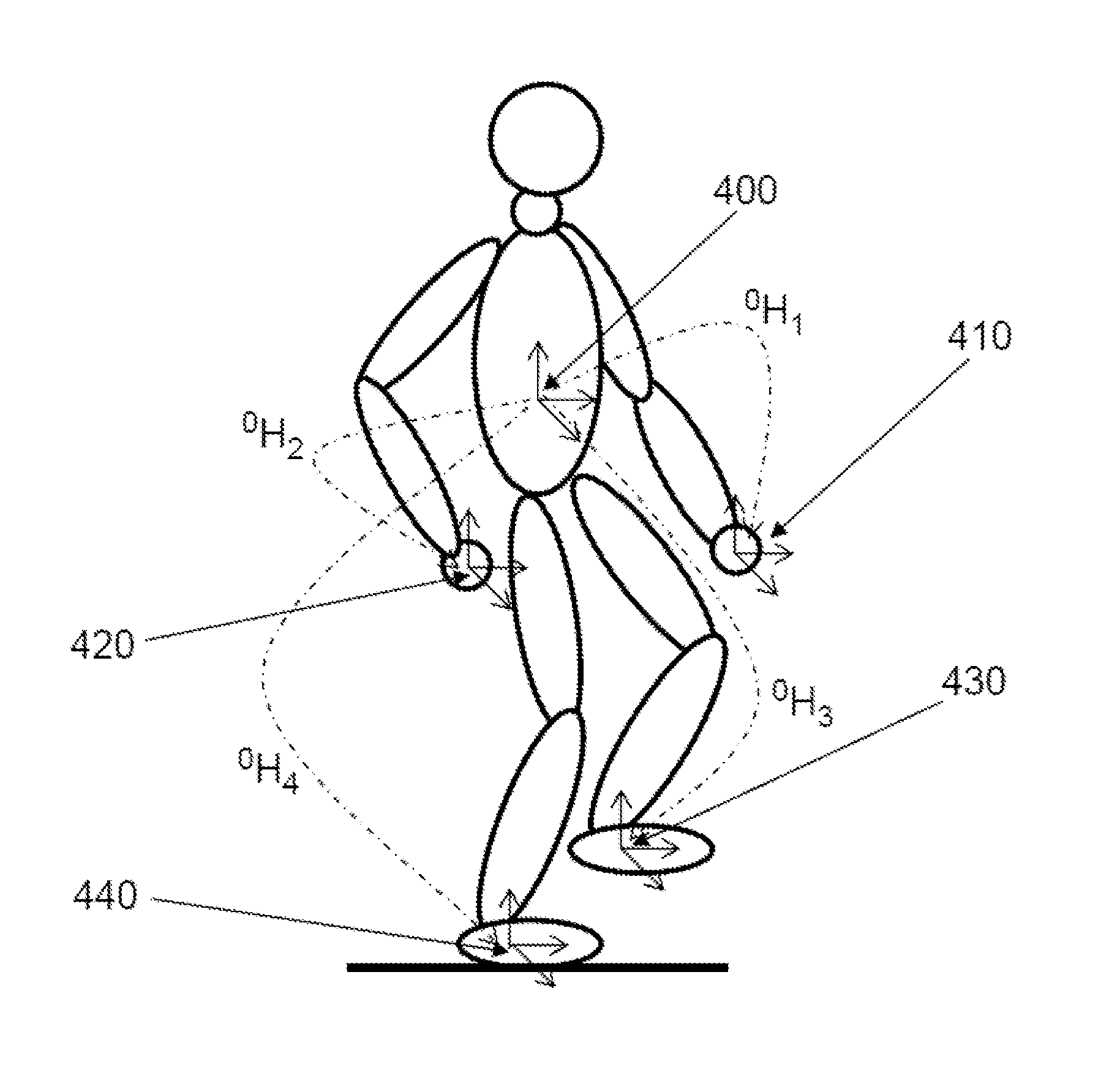
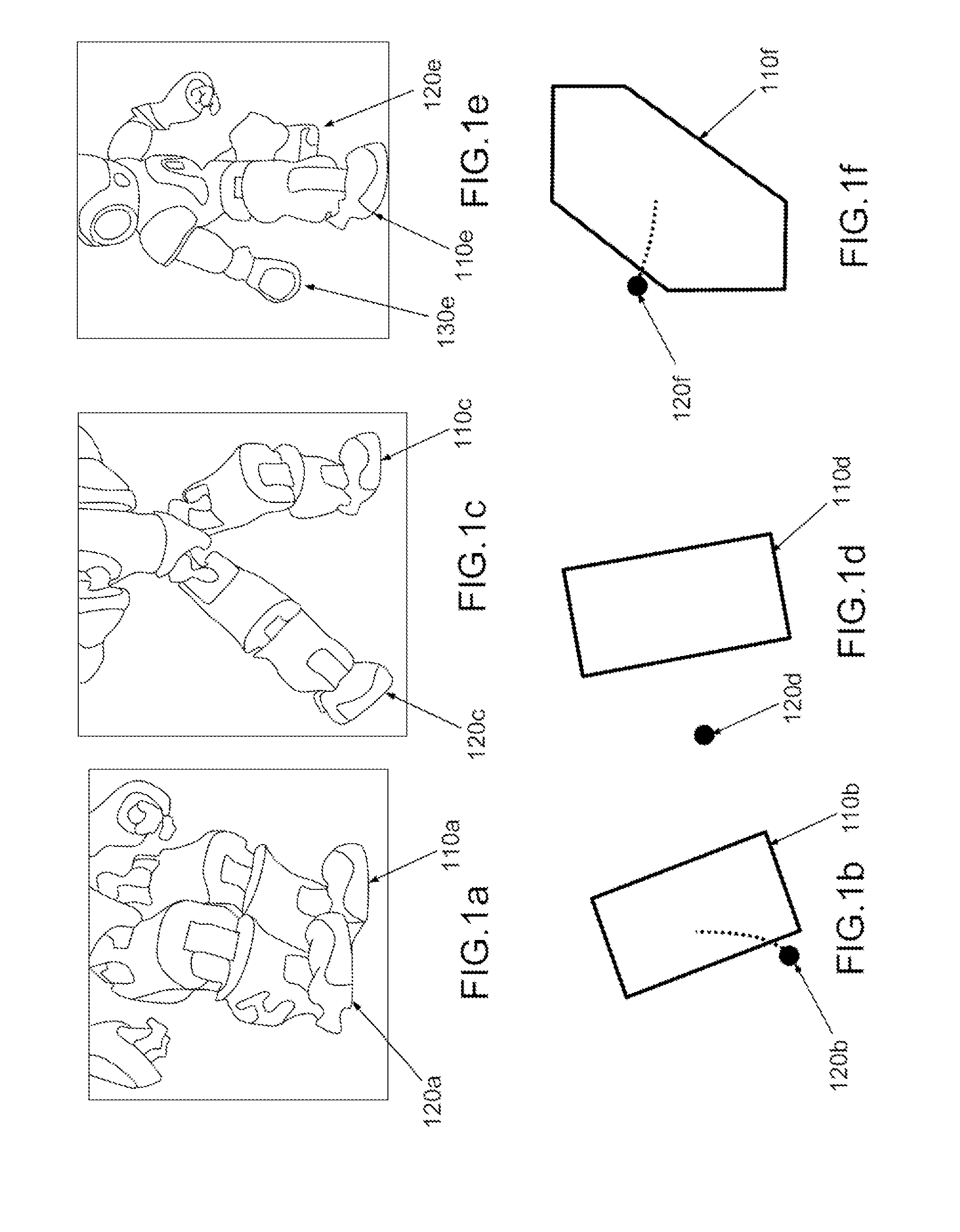
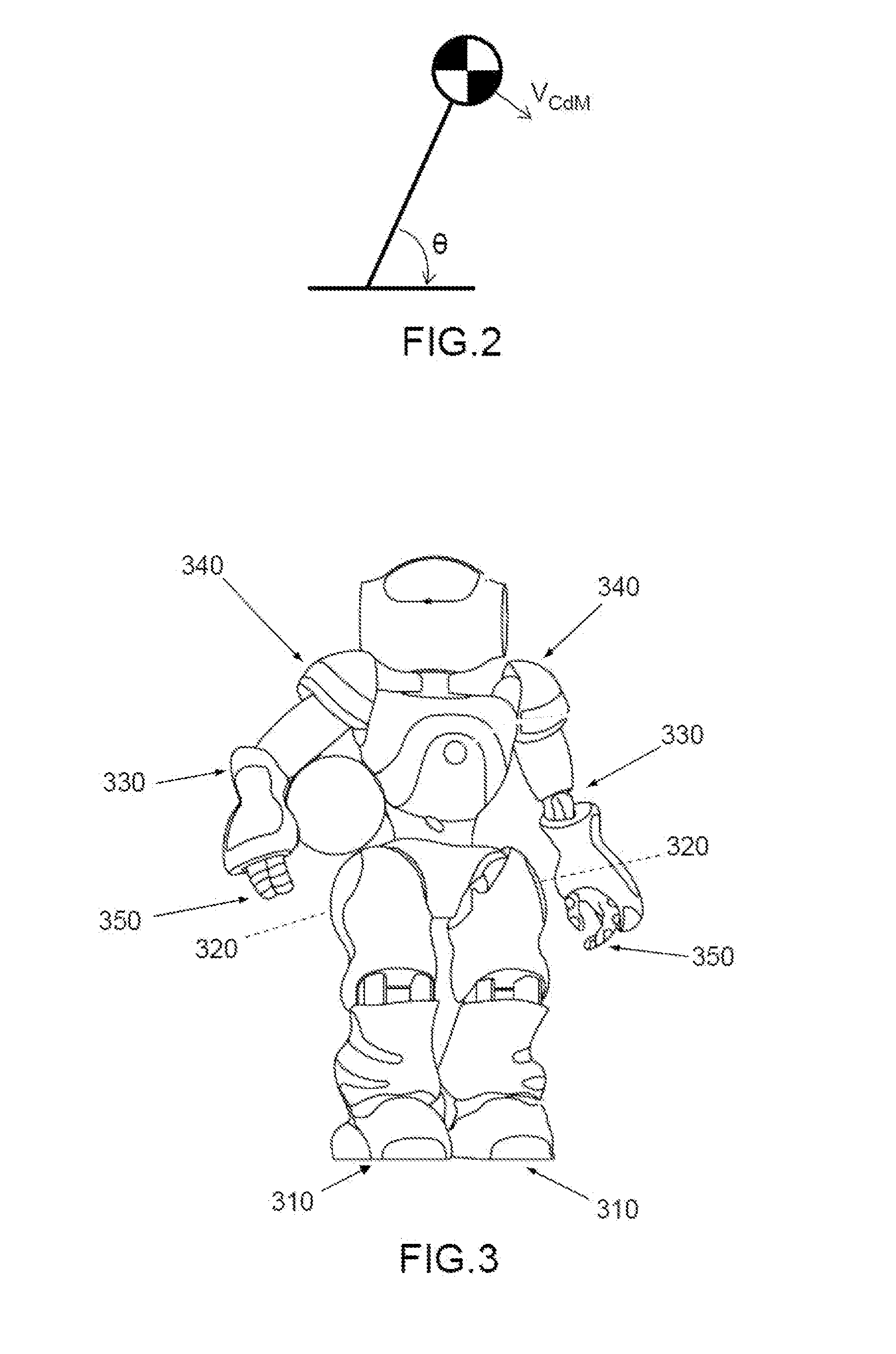
Humanoid robot having fall-management capabilities, and method for managing said falls
ActiveUS20130231822A1Criterion is simpleImprove efficiencyVehicle testingProgramme-controlled manipulatorHumanoid robot naoEngineering
The invention relates to a humanoid robot endowed with particular capabilities for managing falls. The risks of falling limit the development of the mass-market use of humanoid robots. In the prior art, the modalities for detecting falls are not well suited to the case of very dynamic robots since the center of mass is very often outside their support polygons. The modalities for managing falls are also poorly suited to robots which must be economical in their computation resources. According to the invention, the conventional support polygon is supplemented with effectors for which it is determined that they are sufficiently close to the ground. Protection strategies are implemented, chosen from a set of strategies defined by a classification of the angles of fall.
Owner:SOFTBANK ROBOTICS EURO
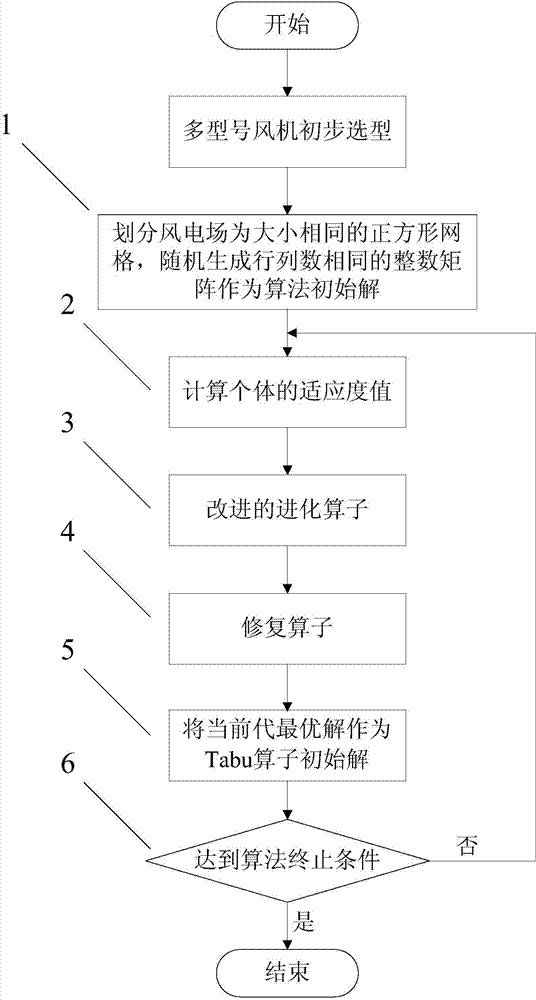
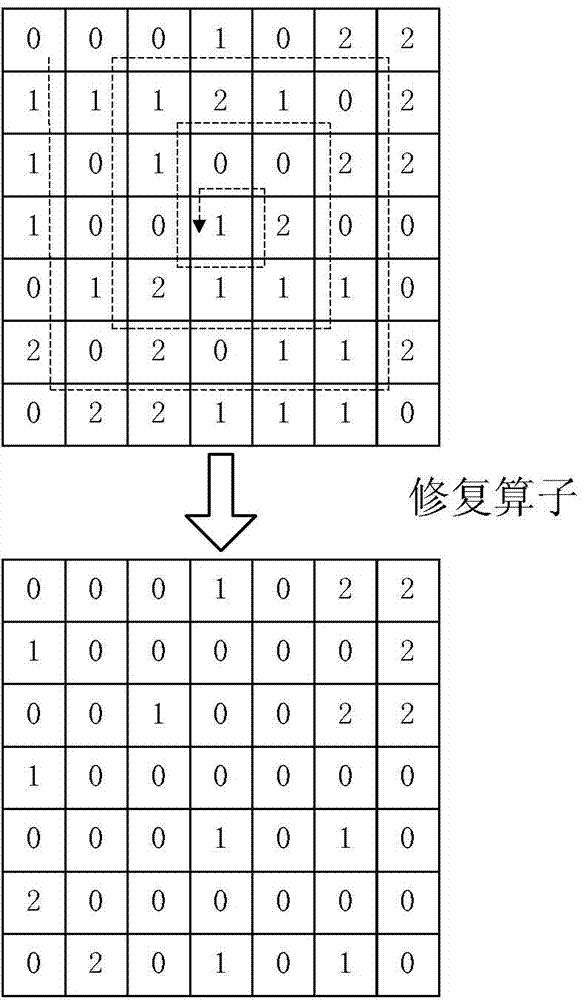
Wind farm multi-model draught fan optimized arrangement method based on genetic algorithm
InactiveCN103793566ACoding is intuitiveIntuitive and accurate position relationshipSpecial data processing applicationsAlgorithmSquare mesh
Owner:TONGJI UNIV
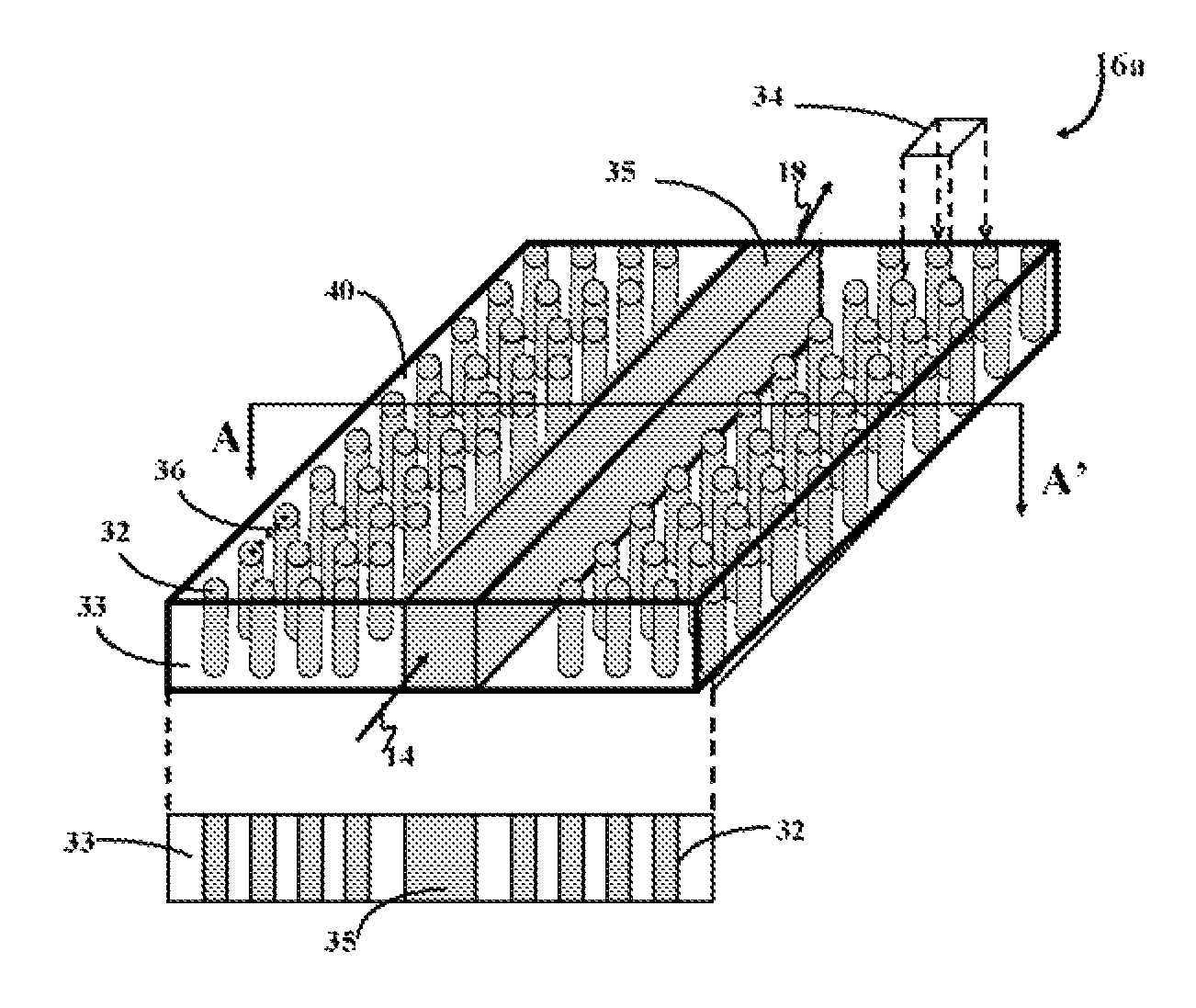
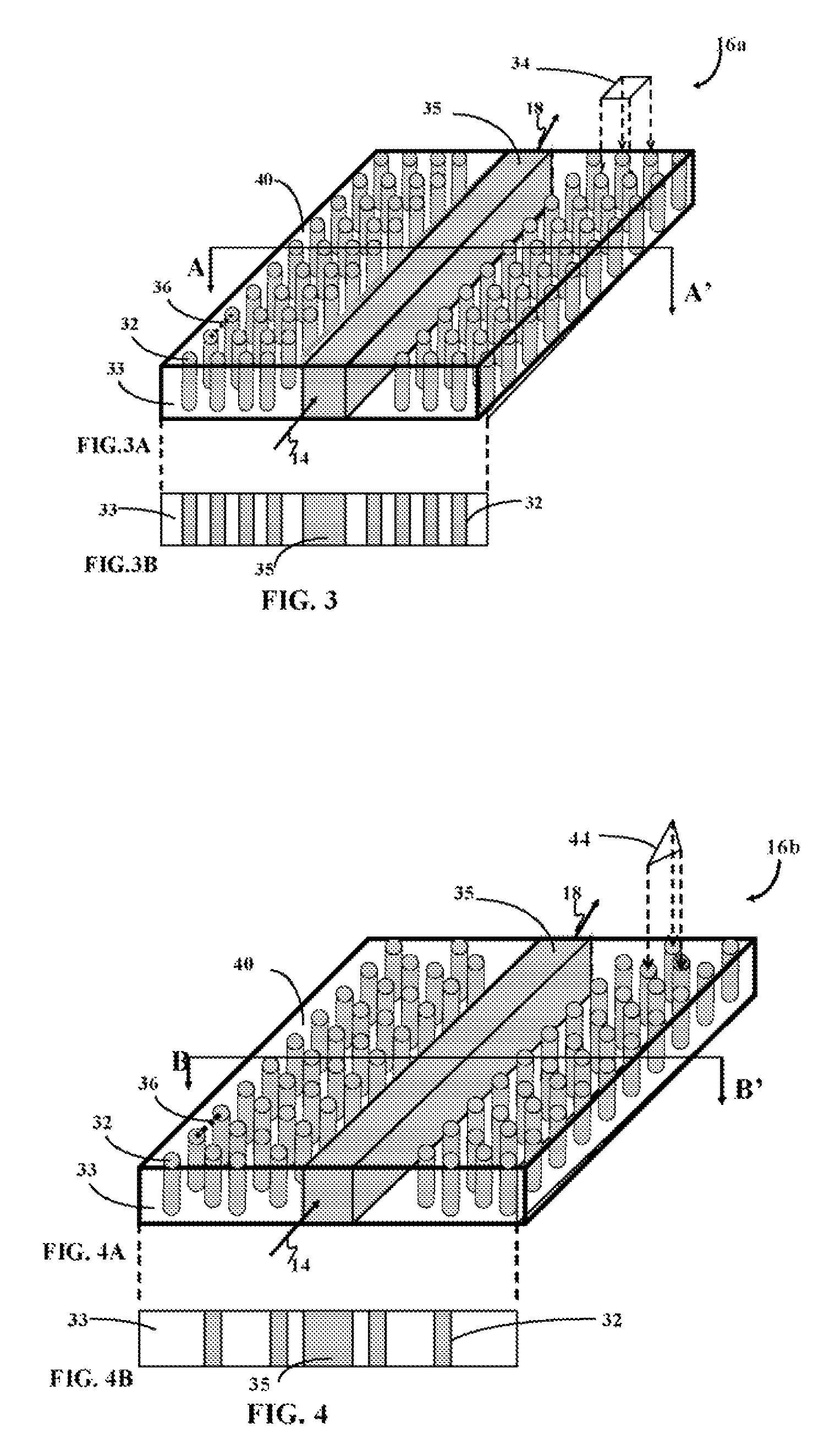
High sensitivity sensor device and manufacturing thereof
ActiveUS7922976B2Reduce total powerAnalysis using chemical indicatorsNanoopticsBiological cellEngineering
Owner:BANPIL PHOTONICS
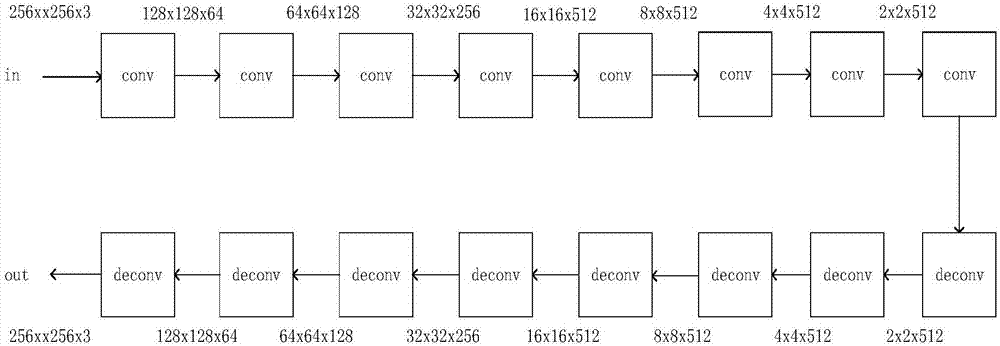
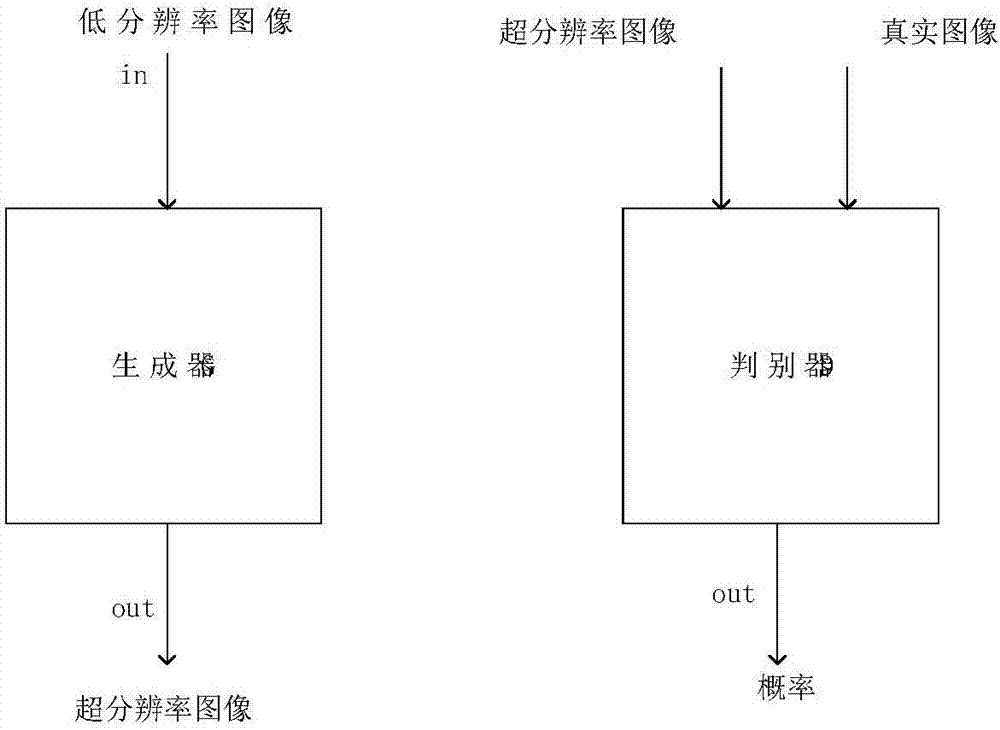
cGAN algorithm-based super-resolution image recovery technology
InactiveCN107274358AShort training timeImprove the display effectImage enhancementGeometric image transformationColor imagePattern recognition
The invention discloses a cGAN algorithm-based super-resolution image recovery technology, and relates to super-resolution recovery for deep convolutional antagonistic neural network images. The existing method needs to carry out a lot of training, the network layers are relatively shallow and the feature weight values included in models obtained through the training are not complete enough, so that the final recovery effect is not ideal. Greyscale maps are used during the training, so that the super-resolution recovery effect for three-channel colored images is not good. Aiming at the defects in the prior art, the invention provides a cGAN algorithm-based super-resolution image recovery method which is capable of training the colored images to achieve better recovery effect. The key points of the method comprises that (1) the training time is short, (2) three-channel colored maps can be directly trained, (3) much image preprocessing is not required, and (4) the models obtained through training can be used once for all.
Owner:GUANGDONG UNIV OF TECH
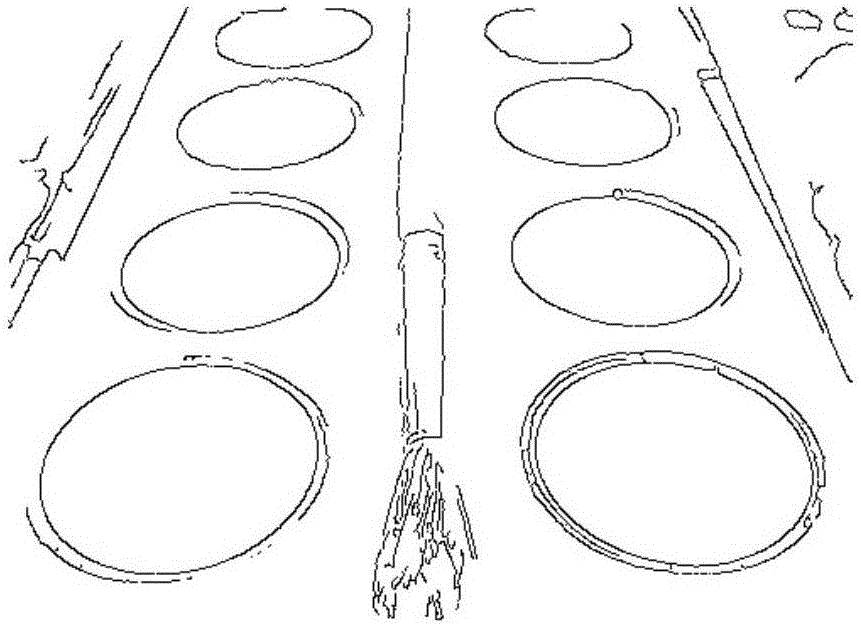
Ellipse rapid detection method based on geometric constraint
ActiveCN105931252AAchieve accelerationSolve problems that take a relatively long timeImage enhancementImage analysisAlgorithmEllipse
The invention discloses an ellipse rapid detection method based on geometric constraint. The method employs a characteristic number to screen a combination of arcs which definitely do not belong to the same ellipse before the ellipse fitting, reduces the unnecessary ellipse fitting operation, and achieves the algorithm acceleration. The method solves a problem that the consumed time is longer in the prior art, and guarantees the ellipse detection accuracy well.
Owner:DALIAN UNIV OF TECH
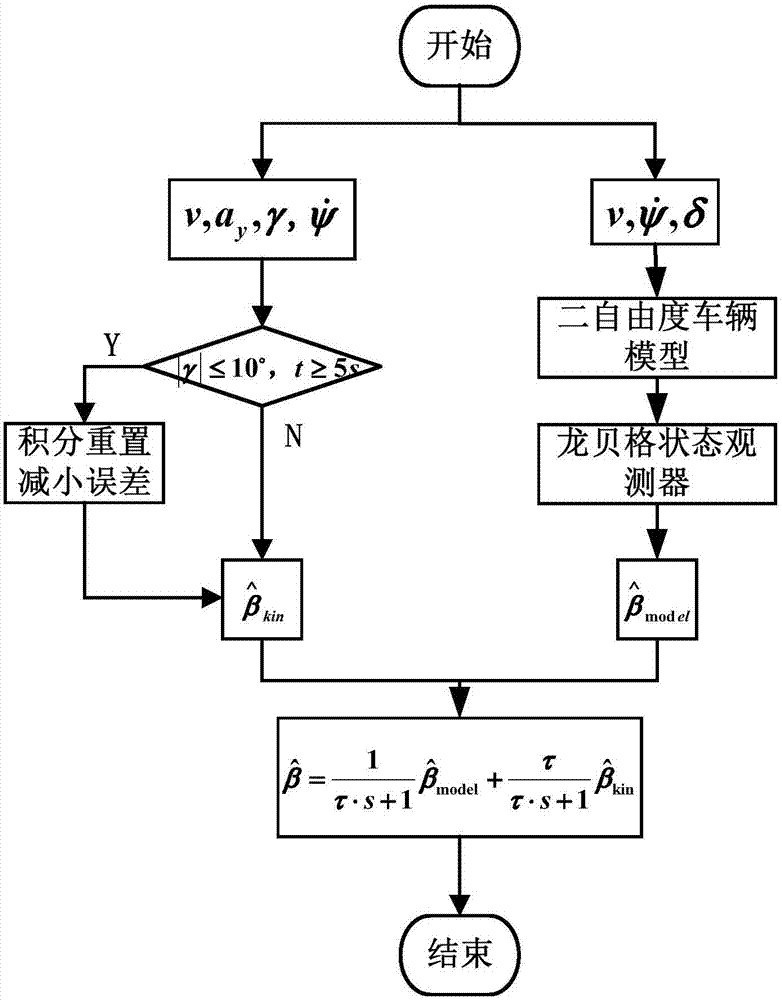
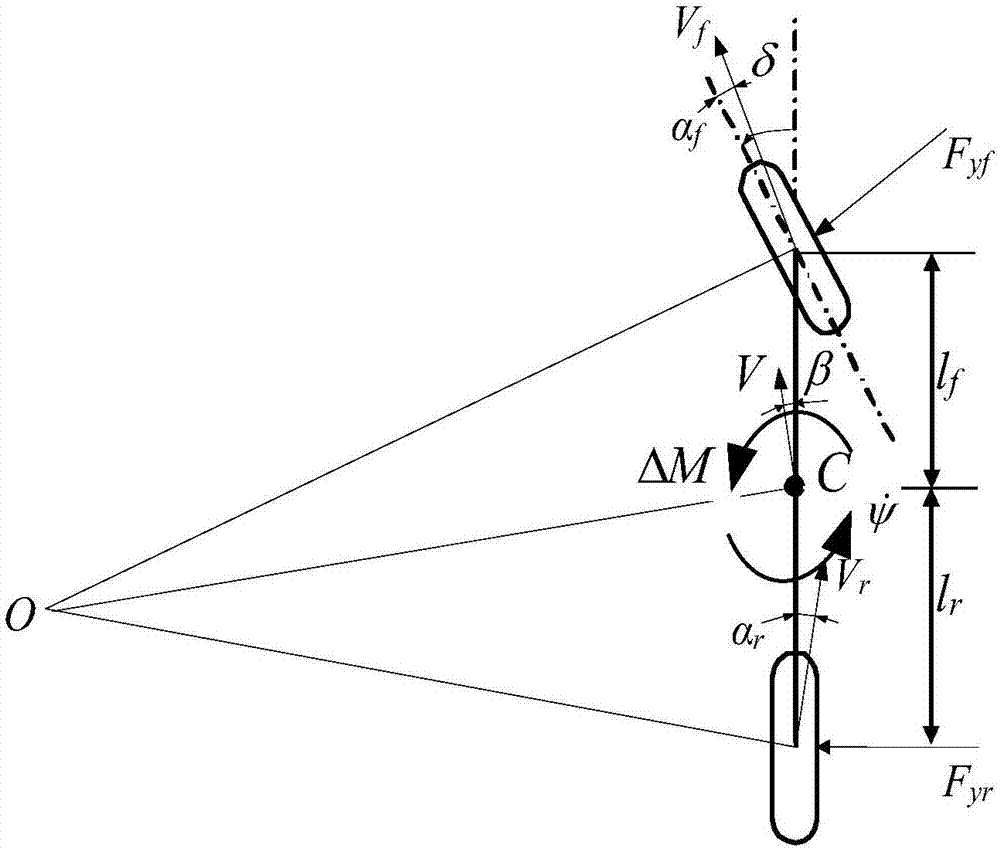
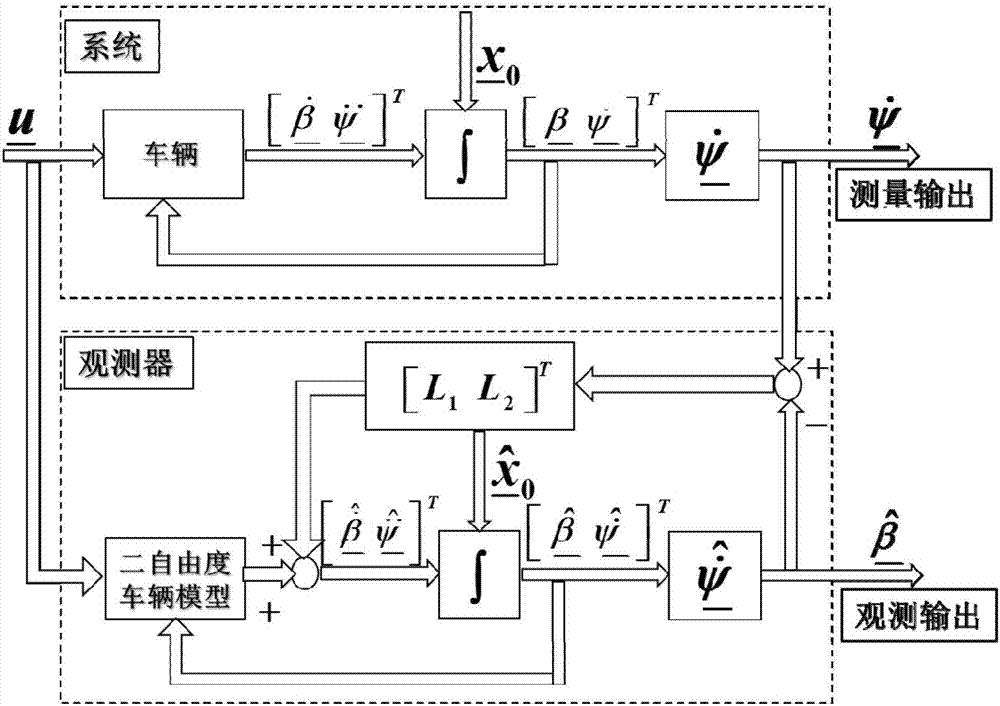
Multi-information fusion vehicle side slip angle estimation method
ActiveCN107031654AImprove robustnessAccurate estimateDriver input parametersKinematicsEstimation methods
The invention relates to a multi-information fusion vehicle side slip angle estimation method. The method comprises the following steps that (1) a kinematics estimation method is adopted to estimate to obtain a kinematics side slip angle measuring estimation value beta <kin>; (2) a linear two-degree-of-freedom monorail vehicle model is adopted to establish a dragonberg observer based on the kinematics, and the observer is adopted to estimate to obtain the kinematics side slip angle measuring estimation value beta <model>; and (3) the kinematics side slip angle measuring estimation value beta is obtained by fusing beta<kin> and beta<model> according to a formula (please see the specifications for the formula), wherein Tau is filter constant, and s is laplacian. Compared with the prior art, the multi-information fusion vehicle side slip angle estimation method has the advantages of high estimation accuracy, good rubustness, wide application and the like.
Owner:TONGJI UNIV
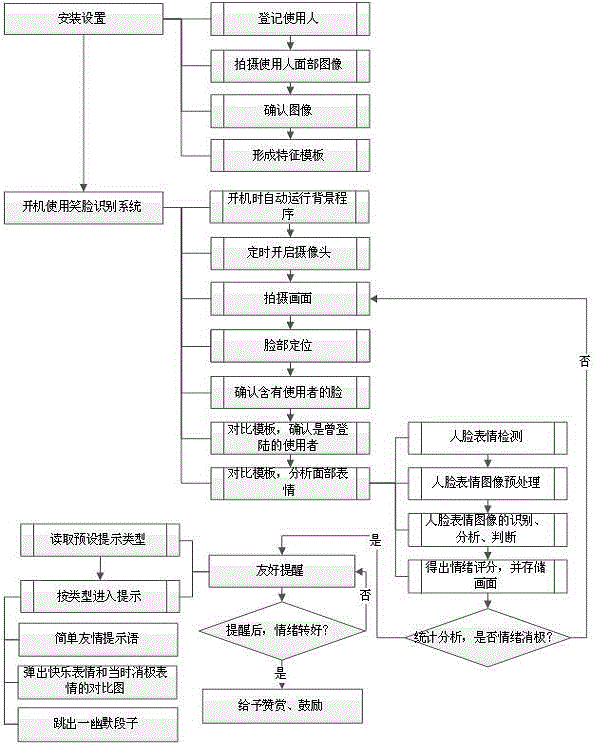
Negative expression identifying and encouraging system
InactiveCN106446753AGood groomingImprove the quality of workAcquiring/recognising facial featuresImaging processingPre treatment
The invention provides a negative expression identifying and encouraging system which belongs to the technical field of image processing and artificial intelligence. The technical schemes of the invention are as follows. A computer camera captures and analyzes a user's expressions to help remove negative emotions. A system firstly pre-acquires the basic expression samples of the user and uses them as a characteristic template. A video is initiated in a fixed time to collect the facial images of the user in the fixed time. Then, the facial images experience pre-treatment, identification and analysis. The facial images that are acquired in real time are matched with the expression characteristic template for the changes in key characteristic parts in terms of European distance difference, geometrical shape, curvature and angle. The similarity is compared to determine whether the user's expressions are angry, anxious, tired or happy ones. A statistic shape and other statistical methods are used to analyze and determine whether the user's mood in a certain period is negative or not and the system reminds the friends of the user of the negative mood of the user; and after the reminding when the user's expressions become good again, rewards and encouragement are given accordingly. With the system, the working mood of an employee can be improved; the working efficiency is raised; and the economic gains of an enterprise go up as well.
Owner:NANJING PERLOVE RADIAL VIDEO EQUIP
Space debris recovery control method based on tethered technology
ActiveCN106516177AOut-of-plane oscillation suppressionStable recyclingCosmonautic vehiclesCosmonautic partsPartial differential equationEngineering
The invention discloses a space debris recovery control method based on a tethered technology. The space debris recovery control method is characterized by comprising the following steps that 1, the tether elasticity is considered, a space tethered debris system is researched by adopting an elastic rod module, and a system dynamics differential equation is built according to a class II Lagrange equation; 2, the system dynamics equation in the step 1 is rewrote into a non-dimensional system dynamics equation; 3, the in-surface outer pivot angle vibration abatement problem of nonlinear time-varying system dynamics equation in the recovery process is researched, and the tether length change analysis control law and the in-surface pitch angle value range in the expectation equilibrium position in the debris recovery process are inferred; and 4, the stability of the system and the value range, keeping stable asymptotically, of a pitch angle in an expectation surface are further analyzed through the Floquet theory. Through the space debris recovery control method, the effect that debris is stably recovered nearby an on-orbit spacecraft can be ensured, and meanwhile the safety in the recovery process especially the safety in the end time can be ensured.
Owner:NANJING UNIV OF AERONAUTICS & ASTRONAUTICS
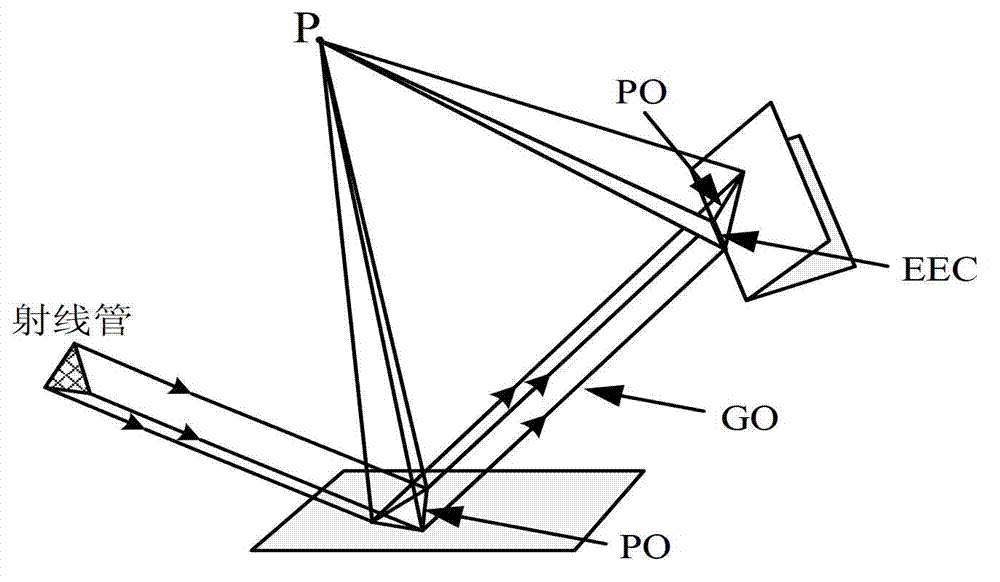
SBR and PO technology-based strong scattering center calculation method
InactiveCN103713284AImprove efficiencyEasy to analyzeRadio wave reradiation/reflectionTarget surfacePhysical optics
The invention belongs to the signal characteristic control technical field and relates to an SBR and PO technology-based strong scattering center calculation method. The calculation method comprises the following steps that: hotspot calculation is performed through ray tracing and physical optics; a distribution diagram which can indicate the radar cross section (RCS) contribution of each surface element of a target surface is obtained; and strong scattering parts can be located through comparing hotspot diagrams. Compared with a low-frequency method, and according to the SBR and PO technology-based strong scattering center calculation method, SBR and PO methods are adopted to calculate target hotspots, and therefore, high efficiency can be realized; hotspot contribution is attached to the surface of a 3D model, and therefore, the strong scattering contribution parts can be analyzed intuitively. The SBR and PO technology-based strong scattering center calculation method of the invention can trace separated two-times and three-times strong coupling structures. Strong multiple-times scattering which is generated through the coupling of separated parts on a target is usually difficult to discover, while, hidden strong scattering structures can be found out through the hotspot diagrams.
Owner:中国航天科工集团第二研究院二〇七所
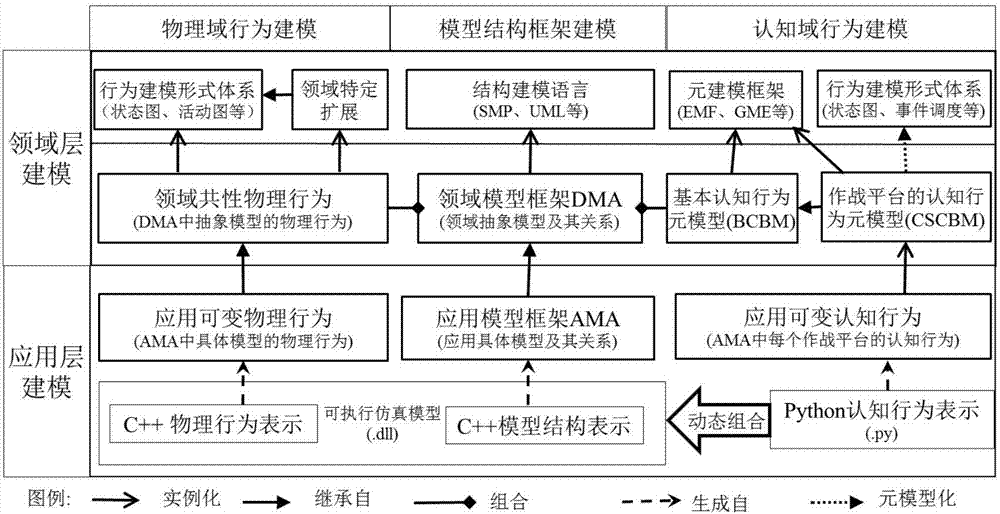
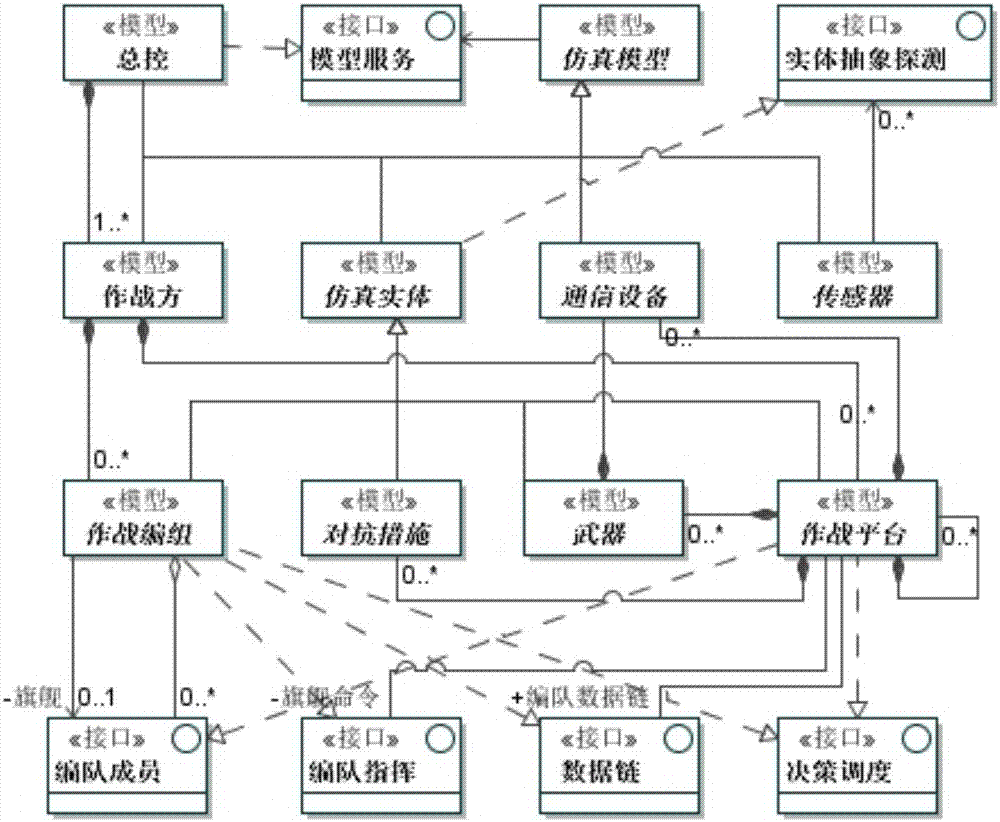
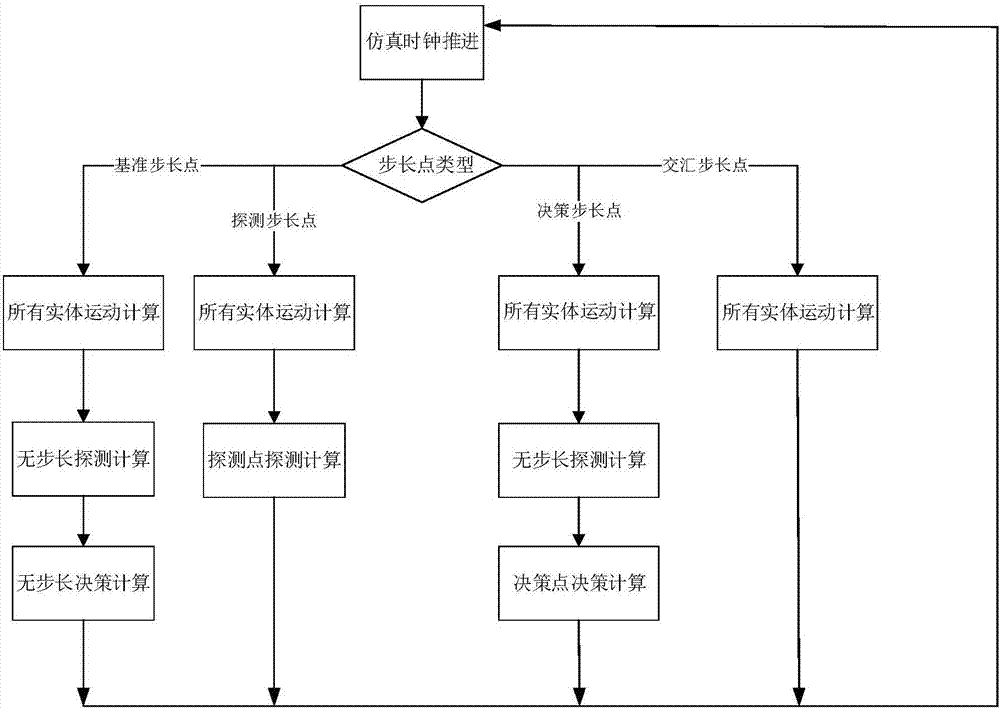
Novel combat effectiveness simulation modeling method
ActiveCN107967134ASupports semantic compositionEfficiently buildSoftware designVisual/graphical programmingMetamodelingProcess behavior
The invention discloses a novel combat effectiveness simulation modeling method, and the problems that a simulation model in combat effectiveness simulation is difficult to combine, reuse, expand andevolve, and a decision behavior model lacks flexibility and problem pertinence are solved. On the one hand, the method emphasizes clear distinction between two levels of knowledge including domain commonness non-variable knowledge and application variable knowledge of the combat effectiveness simulation, and describing the two levels of the knowledge separately; the domain commonness non-variableknowledge is applicable to the entire combat effectiveness field, accordingly a field abstract model is established; the application variable knowledge depends on specific combat effectiveness assessment questions, and an application-specific model which can be instantiated and deployed is established on the basis of the field abstract model. On the other hand, the method emphasizes the distinction between physical process behaviors of weapons and cognitive decision-making behaviors of combat commanders, the cognitive decision-making behaviors compared with the physical process behaviors havegreat difference in different applications according to missions and different choices of the commanders, and dynamic flexibility of the cognitive decision-making behaviors and pertinent expression ofquestions are realized by means of a script technology and a meta-modeling technology.
Owner:NAT UNIV OF DEFENSE TECH
Features
- R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
Why Patsnap Eureka
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com