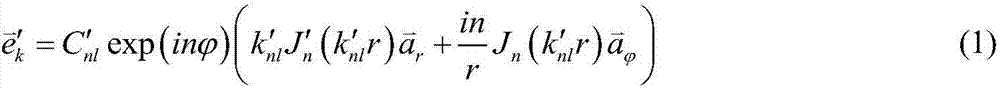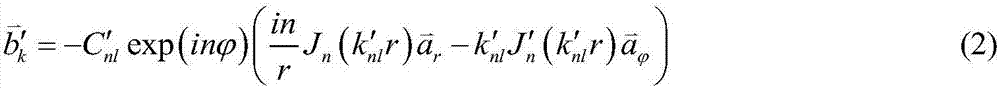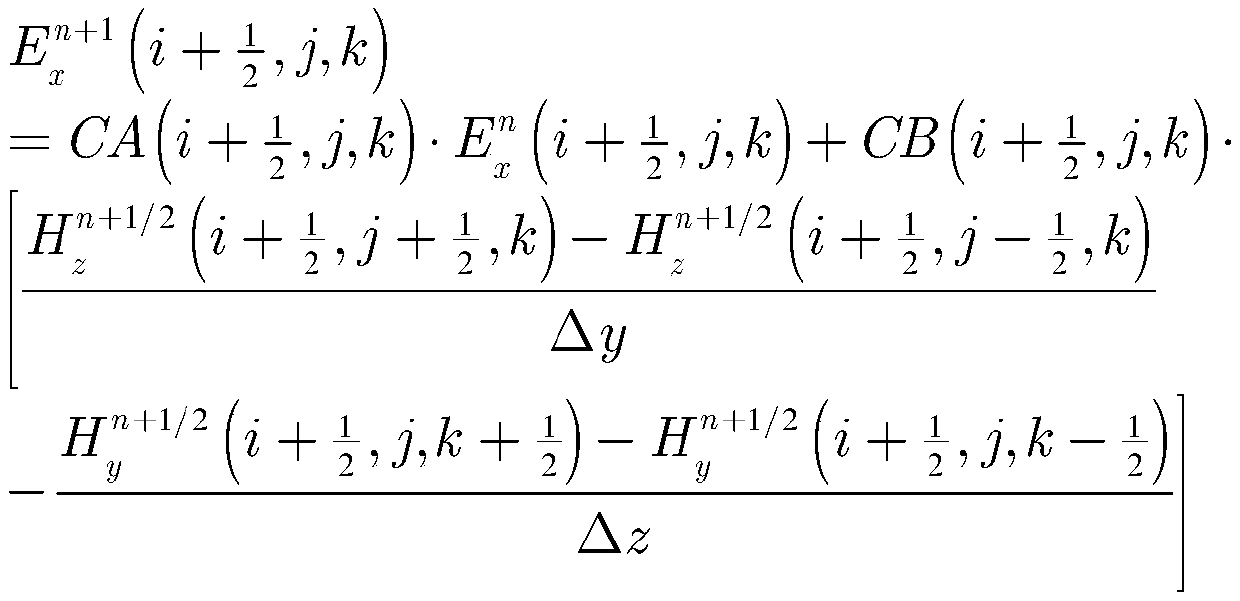Patents
Literature
100 results about "Maxwell's equations" patented technology
Efficacy Topic
Property
Owner
Technical Advancement
Application Domain
Technology Topic
Technology Field Word
Patent Country/Region
Patent Type
Patent Status
Application Year
Inventor
Maxwell's equations are a set of coupled partial differential equations that, together with the Lorentz force law, form the foundation of classical electromagnetism, classical optics, and electric circuits. The equations provide a mathematical model for electric, optical, and radio technologies, such as power generation, electric motors, wireless communication, lenses, radar etc. Maxwell's equations describe how electric and magnetic fields are generated by charges, currents, and changes of the fields. An important consequence of the equations is that they demonstrate how fluctuating electric and magnetic fields propagate at a constant speed (c) in a vacuum. Known as electromagnetic radiation, these waves may occur at various wavelengths to produce a spectrum of light from radio waves to γ-rays. The equations are named after the physicist and mathematician James Clerk Maxwell, who between 1861 and 1862 published an early form of the equations that included the Lorentz force law. Maxwell first used the equations to propose that light is an electromagnetic phenomenon.
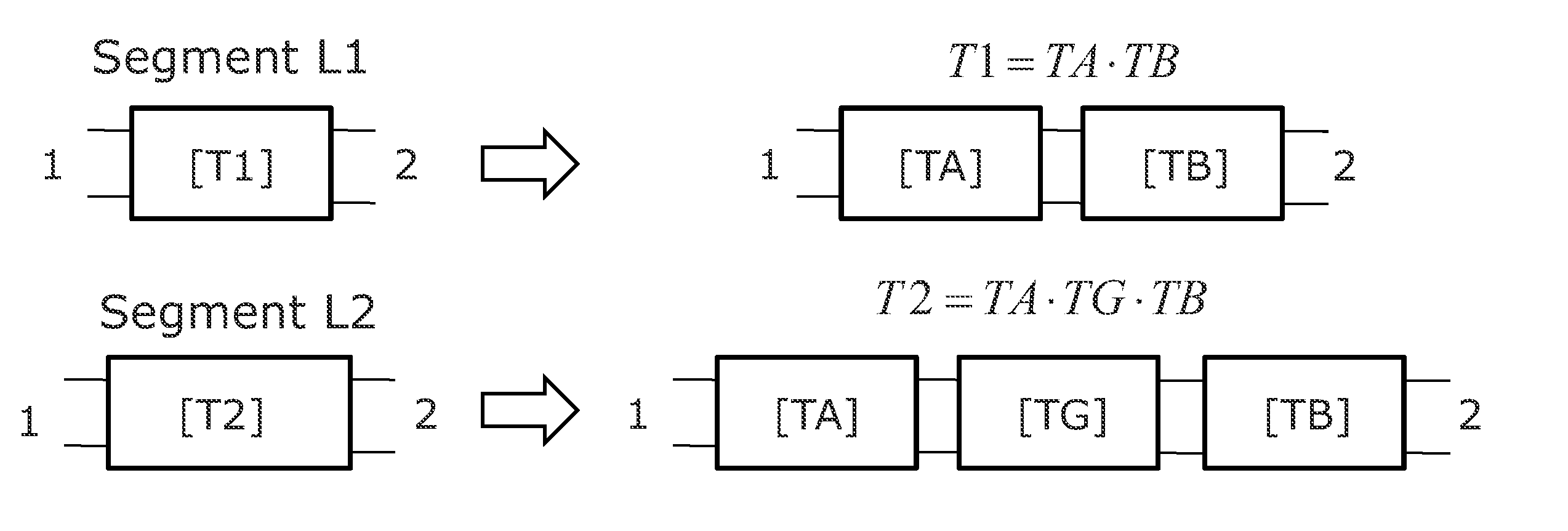
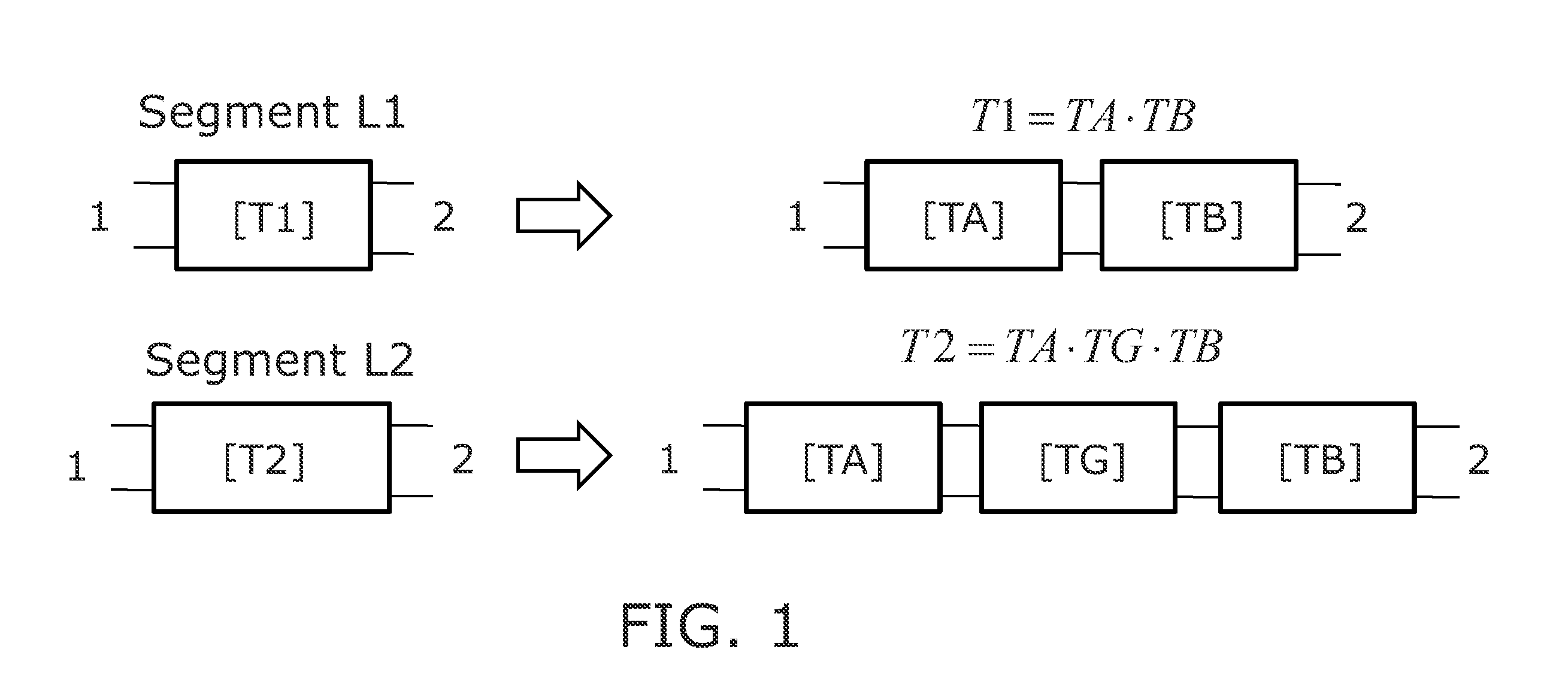
Efficient Computation Method for Electromagnetic Modeling
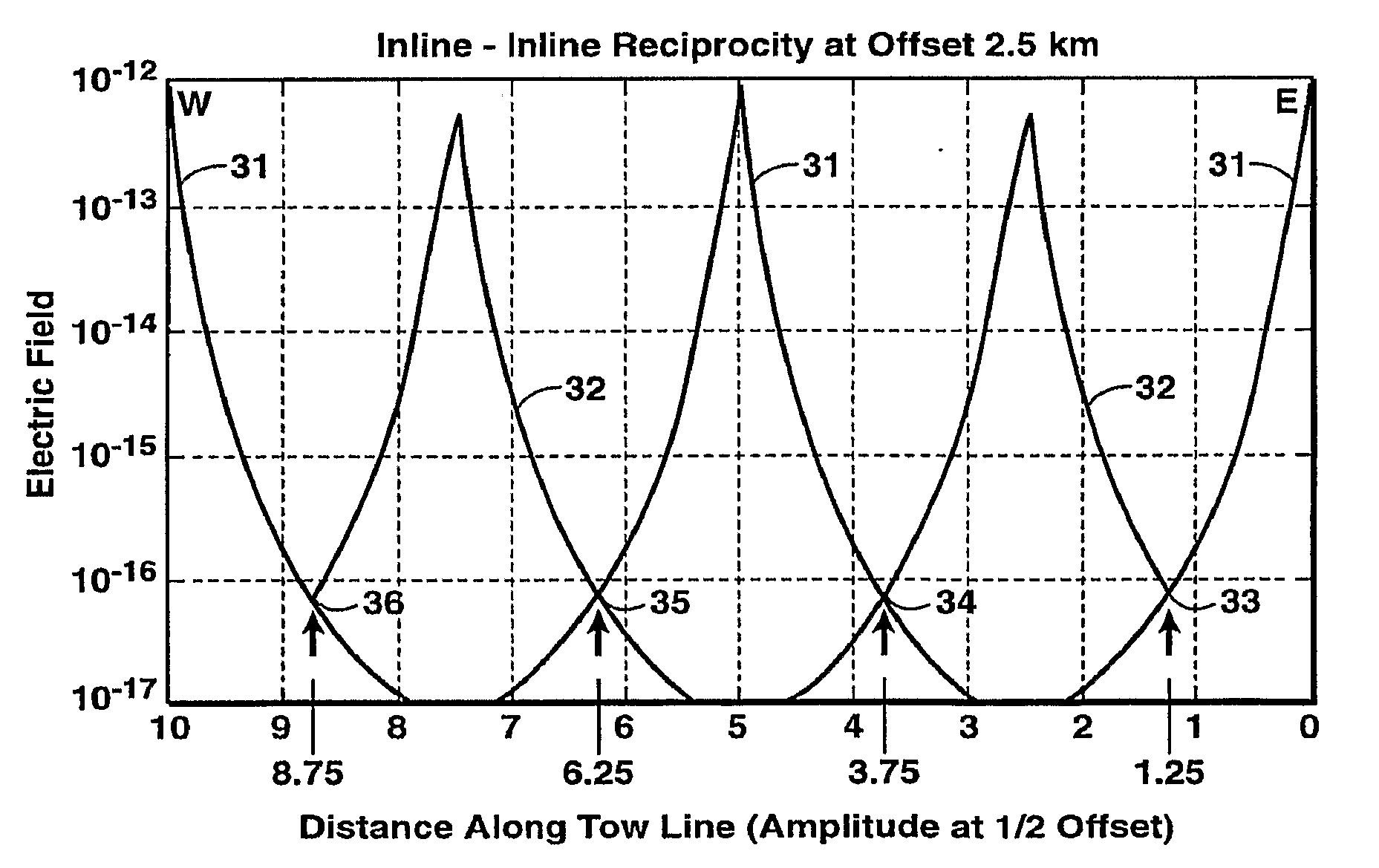
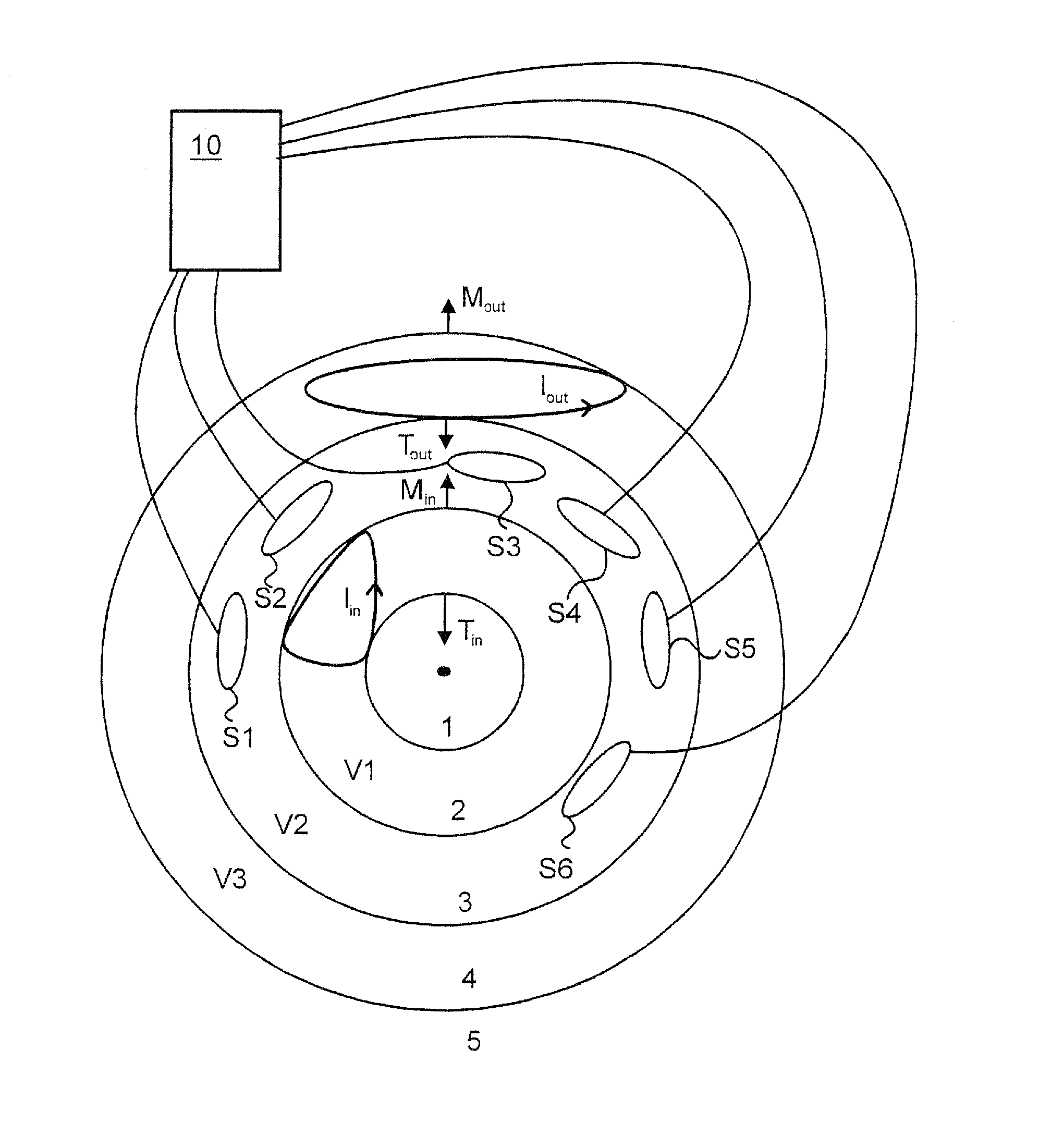
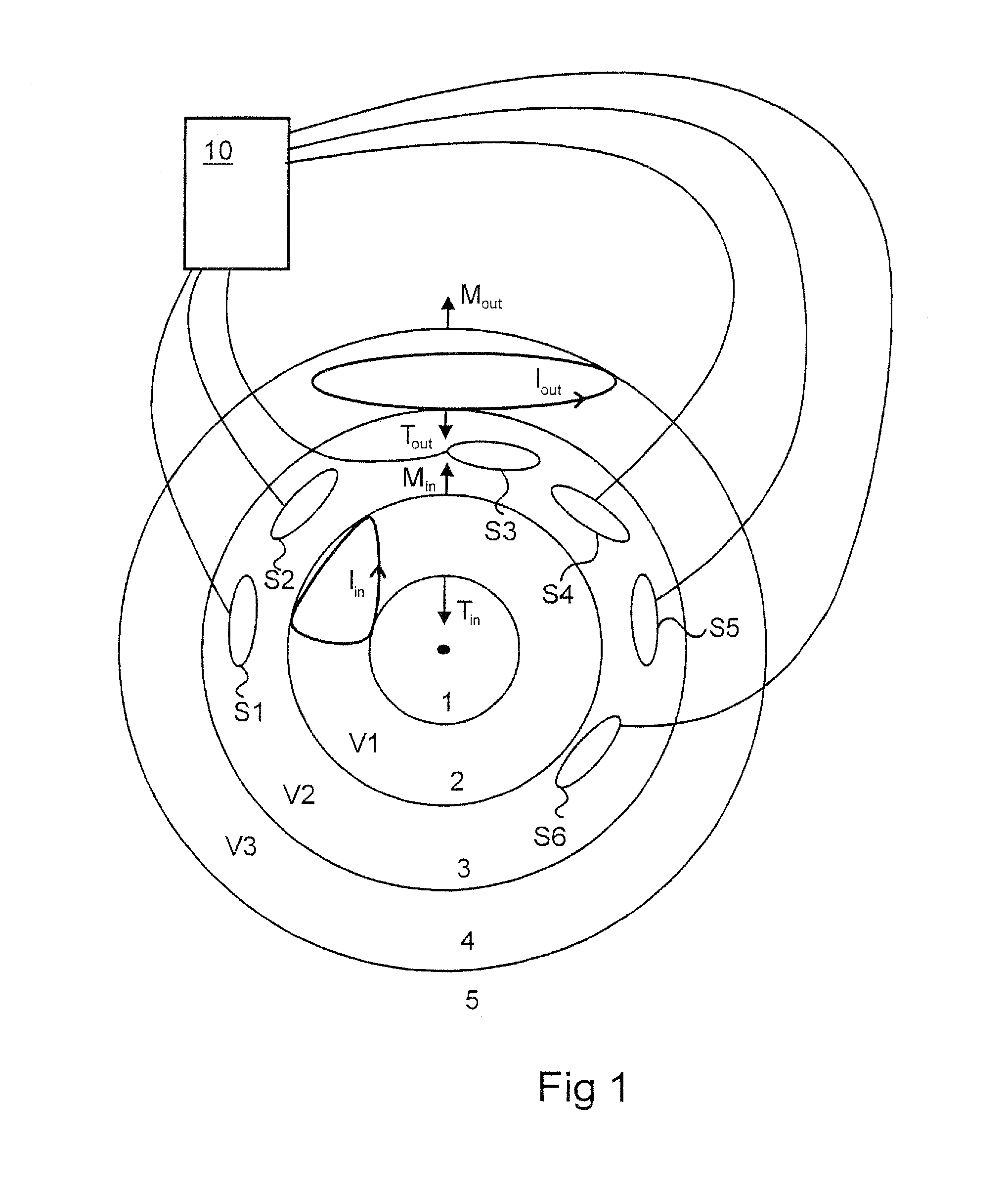
ActiveUS20090006053A1InsulationFluid removalControlled source electro-magneticElectromagnetic shielding
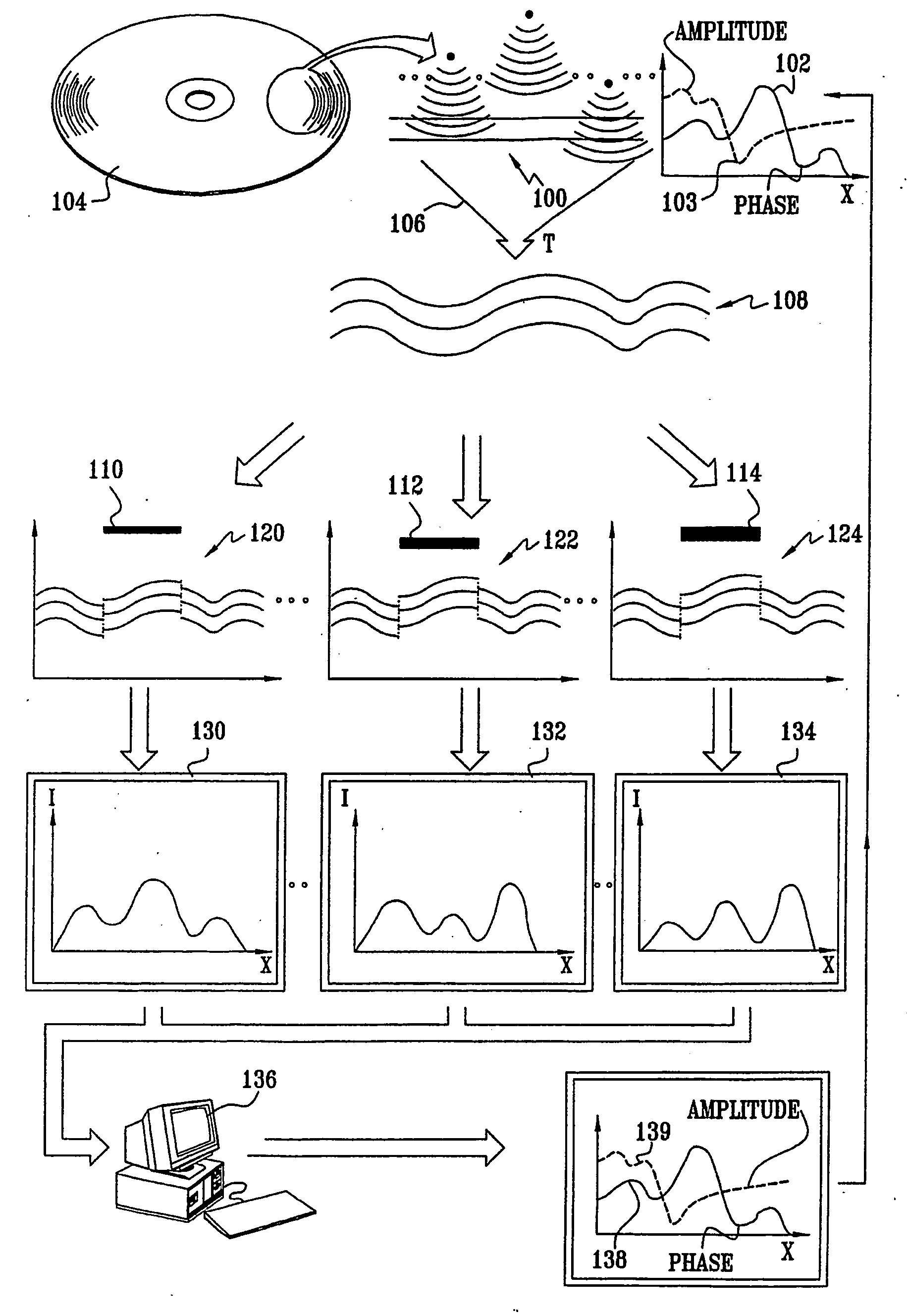
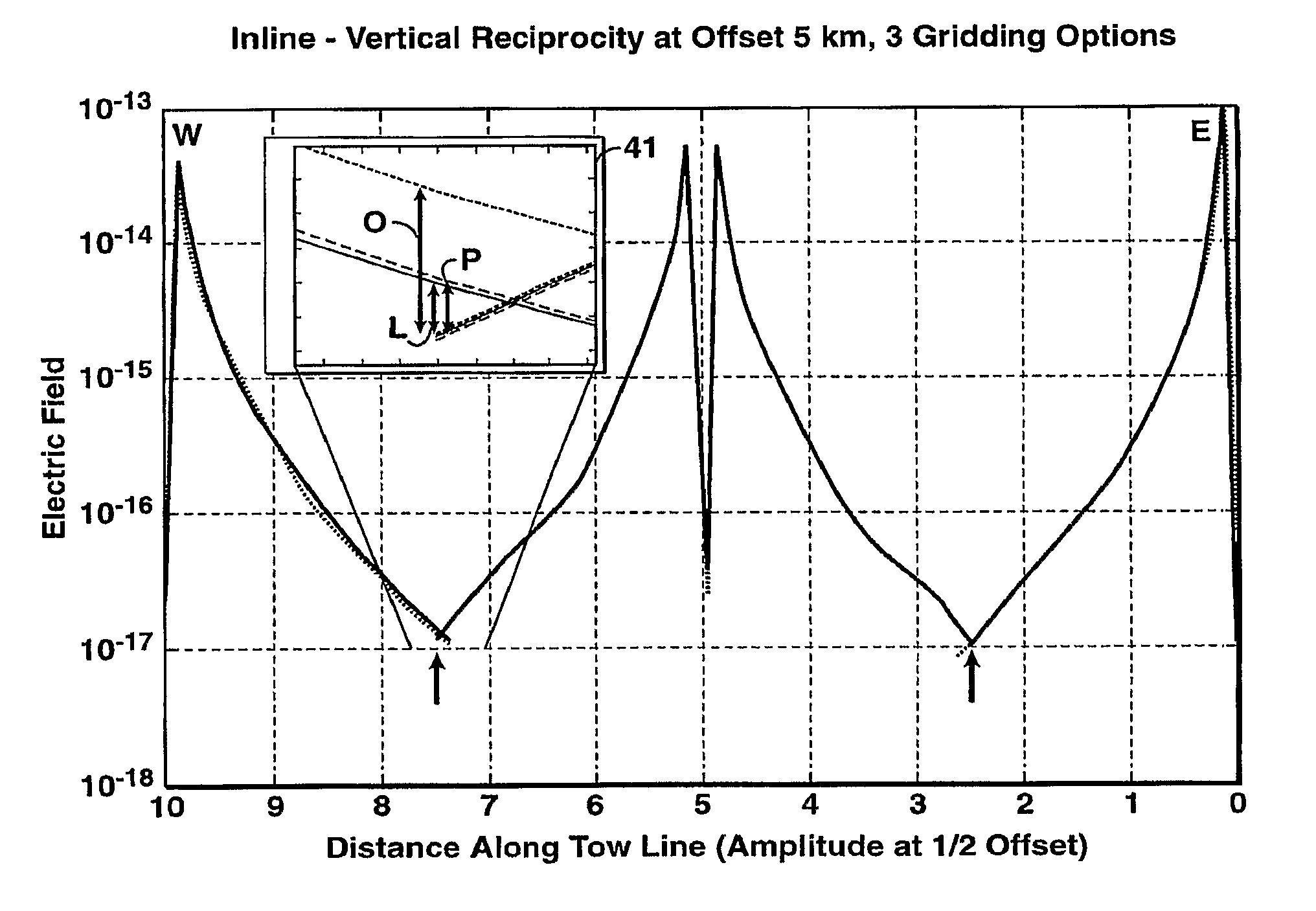
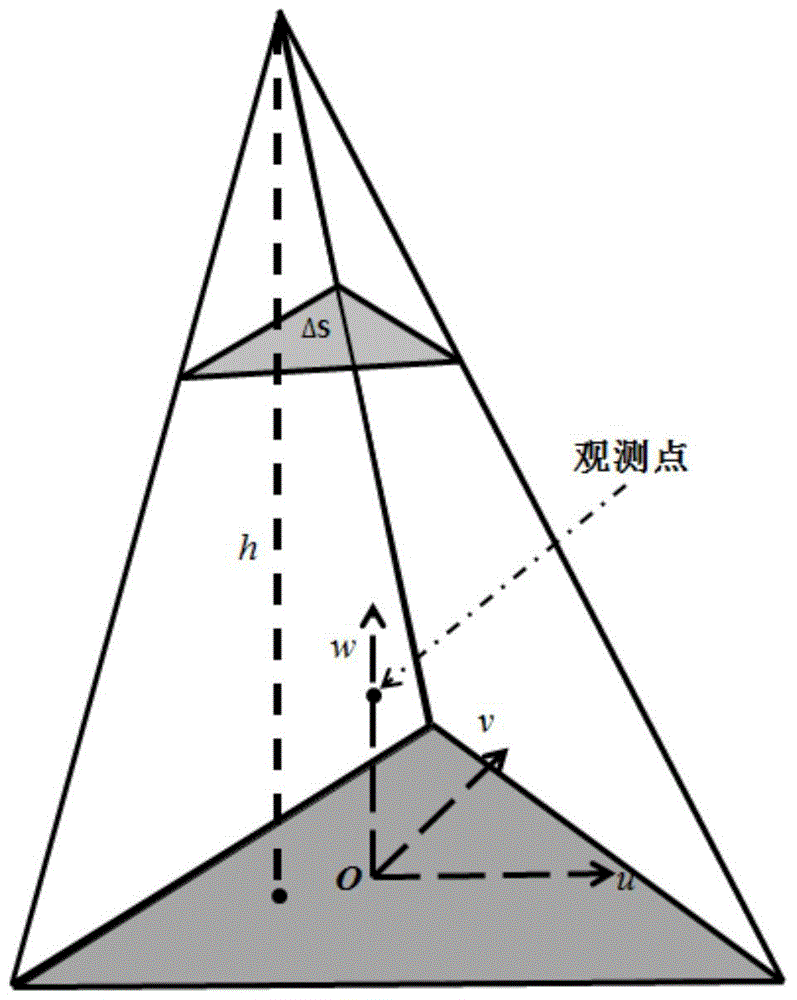
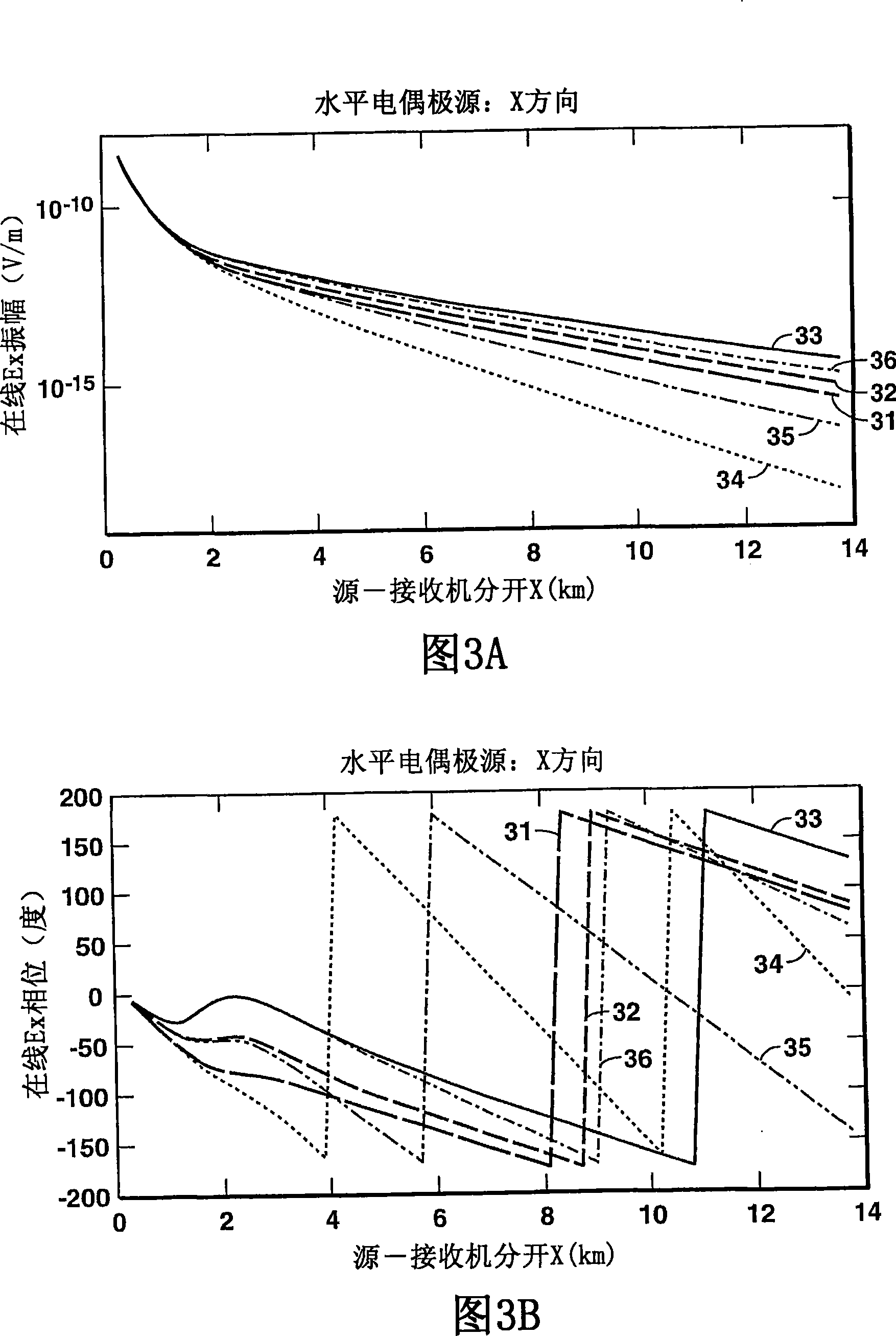
Method for efficient processing of controlled source electromagnetic data, whereby Maxwell's equations are solved [107] by numerical techniques [109] such as finite difference or finite element in three dimensions for each source location and frequency of interest. The Reciprocity Principle is used [103] to reduce the number of computational source positions, and a multi-grid is used [105] for the computational grid to minimize the total number of cells yet properly treat the source singularity, which is essential to satisfying the conditions required for applicability of the Reciprocity Principle. An initial global resistivity model [101] is Fourier interpolated to the computational multi grids [106]. In inversion embodiments of the invention, Fourier prolongation is used to update [120] the global resistivity model based on optimization results from the multi-grids.
Owner:EXXONMOBIL UPSTREAM RES CO
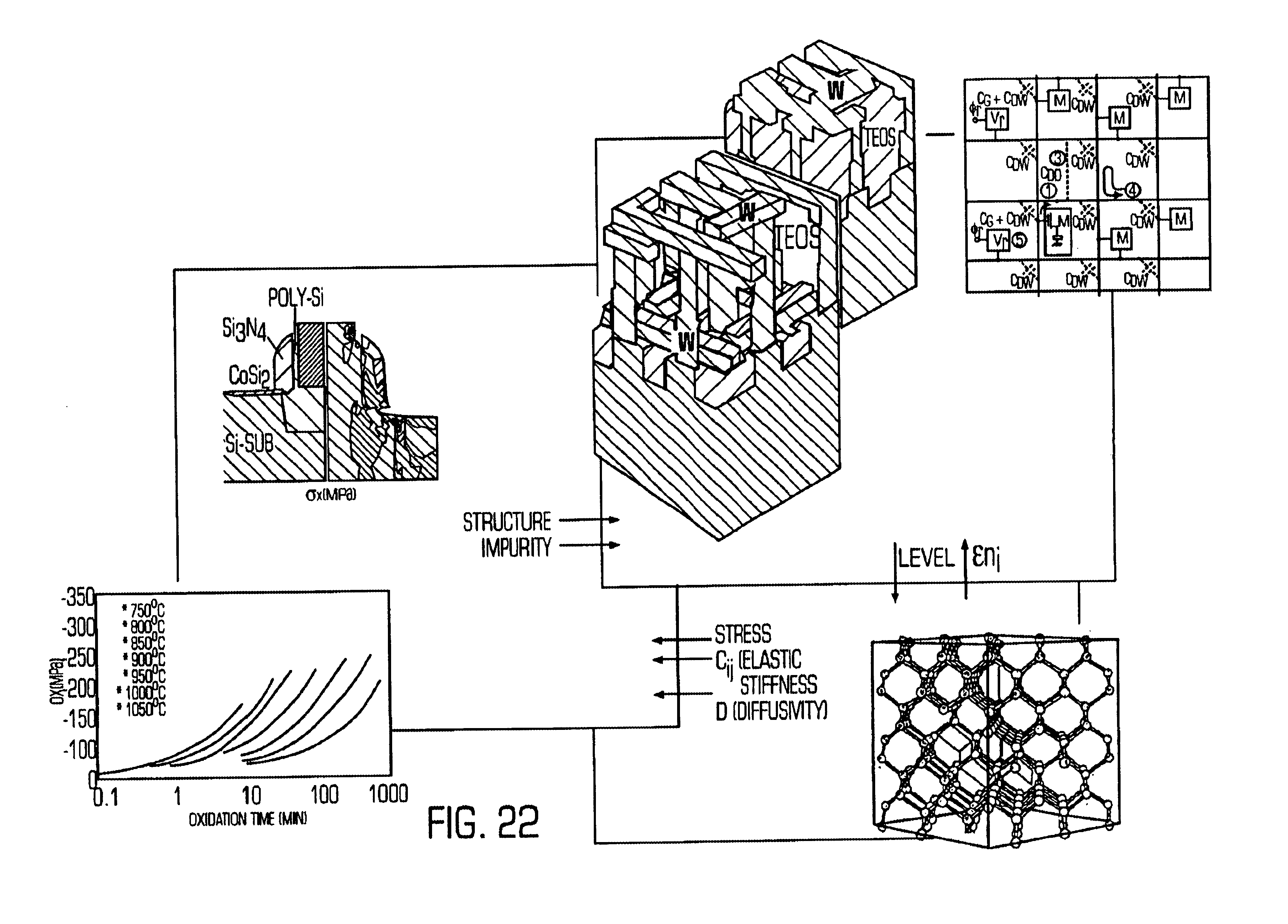
Method and apparatus for simulating manufacturing, electrical and physical characteristics of a semiconductor device
InactiveUS6826517B2Semiconductor/solid-state device detailsDetecting faulty computer hardwareElement modelMaterial Design
An electronic device simulator includes a three-dimensional lumped device model, a three-dimensional visco-elastic process simulation model and a material design model that are interlinked with each other. The three-dimensional lumped device element model comprises a Poisson's equation model, an electron continuity equation model, a hole continuity equation model, a Maxwell's equations model, an eddy current equation model, and an Ohm's law equation model. The simulator accounts for the three dimensional characteristics of the circuit to determine circuit performance.
Owner:KK TOSHIBA
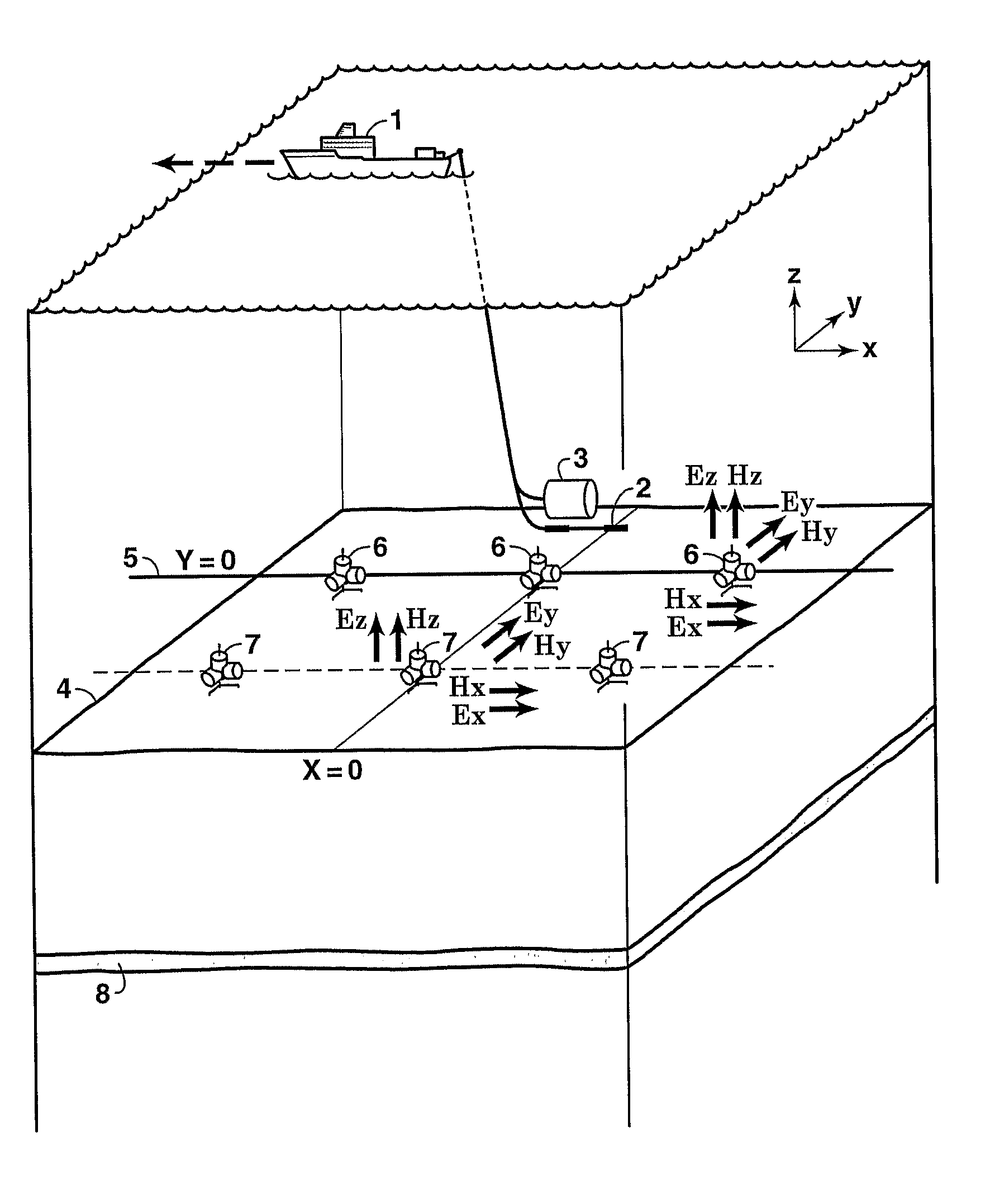
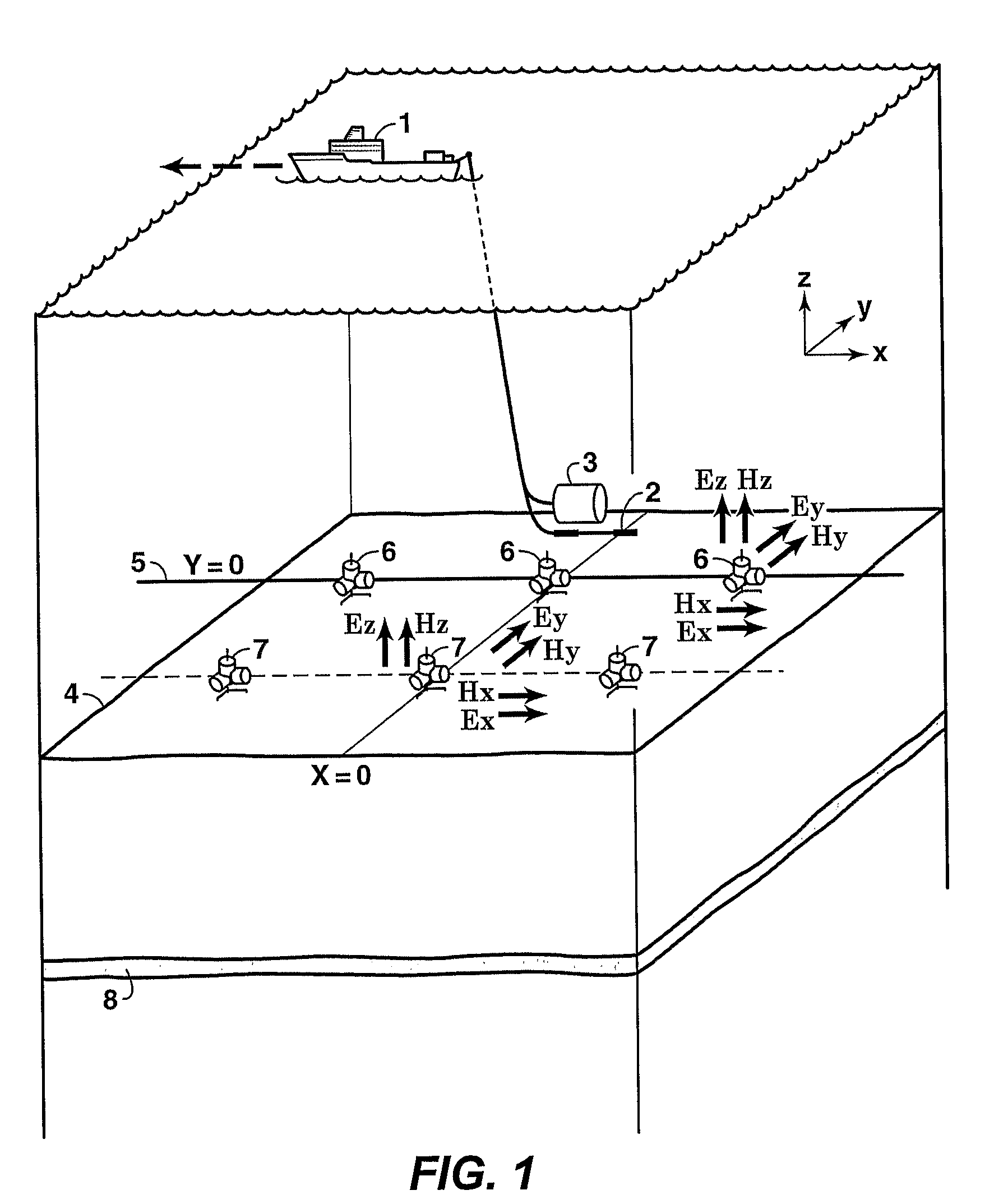
Time Lapse Analysis with Electromagnetic Data
ActiveUS20090005994A1Electric/magnetic detection for well-loggingMeasurement arrangements for variableFluid saturationOnline and offline
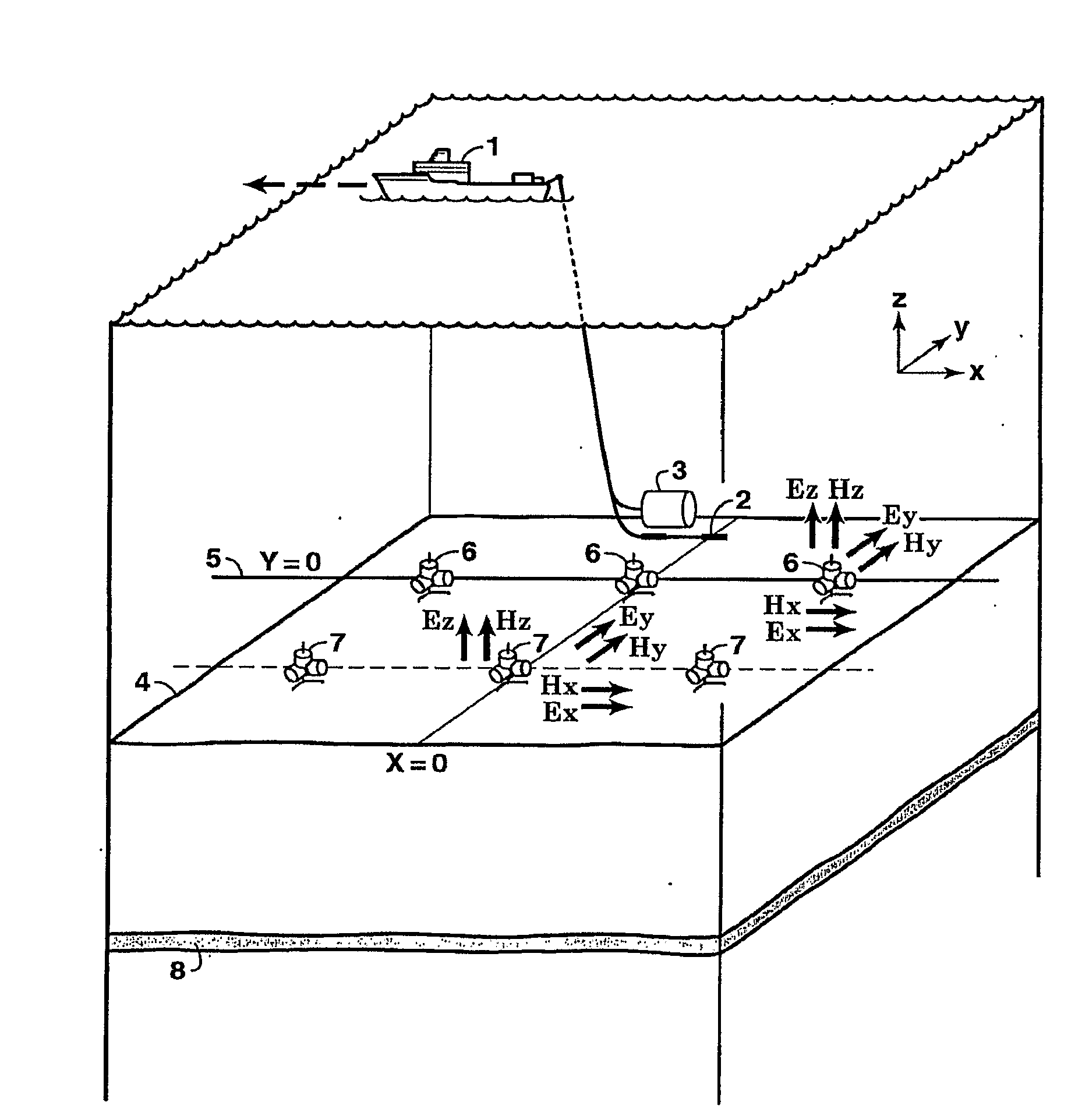
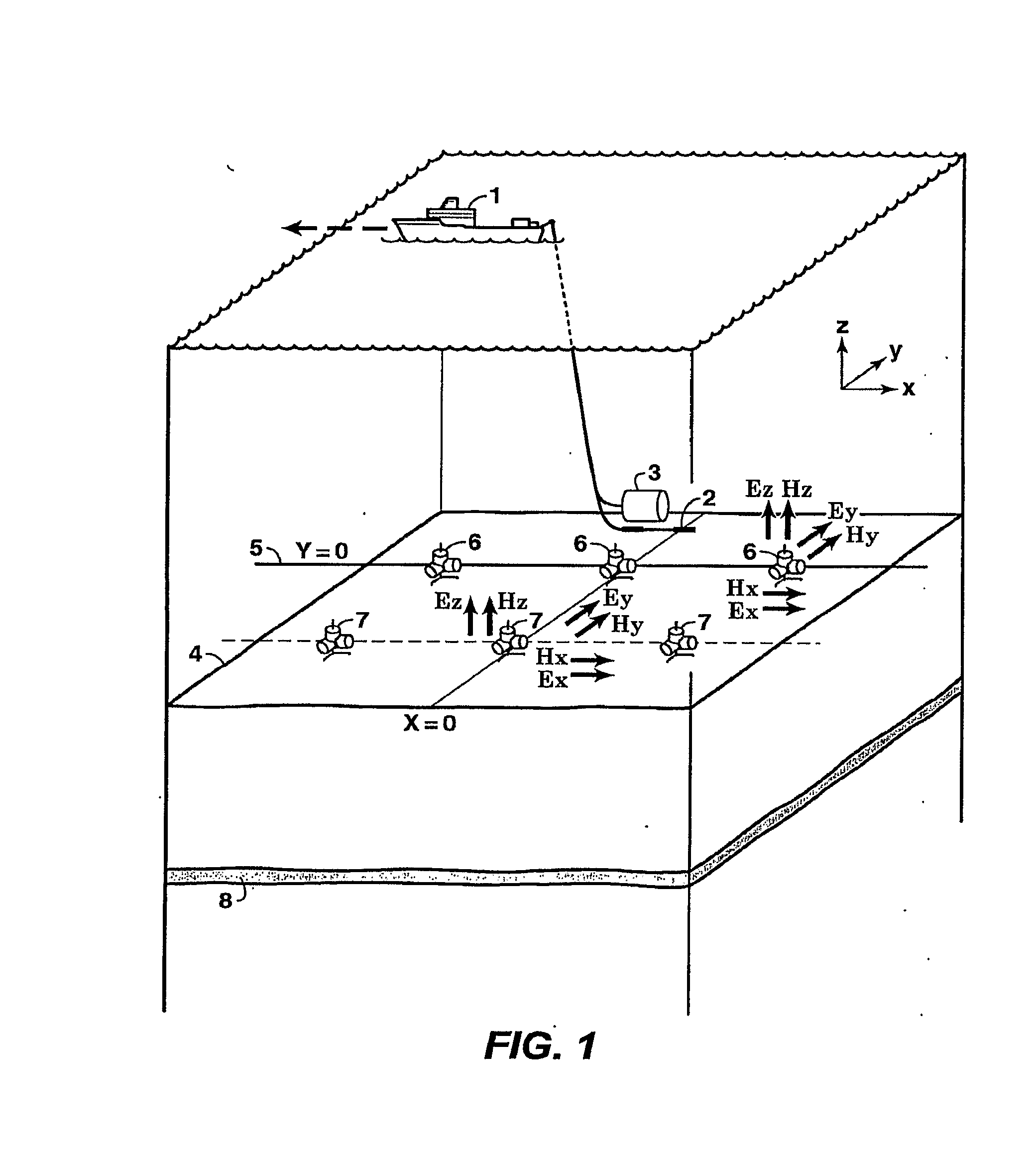
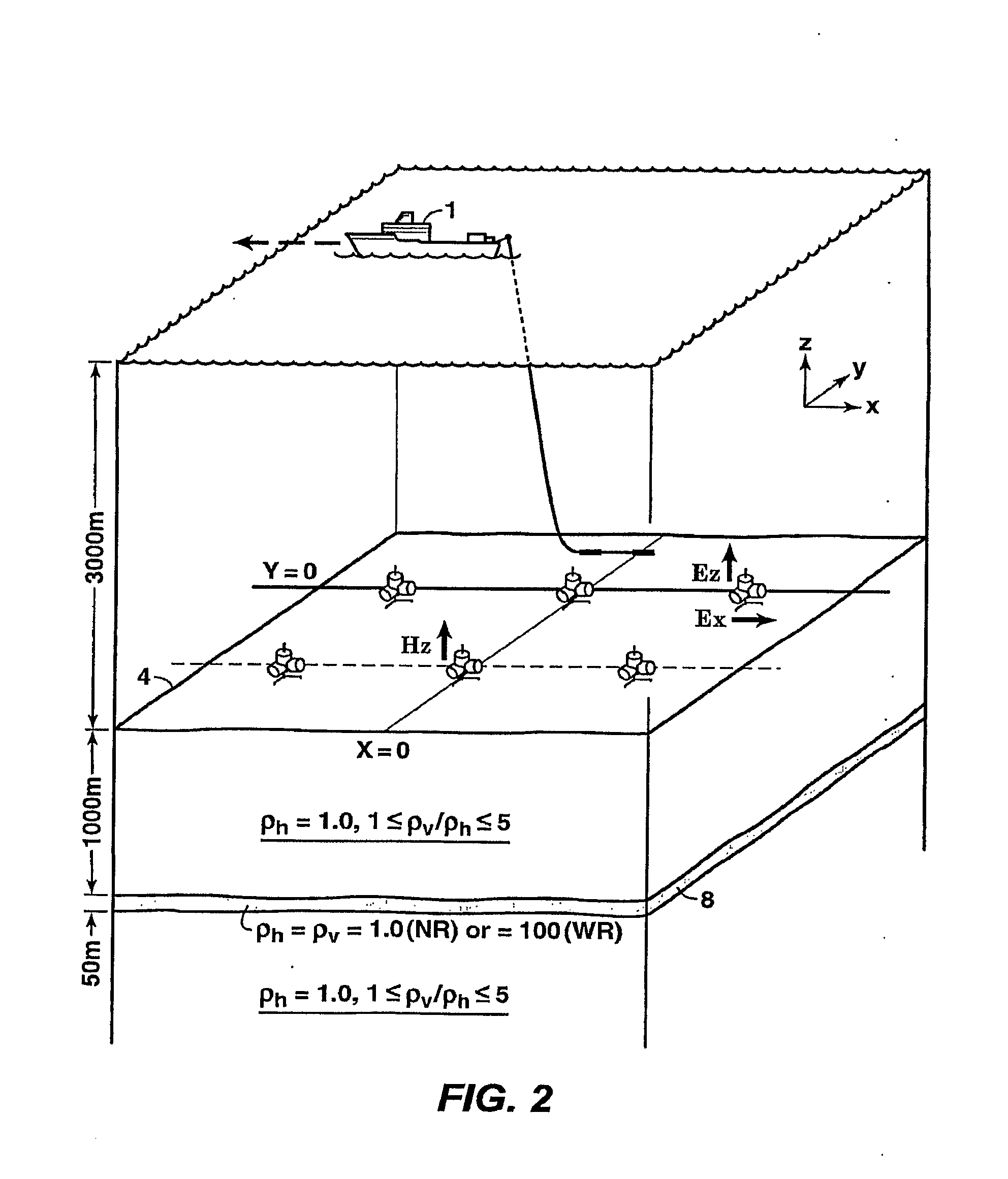
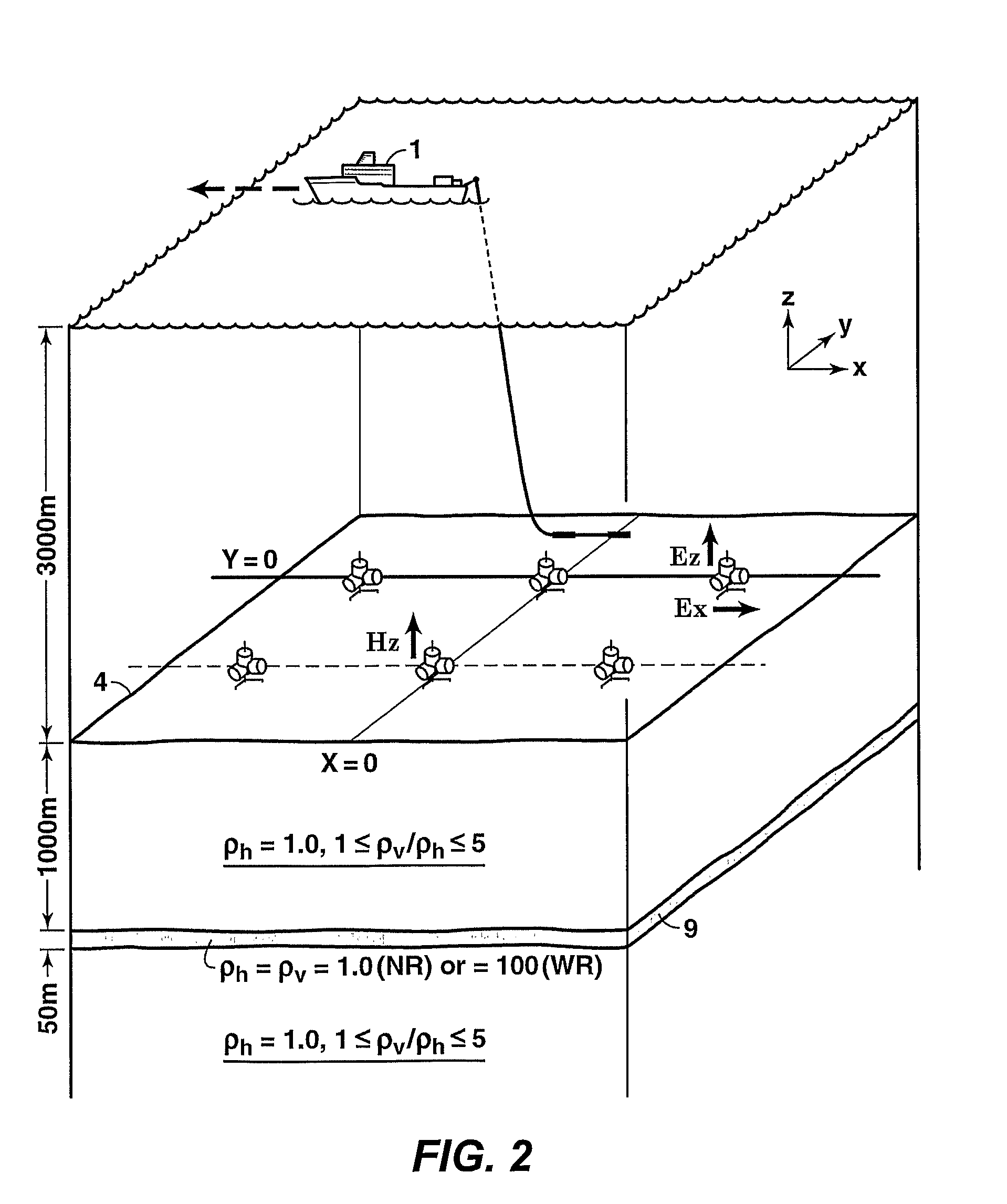
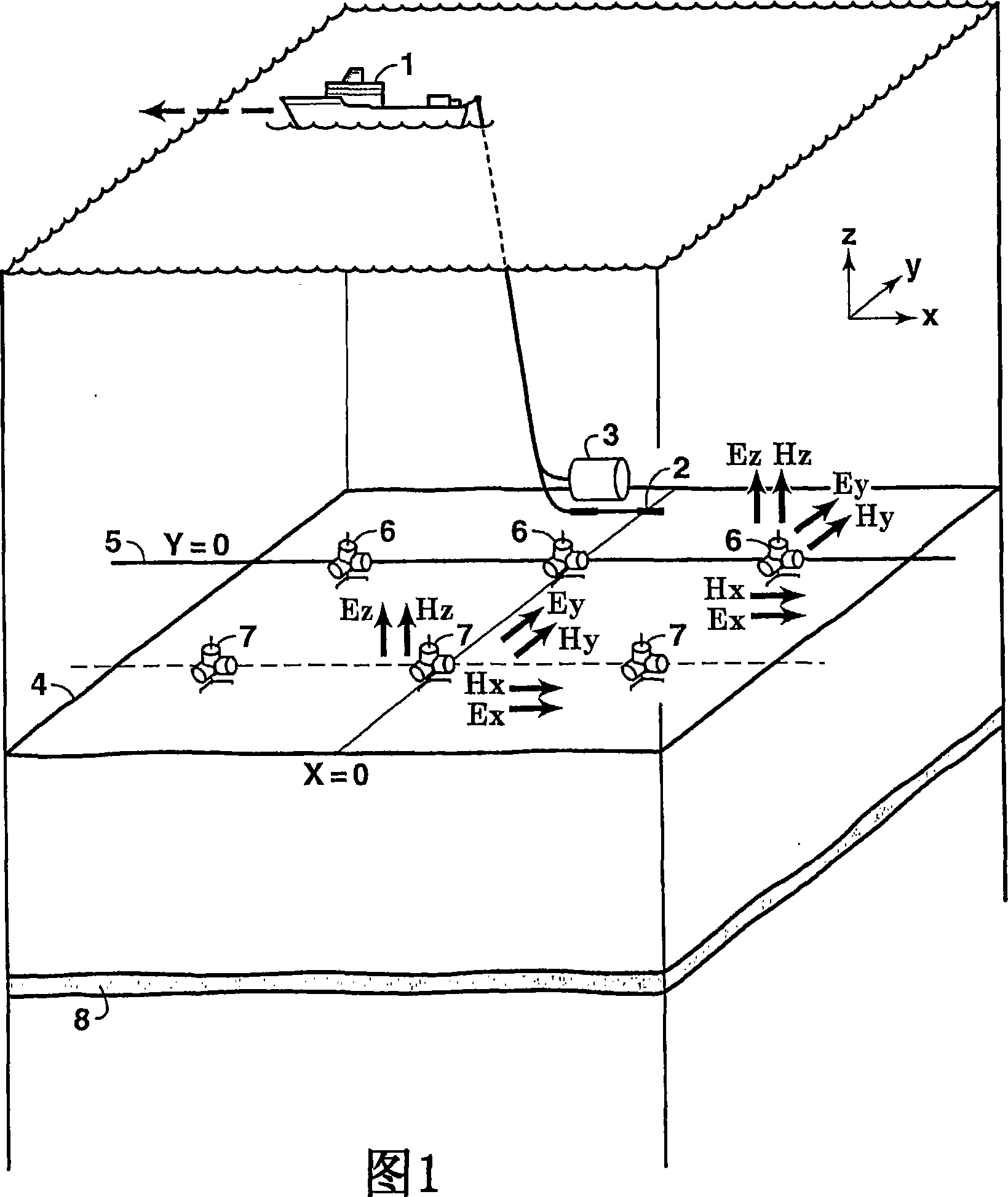
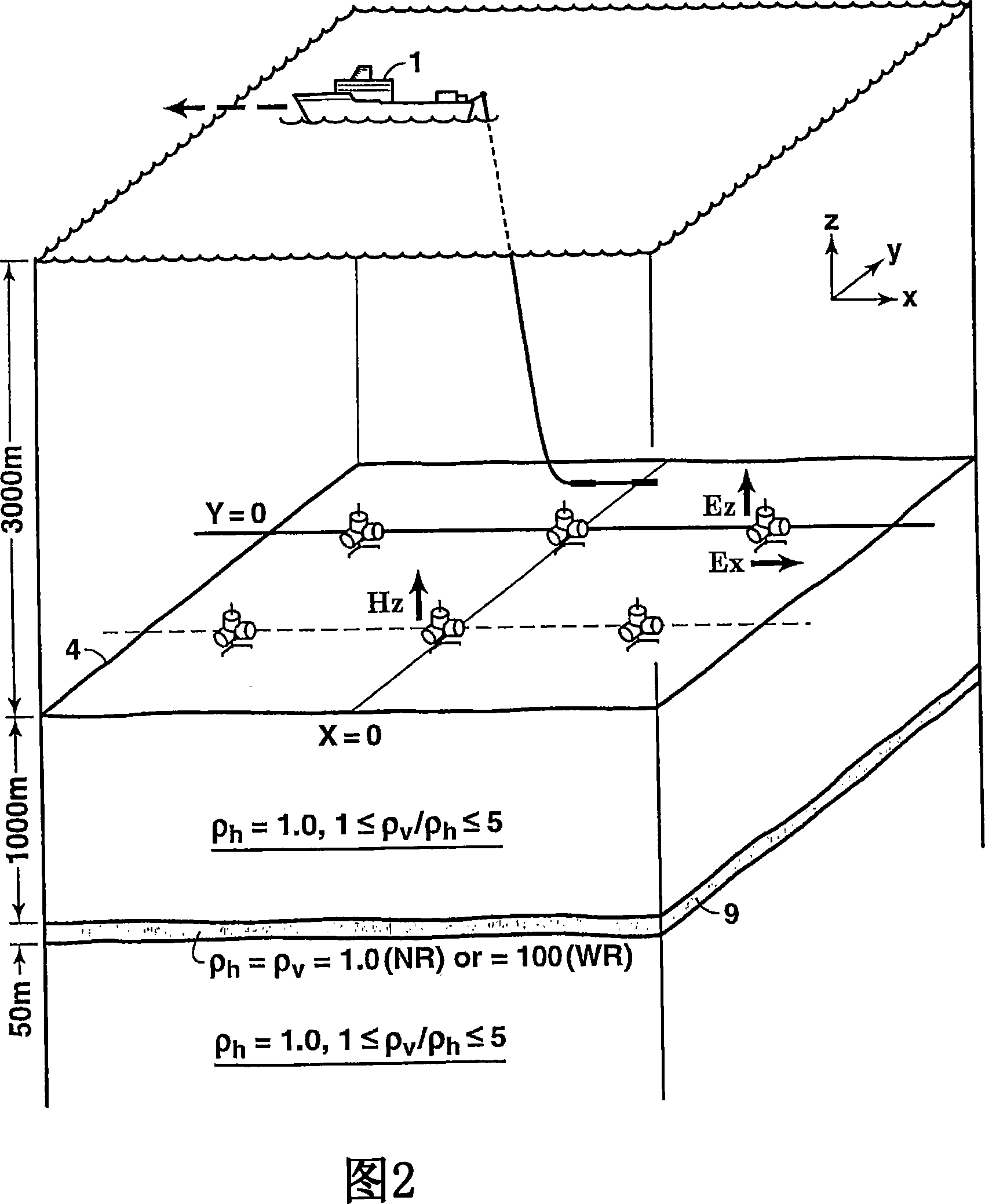
Method for determining time-dependent changes [73] in the earth vertical and horizontal electrical resistivity and fluid saturations from offshore electromagnetic survey measurements. The method requires both online and offline data, which should include at least one electromagnetic field component sensitive at least predominantly to vertical resistivity and another component sensitive at least predominately to horizontal resistivity [62]. Using a horizontal electric dipole source, online Ez and offline Hz measurements are preferred. For a horizontal magnetic dipole source, online H2 and offline E2 data are preferred. Magnetotelluric data may be substituted for controlled source data sensitive at least predominantly to horizontal resistivity. Maxwell's equations are solved by forward modeling [64,65] or by inversion [66,67], using resistivity models of the subsurface that are either isotropic contrast, and [64,66] or anisotropic [65,67]. Fluid saturation is determined from the vertical and horizontal resistivities using empirical relations or rock physics models [70].
Owner:EXXONMOBIL UPSTREAM RES CO
Methods and apparatus for wavefront manipulations and improved 3-D measurements
InactiveUS20100002950A1Accurate calculationPoor spatial resolutionFeeler-pin gaugesUsing subsonic/sonic/ultrasonic vibration meansMaxwell's equations3d measurement
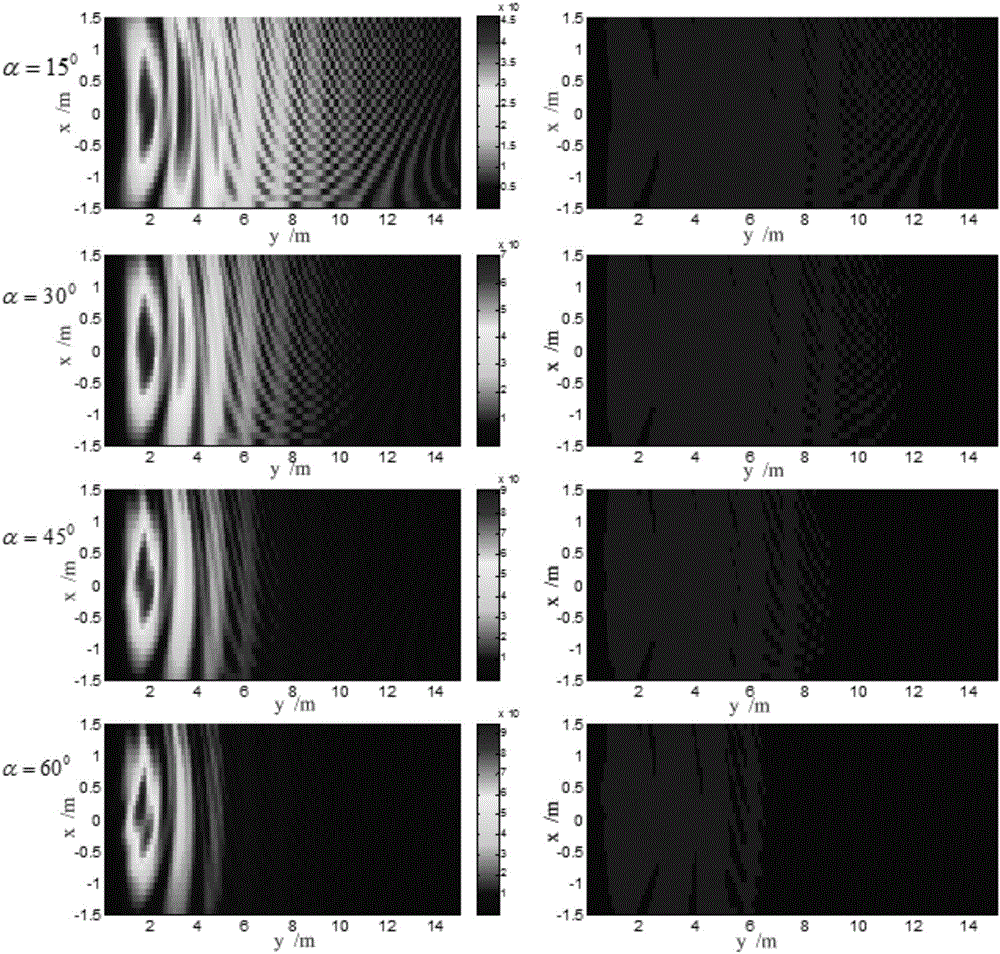
Methods and apparatus to perform wavefront analysis, including phase and amplitude information, and 3D measurements in optical systems, and in particular those based on analyzing the output of an intermediate plane, such as an image plane, of an optical system. Measurement of surface topography in the presence of thin film coatings, or of the individual layers of a multilayered structure is described. Multi-wavelength analysis in combination with phase and amplitude mapping is utilized. Methods of improving phase and surface topography measurements by wavefront propagation and refocusing, using virtual wavefront propagation based on solutions of Maxwell's equations are described. Reduction of coherence noise in optical imaging systems is achieved by such phase manipulation methods, or by methods utilizing a combination of wideband and coherent sources. The methods are applied to Integrated Circuit inspection, to improve overlay measurement techniques, by improving contrast or by 3-D imaging, in single shot imaging. Data supplied from the esp@cenet database—Worldwide
Owner:ICOS VISION SYST
Method and apparatus for simulating manufacturing, electrical and physical characteristics of a semiconductor device
InactiveUS20020123872A1Semiconductor/solid-state device detailsSolid-state devicesElement modelMaterial Design
An electronic device simulator includes a three-dimensional lumped device model, a three-dimensional visco-elastic process simulation model and a material design model that are interlinked with each other. The three-dimensional lumped device element model comprises a Poisson's equation model, an electron continuity equation model, a hole continuity equation model, a Maxwell's equations model, an eddy current equation model, and an Ohm's law equation model. The simulator accounts for the three dimensional characteristics of the circuit to determine circuit performance.
Owner:KK TOSHIBA
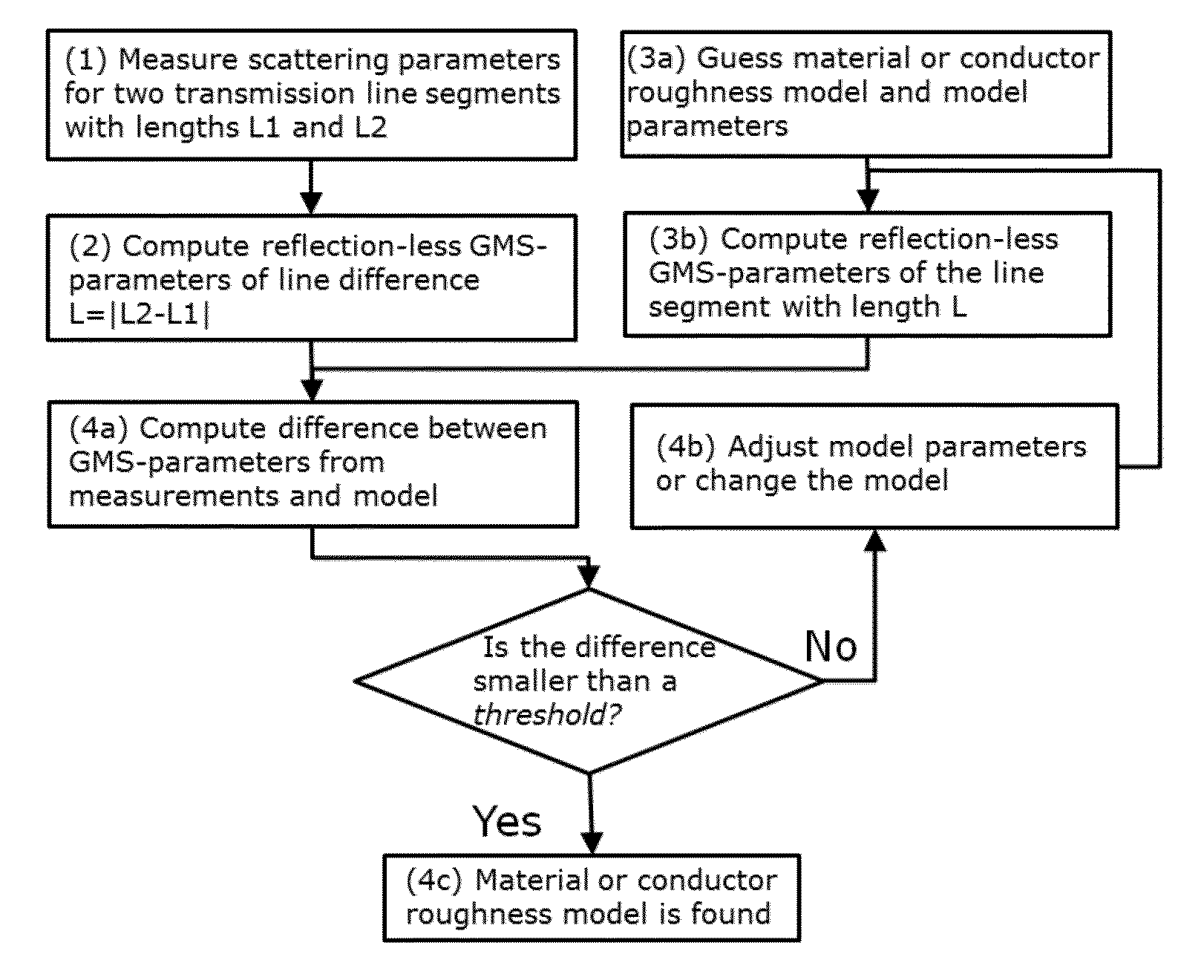
System and method for identification of complex permittivity of transmission line dielectric
InactiveUS20110178748A1Dielectric property measurementsVoltage-current phase angleModel parametersEngineering
A system and method for identification of complex permittivity associated with a transmission line dielectric is proposed. A network analyzer measures scattering parameters over a specified frequency band for at least two line segments of different length and substantially identical cross-section filled with a dielectric. A first engine determines non-reflective (generalized) modal scattering parameters of the difference segment based on the measured scattering parameters of two line segments. A second engine computes generalized modal scattering parameters of the line difference segment by solving Maxwell's equations for geometry of the line cross-section with a given frequency-dependent complex permittivity dielectric model. A third engine performs optimization by changing dielectric model parameters and model type until the computed and measured generalized modal scattering parameters match. The model that produces generalized modal S-parameters closest to the measured is the final dielectric model.
Owner:SIMBERIAN
Method for determining earth vertical electrical anisotropy in marine electromagnetic surveys
ActiveUS7894989B2Beacon systems using ultrasonic/sonic/infrasonic wavesElectric/magnetic detection for well-loggingElectricityOnline and offline
A method is disclosed for determining earth vertical electrical anisotropy from offshore electromagnetic survey measurements. The method requires both online and offline data, which includes at least one electromagnetic field component sensitive at least predominantly to vertical resistivity and another component sensitive at least predominantly to horizontal resistivity. Using a horizontal electric dipole source, online EZ and offline HZ measurements are preferred. For a horizontal magnetic dipole source, online HZ and offline EZ data are preferred. magnetotelluric data may be substituted for controlled source data sensitive to horizontal resistivity. Maxwell's equations are solved by forward modeling or by inversion, using resistivity models of the subsurface that are either isotropic or anisotropic.
Owner:EXXONMOBIL UPSTREAM RES CO
Marine controlled source electromagnetic method finite element forward method of anisotropic media
InactiveCN106980736AAvoid the effects of singularityEasy constructionDesign optimisation/simulationSpecial data processing applicationsScalar potentialMaxwell's equations
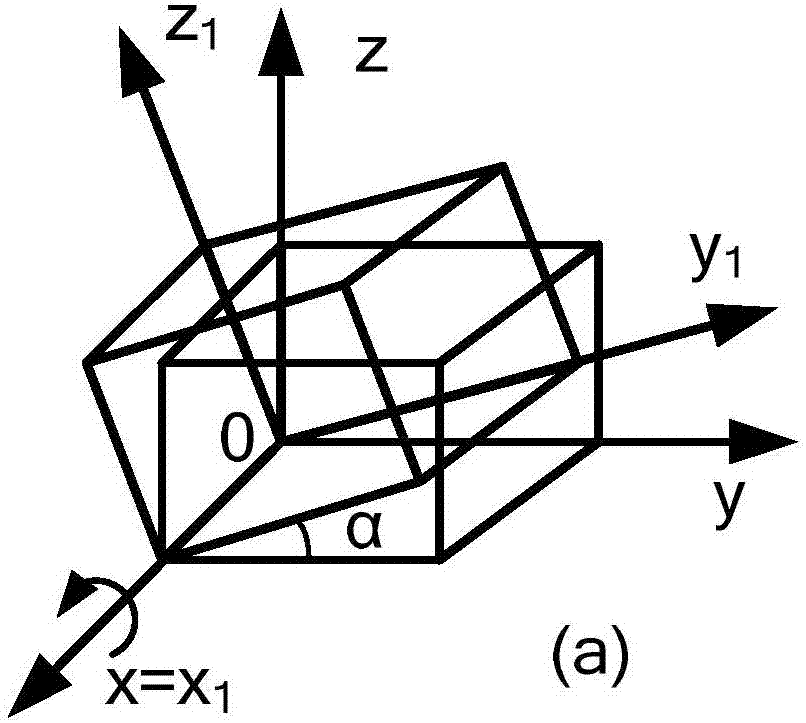
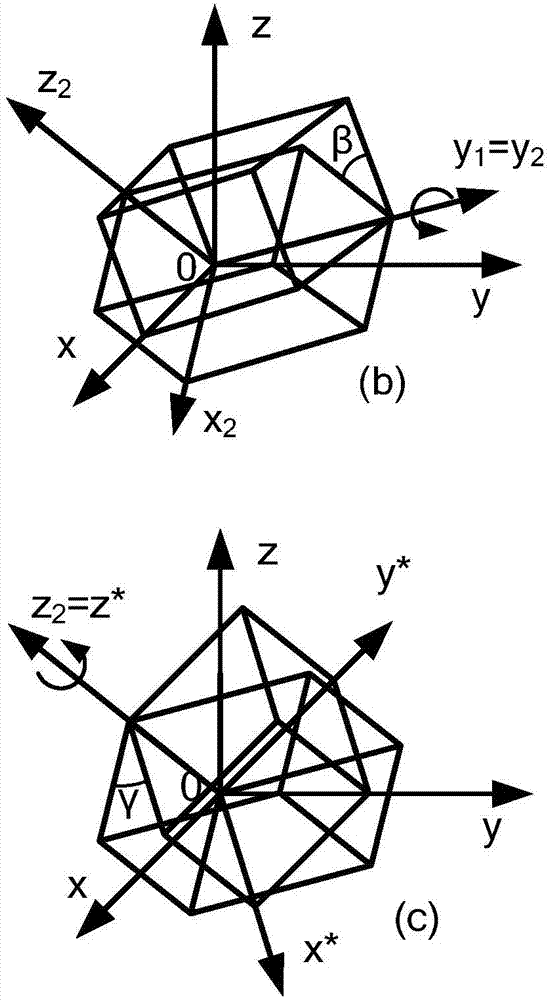
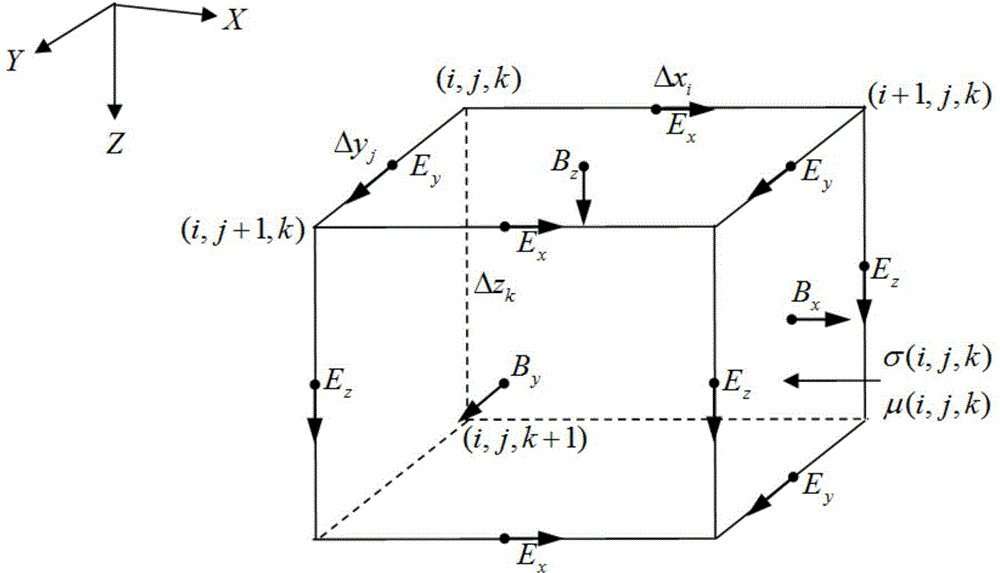
The present invention is a marine controlled source electromagnetic method finite element forward method of anisotropic media. The method comprises: firstly, setting a reference electrical conductivity, wherein three non-zero diagonal elements of the reference electrical conductivity are electrical conductivities in the direction of three main axes: x, y, z; next, setting three Euler rotation angles, and after three times of Euler rotation, obtaining an electrical conductivity tensor model in any direction; then starting from Maxwell equations, obtaining a finite element equation that is satisfied by magnetic vector potential and scalar potential under Coulomb regulations on a condition that the electrical conductivity presents anisotropy; then, performing discrete segmentation on a research region by using a non-structural grid, so that a complicated geoelectric model can be constructed; combining an incomplete LU discomposition pre-condition factor with an IDR(s) algorithm, so as to realize efficient and precise solution of a large sparse linear equation; and finally, deriving vector potential and scalar potential of a secondary field by using weighted moving least squares solution, to obtain each component of an electromagnetic field. The method provided by the present invention has excellent universality and can be promoted for electromagnetic method numerical value simulation with complicated electrical conductivity distribution and high precision.
Owner:JILIN UNIV
Surface wave polarization converter
ActiveUS20170025765A1Enhanced couplingAltered couplingAntenna arraysRadiating elements structural formsElectricityDielectric surface
A method and apparatus for converting electromagnetic surface waves from TE mode to TM mode or from TM mode to TE mode. The apparatus includes a dielectric surface having an anisotropic impedance tensor which is preferably obtained by a plurality of electrically conductive unit cells disposed on the dielectric surface and arranged in a two dimensional array of unit cells, a majority of the unit cells in said array being divided into at least two portions, with at least one gap separating the at least two portions from each other into two or more patches or plates, the array of unit cells having a surface wave input end and a surface wave output end, gaps in the unit cells disposed closest to the surface wave input end having a first orientation and gaps in said unit cells disposed closest to the surface wave output end having a second orientation different than said first orientation. The electromagnetic surface waves have a frequency greater than a TE cutoff frequency determined by a second solution of Maxwell's equations for said dielectric surface.
Owner:HRL LAB
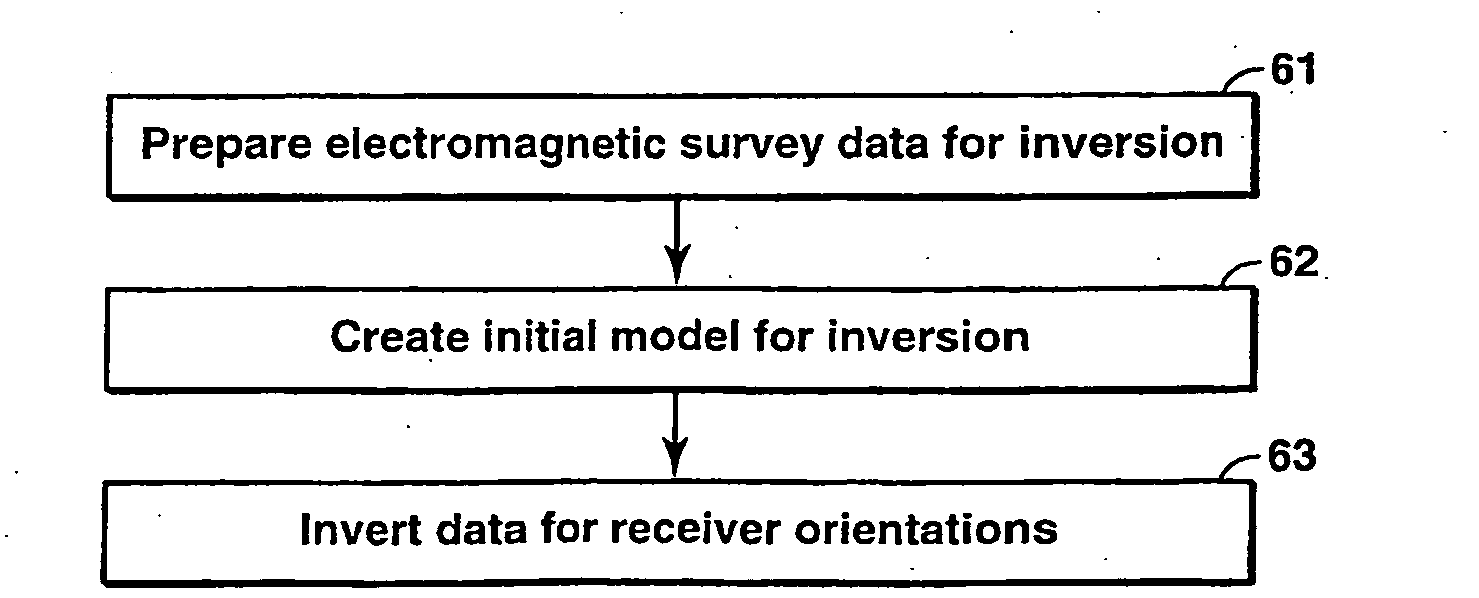
Method for Determining Receiver Orientations
InactiveUS20090171587A1Electric/magnetic detection for well-loggingNoise figure or signal-to-noise ratio measurementOcean bottomNoisy data
Method for completely specifying orientation of electromagnetic receivers dropped to the ocean bottom in an electromagnetic survey. Survey data are selected, rejecting noisy data with long offsets and data where the receiver has saturated with short offsets (61). A model is developed comprising three independent receiver orientation angles completely specifying the receiver orientation in three dimensions, and an earth resistivity model including a water layer and possibly an air layer (62). Maxwell's equations, applied to the model and the selected data, are then inverted to determine the receiver orientations (63).
Owner:EXXONMOBIL UPSTREAM RES CO
Efficient computation method for electromagnetic modeling
Method for efficient processing of controlled source electromagnetic data, whereby Maxwell's equations are solved [107] by numerical techniques [109] such as finite difference or finite element in three dimensions for each source location and frequency of interest. The Reciprocity Principle is used [103] to reduce the number of computational source positions, and a multi-grid is used [105] for the computational grid to minimize the total number of cells yet properly treat the source singularity, which is essential to satisfying the conditions required for applicability of the Reciprocity Principle. An initial global resistivity model [101] is Fourier interpolated to the computational multi grids [106]. In inversion embodiments of the invention, Fourier prolongation is used to update [120] the global resistivity model based on optimization results from the multi-grids.
Owner:EXXONMOBIL UPSTREAM RES CO
Methods and Apparatus for Simulating Interaction of Radiation with Structures, Metrology Methods and Apparatus, Device Manufacturing Method
ActiveUS20170102623A1Economical and robust methodReduce calculationMaterial analysis using wave/particle radiationPhotomechanical exposure apparatusComputation complexityMetrology
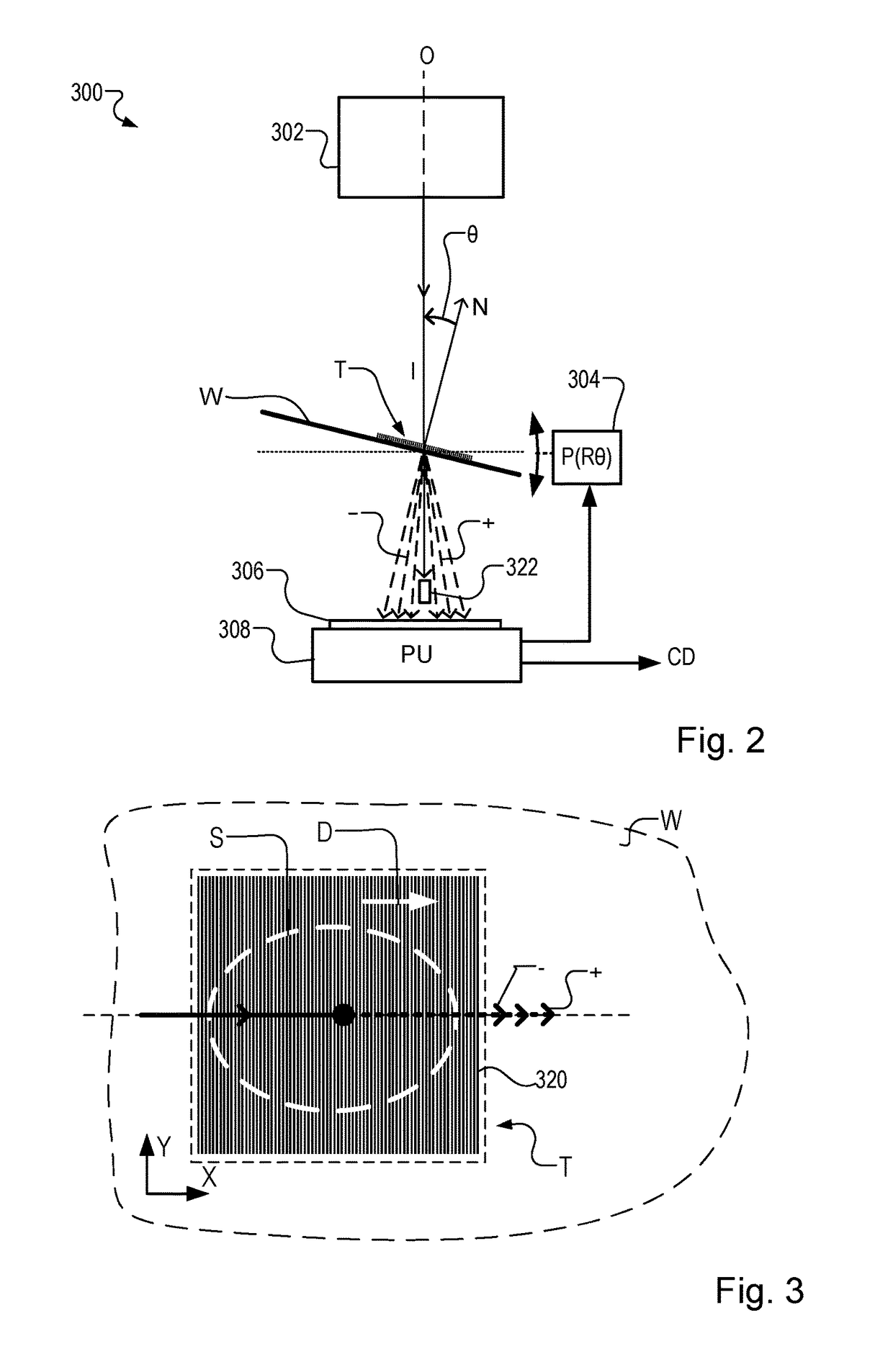
A structure of interest is irradiated with radiation for example in the x-ray or EUV waveband, and scattered radiation is detected by a detector (306). A processor (308) calculates a property such as linewidth (CD) by simulating interaction of radiation with a structure and comparing the simulated interaction with the detected radiation. A layered structure model (600, 610) is used to represent the structure in a numerical method. The structure model defines for each layer of the structure a homogeneous background permittivity and for at least one layer a non-homogeneous contrast permittivity. The method uses Maxwell's equation in Born approximation, whereby a product of the contrast permittivity and the total field is approximated by a product of the contrast permittivity and the background field. A computation complexity is reduced by several orders of magnitude compared with known methods.
Owner:ASML NETHERLANDS BV
MPM hybrid algorithm applied to numerical simulation of ECR ion source
ActiveCN107577639AAccurate descriptionReduce computational complexityComplex mathematical operationsComputation complexityMaxwell's equations
The invention belongs to the field of numerical simulation technology of ECR ion sources, and particularly relates to an MPM hybrid algorithm applied to numerical simulation of an ECR ion source. Thealgorithm is suitable for use in an ECR ion source structure. The MPM hybrid algorithm of simulation of the ECR ion source is established through combining an MAGY theory and PIC / MCC simulation algorithms, a time-varying electromagnetic field is described by the MAGY theory, self-consistent interaction of charged particles and the electromagnetic field is described by the PIC algorithm, and inter-particle collision processes are described by the MCC algorithm. A complex and complete solving process which originally needs to be carried out on Maxwell's equations is enabled to be simplified to solving on a set of coupled one-dimensional partial differential equations about mode amplitudes, relatively larger time step length can also be taken due to that compared with high-frequency cycles, changes of the mode amplitudes are slower, and computational complexity and a computational amount are greatly reduced. In addition, an electromagnetic model is adopted, and thus compared with adoptingan electrostatic model, the algorithm can more accurately describe an actual physical process.
Owner:UNIV OF ELECTRONICS SCI & TECH OF CHINA
Robust tetrahedralization and triangulation method with applications in VLSI layout design and manufacturability
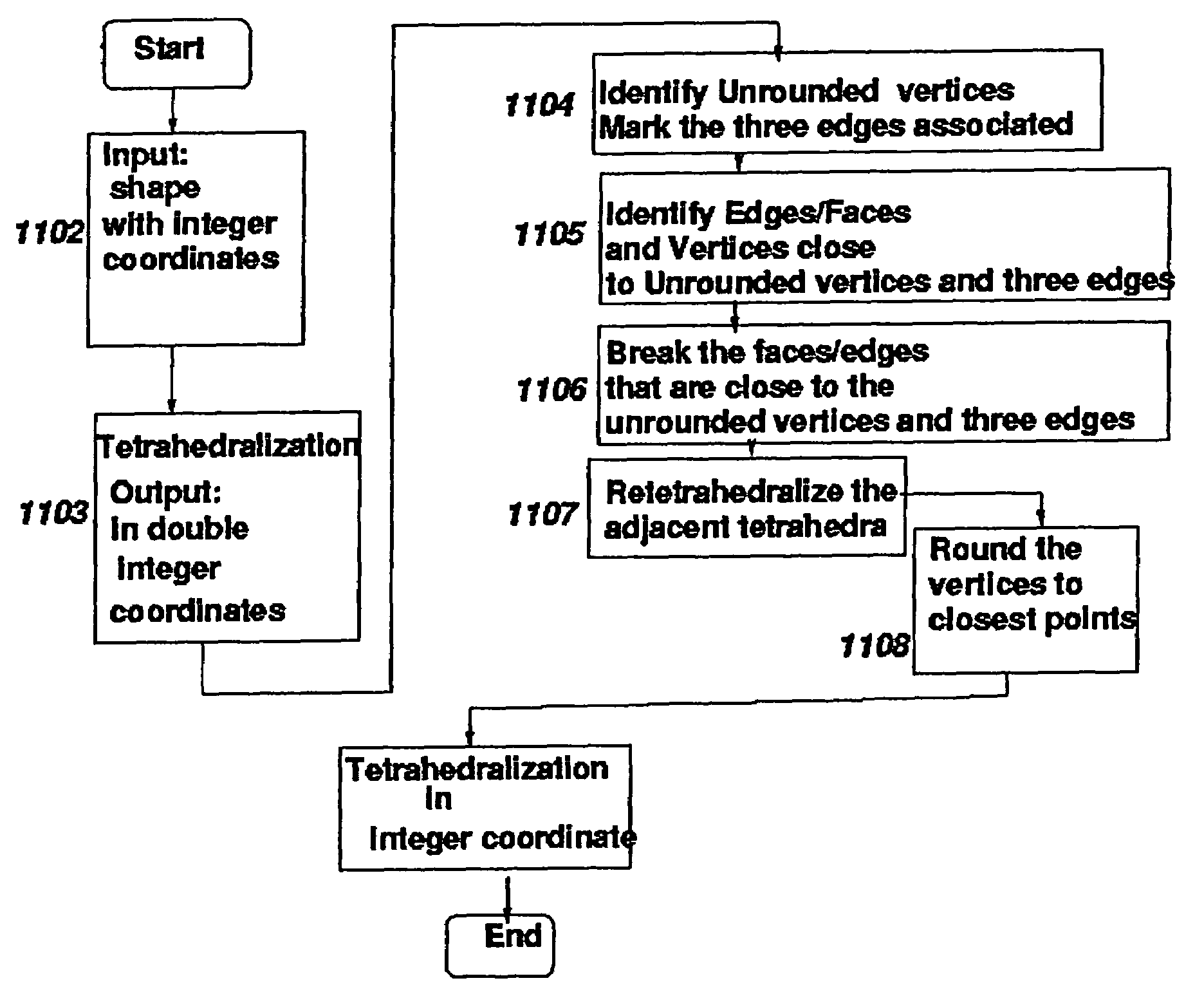
ActiveUS7075532B2Avoid volumePrevent inconsistency in processDetecting faulty computer hardwareCathode-ray tube indicatorsTopological consistencyElement analysis
A tetrahedralization and triangulation method used with the proximity based rounding method to satisfy topological consistency of tetrahedralization with the bounded precision of a digital computer is described. Tetrahedralization is applied to a VLSI design, and more specifically for solving Maxwell's equation to extract parasitic capacitances and 3-D optical proximity correction applications. The exactness of solving Maxwell's equation and finite element analysis depends on the correctness of the topological properties of the tetrahedralization. Among the important aspects of the correctness of the topological properties is the absence of spurious intersection of two or more tetrahedra. In a typical digital computer, numbers are represented using finite sized words. Round-off errors occur when a long number is represented using the finite word size. As a result, tetrahedralization loses its topological consistency. The proximity based rounding method finds potential locations of spurious intersections and pre-corrects these locations to avoid the generation of any topological inconsistencies.
Owner:TWITTER INC
Method for remodeling medium objects by electromagnetic inverse scattering
InactiveCN105677937AMesh quality requirements are lowImprove solution efficiencySpecial data processing applicationsIterative methodologyMaxwell's equations
The invention relates to a method for remodeling medium objects by electromagnetic inverse scattering. The method comprises following steps: utilizing Maxwell's equations and constitutive equations to deduce forward and reverse integral equations for electromagnetic scattering; guessing the shape of an object to be detected and discretizing integral equations with a method in order to obtain matrix equations; utilizing a Gauss-Newton minimization method to regularize ill-conditioned equations during the reverse scattering process following discretization, wherein used regularized parameters are obtained by a multiplicative regularization method; and adopting a born iterative method to carry out iteration and obtaining wave number of detected mediums at the needed precision in order to achieve the objective of remodeling mediums.The method helps to avoid the problem in the conventional method that parameters are obtained by a lot of experiment data so that solving efficiency is increased.
Owner:TONGJI UNIV
Electromagnetic Imaging By Four Dimensional Parallel Computing
ActiveUS20100224362A1Reduce the differenceSurveyFluid removalControlled source electro-magneticFourth Dimension
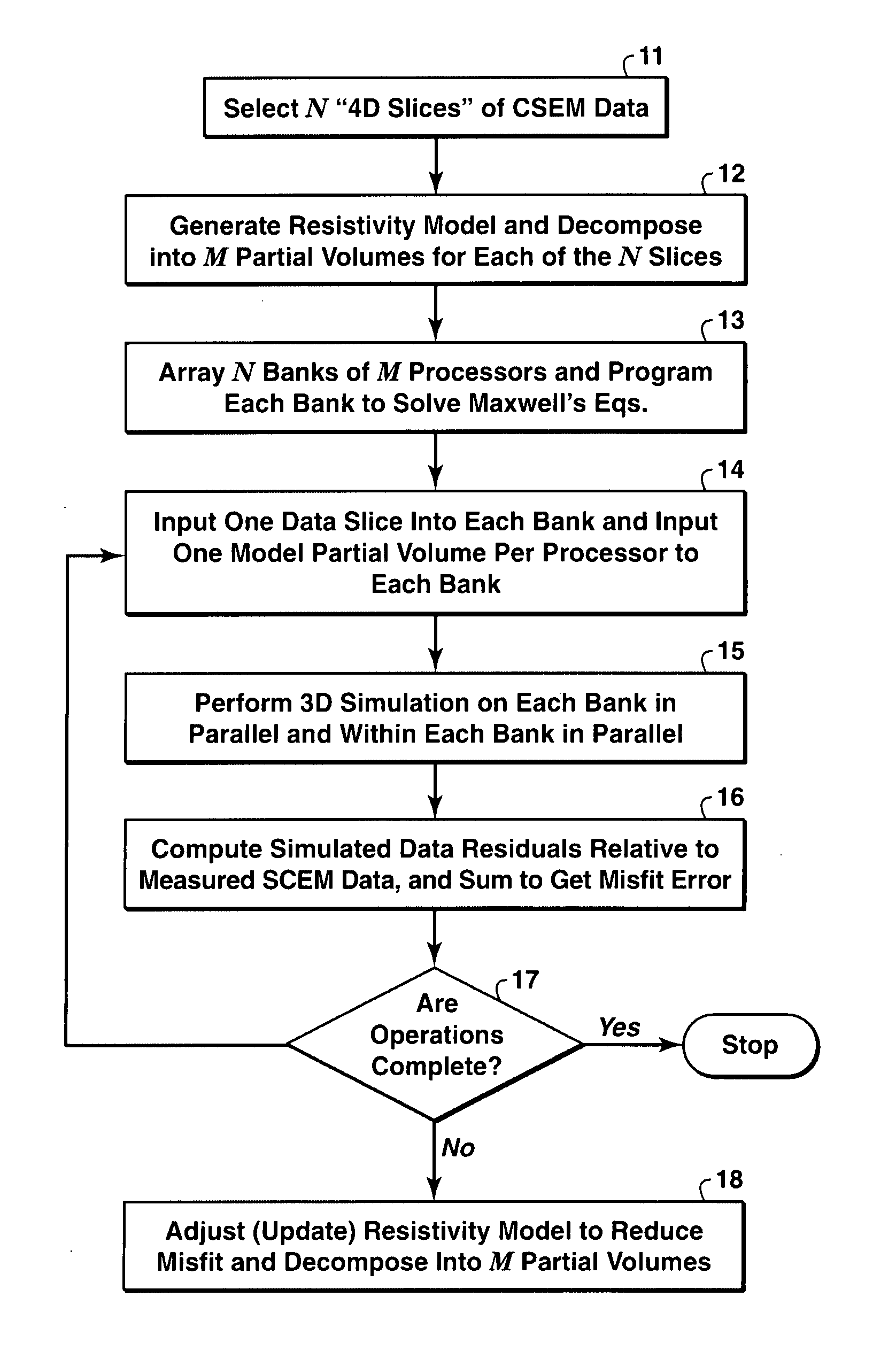
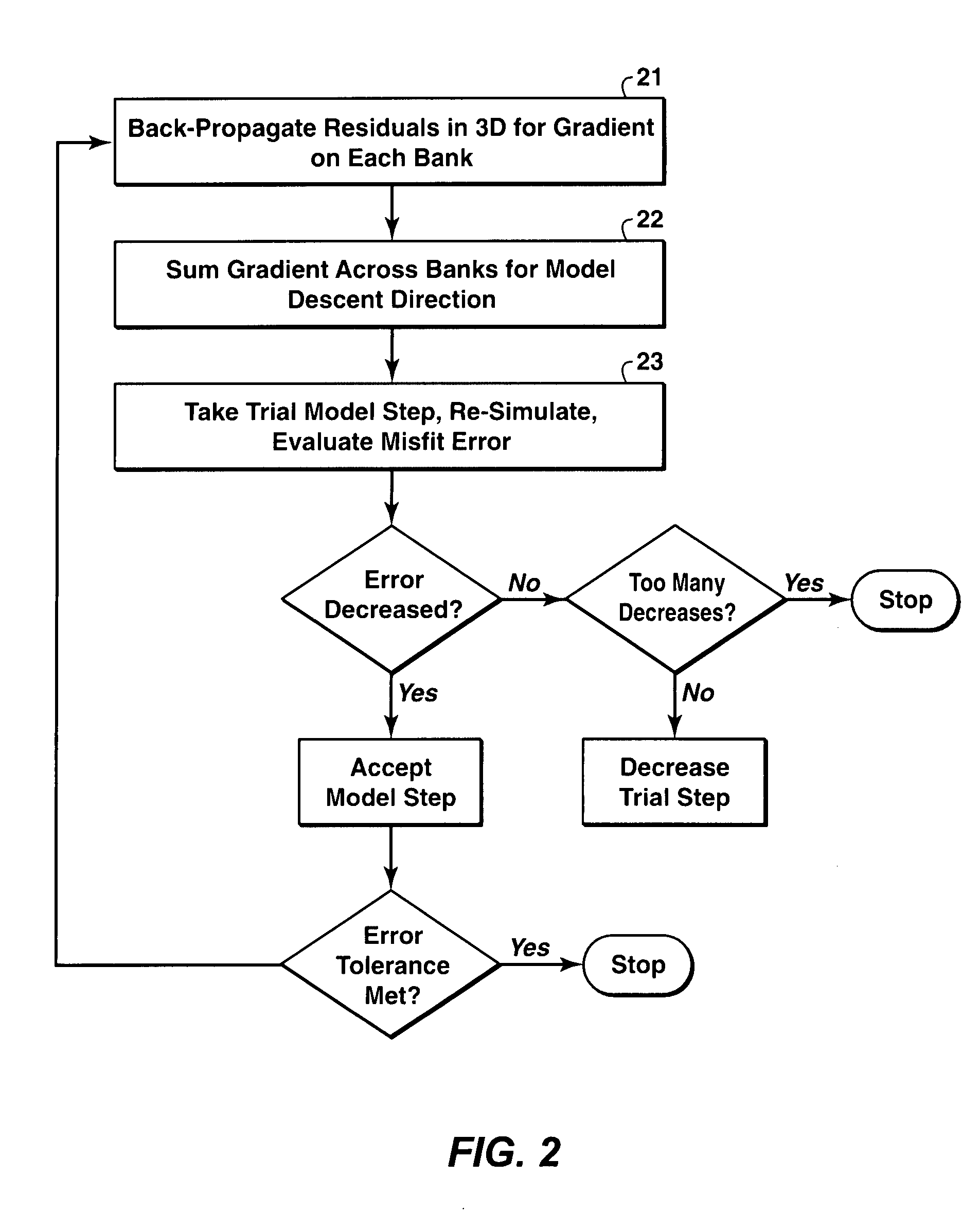
Method for organizing computer operations on a system of parallel processors to invert electromagnetic field data (11) from a controlled-source electromagnetic survey of a subsurface region to estimate resistivity structure (12) within the subsurface region. Each data processor in a bank of processors simultaneously solves Maxwell's equations (13) for its assigned geometrical subset of the data volume (14). Other computer banks are simultaneously doing the same thing for data associated with a different source frequency, position or orientation, providing a “fourth dimension” parallelism, where the fourth dimension requires minimal data passing (15). In preferred embodiments, a time limit is set after which all processor calculations are terminated, whether or not convergence has been reached.
Owner:EXXONMOBIL UPSTREAM RES CO
Caching of intra-layer calculations for rapid rigorous coupled-wave analyses
InactiveUS20050068545A1Reduce computing timeRadiation pyrometrySpectrum investigationAngle of incidenceAtmospheric layer
The diffraction of electromagnetic radiation from periodic grating profiles is determined using rigorous coupled-wave analysis, with intermediate calculations cached to reduce computation time. To implement the calculation, the periodic grating is divided into layers, cross-sections of the ridges of the grating are discretized into rectangular sections, and the permittivity, electric fields and magnetic fields are written as harmonic expansions along the direction of periodicity of the grating. Application of Maxwell's equations to each intermediate layer, i.e., each layer except the atmospheric layer and the substrate layer, provides a matrix wave equation with a wave-vector matrix A coupling the harmonic amplitudes of the electric field to their partial second derivatives in the direction perpendicular to the plane of the grating, where the wave-vector matrix A is a function of intra-layer parameters and incident-radiation parameters. W is the eigenvector matrix obtained from wave-vector matrix A, and Q is a diagonal matrix of square roots of the eigenvalues of the wave-vector matrix A. The requirement of continuity of the fields at boundaries between layers provides a matrix equation in terms of Wand Q for each layer boundary, and the solution of the series of matrix equations provides the diffraction reflectivity. Look-up of W and Q, which are precalculated and cached for a useful range of intra-layer parameters (i.e., permittivity harmonics, periodicity lengths, ridge widths, ridge offsets) and incident-radiation parameters (i.e., wavelengths and angles of incidence), provides a substantial reduction in computation time for calculating the diffraction reflectivity.
Owner:TOKYO ELECTRON US HOLDINGS INC
Method and system of computing and rendering the nature of the excited electronic states of atoms and atomic ions
InactiveUS7689367B2Chemical property predictionRadiation/particle handlingDisplay deviceMaxwell's equations
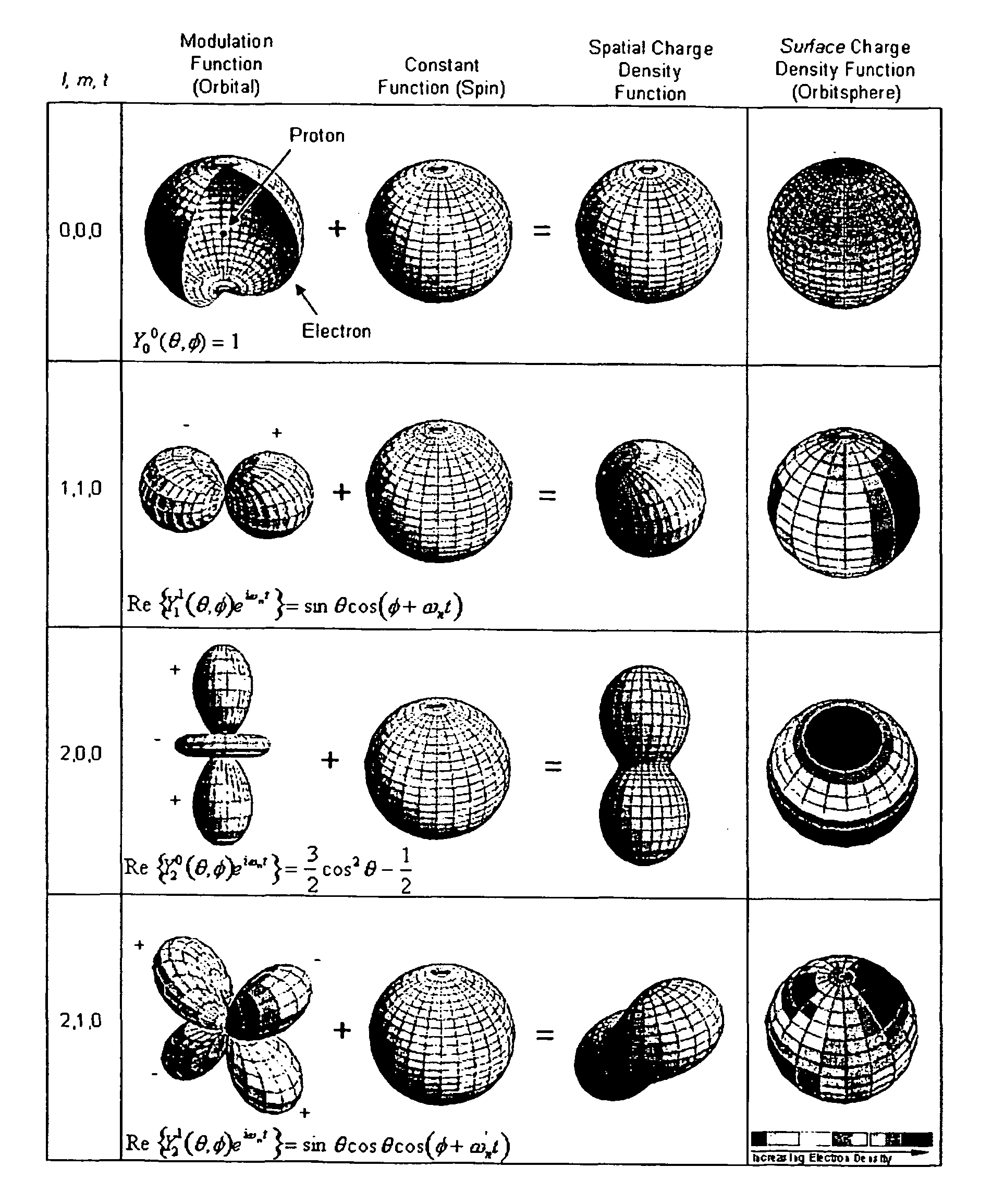
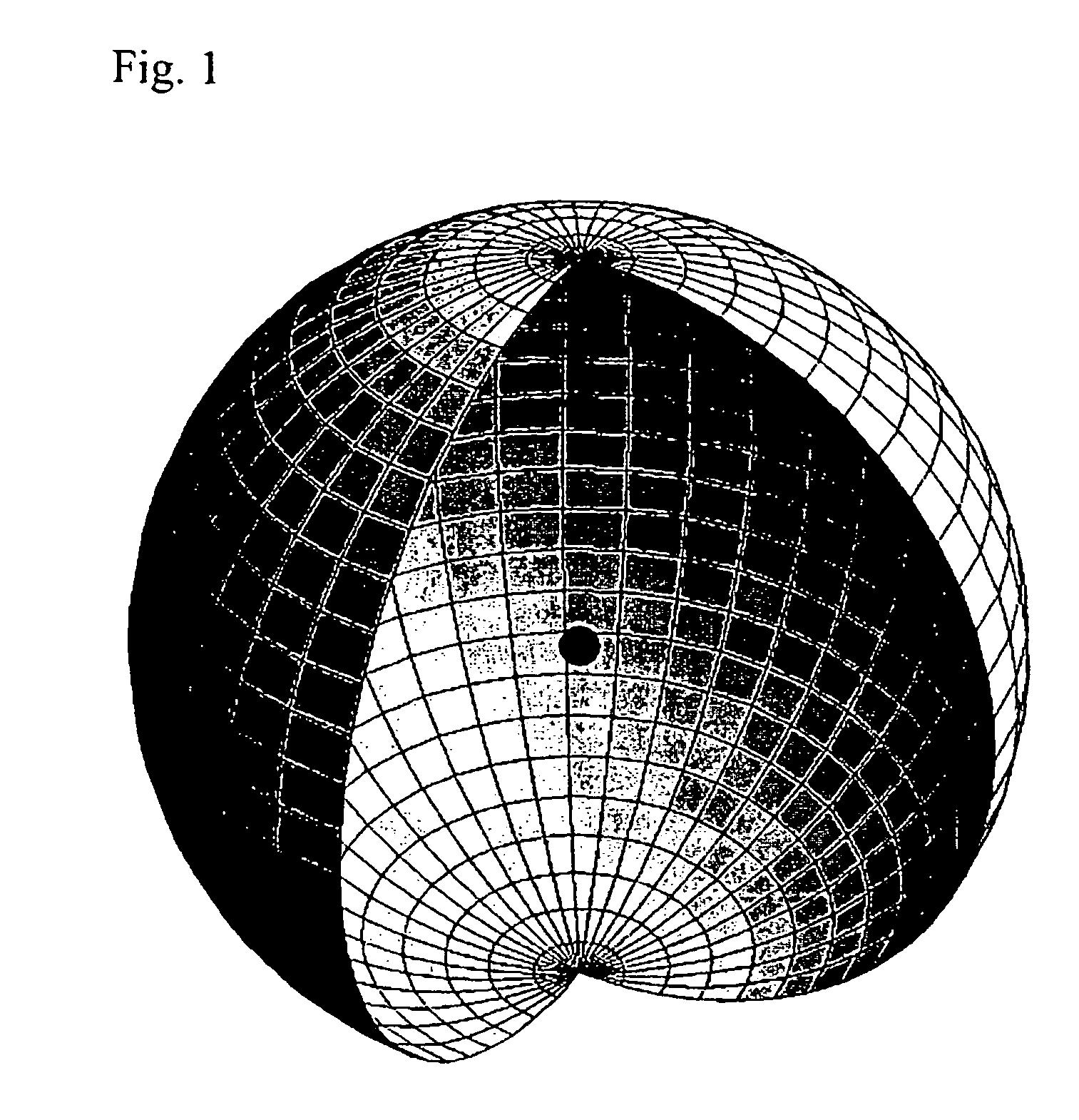
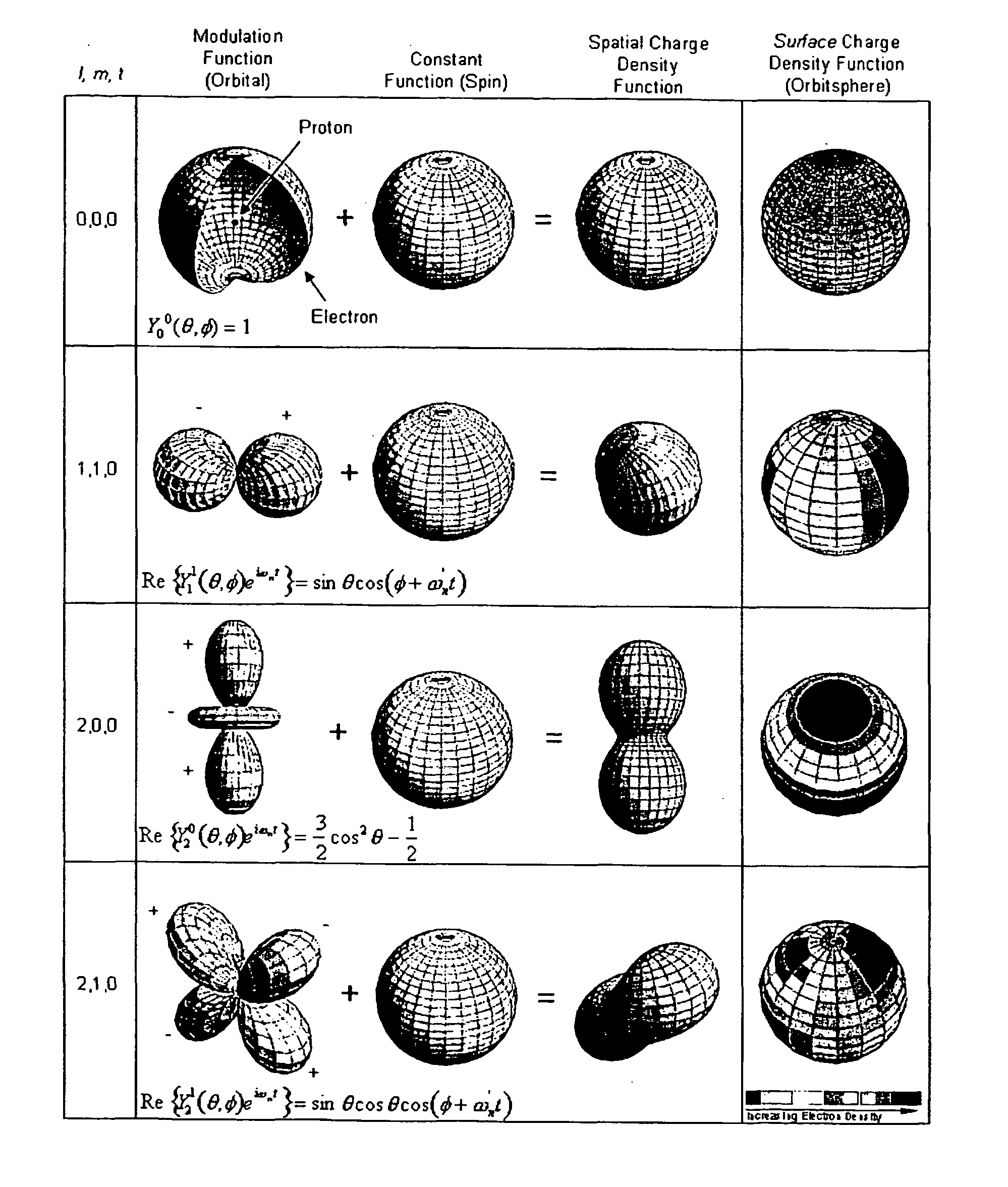
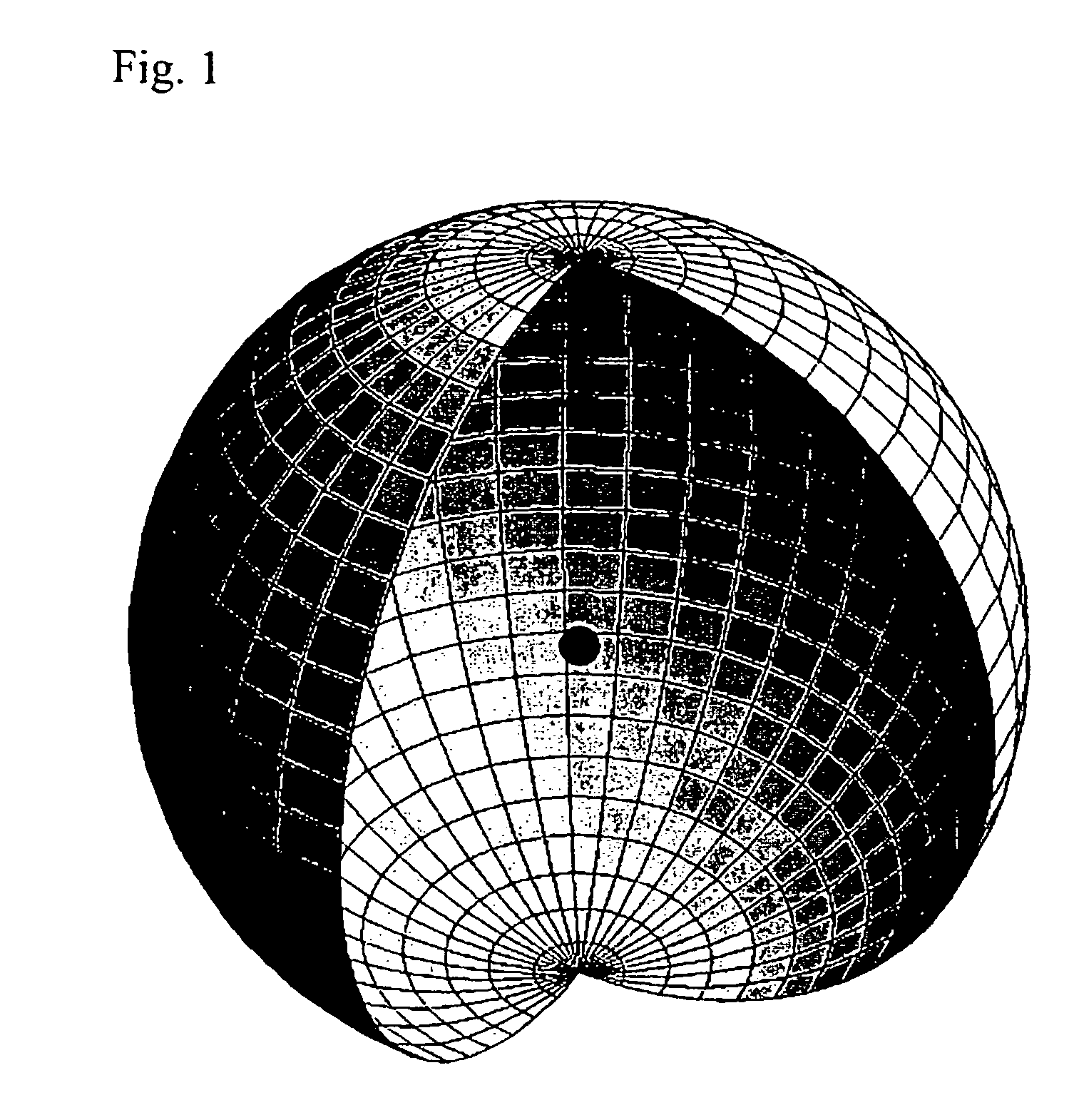
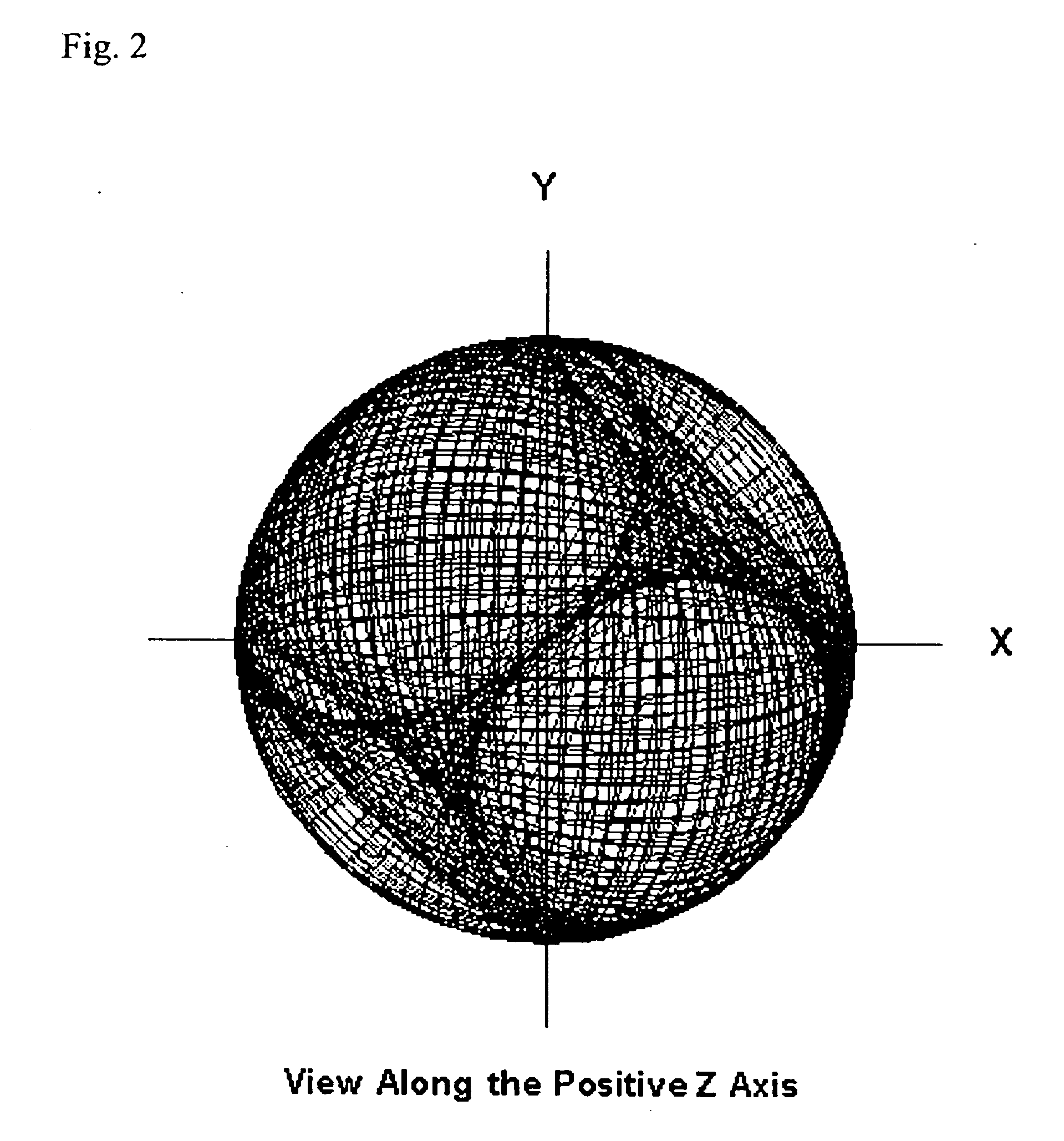
A method and system of physically solving the charge, mass, and current density functions of excited-state atoms and atomic ions using Maxwell's equations and computing and rendering the nature of excited-state electrons using the solutions. The results can be displayed on visual or graphical media. The display can be static or dynamic such that electron spin and rotation motion can be displayed in an embodiment. The displayed information is useful to anticipate reactivity and physical properties. The insight into the nature of excited-state electrons can permit the solution and display of those of other atoms and atomic ions and provide utility to anticipate their reactivity and physical properties as well as spectral absorption and emission to lead to new optical materials and light sources.
Owner:BRILLIANT LIGHT POWER
Electric dipole source three-dimensional time domain finite difference direct interpretation imaging method
InactiveCN104408021AFlexible width adjustmentRich low frequency signalComplex mathematical operationsICT adaptationOcean bottomMaxwell's equations
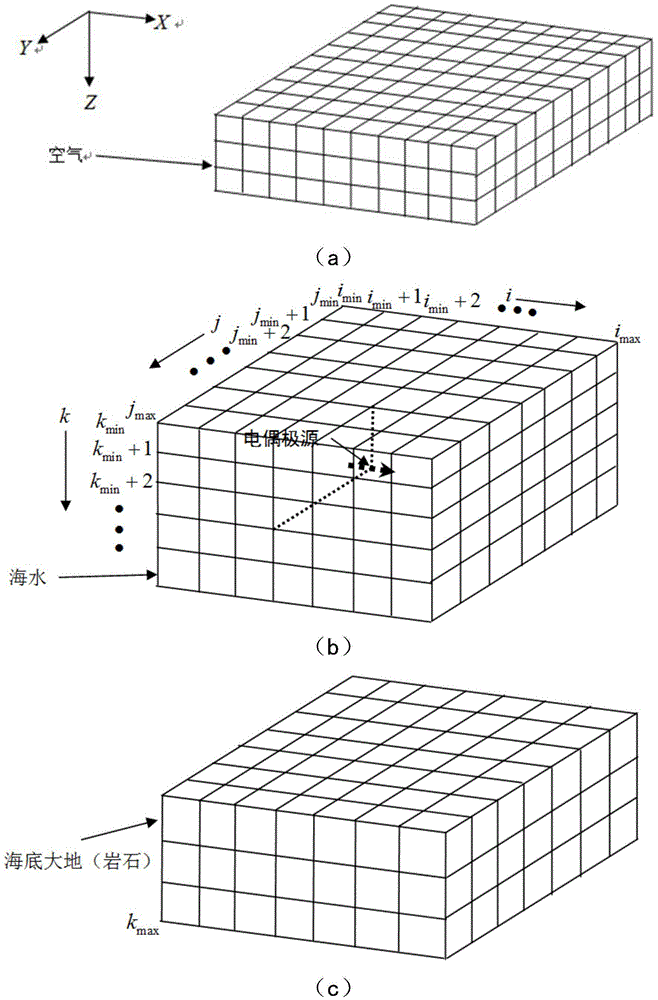
The invention relates to an electric dipole source three-dimensional time domain finite difference direct interpretation imaging method. The method includes the steps of loading Gaussian pulses on an electric dipole source, establishing Maxwell equations and constitutive equations for the ocean air space, the seawater space and the seabed ground space, conducting uniform mesh generation on prism object models of the three spaces, obtaining difference equations of seawater and the seabed ground through a time domain finite difference method according to meshes obtained through mesh generation by consuming that the conductivities and the magnetic conductivities of all the meshes obtained through mesh generation are unchanged, processing the Maxwell equations of ocean air through analysis solutions, calculating the electromagnetic field of the air above the sea surface, processing the boundary conditions of the generation space, setting stabilization conditions, solving the established difference equations through the combination with the processing results of the boundary conditions and the set stability conditions, and obtaining the distribution of the electromagnetic field of the seawater and the seabed ground at any moment.
Owner:CHINA NAT OFFSHORE OIL CORP +2
Microwave passive circuit electromagnetic heat integral analysis method based on time domain spectrum element method
ActiveCN104050307AGood mannersQuickly obtain temperature distributionSpecial data processing applicationsMaxwell's equationsEngineering
The invention discloses a microwave passive circuit electromagnetic heat integral analysis method based on a spectrum element method. According to the method, firstly, a time domain spectrum element method is adopted for solving maxwell's equations, the instantaneous electric field and magnetic field distribution of a circuit under the effect of high-power pulses is worked out, and the electromagnetic loss at the current moment is obtained. If all of the electromagnetic loss inside a mold is converted into heat energy, the obtained heat energy is substituted into a heat conduction equation, and the temperature distribution conditions of each point at the current moment are obtained. Electricity characteristic parameters of materials at a next moment are obtained by utilizing a relational expression of dielectric parameters along with the temperature change, an electromagnetic field equation is calculated again, and the electromagnetic loss is obtained. The operation is repeatedly cycled in such a way until the preset heating time is completed. Through the electromagnetic heat integral analysis, the distribution condition of the temperature inside the mold along the time change when a filter receives the effect of different pulses can be clearly obtained, the modeling is flexible, the subdivision is convenient, formed matrixes have good sparsity, and the solving efficiency is higher.
Owner:NANJING UNIV OF SCI & TECH
Method and apparatus for optically measuring the topography of nearly planar periodic structures
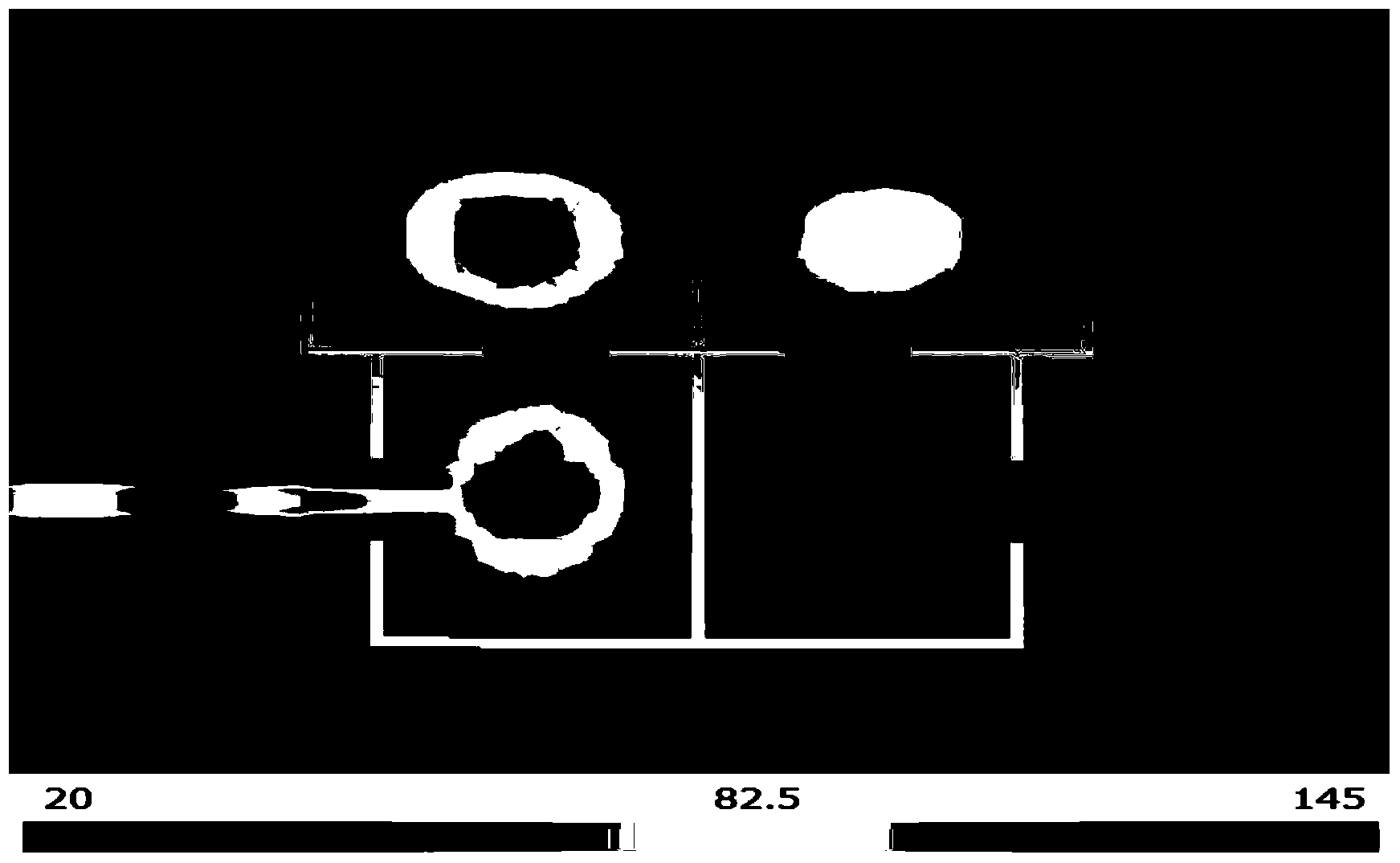
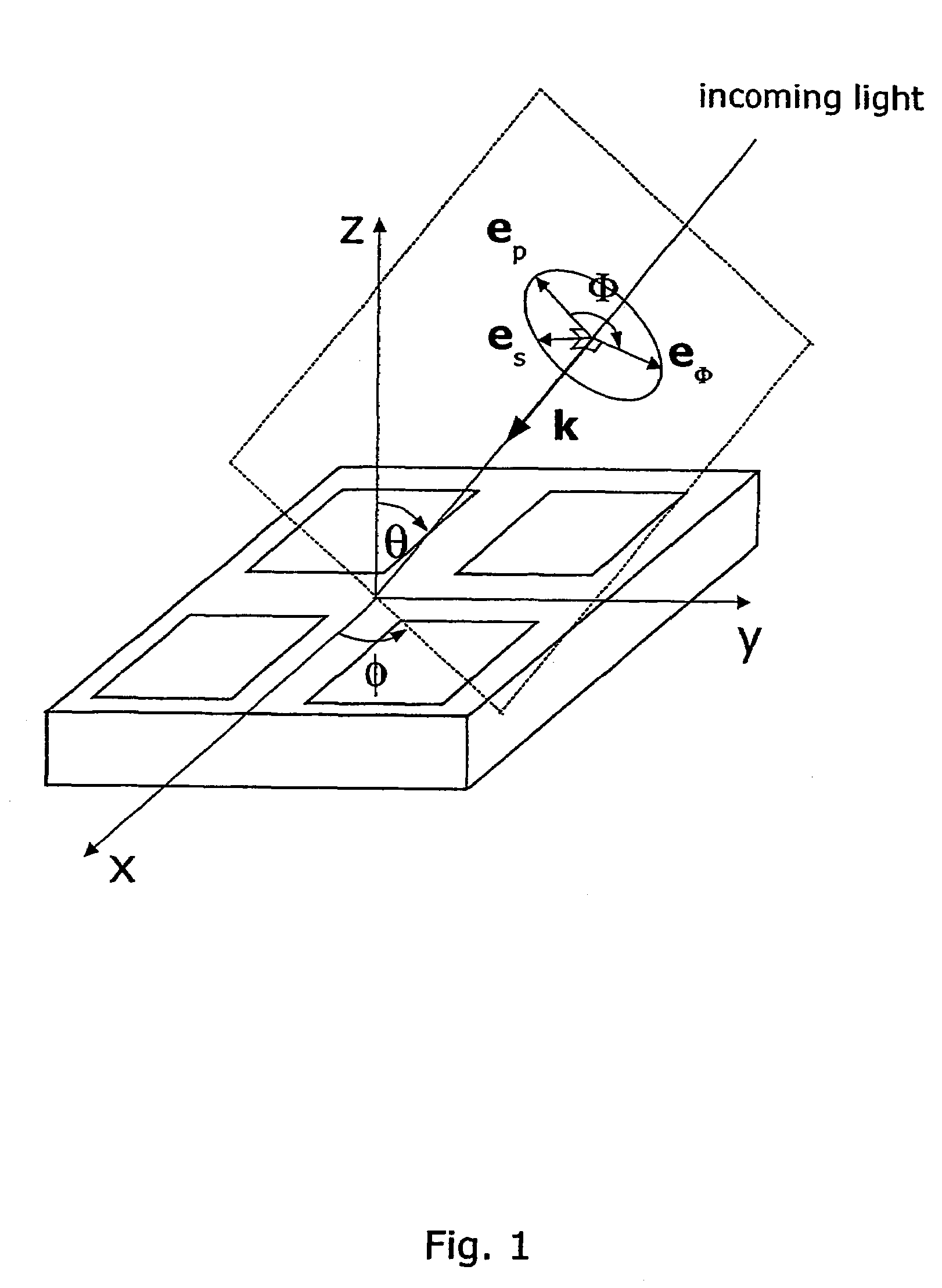
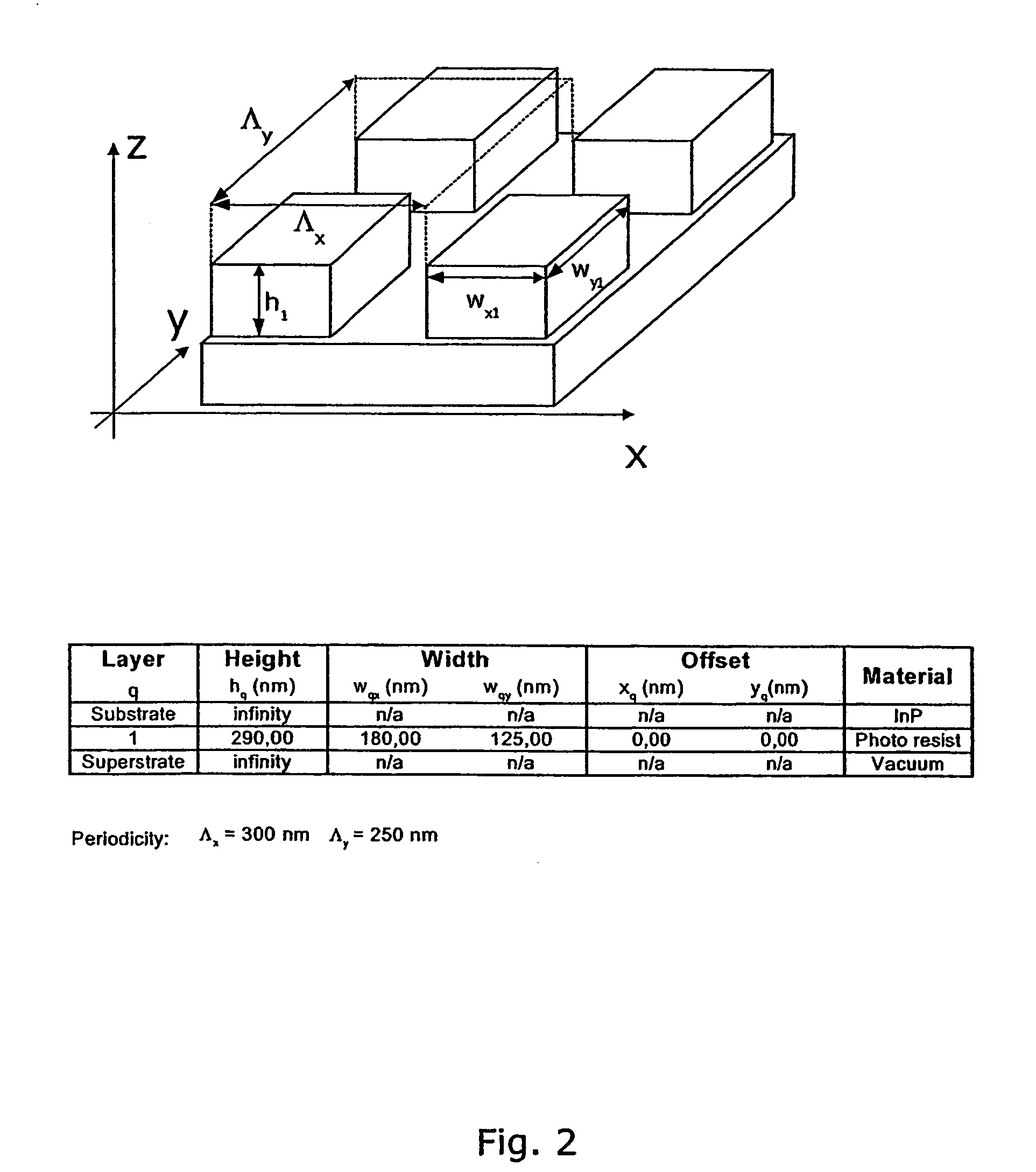
InactiveUS7321433B2Radiation pyrometryAmplifier modifications to reduce noise influenceDiffraction orderMaxwell's equations
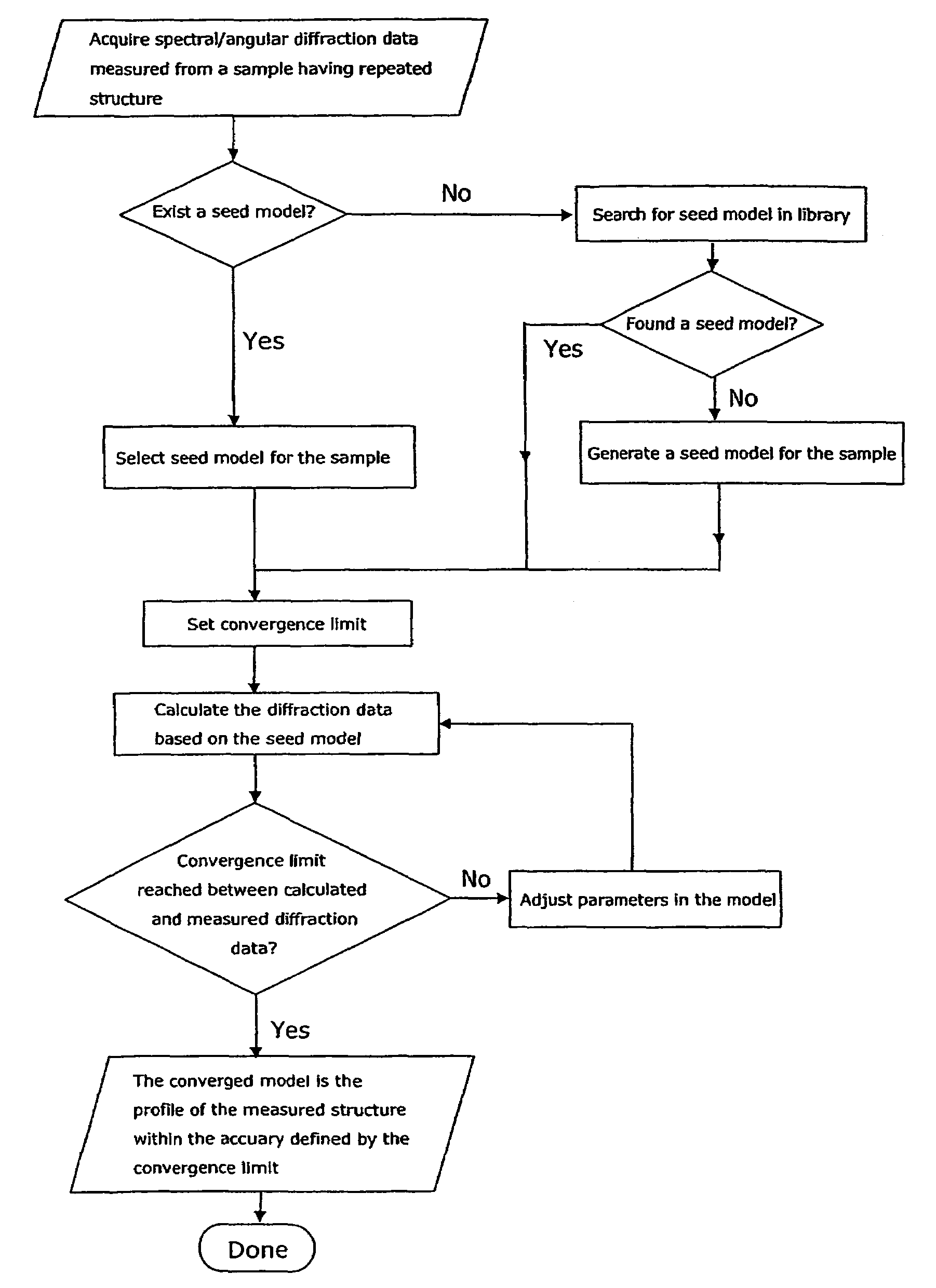
The present invention discloses a non-destructive method and apparatus for measuring the 3D topography of a sample having periodic microstructure deposited onto the surface, or deposited onto a film, or buried into the film or sample. In particular, the present invention relates to an optical system and method utilizing polarized light beam, diffracted from the repeated structure, to measure its spatial geometry giving parameters such as profile height, profile widths, sidewall angles, and arbitrary profile shape. The optical system employs a broadband or semi-monochromatic light source to produce a light beam that is polarized and focused onto the periodic structure being measured. The focused beam consists of a whole range of illumination angles that is provided to the structure simultaneously. Transmitted or reflected diffracted light generated by the interaction of the light with the periodic structure is collected by an imaging detector system. The detector records the diffraction light irradiance resolved into illumination angles, diffraction orders and wavelength. The data is applied to determine the geometrical profile of the periodic structure using a reconstruction algorithm that is based on comparisons between measured diffraction data and modeled diffraction irradiance of a profile model using Maxwell's equations. The reconstruction of the profile is performed by iterative adjustments of a profile seed model until the modeled diffraction irradiance matches the measured data within a predefined convergence tolerance.
Owner:DANSK FUNDAMENTAL METROLOGI
Method and device for processing a multi-channel measurement of magnetic fields
ActiveUS7463024B2Reduce stepsQuick calculationMagnitude/direction of magnetic fieldsMeasurement deviceMaxwell's equations
Owner:MEGIN OY
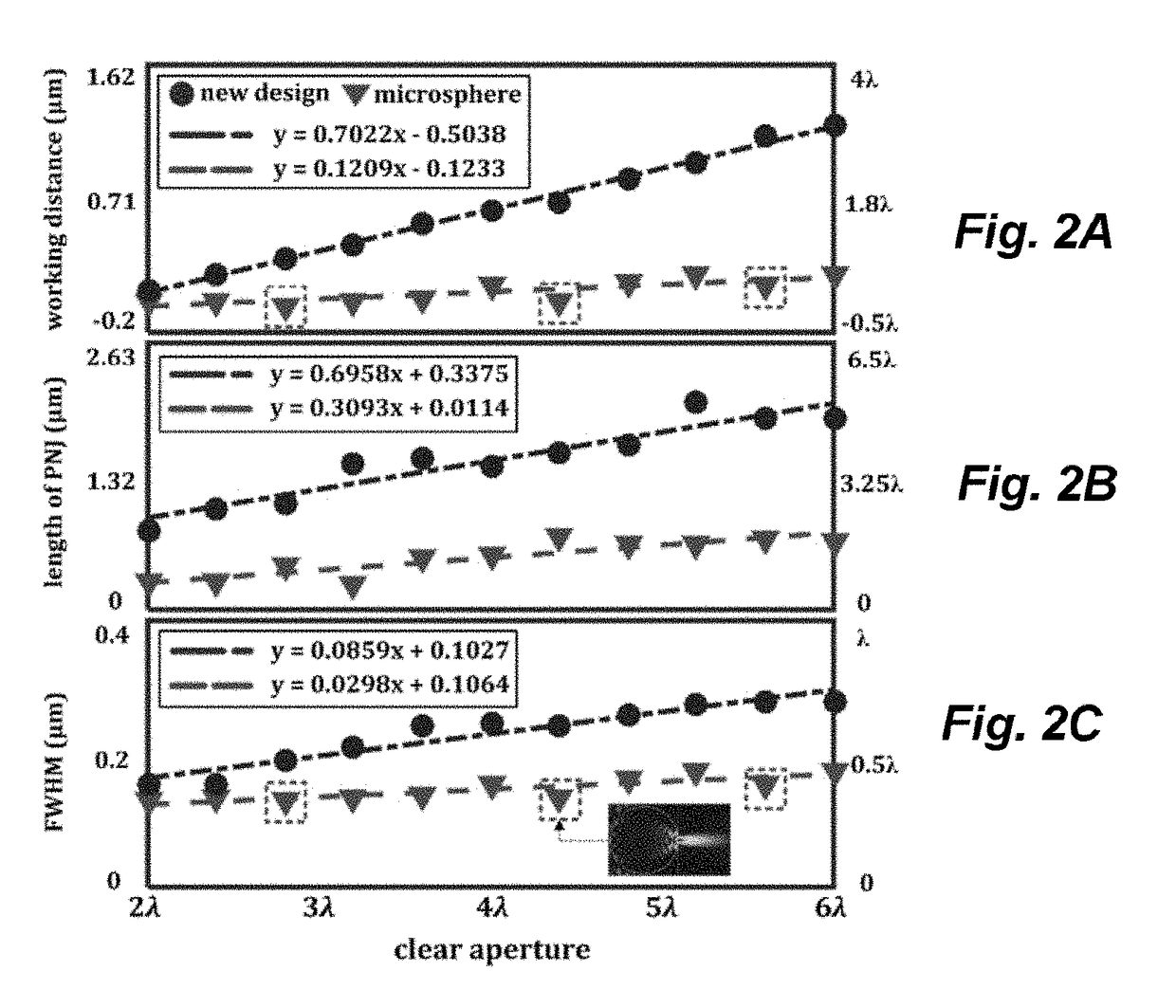
Spatial Control of the Optical Focusing Properties of Photonic Nanojets
Methods and apparatus for concentrating light into a specified focal volume and for collecting light from a specified volume. Incident light is coupled through a plurality of successive transmissive asymmetric microstructure elements. The succession of transmissive asymmetric microstructure elements may be designed by representing an electromagnetic field as a linear combination of eigenmodes of one of the succession of transmissive asymmetric microstructure elements. The asymmetric microstructure elements are represented as a plurality of mesh lattice units and eigenmode solutions to Maxwell's equations are obtained for each mesh lattice unit subject to consistent boundary conditions. S-matrix formalism is employed to calculate a field output and weighting coefficients for the eigenmodes are selected to achieve a specified set of field output characteristics.
Owner:THE BOARD OF TRUSTEES OF THE UNIV OF ILLINOIS
Method for accurately calculating electromagnetic scattering of bianisotropic medium ball
InactiveCN103235888AElectromagnetic scattering appliesSpecial data processing applicationsMaxwell's equationsCondensed matter physics
The invention provides a method for accurately calculating electromagnetic scattering of a bianisotropic medium ball. The method comprises the steps of 1, using passive maxwell's equations and an intrinsic equation of a bianisotropic medium to deduce a differential equation of the magnetic induction intensity B; 2, expressing factors related to the B in the differential equation in the form of spherical vector wave functions, then using orthogonality properties of spherical vector wave functions M and N to obtain a parameter-contained matrix equation, firstly, calculating parameters of the matrix equation under the condition that the matrix equation meets a non-zero solution, and then substituting parameters into the parameter-contained matrix equation to obtain the non-zero solution of the matrix equation; and 3, constructing a new function, expressing the magnetic induction intensity B again through the new function, then an electromagnetic field inside the medium ball is calculated, and substituting the electromagnetic field inside the medium ball and an incident electromagnetic field and a scattering electromagnetic field outside the ball into boundary conditions to obtain a scattering matrix. The method is applicable to solving of the electromagnetic scattering of the bianisotropic medium ball of the small electrical size.
Owner:HANGZHOU DIANZI UNIV
Method for determining earth vertical electrical anisotropy in marine electromagnetic surveys
InactiveCN101194262AElectric/magnetic detection for well-loggingSpecial data processing applicationsOnline and offlineMaxwell's equations
Oceanographic methods for judging the vertical electrical anisotropy of the Earth use offshore electromagnetic survey measurements (1). The method requires on-line and off-line data and includes at least one electromagnetic field component sensitive at least primarily to vertical resistivity, and another component at least primarily sensitive to horizontal resistivity (4). Using a horizontal electric dipole source, online Ez and offline Hz measurements are preferred. For horizontal magnetic dipole sources, online Hz and offline Ez are preferred. Magnetotelluric data can be replaced by controlled source data that is only sensitive to horizontal resistivity. Maxwell's equations are solved using forward modeling or by inversion using isotropic or anisotropic surface resistivity models.
Owner:EXXONMOBIL UPSTREAM RES CO
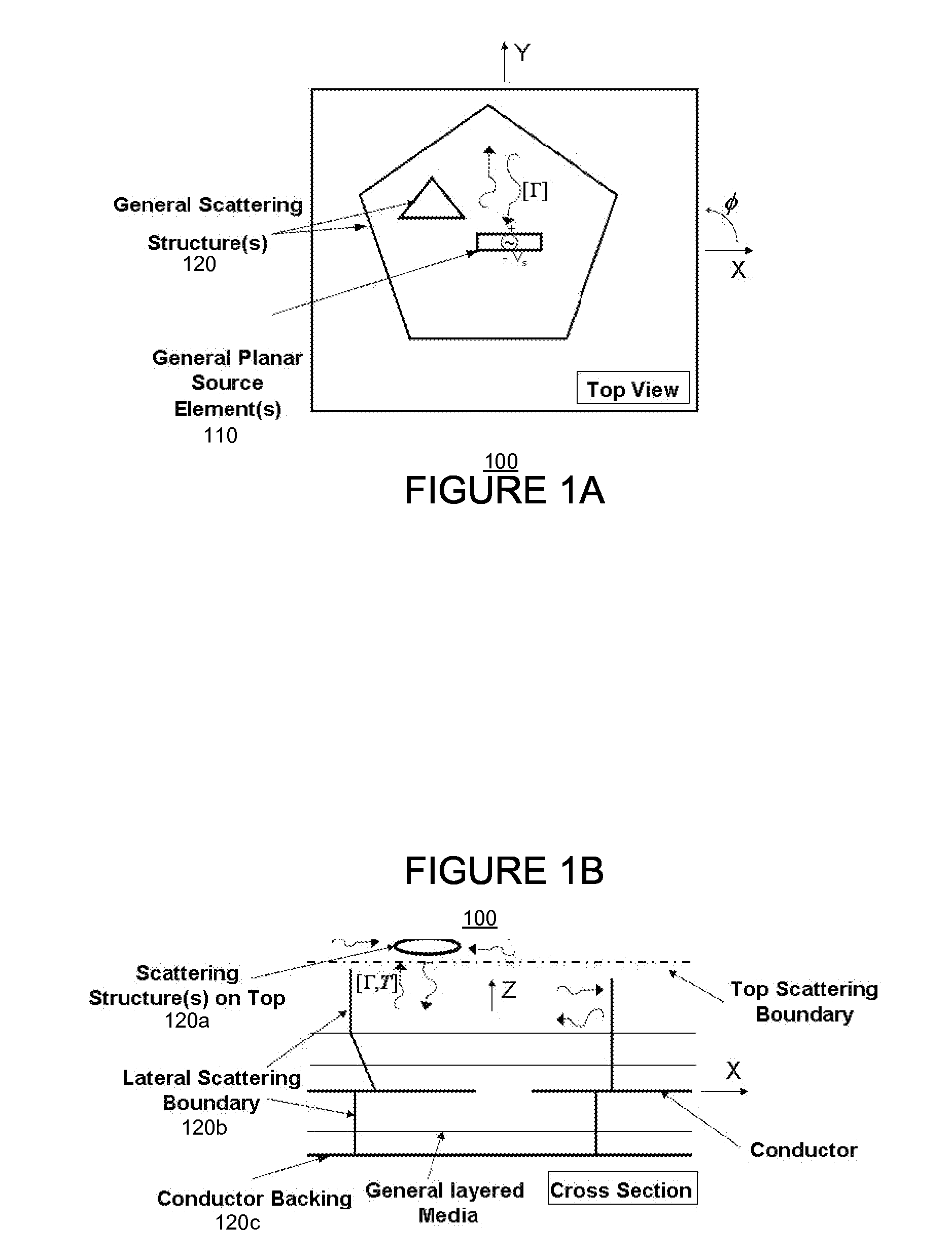
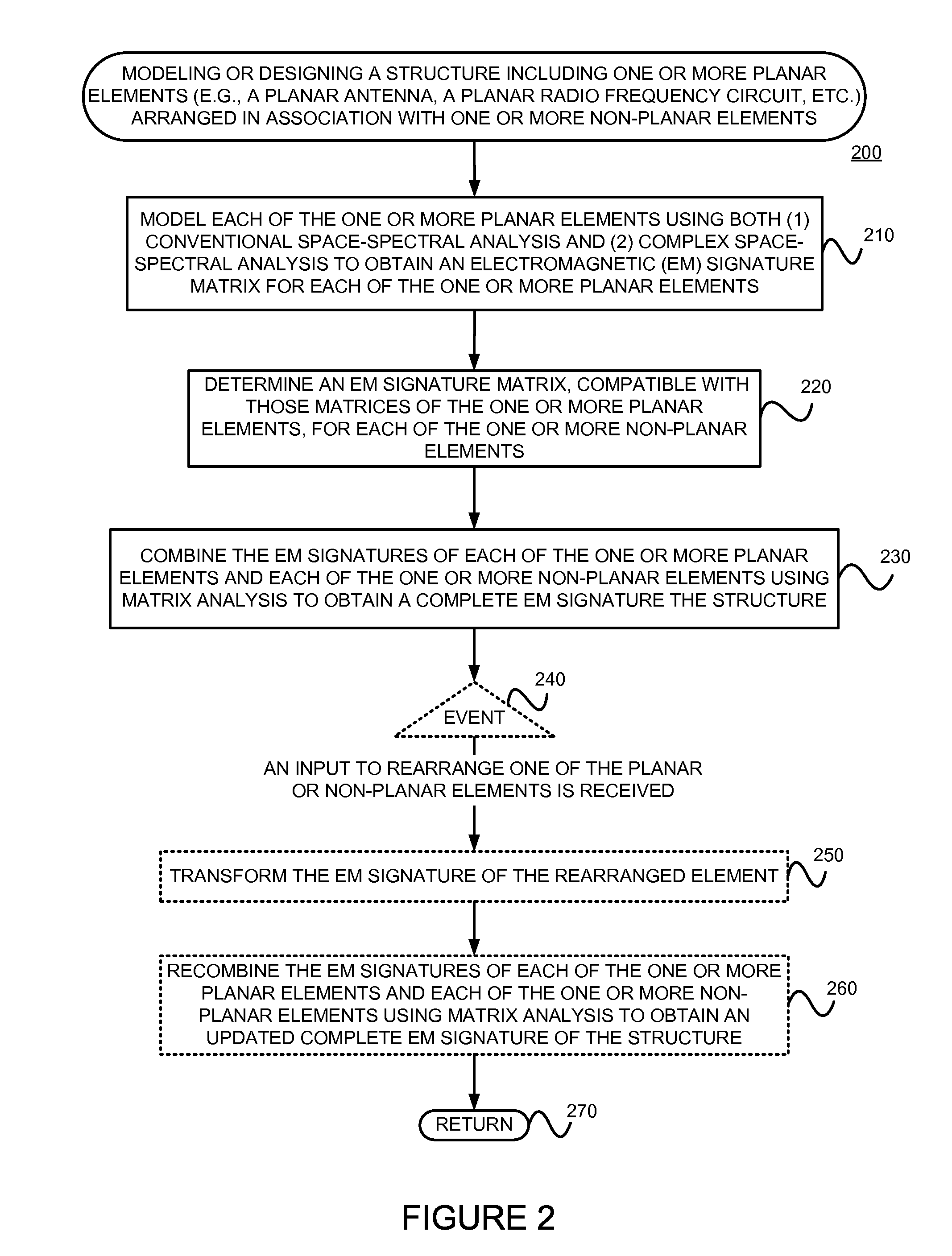
Modular modeling and design of antennas and radio frequency circuits that are arranged in a class of composite structural configurations
InactiveUS20130116980A1Computationally efficientComputer aided designSpecial data processing applicationsBrute forceModularity
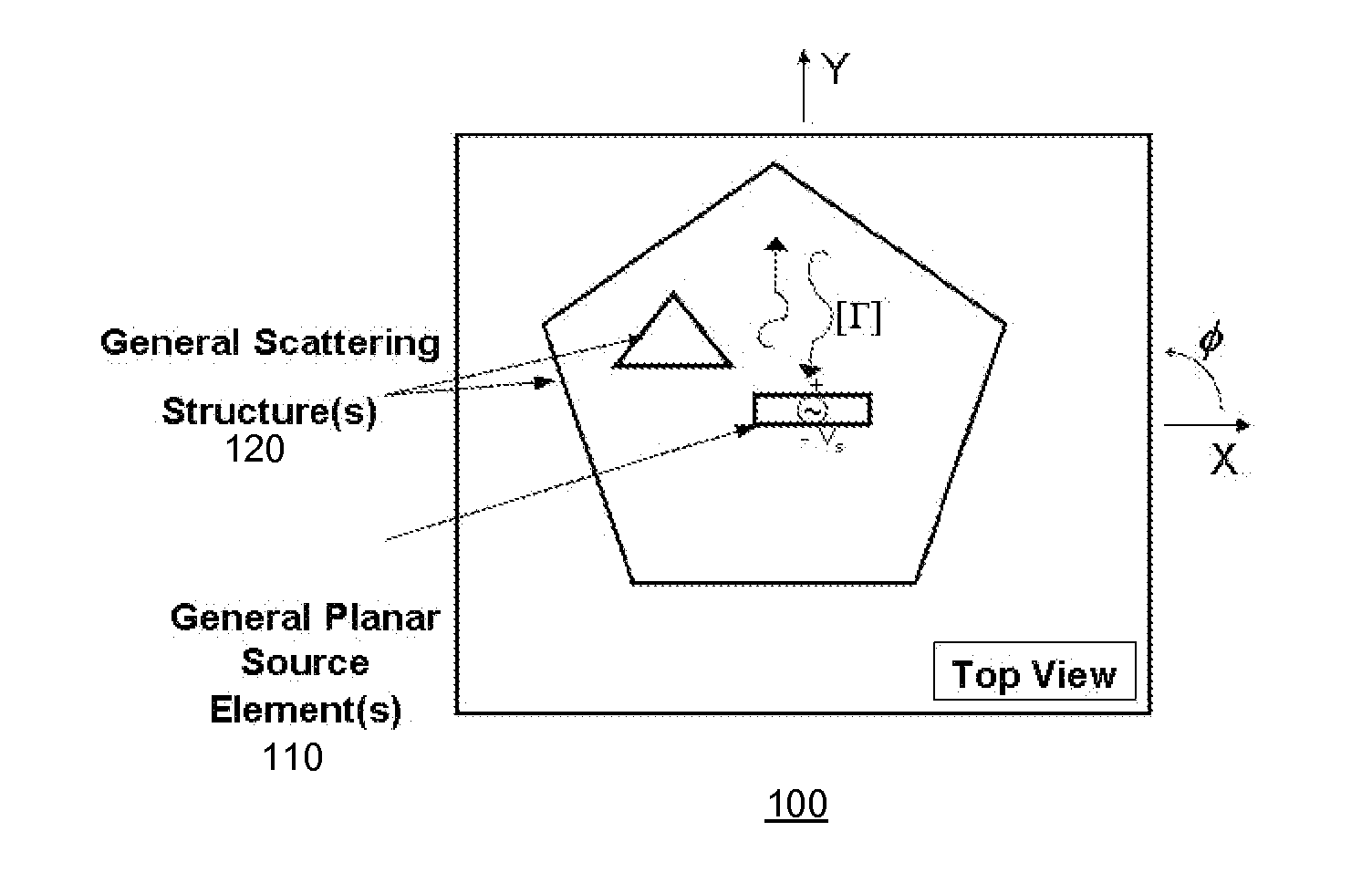
The problem of modeling and designing a structure including a planar element(s) (e.g., antenna, RF circuit, etc.) arranged in association with a non-planar element(s) (e.g., non-planar packaging, a non-planar scattering element, a complex meta material, a periodic array element, etc.), in a computationally efficient and rigorous manner is solved by (1) modeling each of the planar elements using both conventional space-spectral analysis and complex space-spectral analysis to obtain an electro-magnetic (EM) signature matrix for each planar element, (2) determining (e.g., using a brute force modeling based on Maxwell's equations, by measuring experimentally, or by reading one from a stored library) an EM signature matrix (e.g., reflection and scattering matrices) compatible with those of the planar elements, for each of the non-planar elements, and (3) combining the EM signatures of the elements using matrix analysis to obtain a complete EM signature the structure.
Owner:POLYTECHNIC INSTITUTE OF NEW YORK UNIVERSITY
System and method for identification of conductor surface roughness model for transmission lines
InactiveUS20140032190A1Computation using non-denominational number representationDesign optimisation/simulationElectrical conductorSurface roughness
A system and method for identification of conductor surface roughness model associated with a transmission line conductor is proposed. A network analyzer measures scattering parameters over a specified frequency band for at least two line segments of different length and substantially identical cross-section with investigated rough conductors. A first engine determines non-reflective (generalized) modal scattering parameters of the difference segment based on the measured scattering parameters of two line segments. A second engine computes generalized modal scattering parameters of the line difference segment by solving Maxwell's equations for geometry of the line cross-section with a given conductor surface roughness model. A third engine performs optimization by changing conductor surface roughness model parameters and model type until the computed and measured generalized modal scattering parameters match. The model that produces generalized modal S-parameters closest to the measured is the final conductor surface roughness model.
Owner:SIMBERIAN
Microwave component micro-discharge numerical simulation method based on GPU architecture
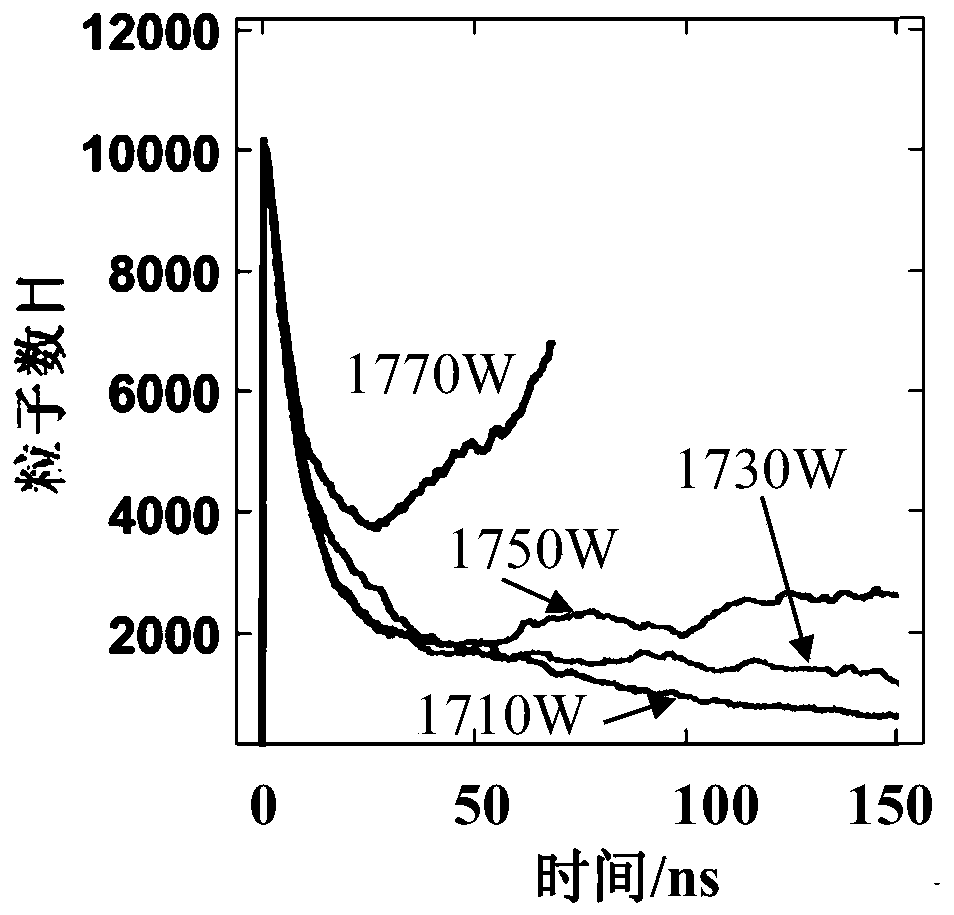
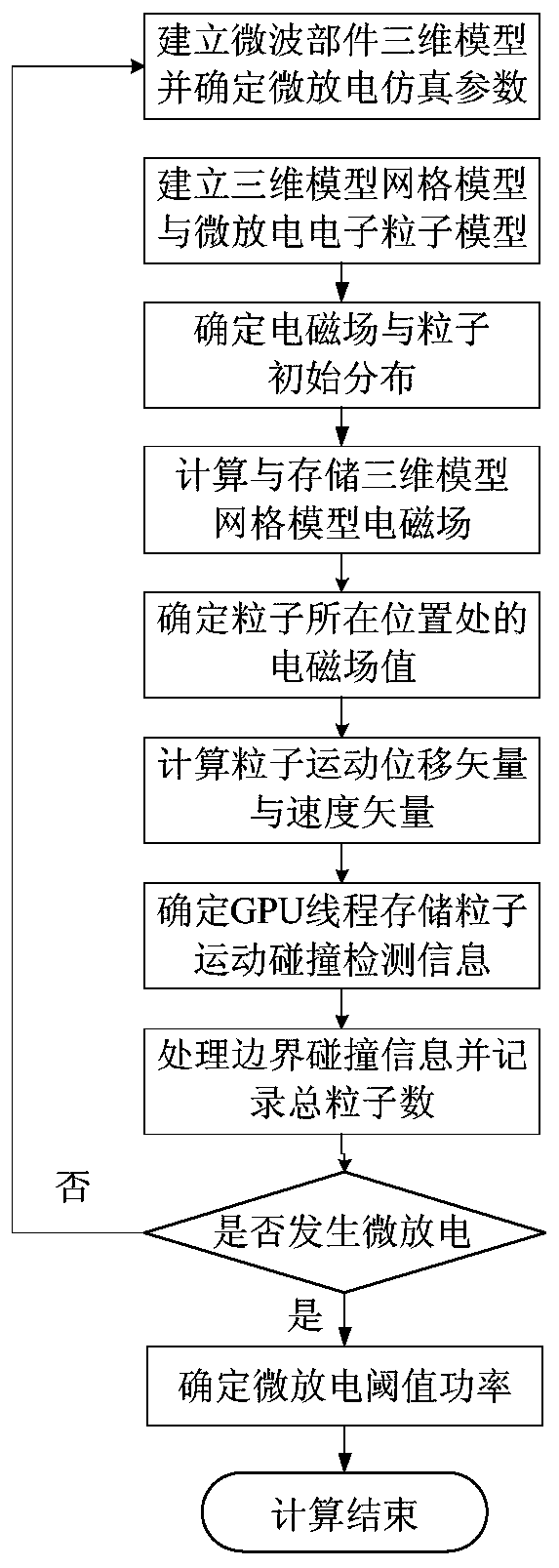
ActiveCN110442919ASimulation is fast and efficientReduce computing timeSpecial data processing applications3D modellingGrid basedMaxwell's equations
The invention relates to a microwave component micro-discharge numerical simulation method based on a GPU architecture, which comprises the following steps of: 1) establishing a three-dimensional model of a microwave component, determining a material of the three-dimensional model and secondary electron emission characteristic parameters of the material, and determining micro-discharge simulationparameters of the microwave component; 2) establishing a grid model of the microwave component three-dimensional model and a particle model of micro-discharge electrons; 3) determining initial distribution of an electromagnetic field and initial distribution of particles in the three-dimensional model grid model; 4) solving a Maxwell equation set in each small grid based on a GPU technology to iteratively update electromagnetic field distribution, and obtaining all electromagnetic field values of M time steps; and 5) solving the Lorentz force equation set to iteratively update the particle motion, obtaining the total particle number of each time step of the M time steps, completing the micro-discharge numerical simulation when the input power is P, and determining whether the micro-discharge occurs or not when the input power is P.
Owner:XIAN INSTITUE OF SPACE RADIO TECH
Label reception power prediction method of ultra high frequency (UHF) radio frequency identification (RFID) electronic toll collection (ETC) applications
ActiveCN106446733AImprove forecast accuracyImprove recognition rateSpecial data processing applicationsSensing by electromagnetic radiationMaxwell's equationsPlane equation
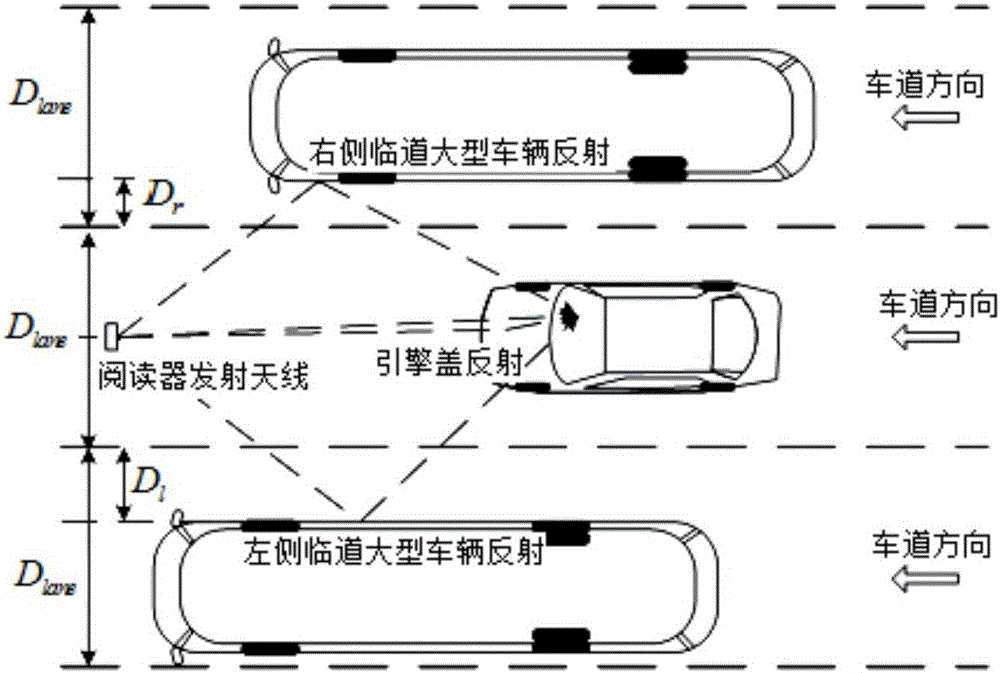
The present invention discloses a label reception power prediction method of UHF RFID ETC applications. The method comprises the steps of setting a reader antenna as a Cartesian coordinate origin, setting the Cartesian coordinate of a label as unknown, and solving a first-order reflection surface equation by the application scene geometrical parameters and the geometrical relationships, namely a plane equation of an automobile engine hood plane, a left temporary road vehicle right side surface and a right temporary road left side surface; by a free space radio wave propagation formula, calculating a visual range electric field intensity vector from the reader antenna to the label; separately calculating the coordinates of the reflection points on the above reflection surface; by a first-order reflection matrix equation of an electromagnetic wave, separately calculating the electric field intensity vectors of an incident wave and a reflection wave arriving at the label at the reflection surface; solving the label electric field vector sum, a label chip antenna port matching coefficient and a polarization matching coefficient, and finally obtaining a label reception power calculation result in the space. The label reception power prediction method of the present invention can obtain a higher prediction precision than the conventional lognormal model and Leslie Model, and obtain the prediction speed more convenient and faster than a commercial electromagnetic calculation software based on Maxwell's equations.
Owner:HUNAN UNIV
Method and System of Computing and Rendering the Nature of the Excited Electronic States of Atoms and Atomic Ions
InactiveUS20080034287A1Chemical property predictionRadiation/particle handlingDisplay deviceMaxwell's equations
A method and system of physically solving the charge, mass, and current density functions of excited-state atoms and atomic ions using Maxwell's equations and computing and rendering the nature of excited-state electrons using the solutions. The results can be displayed on visual or graphical media. The display can be static or dynamic such that electron spin and rotation motion can be displayed in an embodiment. The displayed information is useful to anticipate reactivity and physical properties. The insight into the nature of excited-state electrons can permit the solution and display of those of other atoms and atomic ions and provide utility to anticipate their reactivity and physical properties as well as spectral absorption and emission to lead to new optical materials and light sources.
Owner:BRILLIANT LIGHT POWER
Features
- R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
Why Patsnap Eureka
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com