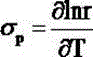Patents
Literature
316 results about "Specific impulse" patented technology
Efficacy Topic
Property
Owner
Technical Advancement
Application Domain
Technology Topic
Technology Field Word
Patent Country/Region
Patent Type
Patent Status
Application Year
Inventor
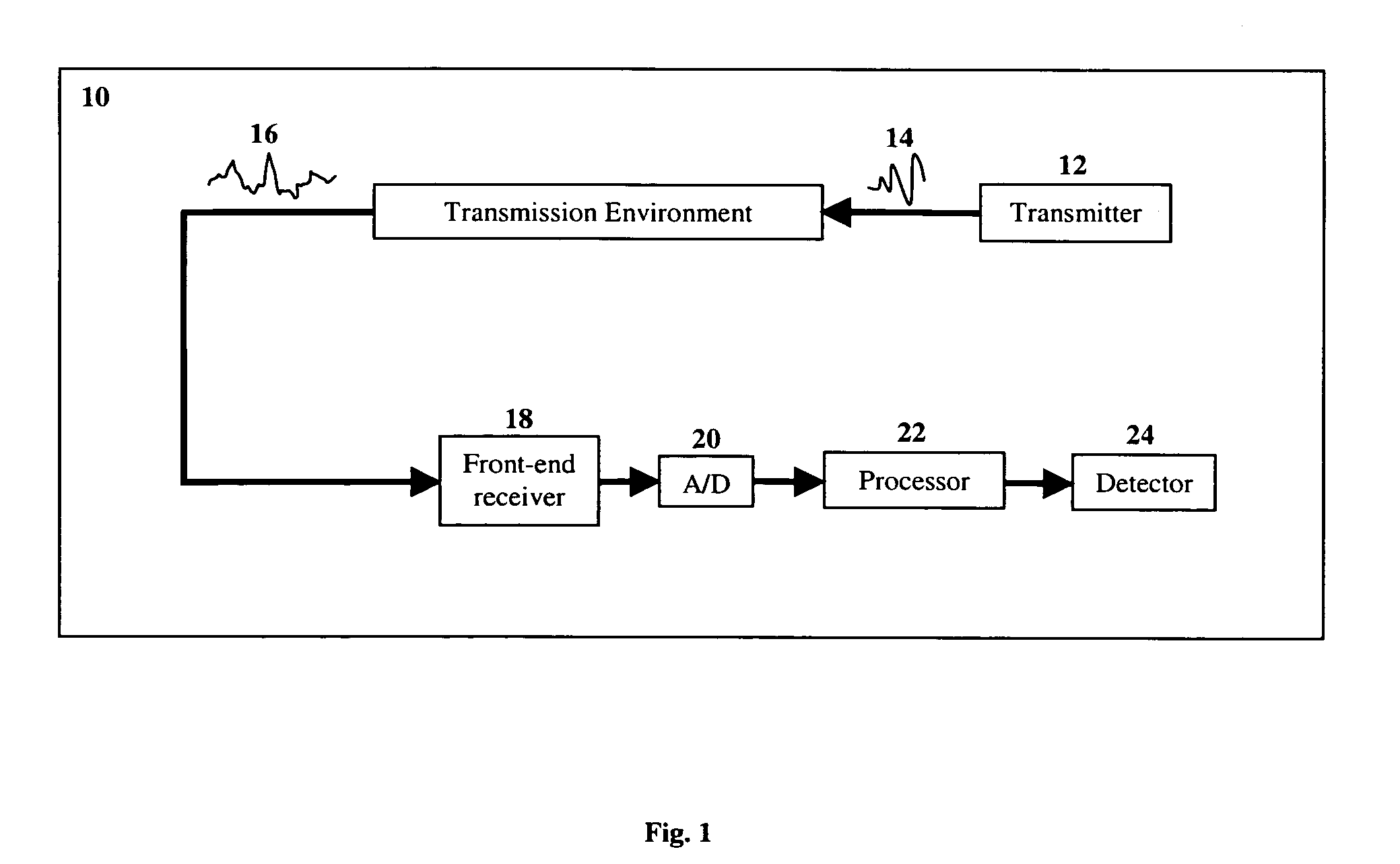
Specific impulse (usually abbreviated Iₛₚ) is a measure of how effectively a rocket uses propellant or a jet engine uses fuel. Specific impulse can be calculated in a variety of different ways with different units. By definition, it is the total impulse (or change in momentum) delivered per unit of propellant consumed and is dimensionally equivalent to the generated thrust divided by the propellant mass flow rate or weight flow rate. If mass (kilogram, pound-mass, or slug) is used as the unit of propellant, then specific impulse has units of velocity. If weight (newton or pound-force) is used instead, then specific impulse has units of time (seconds). Multiplying flow rate by the standard gravity (g₀) converts specific impulse from the weight basis to the mass basis.
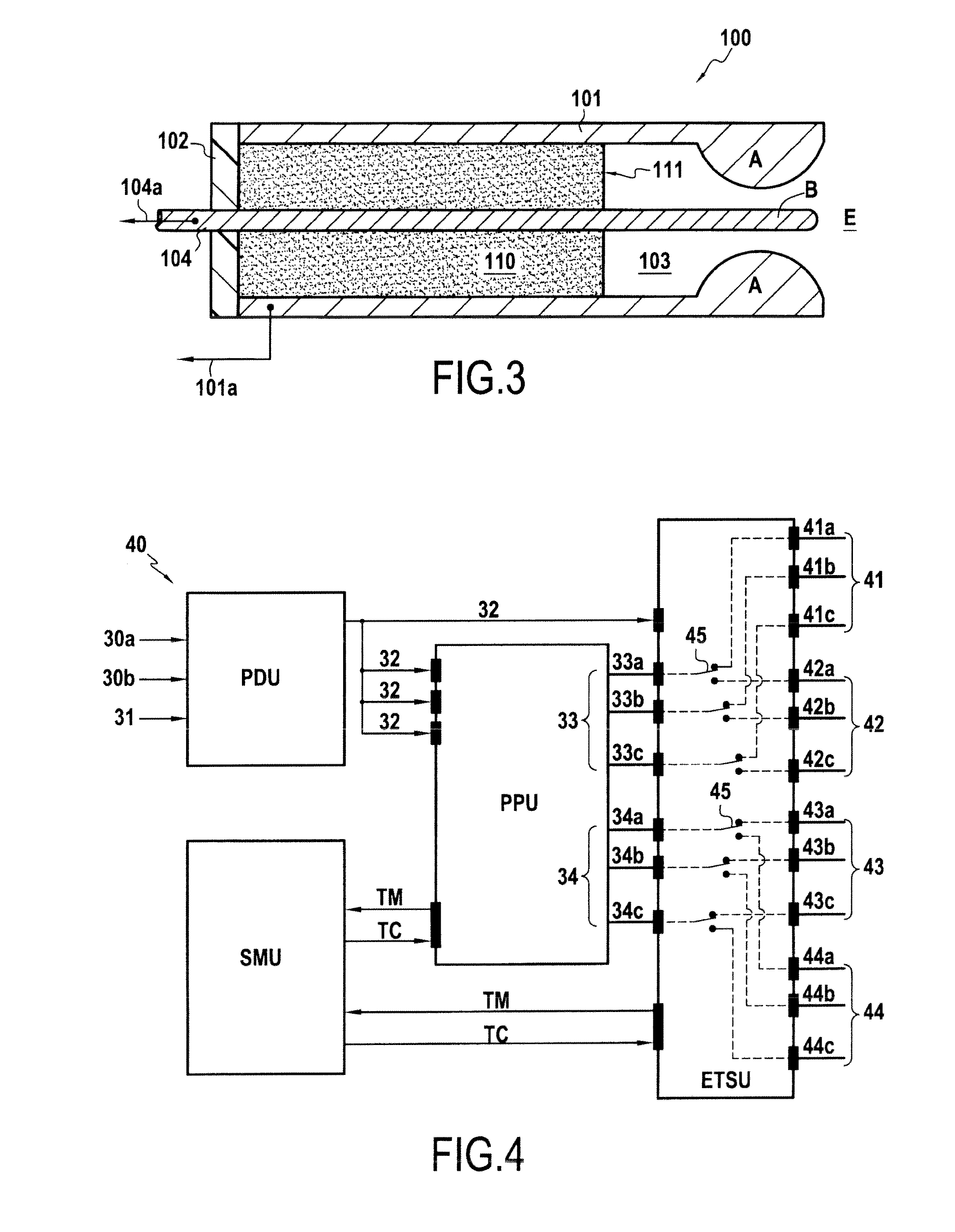
Practical orbit raising system and method for geosynchronous satellites
InactiveUS7113851B1Maximizing payload massMaximizing mission lifeLaunch systemsCosmonautic propulsion system apparatusElectricitySynchronous orbit
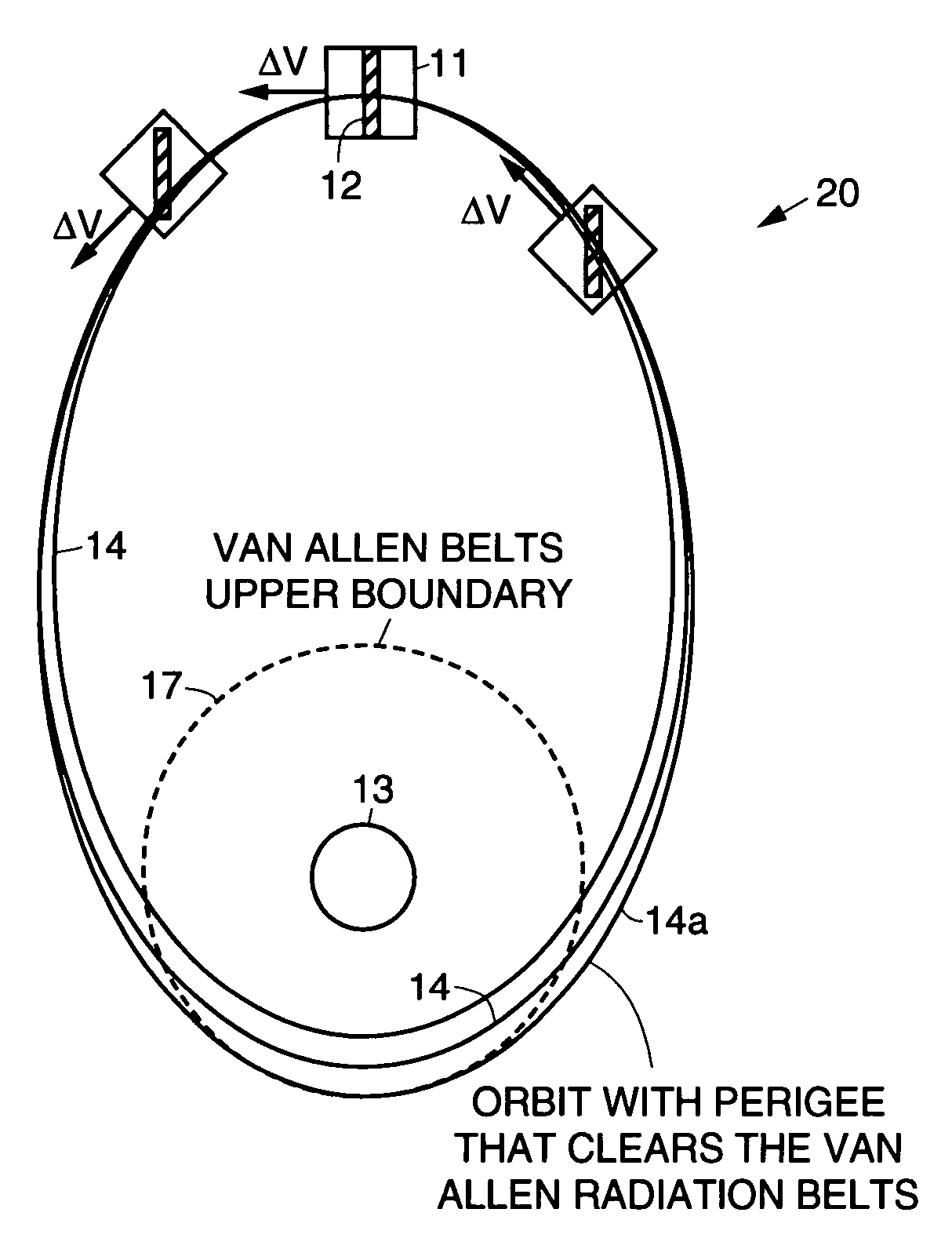
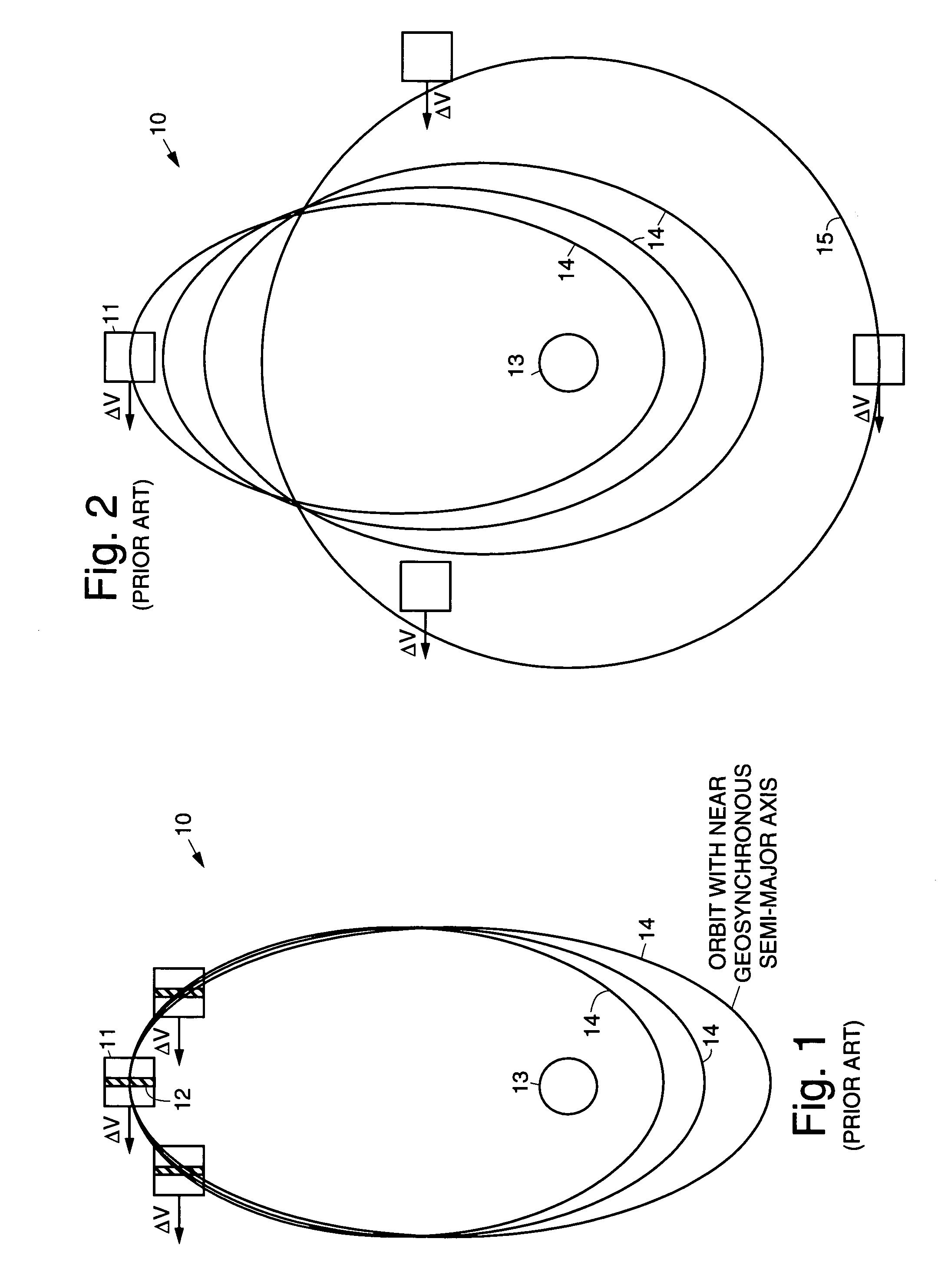
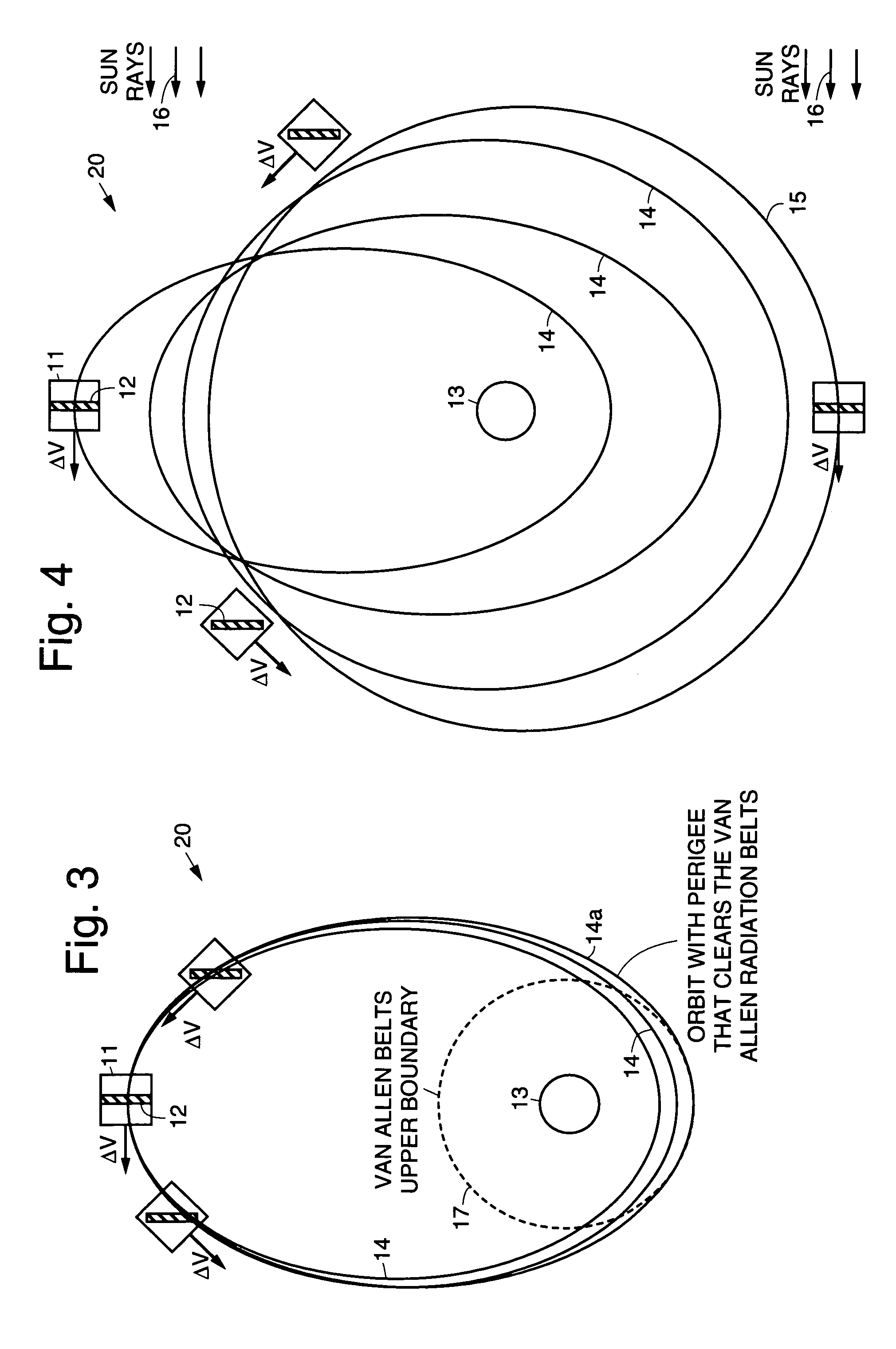
A practical orbit raising method and system wherein a satellite quickly escapes the Van Allen radiation belts and payload mass and mission life are maximized. A satellite is launched that contains high thrust chemical propulsion thrusters, high specific impulse electric propulsion thrusters and a solar array. The satellite quickly escapes the Van Allen radiation belts by firing the high thrust chemical propulsion thrusters at apogees of intermediate orbits, starting from the transfer orbit initiated by a launch vehicle, to successively raise the perigees until the perigee clears the Van Allen radiation belts. The payload mass and mission life are maximized by firing high specific impulse electric propulsion thrusters to raise the satellite to near synchronous orbit, while steering the thrust vector and solar array to maintain the sun's illumination on the solar array. The chemical and / or electric propulsion thrusters are then fired to achieve geosynchronous orbit.
Owner:SPACE SYST LORAL INC
Gas generating process for propulsion and hydrogen production
InactiveUS6849247B1Reduce the temperatureProducing energyLoomsHydrogen productionMetallic materialsSlurry
Owner:THE GOVERNMENT OF THE UNITED STATES OF AMERICA AS REPRESENTED BY THE SEC OF THE NAVY NAVAL RES LAB WASHINGTON
Method and a system for putting a space vehicle into orbit, using thrusters of high specific impulse
InactiveUS6116543AReduce thrustReached efficientlyLaunch systemsCosmonautic propulsion system apparatusFlight vehicleOrbital inclination
The method serves to place a space vehicle, such as a satellite, on a target orbit such as the orbit adapted to normal operation of the space vehicle and starting from an elliptical initial orbit that is significantly different from, and in particular more eccentric than the target orbit. The space vehicle is caused to describe a spiral trajectory made up of a plurality of intermediate orbits while a set of high specific impulse thrusters mounted on the space vehicle are fired continuously and without interruption, thereby causing the spiral trajectory to vary so that on each successive revolution, at least during a first stage of the maneuver, perigee altitude increases, apogee altitude varies in a desired direction, and any difference in inclination between the intermediate orbit and the target orbit is decreased, after which, at least during a second stage of the maneuver, changes in perigee altitude and in apogee altitude are controlled individually in predetermined constant directions, while any difference in inclination between the intermediate orbit and the target orbit continues to be reduced until the apogee altitude, the perigee altitude, and the orbital inclination of an intermediate orbit of the space vehicle have substantially the values of the target orbit.
Owner:SN DETUDE & DE CONSTR DE MOTEURS DAVIATION S N E C M A
Laser propulsion device
InactiveCN101737201AIncrease the actual specific impulseAvoid lostRocket engine plantsSputteringCombustion chamber
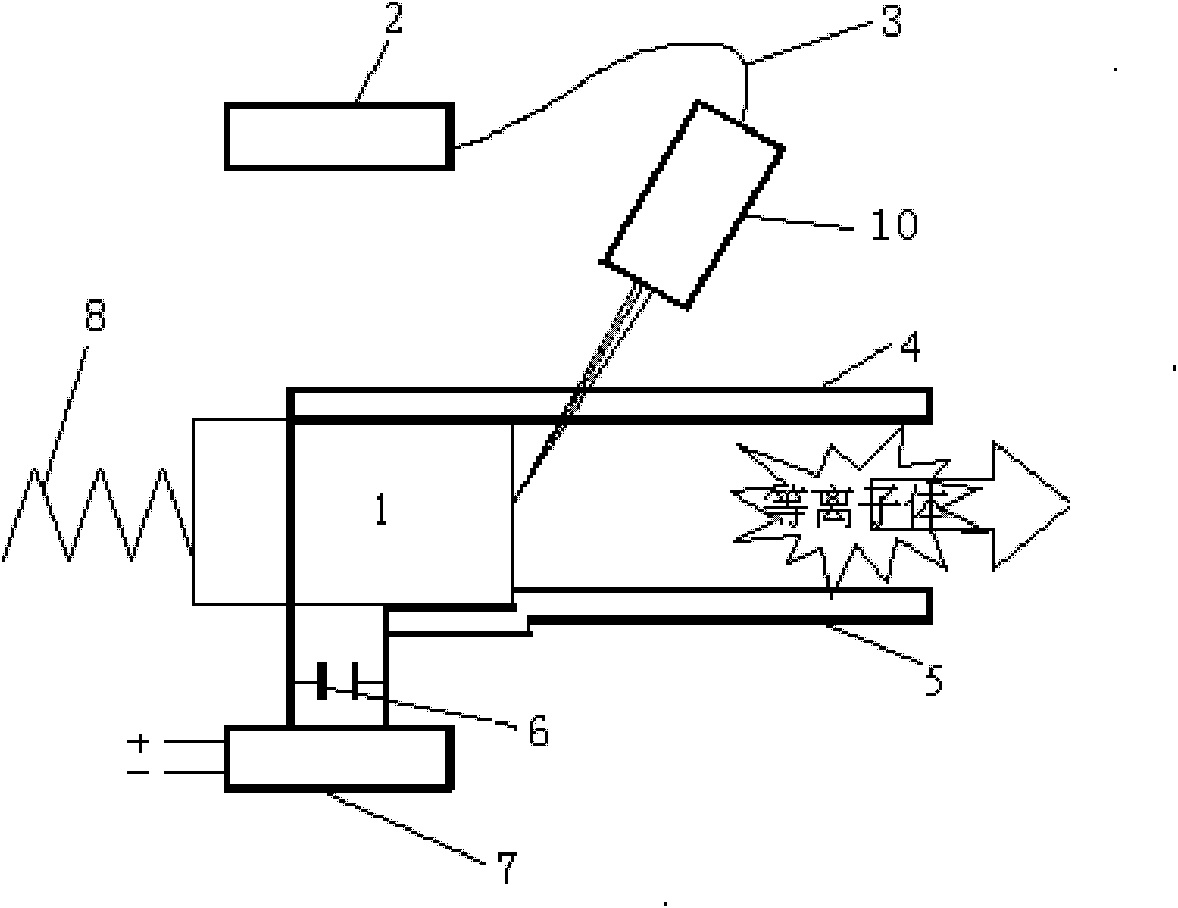
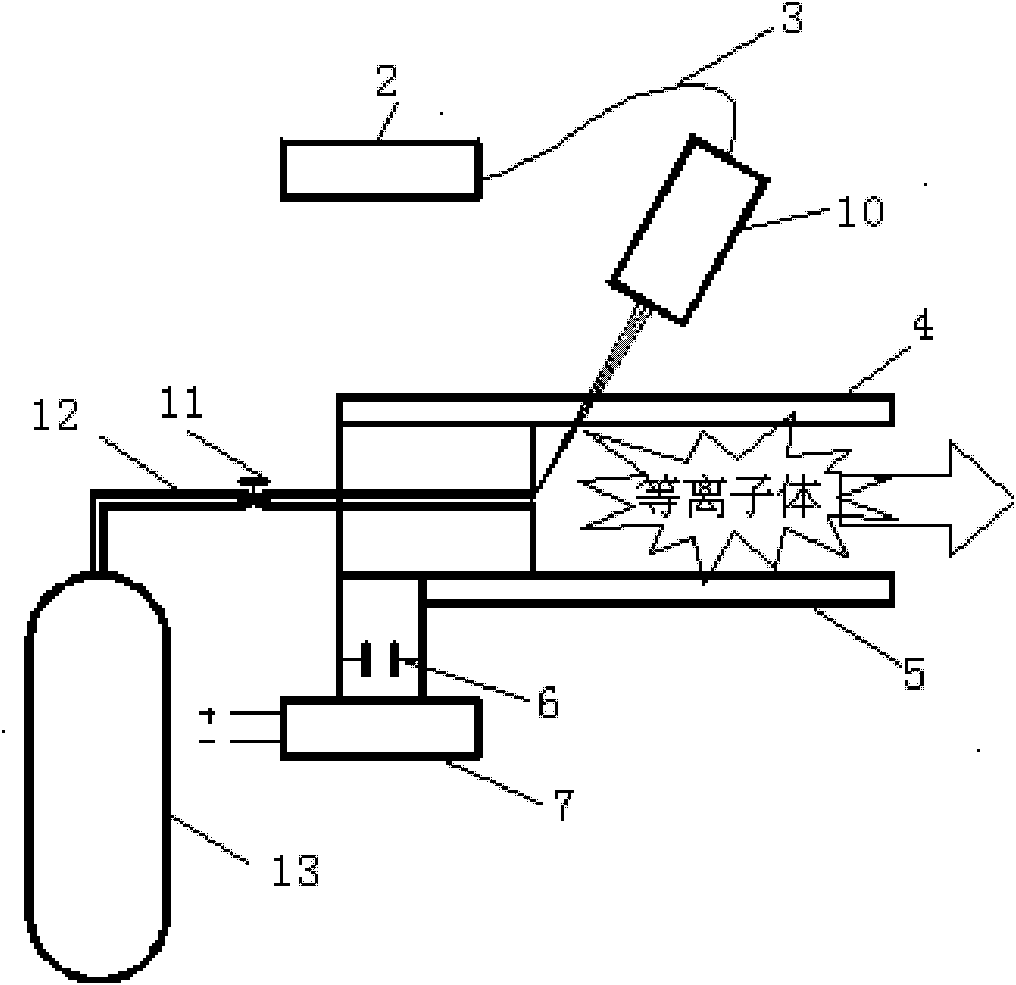
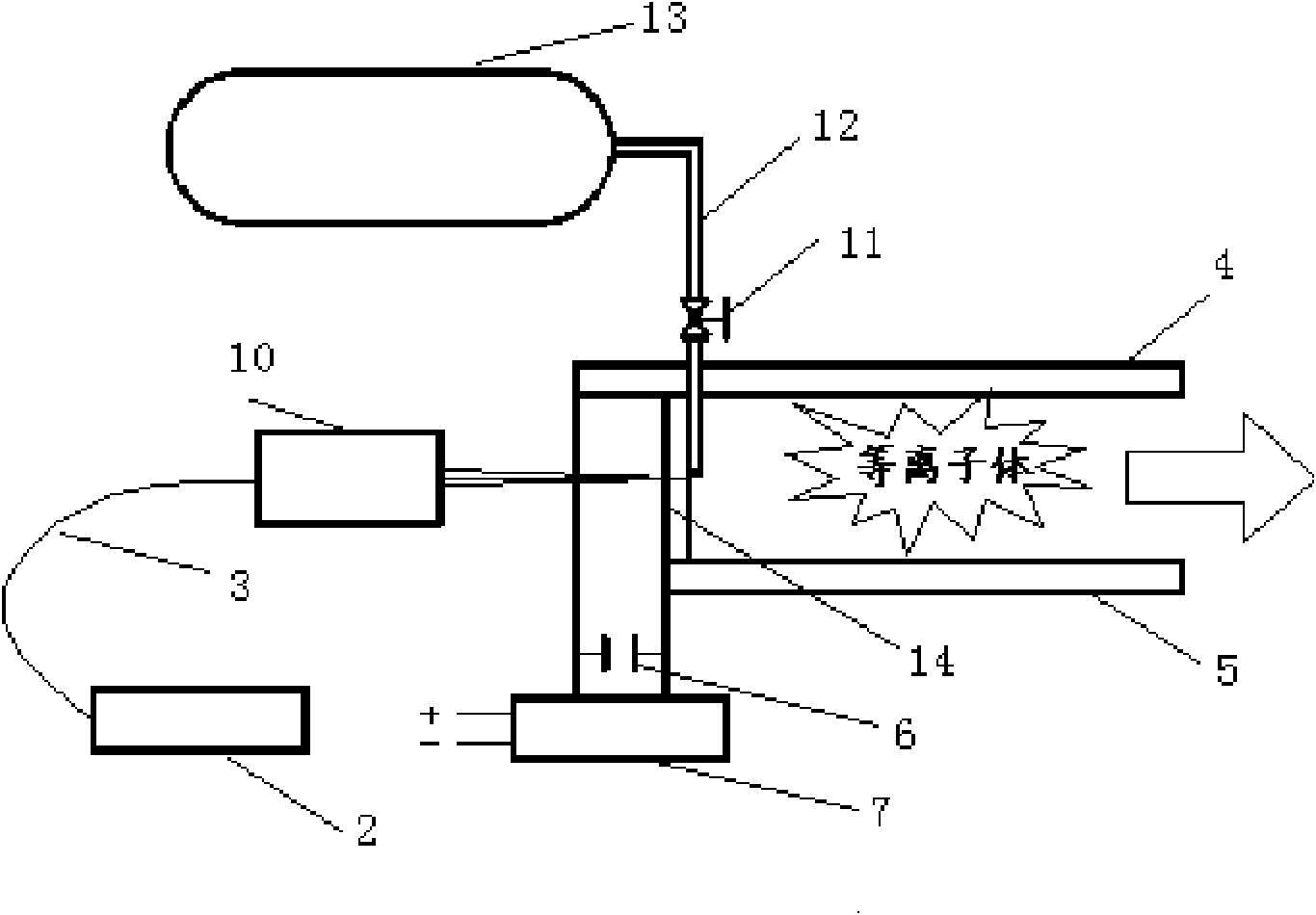
The invention discloses a laser propulsion device. The device comprises a laser device, a propellant feeding device, laser focusing equipment and a combustion chamber, wherein the laser device is used for generating laser; the laser focusing equipment is used for focusing the laser on a propellant; the propellant feeding device is used for providing the propellant and the propellant within a laser irradiation area is mainly converted into plasma; and the combustion chamber is used for transmitting the energy of the plasma to a lightcraft. The laser propulsion device can avoid heat conduction generated when the laser ablates a solid propellant and propellant loss caused by material sputtering, thereby increasing the actual specific impulse of laser propulsion.
Owner:INST OF PHYSICS - CHINESE ACAD OF SCI
Pulsed plasma thruster with water working medium
The invention provides a pulsed plasma thruster with water as a working medium. The thruster comprises two parts, namely a thruster body and a power supply processing unit, wherein the thruster body consists of a thruster structure and an energy storage capacitor; the thruster structure comprises a positive pole, a negative pole, a trigger, a wording medium feeding mechanism and a nozzle; the power supply processing unit consists of a main power supply and a triggering power supply; the main power supply is connected to the wiring terminals of the positive pole and the negative pole by wires,and is simultaneously connected with the energy storage capacitor; and the triggering power supply is connected with the trigger. A water working medium is added with sodium chloride or potassium chloride solution in which elements are easily ionized at the molar percentage of 0.5-2.2%. The specific impulse of the pulsed plasma thruster with water as the working medium provided by the invention is higher than that of the Teflon pulsed plasma thruster, and is adapted to the operation of low-power pulsed plasma thrusters; and when used in spacecrafts, the pulsed plasma thruster can be used for improving the efficiency, greatly saving the cost and space, and solving the problem of space replenishment of thrusters.
Owner:ZHONGBEI UNIV
Method of electrically exploding wires to generate shock waves in water by driving energy containing mixtures
ActiveCN108180003AReduce volumeImproving the efficiency of energy storage conversion to plasma energyFluid removalShock waveLow voltage
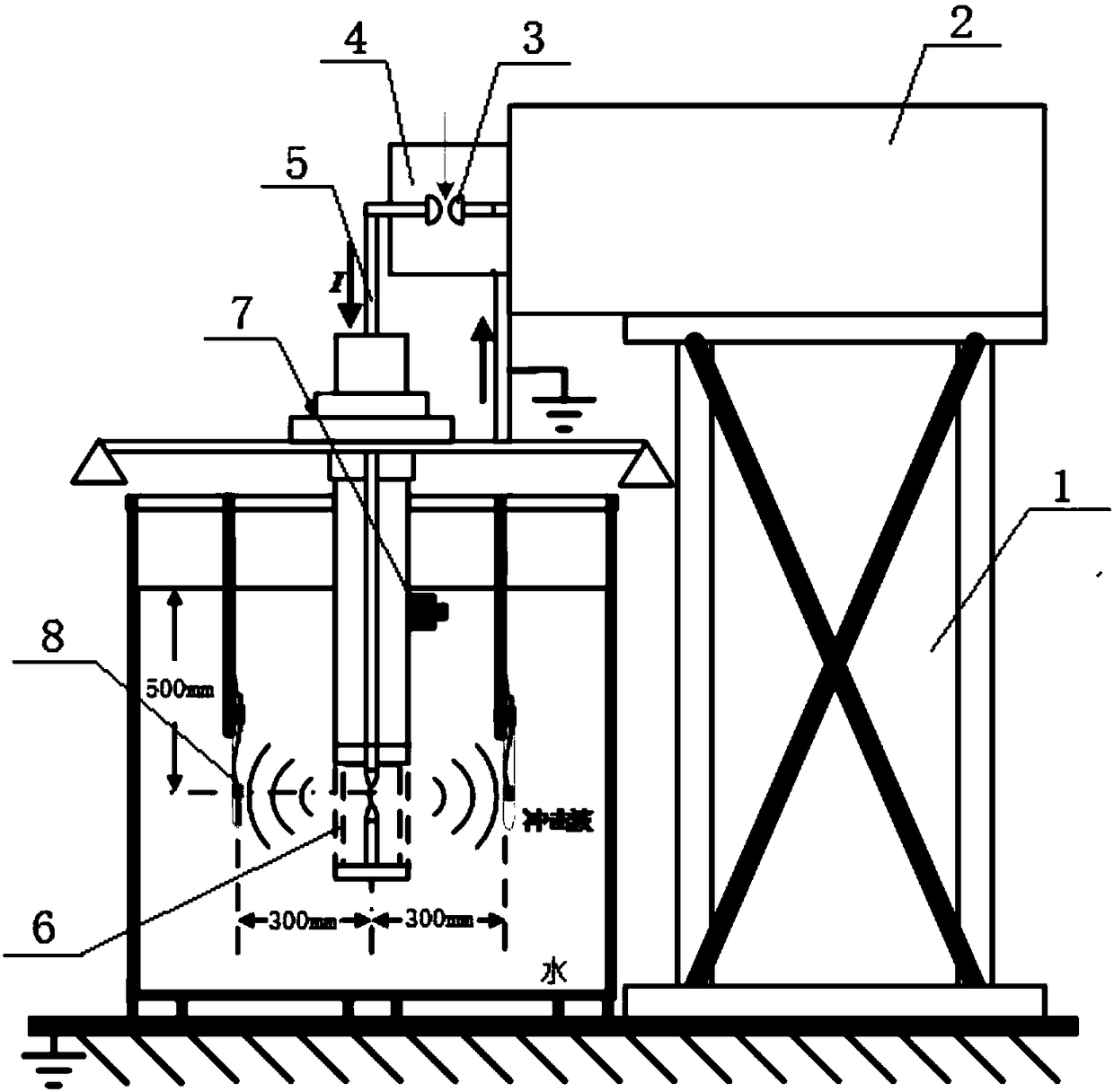
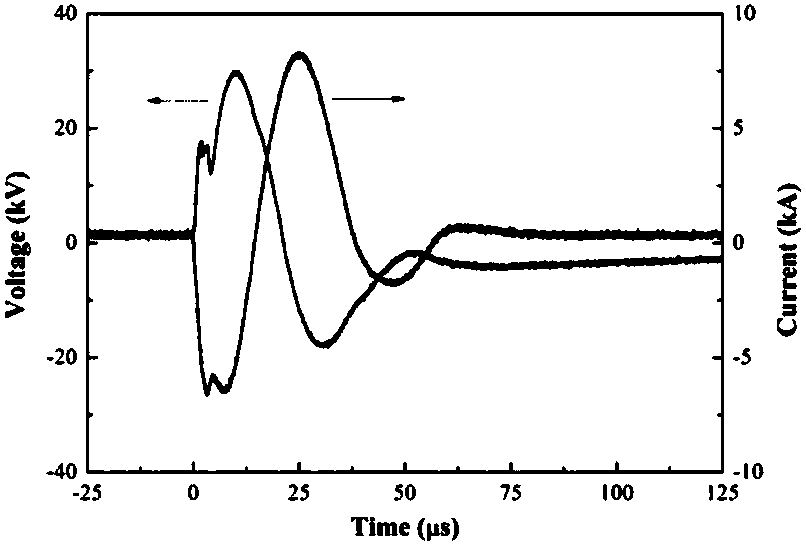
The invention relates to the field of pulse power technology applications and energy exploitation technology, in particular to a method of electrically exploding wires to generate shock waves in waterby driving energy containing mixtures. The method of the electrically exploding wires to generate the shock waves in water by driving the energy containing mixtures comprises the following steps thata specific pulse power drive source is used to drive the wires of different materials, different diameters, and different lengths to cause an electrical explosion, the phase transition time, discharge current waveform and emission spectrum intensity of the corresponding wires are recorded; shock wave loads of different formulations are made and underwater shock wave experiments are correspondingly performed; shock wave probes are used to measure shock wave waveform and compared with the required waveform to determine the corresponding relationship between shock wave specific impulse and the shock wave loads; and according to the required shock wave parameters and the corresponding relationship between the shock wave specific impulse and the shock wave loads, a corresponding shock wave load is selected to be placed between the high and low voltage electrodes at the output end of the pulse power drive source and is driven under water to generate a controlled shock wave.
Owner:XI AN JIAOTONG UNIV +1
Method and a system for putting a space vehicle into orbit, using thrusters of high specific impulse
InactiveUS6213432B1High specific impulseReduce thrustLaunch systemsCosmonautic propulsion system apparatusFlight vehicleOrbital inclination
The method serves to place a space vehicle, such as a satellite, on a target orbit such as the orbit adapted to normal operation of the space vehicle and starting from an elliptical initial orbit that is significantly different from, and in particular more eccentric than the target orbit. The space vehicle is caused to describe a spiral trajectory made up of a plurality of intermediate orbits while a set of high specific impulse thrusters mounted on the space vehicle are fired continuously and without interruption, thereby causing the spiral trajectory to vary so that on each successive revolution, at least during a first stage of the maneuver, perigee altitude increases, apogee altitude varies in a desired direction, and any difference in inclination between the intermediate orbit and the target orbit is decreased, after which, at least during a second stage of the maneuver, changes in perigee altitude and in apogee altitude are controlled individually in predetermined constant directions, while any difference in inclination between the intermediate orbit and the target orbit continues to be reduced until the apogee altitude, the perigee altitude, and the orbital inclination of an intermediate orbit of the space vehicle have substantially the values of the target orbit.
Owner:SN DETUDE & DE CONSTR DE MOTEURS DAVIATION S N E C M A
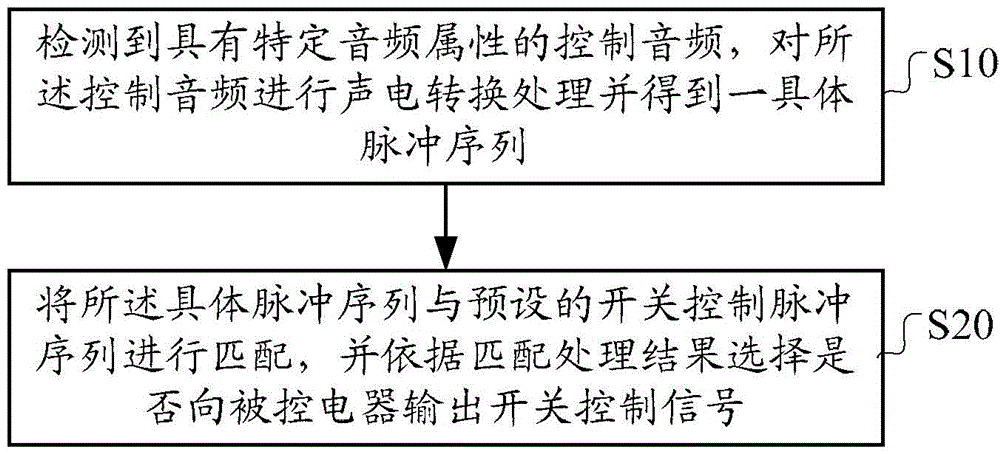
On-off device and control realization method thereof
InactiveCN103957635AImprove visibilityImprove reliabilityElectric light circuit arrangementElectricityControl signal
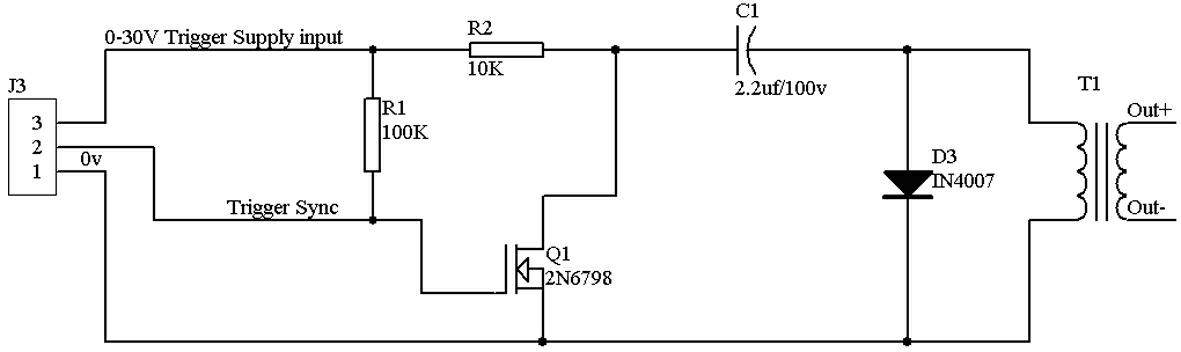
The invention discloses an on-off device and a control realization method thereof. The method includes the steps that a control audio frequency with specific audio frequency attributes is detected, and acoustic-electric conversion processing is conducted on the control audio frequency to obtain a specific impulse sequence; matching is conducted on the specific impulse sequence and a preset on-off control impulse sequence, and whether an on-off control signal is output to a controlled electric appliance or not is selected according to a matching processing result. In the on-off device and the control realization method of the on-off device, a user can use clapping sound or other control audio frequencies with specific audio frequency attributes to achieve on-off control of controlled electric appliances; in the specific realization process, the voice recognition technology and an unconventional voice operated switch do not need to be used, and the on-off device and the control realization method of the on-off device have multiple advantages of being high in identification, high in reliability, high in adaptability and low in cost.
Owner:梁涛
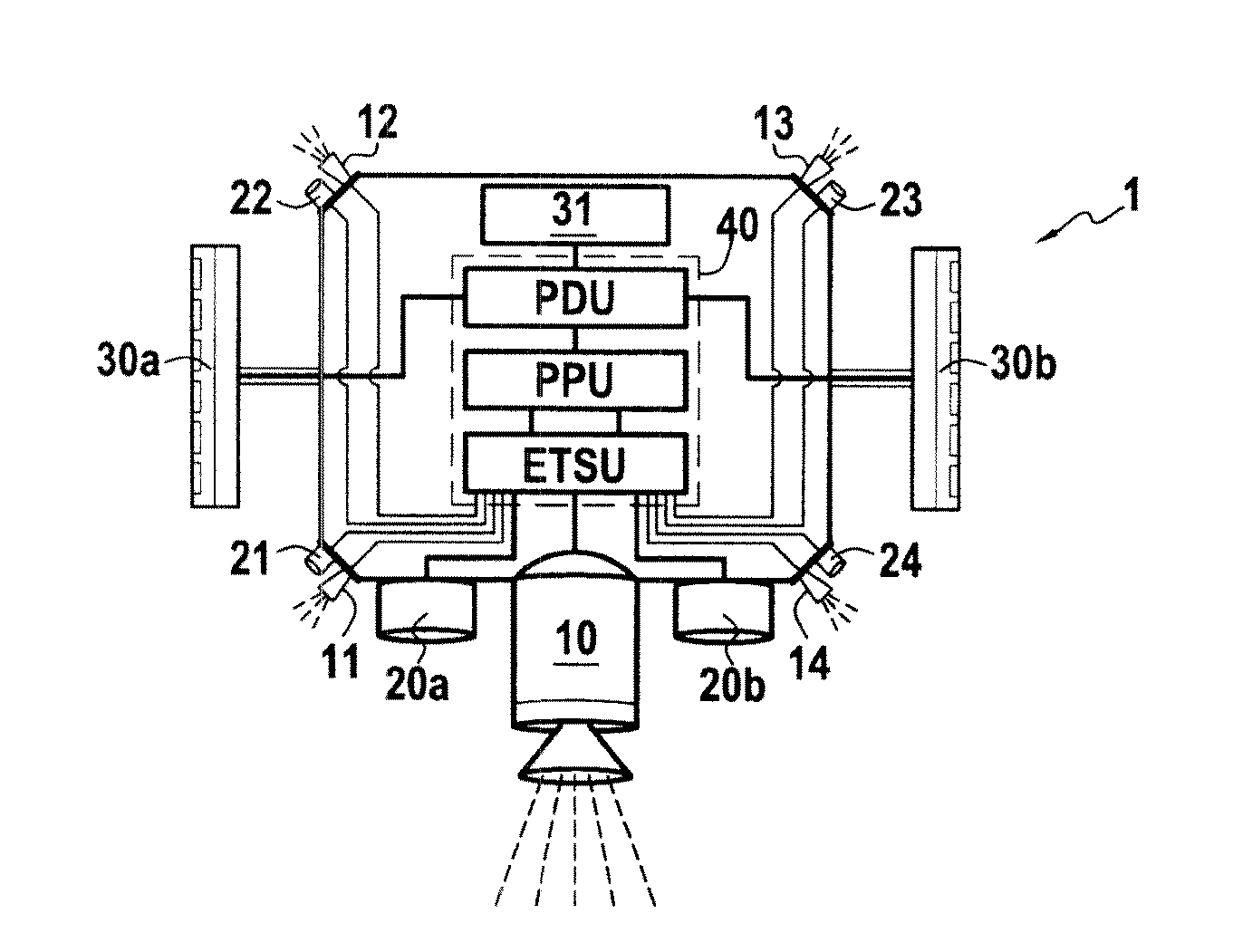
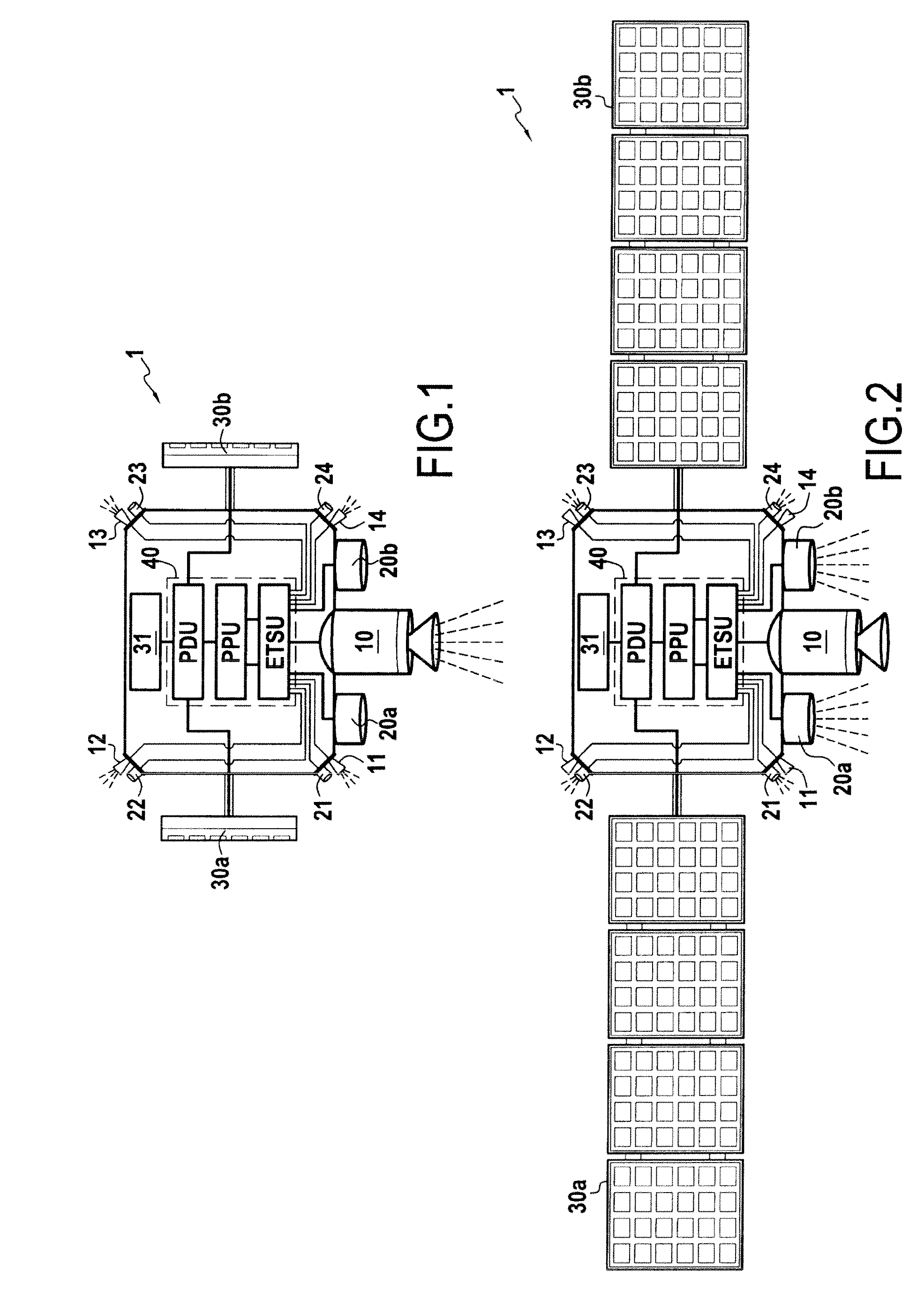
Space vehicle with electric propulsion and solid propellant chemical propulsion
ActiveUS20150021439A1Easy transitionSimple control systemCosmonautic propulsion system apparatusCosmonautic power supply systemsElectric powerSatellite
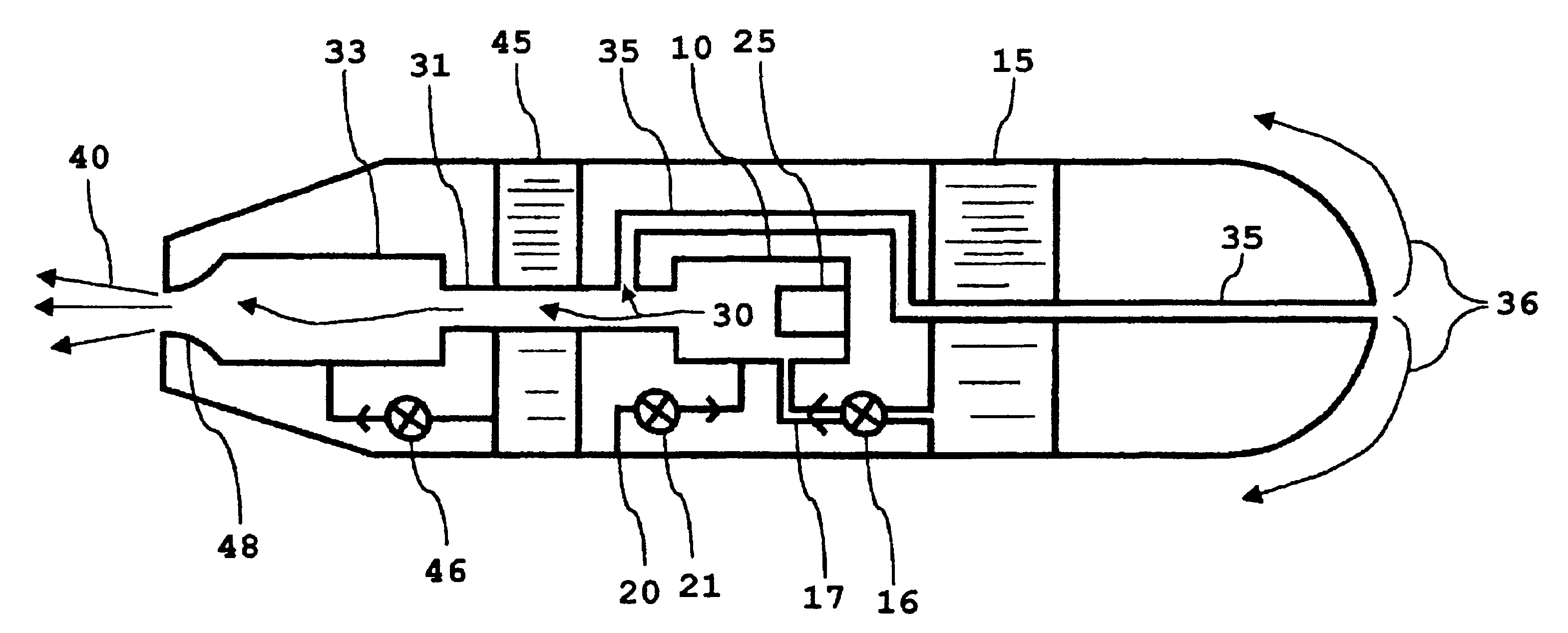
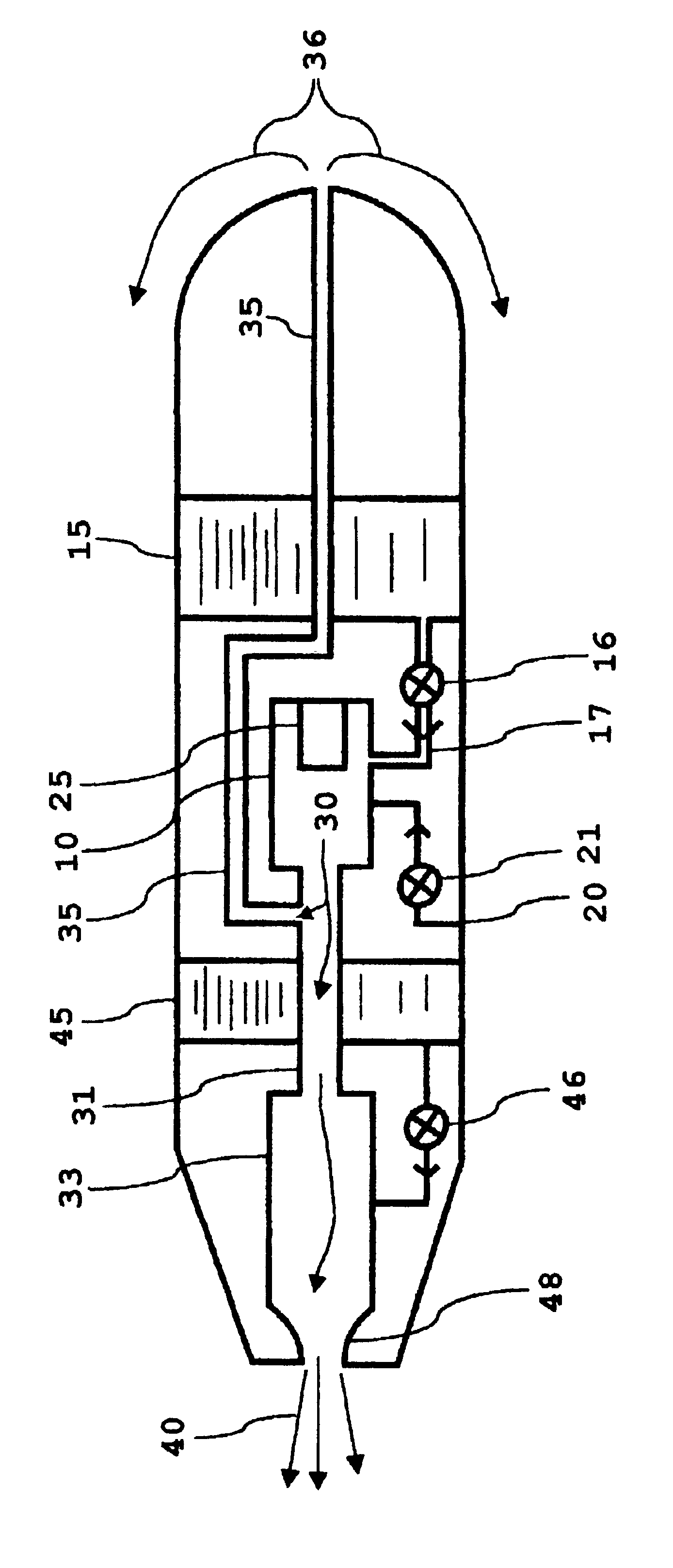
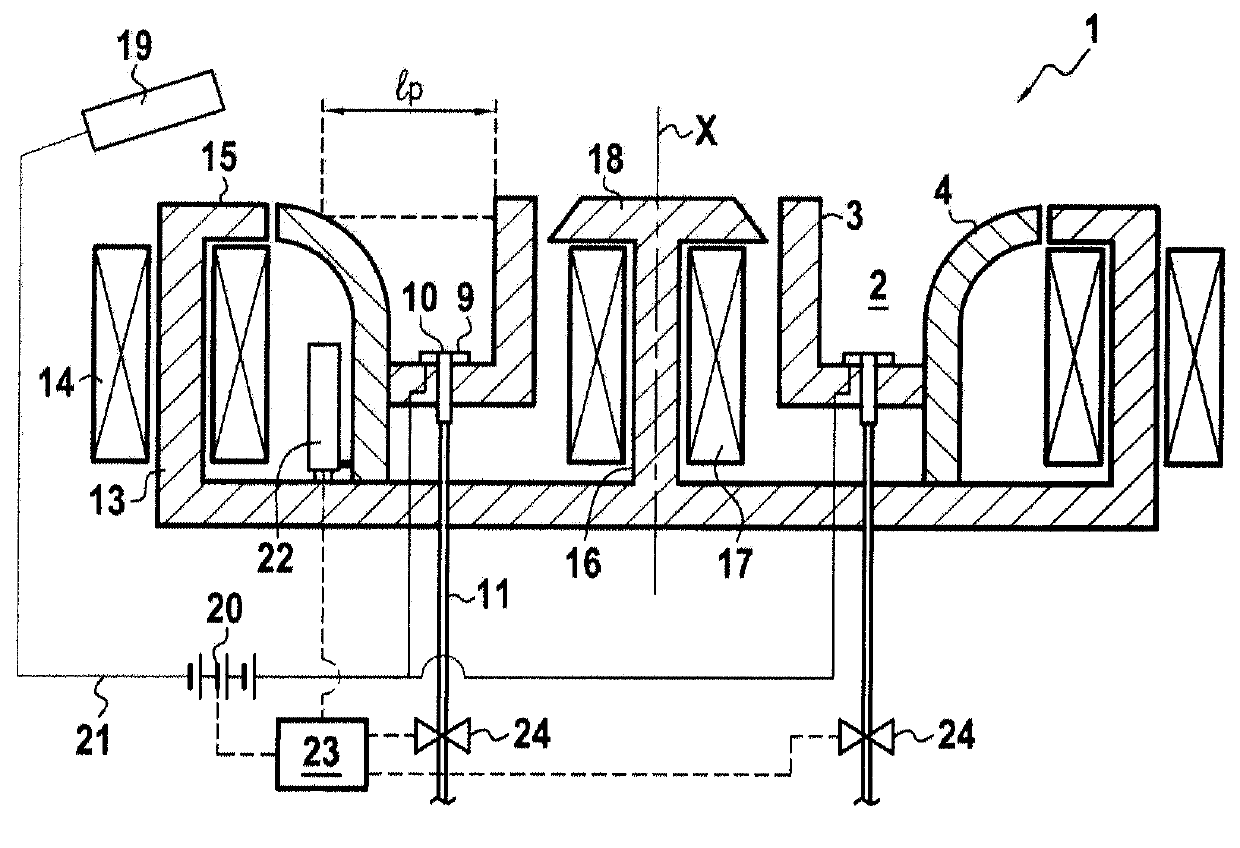
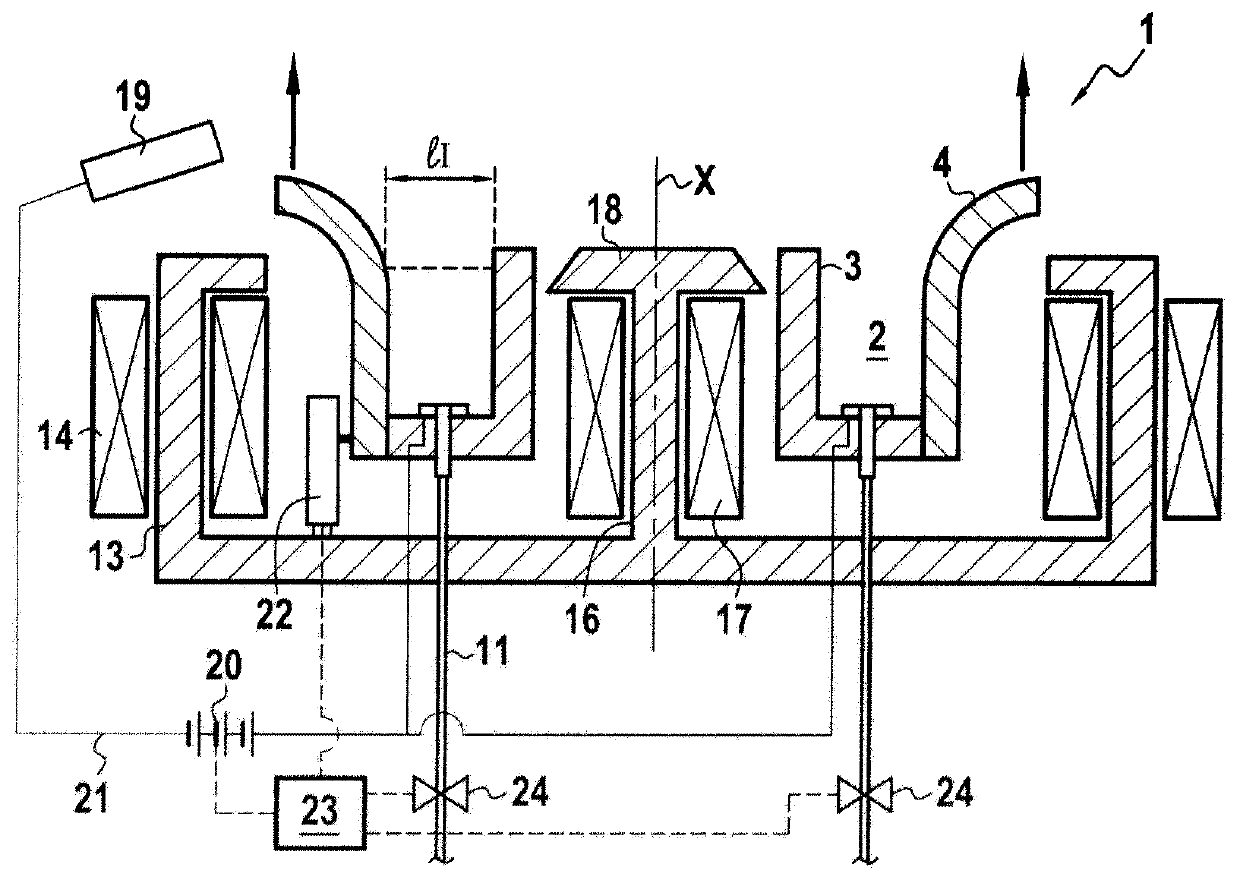
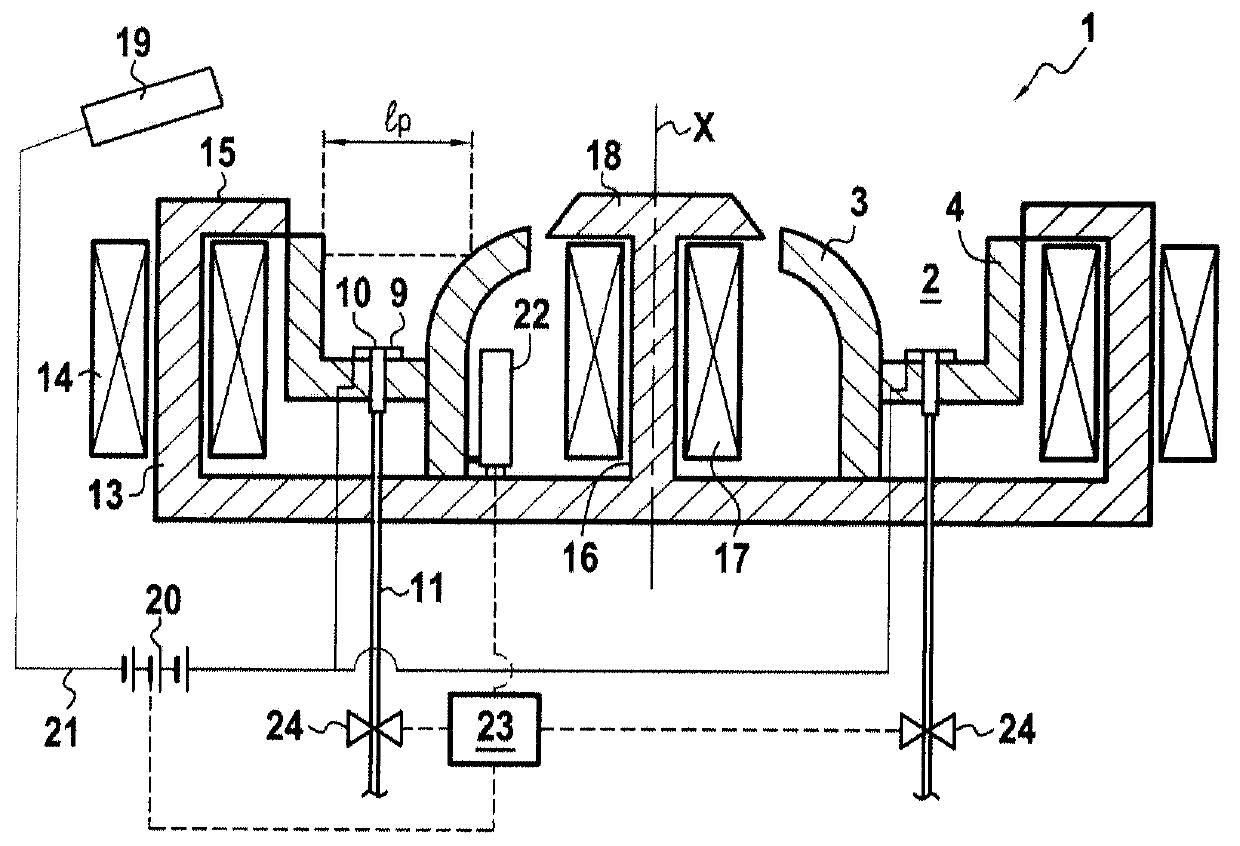
A space vehicle (1), in particular a satellite or a probe, capable of executing high-thrust maneuvers or high specific impulse maneuvers. According to the invention, the space vehicle (1) includes at least one solid-propellant chemical thruster (10-14) and at least one electric thruster (20-24).
Owner:GERAKL
Robust predictive deconvolution system and method
InactiveUS7106250B2High-fidelity impulse response estimationReduce ambiguityRadio wave reradiation/reflectionAmbiguityCircumflex
Owner:THE U S A AS REPRESENTED BY THE SEC OF THE NAVY
Propellant with high energy and low temperature sensitive coefficient of burning
ActiveCN105130720ABoost energy levelsLow burning rate temperature sensitivity coefficientExplosivesAl powderExplosive Agents
A propellant with high energy and low temperature sensitive coefficient of burning comprises 12-15% of an adhesive, 10-13% of a plasticizer, 15-18% of an oxidant, 38-50% of an energetic explosive, 10-18% of a metal fuel and 1.5-2.0% of a small group, wherein the adhesive is glycidyl azide polymer; the plasticizer is triethylene glycol dinitrate or 2,4-dinitro-2,4-diazaalkane; the oxidant is ammonium perchlorate; the energetic explosive is octogen; and the metal fuel is aluminum powder. The propellant has the characteristics of high energy (standard measured specific impulse is greater than 2450N.s / kg) and low temperature sensitive coefficient of burning (not greater than 0.15%K<-1>), and is suitable for tactical missile engines with far required range, strong penetration ability, high reliability and accurate guidance.
Owner:HUBEI INST OF AEROSPACE CHEMOTECH
Plume neutralizer of space electric thruster
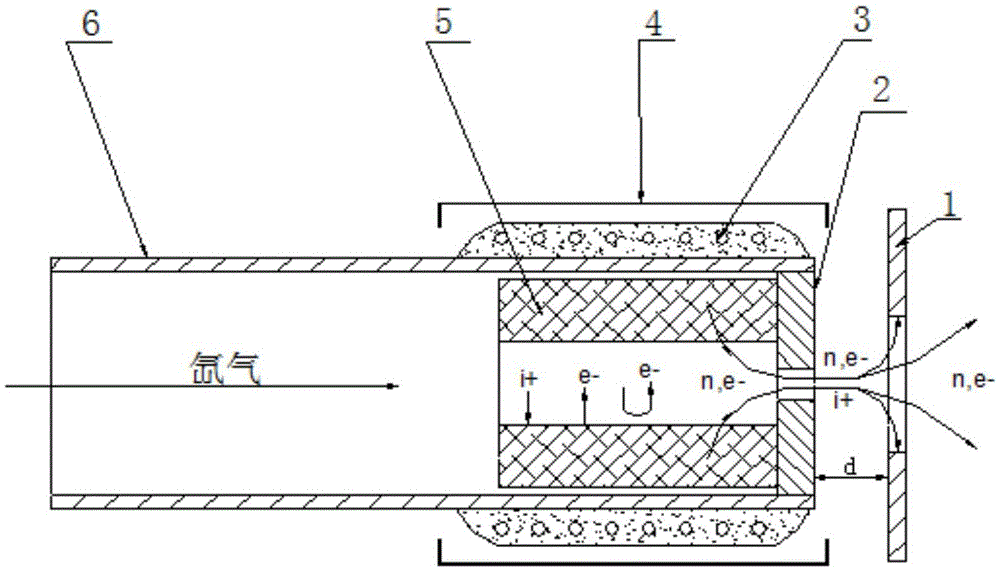
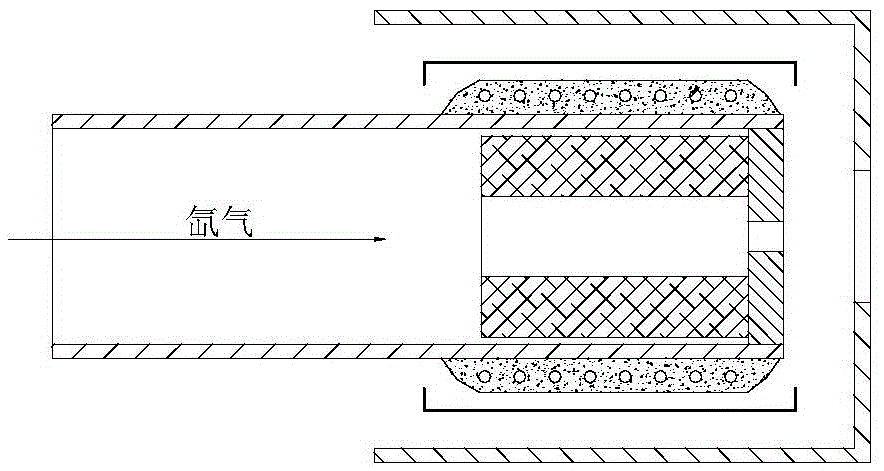
ActiveCN105626410AAvoid harmful effectsGuaranteed dockingMachines/enginesUsing plasmaGas-discharge lampPower flow
The invention discloses a plume neutralizer of a space electric thruster. The neutralizer comprises an ignition electrode, a top hole plate, a heater, a heat shielding cylinder, an emitting body and a support pipe; the emitting body is mounted in the support pipe; the top hole plate shields out of the emitting body, and is fixedly connected with the support pipe; the heater is mounted out of the support pipe opposite to the emitting body; a heating area covers the whole emitting body; the heater is wrapped with an insulation ceramic layer; the heat shielding cylinder covers the heater, and forms gaps with the heater and the insulation ceramic layer; the ignition electrode is mounted at the downstream of the top hole plate, and forms a gap with a small hole of the top hole plate; and a center hole of the ignition electrode is coaxial with the small hole of the top hole plate. The neutralizer generates a lot of electrons through a hot electron ionized gas discharge mode; continuously emitted electrons are high in density; after the gas discharge is stabilized, the self-heating can be performed to maintain discharge, so that the system power consumption is saved; the equivalent potential is low; the effective acceleration voltage of the thruster is higher; and the specific impulse of the thruster is high.
Owner:SHANGHAI INST OF SPACE PROPULSION
Pulse laser plasma electricity hybrid micro-propulsion unit and method
ActiveCN102374146AImprove specific impulseHigh thrust power ratioMachines/enginesUsing plasmaElectric fieldPulsed laser
The invention discloses a plasma laser plasma electricity hybrid micro-propulsion unit which comprises a pulse laser ablation device, a propellant supply device and a plasma accelerating device, wherein the pulse laser ablation device irradiates a propellant supplied by the propellant supply device to generate high-speed plasma; and the plasma accelerating device is used for accelerating the high-speed plasma again. The invention also provides a pulse laser plasma electricity hybrid micro-propulsion method which comprises the following steps of: generating high-temperature and high-speed plasma through the high-frequency pulse laser ablation propellant; and accelerating the high-temperature and high-speed plasma through an electric field or magnetic field. According to the invention, a pushing force with high specific impulse and high thrust-to-power ratio can be provided for a mini satellite.
Owner:苏州纳飞卫星动力科技有限公司
Laser microthruster
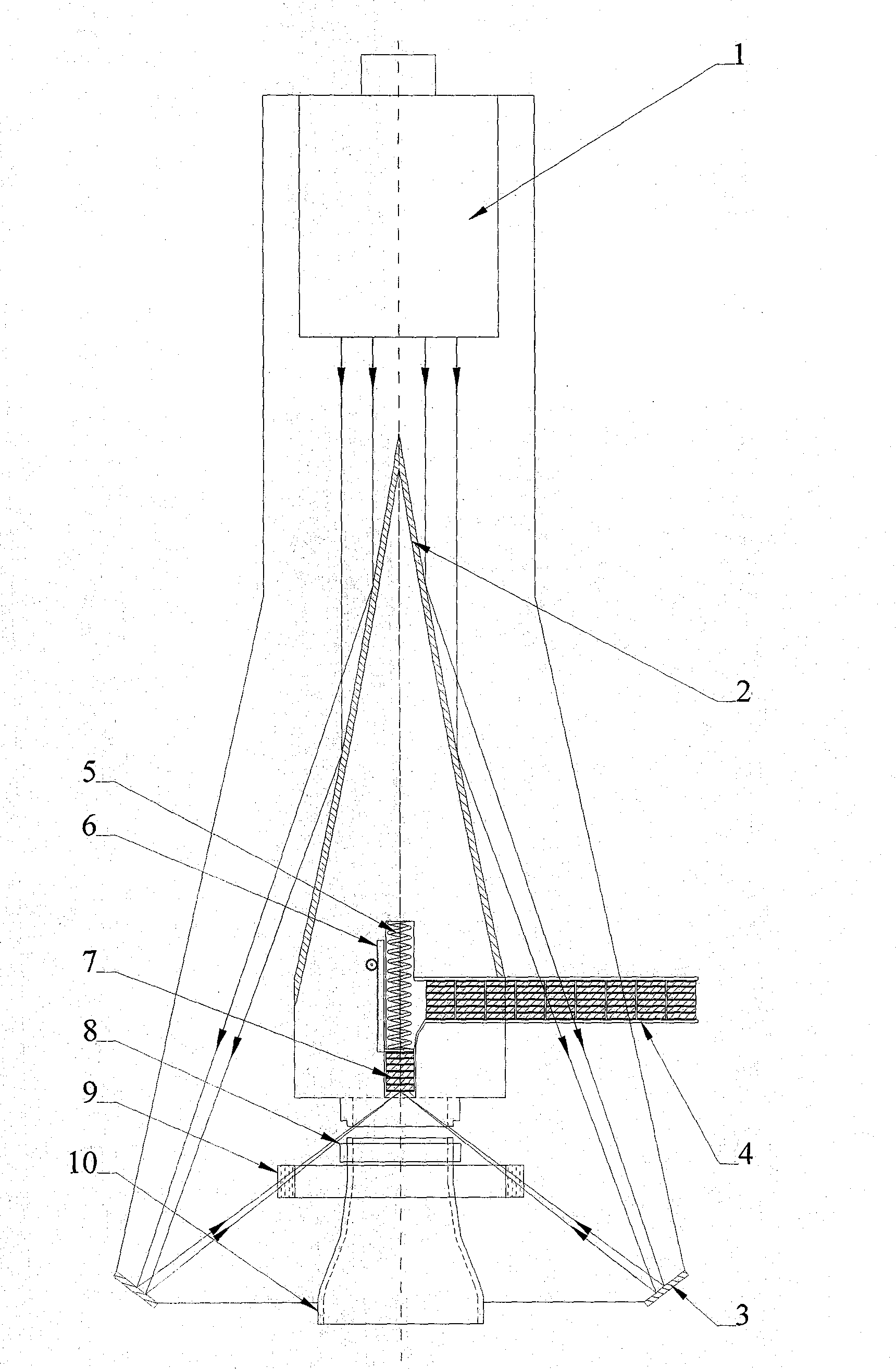
InactiveCN102022299AReduce pollutionPrecise control of impulse sizeMachines/enginesUsing plasmaOptoelectronicsSymmetric axis
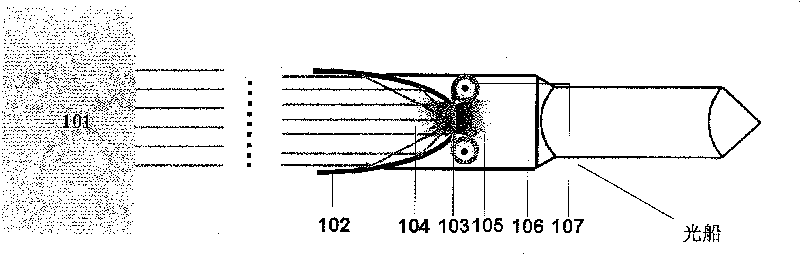
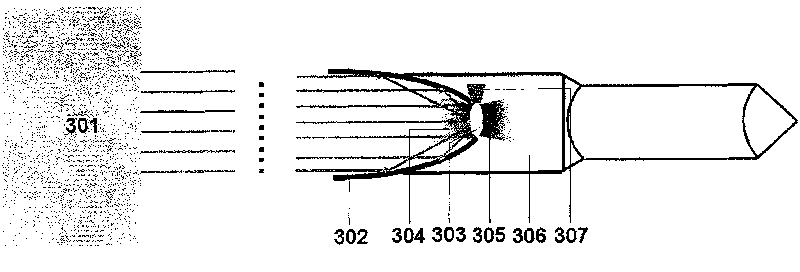
The invention relates to a laser microthruster which comprises a rotator parabolic reflecting mirror (2), an annular reflecting mirror (3), a jet pipe (10) with a slit, a shutter (8) for preventing optical mirror faces from being polluted, and an anti-pollution transparent glass loop (9), wherein the symmetry axis of the rotator parabolic reflecting mirror (2), the annular reflecting mirror (3) and the jet pipe (10) with a slit coincides with the central axis of the laser microthruster. The invention reduces the pollution of optical devices of a reflection-type laser thruster, and can effectively increase the specific impulse; the mass of the ablated working medium per impulse and the magnitude of the impulse of the thruster can be accurately controlled; and a flame-retardant film can be ablated by the laser or used for generating partial thrust.
Owner:深圳巡天空间技术有限公司
Pinhole array miniature electrostatic electric thruster
ActiveCN105649906ASimple structureImprove reliabilityMachines/enginesUsing plasmaMicrosatelliteComputer module
The invention discloses a pinhole array miniature electrostatic electric thruster. The pinhole array miniature electrostatic electric thruster comprises a neutralizer and a thruster body which are mutually connected, wherein the thruster body sequentially comprises a grid component, a pinhole array component and a propellant storage chamber which are cooperatively connected from top to bottom; the pinhole array component is formed by conveying plates and a pinhole array plate; the conveying plates are arranged on the lower surface of the pinhole array plate; pinhole arrays are uniformly distributed in the pinhole array plate; the grid component consists of an extraction grid, an acceleration grid and an insulation bracket; the extraction grid, the acceleration grid and the pinhole array plate are sequentially connected through the insulation bracket; and coaxial pinholes corresponding to the pinhole arrays are formed in the extraction grid and the acceleration grid; and heaters and the propellant are all located in the propellant storage chamber. The pinhole array miniature electrostatic electric thruster has the advantages that the structure is simple; the size is small; the specific impulse can reach 700-2000 s; the propellant storage function and the conveying function are integrated; the propellant is stored in a pressure-free mode; no movable components exist; and the like. The pinhole array miniature electrostatic electric thruster can be packaged in a chip mode, and can be applied to microsatellites as a standard thrusting module.
Owner:SHANGHAI INST OF SPACE PROPULSION
Hall effect thruster
The invention relates to the field of Hall effect thrusters, and in particular to a thruster (1). The downstream end of the annular channel (2) of the thruster has a variable cross-section so as to be capable of varying the thrust and the specific impulse.
Owner:SN DETUDE & DE CONSTR DE MOTEURS DAVIATION (S N E C M A)
Solid-and-liquid attitude-control rocket engine
ActiveCN106194502ASimple structureImprove reliabilityRocket engine plantsCombustion chamberSolenoid valve
The invention discloses a solid-and-liquid attitude-control rocket engine. The solid-and-liquid attitude-control rocket engine comprises an oxidizing agent conveying system, a direct-action solenoid valve, a honeycomb-type catalytic bed, a combustion chamber and a spraying pipe, wherein the conveying system is used for supplying hydrogen peroxide by adopting a nitrogen extrusion mode; the supplying amount of the hydrogen peroxide is controlled by the direct-action solenoid valve, so that rapid response of the solid-and-liquid attitude-control rocket engine can be realized; the honeycomb-type catalytic bed is adopted for catalyzing, and an oxidizing agent is resolved to generate high-temperature oxygen which enters the combustion chamber through a spraying and jetting panel; and six passages are formed in the middle part of an end-burning grain, and the high-temperature oxygen reaches a grain section through the above passages and generates action with 1-3 butadiene which is a product of decomposition of HTPB, so that the engine starts to work. According to the solid-and-liquid attitude-control rocket engine, double-mode work is adopted, and the advantages of a single-unit attitude-control rocket engine of simple structure and high reliability and the advantages of a double-unit attitude-control rocket engine of high specific impulse and rapid switching-on and switching-off are combined; besides, the structure is simple; cost is low; safety is high; and the solid-and-liquid attitude-control rocket engine is environment-friendly.
Owner:BEIHANG UNIV
Spatial high-power nuclear power system based on closed Brayton cycle
ActiveCN109677639AEfficient conversionReduce weightCosmonautic vehiclesCosmonautic propulsion system apparatusLow voltageMixed gas
The invention provides a spatial high-power nuclear power system based on a closed Brayton cycle. The spatial high-power nuclear power system comprises a spatial nuclear reactor, a Brayton thermoelectric conversion subsystem, a heat dissipation subsystem, a cycle working medium storage and supply subsystem, an electric propulsion subsystem and an electric loading subsystem. Helium-xenon mixed gasis taken as a cycle working medium so as to realize efficient thermoelectric conversion, and a high-specific-impulse high-thrust electric thruster directly driven by high voltage is utilized for realizing efficient propulsion. According to the spatial high-power nuclear power system, the efficient thermoelectric conversion problem of a nuclear power air vehicle and the large-range electric power adjusting problem are solved, and the problem that the high voltage of a motor end is not matched with the lower voltage of the electric thruster is solved.
Owner:SHANGHAI INST OF SPACE PROPULSION
Bi-order grid spiral wave ion propulsion device
InactiveCN104454417AImprove specific impulseImprove convenienceMachines/enginesUsing plasmaRadio frequencyAtomic physics
The invention discloses a bi-order grid spiral wave ion propulsion device which comprises a discharge chamber, a spiral wave excitation antenna, a metal sleeve, an electromagnetic coil and a bi-order grid system. The spiral wave excitation antenna is connected with a radio-frequency power source and is arranged outside the discharge chamber in a sleeving mode, the spiral wave excitation antenna and the discharge chamber are both arranged inside the metal sleeve, and the metal sleeve is sleeved with the electromagnetic coil. The bi-order grid system is arranged at the tail end of the discharge chamber. The bi-order grid system comprises a screen grid, an extraction grid, an accelerating grid and a decelerating grid which are sequentially arranged away from the discharge chamber from near to far, and the screen grid, the extraction grid, the accelerating grid and the decelerating grid are all provided with grid holes. According to the bi-order grid spiral wave ion propulsion device, the mode that a spiral wave plasma source and the bi-order grid system are combined is adopted, the propulsion device can work under high power, and thus the reliable performance of high specific impulse and high propulsion capability can be achieved.
Owner:DALIAN UNIV OF TECH
Low-power cylinder-type electromagnetic plasma thruster with adjustable magnetic field
ActiveCN106351811ASolve the problem of high corrosion rateImprove ionization efficiencyMachines/enginesUsing plasmaElectricityEngineering
The invention provides a low-power cylinder-type electromagnetic plasma thruster with an adjustable magnetic field and belongs to the field of electric propulsion. The thruster comprises a front coil, a rear coil, a ceramic discharging channel, a pure iron sleeve, an iron core, a front seal cover, a rear seal cover and others. A discharging chamber formed by the ceramic discharging channel is cylindrical. The front coil and the rear coil are installed in front and back of the ceramic discharging channel respectively, and the distribution of the magnetic field inside the discharging chamber is changed by adjusting the current of the coils. A magnetic guide ring is installed at the outlet end of the ceramic discharging channel, a plasma generating region and an accelerating region inside the discharging chamber are easily separated, ions are fully accelerated, and the specific impulse of the thruster is improved. According to the thruster, a discharging chamber of a common Hall thruster is improved into a complete cylinder, in this way, the annular Hall thruster is high in corrosion rate under low power, ionization efficiency is obviously improved, and the low-power cylinder-type electromagnetic plasma thruster can stably work under 100 W or less and has expanded application in the low-power field compared with the common electric thruster.
Owner:BEIHANG UNIV
Aerospace laser ignition/ablation variable high precision thruster
InactiveUS9021782B1Cosmonautic vehiclesCosmonautic propulsion system apparatusAviationLaser ignition
A laser ignition / ablation propulsion system that captures the advantages of both liquid and solid propulsion. A reel system is used to move a propellant tape containing a plurality of propellant material targets through an ignition chamber. When a propellant target is in the ignition chamber, a laser beam from a laser positioned above the ignition chamber strikes the propellant target, igniting the propellant material and resulting in a thrust impulse. The propellant tape is advanced, carrying another propellant target into the ignition chamber. The propellant tape and ignition chamber are designed to ensure that each ignition event is isolated from the remaining propellant targets. Thrust and specific impulse may by precisely controlled by varying the synchronized propellant tape / laser speed. The laser ignition / ablation propulsion system may be scaled for use in small and large applications.
Owner:NASA
Solid-liquid scramjet engine
The invention discloses a solid-liquid scramjet engine, and belongs to the technical field of engines. The engine comprises an air inlet channel, a combustion chamber, a tail spray pipe, a fuel gas generator, an oil tank system, a control system and the like. The oil tank system comprises a high-pressure gas cylinder, a pressure reducing valve, a safety valve, fuel oil, an oil filter, a leather bag and the like, and the control system provides fuel oil flow meeting requirements for the scramjet engine according to set requirements. The fuel gas generator is mainly composed of a heat insulation combustion chamber, a wrapped grain, a long tail pipe spray pipe component and an igniter. The fuel gas generator is fixedly arranged in the oil tank system, and a long tail pipe of the fuel gas generator penetrates through the head portion of the combustion chamber and stretches into the combustion chamber. The solid-liquid scramjet engine can keep the advantages that the specific impulse of the liquid fuel scramjet engine is high, and the solid fuel scramjet engine is not prone to being shut down under a large attack angle, and meanwhile the defects that the liquid scramjet engine is prone to being shut down under the large attack angle, the thrust of the solid fuel scramjet engine is hard to adjust, and the specific impulse is low are overcome.
Owner:BEIJING POWER MACHINERY INST
Electric hydrodynamic force propeller
InactiveCN103912466ABreak through bottlenecks such as high temperature and high pressureImprove efficiencyMachines/enginesUsing plasmaPlasma generatorCorona discharge
The invention relates to an electric hydrodynamic force propeller which comprises a contracting nozzle connected with a synchronous multistage accelerator. An alternating positive-negative plasma generator is fixed at the air inlet end of the synchronous multistage accelerator. A support plate is disposed at the outer edge of the alternating positive-negative plasma generator. Connecting plates are located on the inner side of the support plate. Every two adjacent layers of connecting plates and the corresponding hollow connecting plate enclose an air passage. Each annular electrode is connected with a high-frequency pulse power supply, which is grounded, through a wire. An alternating positive-negative plasma emitting unit is disposed in each mounting hole. Each high-frequency tip electrode and the corresponding high-frequency circular electrode form corona discharge, the plasma of the corresponding alternating positive-negative plasma emitting unit is sprayed, the plasma mixed with the air flowing in from the air passage enters the synchronous multistage accelerator, and charge particles and the air accelerated by the synchronous multistage accelerator enter the contracting nozzle and are sprayed out by the same after acceleration. By the electric hydrodynamic force propeller, bottlenecks of high temperature and high pressure are overcome, aero-space flight is achieved, high specific impulse and propelling efficiency are achieved, and propellant mass is reduced.
Owner:XIAN RUOSHUI ELECTRICAL EQUIP CO LTD
Hydrogen-peroxide-based RBCC (Rocket Based Combined Cycle) engine pressure pumping and squeezing integrated fuel system
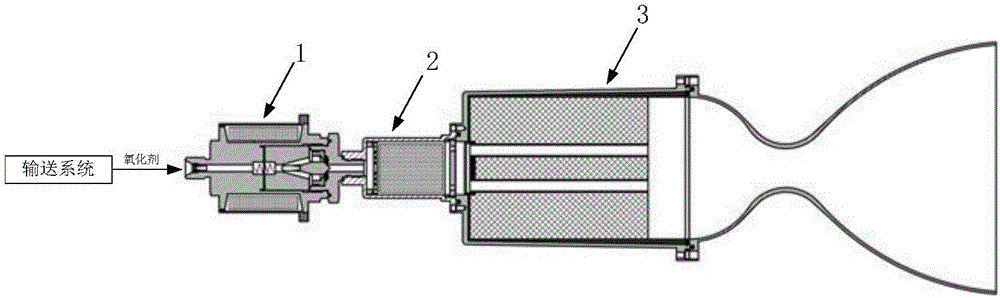
ActiveCN103696883AOvercoming complexityOvercome the huge disadvantageRocket engine plantsCombustion chamberKerosene
The invention provides a hydrogen-peroxide-based RBCC (Rocket Based Combined Cycle) engine pressure pumping and squeezing integrated fuel system. The hydrogen-peroxide-based RBCC engine pressure pumping and squeezing integrated fuel system comprises a pressurization unit, a supplying unit, an engine body and a connecting pipeline unit; the pressurization unit is used for performing pressurization on the supplying unit; the supplying unit which is connected with the engine body through the connecting pipeline unit supplies propellant to the engine body. The hydrogen-peroxide-based RBCC engine pressure pumping and squeezing integrated fuel system has the advantages of overcoming disadvantages of a complex and huge system due to the fact that a rocket thrust chamber and a stamping combustion chamber separately supply fuel, synthesizing respective advantages of the hydrogen peroxide and kerosene propellant, being high in density specific impulse, satisfying combination engine design requirements for integrated fuel supplying and an integrated cooling structure and being mature in utilization and maintenance technology, relatively simple in system composition and easy to achieve.
Owner:NO 11 INST OF NO 6 ACADEMY OF CHINA AEROSPACE SCI & TECH
Magnetic nozzle of variable specific impulse magnetic plasma rocket
InactiveCN102434414AChange the strength of the magnetic fieldWide range of workMachines/enginesUsing plasmaSprayerAlloy
The invention relates to a magnetic nozzle of a variable specific impulse magnetic plasma rocket, aiming at solving the problem of speed waste during acceleration of a plasma body in an electric propulsion system and relating to the design technology of the magnetic nozzle of the variable specific impulse magnetic plasma rocket. The magnetic nozzle of the variable specific impulse magnetic plasma rocket is used for changing a circumferential speed of the plasma body to an axial speed and belongs to the magnetic fluid technology field. The magnetic nozzle which is used as the last stage of the variable specific impulse magnetic plasma rocket is arranged at the tail end of a rocket engine and consists of a sprayer nozzle and a superconducting coil, wherein, the sprayer nozzle is arranged at the tail end of a shell body of the rocket engine and is an expanding nozzle, the nozzle expansion ratio which is the ratio between a nozzle exit area and a nozzle throat area is 40:1, the nozzle is made of a heat-resisting and ablation-resisting alloy material to reduce ablation and thrust eccentricity.
Owner:BEIJING INSTITUTE OF TECHNOLOGYGY
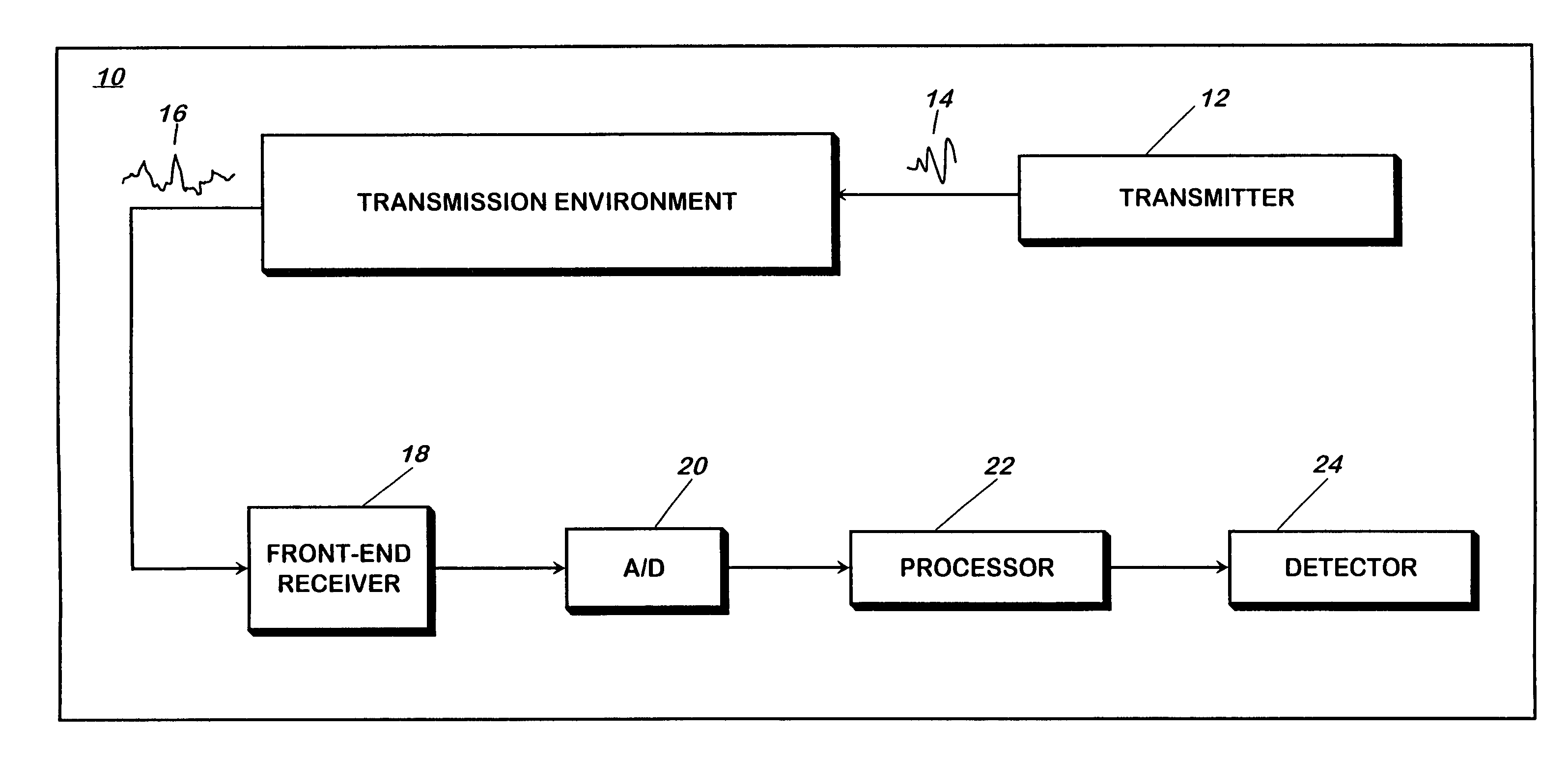
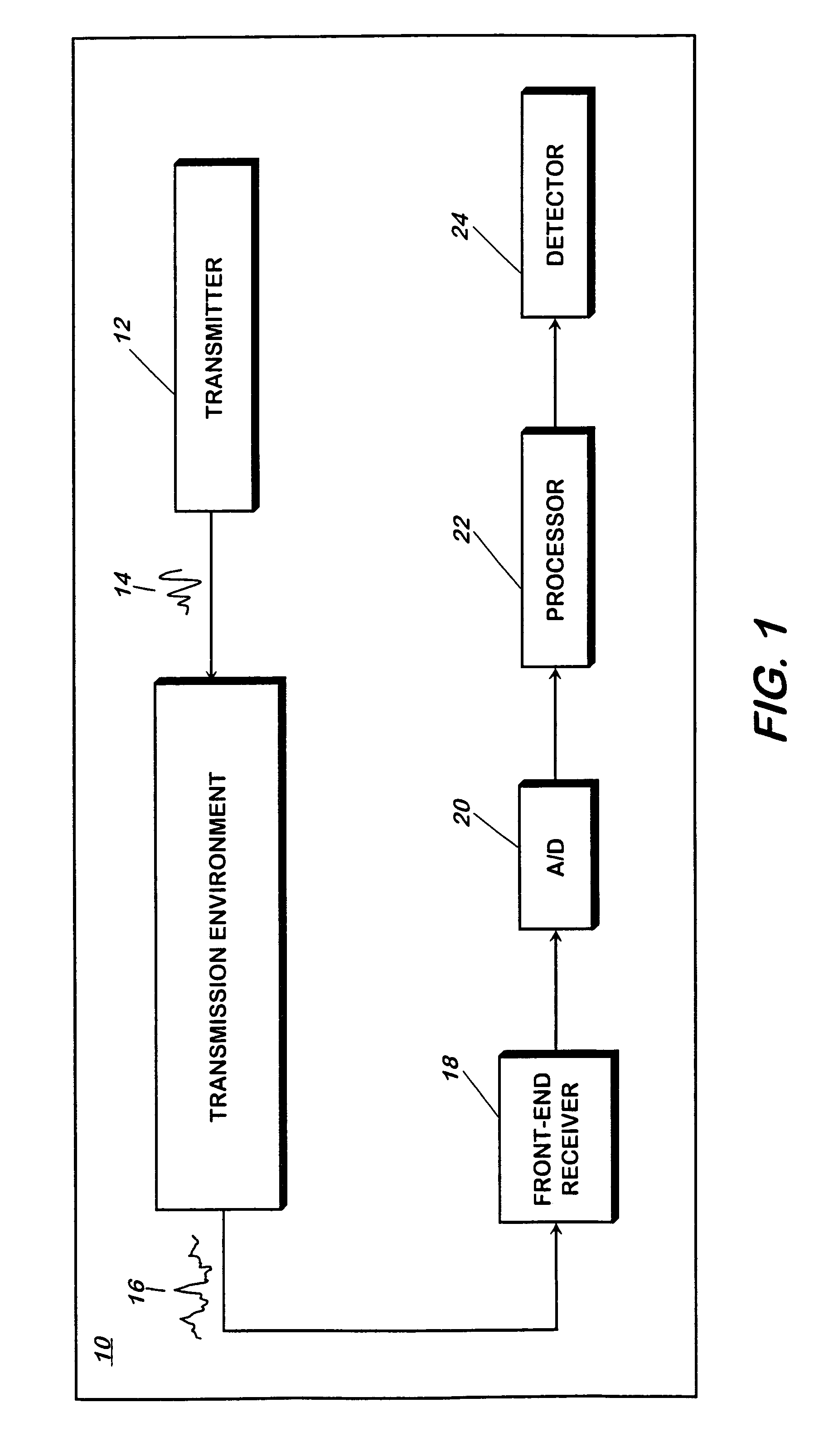
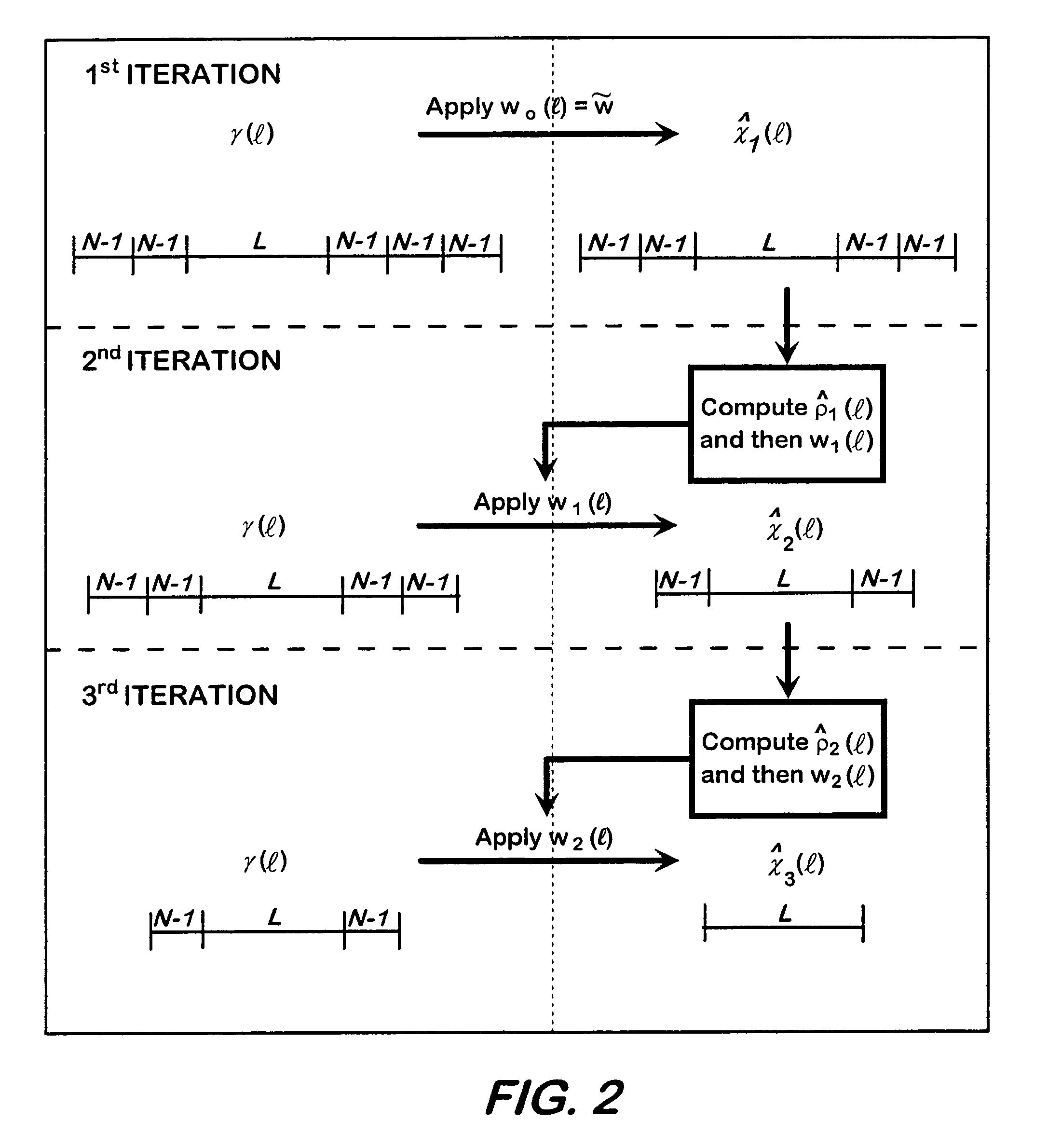
Robust predictive deconvolution system and method
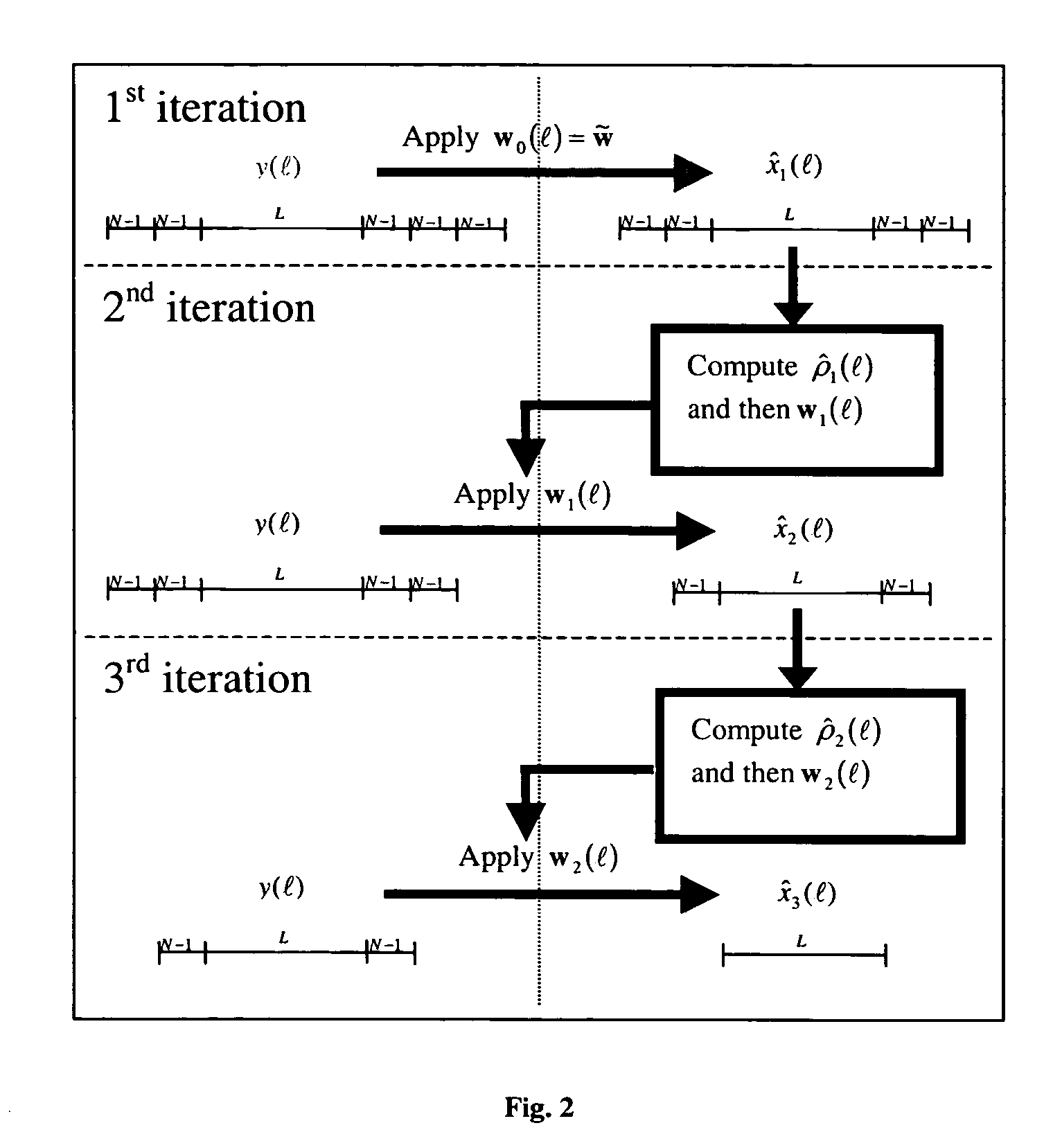
InactiveUS20050046612A1High-fidelity impulse responseEliminates spatial ambiguityRadio wave reradiation/reflectionAmbiguityEngineering
A method for processing a received, modulated pulse (i.e. waveform) that requires predictive deconvolution to resolve a scatterer from noise and other scatterers includes receiving a return signal; obtaining L+(2M−1)(N−1) samples y of the return signal, where y(l)={tilde over (x)}T(l)s+ν(l); applying RMMSE estimation to each successive N samples to obtain initial impulse response estimates [{circumflex over (x)}1{−(M−1)(N−1)}, . . . ,{circumflex over (x)}1{−1},{circumflex over (x)}1{0}, . . . ,{circumflex over (x)}1{L−1},{circumflex over (x)}1{L}, . . . ,{circumflex over (x)}1{L−1+(M−1)(N−1)}]; computing power estimates {circumflex over (ρ)}1(l)=|{circumflex over (x)}1(l)|2 for l=−(M−1)(N−1), . . . ,L−1+(M−1)(N−1); computing MMSE filters according to w(l)=ρ(l)(C(l)+R)−1s, where ρ(l)=|x(l)|2 is the power of x(l), and R=E[v(l)vH(l)] is the noise covariance matrix; applying the MMSE filters to y to obtain [{circumflex over (x)}2{−(M−2)(N−1)}, . . . ,{circumflex over (x)}2{−1},{circumflex over (x)}2{0}, . . . ,{circumflex over (x)}2{L−1},{circumflex over (x)}2{L}, . . . ,{circumflex over (x)}2{L−1+(M−2)(N−1)}]; and repeating (d)-(f) for subsequent reiterative stages until a desired length-L range window is reached, thereby resolving the scatterer from noise and other scatterers. The RMMSE predictive deconvolution approach provides high-fidelity impulse response estimation. The RMMSE estimator can reiteratively estimate the MMSE filter for each specific impulse response coefficient by mitigating the interference from neighboring coefficients that is a result of the temporal (i.e. spatial) extent of the transmitted waveform. The result is a robust estimator that adaptively eliminates the spatial ambiguities that occur when a fixed receiver filter is used.
Owner:THE UNITED STATES OF AMERICA AS REPRESENTED BY THE SECRETARY OF THE NAVY
Miniature propeller based on MEMS nozzle chip
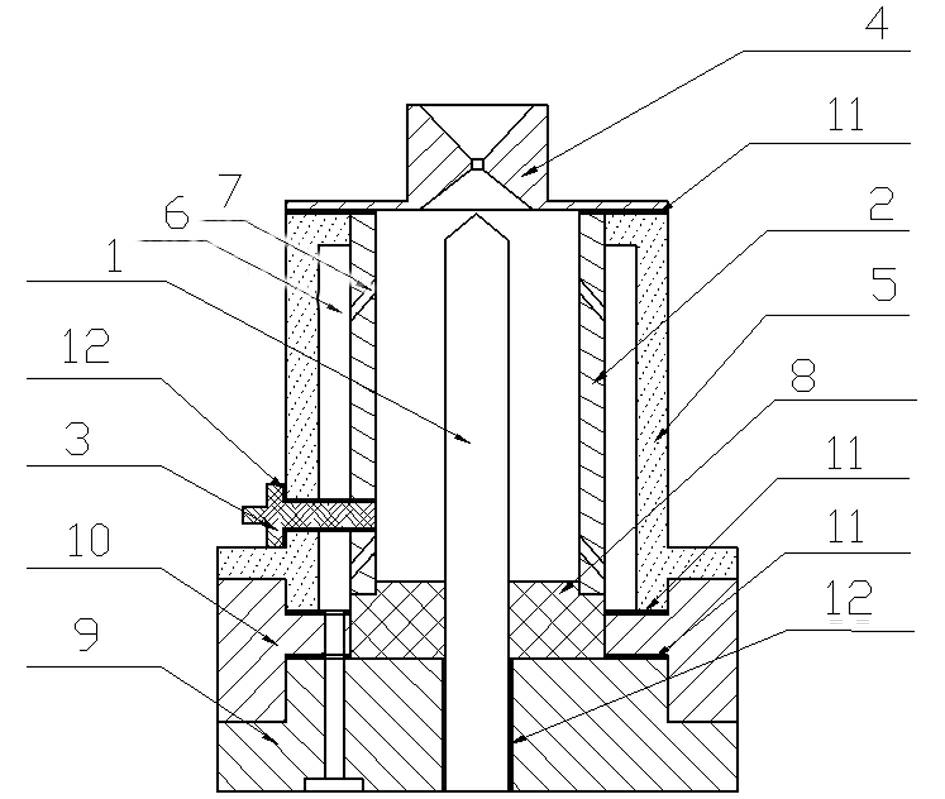
InactiveCN101476523AReduce volumeReduce power consumptionRocket engine plantsBiochemical engineeringThermal insulation
The invention discloses a miniature propeller based on an MEMS nozzle chip. The miniature propeller comprises a radiation thermal insulation casing, a catalytic reaction cavity and a top cover. The catalytic reaction cavity comprises a catalytic cavity arranged inside the radiation thermal insulation casing, and an inlet passage of the catalytic reaction cavity. One end of the inlet passage of the catalytic reaction cavity is communicated with the catalytic cavity; and the other end of the inlet passage of the catalytic reaction cavity passes through the radiation thermal insulation casing. A central covering piece hermetically covers the front end of the catalytic cavity; a top cover seal sleeve is inserted into the periphery of the central covering piece; and the MEMS nozzle chip passes through the middle part of the central covering piece. One end of the MEMS nozzle chip is communicated with the catalytic cavity; and the other end of the MEMS nozzle chip passes through the top cover. The miniature propeller also comprises a heater wire for heating the catalytic cavity. The miniature liquid fuel propeller has a small size, light mass, low power consumption, and higher specific impulse. The miniature propeller is very suitable for an attitude control system of a tiny satellite.
Owner:GUANGZHOU INST OF ENERGY CONVERSION - CHINESE ACAD OF SCI
RBCC fuel gas generator integrated supplying and adjusting system based on liquid oxygen
The invention provides an RBCC fuel gas generator integrated supplying and adjusting system based on liquid oxygen. The system comprises a pressurization unit, a supply unit, an engine body and a connecting pipeline unit. The pressurization unit is used for conducting pressurization on the supply unit. The supply unit is connected with the engine body through the connecting pipeline unit, and supplies propellants to the engine body. According to the RBCC fuel gas generator integrated supplying and adjusting system based on the liquid oxygen, the defect that an original system is complex and large due to the fact that a rocket thrust chamber and a ramjet combustion chamber are independently supplied with fuel oil is overcome, the respective advantages of the liquid oxygen, hydrogen peroxide and kerosene propellants are combined, the engine specific impulse and density specific impulse are high, the requirement for the combined engine integrated fuel oil supply and integrated cooling structural design is met, the system using and maintaining technology is mature, the system composition is relatively simple, and implementation is easy.
Owner:NO 11 INST OF NO 6 ACADEMY OF CHINA AEROSPACE SCI & TECH
Rocket-based combined cycle engine thrust calculation method
InactiveCN110362783AThrust Quick EstimationQuick Estimation of Specific Impulse PerformanceComplex mathematical operationsFlight heightCombustion chamber
The invention provides a rocket-based combined cycle engine thrust calculation method. Firstly, one-dimensional geometrical parameters of an inner flow channel of the rocket-based combined cycle engine are determined and include an air inlet channel inlet sectional area, an air inlet channel compression angle, an e isolation section sectional area, a sub-expansion section expansion ratio, a combustion chamber expansion ratio, a rocket combustion chamber sectional area, a rocket nozzle size and an engine exhaust nozzle expansion ratio; the flight height, the flight Mach number and the mainstream flow are input; and then thrust estimation is conducted on the rocket-based combined cycle engine, and the final thrust of an outlet of an exhaust nozzle of the rocket-based combined cycle engine and the specific impulse of the engine are obtained. According to the method, rapid estimation of thrust and specific impulse performance of the rocket-based combined cycle engine is achieved, and a newtool is provided for initial design of the engine and trajectory planning of an aircraft.
Owner:NAT UNIV OF DEFENSE TECH
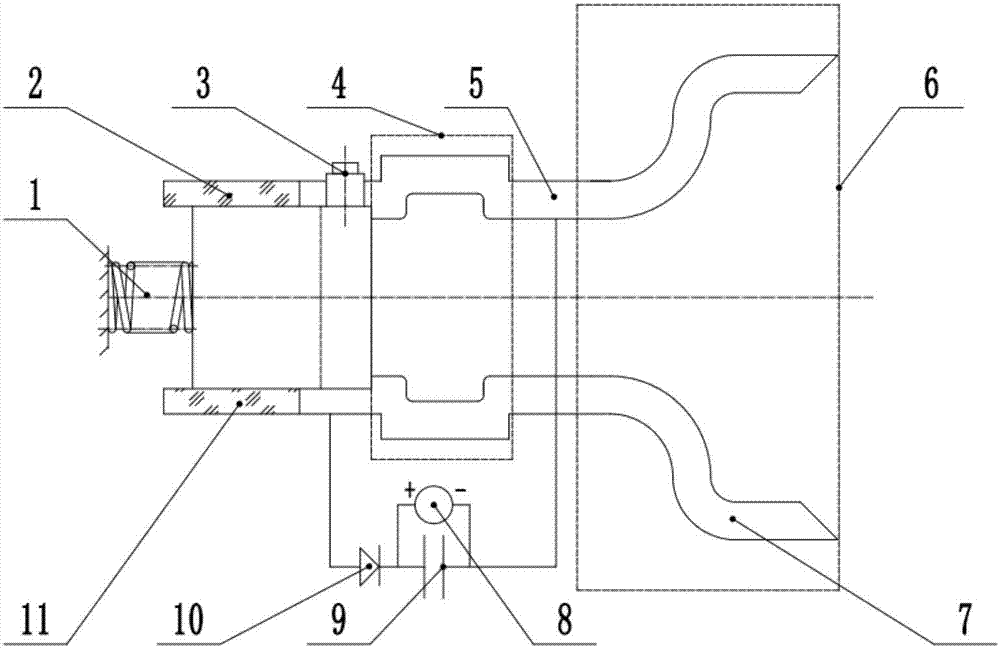
Solid pulse plasma thruster with high propellant utilization rate and working method
InactiveCN107178479AIncrease profitIncrease the probability of collisionMachines/enginesUsing plasmaMicro nanoHigh pressure
The invention discloses a solid pulse plasma thruster with high propellant utilization rate and a working method, and belongs to the technical field of aerospace propulsion of micro-satellites. The solid pulse plasma thruster with high propellant utilization rate comprises a constant-force spring, an upper insulating plate for fixing a propellant, a semiconductor spark plug, a permanent magnet for increasing impulse bit, a cathode plate, a permanent magnet for increasing specific impulse, an anode plate, a high-voltage power supply, a main spark-gap capacitor, a diode, a lower insulating plate for fixing the propellant and a solid propellant; gas storage cavities for reducing the forward movement speed of neutral gas are respectively formed in the cathode plate and the anode plate; the distance between the cathode plate and the anode plate is increased on the rear sides of the gas storage cavities; tail ends, which are close to a nozzle, of the cathode plate and the anode plate are parallel to each other; the permanent magnet for increasing the impulse bit is added in the direction which is opposite to the direction of a self-inductance magnetic field; and the permanent magnet for increasing the specific impulse is added in the direction which is the same as the direction of the self-inductance magnetic field. The propellant utilization rate of the solid pulse plasma thruster can be increased. The solid pulse plasma thruster has the advantage of low cost, and is suitable for being used as a main thruster of a micro-nano satellite or an adjusting device of various large satellites.
Owner:BEIJING INSTITUTE OF TECHNOLOGYGY
Features
- R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
Why Patsnap Eureka
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com